Applicability and Limitations of Ru’s Formulation for Vibration Modelling of Double-Walled Carbon Nanotubes
Abstract
1. Introduction
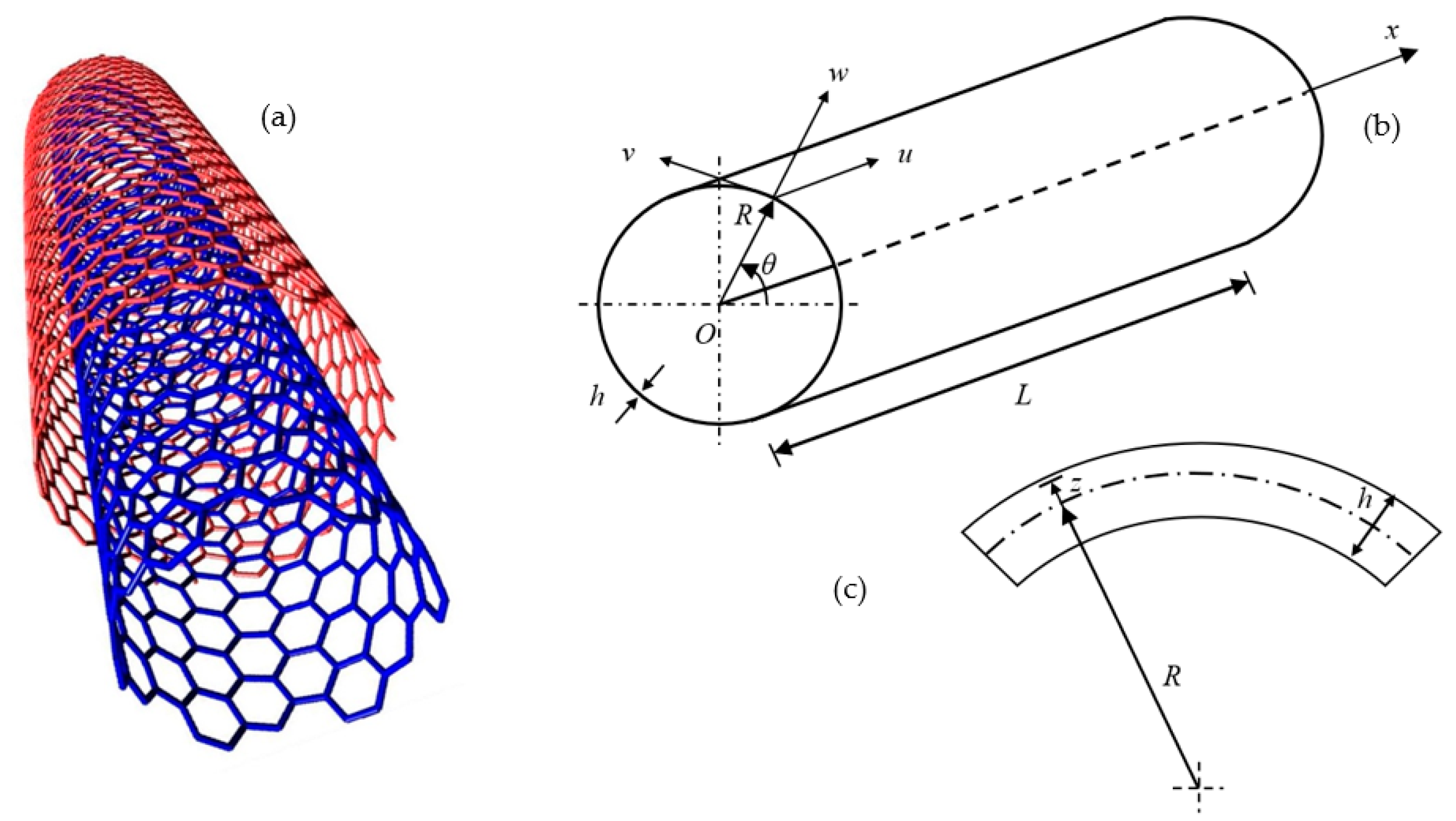
2. Donnell Shell Theory for DWCNTs
2.1. Displacement Field
2.2. Strain-Displacement Relationships
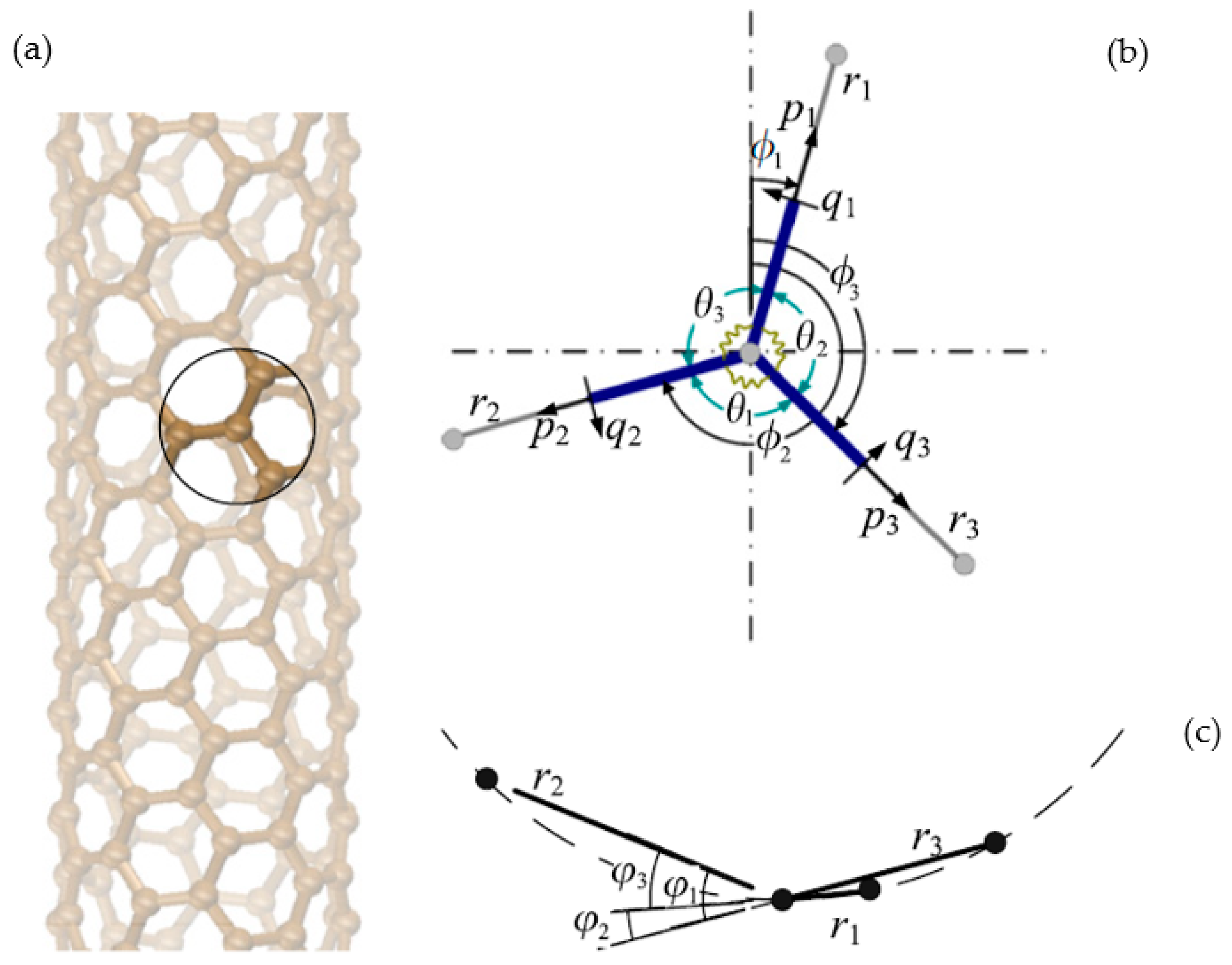
3. Anisotropic Elastic Shell Model for DWCNTs
3.1. Stress–Strain Relationships
3.2. Force and Moment Resultants
3.3. Elastic Strain Energy
3.4. Kinetic Energy
3.5. Van der Waals Interaction Forces
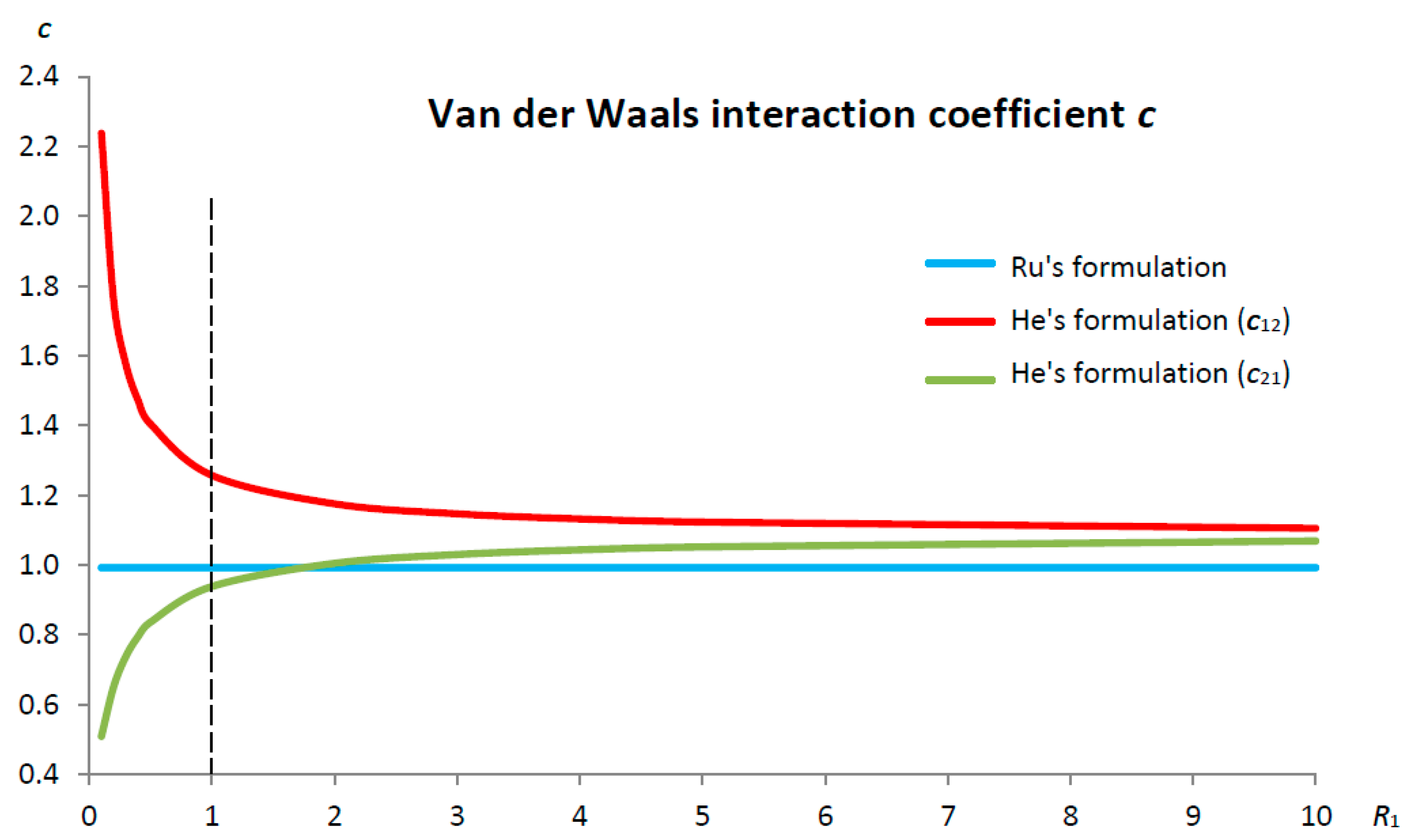
3.5.1. Van der Waals Interaction Coefficient: Ru’s Formulation
3.5.2. Van der Waals Interaction Coefficient: He’s Formulation
3.5.3. Van der Waals Interaction Energy
4. Vibration Modelling of DWCNTs
4.1. Boundary Conditions
4.2. Rayleigh–Ritz Method
5. Numerical Results
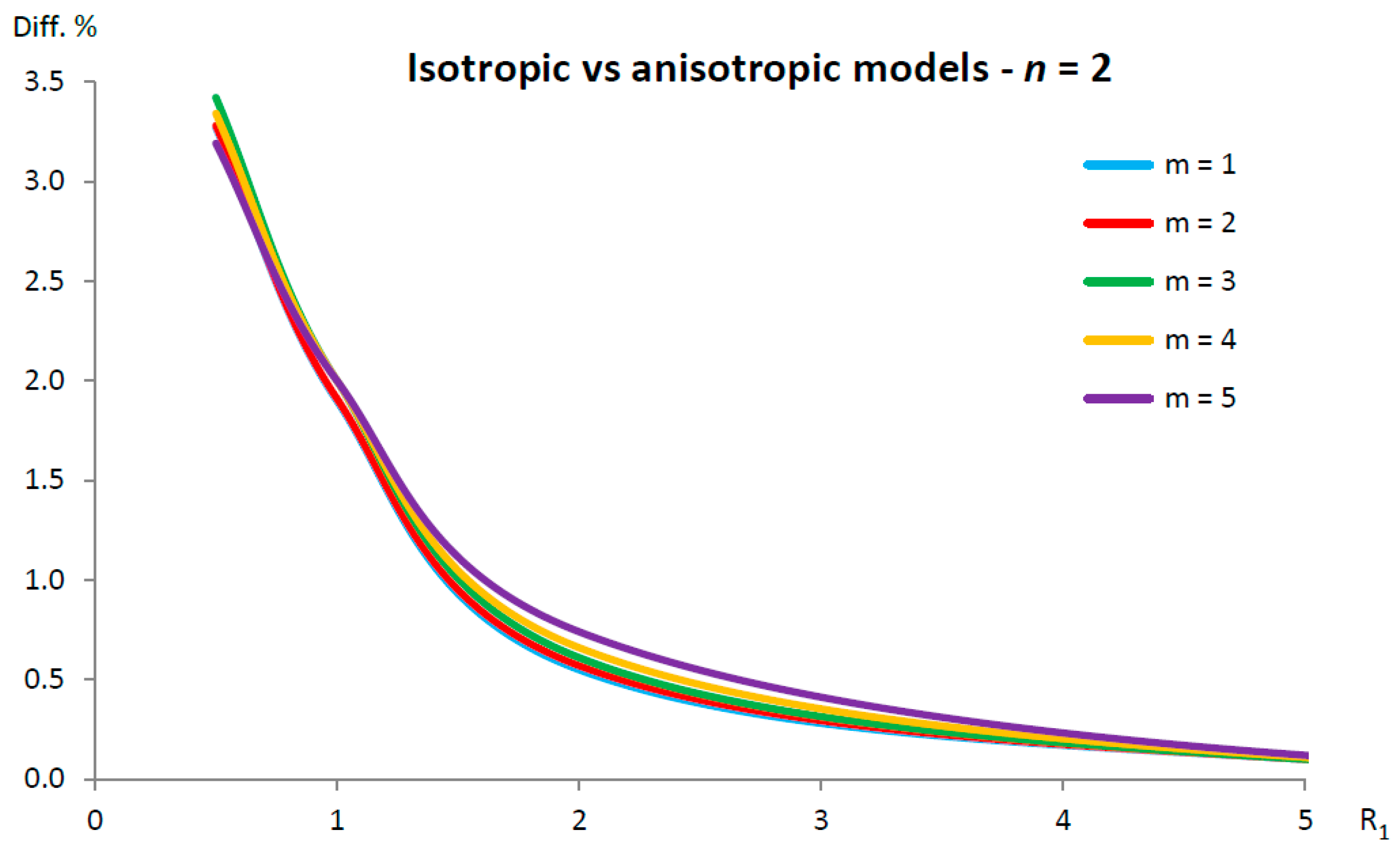
5.1. Validation of the Proposed Model in the Isotropic Case
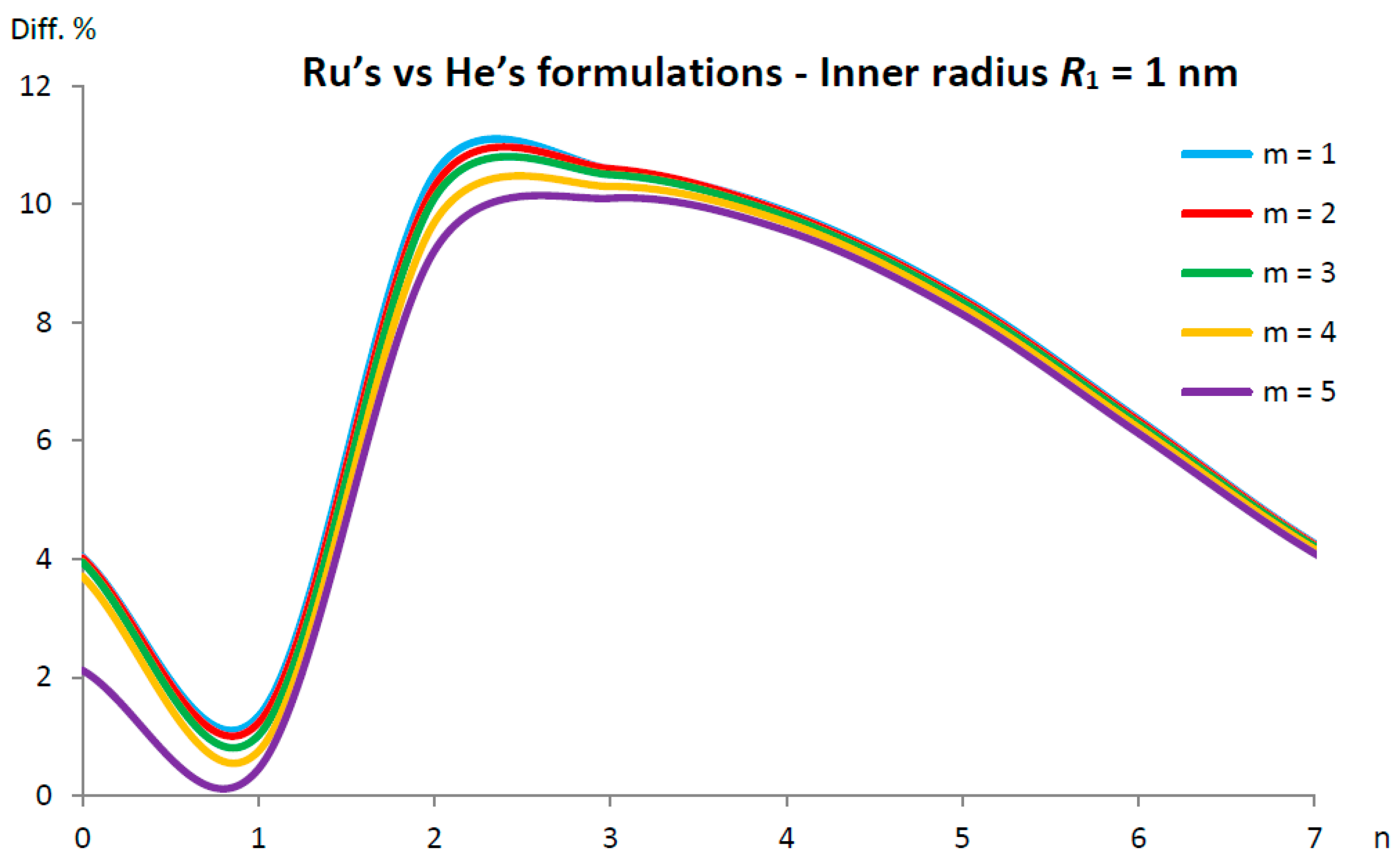
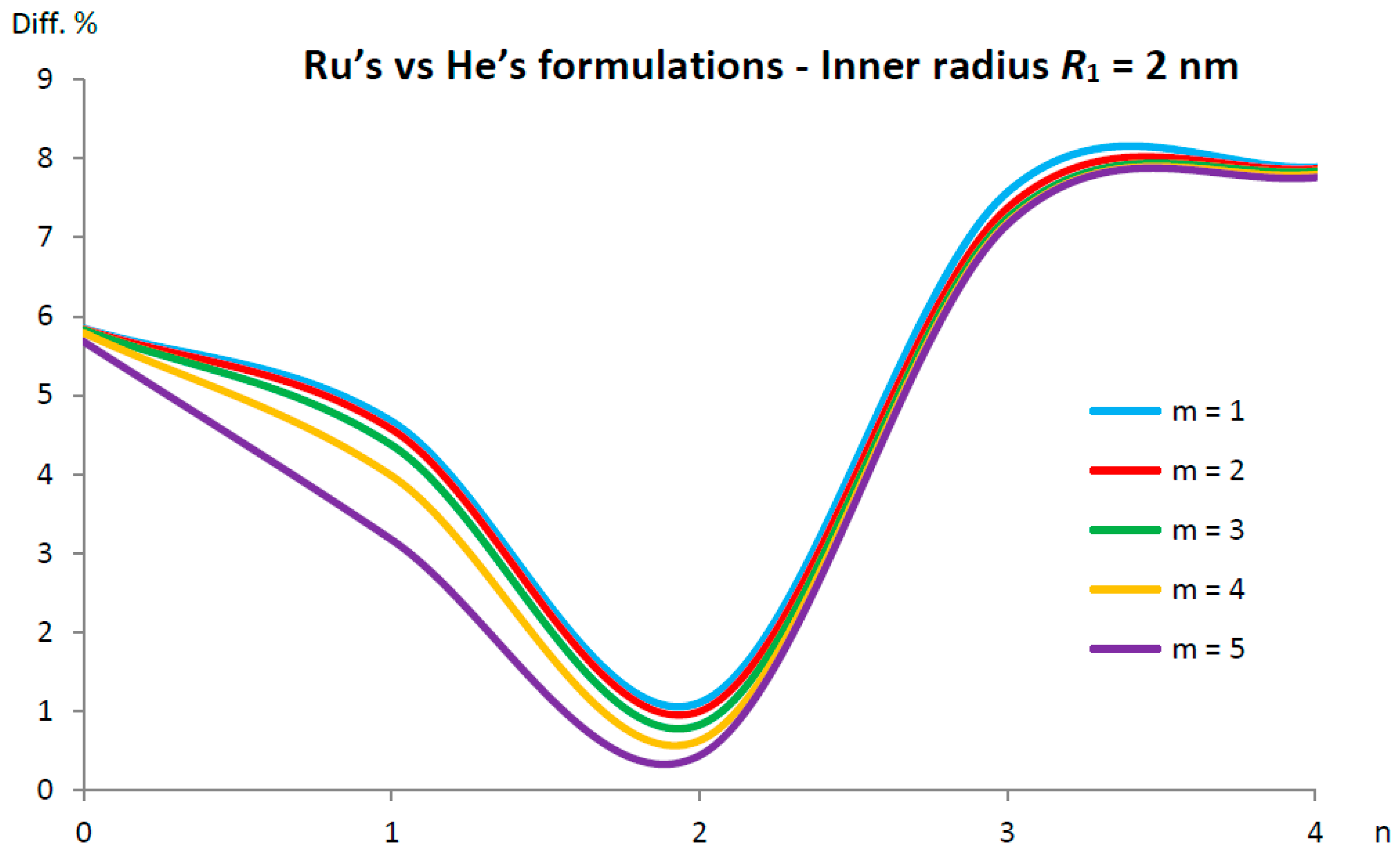
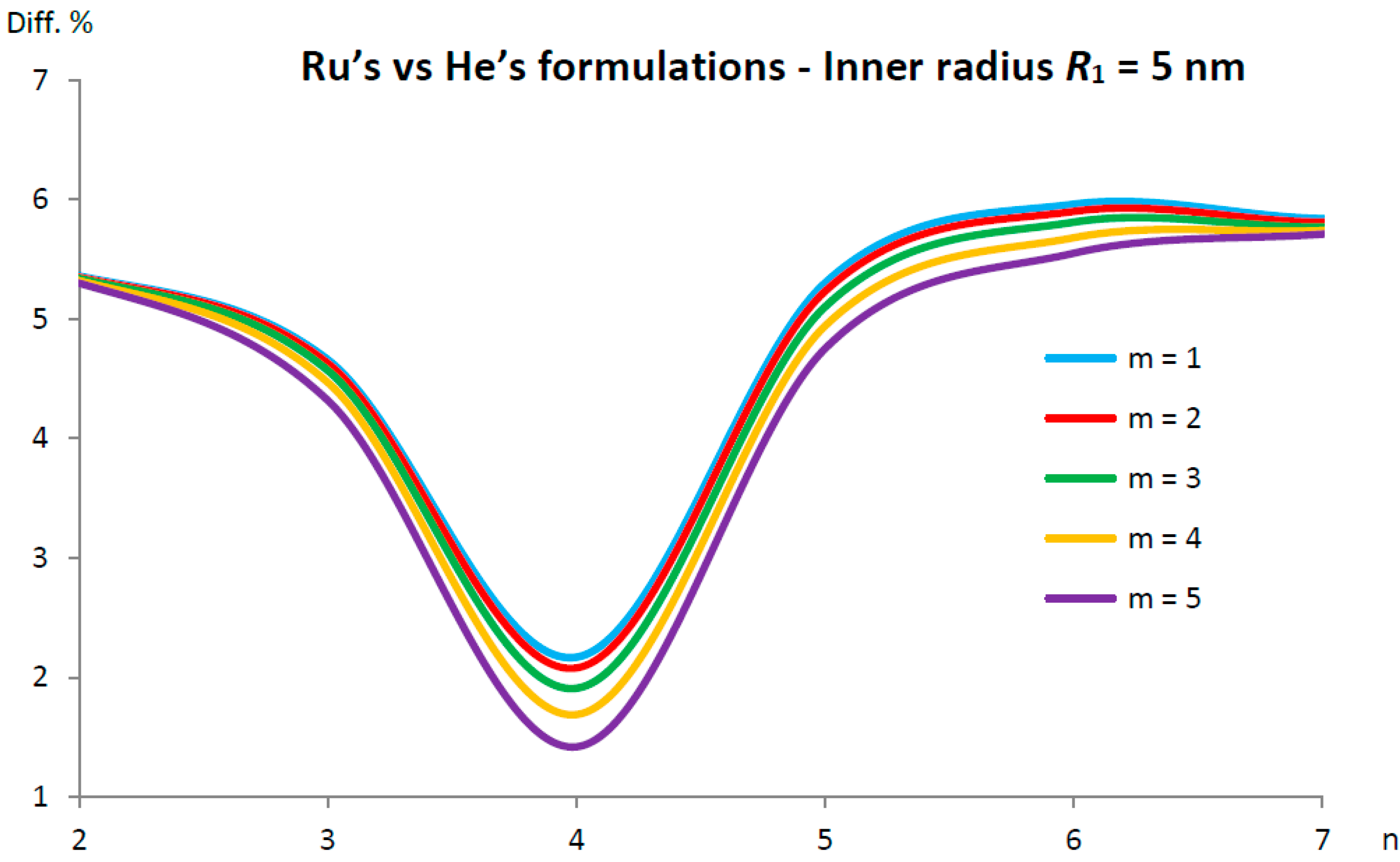
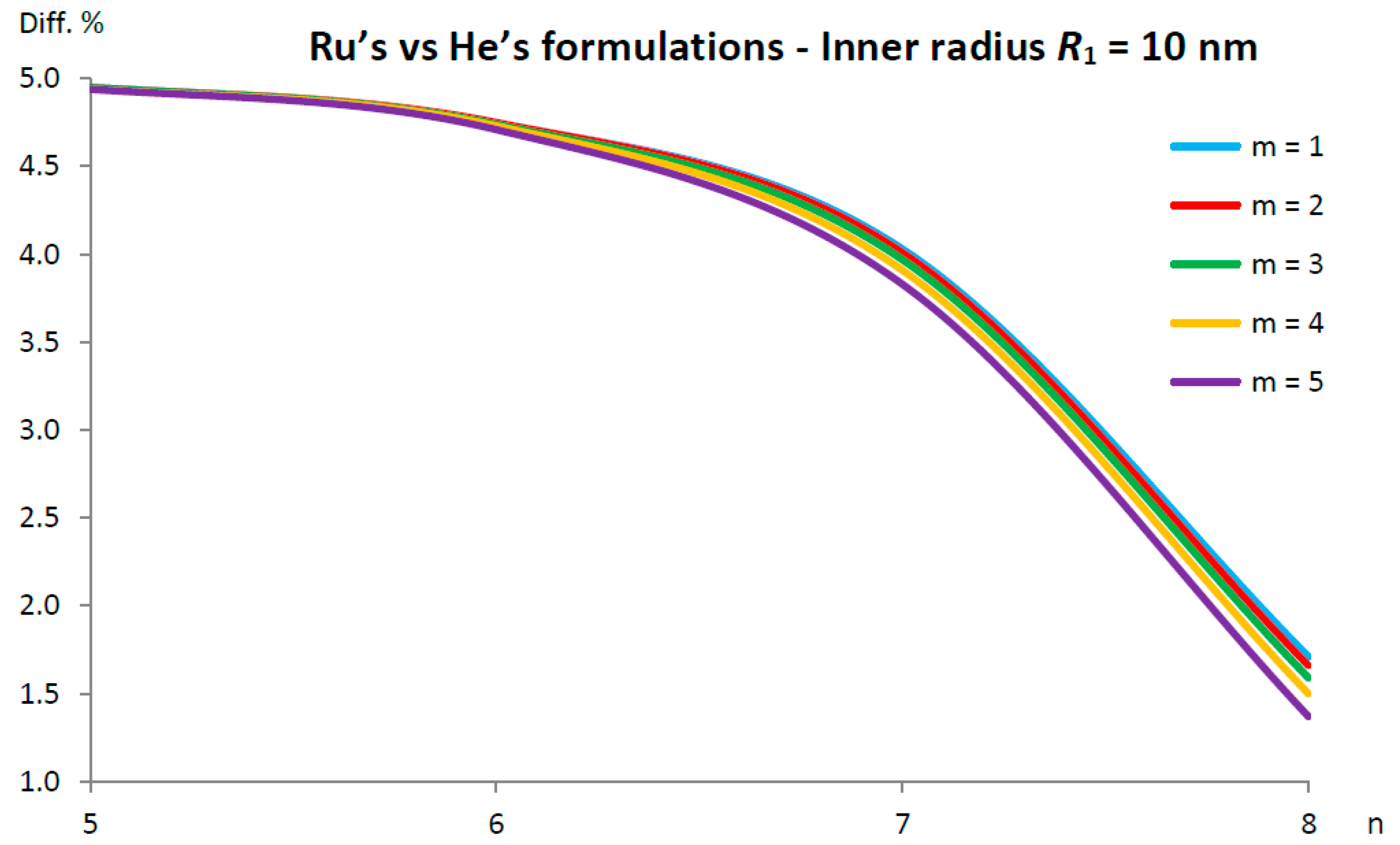
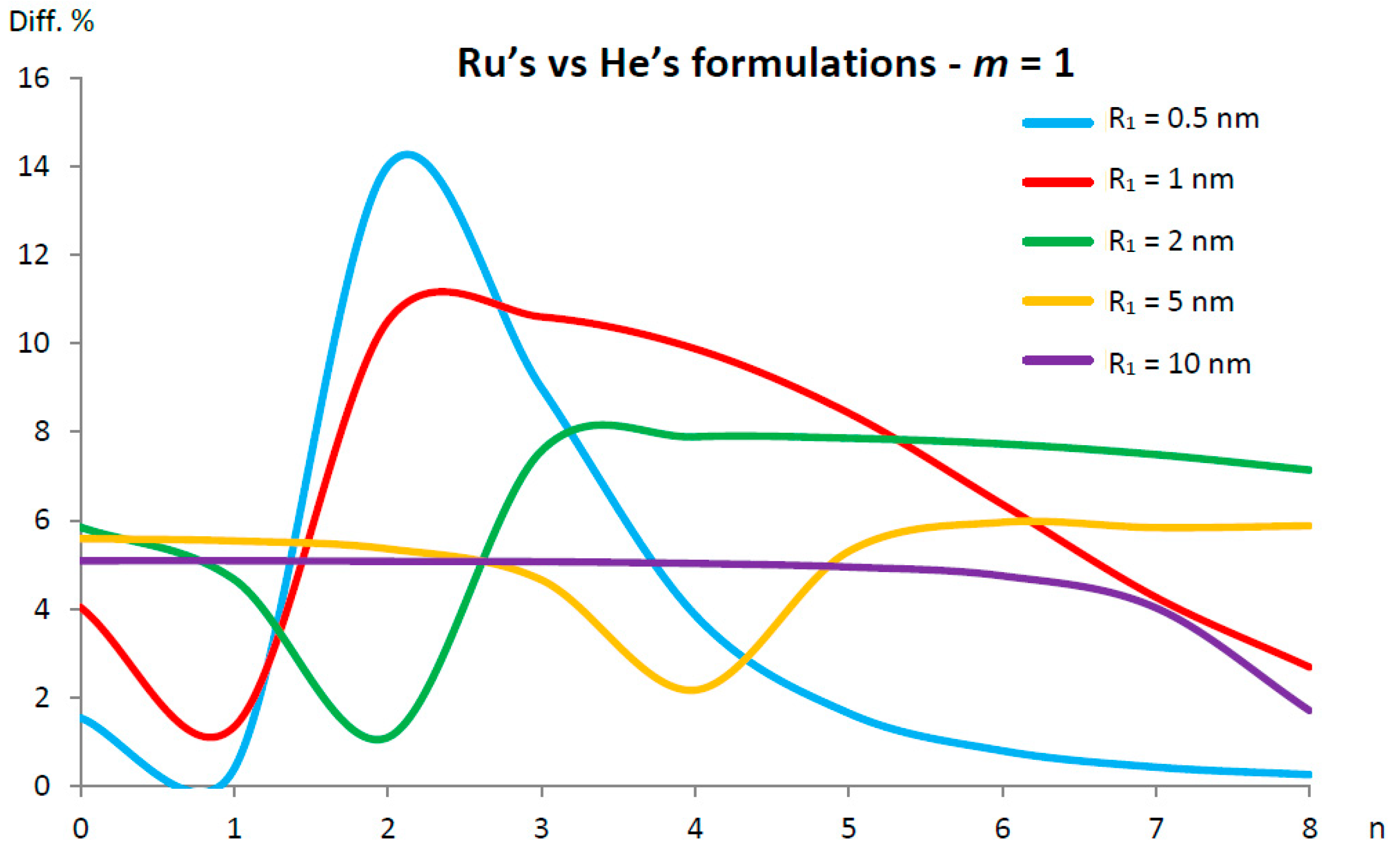
5.2. Ru’s vs. He’s Formulations of the van der Waals Interaction Coefficient for DWCNTs
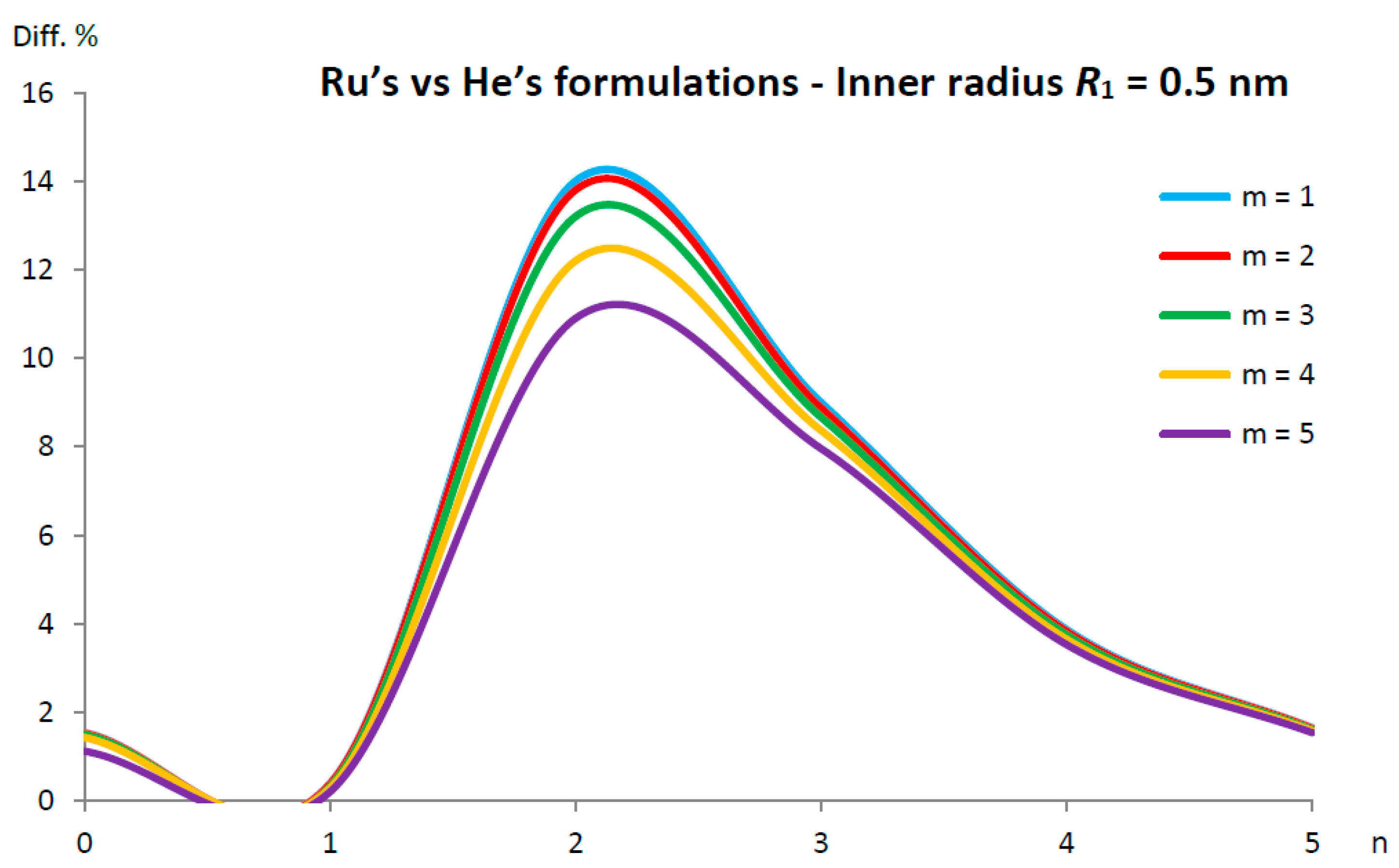
5.3. Applicability and Limitations of Ru’s Formulation for DWCNTs
- for the percentage difference is initially very low , then it increases, finally stabilizing at ;
- for , the percentage difference is initially extremely high , then it decreases by assuming a minimum value of and finally increases, stabilizing at ;
- for , the percentage difference is initially very high , then it reduces, stabilizing at ;
- for , the percentage difference is initially relatively low , then it increases until a maximum value of , it decreases until a minimum value of and finally it increases, stabilizing at ;
- for , the percentage difference is initially very low , then it increases until a maximum value of and finally decreases at a value lower than .
- (axisymmetric modes), for every value of ;
- (beam-like modes), for every value of ;
- (circumferential flexure modes), for ;
- (shell-like modes), for ;
- (shell-like modes), for and for ;
- (shell-like modes), for and for ;
- (shell-like modes), for and for ;
- (circumferential flexure modes), for ;
- (shell-like modes), for ;
- (shell-like modes), for ;
- (shell-like modes), for ;
- (shell-like modes), for .
- (very low inner radius), for and for ;
- (low inner radius), for and for ;
- (intermediate inner radius), for ;
- (high inner radius), for ;
- (very high inner radius), for every number of ;
- (very low inner radius), for ;
- (low inner radius), for ;
- (intermediate inner radius), for ;
- (high inner radius), for .
6. Conclusions
- for a small inner radius, the interaction coefficient strongly depends on the radius, and therefore it assumes very different values for Ru’s and He’s formulations;
- for a large inner radius, the interaction coefficient no longer depends on the radius, and it assumes a constant value, which is similar for Ru’s and He’s formulations;
- He’s formulation is able to simulate the actual anisotropic behaviour of CNTs more accurately than Ru’s formulation, and is assumed as reference for the comparisons;
- the difference in the results between Ru’s and He’s formulations is localised in the highest radial natural frequencies;
- for axisymmetric and beam-like modes, Ru’s formulation can be applied for every value of the inner radius;
- for shell-like modes with a relative low number of circumferential waves, Ru’s formulation cannot be applied for a small inner radius;
- for shell-like modes with a high number of circumferential waves, Ru’s formulation can be applied for every value of the inner radius;
- for a large inner radius, Ru’s formulation can be applied for every number of circumferential waves;
- the behaviour is almost the same for every number of longitudinal half-waves.
Funding
Acknowledgments
Conflicts of Interest
References
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Ibrahim, K.S. Carbon nanotubes, properties and applications: A review. Carbon Lett. 2013, 14, 131–144. [Google Scholar] [CrossRef]
- Khan, D.; Ali, Z.; Asif, D.; Panjwani, M.K.; Khan, I. Incorporation of carbon nanotubes in photoactive layer of organic solar cells. Ain Shams Eng. J. 2021, 12, 897–900. [Google Scholar] [CrossRef]
- Luo, C.; Xie, H.; Wang, Q.; Luo, G.; Liu, C. A Review of the Application and Performance of Carbon Nanotubes in Fuel Cells. J. Nanomater. 2015, 2015, 4. [Google Scholar] [CrossRef]
- Rao, A.M.; Richter, E.; Bandow, S.; Chase, B.; Eklund, P.C.; Williams, K.A.; Fang, S.; Subbaswamy, K.R.; Menon, M.; Thess, A.; et al. Diameter-Selective Raman Scattering from Vibrational Modes in Carbon Nanotubes. Science 1997, 275, 187–191. [Google Scholar] [CrossRef]
- Bandow, S.; Asaka, S.; Saito, Y.; Rao, A.M.; Grigorian, L.; Richter, E.; Eklund, P.C. Effect of the Growth Temperature on the Diameter Distribution and Chirality of Single-Wall Carbon Nanotubes. Phys. Rev. Lett. 1998, 80, 3779–3782. [Google Scholar] [CrossRef]
- Dresselhaus, G.; Dresselhaus, M.S.; Hafner, J.H.; Hunter, M.; Jorio, A.; Lieber, C.M.; McClure, T.; Saito, R. Structural (n, m) Determination of Isolated Single-Wall Carbon Nanotubes by Resonant Raman Scattering. Phys. Rev. Lett. 2001, 86, 1118. [Google Scholar] [CrossRef]
- Gupta, S.S.; Bosco, F.G.; Batra, R.C. Breakdown of structural models for vibrations of single-wall zigzag carbon nanotubes. J. Appl. Phys. 2009, 106, 063527. [Google Scholar] [CrossRef]
- Cheng, H.C.; Liu, Y.L.; Wu, C.; Chen, W.H. On radial breathing vibration of carbon nanotubes. Comput. Methods Appl. Mech. Eng. 2010, 199, 2820–2827. [Google Scholar] [CrossRef]
- Duan, W.H.; Wang, C.; Zhang, Y. Calibration of nonlocal scaling effect parameter for free vibration of carbon nanotubes by molecular dynamics. J. Appl. Phys. 2007, 101, 024305. [Google Scholar] [CrossRef]
- Odegard, G.M.; Gates, T.S.; Nicholson, L.M.; Wise, K.E. Equivalent-Continuum Modeling of Nano-Structured Materials. Compos. Sci. Technol. 2002, 62, 1869–1880. [Google Scholar] [CrossRef]
- Arroyo, M.; Belytschko, T. Continuum Mechanics Modeling and Simulation of Carbon Nanotubes. Meccanica 2005, 40, 455–469. [Google Scholar] [CrossRef]
- Zhang, P.; Huang, Y.; Geubelle, P.H.; Hwang, K. On the continuum modeling of carbon nanotubes. Acta Mech. Sin. 2002, 18, 528–536. [Google Scholar] [CrossRef]
- Yakobson, B.I.; Brabec, C.J.; Bernholc, J. Nanomechanics of Carbon Tubes: Instabilities beyond Linear Response. Phys. Rev. Lett. 1996, 76, 2511–2514. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Ru, C.Q.; Mioduchowski, A. Applicability and Limitations of Simplified Elastic Shell Equations for Carbon Nanotubes. J. Appl. Mech. 2004, 71, 622–631. [Google Scholar] [CrossRef]
- Silvestre, N.; Wang, C.; Zhang, Y.; Xiang, Y. Sanders shell model for buckling of single-walled carbon nanotubes with small aspect ratio. Compos. Struct. 2011, 93, 1683–1691. [Google Scholar] [CrossRef]
- Silvestre, N. On the accuracy of shell models for torsional buckling of carbon nanotubes. Eur. J. Mech.-A/Solids 2012, 32, 103–108. [Google Scholar] [CrossRef]
- Strozzi, M.; Manevitch, L.I.; Pellicano, F.; Smirnov, V.V.; Shepelev, D.S. Low-frequency linear vibrations of single-walled carbon nanotubes: Analytical and numerical models. J. Sound Vib. 2014, 333, 2936–2957. [Google Scholar] [CrossRef]
- Strozzi, M.; Smirnov, V.V.; Manevitch, L.I.; Pellicano, F. Nonlinear vibrations and energy exchange of single-walled carbon nanotubes. Radial breathing modes. Compos. Struct. 2018, 184, 613–632. [Google Scholar] [CrossRef]
- Strozzi, M.; Pellicano, F. Nonlinear Resonance Interaction between Conjugate Circumferential Flexural Modes in Single-Walled Carbon Nanotubes. Shock Vib. 2019, 2019, 3241698. [Google Scholar] [CrossRef]
- Strozzi, M.; Smirnov, V.V.; Manevitch, L.I.; Pellicano, F. Nonlinear normal modes, resonances and energy exchange in single-walled carbon nanotubes. Int. J. Non-Linear Mech. 2020, 120, 103398. [Google Scholar] [CrossRef]
- Chang, T.; Geng, J.; Guo, X. Prediction of chirality- and size-dependent elastic properties of single-walled carbon nanotubes via a molecular mechanics model. Proc. R. Soc. A Math. Phys. Eng. Sci. 2006, 462, 2523–2540. [Google Scholar] [CrossRef]
- Chang, T. A molecular based anisotropic shell model for single-walled carbon nanotubes. J. Mech. Phys. Solids 2010, 58, 1422–1433. [Google Scholar] [CrossRef]
- Ghavanloo, E.; Fazelzadeh, S. Vibration characteristics of single-walled carbon nanotubes based on an anisotropic elastic shell model including chirality effect. Appl. Math. Model. 2012, 36, 4988–5000. [Google Scholar] [CrossRef]
- Fazelzadeh, S.A.; Ghavanloo, E. Nonlocal anisotropic elastic shell model for vibrations of single-walled carbon nanotubes with arbitrary chirality. Compos. Struct. 2012, 94, 1016–1022. [Google Scholar] [CrossRef]
- Leissa, A.W. Vibration of Shells; Acoustical Society of America: Columbus, OH, USA, 1993. [Google Scholar]
- Yamaki, N.; Simitses, G.J. Elastic Stability of Circular Cylindrical Shells. J. Appl. Mech. 1985, 52, 501–502. [Google Scholar] [CrossRef]
- Soedel, W.; Qatu, M.S. Vibrations of Shells and Plates, Third Edition. J. Acoust. Soc. Am. 2005, 117, 1683. [Google Scholar] [CrossRef]
- Ventsel, E.; Krauthammer, T.; Carrera, E. Thin Plates and Shells: Theory, Analysis, and Applications. Appl. Mech. Rev. 2002, 55, B72–B73. [Google Scholar] [CrossRef]
- Jones, J.E. On the determination of molecular fields.—I. From the variation of the viscosity of a gas with temperature. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1924, 106, 441–462. [Google Scholar] [CrossRef]
- Ru, C.Q. Elastic Models for Carbon Nanotubes. Encycl. Nanosci. Nanotechnol. 2004, 2, 731–744. [Google Scholar]
- Ru, C.Q. Axially compressed buckling of a double-walled carbon nanotube embedded in an elastic medium. J. Mech. Phys. Solids 2001, 49, 1265–1279. [Google Scholar] [CrossRef]
- Ru, C.Q. Column buckling of multiwalled carbon nanotubes with interlayer radial displacements. Phys. Rev. B 2000, 62, 16962–16967. [Google Scholar] [CrossRef]
- Girifalco, L.A.; Lad, R.A. Energy of Cohesion, Compressibility, and the Potential Energy Functions of the Graphite System. J. Chem. Phys. 1956, 25, 693–697. [Google Scholar] [CrossRef]
- Pentaras, D.; Elishakoff, I. Effective Approximations for Natural Frequencies of Double-Walled Carbon Nanotubes Based on Donnell Shell Theory. J. Nanotechnol. Eng. Med. 2011, 2, 021013. [Google Scholar] [CrossRef]
- Elishakoff, I.; Pentaras, D. Fundamental natural frequencies of double-walled carbon nanotubes. J. Sound Vib. 2009, 322, 652–664. [Google Scholar] [CrossRef]
- Pentaras, D.; Elishakoff, I. Free vibration of triple-walled carbon nanotubes. Acta Mech. 2011, 221, 239–249. [Google Scholar] [CrossRef]
- Ehteshami, H.; Hajabasi, M.A. Analytical approaches for vibration analysis of multi-walled carbon nanotubes modeled as multiple nonlocal Euler beams. Phys. E Low-Dimens. Syst. Nanostructures 2011, 44, 270–285. [Google Scholar] [CrossRef]
- Xu, K.Y.; Guo, X.N.; Ru, C.Q. Vibration of a double-walled carbon nanotube aroused by nonlinear intertube van der Waals forces. J. Appl. Phys. 2006, 99, 064303. [Google Scholar] [CrossRef]
- Xu, K.-Y.; Aifantis, E.C.; Yan, Y.-H. Vibrations of Double-Walled Carbon Nanotubes With Different Boundary Conditions Between Inner and Outer Tubes. J. Appl. Mech. 2008, 75, 021013. [Google Scholar] [CrossRef]
- He, X.; Kitipornchai, S.; Liew, K. Buckling analysis of multi-walled carbon nanotubes: A continuum model accounting for van der Waals interaction. J. Mech. Phys. Solids 2005, 53, 303–326. [Google Scholar] [CrossRef]
- He, X.Q.; Eisenberger, M.; Liew, K.M. The effect of van der Waals interaction modeling on the vibration characteristics of multiwalled carbon nanotubes. J. Appl. Phys. 2006, 100, 124317. [Google Scholar] [CrossRef]
- He, X.Q.; Kitipornchai, S.; Wang, C.; Liew, K. Modeling of van der Waals force for infinitesimal deformation of multi-walled carbon nanotubes treated as cylindrical shells. Int. J. Solids Struct. 2005, 42, 6032–6047. [Google Scholar] [CrossRef]
- Strozzi, M.; Pellicano, F. Linear vibrations of triple-walled carbon nanotubes. Math. Mech. Solids 2018, 23, 1456–1481. [Google Scholar] [CrossRef]
- Strozzi, M.; Gendelman, O.; Elishakoff, I.; Pellicano, F. Applicability and Limitations of Simplified Elastic Shell Theories for Vibration Modelling of Double-Walled Carbon Nanotubes. C 2021, 7, 61. [Google Scholar] [CrossRef]
- Strozzi, M.; Elishakoff, I.E.; Manevitch, L.I.; Gendelman, O.V. Applicability and limitations of Donnell shell theory for vibration modelling of double-walled carbon nanotubes. Thin-Walled Struct. 2022, 178, 109532. [Google Scholar] [CrossRef]
- Strozzi, M.; Smirnov, V.V.; Pellicano, F.; Kovaleva, M. Nonlocal anisotropic elastic shell model for vibrations of double-walled carbon nanotubes under nonlinear van der Waals interaction forces. Int. J. Non-Linear Mech. 2022, 146, 104172. [Google Scholar] [CrossRef]
- Natsuki, T.; Ni, Q.-Q.; Endo, M. Analysis of the vibration characteristics of double-walled carbon nanotubes. Carbon 2008, 46, 1570–1573. [Google Scholar] [CrossRef]
- Natsuki, T.; Lei, X.-W.; Ni, Q.-Q.; Endo, M. Free vibration characteristics of double-walled carbon nanotubes embedded in an elastic medium. Phys. Lett. A 2010, 374, 2670–2674. [Google Scholar] [CrossRef]
- Kumar, B.R. Investigation on mechanical vibration of double-walled carbon nanotubes with inter-tube van der Waals forces. Adv. Nano Res. 2018, 6, 135–145. [Google Scholar]
- Afsharirad, F.; Mousanezhad, S.; Biglari, H.; Rahmani, O. Molecular dynamics of axial interwall van der Waals force and mechanical vibration of double-walled carbon nanotubes. Mater. Today Commun. 2021, 28, 102708. [Google Scholar] [CrossRef]
- Asghar, S.; Naeem, M.N.; Hussain, M. Non-local effect on the vibration analysis of double walled carbon nanotubes based on Donnell shell theory. Phys. E Low-Dimens. Syst. Nanostructures 2020, 116, 113726. [Google Scholar] [CrossRef]
- Gul, U.; Aydogdu, M. Noncoaxial vibration and buckling analysis of embedded double-walled carbon nanotubes by using doublet mechanics. Compos. Part B: Eng. 2018, 137, 60–73. [Google Scholar] [CrossRef]
- Senthilkumar, V. Axial vibration of double-walled carbon nanotubes using double-nanorod model with van der Waals force under Pasternak medium and magnetic effects. Vietnam J. Mech. 2022, 44, 29–43. [Google Scholar] [CrossRef]
- Natsuki, J.; Wu, P.; Jiang, H.; Natsuki, T. Dynamic analysis of double-walled carbon nanotubes embedded in elastic medium under a nanoparticle delivery. Diam. Relat. Mater. 2022, 128, 109194. [Google Scholar] [CrossRef]
| Tensile rigidity | |
| Bending rigidity | |
| Surface density | |
| Poisson’s ratio |
| Natural Frequency (THz) | Diff. (%) | ||||
|---|---|---|---|---|---|
| Mode (m,n) | Prevalent Displacement | Prevalent Mode Shape | Present Model (Ru) | Ref. [35] Model (Ru) | |
| (1,2) | w | R1 | 0.0163 | 0.0162 | 0.62 |
| (2,2) | w | R1 | 0.0511 | 0.0509 | 0.39 |
| (3,2) | w | R1 | 0.1025 | 0.1020 | 0.49 |
| (1,2) | u | R2 | 0.8508 | 0.8438 | 0.83 |
| (2,2) | u | R2 | 0.8850 | 0.8775 | 0.85 |
| (1,2) | u | R1 | 0.9070 | 0.8999 | 0.79 |
| (3,2) | u | R2 | 0.9334 | 0.9254 | 0.86 |
| (2,2) | u | R1 | 0.9446 | 0.9375 | 0.76 |
| (3,2) | u | R1 | 1.0050 | 0.9977 | 0.73 |
| (1,2) | v | R2 | 1.3114 | 1.3080 | 0.26 |
| (2,2) | v | R2 | 1.3601 | 1.3567 | 0.25 |
| (3,2) | v | R2 | 1.4371 | 1.4334 | 0.26 |
| (1,2) | v | R1 | 1.5384 | 1.5371 | 0.08 |
| (2,2) | v | R1 | 1.5692 | 1.5679 | 0.08 |
| (3,2) | v | R1 | 1.6214 | 1.6201 | 0.08 |
| (1,2) | w | R1 | 2.7006 | 2.7000 | 0.02 |
| (2,2) | w | R1 | 2.7011 | 2.7005 | 0.02 |
| (3,2) | w | R1 | 2.7021 | 2.7015 | 0.02 |
| Natural Frequency (THz) | Diff. (%) | ||||
|---|---|---|---|---|---|
| Mode (m,n) | Prevalent Displacement | Prevalent Mode Shape | Present Model (He) | Ref. [42] Model (He) | |
| (1,2) | w | R1 | 0.0163 | 0.0163 | 0.00 |
| (2,2) | w | R1 | 0.0511 | 0.0509 | 0.39 |
| (3,2) | w | R1 | 0.1025 | 0.1021 | 0.39 |
| (1,2) | u | R2 | 0.8508 | 0.8440 | 0.81 |
| (2,2) | u | R2 | 0.8852 | 0.8782 | 0.80 |
| (1,2) | u | R1 | 0.9071 | 0.8998 | 0.81 |
| (3,2) | u | R2 | 0.9339 | 0.9266 | 0.79 |
| (2,2) | u | R1 | 0.9447 | 0.9372 | 0.80 |
| (3,2) | u | R1 | 1.0052 | 0.9972 | 0.80 |
| (1,2) | v | R2 | 1.3157 | 1.3130 | 0.21 |
| (2,2) | v | R2 | 1.3642 | 1.3620 | 0.16 |
| (3,2) | v | R2 | 1.4409 | 1.4380 | 0.20 |
| (1,2) | v | R1 | 1.5387 | 1.5360 | 0.18 |
| (2,2) | v | R1 | 1.5696 | 1.5670 | 0.17 |
| (3,2) | v | R1 | 1.6218 | 1.6190 | 0.17 |
| (1,2) | w | R1 | 2.7831 | 2.7830 | 0.00 |
| (2,2) | w | R1 | 2.7835 | 2.7840 | 0.02 |
| (3,2) | w | R1 | 2.7843 | 2.7840 | 0.01 |
| Natural Frequency (THz) | Diff. (%) | ||||
|---|---|---|---|---|---|
| Mode (m,n) | Prevalent Displacement | Prevalent Mode Shape | Anisotropic Model (Ru) | Anisotropic Model (He) | |
| (1,2) | w | R1 | 0.0162 | 0.0162 | 0.00 |
| (2,2) | w | R1 | 0.0510 | 0.0510 | 0.00 |
| (3,2) | w | R1 | 0.1023 | 0.1023 | 0.00 |
| (1,2) | u | R2 | 0.8593 | 0.8594 | 0.01 |
| (2,2) | u | R2 | 0.8936 | 0.8943 | 0.08 |
| (1,2) | u | R1 | 0.9160 | 0.9161 | 0.01 |
| (3,2) | u | R2 | 0.9421 | 0.9437 | 0.17 |
| (2,2) | u | R1 | 0.9538 | 0.9541 | 0.03 |
| (3,2) | u | R1 | 1.0149 | 1.0152 | 0.03 |
| (1,2) | v | R2 | 1.2975 | 1.3086 | 0.85 |
| (2,2) | v | R2 | 1.3462 | 1.3567 | 0.77 |
| (3,2) | v | R2 | 1.4230 | 1.4327 | 0.68 |
| (1,2) | v | R1 | 1.5248 | 1.5257 | 0.06 |
| (2,2) | v | R1 | 1.5550 | 1.5560 | 0.06 |
| (3,2) | v | R1 | 1.6063 | 1.6074 | 0.07 |
| (1,2) | w | R1 | 2.6313 | 2.8507 | 7.70 |
| (2,2) | w | R1 | 2.6319 | 2.8510 | 7.69 |
| (3,2) | w | R1 | 2.6329 | 2.8517 | 7.67 |
| C-C Bond Parameters | |
| C-C bond length | |
| C-C bond elongation | |
| C-C bond angle variance | |
| C-C distance parameters | |
| C-C potential depth | |
| C-C equilibrium separation distance | |
| CNT equivalent parameters | |
| Thickness | |
| Mass density | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Strozzi, M. Applicability and Limitations of Ru’s Formulation for Vibration Modelling of Double-Walled Carbon Nanotubes. C 2022, 8, 59. https://doi.org/10.3390/c8040059
Strozzi M. Applicability and Limitations of Ru’s Formulation for Vibration Modelling of Double-Walled Carbon Nanotubes. C. 2022; 8(4):59. https://doi.org/10.3390/c8040059
Chicago/Turabian StyleStrozzi, Matteo. 2022. "Applicability and Limitations of Ru’s Formulation for Vibration Modelling of Double-Walled Carbon Nanotubes" C 8, no. 4: 59. https://doi.org/10.3390/c8040059
APA StyleStrozzi, M. (2022). Applicability and Limitations of Ru’s Formulation for Vibration Modelling of Double-Walled Carbon Nanotubes. C, 8(4), 59. https://doi.org/10.3390/c8040059






