Model Predictive Control—A Stand Out among Competitors for Fed-Batch Fermentation Improvement

Abstract

The fed-batch cultivation is in many ways a benchmark for fermentation processes, and it has been an attractive choice for the biotechnological production of various products in the past decades. The majority of biopharmaceuticals that are presently undergoing clinical trials or are available on the market are manufactured through fed-batch fermentations. A crucial process parameter in fed-batch cultivations is the substrate feed rate, which directly influences the overall process productivity, product quality and process repeatability; henceforth, effective control of this parameter is imperative for a successful fed-batch fermentation process. Two distinct control strategies can be distinguished—open-loop and closed-loop (feedback) control. Each of these methods has its own set of benefits, limitations and suitability for specific bioprocesses. This article surveys and compares the most popular open- and closed-loop methods for substrate feed rate control in fed-batch fermentations. Emphasis is placed on model-predictive feed rate control (MPC)—a stand out among other methods that offers a promising application perspective. The authors also demonstrate a practical example of the implementation of a robust, flexible MPC solution that is suitable for various cultures and runs on standard computer hardware, thus overcoming one of the main reported MPC drawbacks—high computational requirements.

1. Introduction

Three main modes exist for operating a fermentation process, namely batch, fed batch and continuous cultivation. Each operational mode has its own set of advantages and disadvantages. To create a cost-effective process, bioengineers must take into account various factors, such as media and supplement costs, process duration, biomass growth and viability, product yield and product quality. Moreover, the concentrations of growth-associated nutrients and by-products in the culture medium are also important considerations. Therefore, during process development, bioengineers must carefully weigh the options of batch, fed batch or continuous cultivation approaches [1].

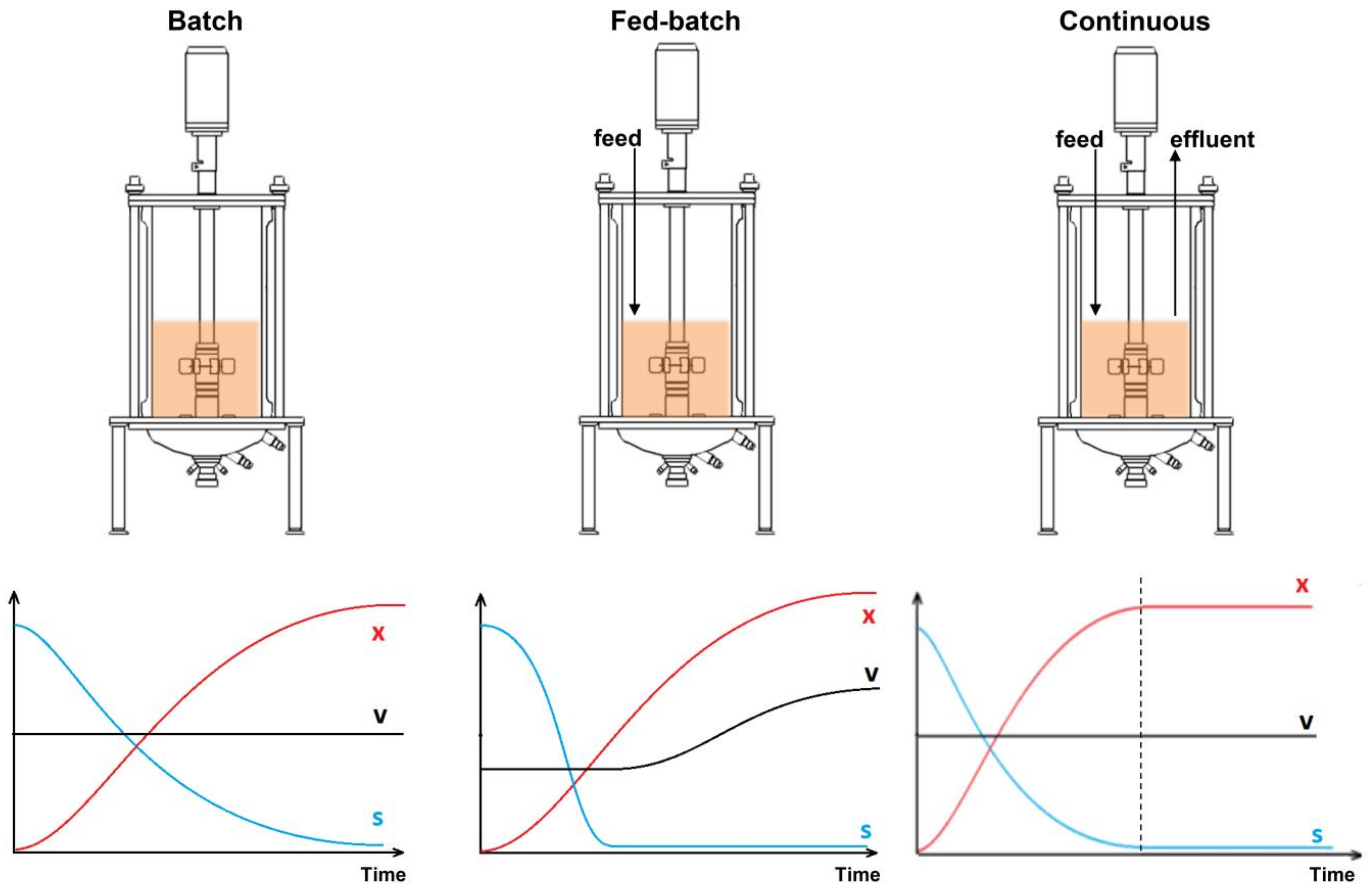
In a batch process, a fixed volume of a medium is introduced to a microbial culture (Figure 1, Batch). As the microorganisms multiply, they use up the nutrients in the medium and generate by-products, which gradually slows their growth and causes them to enter the stationary growth phase. In contrast, continuous fermentation involves a constant flow of fresh cultivation medium into the bioreactor, typically at a constant rate, while the spent medium and cells are simultaneously collected, thereby maintaining a constant medium level in the bioreactor (Figure 1, continuous). This process enables the replenishment of consumed nutrients and removal of toxic metabolites from the culture while keeping the culture volume constant.

Fed-batch fermentation is comparable to the batch process, but after the microorganisms consume all the substrate and nutrients in the cultivation medium, additional substrate and nutrients are added to the bioreactor (Figure 1, fed batch), thereby extending the active growth phase. The feed rate can be adjusted to regulate both the microorganism growth or the product formation rate. When designing a feed profile, it is essential to consider the maximum specific substrate utilization rate for the employed microbial strain. If more substrate is provided to the bioreactor than the cells can utilize, it will eventually start to accumulate and, upon reaching high concentrations, could potentially impede biomass growth, either directly or by promoting the synthesis of inhibitory metabolites. A similar situation may arise when the product has an inhibitory effect on the cells; thus, it gradually slows growth as the product accumulates in the reactor. A fed-batch operation typically results in significant biomass accumulation, making it particularly beneficial for bioprocesses that seek to generate high cell densities and product titers, especially when the target product is positively linked with microbial growth. Additionally, because the substrate is not overfed during the process and by-product accumulation is limited, both product and biomass yields per fed substrate are elevated [2]. In general, a higher product titer can be obtained per fermentation using a fed-batch operation, which practically increases the product space time yields when compared to batch processes. To illustrate, Muradi et al. improved bioethanol productivity 1.8 fold in S. cerevisiae fermentation, in comparison of a 72 h long batch versus a 72 h long fed-batch fermentation, thus increasing the overall process productivity [3].

Fed batch has become a benchmark for bioprocesses, and it has been a popular choice for production for several decades due to its robustness and elevated product yields per run and per time. Currently, most biotherapeutics in the market or clinical phases are produced using fed-batch fermentations [4]. Moreover, a vast range of amino acids, antibiotics, enzymes, solvents, vitamins and other products are now produced using this approach [2]. Human insulin was historically the first “golden molecule” produced in the biotech industry using an E. coli fed-batch cultivation. In this process, additional substrate is fed into the reactor at a rate to maintain low growth rates, which in turn suppresses by-product (acetate) formation and allows the culture to grow to high cell densities [5]. The fed-batch strategy is also commonly used in large-scale cultivations to address limiting factors such as mass and heat transfer. For example, the substrate feed is adjusted to maintain sufficient mixing, oxygenation and cooling conditions. This helps to ensure the optimal growth and productivity of the microbial culture throughout the fermentation process [6]. Therefore, the fed-batch mode of operation is commonly used in the bioprocess industry since it can overcome most of the limitations of batch and continuous processes. However, achieving an efficient and consistent fed-batch operation can be challenging due to the need to maintain an optimal substrate feed rate.

The rate at which substrate is fed into the bioreactor has a significant impact on both the metabolic processes and the volume changes in the system. The concentration of substrate in the growth medium is a critical factor that directly influences various aspects of the fermentation process. Specifically, it affects the rate of cell growth, oxygen utilization and the formation rates of both product and by-products. Therefore, maintaining an optimal substrate concentration is essential to ensure the efficient use of nutrients, minimize the production of undesirable by-products and maximize the yield of desired products. In turn, changes in the volume dynamics affect the concentration of all the elements in the bioreactor, and the medium’s viscosity can also impact both oxygen uptake and transfer rates. If the substrate feed rate is too low, the process will not reach its maximum productivity. If it is too high, it could result in an overflow metabolism and an increase in by-product formation. Additionally, during exponential growth, changes in metabolic processes, volume dynamics and other potential disturbances cause the maximum substrate uptake rate value to continuously change in a nonlinear manner, making the task of controlling the feed rate a challenging one [7].

Two distinct groups of feed rate control principles can be distinguished—open- and closed-loop control. Each of these approaches has its own strengths and limitations. However, the ultimate goal of any strategy is to achieve a balance between system implementation costs and control efficiency. This balance can affect the overall cost effectiveness of the process. Since microorganisms are fairly complex living systems, process productivity, product characteristics and the overall nature of each fermentation run can vary even when the same process parameters are used. As a result, feedback-based control methods are typically used in fed-batch fermentations to automatically adjust the substrate feed rate profile. This approach can provide significant benefits for overall process reproducibility by accommodating the dynamic and nonlinear changes in the system and ensuring that the nutrient demand is met consistently throughout the fermentation process.

This study examines some of the widely used substrate feed rate control strategies in fed-batch fermentations by comparing them based on the reports available in the literature. The analysis of practical examples from the authors’ previous experience provides a more comprehensive understanding of various practical aspects when selecting a particular substrate feed rate control strategy. Additionally, the paper presents a practical example of developing a robust and flexible model predictive control (MPC) solution, which runs on standard hardware. The study highlights the strengths of the MPC method and demonstrates how it can overcome one of its primary drawbacks—high computational demands. The presented example showcases the possibility of achieving an efficient and effective substrate feed rate control while also reducing computational demands, making the process more practical and cost effective.

2. Open-Loop Feed Rate Control

In an open-loop feed rate controller (also known as a nonfeedback controller), the control action taken is not dependent on the current process output. This type of control does not use feedback to assess whether the output has achieved the desired input or process set point. In fermentation systems, this approach is typically implemented in the form of a precalculated substrate feed rate time profile. The controller relies solely on the predetermined feed rate profile, which is based on the expected nutrient demand of the microorganisms and does not take into account any deviations in the actual nutrient demand or fluctuations in the system. Open-loop control can be a simple and cost-effective solution for certain systems, but it may not be as accurate or reliable as the feedback-based methods in more complex systems. The system is schematically illustrated in Figure 2.

Many industrial substrate-limited fermentation processes are operated in an open loop as this is the easiest way to organize a fed-batch process [8]. The feed rate time profile is calculated based on the initial conditions of the process. The first step is usually to calculate the initial feed rate at the start of the fed-batch phase. The equation for the initial feed rate (F₀) calculation is presented in Equation (1):

$$F_0=\left(\frac{\mu }{Y_{X/S,max}}+m_S\right)\times \frac{V_0{X}_0}{F_S} \left[\mathrm{L}/\mathrm{h}\right]$$

(1)

where µ—specific cell growth rate (h⁻¹), Y_X/S,max—maximum cell biomass yield from substrate (g g⁻¹), m_S—specific cell maintenance coefficient (g g⁻¹ h⁻¹), V₀—initial culture volume (L), X₀—initial cell biomass concentration (g L⁻¹) and F_S—substrate mass fraction in the feed solution (g g⁻¹) [9].

Once the initial feed rate has been determined, the remaining substrate feed rate time profile can be calculated using open-loop control methods. The specific approach used to calculate the feed rate profile will depend on the defined control goal of the fermentation process. There are several strategies that can be employed to determine the open-loop feed rate time profile for fed-batch fermentation. The choice of the appropriate strategy will depend on the specific goals of the fermentation process and the characteristics of the microorganisms being used.

A linear feed rate increase is the most commonly used feed rate profile, where the feed rate is gradually increased at a constant rate over time. A linear feed rate increase can be implemented by determining the initial feed rate, the final feed rate and the length of the fermentation process, and then calculating the rate of increase in the feed rate. The mathematical expression of this method is presented in Equation (2).

The exponential feed rate increase involves an exponential increase in the feed rate over time. The exponential feed rate increase strategy can be more effective than the linear feed rate increase strategy in achieving a faster increase in product concentration, but it may not be suitable for all types of processes or for achieving certain control goals. In fed-batch fermentation processes, using an exponential feed rate is a simple, predetermined method to maintain a steady specific growth rate below a critical level in order to prevent the formation of undesired by-products. This approach allows for better control of the growth rate and the formation of the end product [10]. The mathematical expression of this method is presented in Equation (3):

$$F_{lin}\left(t\right)=F_0+\left(F_{end}-F_0\right)\times \left(t/T\right) \left[\mathrm{L}/\mathrm{h}\right]$$

(2)

$$F_{exp}\left(t\right)=F_0\times e^{\mu t} \left[\mathrm{L}/\mathrm{h}\right]$$

(3)

where F₀—initial feed rate [L/h], F_end—feed rate at the end of substrate feeding (L/h), t—time after starting feed (h), T—process end time (h), µ—specific cell growth rate (h⁻¹).

Some other strategies include step-wise feed rate change (a sudden change in the feed rate at a specific point in time), pulse feeding (adding a pulse of substrate to the reactor at certain intervals), feed-on-demand (adding substrate to the reactor only when it is needed, based on the current state of the process) and gradual feed rate decrease (gradually decreasing the feed rate over time). It is important to note that the best substrate feed rate time profile will depend on the specific process, the control goal and the available resources. Some strategies may be more appropriate for certain types of processes or for achieving certain control goals.

In addition to basic strategies, more advanced methods can be used to calculate substrate feed rate time profiles, such as following a selected specific growth rate time profile [11,12]. The specific growth rate (µ) is a crucial variable in biotechnological processes as it greatly impacts the physiological state of the microbial culture, the production of cell biomass and the quantity and quality of desired products [13,14]. It is a key factor that shapes the outcome of the fermentation process; hence, efficiently controlling this parameter may prove beneficial for process productivity and repeatability.

Open-loop feed rate profiles can also be calculated based on a process model (also called model-based control). Understandably, this method requires a robust process model, and its accuracy is dependent on the accuracy of the model itself. Several examples of the successful use of this method have been reported [15,16,17].

Although easy to implement, such systems are not able to predict or react to unexpected disturbances during cultivation. For example, some inhibitory factors can cause changes in the specific substrate utilization rate, and the selected cell growth rate can no longer be attained. This can lead to lowered product yields, higher batch-to-batch variability and potentially even to whole-batch discard. In some cases, unexpected deviations from the expected performance of a fed-batch bioprocess can be addressed by an operator who manually adjusts the feed rate profile. However, this approach depends heavily on the operator’s experience and introduces a significant “human factor” into the process. In industries such as biopharmaceutical production, relying on manual adjustments may not be sustainable or compliant with current Good Manufacturing Practice guidelines. Therefore, it is important to develop and implement reliable feed rate control strategies that minimize the need for operator intervention and ensure consistent process performance.

In practice, the selected feed rate control strategy is very much dependent on the characteristics of the cultivation process in question. Sometimes high process productivity can be achieved with relatively simple feed rate control strategies, thus excluding the need to develop sophisticated and labor-intensive control schemes. One example, where an open-loop substrate feed profile can provide sufficient productivity, is the classic Invitrogen corporations’ Pichia pastoris cultivation protocol for recombinant protein production [18]. The methanol feed profile in this particular protocol suggests a step-wise feed rate increase, starting with a feed rate of 3.6 mL/h/L for the first 3–5 h, which is then doubled to 7.3 mL/h/L for 2 h and, finally, increased to 10.9 mL/h/L for the rest of the cultivation. Such a feed profile may not be entirely optimal from a maximum-productivity standpoint, for example, because with a constant feed rate, the amount of substrate per cells decreases during cultivation (cell biomass increases, feed rate remains constant), causing a decrease in the specific growth rate with time [9].

Regardless, this cultivation strategy is still able to produce high recombinant protein yields. We have reported a case in which this particular feed profile produced the highest yet reported recombinant hepatitis B core antigen virus-like particle (HBcAg VLPs) yield [19]. In this particular research, the effect of residual methanol in the concentration range of 0.1–2.0 g/L (usually associated with an increased recombinant protein productivity) on HBcAg VLP production was screened. The residual methanol concentration was controlled using a methanol sensor and by manipulating the methanol feed rate using a feedback PI-based feed rate control algorithm. Despite employing this closed-loop feed rate control method, the highest HBcAg VLP yield was produced in the cultivation conducted according to the Invitrogen cultivation guidelines with an open-loop feed profile, where no significant accumulation of methanol occurred and the methanol concentration was limiting for most of the induction phase (see Figure 3).

There are plenty of reports where the optimization of the Invitrogen protocol leads to elevated recombinant protein yields. The cultivation media composition, induction temperature, dissolved oxygen concentration (DO) and residual methanol concentration are most often the targets for product yield optimization in P. pastoris [9,20,21]. However, the substrate feed rate profile can also play a significant role in maximizing process productivity. For example, the length of the glycerol fed-batch phase and reached cell biomass concentration can have a significant effect on recombinant protein biosynthesis [22,23,24]. A similar case is true for the methanol induction phase, as the selection of an optimal feed rate profile can be crucial to the product concentration at the end of the fermentation. The open-loop profiles most often employed are either linear or exponential (to maintain a constant specific growth rate or induction pressure) [22,25].

Garcia et al. compared two open-loop substrate feed systems—offline optimizing control and exponential feeding—in a C. necator fermentation producing a poly(3-hydroxybutyrate-co-3-hydroxyvalerate) (PHA) copolymer. The offline optimizing control approach employed an unstructured process model to calculate the feed profile, whereas the exponential feed profile was calculated to maintain a constant specific growth rate of 0.15 h⁻¹. The fed-batch optimizing control strategy resulted in the highest reaction yield, highest PHA content and highest productivity. However, the attained product yield obtained (mass of polymer produced per mass of substrate consumed by the microorganism) was not satisfactory. Furthermore, the fed-batch-exponential strategy resulted in the lowest reaction yield, showing that this strategy is not at all suitable. To further improve the process productivity, the authors implemented a closed-loop control strategy, which uses biomass and substrate information predicted online by soft sensors to maintain a preset substrate concentration in a 500 L bioreactor process. However, the produced polymer concentration was even lower than in the previous 5 L open-loop experiments [26]. Vanichsriratana et al. compared two optimal open-loop and closed-loop feed rate control strategies in a simulated fermentation process. The authors found that the closed-loop optimal feed rate control provided a better result mainly due to the feedback property allowing the system to compensate for the modeling error [27]. In a different article, the authors compared an open-loop and a closed-loop control system and concluded that when the process model was an exact representation of the plant, both methods gave similar results in a fermentation producing primary and secondary metabolites [28].

In general, open-loop control may not always lead to the highest product yields and does not account for system disturbances. However, depending on the specifics of a given bioprocess, it can still be a valid approach for feed rate control. As demonstrated in the previous examples, open-loop control can sometimes even outperform closed-loop systems. Despite its limitations, the main benefit of open-loop control is its ease of implementation and the fact that it does not rely on measured variables. It is important to carefully evaluate the specific requirements of each bioprocess to determine whether open-loop control is an appropriate choice for feed rate control.

3. Closed-Loop Feed Rate Control

In a closed-loop feed rate controller, the input is adjusted based on the output of the system, which is typically a measured process variable (PV) signal. This allows the system to compensate for any disturbances that may affect the process and ensure that the output remains within the desired range. The system is schematically illustrated in Figure 4.

Closed-loop feed rate control strategies cover a wide range of methods, but the common denominator is the variation in the control action in order to respond to nonlinear dynamics or uncertainties during fed batch processes. The type of controller is determined by the control action calculation method employed. Closed-loop strategies may also be adaptive and thus able to adapt to the unexpected variance in the system parameters. An adaptive control system is one in which the controller parameters are adjusted automatically to compensate for changing process conditions [29]. Due to the complex and nonlinear dynamics of a biological system, the use of adaptive strategies is very compelling for fermentation processes. The most popular closed-loop strategies are briefly presented further.

3.1. PID Control

The most common closed-loop feed rate control method is the proportional–integral–derivative or PID controller. It works by continuously calculating the error signal value as the difference between the desired set point (SP) and the measured process variable (PV) and applies a correction to the input based on proportional, integral and derivative terms. Of these three terms, the first is proportional to the deviation between the targeted value and the currently observed value, the second is proportional to the integral of the deviation and the third term is proportional to the derivative of the deviation. Namely, the proportional term responds to the current error, the integral term responds to the accumulated error over time and the derivative term responds to the rate of change of the error. The overall control function for the substrate feed rate control in its classical mathematical form is presented in Equation (4):

$$F\left(t\right)=K_{p}e\left(t\right)+K_i{{\displaystyle \int }}_0^{t}e\left(t\right)dt+K_d\frac{de\left(t\right)}{dt}$$

(4)

where F(t)—feed rate correction signal value; K_p, K_i and K_d—the coefficients denoting the proportional, integral and derivative terms, respectively; e(t)—deviation from set-point value (SP-PV).

To implement digital controllers, which is the case for most biotechnical applications, discrete sampling periods are used, requiring the use of a discrete form of the PID equation to approximate the integral of the error and derivative. This discrete modification involves replacing the continuous integral with a summation of the error, with T representing the time between sampling instances and n representing the number of sampling instances [30]. The discrete three-term controller allows for the independent tuning of each term, which can be an advantage for the control of nonlinear processes. The discrete (sampled) form of the algorithm has many forms based on the technique used for discretization [31,32], but can, for example, be expressed as:

$$F\left(t\right)=F_{t-1}+K_p\left(e_t-e_{t-1}\right)+K_i{e}_{t}T+K_d\frac{\left(e_t+e_{t-2}-2e_{t-1}\right)}{T}$$

(5)

where F(t)—the control output at time step t; e—the difference between the setpoint and measured output (error) at current (t) or previous (t − 1, t − 2) sampling times; T—the time between sampling instances (sampling time) [33].

In fed-batch processes, PID control is usually implemented in the form of indirect feedback control schemes that couple the substrate feed rate with measurements of pH (pH-stat) and/or dissolved oxygen concentration (DO-stat) [34,35]. The pH-stat method is based on the phenomena that pH usually decreases when the substrate is consumed (due to the consumption of NH₄⁺ ions) and rises along with the excretion of ammonium ions, usually due to the depletion of the carbon source or cell lysis [34,36]. Similarly, the DO-stat is based on the fact that DO increases sharply when a key substrate is depleted [35,37].

Several other PID control schemes are also widely used in the biotechnological industry. In Saccharomyces cerevisiae (baker’s yeast) cultivations, the ethanol concentration in the medium can be maintained at a constant low level. In this way, the specific growth rate is kept at maximum while avoiding growth-inhibitory ethanol formation [38]. The PID-based control shows favorable results as the overall performance of the process is better than in the case of open-loop control and the overall implementation complexity is not that high. Despite this, the use of this method is limited in some cases due to the lack of reliable on-line or express at-line measurement systems for determining the values of control parameters and due to the general nonlinearity of biological processes [39]. For example, it is difficult to accurately estimate the concentrations of cell biomass or most substrates on line.

The signal quality of optical or capacitive biomass sensors are often influenced by such disturbances as mixing, aeration, foam and the state of the culture, while the enzymatic sensors used to measure the substrate concentrations often do not provide sufficient accuracy and reliability [40]. The availability of accurate substrate concentration measurement systems, however, depend on the substrate in question as, for example, there are several systems to precisely estimate the concentration of methanol in recombinant Picha pastoris cultivations [41,42]. More accurate measurements of the mentioned control parameters can be obtained by in-line chromatography or flow cytometry; nevertheless, the said approaches do not guarantee that the state of the system will be correctly evaluated. For example, the lack of culture growth does not necessarily indicate malnutrition but may be a result of inhibitory metabolite formation. Additionally, maintaining a certain critical substrate concentration (S_crit) does not guarantee that there is no overflow metabolism in the system, since S_crit can change from process to process [43].

The critical factor in ensuring high-quality bioreactor operation is the effective setup and tuning of the controller parameters to address the sources of process variability [44]. Due to substantial fluctuations in the process dynamics during operation, standard PID controllers with fixed tuning parameters are insufficient for precise process control. As a result, several methods have been suggested for tuning the PID controller parameters in biotechnological processes under conditions that change over time. A continuous cultivation process has an equilibrium for which the controller can be tuned. Fed-batch processes, however, have no such point, as the system constantly changes and thus cannot be linearized. Therefore, it is necessary to use nonclassical tuning methods to achieve the best overall PID control for the entire operating range of the given system [31]. Numerous PID parameter tuning methods are available—both manual and automatic (online) [45,46]. Some of the most commonly used tuning methods are gain scheduling [12,47,48,49], first-principle models [50,51], fuzzy rule-based systems [52], metaheuristic models [31,45] and other techniques [30,46,53]. By introducing an automatic tuning procedure, the closed-loop system is periodically tested, and the test characteristics automatically determine new controller settings and thus introduce adaptive control [29].

To present an actual example of the role that PID parameter tuning plays in fed-batch cultivations, we can look to our previous experience, controlling the residual methanol concentration via a PI-based substrate feed rate control algorithm in P. pastoris cultivations. The cell biomass growth, methanol concentration and feed rate time profiles of three experiments are presented in Figure 5. In Exp. 3, methanol was successfully controlled at 1.0 g/L; however, in both Exps. 4 and 5, a residual methanol concentration of 2.0 g/L was selected as the set-point value. In Exp. 4, the same control parameters were used as in Exp. 3 and, consequently, the system was unable to successfully maintain a methanol concentration of 2.0 g/L, illustrated by the wild fluctuations (±1.0 g/L) around the set-point value. After manually tuning the PI control algorithm parameters in a process simulation, the experiment was repeated (Exp. 5). Now, the residual methanol concentration control was much more accurate and the deviation around the set-point value much lower (±0.39 g/L) [19].

Despite the difficulties posed by the necessary parameter tuning procedures, PID, PD and PI closed-loop feed rate control can efficiently control the substrate feed in a way to achieve the set process goals. For example, we reported a case of recombinant hepatitis B surface antigen virus-like particle (HBsAg VLPs) production in the yeast P. pastoris, where sufficient productivity could not be achieved by open-loop feed rate control methods [54]. The product would be mainly in nonsoluble form (not suitable for VLP formation) and disappear during the initial purification steps. However, cultivation in an elevated residual methanol concentration of 6.0 g/L would prove to be beneficial to the product, and 186 mg/L of purified HBsAg VLPs were successfully produced. Case in point, the residual methanol concentration was controlled using a PI-based methanol feed rate control algorithm and adjusted according to the real-time methanol concentration measurement of a methanol sensor probe.

Priyanka et al. compared the performance of an augmented decoupled adaptive control strategy that uses the substrate and the DO as controlled variables vs. a PID controller in a P. pastoris X-33 Mut⁺ fermentation to produce rHSA. The augmented controller consisted of a decoupled adaptive control (DAC) and a decoupled input–output linearizing control (DIOLC) in a combined architecture, allowing for the simultaneous control of both the substrate and dissolved oxygen concentration. The performance of the augmented DAC-DIOLC controller showed deviations of only 0.021 g/L from the substrate set point compared to 0.09 g/L in PID, and a 1.12% deviation from the DO set point compared to 11.86% in PID. Overall, the use of the augmented controller resulted in a 1.5-fold increase in rHSA production [55]. Brignoli et al. implemented and optimized a novel proportional-integral (PI) feedforward–feedback controller to maintain a desired specific growth rate of a K. marxianus culture. The proposed control logic provided robust set-point tracking of an exponentially evolving fed-batch culture while ensuring improved noise and oscillation management. It was demonstrated that a strain of K. marxianus could be grown successfully in fed-batch mode under substrate-limited, aerobic conditions at different set points ranging from 0.1 h⁻¹ to 0.4 h⁻¹ [12]. Kager et al. implemented a nonlinear model predictive controller (MPC) in a P. chrysogenum fed-batch process and compared it to a PI(D) and an open loop feedback control scheme. The authors found that the implemented PI(D) controller showed some instabilities due to changing process dynamics, and the open-loop feedback inverse control (MBC) was limited in its linearized control space. The authors concluded that to optimally control the nonlinearities and discontinuities of the process, MPC is needed to satisfy multiple objectives and to predict process events in order to prevent the formation of gluconic acid and mannitol during the first phase of the experiment. This enabled an ongoing product formation, which led to 14% higher product concentrations and improved product and biomass yields [56].

To summarize, a PID controller can enhance the overall stability and efficiency of the process by regulating the substrate feed rate and compensating for unexpected disturbances. However, for the controller to be effective, it must be properly tuned, which can be challenging due to the nonlinearity of bioprocesses. Controllers with fixed tuning parameters may not be accurate throughout the entire process, thus requiring careful attention to tuning during operation [13].

3.2. Artificial Neural Networks (ANN)

An artificial neural network (ANN) is a computational algorithm that mimics the structure of a biological brain network. ANNs are used to estimate and predict bioprocess variables based on environmental and physiological information available from on-line sensors. They can describe complex nonlinear systems without the need for complex model equations, but require significant amounts of past process data to train the network accurately and predict the relationship between system inputs and outputs [7].

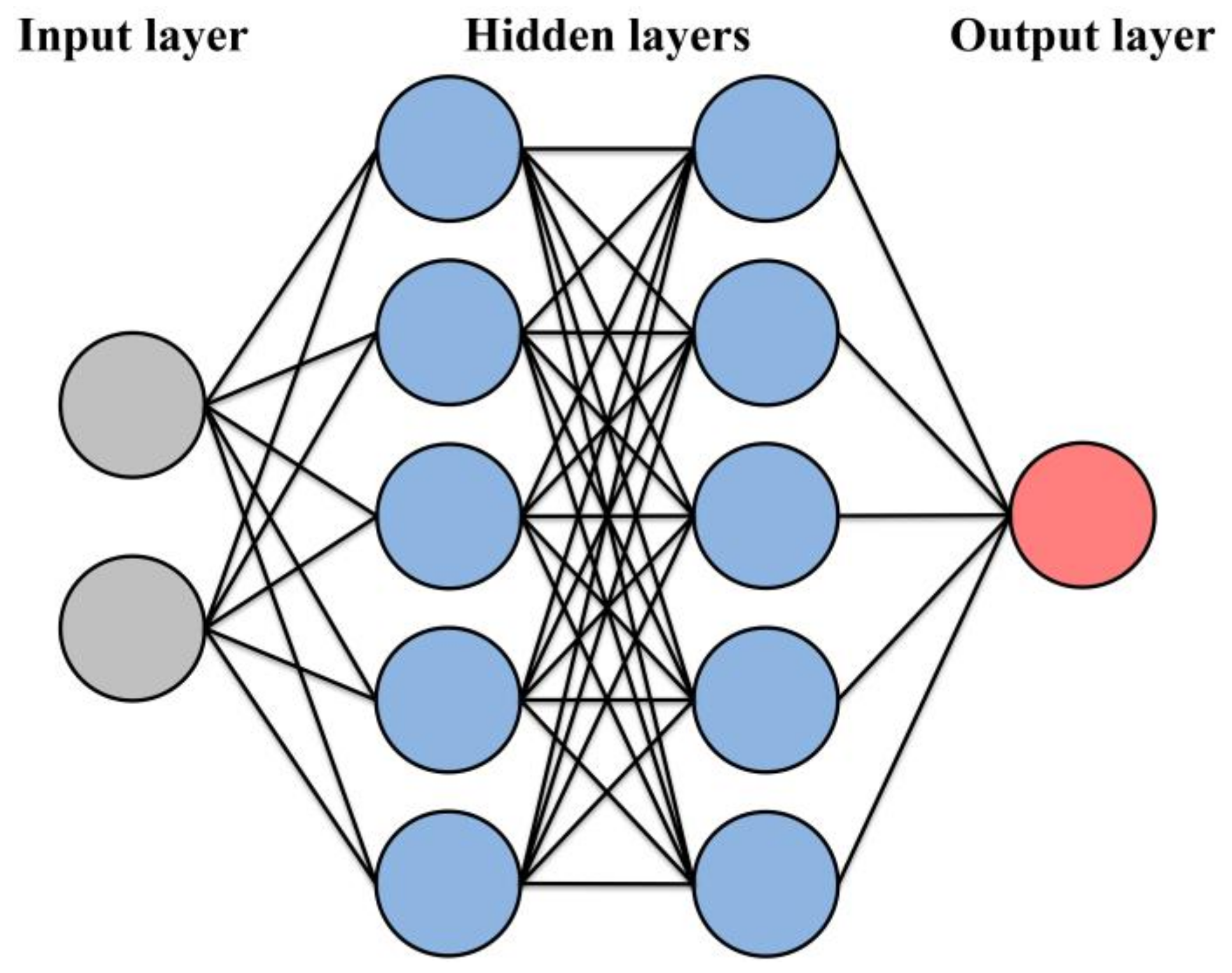
ANNs have layers of nodes, also called artificial neurons, which are typically grouped into subsets or layers, including an input layer, one or more hidden layers and an output layer. Each node is connected to others and has a weight and a threshold. A node is activated and sends data to the next layer of the network if its output exceeds the threshold value. If not, no data are passed to the next layer. The outputs of the neurons from one layer represent the inputs for the next layer. A neuron can have any number of inputs, but only one output that is usually related to the inputs by a transfer function. The most common transfer functions are the sigmoid, hyperbolic tangent, sine, linear and saturated linear functions. The argument for these functions is calculated by adding the inputs to a neuron, where each input is multiplied by its corresponding weight, indicating the connection strength between neurons [39]. Figure 6 shows a schematic representation of an artificial neural network.

Although ANNs are generally quick and straightforward to implement and perform well, they lack interpretability; thus, limited process knowledge is gained. Additionally, the network is trained for a certain scale and, therefore, will need to be retrained during the process scale up [57]. Furthermore, ANNs have limited ability to extrapolate beyond the range of data used for training, in contrast to physically based mathematical models or rule-based systems, which can be more flexible and widely applicable [58].

It is possible either to apply the ANN as a predictor for a variable of interest and then incorporate this into a feedback control algorithm or to utilize the ANN directly in an optimization algorithm to solve for optimal control solutions [59,60]. ANNs have previously been shown to be successful at predicting the behavior of various fermentation systems and, consequently, have been employed in bioprocess control applications. The current reported applications include the use of ANN models to control reactor temperature [39], specific growth rate [61], maximize cell biomass [60,62,63], product concentration [63,64,65,66,67] and to estimate [63,67] or follow a preselected substrate concentration trajectory [59].

Chaudhuri et al. demonstrated the applicability of an ANN to calculate optimal substrate feed profiles in two simulations in comparison to reported kinetic models. The simulation results for the secreted protein and invertase production demonstrated that the ANN model managed to capture the essential features of the process kinetics, and therefore, the model can be used for the dynamic simulation of the process. The optimal feeding policies obtained with the model agrees reasonably well with the previously reported results, which allows the authors to conclude that the main advantage of the approach lies in the fact that optimization can be achieved without knowledge of the detailed kinetic model of the process [68]. Galvanauskas et al. compared the specific growth rate control performance of an adaptive PI controller based on the gain scheduling technique and a model-free adaptive controller based on an artificial neural network. Both controllers delivered a comparable control performance and were suitable for application when using the substrate limitation approach and substrate feeding rate manipulation. However, the authors concluded that considering the efforts for controller design and tuning (including the development of the adaptation/learning algorithms), the model-free adaptive control algorithm proved to be more attractive for industrial applications, especially when only limited knowledge of the process and its mathematical model is available. Additionally, the model-free adaptive controller also tended to deliver a better control quality under low specific growth rate conditions during the recombinant protein production phase [49]. Zelic et al. investigated three different models: the unstructured mechanistic black-box model, the input–output neural-network-based model and the externally recurrent neural network model to describe the pyruvate production process from glucose and acetate using a genetically modified E. coli YYC202 strain. The unstructured mechanistic model could not adequately fit the experimental data obtained in the different processes; however, the results obtained using the neural networks showed satisfactory compliance with experimental values. The performance of the neural networks conclusively showed that they have the potential to be implemented as an online state estimator, facilitating the control of pyruvate production, and can also be used in process optimization [69]. Rashid et al. conducted a study where neural network and fuzzy logic methods are used in the design of a controller for baker’s yeast production. After the first iteration, the ANN-based controller showed unsatisfactory results; hence, a set of fuzzy rules were introduced to characterize the biomass concentration. To obtain a reliable assessment, the results were then compared with those of the PI controller. Unlike the PI controller, the developed controller proved capable to follow the time-varying characteristics of the process and deal with the nonlinearity of the process [70]. Pantano et al. successfully implemented a closed-loop controller integrated with a neural network state estimator to track three optimal profiles of an important nonlinear biological process by manipulating the nutrient and inductor feed rates. The proposed controller was compared with a PI controller, showing a better control response. Moreover, through several closed-loop simulation tests, the proposed controller was shown to be not only simple and efficient with the neural state estimation, but also sufficiently robust to compensate for the mismatches in the model parameters as well as the internal and external perturbations of the system [71].

In summary, ANNs have demonstrated the successful prediction of fermentation system behavior based on measured variables and have been applied to various control applications. Although they can be relatively easy to implement, building an accurate ANN requires significant historical process data, and limited process knowledge is gained from the network. Additionally, ANNs are trained on a single scale and are limited in their ability to extrapolate data, which restricts their application.

3.3. Fuzzy Control

Fuzzy logical control is a control strategy intended to address uncertainties in nonlinear systems, such as batch, fed-batch and continuous fermentations. It leverages the knowledge and expertise of the process operator to control the fermentation. The fundamental principle of fuzzy control is to convert quantitative data into qualitative parameters [7].

A set of fuzzy if–then rules and an inference mechanism are used to determine the input–output mapping of the system. First, the input data are fuzzified—converted from numerical data into ‘membership functions’ based on the degree to which they fit in a fuzzy set (given a value from 0 to 1). To perform fuzzification, a range of possible values is defined for each input variable. This range serves as a scale for comparing the data values. The variable is then described using a fuzzy set and is assigned a degree of membership. For instance, a substrate concentration reading of 2.0 g/L might be compared to the range of 0–10 g/L and assigned to the fuzzy set “Low” with a degree of membership of 0.8 and to the fuzzy set “OK” with a degree of membership of 0.2. It is important to note that the total degree of membership for all fuzzy sets for a given variable must equal one. A fuzzy set is described by a matrix that includes the original value of the variable and the degree to which it belongs to a category on a scale from 0 to 1. The current state of the system is interpreted using the fuzzy sets. Fuzzy control is based on a set of “fuzzy rules” that describe the conditions of the system and are derived from the operators’ experience with the process in the form of conditional statements using such terms as ‘if’ and ‘then’. For example, If S (substrate concentration) is “Low”, Then F (substrate feed rate) is “High”. In this case, the controller assesses the substrate concentration as low and, consequently, increases substrate feed rate. The operator’s experience is incorporated into the controller via a process called defuzzification—the process of transforming a fuzzy output into a numerical value that represents the best estimate of the actual output that can be used to make decisions [7,72]. A fuzzy logic controller is schematically illustrated in Figure 7.

In contrast to ANNs, the outcome of fuzzy control is to identify the current state of the system, and it therefore provides some information to the operator. The main advantage of the fuzzy logic approach is the greater flexibility to capture incomplete and imperfect aspects of the process.

Fuzzy controllers have also previously been successfully employed in bioprocess applications; for example, to estimate substrate concentrations [73,74,75,76], cell biomass [74], fermentation temperature [77] and adjust the substrate feed rate [75].

Ye et al. developed a five-layer neural–fuzzy network to control the fed-batch cultivation conditions of a recombinant E. coli strain for maximum β-galactosidase production [78]. The authors applied a fuzzy network to control the glucose feed rate based on deviations from set points of the pH value, which can be used to indirectly measure the glucose concentration in the broth, and the specific cell-growth rate. The specific growth rate is the most important variable, influencing both cell growth and recombinant product expression. The biomass concentration of recombinant E. coli improved from 20 g dry cell weight/L under conventional control to 84 g dry cell weight/L under neural–fuzzy control. However, the relative activity of β-galactosidase was not high due to a high residual glucose concentration after induction. To overcome the low relative activity, the researchers created two fuzzy networks—one for the period before induction and one for after. Adding the second fuzzy network increased the relative activity of β-galactosidase four fold while a biomass of 50 g (dry cell weight)/L was reached, which still represents a significant improvement over conventional techniques [78,79].

Fonseca et al. proposed an adaptive fuzzy feedforward–feedback control structure (A4FB) in which a Mamdani fuzzy system was used to adapt the feedforward control law parameters. The A4FB was tested in a CSTR reactor, in which an enzymatic reaction of starch hydrolysis by Aspergillus niger glucoamylase takes place. A comparison between the A4FB and the classical feedforward–feedback control was also provided. The results indicated that the adaptive fuzzy feedforward control performed better in terms of disturbance rejection since its performance index was 0.645 while the classical feedforward–feedback control achieved only 0.406. In conclusion, the authors list the main advantages of the developed adaptive fuzzy control system: easy deployment of a regulatory control action without prior nonlinear process modeling; ease to adapt from the fuzzy logic to other systems; and better rejection of the process disturbances [75]. Choi et al. investigated the effect of controlling the substrate feed rate with an ANN and fuzzy logic controllers to enhance flavonoid production in a Scutellaria baicalensis Georgi plant cell fed-batch fermentation. The experimental results showed that the ANN controller with a genetic algorithm improved the flavonoid production compared with a simple fuzzy logic control system. Furthermore, the specific production yield and flavonoid productivity also increased. Therefore, the authors concluded that an artificial neural network is a more suitable controller than a fuzzy logic controller in the fed-batch cultivation of S. baicalensis G. [80]. Yuan et al. investigated an approach in which a fuzzy logic controller was developed based on an artificial neural network model. The controller was then tested online with an objective to obtain a high concentration of cell mass in the shortest fed-batch culture time. The experimental results revealed that the fuzzy neural network controller on-line feeding of the substrate performed, as the authors described, “well” [81].

In summary, fuzzy control methods are useful for dealing with nonlinear systems such as fermentations and are considered more intuitive to users. However, there is a lack of recent examples of their use in substrate feed rate control applications. Fuzzy logic controllers require a good understanding of the bioprocess to establish a comprehensive rule base, which is dependent on human expertise. While they provide insight into the dynamics of complex systems, their effectiveness is limited by the need for human input and the lack of recent examples of their application in this specific area.

3.4. Model Predictive Control

One of the most promising methods for closed-loop control in fermentation systems is currently model predictive control (MPC). This method evaluates the difference between the predicted and reference values of the controlled variable in order to determine an appropriate control action. A robust prediction process model is required to simulate the fermentation process up to a future time horizon, which allows for predictions of both the current output and future system states. These predictions are then assessed based on an optimization of a cost function over the entire process time, which ultimately determines the appropriate control action (i.e., feed rate correction) required at the current time. An MPC controller is schematically illustrated in Figure 8.

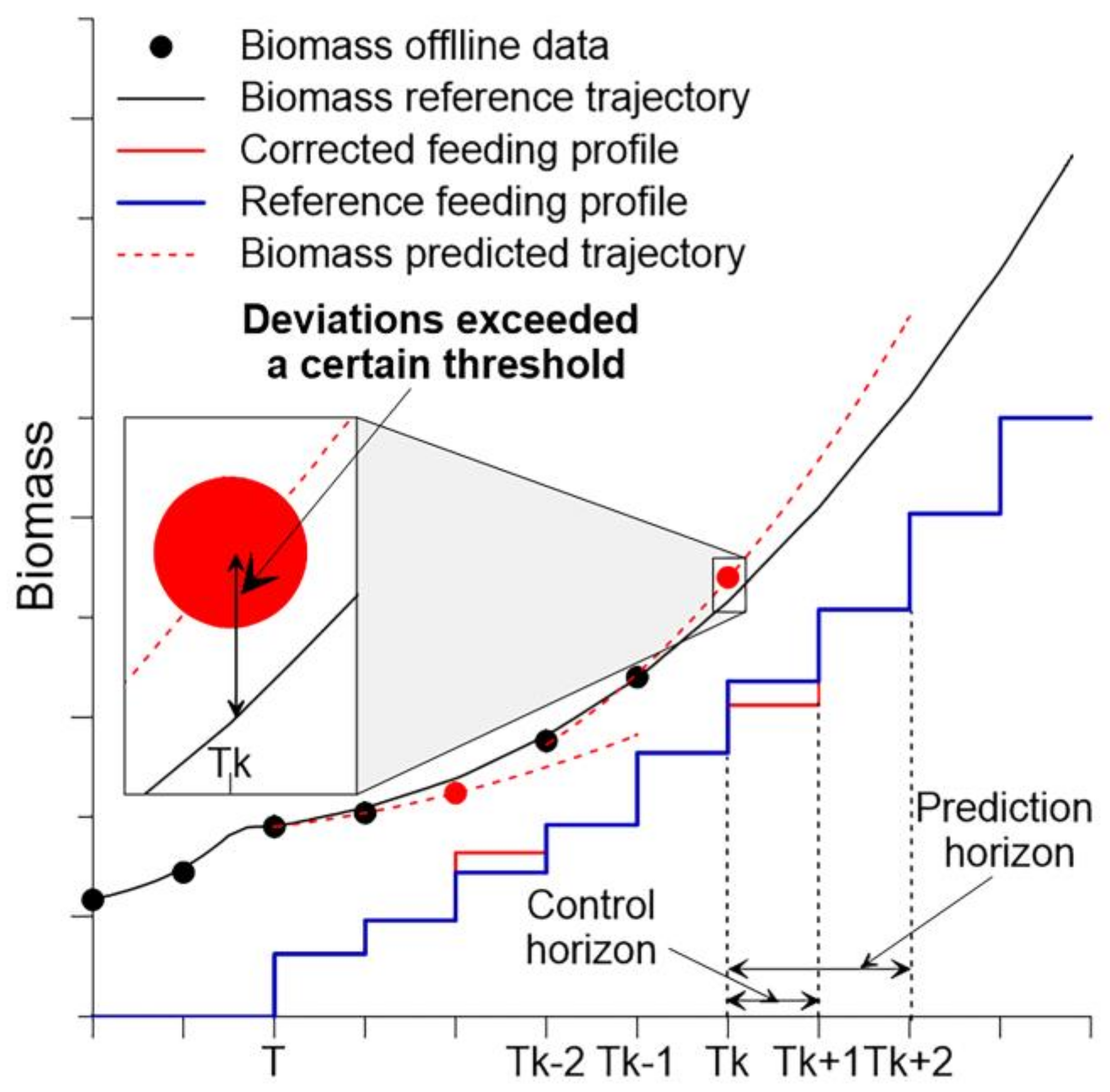
The basic operating principle of model predictive control (MPC) involves several steps. First, the initial process parameter values are defined, and the desired process reference trajectories are established. Then, using historical process data, a model is constructed to simulate the behavior of the fermentation process over a defined time period (the prediction horizon), allowing for the prediction of the system state. The predicted trajectories are then compared to the reference trajectories, and if the deviation exceeds a defined threshold, the MPC algorithm modifies the feed rate profile within a predetermined range over a specific time period (the control horizon) until new data are supplied. The operational principle of an MPC controller is presented in Figure 9, where T_k is the actual point in time, T_k−1 and T_k−2 are past (measured) values and T_k+1 and T_k+2 are future (predicted) values.

To control the feed rate using MPC, choosing an appropriate optimization function is a crucial aspect. Two commonly used approaches are following a reference trajectory for either cell biomass or substrate concentration during cultivation. The reference trajectories can be obtained from previously reported processes [83], calculated using mathematical process models [84] or determined experimentally, for example, by employing the probing method [85].

Both classic mechanistic [86,87] and empirical models (ANN [88,89], partial least squares [90]) can be used to develop predictions. Empirical models can be quite accurate within the boundaries of the process parameters they are originally derived from, but they are poorly scalable and present less predictive and analytical insight, in contrast to mechanistic models [90]. Additionally, the employment of a model predicting the behavior of the system, along with a desired reference trajectory, permits the prediction of possible process parameter deviations in advance, which is not possible using other methods of direct control.

Many examples for the application of MPC for the control of yeast [88,89], bacteria [84,87,91] and mammalian cell cultivations [83,86,92] can be found in the literature. Some examples of use in alcohol biosynthesis [88,89], recombinant proteins [83], hormones [84], flavonoids [93] and antibiotic [90] production have been also reported. However, half of these studies were carried out on various kinds of simulators [88,89,90,91,92] and not dedicated towards direct operation in real systems.

Kuprijanov et al. demonstrated how an MPC controller can be easily implemented in industrial bioreactor automation systems for fed-batch fermentation processes. Using only standard sensors (pH, DO) and at-line biomass and glucose measurements, and by varying the substrate feed rate, the authors were able to demonstrate the ability of the MPC controller to follow a preset biomass growth profile and thus improved process repeatability and safety [87].

Lupenza et al. developed an Event-Triggered Feed-Forward Control (ET-FFC) scheme for the K12 E. coli fed-batch fermentation process. Based on the data, a Proportional Integral (PI) and a model predictive (MPC) controllers were designed to control the cell biomass concentration by manipulating the substrate feed rate. The closed-loop performances of the proposed controllers were evaluated and analyzed through a simulation of an E. coli fermentation process. The results showed that the MPC-based ET-FFC scheme provided better performances with a minimum integral square error over the PI-based ET-FFC scheme [94]. Ulonska et al. compared the performance of two different model-based control strategies with respect to the simultaneous set-point control of two individual substrate uptake rates by two substrate feeds in an E. coli fed-batch process. The compared controllers were an elemental balance controller (EBC) and a model predictive controller (MPC) based on a mechanistic model. Both controllers showed comparable behavior and were generally capable of fulfilling their tasks. The MPC was based on a better and more flexible description of the system, whereas the EBC was easier and showed more stable behavior. The authors concluded that for the investigated application, the EBC was preferable due to its simplicity. However, the potential of the MPC was clearly in its prediction power and flexibility towards objective functions. Therefore, it would be the controller of choice in the case of product-related objective functions [95]. Schneider et al. compared the performance of two model predictive controllers—a nonlinear open-loop feedback optimal (OLFO) and a linear dynamic matrix control (DMC)—in Cyathus striatus fermentation. The authors found that the DMC controller performed unexpectedly well in this particular process as it is more suited for fast, discrete and linear systems. However, the authors concluded that better results can be achieved with the OLFO controller with more frequent model parameter identification and if the time horizon for the identification process is the past 24 h and not the entire process time [96]. Aehle et al. employed an MPC system to ensure a high batch-to-batch reproducibility in an animal cell (CHO-cell) culture for recombinant therapeutic protein (EPO) production. The control objective was to identify and control an optimal specific growth rate by controlling the oxygen mass consumed by the cells by manipulating the glutamine feed rate. The authors judged the performance of the controller to be fairly good, which could best be judged by high batch-to-batch reproducibility obtained in cultures that are operated with this controller [83].

To summarize, model predictive control (MPC) is a powerful closed-loop control method for substrate feed rate control that optimizes the control actions for the full process time, not just at the current time instant. MPC also models the impact of disturbances as part of the optimization problem. However, the effectiveness of this method heavily depends on the accuracy of the process model and its ability to handle unexpected disturbances. Some of the main drawbacks of this method include the requirement for robust process models, which may not always be available, and its computational expense.

4. A Practical Example of MPC Implementation

In practice, MPC is a powerful and prospective feed rate control approach in a wide variety of fed-batch bioprocesses. There are also some commercial MPC solutions available; however, they are highly process specific and are designed to be employed mainly in the biopharma industry. For example, ABB offers a nonlinear MPC system for mammalian cell (CHO) cultivation for biopharmaceutical production [86,97]. A similar system was also announced to be in development by Bilfinger [98]. The market currently lacks universal, sufficiently robust, affordable and easy-to-use MPC options for a wide range of advanced bioprocess control applications; therefore, it may be necessary to tailor the MPC system to one’s specific process.

However, implementing this approach demands proficiency in bioprocess modeling and programming. In the case of adapting the MPC system to a different bioprocess, most of the development process has to be repeated. To showcase the feasibility of this approach and to provide a clearer picture of the development process, we have previously designed an MPC system, which was constructed using a standard hardware PC and a Siemens Simatic S7-1200/1500 series programmable logic controller (PLC). The module communication scheme and hardware implementation of the proposed system are illustrated in Figure 10 and Figure 11, respectively. SCADA, installed on a standard hardware personal computer, was connected to the Siemens Simatic S7-1500 PLC through the router via an Ethernet link. The implementation of the proposed MPC algorithm was realized using a PC-based program, developed in a Matlab (Mathworks, USA) environment. The data exchange of the process and control variables between the MPC control algorithm and SCADA, programmed in a PcVue (PcVue Solutions, France) environment, was implemented every 1 s through an OPC server. The feeding was controlled gravimetrically using the scale module (Bioreactors.net, Latvia) or volumetrically by means of an analogue peristaltic pump.

To employ this MPC system, it is first necessary to establish the optimal trajectories for either biomass growth or substrate concentration (so-called “golden batch”) [99]. Both the empirical (modeling) and experimental methods mentioned in the previous paragraphs can be employed to construct said reference trajectories. Before starting the process, the initial X₀, S₀ and V₀ values must be defined, and the program then calculates a possible feeding profile and models the reference trajectory of X(t), S(t) and V(t) for the entire cultivation. After starting the MPC control program, sampling must be carried out. After each sampling procedure, the biomass and sugar measurements are entered in the system, a prediction trajectory is calculated and the deviation from the reference trajectory is estimated. If it is within preset boundaries, no action is carried out; however, if the deviation is too great, a corrective feed action is implemented in order to minimize the difference between the measured process and reference values. This MPC algorithm is schematically illustrated in Figure 12.

We have previously reported several cases where this MPC approach has been successfully employed [82,99].

For example, this MPC solution was used in a recombinant E. coli BL21 process to successfully follow a predefined cell biomass reference trajectory in a glucose-limited fed-batch process. The proposed approach was implemented and tested in a lab-scale bioreactor system EDF-5.4/BIO-4 (Bioreactors.net, Riga, Latvia). An additional test run using the proposed approach was performed on a system consisting of a single-use bioreactor (SUB) CellVessel 5.7 (CerCell, Herlev, Denmark) connected to a BIO-4 controller. Fermentations were started as batch cultures and continued as fed-batch when the MPC controller activated feeding to follow the predefined reference growth trajectory.

The time profiles of the cell biomass growth, substrate (glucose) concentration and feed rate are presented in Figure 13. A cell biomass concentration of 93.6 g/L was reached in the most productive run (Exp-3); however, significant glucose accumulation was noted towards the end of the process due to culture overfeeding, and significant corrective actions were necessary. In a more stable and safer yet still very productive run (Exp-2), a cell biomass concentration of 79.8 g/L, in contrast to 65.8 g/L, produced in the initial experiment (Exp-1) was reached after 24 h, employing the proposed system. The estimated and experimentally measured cell biomass mean deviations from the preset reference value at the end of the processes were 4.6% and 3.8%, respectively. The developed and implemented MPC system was used to track the selected biomass reference trajectories. The MPC system demonstrated a good control performance and reduced process variability as compared to the system with an open-loop feeding profile control. Importantly, it was also proven that the results produced in the best run (Exp-2) were reproducible in a different system—in this case, a single-use bioreactor vessel [99].

Another successful example of this system’s use was reported in a yeast Kluyveromyces marxianus fed-batch cultivation process [82]. Laboratory-scale cultivations were performed in a 5.4 L working volume bioreactor EDF-5.4_1 (Bioreactors.net, Latvia). During cultivations, offline glucose and biomass measurements were carried out every 30–120 min, and the obtained results were uploaded into SCADA, which passed the updated information to the MPC software. The reference trajectories X_ref, S_ref, V_ref and F_ref were calculated using the model described by Grigs et al. [99].

The MPC algorithm was successfully applied for substrate feed rate control during cultivation. Mathematical model parameters were fine tuned during the experimental work to successfully estimate the yeast biomass growth and substrate consumption kinetics, which in turn allowed for the successful construction of desirable reference growth trajectories to maintain a constant specific growth rate. Along with a novel optimized synthetic cultivation medium, the employed MPC feed rate control system facilitated the production of 70 g/L yeast dry biomass concentration and a 2-Phenylethanol biosynthesis rate of 0.372 g/L/h (74% conversion from 2-phenylalanine) (Figure 14) [82].

Overall, the presented MPC system is flexible enough to potentially be employed for a wide range of microorganisms, while at the same time providing good control accuracy and being relatively easy to use. It has the potential to produce comparable results to other, much more sophisticated MPC systems with lower resource requirements, while still being user friendly and widely applicable.

5. Discussion

With the rise in popularity and accessibility of computers, advanced process engineering tools for biotechnology have also emerged, including modeling, process control and optimization. However, applying these tools to cultivation processes remains challenging due to the limited availability of experimental data for model building, as well as uncertainties associated with bioprocess dynamics. In addition, the lack of reliable and cost-effective online sensors to monitor certain key process variables poses a further challenge [100]. The industry is increasingly adopting the Quality-by-Design (QbD) approach, which involves designing quality into the product. To achieve this, advanced bioprocess control and insight are essential, which can only be attained by utilizing advanced process engineering tools, such as comprehensive data analysis and process modeling [101].

To reduce implementation costs, many industrial fed-batch cultivation processes still employ open-loop feeding strategies. With this approach, there is no need for online measurements or prior user experience. However, it may not be the most optimal control strategy and may result in reduced process efficiency and product quality [100,102]. However, this approach has limitations in reacting to unexpected system deviations and accounting for nonlinear behavior, potentially decreasing overall batch-to-batch reproducibility and resulting in poor performance. Furthermore, it also provides limited process insight. Despite these limitations, the open-loop approach may still be appropriate for certain bioprocesses and product requirements and should not be entirely dismissed.

Closed-loop strategies are an alternative to open-loop feeding strategies, which allow for the calculation of the substrate feed rate based on measured online data or their estimates (soft sensors), and can react to system disturbances [100]. While the use of soft sensors may seem appealing, they are often difficult to implement and require extensive data from previous processes. Most closed-loop solutions use a PID controller, which requires extensive parameter tuning and may not account for the dynamic and nonlinear behavior of living systems. More advanced controllers, such as ANN and fuzzy logic controllers, can handle the dynamic and nonlinear behavior of living cells, but they require historical data to create empirical process models, which are difficult to interpret and provide little insight into the nature of the system. Fuzzy logic controllers also require previous operator experience to evaluate the state of the process. Despite their drawbacks, closed-loop strategies are superior to open-loop strategies as they can react to disturbances and provide better batch-to-batch reproducibility.

Model predictive control (MPC) is a promising approach for substrate feed rate control in fed-batch cultivations, provided a robust process model is available. This method can effectively account for disturbances and the nonlinear dynamics of living organisms, while also offering important insights into the process. MPC also allows for the use of at-line measurements to track deviations from the reference growth trajectory and make automatic corrections. Based on our experience, MPC is particularly suitable for controlling the feed rate in fast-growing microorganism fermentations such as yeasts and bacteria.

MPC has some limitations that should be considered. One of the main requirements for the successful implementation of MPC is a robust process model, which can be a challenge in cases where the system has not been well characterized or there is limited information available. Furthermore, the accuracy of the model must be validated through experimental data, which may require several runs. The development of bioprocess models also necessitates a specialized skill set, including a solid understanding of bioengineering and basic programming. There are also reports of the use of ANN [88,103,104] and fuzzy logic [105] models in MPC systems. The second limitation of MPC is that it involves computationally intensive calculations, which can be time consuming. In addition, it has high hardware and software requirements, similar to ANNs. However, it is possible to overcome these limitations, as demonstrated in the previous section, by using a standard personal computer and replacing expensive online sensors with standard at-line measurements. This makes MPC more appealing to a wider audience and promotes its use in fed-batch fermentations.

There are several reports where the performance of MPC solutions have been compared in fed-batch fermentations. For example, Jabarivelisdeh et al. implemented and applied a closed-loop bilevel problem based on MPC in order to handle uncertainties in modeling parameters in an E. coli fermentation for ethanol production. To evaluate the results, the authors compared the maximum ethanol productivity with an open-loop controller. The MPC solution showed a better performance and allowed the system to achieve both higher cell biomass concentrations and ethanol yields [106]. Joynes and Zhang designed a feedback control loop by using MPC and a conventional proportional and integral (PI) controller to control the glucose concentration at 15 min sampling intervals. The authors found that incorporating a linear ARX model in both controllers improved the control performance in both cases. The adaptive MPC had the lowest integral absolute error (IAE) on average, outperforming PI control, though the results varied run to run [107]. Eaton and Rawlings compared an MPC system with a conventional feedback control and found that MPC provided a superior performance in the case for nonminimum phase systems with input constraints when future set points were known [108]. Finally, Karra et al. developed a novel adaptive MPC formulation for multivariable time-varying systems. The proposed adaptive MPC (AMPC) scheme was able to achieve tight control of time-varying semi-batch processes and was capable of managing large transitions in the operating point of a continuously operated complex multivariable process. The authors also demonstrated that the AMPC scheme performed considerably better than the conventional nonadaptive MPC scheme for the servo control problems [109].

The main takeaway is that there are currently no universal substrate feed rate control methods that are ideal for every possible application. Each method has its strengths and weaknesses and varying applicability in bioprocesses. A comparison of both the benefits and drawbacks of the mentioned substrate feed rate control methods can be seen in

Table 1. A comparison of substrate feed rate control methods in fed-batch bioprocesses.

Feed Rate Control Method	Benefits	Drawbacks
Open loop	Easy implementation	Inability to react to disturbances Reduced batch-to-batch repeatability
PID	Ability to react to disturbances Simple implementation	Requires accurate parameter tuning Unable to account for nonlinear system dynamics
ANN	Able to account for nonlinear system dynamics Relatively easy and fast to implement	Historical process data required for training Provides little insight into the process
Fuzzy logic	Provides some insight into the process More intuitive to the user	Requires human interpretation and a high degree of understanding of the bioprocess
MPC	Provides high process repeatability	Reliant on process model accuracy Requires historical process data for model parameter fine tuning

.

An excellent review of the future perspectives of bioprocess control was presented by Rathore et al. [110]. Despite the significant progress in this field, it is evident that the future holds immense potential for further advancements. More advanced closed-loop substrate feed rate control methods, such as MPC, ANNs and fuzzy logic controllers, provide promising opportunities for the successful automation of fed-batch fermentations, addressing some of the challenges faced by commercial-scale production. Enhanced knowledge in process modeling will lead to a better understanding of the bioprocess, even facilitating the creation of process digital twins—a virtual model capable of accurately simulating the fermentation process. The improvements in process monitoring with more robust at- and in-line sensors will drive an increase in the overall productivity of the fermentation process. Lastly, the use of sophisticated and improved bioprocess data analysis techniques will enable the analysis of the ever-increasing amount of data generated, which is becoming increasingly complex and voluminous.

6. Conclusions

Accurately controlling the substrate feed rate in fed-batch bioprocesses is critical to achieving high overall process productivity, and thus requires careful optimization. Several substrate feed rate control strategies are available, each with their own strengths and weaknesses. However, there is no universally perfect control method that can be applied to all bioprocesses. As such, selecting the control method that is best suited for the specific application is essential.

Model predictive control has emerged as a promising substrate feed rate control method, despite being described as computationally expensive, process specific and difficult to implement. However, as demonstrated in this article, our past experience has shown that implementing a simple, robust and accurate MPC system may not always be challenging. We showcased that a standard hardware personal computer can be used to implement an MPC system that provides accurate microbial biomass control along a predefined growth trajectory in bacteria and yeast fed-batch fermentations. This example indicates that the main drawbacks of MPC can be surmounted, and hopefully, it will encourage the wider adoption of model predictive control in various bioprocess applications.