Non-Destructive Testing of the Internal Quality of Korla Fragrant Pears Based on Dielectric Properties
Abstract
:1. Introduction
2. Materials and Methods
2.1. Test Materials
Sampling of Korla Fragrant Pears
2.2. Measurement Methods
2.2.1. Measurement of Dielectric Parameters
2.2.2. Measurement of Hardness
2.2.3. Measurement of SSC
2.2.4. Data Assignment
2.3. Modelling Methods
2.3.1. PLSR Model
2.3.2. SVR Model
2.3.3. PSO-LSSVR Model
2.4. Model Evaluations
3. Results and Analysis
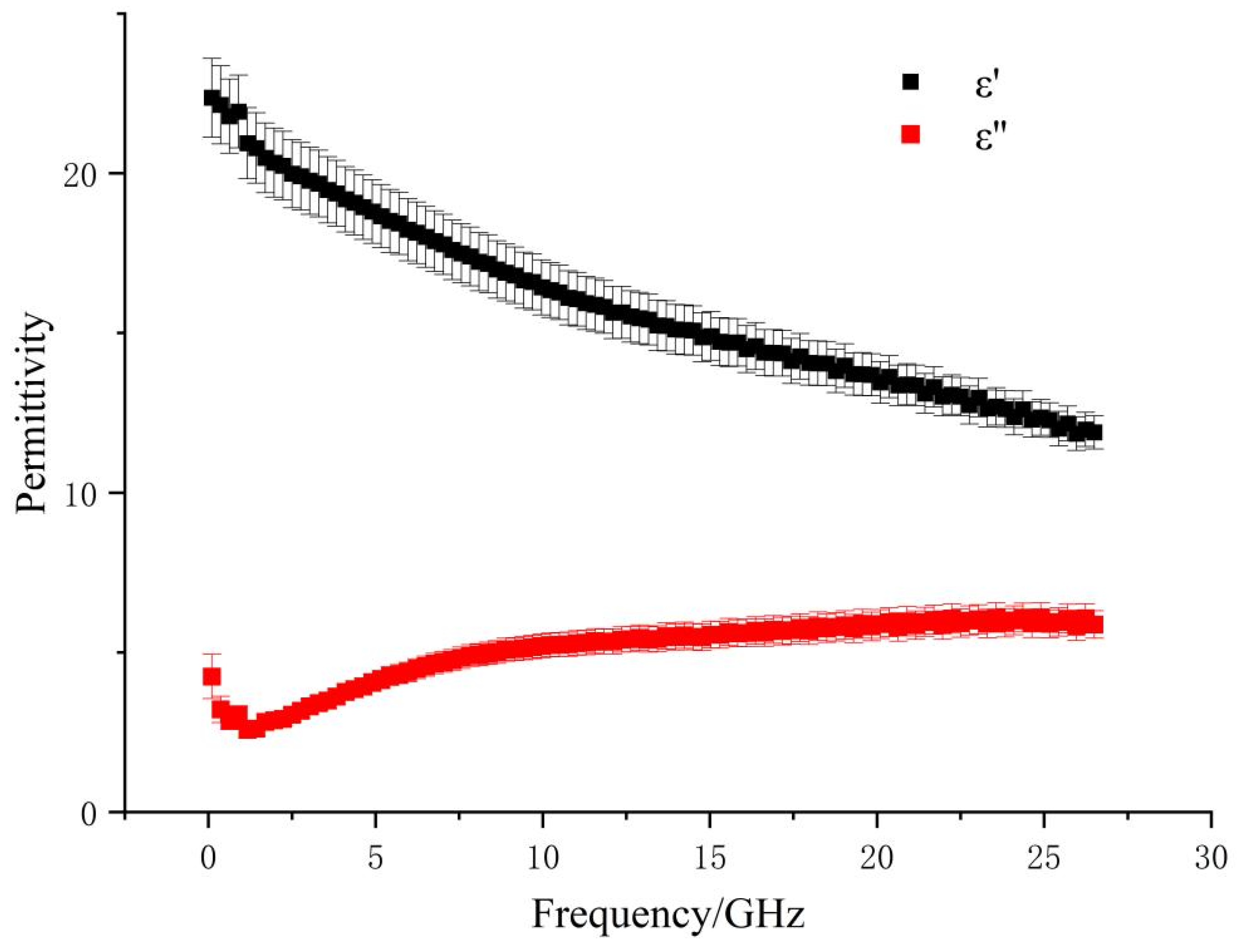
3.1. Linear Correlation between Dielectric Parameters and the Internal Quality of Fragrant Pears
3.2. Sample Division
3.3. Prediction of Hardness
3.4. Prediction of SSC
3.5. Model Verification
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, J.; Guo, K.Q. Dynamic viscoelastic behaviour and microstructural changes of Korla pear (Pyrus bretschneideri rehd) under varying turgor levels. Biosyst. Eng. 2010, 106, 485–492. [Google Scholar] [CrossRef]
- Wang, B.; Sun, X.; Dong, F.; Zhang, F.; Niu, J. Cloning and expression analysis of an MYB gene associated with calyx persistence in Korla fragrant pear. Plant Cell Rep. 2014, 33, 1333–1341. [Google Scholar] [CrossRef] [PubMed]
- Jia, X.H.; Wang, W.H.; Du, Y.M.; Tong, W.; Wang, Z.-H.; Gul, H. Optimal storage temperature and 1-MCP treatment combinations for different marketing times of Korla Xiang pears. J. Integr. Agric. 2018, 17, 693–703. [Google Scholar] [CrossRef]
- Nicolaï, B.; Verlinden, B.; Desmet, M.; Saevels, S.; Saeys, W.; Theron, K.; Cubeddu, R.; Pifferi, A.; Torricelli, A. Time-resolved and continuous wave NIR reflectance spectroscopy to predict soluble solids content and firmness of pear. Postharvest Biol. Technol. 2008, 47, 68–74. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, T.; Su, R.; Hu, C.; Chen, F.; Cheng, J. Quantitative evaluation of color, firmness, and soluble solid content of Korla fragrant pears via IRIV and LS-SVM. Agriculture 2021, 11, 731. [Google Scholar] [CrossRef]
- Liu, Y.; Niu, X.; Tang, Y.; Li, S.; Lan, H.; Niu, H. Internal quality prediction method of damaged Korla fragrant pears during storage. Horticulturae 2023, 9, 666. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, Y.; Tang, Y.; Lan, H.; Niu, H.; Zhang, H. Non-destructive detection of the fruit firmness of Korla fragrant pear based on electrical properties. Int. J. Agric. Biol. Eng. 2022, 15, 216–221. [Google Scholar] [CrossRef]
- Guo, W.; Nelson, S.; Trabelsi, S.; Kays, S. 10–1800-MHz dielectric properties of fresh apples during storage. J. Food Eng. 2007, 83, 562–569. [Google Scholar] [CrossRef]
- Nelson, S.; Guo, W.; Trabelsi, S.; Kays, S. Dielectric properties of watermelons for quality sensing. Meas. Sci. Technol. 2007, 18, 1887–1892. [Google Scholar] [CrossRef]
- Lan, H.; Wang, Z.; Niu, H.; Zhang, H.; Zhang, Y.; Tang, Y.; Liu, Y. A nondestructive testing method for soluble solid content in Korla fragrant pears based on electrical properties and artificial neural network. Food Sci. Nutr. 2020, 8, 5172–5181. [Google Scholar] [CrossRef]
- Shang, L.; Gu, J.; Guo, W. Non-destructively detecting sugar content of nectarines based on dielectric properties and ANN. Trans. Chin. Soc. Agric. Eng. 2013, 29, 257–264. [Google Scholar]
- Guo, W.; Shang, L.; Zhu, X.; Nelson, S. Nondestructive detection of soluble solids content of apples from dielectric spectra with ANN and chemometric methods. Food Bioprocess Technol. 2015, 8, 1126–1138. [Google Scholar] [CrossRef]
- Guo, W.; Fang, L.; Liu, D.; Wang, Z. Determination of soluble solids content and firmness of pears during ripening by using dielectric spectroscopy. Comput. Electron. Agric. 2015, 117, 226–233. [Google Scholar] [CrossRef]
- Guo, W.; Zhu, X.; Nelson, O.; Yue, R.; Liu, H.; Liu, Y. Maturity effects on dielectric properties of apples from 10 to 4500 MHz. LWT-Food Sci. Technol. 2011, 44, 224–230. [Google Scholar] [CrossRef]
- Li, Y.; Li, C. The agricultural product wholesale price index forecasting model based on LSSVR optimized by PSO. J. Cover. Inf. Technol. 2012, 7, 531–539. [Google Scholar]
- Nelson, S. Agricultural applications of dielectric measurements. IEEE Trans. Dielectr. Electr. Insul. 2006, 4, 688–702. [Google Scholar] [CrossRef]
- Sosa, M.; Valerio, J.; Lopez, M.; Garcia, H. Dielectric properties of food: Reported data in the 21st century and their potential applications. Food Sci. Technol. 2010, 43, 1169–1179. [Google Scholar]
- Carrascal, L.; Galvcln, I.; Gordo, O. Partial least squares regression as an alternative to current regression methods used in ecology. Oikos A J. Ecol. 2009, 118, 681–690. [Google Scholar] [CrossRef]
- Wang, Z.; Fu, Z.; Weng, W.; Yang, D.; Wang, J. An efficient method for the rapid detection of industrial paraffin contamination levels in rice based on hyperspectral imaging. LWT 2022, 171, 114125. [Google Scholar] [CrossRef]
- Hu, S.; Meng, Y.; Zhang, Y. Prediction method for sugarcane syrup brix based on improved support vector regression. Electronics 2023, 12, 1535. [Google Scholar] [CrossRef]
- Cao, W.; Li, G.; Song, H.; Quan, B.; Liu, Z. Research on grain moisture model based on improved SSA-SVR algorithm. Appl. Sci. 2024, 14, 3171. [Google Scholar] [CrossRef]
- Liu, W.; Huo, H.; Zhou, P.; Li, M.; Wang, Y. Research on hyperspectral modeling of total iron content in soil applying LSSVR and CNN based on shannon entropy wavelet packet transform. Remote Sens. 2023, 15, 4681. [Google Scholar] [CrossRef]
- Wang, L.; Rong, X.; Chen, Z.; Mu, L.; Jiang, S. A real estate early warning system based on an improved PSO-LSSVR model-a beijing case study. Buildings 2022, 12, 706. [Google Scholar] [CrossRef]
- Yeh, W.; Zhu, W. Forecasting by combining chaotic PSO and automated LSSVR. Technologies 2023, 11, 50. [Google Scholar] [CrossRef]
- Bishara, A.J.; Hittner, J.B. Testing the significance of a correlation with nonnormal data: Comparison of Pearson, Spearman, transformation, and resampling approaches. Psychol. Methods 2012, 17, 399–417. [Google Scholar] [CrossRef]
- Fu, T.; Tang, X.; Cai, Z. Correlation research of phase angle variation and coating performance by means of Pearson’s correlation coefficient. Prog. Org. Coat. 2020, 139, 105459. [Google Scholar] [CrossRef]
- Cao, M.; Zeng, S.; Wang, J.; Guo, W. Assessment of SSC and soluble sugar content of three pear cultivars during storage using dielectric method. Postharvest Biol. Technol. 2024, 6, 112906. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, X.; Yu, X. Progress in the application of non-destructive testing technology in fruit and vegetable quality detection. J. Zhejiang Univ.-SCIENCE B. 2020, 46, 27–37. [Google Scholar] [CrossRef]
- Cao, M.; Zeng, S.; Wang, J.; Guo, W. Dielectric properties of peaches with and without skin during storage and their relationship to internal quality. Postharvest Biol. Technol. 2023, 204, 112433. [Google Scholar] [CrossRef]
- Lin, F.; Chen, D.; Liu, C.; He, J. Non-destructive detection of golden passion fruit quality based on dielectric characteristics. Appl. Sci. 2024, 14, 2200. [Google Scholar] [CrossRef]
- Trabelsi, S.; Mckeown, M.; Nelson, S. Dielectric properties-based method for rapid and nondestructive moisture sensing in almonds. J. Microw. Power Ee. 2016, 50, 94–105. [Google Scholar] [CrossRef]
- Cruz, S.; Guerra, R.; Brazio, A.; Cavaco, A.; Antunes, D.; Passos, D. Nondestructive simultaneous prediction of internal browning disorder and quality attributes in ‘Rocha’ pear (Pyrus communis L.) using VIS-NIR spectroscopy. Postharvest Biol. Technol. 2021, 179, 111562. [Google Scholar] [CrossRef]
- Cavaco, A.; Pires, R.; Antunes, M.; Panagopoulos, T.; Brázio, A.; Afonso, A.; Silva, L.; Lucas, M.; Cadeiras, B.; Cruz, S.; et al. Validation of short wave near infrared calibration models for the quality and ripening of ‘Newhall’ orange on tree across years and orchards. Postharvest Biol. Technol. 2018, 141, 86–97. [Google Scholar] [CrossRef]
- Fang, L.; Guo, W. Nondestructive determination of sugar content and hardness of Korla fragrant pear based on dielectric spectrum. Mod. Food Sci. Technol. 2016, 32, 295–301. [Google Scholar]


| Quality Indicators | Sample Set | Minimum | Maximum | Mean ± Standard Deviation |
|---|---|---|---|---|
| Hardness | Total sample | 4.06 | 7 | 5.46 ± 0.50 |
| training set | 4.06 | 7 | 5.44 ± 0.49 | |
| test set | 4.58 | 6.44 | 5.50 ± 0.52 | |
| SSC | Total sample | 10.97 | 14.80 | 12.65 ± 0.65 |
| training set | 10.97 | 14.80 | 12.62 ± 0.65 | |
| test set | 11.70 | 14.33 | 12.72 ± 0.65 |
| Modeling Methods | Modeling Variables | Training Set | Test Set | ||
|---|---|---|---|---|---|
| R | MSE | R | MSE | ||
| PLSR | ε′ | 0.82 | 0.054 | 0.77 | 0.073 |
| ε″ | 0.81 | 0.055 | 0.64 | 0.148 | |
| SVR | ε′ | 0.74 | 0.112 | 0.39 | 0.233 |
| ε″ | 0.96 | 0.019 | 0.26 | 0.328 | |
| PSO-LSSVR | ε′ | 0.79 | 0.098 | 0.41 | 0.220 |
| ε″ | 0.89 | 0.046 | 0.46 | 0.300 | |
| Modeling Methods | Modeling Variables | Training Set | Test Set | ||
|---|---|---|---|---|---|
| R | MSE | R | MSE | ||
| PLSR | ε′ | 0.91 | 0.055 | 0.84 | 0.090 |
| ε″ | 0.92 | 0.063 | 0.91 | 0.087 | |
| SVR | ε′ | 0.86 | 0.118 | 0.27 | 0.433 |
| ε″ | 0.97 | 0.04 | 0.15 | 0.378 | |
| PSO-LSSVR | ε′ | 0.95 | 0.055 | 0.45 | 0.347 |
| ε″ | 0.83 | 0.186 | 0.40 | 0.300 | |
| Modeling Methods | Modeling Variables | Quality Indicators | Model Accuracy | |
|---|---|---|---|---|
| R | MSE | |||
| PLSR | ε′ | Hardness | 0.76 | 0.129 |
| PLSR | ε″ | SSC | 0.85 | 0.095 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Y.; Zhang, H.; Liang, Q.; Xia, Y.; Che, J.; Liu, Y. Non-Destructive Testing of the Internal Quality of Korla Fragrant Pears Based on Dielectric Properties. Horticulturae 2024, 10, 572. https://doi.org/10.3390/horticulturae10060572
Tang Y, Zhang H, Liang Q, Xia Y, Che J, Liu Y. Non-Destructive Testing of the Internal Quality of Korla Fragrant Pears Based on Dielectric Properties. Horticulturae. 2024; 10(6):572. https://doi.org/10.3390/horticulturae10060572
Chicago/Turabian StyleTang, Yurong, Hong Zhang, Qing Liang, Yifan Xia, Jikai Che, and Yang Liu. 2024. "Non-Destructive Testing of the Internal Quality of Korla Fragrant Pears Based on Dielectric Properties" Horticulturae 10, no. 6: 572. https://doi.org/10.3390/horticulturae10060572
APA StyleTang, Y., Zhang, H., Liang, Q., Xia, Y., Che, J., & Liu, Y. (2024). Non-Destructive Testing of the Internal Quality of Korla Fragrant Pears Based on Dielectric Properties. Horticulturae, 10(6), 572. https://doi.org/10.3390/horticulturae10060572







