A Machine Learning Model for Photorespiration Response to Multi-Factors
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Access
2.2. Data Preprocessing
2.3. Approach to Building the Model
2.3.1. Polynomial Regression
2.3.2. K-Nearest Neighbors
2.3.3. Gaussian Process Regression
2.3.4. Support Vector Regression
2.3.5. Adaptive Boosting
2.3.6. Gradient Boosting Decision Tree
2.3.7. Extreme Gradient Boosting
2.3.8. Neural Network
2.4. Optimization Technologies
2.5. Performance Evaluation
3. Results and Discussion
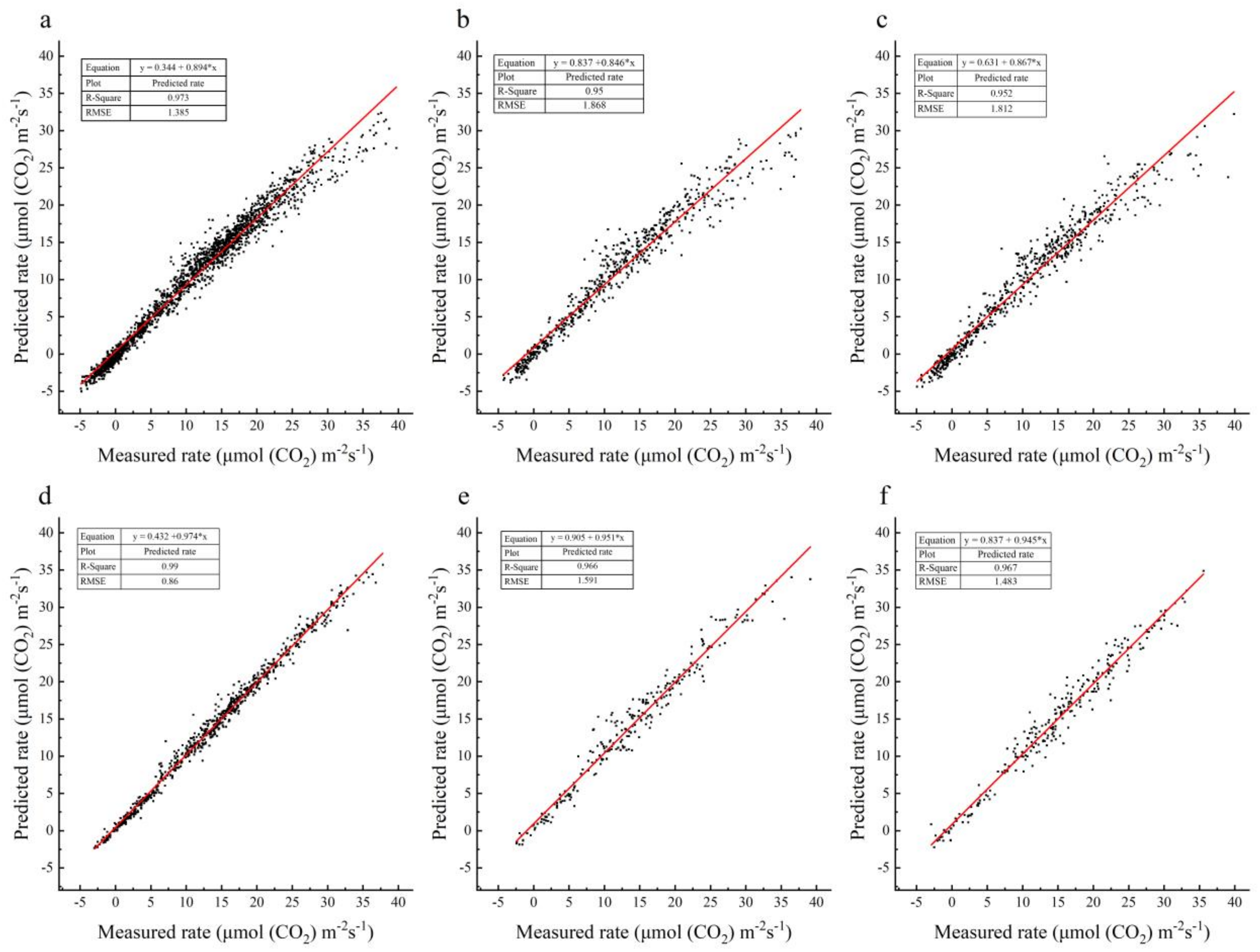
3.1. Performance of the Models
3.2. Potential for Model Performance Enhancing
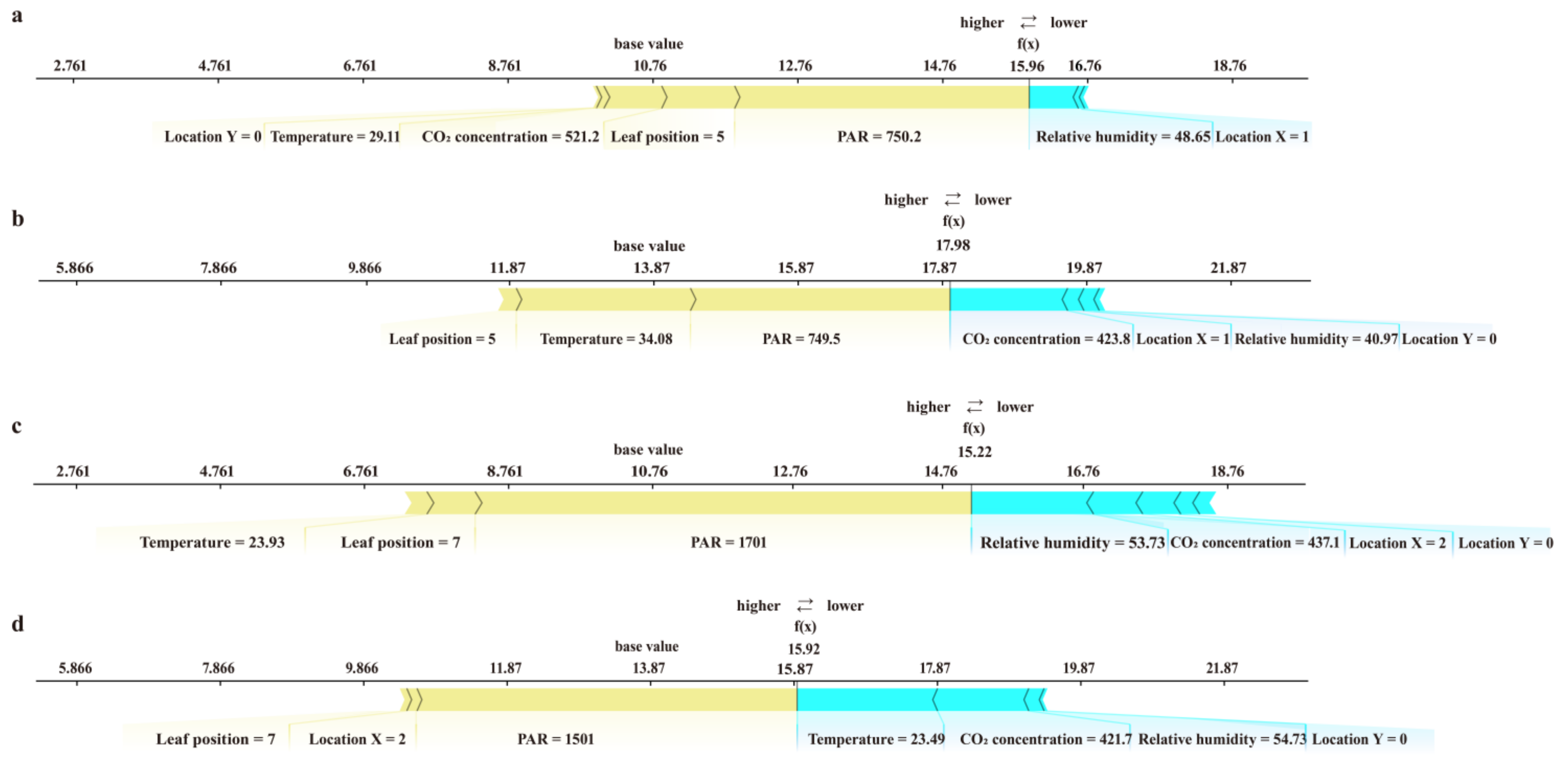
3.3. Interpretability of the Model and the Main Factors Affecting the Photorespiration
3.4. Soft Sensors and Ability to Promote
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liang, Y.; Kang, C.; Kaiser, E.; Kuang, Y.; Yang, Q.; Li, T. Red/Blue Light Ratios Induce Morphology and Physiology Alterations Differently in Cucumber and Tomato. Sci. Hortic. 2021, 281, 109995. [Google Scholar] [CrossRef]
- Li, Y.; Liu, C.; Shi, Q.; Yang, F.; Wei, M. Mixed Red and Blue Light Promotes Ripening and Improves Quality of Tomato Fruit by Influencing Melatonin Content. Environ. Exp. Bot. 2021, 185, 104407. [Google Scholar] [CrossRef]
- Takahashi, S.; Murata, N. Glycerate-3-Phosphate, Produced by CO2 Fixation in the Calvin Cycle, Is Critical for the Synthesis of the D1 Protein of Photosystem II. Biochim. Biophys. Acta Bioenergy 2006, 1757, 198–205. [Google Scholar] [CrossRef] [Green Version]
- Kimura, K.; Yasutake, D.; Koikawa, K.; Kitano, M. Spatiotemporal Variability of Leaf Photosynthesis and Its Linkage with Microclimates across an Environment-Controlled Greenhouse. Biosyst. Eng. 2020, 195, 97–115. [Google Scholar] [CrossRef]
- Fara, S.J.; Teixeira Delazari, F.; Silva Gomes, R.; Araújo, W.L.; da Silva, D.J.H. Stomata Opening and Productiveness Response of Fresh Market Tomato under Different Irrigation Intervals. Sci. Hortic. 2019, 255, 86–95. [Google Scholar] [CrossRef]
- Flügel, F.; Timm, S.; Arrivault, S.; Florian, A.; Stitt, M.; Fernie, A.R.; Bauwe, H. The Photorespiratory Metabolite 2-Phosphoglycolate Regulates Photosynthesis and Starch Accumulation in Arabidopsis. Plant Cell 2017, 29, 2537–2551. [Google Scholar] [CrossRef] [Green Version]
- De FC Carvalho, J.; Madgwick, P.J.; Powers, S.J.; Keys, A.J.; Lea, P.J.; Parry, M.A.J. An Engineered Pathway for Glyoxylate Metabolism in Tobacco Plants Aimed to Avoid the Release of Ammonia in Photorespiration. BMC Biotechnol. 2011, 11, 111. [Google Scholar] [CrossRef] [Green Version]
- López-Calcagno, P.E.; Fisk, S.; Brown, K.L.; Bull, S.E.; South, P.F.; Raines, C.A. Overexpressing the H-Protein of the Glycine Cleavage System Increases Biomass Yield in Glasshouse and Field-Grown Transgenic Tobacco Plants. Plant Biotechnol. J. 2019, 17, 141–151. [Google Scholar] [CrossRef]
- Rae, B.D.; Long, B.M.; Förster, B.; Nguyen, N.D.; Velanis, C.N.; Atkinson, N.; Hee, W.Y.; Mukherjee, B.; Price, G.D.; McCormick, A.J. Progress and Challenges of Engineering a Biophysical CO2-Concentrating Mechanism into Higher Plants. J. Exp. Bot. 2017, 68, 3717–3737. [Google Scholar] [CrossRef]
- South, P.F.; Cavanagh, A.P.; Liu, H.W.; Ort, D.R. Synthetic Glycolate Metabolism Pathways Stimulate Crop Growth and Productivity in the Field. Science 2019, 363, eaat9077. [Google Scholar] [CrossRef] [Green Version]
- Zhu, X.G.; Portis, A.R.; Long, S.P. Would Transformation of C3 Crop Plants with Foreign Rubisco Increase Productivity? A Computational Analysis Extrapolating from Kinetic Properties to Canopy Photosynthesis. Plant Cell Environ. 2004, 27, 155–165. [Google Scholar] [CrossRef]
- Galmés, J.; Hermida-Carrera, C.; Laanisto, L.; Niinemets, Ü. A Compendium of Temperature Responses of Rubisco Kinetic Traits: Variability among and within Photosynthetic Groups and Impacts on Photosynthesis Modeling. J. Exp. Bot. 2016, 67, 5067–5091. [Google Scholar] [CrossRef] [Green Version]
- Hermida-Carrera, C.; Kapralov, M.V.; Galmés, J. Rubisco Catalytic Properties and Temperature Response in Crops. Plant Physiol. 2016, 171, 2549–2561. [Google Scholar] [CrossRef] [Green Version]
- Busch, F.A. Photorespiration in the Context of Rubisco Biochemistry, CO2 Diffusion and Metabolism. Plant J. 2020, 101, 919–939. [Google Scholar] [CrossRef] [Green Version]
- Huang, W.; Hu, H.; Zhang, S.-B. Photorespiration Plays an Important Role in the Regulation of Photosynthetic Electron Flow under Fluctuating Light in Tobacco Plants Grown under Full Sunlight. Front. Plant Sci. 2015, 6, 621. [Google Scholar] [CrossRef] [Green Version]
- Kangasjarvi, S.; Neukermans, J.; Li, S.; Aro, E.M.; Noctor, G. Photosynthesis, Photorespiration, and Light Signalling in Defence Responses. J. Exp. Bot. 2012, 63, 1619–1636. [Google Scholar] [CrossRef] [Green Version]
- Lin, Z.; Peng, C.; Sun, Z.; Lin, G. Effect of Light Intensity on Partitioning of Photosynthetic Electron Transport to Photorespiration in Four Subtropical Forest Plants. Sci. China Ser. C Life Sci. 2000, 43, 347–354. [Google Scholar] [CrossRef]
- Ye, Z.P. A New Model for Relationship between Irradiance and the Rate of Photosynthesis in Oryza Sativa. Photosynthetica 2007, 45, 637–640. [Google Scholar] [CrossRef]
- Ye, Z.P.; Duan, S.H.; Chen, X.M.; Duan, H.L.; Gao, C.P.; Kang, H.J.; An, T.; Zhou, S.X. Quantifying Light Response of Photosynthesis: Addressing the Long-Standing Limitations of Non-Rectangular Hyperbolic Model. Photosynthetica 2021, 59, 185–191. [Google Scholar] [CrossRef]
- Lanoue, J.; Leonardos, E.D.; Grodzinski, B. Effects of Light Quality and Intensity on Diurnal Patterns and Rates of Photo-Assimilate Translocation and Transpiration in Tomato Leaves. Front. Plant Sci. 2018, 9, 756. [Google Scholar] [CrossRef] [Green Version]
- Farquhar, G.D.; von Caemmerer, S.; Berry, J.A. A Biochemical Model of Photosynthetic CO2 Assimilation in Leaves of C 3 Species. Planta 1980, 149, 78–90. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gu, L.; Pallardy, S.G.; Tu, K.; Law, B.E.; Wullschleger, S.D. Reliable Estimation of Biochemical Parameters from C3 Leaf Photosynthesis-Intercellular Carbon Dioxide Response Curves. Plant Cell Environ. 2010, 33, 1852–1874. [Google Scholar] [CrossRef]
- Miranda-Apodaca, J.; Marcos-Barbero, E.L.; Morcuende, R.; Arellano, J.B. Surfing the Hyperbola Equations of the Steady-State Farquhar–von Caemmerer–Berry C3 Leaf Photosynthesis Model: What Can a Theoretical Analysis of Their Oblique Asymptotes and Transition Points Tell Us? Bull. Math. Biol. 2020, 82, 3. [Google Scholar] [CrossRef] [Green Version]
- Moualeu-Ngangue, D.P.; Chen, T.-W.; Stützel, H. A New Method to Estimate Photosynthetic Parameters through Net Assimilation Rate–Intercellular Space CO2 Concentration (A–C i) Curve and Chlorophyll Fluorescence Measurements. New Phytol. 2017, 213, 1543–1554. [Google Scholar] [CrossRef]
- Coursolle, C.; Otis Prud Homme, G.; Lamothe, M.; Isabel, N. Measuring Rapid A–Ci Curves in Boreal Conifers: Black Spruce and Balsam Fir. Front. Plant Sci. 2019, 10, 1276. [Google Scholar] [CrossRef] [Green Version]
- Han, T.; Zhu, G.; Ma, J.; Wang, S.; Zhang, K.; Liu, X.; Ma, T.; Shang, S.; Huang, C. Sensitivity Analysis and Estimation Using a Hierarchical Bayesian Method for the Parameters of the FvCB Biochemical Photosynthetic Model. Photosynth. Res. 2020, 143, 45–66. [Google Scholar] [CrossRef]
- Wang, Q.; Chun, J.; Fleisher, D.; Reddy, V.; Timlin, D.; Resop, J. Parameter Estimation of the Farquhar—von Caemmerer—Berry Biochemical Model from Photosynthetic Carbon Dioxide Response Curves. Sustainability 2017, 9, 1288. [Google Scholar] [CrossRef] [Green Version]
- Xiong, D.; Liu, X.; Liu, L.; Douthe, C.; Li, Y.; Peng, S.; Huang, J. Rapid Responses of Mesophyll Conductance to Changes of CO2 Concentration, Temperature and Irradiance Are Affected by N Supplements in Rice. Plant Cell Environ. 2015, 38, 2541–2550. [Google Scholar] [CrossRef]
- Kaiser, E.; Morales, A.; Harbinson, J.; Kromdijk, J.; Heuvelink, E.; Marcelis, L.F.M. Dynamic Photosynthesis in Different Environmental Conditions. J. Exp. Bot. 2015, 66, 2415–2426. [Google Scholar] [CrossRef] [Green Version]
- Morales, A.; Kaiser, E.; Yin, X.; Harbinson, J.; Molenaar, J.; Driever, S.M.; Struik, P.C. Dynamic Modelling of Limitations on Improving Leaf CO2 Assimilation under Fluctuating Irradiance. Plant Cell Environ. 2018, 41, 589–604. [Google Scholar] [CrossRef] [Green Version]
- Li, P.-P.; Wang, J.-Z.; Chen, X.; Liu, W.-H. Studies on Photosynthesis Model of Mini-Cucumber Leaf in Greenhouse. In Crop Modeling and Decision Support; Springer: Berlin, Germany, 2009; pp. 24–29. ISBN1 978-3-642-01131-3. ISBN2 978-3-642-01132-0. [Google Scholar]
- Peri, P.L.; Arena, M.; Martínez Pastur, G.; Lencinas, M.V. Photosynthetic Response to Different Light Intensities, Water Status and Leaf Age of Two Berberis Species (Berberidaceae) of Patagonian Steppe, Argentina. J. Arid. Environ. 2011, 75, 1218–1222. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, S. Simulation of the Canopy Photosynthesis Model of Greenhouse Tomato. Procedia Eng. 2011, 16, 632–639. [Google Scholar] [CrossRef] [Green Version]
- Goltsev, V.; Zaharieva, I.; Chernev, P.; Kouzmanova, M.; Kalaji, H.M.; Yordanov, I.; Krasteva, V.; Alexandrov, V.; Stefanov, D.; Allakhverdiev, S.I.; et al. Drought-Induced Modifications of Photosynthetic Electron Transport in Intact Leaves: Analysis and Use of Neural Networks as a Tool for a Rapid Non-Invasive Estimation. Biochim. Biophys. Acta Bioenergy 2012, 1817, 1490–1498. [Google Scholar] [CrossRef] [Green Version]
- Heckmann, D.; Schlüter, U.; Weber, A.P.M. Machine Learning Techniques for Predicting Crop Photosynthetic Capacity from Leaf Reflectance Spectra. Mol. Plant 2017, 10, 878–890. [Google Scholar] [CrossRef] [Green Version]
- Jian, Y.; Xinying, L.; Man, Z.; Han, L. Photosynthetic Rate Prediction of Tomato Plant Population Based on PSO and GA. IFAC-PapersOnLine 2018, 51, 61–66. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Huang, Z.; Su, X.; Siu, A.; Song, Y.; Zhang, D.; Fang, Q. Machine Learning Models for Net Photosynthetic Rate Prediction Using Poplar Leaf Phenotype Data. PLoS ONE 2020, 15, e0228645. [Google Scholar] [CrossRef] [Green Version]
- Dusenge, M.E.; Duarte, A.G.; Way, D.A. Plant Carbon Metabolism and Climate Change: Elevated CO2 and Temperature Impacts on Photosynthesis, Photorespiration and Respiration. New Phytol. 2019, 221, 32–49. [Google Scholar] [CrossRef] [Green Version]
- Huang, S.; Jacoby, R.P.; Shingaki-Wells, R.N.; Li, L.; Millar, A.H. Differential Induction of Mitochondrial Machinery by Light Intensity Correlates with Changes in Respiratory Metabolism and Photorespiration in Rice Leaves. New Phytol. 2013, 198, 103–115. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Slot, M.; Garcia, M.N.; Winter, K. Temperature Response of CO2 Exchange in Three Tropical Tree Species. Funct. Plant Biol. 2016, 43, 468–478. [Google Scholar] [CrossRef]
- Walker, B.J.; Orr, D.J.; Carmo-Silva, E.; Parry, M.A.J.; Bernacchi, C.J.; Ort, D.R. Uncertainty in Measurements of the Photorespiratory CO2 Compensation Point and Its Impact on Models of Leaf Photosynthesis. Photosynth. Res. 2017, 132, 245–255. [Google Scholar] [CrossRef]
- Busch, F.A. Current Methods for Estimating the Rate of Photorespiration in Leaves. Plant Biol. 2013, 15, 648–655. [Google Scholar] [CrossRef]
- Shalaby, T.A.; Abd-Alkarim, E.; El-Aidy, F.; Hamed, E.-S.; Sharaf-Eldin, M.; Taha, N.; El-Ramady, H.; Bayoumi, Y.; dos Reis, A.R. Nano-Selenium, Silicon and H2O2 Boost Growth and Productivity of Cucumber under Combined Salinity and Heat Stress. Ecotoxicol. Environ. Saf. 2021, 212, 111962. [Google Scholar] [CrossRef]
- Tang, F.; Ishwaran, H. Random Forest Missing Data Algorithms. Stat. Anal. Data Min. 2017, 10, 363–377. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Elavarasan, D.; Vincent, D.R.; Sharma, V.; Zomaya, A.Y.; Srinivasan, K. Forecasting Yield by Integrating Agrarian Factors and Machine Learning Models: A Survey. Comput. Electron. Agric. 2018, 155, 257–282. [Google Scholar] [CrossRef]
- Goh, A.H.A.; Ali, Z.; Nor, N.M.; Baharum, A.; Ahmad, W.M.A.W. A Quadratic Regression Modelling on Paddy Production in the Area of Perlis. AIP Conf. Proc. 2017, 1870, 060015. [Google Scholar] [CrossRef]
- Ebrahimi, M.A.; Khoshtaghaza, M.H.; Minaei, S.; Jamshidi, B. Vision-Based Pest Detection Based on SVM Classification Method. Comput. Electron. Agric. 2017, 137, 52–58. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef] [Green Version]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the KDD ’16: 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining 2016, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef] [Green Version]
- Gilpin, L.H.; Bau, D.; Yuan, B.Z.; Bajwa, A.; Specter, M.; Kagal, L. Explaining Explanations: An Overview of Interpretability of Machine Learning. In Proceedings of the 2018 IEEE 5th International Conference on Data Science and Advanced Analytics (DSAA), Turin, Italy, 1–4 October 2018; pp. 80–89. [Google Scholar]
- Liakos, K.G.; Busato, P.; Moshou, D.; Pearson, S.; Bochtis, D. Machine Learning in Agriculture: A Review. Sensors 2018, 18, 2674. [Google Scholar] [CrossRef] [Green Version]
- Cardoso, J.; Gloria, A.; Sebastiao, P. Improve Irrigation Timing Decision for Agriculture Using Real Time Data and Machine Learning. In Proceedings of the 2020 International Conference on Data Analytics for Business and Industry: Way Towards a Sustainable Economy (ICDABI), Sakheer, Bahrain, 26–27 October 2020; pp. 1–5. [Google Scholar]
- Elavarasan, D.; Vincent, D.R. Reinforced XGBoost Machine Learning Model for Sustainable Intelligent Agrarian Applications. J. Intell. Fuzzy Syst. 2020, 39, 7605–7620. [Google Scholar] [CrossRef]
- Conţiu, Ş.; Groza, A. Improving Remote Sensing Crop Classification by Argumentation-Based Conflict Resolution in Ensemble Learning. Expert Syst. Appl. 2016, 64, 269–286. [Google Scholar] [CrossRef]
- Wu, T.; Zhang, W.; Jiao, X.; Guo, W.; Alhaj Hamoud, Y. Evaluation of Stacking and Blending Ensemble Learning Methods for Estimating Daily Reference Evapotranspiration. Comput. Electron. Agric. 2021, 184, 106039. [Google Scholar] [CrossRef]
- Bi, Y.; Xiang, D.; Ge, Z.; Li, F.; Jia, C.; Song, J. An Interpretable Prediction Model for Identifying N7-Methylguanosine Sites Based on XGBoost and SHAP. Mol. Ther. Nucleic Acids 2020, 22, 362–372. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the NIPS’17: 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Long Beach, CA, USA, 2017; Volume 2017, pp. 4768–4777. [Google Scholar]
- Jung, D.H.; Kim, H.S.; Jhin, C.; Kim, H.J.; Park, S.H. Time-Serial Analysis of Deep Neural Network Models for Prediction of Climatic Conditions inside a Greenhouse. Comput. Electron. Agric. 2020, 173, 105402. [Google Scholar] [CrossRef]
- Liu, T.; Yuan, Q.Y.; Wang, Y.G. Prediction Model of Photosynthetic Rate Based on Sopso-Lssvm for Regulation of Greenhouse Light Environment. Eng. Lett. 2021, 29, 297–301. [Google Scholar]






| Method | Model | Hyper-Parameters 1 | Value | Dataset | EV | MAPE | RMSE | R2 | Time-Consuming |
|---|---|---|---|---|---|---|---|---|---|
| Polynomial regression | Air based | degree | 2 | Validation set | 0.905 | 1.093 | 2.974 | 0.905 | 25 ms |
| interaction_only | FALSE | ||||||||
| include_bias | TRUE | Test set | 0.899 | 1.010 | 2.947 | 0.899 | |||
| 2% O2 based | degree | 3 | Validation set | 0.937 | 0.443 | 2.236 | 0.937 | ||
| interaction_only | FALSE | ||||||||
| include_bias | TRUE | Test set | 0.938 | 0.363 | 2.125 | 0.937 | |||
| k-nearest neighbors (KNN) | Air based | n_neighbors | 2 | Validation set | 0.919 | 0.714 | 2.815 | 0.915 | 356 ms |
| weights | ‘distance’ | ||||||||
| algorithm | ‘brute’ | ||||||||
| leaf_size | 40 | Test set | 0.912 | 0.698 | 2.770 | 0.910 | |||
| p | 2 | ||||||||
| 2% O2 based | n_neighbors | 2 | Validation set | 0.861 | 1.533 | 3.328 | 0.86 | ||
| weights | ‘distance’ | ||||||||
| algorithm | ‘ball_tree’ | ||||||||
| leaf_size | 70 | Test set | 0.881 | 0.486 | 2.945 | 0.879 | |||
| p | 2 | ||||||||
| Gaussian process (GP) | Air based | kernel | Rational Quadratic | Validation set | 0.851 | 2.179 | 3.750 | 0.848 | 24.5 s |
| length_scale | 1.2 | ||||||||
| alpha | 1 | Test set | 0.859 | 2.317 | 3.477 | 0.859 | |||
| 2% O2 based | kernel | Rationa lQuadratic | Validation set | 0.906 | 1.302 | 2.729 | 0.906 | ||
| length_scale | 1 | ||||||||
| alpha | 1.3 | Test set | 0.923 | 0.369 | 2.378 | 0.921 | |||
| Support vector regression (SVR) | Air based | C | 385.49 | Validation set | 0.954 | 0.525 | 2.083 | 0.953 | 17.2 s |
| kernel | rbf | Test set | 0.947 | 0.550 | 2.139 | 0.947 | |||
| 2% O2 based | C | 598.15 | Validation set | 0.924 | 0.746 | 2.454 | 0.924 | ||
| kernel | rbf | Test set | 0.936 | 0.355 | 2.147 | 0.936 | |||
| Random Forest (RF) | Air based | n_estimators | 280 | Validation set | 0.962 | 0.366 | 1.894 | 0.961 | 945 ms |
| criterion | ‘mse’ | ||||||||
| max_depth | 24 | ||||||||
| min_samples_split | 6 | Test set | 0.961 | 0.370 | 1.835 | 0.961 | |||
| min_samples_leaf | 3 | ||||||||
| max_features | ‘log2’ | ||||||||
| 2% O2 based | n_estimators | 190 | Validation set | 0.955 | 0.480 | 1.894 | 0.955 | ||
| criterion | ‘mse’ | ||||||||
| max_depth | 15 | ||||||||
| min_samples_split | 6 | Test set | 0.963 | 0.153 | 1.634 | 0.963 | |||
| min_samples_leaf | 3 | ||||||||
| max_features | ‘auto’ | ||||||||
| Adaboost | Air based | loss | ‘linear’ | Validation set | 0.869 | 1.391 | 3.485 | 0.869 | 295 ms |
| n_estimators | 154 | ||||||||
| learning_rate | 3.675 | Test set | 0.864 | 1.125 | 3.421 | 0.863 | |||
| 2% O2 based | loss | ‘linear’ | Validation set | 0.908 | 1.136 | 2.718 | 0.907 | ||
| n_estimators | 88 | ||||||||
| learning_rate | 3.04 | Test set | 0.911 | 0.257 | 2.537 | 0.910 | |||
| Gradient Boosting Decision Tree (GBDT) | Air based | loss | ‘huber’ | Validation set | 0.959 | 0.400 | 1.949 | 0.959 | 705 ms |
| learning_rate | 0.24 | ||||||||
| n_estimators | 169 | ||||||||
| subsample | 0.84 | Test set | 0.960 | 0.409 | 1.843 | 0.960 | |||
| criterion | ‘friedman_mse’ | ||||||||
| 2% O2 based | loss | ‘ls’ | Validation set | 0.959 | 0.589 | 1.810 | 0.959 | ||
| learning_rate | 0.38 | ||||||||
| n_estimators | 177 | ||||||||
| subsample | 0.66 | Test set | 0.959 | 0.260 | 1.732 | 0.958 | |||
| criterion | ‘friedman_mse’ | ||||||||
| XGBoost | Air based | num_round | 400 | Validation set | 0.970 | 0.334 | 1.667 | 0.970 | 779 ms |
| obj | ‘reg:linear’ | ||||||||
| max_depth | 5 | ||||||||
| eta | 0.08 | ||||||||
| gamma | 4 | Test set | 0.970 | 0.327 | 1.607 | 0.970 | |||
| alpha | 4 | ||||||||
| colsample_bytree | 0.85 | ||||||||
| 2% O2 based | num_round | 400 | Validation set | 0.971 | 0.271 | 1.523 | 0.971 | ||
| obj | ‘reg:linear’ | ||||||||
| max_depth | 4 | ||||||||
| eta | 0.07 | ||||||||
| gamma | 0 | Test set | 0.970 | 0.181 | 1.469 | 0.970 | |||
| alpha | 4 | ||||||||
| colsample_bytree | 0.9 | ||||||||
| Neural network (NN) | Air based | layers | 4 | Validation set | 0.958 | 1.465 | 1.992 | 0.957 | 85.3 s |
| each_layer_nodes | [20, 22, 19, 1] | ||||||||
| activation_function | ‘sigmoid’ | ||||||||
| optimizer | ‘SGD’ | ||||||||
| learning_rate | 0.1 | Test set | 0.959 | 1.501 | 1.893 | 0.958 | |||
| momentum | 0.8 | ||||||||
| epochs | 1000 | ||||||||
| 2% O2 based | layers | 3 | Validation set | 0.924 | 0.862 | 2.450 | 0.924 | ||
| each_layer_nodes | [23, 8, 1] | ||||||||
| activation_function | ‘sigmoid’ | ||||||||
| optimizer | ‘SGD’ | ||||||||
| learning_rate | 0.1 | Test set | 0.933 | 0.435 | 2.183 | 0.933 | |||
| momentum | 0.8 | ||||||||
| epochs | 1000 |
| Method | Model | Hyper-Parameters 1 | Value | Dataset | EV | MAPE | RMSE | R2 | Time-Consuming |
|---|---|---|---|---|---|---|---|---|---|
| XGBoost | air based | num_round | 1000 | Validation set | 0.975 | 0.254 | 1.527 | 0.975 | 1.62 s |
| obj | ‘reg:linear’ | ||||||||
| max_depth | 6 | ||||||||
| eta | 0.15 | ||||||||
| lambda | 3 | Test set | 0.976 | 0.365 | 1.439 | 0.976 | |||
| alpha | 0 | ||||||||
| colsample_bylevel | 0.4 | ||||||||
| colsample_bynode | 1 | ||||||||
| 2% O2 based | num_round | 275 | Validation set | 0.968 | 0.255 | 1.584 | 0.968 | ||
| obj | ‘reg:linear’ | ||||||||
| max_depth | 4 | ||||||||
| eta | 0.07 | ||||||||
| lambda | 0.9 | Test set | 0.970 | 0.199 | 1.483 | 0.969 | |||
| alpha | 4 | ||||||||
| colsample_bylevel | 1 | ||||||||
| colsample_bynode | 0.5 |
| Photosynthesis Model | Photorespiration Model | ||
|---|---|---|---|
| Term 1 | Coefficient | Term 2 | Coefficient |
| PAR | 8.221 | Leaf position × Location Y | 18.015 |
| CO2 concentration | 3.122 | Temperature | 13.639 |
| Location Y | 2.089 | Temperature × Growth stage 2 | 13.418 |
| Leaf position | 1.503 | Location X | 12.691 |
| Relative humidity | 1.500 | Leaf position × Location X × Location Y | 12.439 |
| Temperature × Growth stage | 1.314 | Growth stage 2 × Location X | 12.349 |
| CO2 concentration × PAR | 1.280 | Temperature × Location X × Location Y | 10.540 |
| Temperature × PAR | 1.190 | Relative humidity × Location X × Location Y | 9.122 |
| … | … | … | … |
| … | … | … | … |
| … | … | … | … |
| CO2 concentration × Growth stage | −0.485 | Temperature × Location X | −11.009 |
| Temperature 2 | −0.505 | Leaf position × Location X | −11.591 |
| PAR × Location X | −0.737 | Growth stage × Leaf position × Location X | −11.620 |
| Growth stage × Location Y | −0.892 | Location X × Location Y 2 | −14.085 |
| Growth stage × Location X | −1.089 | Leaf position | −15.735 |
| Relative humidity × Growth stage | −1.094 | Location X 2 × Plant Location Y | −15.925 |
| Location Y 2 | −1.266 | Growth stage 2 × Plant Location Y | −18.780 |
| PAR 2 | −3.704 | Location Y | −20.869 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, K.; Bo, Y.; Bao, Y.; Zhu, X.; Wang, J.; Wang, Y. A Machine Learning Model for Photorespiration Response to Multi-Factors. Horticulturae 2021, 7, 207. https://doi.org/10.3390/horticulturae7080207
Zheng K, Bo Y, Bao Y, Zhu X, Wang J, Wang Y. A Machine Learning Model for Photorespiration Response to Multi-Factors. Horticulturae. 2021; 7(8):207. https://doi.org/10.3390/horticulturae7080207
Chicago/Turabian StyleZheng, Kunpeng, Yu Bo, Yanda Bao, Xiaolei Zhu, Jian Wang, and Yu Wang. 2021. "A Machine Learning Model for Photorespiration Response to Multi-Factors" Horticulturae 7, no. 8: 207. https://doi.org/10.3390/horticulturae7080207
APA StyleZheng, K., Bo, Y., Bao, Y., Zhu, X., Wang, J., & Wang, Y. (2021). A Machine Learning Model for Photorespiration Response to Multi-Factors. Horticulturae, 7(8), 207. https://doi.org/10.3390/horticulturae7080207






