Estimating Nitrogen Release from Organic Fertilizers for Soilless Production by Analysis of C and N Pools
Abstract
1. Introduction
2. Materials and Methods
2.1. Commercial Organic Fertilizers
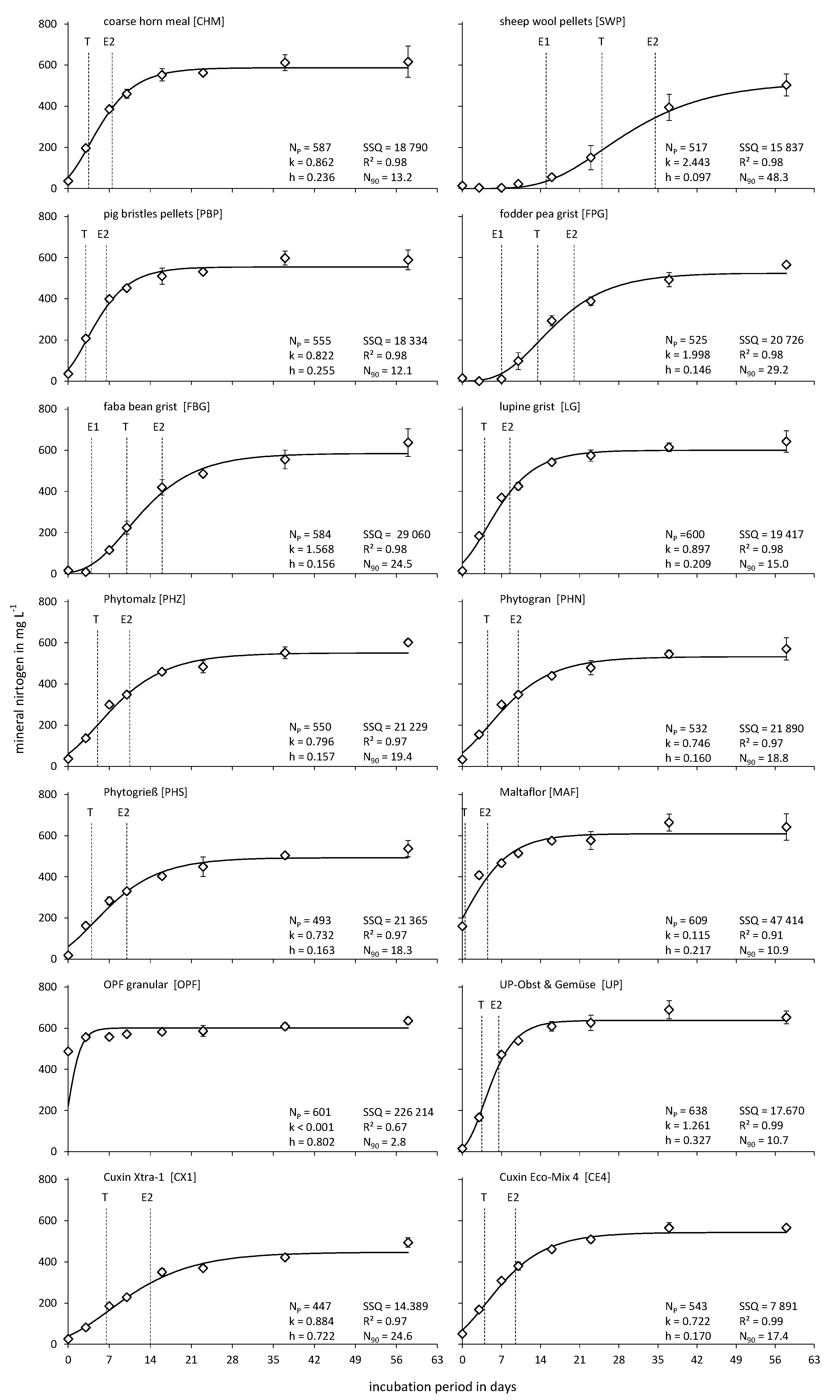
- Coarse horn meal (CHM; 13.8 + 0.6 + 0.0 + 0.1 + 2.0): CHM is made of the horns and hooves of slaughtered ungulates, mainly cattle, with minor adhesions of fur, meat, bones, blood, and manure. According to the regulations of the European Union, hygienization by heating or treatment with propionic acid is mandatory [35]. The main component of horns and hooves is keratin, a group of fibrous proteins [36]. The CHM was purchased from Beckmann & Brehm GmbH (Beckeln/Germany).
- Sheep wool pellets (SWPs; 9.7 + 0.1 + 3.5 + 0.1 + 2.1): SWPs were obtained from Düngepellet Produkt und Vertriebs GmbH (Lauchammer/Germany). Raw and uncleaned wool is a waste product from sheep husbandry and it is pelletized by a thermal–mechanical process. The primary N source of SWPs is keratin. However, the usually unwashed wool contains many waxes, dirt, and feces [37].
- Pig bristle pellets (PBPs; 13.9 + 0.1 + 0.1 + 0 + 2.1): PBPs, also named hair meal pellets, are slaughterhouse waste. The bristles are removed from slaughtered carcasses and typically pasteurized, dried, ground, and pelletized [35]. As with CHM and SWPs, keratin is the primary N source of PBPs. However, pig bristles are less soiled than CHM and SWPs, respectively. The pig bristles were purchased from Beckmann & Brehm GmbH (Beckeln/Germany).
- Fodder pea grist (FPG; 4.3 + 0.3 + 1 + 0.1 + 0.1): The seeds of fodder peas were crushed by us in a malt mill, as this is the current practice for legumes used as fertilizers in organic agriculture [35].
- Faba bean grist (FBG; 3.2 + 0.2 + 0.8 + 0.1 + 0.1): Similar to the seeds of fodder peas, faba bean seeds were also crushed by us.
- Lupine grist (LG; 5.2 + 0.2 + 0.7 + 0.2 + 0.3): Similar to the fodder pea and faba bean seeds, lupine seeds were crushed by us.
- Phytomalz (PHZ; 5.8 + 0.7 + 1.1 + 0.2 + 0.6): Provita® Phytomalz (Beckmann & Brehm, Beckeln/Germany) is made from protein-rich residues from the food-processing industry. The principal components are malt culms and corn, which are pressed into small pellets, with the addition of vinasse.
- Phytogran (PHN; 5.3 + 0.5 + 1.7 + 0.5 + 0.5): Provita® Phytogran (Beckmann & Brehm, Beckeln/Germany) is a granulate with a particle size of 2–5 mm. The raw material (residues from the food-processing industry) is dissolved in water, steam-sterilized, and fermented by yeasts. Afterwards, the fermented biomass is dried at about 100 °C, mixed with molasses, and granulated.
- Phytogrieß (PHS; 6.2 + 0.8 + 0.8 + 0.2 + 1.1): Provita® Phytogrieß (Beckmann & Brehm, Beckeln/Germany) is derived from the fermented residues and glucose of corn gluten production. The granules have a particle size between 0.2 and 2 mm.
- Maltaflor (MAF; 4.9 + 0.6 + 1.2 + 0.4 + 0.7): Maltaflor® (Maltaflor EUROPA GmbH, Boppard/Germany) is made of malt culms from breweries, vinasse, and vinasse–potassium, as well as grain hulls. After the malting process, the culms are dried, pelletized, and mixed with the vinasse [35].
- OPF granular (OPF; 7.0 + 1.2 + 8.8 + 0.2 + 7): According to the supplier (Plant Health Cure B.V., Oisterwijk/Netherlands), OPF is made of various herbal substances, e.g., fermented sugar beets, and is adjusted to promote the growth of beneficial soil bacteria and mycorrhizal fungi. Most of the nitrogen is amino-derived. The British Soil Association tests all raw materials.
- UP—fruit and vegetables (UP; 8.3 + 1 + 4.6 + 0.2 + 3.8): UP was purchased from Umweltpionier GmbH (Perg/Austria). Similar to OPF, no specific information about the raw materials and processing was available. However, according to the supplier, the fertilizer is a mixture of plant material, clay minerals, and microorganisms. A unique feature of UP is its classification as a foodstuff.
- Cuxin Xtra-1 (CX1; 10.7 + 0.1 + 3.3 + 0.7 + 4.8): DCM ECO-XTRA® 1 (Deutsche CUXIN Marketing GmbH, Telgte/Germany) is a mixture of animal residues (slaughterhouse waste according to EU ordinance No. 1069/2009), residues of the food, beverage, and feed industry, and tannins from forestry. CX1 is formulated as fine granules, with a particle size between 0.8 and 2.5 mm.
- Cuxin Eco-Mix 4 (CE4; 6.3 + 0.1 + 0.3 + 0.2 + 0.6): DCM Öko-Mix® 4 (Deutsche CUXIN Marketing GmbH, Telgte/Germany), similar to CX1, is a mixture of animal residues (slaughterhouse waste according to EU ordinance No. 1069/2009), residues of the food, beverage, and feed industry, and cocoa shells or vinasse. The particle size of CE4 is similar to that of CX1.
2.2. Characterization of Carbon and Nitrogen Pools
2.3. Incubation Experiment
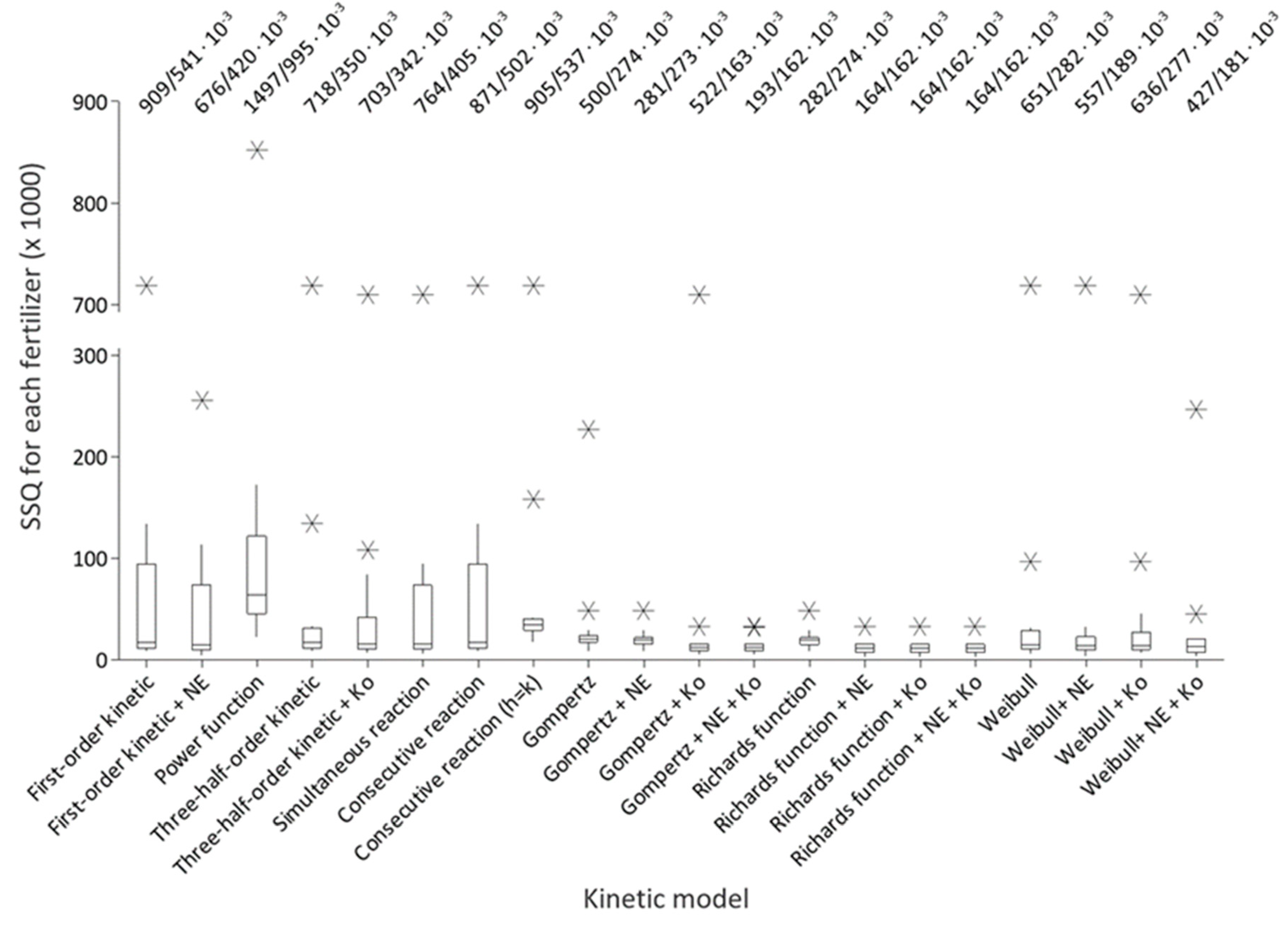
2.4. Calculations and Statistical Analyses
| Kinetic Model (Number of Parameters) | Equation [Reference] | |
|---|---|---|
| First-order kinetic (2) | [7] | |
| First-order kinetic plus readily available N (NE) (3) | [49] | |
| Power function (2) | [50] | |
| Three-half-order kinetic model (3) | [51] | |
| Three-half-order kinetic model plus zero order rate constant (k0) (4) | [51] | |
| Simultaneous reaction model (4) | [52] | |
| Consecutive reaction model (3) | [53] | |
| Consecutive reaction model with rate constants h = k (2) | [53] | |
| Gompertz function (3) | [14] | |
| Gompertz function + NE (4) | [14] | |
| Gompertz function + k0 (4) | [14] | |
| Gompertz function + NE + K0 (5) | [14] | |
| Richards function (4) | [54] | |
| Richards function + NE (5) | [54] | |
| Richards function + k0 (5) | [54] | |
| Richards function + NE + K0 (6) | [54] | |
| Weibull function (3) | [15] | |
| Weibull function + NE (4) | [15] | |
| Weibull function + k0 (4) | [15] | |
| Weibull function + NE + K0 (5) | [15] |
3. Results and Discussion
3.1. Characterization of Nitrogen and Carbon Pools
3.2. Nitrogen Release
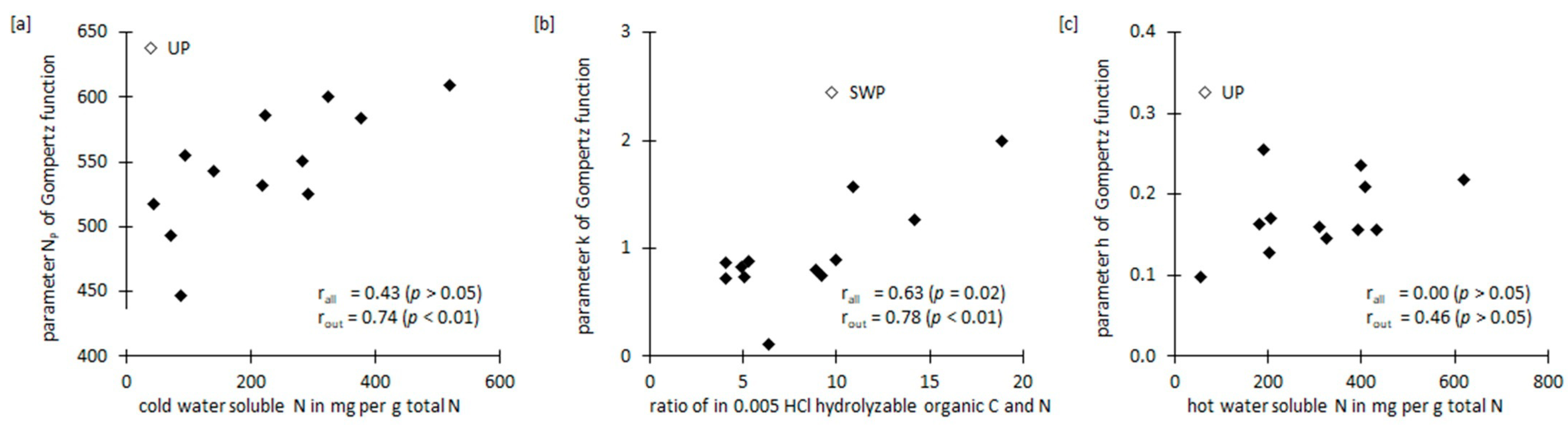
3.3. Relative Importance of N and C Pools
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Granatstein, D.; Kirby, E.; Willer, H. Organic horticulture expands globally. Chron. Hortic. 2010, 50, 31–38. [Google Scholar]
- Yue, C.; Dennis, J.H.; Behe, B.K.; Hall, C.R.; Campbell, B.L.; Lopez, R.G. Investigating consumer preference for organic, local, or sustainable plants. HortScience 2011, 46, 610–615. [Google Scholar] [CrossRef]
- Reganold, J.P.; Wachter, J.M. Organic agriculture in the twenty-first century. Nat. Plants 2016, 2, 15221. [Google Scholar] [CrossRef]
- Willer, H.; Lernoud, J. The World of Organic Agriculture. Statistics and Emerging Trends; Research Institute of Organic Agriculture FiBL: Frick, Switzerland; IFOAM-Organics International: Bonn, Germany, 2017; pp. 1–336. [Google Scholar]
- Burnett, S.E.; Stack, L.B. Survey of the research needs of the potential organic ornamental bedding plant industry in Maine. HortTechnology 2009, 19, 743–747. [Google Scholar] [CrossRef]
- Bergstrand, K.J. Organic fertilizers in greenhouse production systems–A review. Sci. Hortic. 2022, 295, 110855. [Google Scholar] [CrossRef]
- Stanford, G.; Smith, S.J. Nitrogen mineralization potentials of soils. Soil Sci. Soc. Am. J. 1972, 36, 465–472. [Google Scholar] [CrossRef]
- Frankenberger, W.T.; Abdelmagid, H.M. Kinetic parameters of nitrogen mineralization rates of leguminous crops incorporated into soil. Plant Soil 1985, 87, 257–271. [Google Scholar] [CrossRef]
- De Neve, S.; Hofman, G. Modelling N mineralization of vegetable crop residues during laboratory incubations. Soil Biol. Biochem. 1996, 28, 1451–1457. [Google Scholar] [CrossRef]
- Cabrera, M.L.; Kissel, D.E.; Vigil, M.F. Nitrogen mineralization from organic residues: Research opportunities. J. Environ. Qual. 2005, 34, 75–79. [Google Scholar] [CrossRef]
- Nendel, C.; Reuter, S. Kinetics of net nitrogen mineralisation from soil-applied grape residues. Nutr. Cycl. Agroecosyst. 2007, 79, 233–241. [Google Scholar] [CrossRef]
- Nakhone, L.N.; Tabatabai, M.A. Nitrogen mineralization of leguminous crops in soils. J. Plant Nutr. Soil Sci. 2008, 171, 231–241. [Google Scholar] [CrossRef]
- Diaz-Fierros, F.; Villar, M.C.; Gil, F.; Carballas, M.; Leiros, M.C.; Carballas, T.; Cabaneiro, A. Effect of cattle slurry fractions on nitrogen mineralization in soil. J. Agric. Sci. 1988, 110, 491–497. [Google Scholar] [CrossRef]
- Ellert, B.H.; Bettany, J.R. Comparison of kinetic models for describing net sulfur and nitrogen mineralization. Soil Sci. Soc. Am. J. 1988, 52, 1692–1702. [Google Scholar] [CrossRef]
- White, C.S.; Marinakis, Y.D. A flexible model for quantitative comparisons of nitrogen mineralization patterns. Biol. Fertil. Soils 1991, 11, 239–244. [Google Scholar] [CrossRef]
- Simard, R.R.; N’dayegamiye, A. Nitrogen-mineralization potential of meadow soils. Can. J. Soil Sci. 1993, 73, 27–38. [Google Scholar] [CrossRef]
- Agbenin, J.O.; Agbaji, E.B.; Suleiman, I.; Agbaji, A.S. Assessment of nitrogen mineralization potential and availability from neem seed residue in a savanna soil. Biol. Fertil. Soils 1999, 29, 408–412. [Google Scholar] [CrossRef]
- Deenik, J.L.; Yost, R.S. Nitrogen mineralization potential and nutrient availability from five organic materials in an atoll soil from the Marshall Islands. Soil Sci. 2008, 173, 54–68. [Google Scholar] [CrossRef]
- Trinsoutrot, I.; Recous, S.; Bentz, B.; Linères, M.; Chèneby, D.; Nicolardot, B. Biochemical quality of crop residues and carbon and nitrogen mineralization kinetics under nonlimiting nitrogen conditions. Soil Sci. Soc. Am. J. 2000, 64, 918–926. [Google Scholar] [CrossRef]
- Iritani, W.M. The Nitrogen Release of Vegetable Crop Residues During Incubation as Related to Their Chemical Composition. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Champaign, IL, USA, 1958. [Google Scholar]
- Fox, R.H.; Myers, R.J.K.; Vallis, I. The nitrogen mineralization rate of legume residues in soil as influenced by their polyphenol, lignin, and nitrogen contents. Plant Soil 1990, 129, 251–259. [Google Scholar] [CrossRef]
- Henriksen, T.M.; Breland, T.A. Evaluation of criteria for describing crop residue degradability in a model of carbon and nitrogen turnover in soil. Soil Biol. Biochem. 1999, 31, 1135–1149. [Google Scholar] [CrossRef]
- Pansu, M.; Thuriès, L.; Larré-Larrouy, M.C.; Bottner, P. Predicting N transformations from organic inputs in soil in relation to incubation time and biochemical composition. Soil Biol. Biochem. 2003, 35, 353–363. [Google Scholar] [CrossRef]
- Jensen, L.S.; Salo, T.; Palmason, F.; Breland, T.A.; Henriksen, T.M.; Stenberg, B.; Pedersen, A.; Lundström, C.; Esala, M. Influence of biochemical quality on C and N mineralisation from a broad variety of plant materials in soil. Plant Soil 2005, 273, 307–326. [Google Scholar] [CrossRef]
- Redin, M.; Recous, S.; Aita, C.; Dietrich, G.; Skolaude, A.C.; Ludke, W.H.; Schmatz, R.; Giacomini, S.J. How the chemical composition and heterogeneity of crop residue mixtures decomposing at the soil surface affects C and N mineralization. Soil Biol. Biochem. 2014, 78, 65–75. [Google Scholar] [CrossRef]
- Noirot-Cosson, P.E.; Dhaouadi, K.; Etievant, V.; Vaudour, E.; Houot, S. Parameterisation of the NCSOIL model to simulate C and N short-term mineralisation of exogenous organic matter in different soils. Soil Biol. Biochem. 2017, 104, 128–140. [Google Scholar] [CrossRef]
- Heuberger, H.; Kreuzmair, A.; Weh, F.; Schnitzler, W.H. Vegetabile Dünger als Stickstoffquelle für Topfbasilikum.-Freisetzung und Aufnahme von Stickstoff aus vegetabilen Düngern bei Basilikum (Ocimum basilicum L.) in Topfkultur. Z. Für Arznei-Und Gewürzpflanzen 2005, 10, 140–143. [Google Scholar]
- Müller, T.; von Fragstein und Niemsdorff, P. Organic fertilizers derived from plant materials Part I: Turnover in soil at low and moderate temperatures. J. Plant Nutr. Soil Sci. 2006, 169, 255–264. [Google Scholar] [CrossRef]
- Müller, T.; von Fragstein und Niemsdorff, P. Organic fertilizers derived from plant materials Part II: Turnover in field trials. J. Plant Nutr. Soil Sci. 2006, 169, 265–273. [Google Scholar] [CrossRef]
- Stadler, C.; Von Tucher, S.; Schmidhalter, U.; Gutser, R.; Heuwinkel, H. Nitrogen release from plant-derived and industrially processed organic fertilizers used in organic horticulture. J. Plant Nutr. Soil Sci. 2006, 169, 549–556. [Google Scholar] [CrossRef]
- Lü, H.; He, H.; Zhao, J.; Zhang, W.; Xie, H.; Hu, G.; Liu, X.; Wu, Y.; Zhang, X. Dynamics of fertilizer-derived organic nitrogen fractions in an arable soil during a growing season. Plant Soil 2013, 373, 595–607. [Google Scholar] [CrossRef]
- Ros, G.H.; Hanegraaf, M.C.; Hoffland, E.; van Riemsdijk, W.H. Predicting soil N mineralization: Relevance of organic matter fractions and soil properties. Soil Biol. Biochem. 2011, 43, 1714–1722. [Google Scholar] [CrossRef]
- Von Lützow, M.; Kögel-Knabner, I.; Ekschmitt, K.; Flessa, H.; Guggenberger, G.; Matzner, E.; Marschner, B. SOM fractionation methods: Relevance to functional pools and to stabilization mechanisms. Soil Biol. Biochem. 2007, 39, 2183–2207. [Google Scholar] [CrossRef]
- Stevenson, F.J. Gross Chemical Fractionation of Organic Matter. Methods of Soil Analysis: Part 2 Chemical and Microbiological Properties; American Society of Agronomy: Madison, WI, USA, 1965; pp. 1409–1421. [Google Scholar] [CrossRef]
- Möller, K.; Schultheiß, U. Organische Handelsdüngemittel Tierischer und Pflanzlicher Herkunft für den Ökologischen Landbau—Charakterisierung und Empfehlungen für die Praxis. Kuratorium für Technik und Bauwesen in der Landwirtschaft (KTBL) e.V.: Darmstadt, Germany, 2013. [Google Scholar]
- Block, R.J.; Bolling, D. The amino acid composition of keratins: The composition of gorgonin, spongin, turtle scutes, and other keratins. J. Biol. Chem. 1939, 127, 685–693. [Google Scholar] [CrossRef]
- Górecki, R.S.; Górecki, M.T. Utilization of waste wool as substrate amendment in pot cultivation of tomato, sweet pepper, and eggplant. Pol. J. Environ. Stud. 2010, 19, 1083–1087. [Google Scholar]
- VDLUFA Method Book II.1: Analysis of Fertilizers, 4th ed.; with 1–6 Supplement; VDLUFA-Verlag: Darmstadt, Germany, 2014.
- VDLUFA Method Book I: Analysis of Soils, 4th ed.; with 1–7 Supplements; VDLUFA-Verlag: Darmstadt, Germany, 2016.
- Meinken, E.; Lohr, D.; Wöck, C. Colonization of growing media by saprophytic fungi-importance of carbon and nitrogen fractions. Acta Hortic. 2017, 1168, 325–332. [Google Scholar] [CrossRef]
- Kroon, H. Determination of nitrogen in water: Comparison of a continuous-flow method with on-line UV digestion with the original Kjeldahl method. Anal. Chim. Acta 1993, 276, 287–293. [Google Scholar] [CrossRef]
- Oweczkin, I.J.; Kerven, G.L.; Ostatek-Boczynski, Z. Determination of dissolved organic carbon by inductively coupled plasma atomic emission spectrometry. Commun. Soil Sci. Plant Anal. 1995, 26, 2739–2747. [Google Scholar] [CrossRef]
- Lohr, D.; Wöck, C.; Meinken, E. Pyrolytic combustion analysis of carbon-a new approach for characterizing growing media. Acta Hortic. 2017, 1168, 341–348. [Google Scholar] [CrossRef]
- DIN 11540:2019-03; Peats for Horticulture and Landscape Gardening—Properties, Test Methods, Specifications. Beuth Verlag GmbH: Berlin, Germany, 2019.
- Methodbook for Analysis of Organic Fertilizers, Soil Improvers and Growing Media, 1st ed.; with 1–6 Supplements; Bundesgütegemeinschaft Kompost (BGK): Köln, Germany, 2021.
- Brown, A.M. A step-by-step guide to non-linear regression analysis of experimental data using a Microsoft Excel spreadsheet. Comput. Methods Programs Biomed. 2001, 65, 191–200. [Google Scholar] [CrossRef]
- Kemmer, G.; Keller, S. Nonlinear least-squares data fitting in Excel spreadsheets. Nat. Protoc. 2010, 5, 267–281. [Google Scholar] [CrossRef]
- Blatná, D. Outliers in regression. Trutnov 2006, 30, 1–6. [Google Scholar]
- Jones, C.A. Estimation of an active fraction of soil nitrogen. Commun. Soil Sci. Plant Anal. 1984, 15, 23–32. [Google Scholar] [CrossRef]
- Pal, D.; Broadbent, F.E. Kinetics of rice straw decomposition in soils. J. Environ.-Qual. 1975, 4, 256–260. [Google Scholar] [CrossRef]
- Brunner, W.; Focht, D.D. Deterministic three-half-order kinetic model for microbial degradation of added carbon substrates in soil. Appl. Environ. Microbiol. 1984, 47, 167–172. [Google Scholar] [CrossRef]
- Molina, J.A.E.; Clapp, C.E.; Larson, W.E. Potentially mineralizable nitrogen in soil: The simple exponential model does not apply for the first 12 weeks of incubation. Soil Sci. Soc. Am. J. 1980, 44, 442–443. [Google Scholar] [CrossRef]
- Noggle, J.H. Chapter 9 Physical Chemistry; Little, Brown and Company: Boston, MA, USA, 1985; pp. 445–449. [Google Scholar]
- Hara, Y. Application of the Richards function to nitrogen release from coated urea at a constant temperature and relationships among the calculated parameters. Soil Sci. Plant Nutr. 2000, 46, 683–691. [Google Scholar] [CrossRef]
- Rubins, E.J.; Bear, F.E. Carbon-nitrogen ratios in organic fertilizer materials in relation to the availability of their nitrogen. Soil Sci. 1942, 54, 411–424. [Google Scholar] [CrossRef]
- Silveira, M.L.; Comerford, N.B.; Reddy, K.R.; Cooper, W.T.; El-Rifai, H. Characterization of soil organic carbon pools by acid hydrolysis. Geoderma 2008, 144, 405–414. [Google Scholar] [CrossRef]
- Leinweber, P.; Schulten, H.R. Nonhydrolyzable forms of soil organic nitrogen: Extractability and composition. J. Plant Nutr. Soil Sci. 2000, 163, 433–439. [Google Scholar] [CrossRef]
- Delics, B.; Lohr, D.; Meinken, E. Nitrogen mineralization and subsequent nitrification of horn as affected by particle size and compost amendment to the growing medium. DGG-Proceedings 2017, 7, 1–5. [Google Scholar] [CrossRef]
- Rahn, C.R.; Lillywhite, R.D. A study of the quality factors affecting the short-term decomposition of field vegetable residues. J. Sci. Food Agric. 2002, 82, 19–26. [Google Scholar] [CrossRef]
- Arancon, N.Q.; Edwards, C.A.; Bierman, P. Influences of vermicomposts on field strawberries: Part 2. Effects on soil microbiological and chemical properties. Bioresour. Technol. 2006, 97, 831–840. [Google Scholar] [CrossRef] [PubMed]
- Dinesh, R.; Srinivasan, V.; Hamza, S.; Manjusha, A. Short-term incorporation of organic manures and biofertilizers influences biochemical and microbial characteristics of soils under an annual crop [Turmeric (Curcuma longa L.)]. Bioresour. Technol. 2010, 101, 4697–4702. [Google Scholar] [CrossRef] [PubMed]
- Lazcano, C.; Gómez-Brandón, M.; Revilla, P.; Domínguez, J. Short-term effects of organic and inorganic fertilizers on soil microbial community structure and function: A field study with sweet corn. Biol. Fertil. Soils 2013, 49, 723–733. [Google Scholar] [CrossRef]
- Zwietering, M.H.; Jongenburger, I.; Rombouts, F.M.; Van’t Riet, K.J.A.E.M. Modeling of the bacterial growth curve. Appl. Environ. Microbiol. 1990, 56, 1875–1881. [Google Scholar] [CrossRef] [PubMed]
- Buchanan, R.L.; Whiting, R.C.; Damert, W.C. When is simple good enough: A comparison of the Gompertz, Baranyi, and three-phase linear models for fitting bacterial growth curves. Food Microbiol. 1997, 14, 313–326. [Google Scholar] [CrossRef]
- Prasad, M.; Simmons, P.; Maher, M.J. Release characteristics of organic fertilizers. Acta Hortic. 2004, 644, 163–170. [Google Scholar] [CrossRef]
- Dion, P.P.; Jeanne, T.; Thériault, M.; Hogue, R.; Pepin, S.; Dorais, M. Nitrogen release from five organic fertilizers commonly used in greenhouse organic horticulture with contrasting effects on bacterial communities. Can. J. Soil Sci. 2020, 100, 120–135. [Google Scholar] [CrossRef]
- Koch, R.; Emmel, M.; Lohr, D.; Frankenberg, A.; Degen, B.; Meinken, E.; Haas, H.P.; Fischinger, S. Organische Dünger in Topfkulturen auf dem Prüfstand—Wie steht es mit der Stickstofffreisetzung? In Beiträge zu 14. Wissenschaftstagung Ökologischer Landbau, N-Düngung und Verluste; Dr. Köster: Berlin, Germany, 2017; pp. 334–337. [Google Scholar]
- Frerichs, C.; Daum, D.; Pacholski, A.S. Ammonia and ammonium exposure of basil (Ocimum basilicum L.) growing in an organically fertilized peat substrate and strategies to mitigate related harmful impacts on plant growth. Front. Plant Sci. 2020, 10, 1696. [Google Scholar] [CrossRef]
- Vandecasteele, B.; Van Loo, K.; Ommeslag, S.; Vierendeels, S.; Rooseleer, M.; Vandaele, E. Sustainable growing media blends with woody green composts: Optimizing the n release with organic fertilizers and interaction with microbial biomass. Agronomy 2022, 12, 422. [Google Scholar] [CrossRef]
- Bushong, J.T.; Roberts, T.L.; Ross, W.J.; Norman, R.J.; Slaton, N.A.; Wilson, C.E., Jr. Evaluation of distillation and diffusion techniques for estimating hydrolyzable amino sugar-nitrogen as a means of predicting nitrogen mineralization. Soil Sci. Soc. Am. J. 2008, 72, 992–999. [Google Scholar] [CrossRef]
- Ahn, M.Y.; Zimmerman, A.R.; Comerford, N.B.; Sickman, J.O.; Grunwald, S. Carbon mineralization and labile organic carbon pools in the sandy soils of a North Florida watershed. Ecosystems 2009, 12, 672–685. [Google Scholar] [CrossRef]
- Zoccola, M.; Montarsolo, A.; Mossotti, R.; Patrucco, A.; Tonin, C. Green hydrolysis as an emerging technology to turn wool waste into organic nitrogen fertilizer. Waste Biomass Valorization 2015, 6, 891–897. [Google Scholar] [CrossRef]
- Arunkumar, N.; Gulsar Banu, J.; Gopalakrishnan, N.; Prakash, A.H. Wax degrading bacteria: Scope and applications in agriculture. Int. J. Curr. Microbiol. Appl. Sci. 2017, 6, 649–664. [Google Scholar] [CrossRef]
- Goodrich, B.S.; Roberts, D.S. Antimicrobial factors in wool wax. Aust. J. Chem. 1971, 24, 153–159. [Google Scholar] [CrossRef]
- Sengupta, A.; Behera, J. Comprehensive view on chemistry, manufacturing and applications of lanolin extracted from wool pretreatment. Am. J. Eng. Res. 2014, 3, 33–43. [Google Scholar]
- Zaghloul, T.I.; Embaby, A.M.; Elmahdy, A.R. Key determinants affecting sheep wool biodegradation directed by a keratinase-producing Bacillus subtilis recombinant strain. Biodegradation 2011, 22, 111–128. [Google Scholar] [CrossRef]
- Fellahi, S.; Zaghloul, T.I.; Feuk-Lagerstedt, E.; Taherzadeh, M.J. A Bacillus strain able to hydrolyze alpha-and beta-keratin. J. Bioprocess. Biotech. 2014, 4, 1–7. [Google Scholar] [CrossRef]
- Sharma, S.; Gupta, A. Sustainable management of keratin waste biomass: Applications and future perspectives. Braz. Arch. Biol. Technol. 2016, 59, 1–14. [Google Scholar] [CrossRef]
- Balliu, A.; Zheng, Y.; Sallaku, G.; Fernández, J.A.; Gruda, N.S.; Tuzel, Y. Environmental and cultivation factors affect the morphology, architecture and performance of root systems in soilless grown plants. Horticulturae 2021, 7, 243. [Google Scholar] [CrossRef]
- Gruda, N.; Schnitzler, W.H. Influence of wood fiber substrates and application rates on the growth of tomato transplants. Adv. Hortic. Sci. 1999, 13, 20–24. [Google Scholar]
- Vives-Peris, V.; De Ollas, C.; Gómez-Cadenas, A.; Pérez-Clemente, R.M. Root exudates: From plant to rhizosphere and beyond. Plant Cell Rep. 2020, 39, 3–17. [Google Scholar] [CrossRef] [PubMed]
- Helal, H.M.; Sauerbeck, D. Effect of plant roots on carbon metabolism of soil microbial biomass. Z. Für Pflanz. Und Bodenkd. 1986, 149, 181–188. [Google Scholar] [CrossRef]
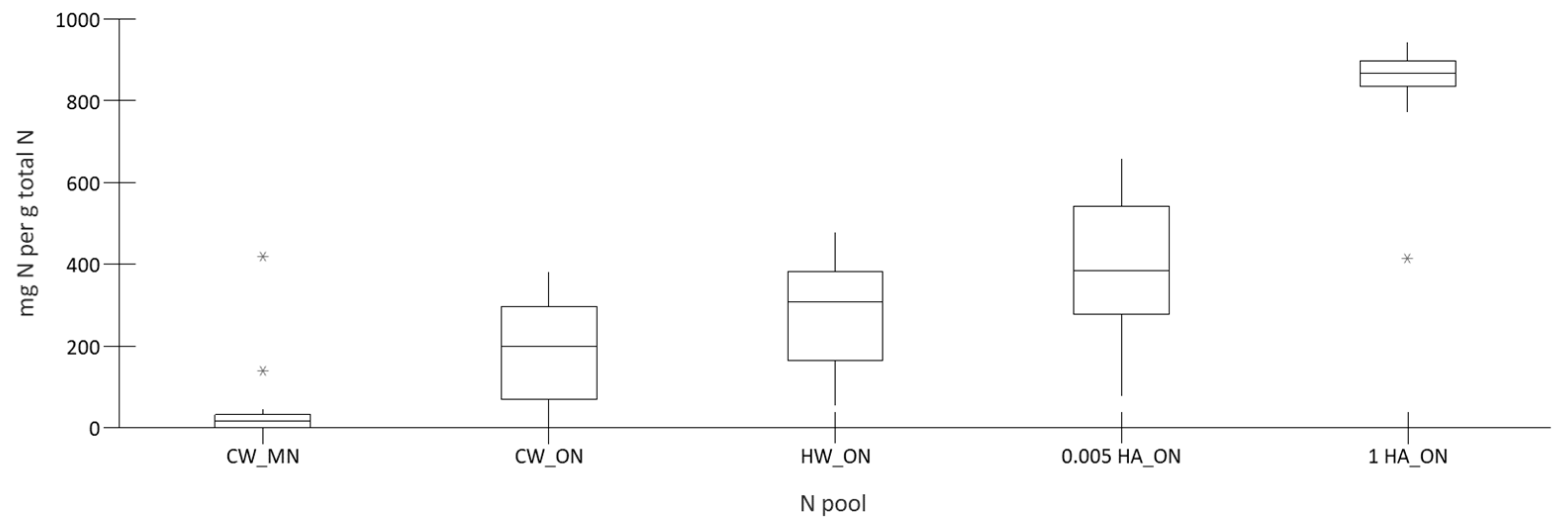
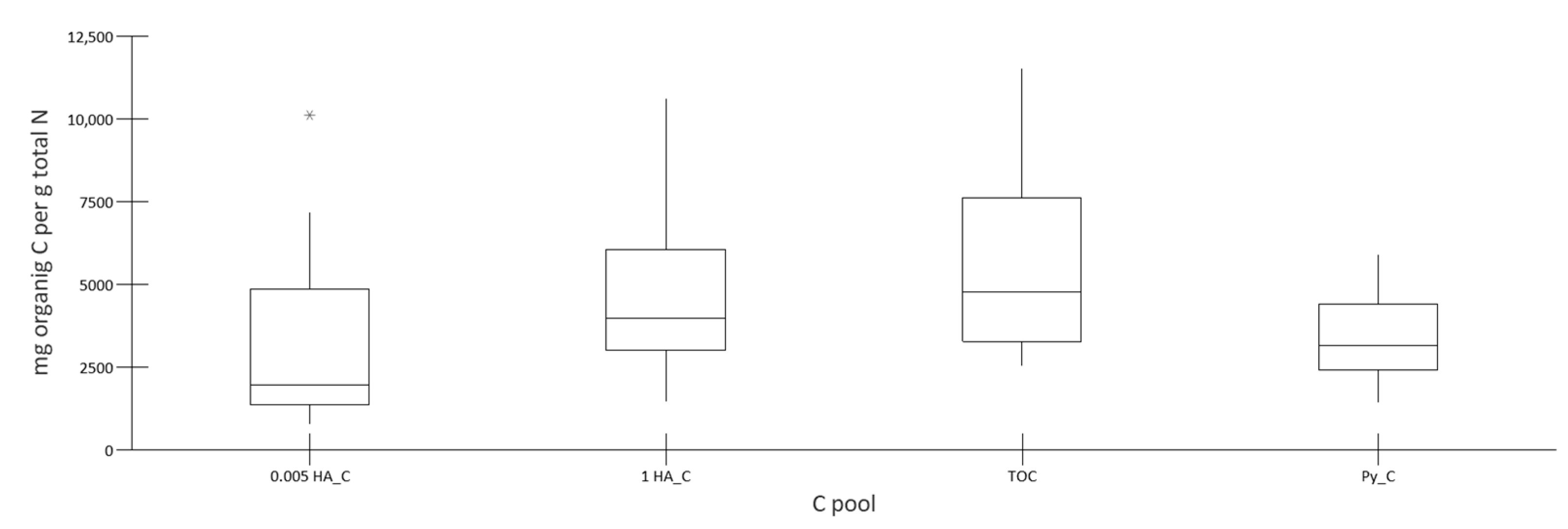

| Total N Soluble in | Organic N Soluble in | |||||
|---|---|---|---|---|---|---|
| Cold Water | Hot Water | 0.005 M HCl | Cold Water | Hot Water | 0.005 M HCl | |
| Hot water | 0.98 (<0.01) | 0.95 (<0.01) | ||||
| 0.005 M HCl | 0.94 (<0.01) | 0.94 (<0.01) | 0.92 (<0.01) | 0.91 (<0.01) | ||
| 1 M HCl | 0.01 (0.99) | −0.10 (0.75) | 0.09 (0.76) | −0.09 (0.77) | −0.20 (0.48) | 0.03 (0.91) |
| TOC/ TN | TOC/ TON | TOC/ CW_ON | TOC/ HW_ON | TOC/ 0.005 HA_ON | TOC/ 1 HA_ON | 0.005 HA C/ON | |
|---|---|---|---|---|---|---|---|
| TOC/TON | 0.98 (<0.01) | ||||||
| TOC/ CW_ON | −0.19 (0.51) | −0.29 (0.31) | |||||
| TOC/ HW_ON | 0.01 (0.99) | −0.08 (0.79) | 0.90 (<0.01) | ||||
| TOC/ 0.005H A_ON | 0.04 (0.88) | −0.03 (0.92) | 0.77 (<0.01) | 0.93 (<0.01) | |||
| TOC/ 1 HA_ON | 0.95 (<0.01) | 0.99 (<0.01) | −0.34 (0.24) | −0.13 (0.67) | 0.08 (0.80) | ||
| 0.005 HA_C/ ON | 0.76 (<0.01) | 0.71 (<0.01) | 0.33 (0.25) | 0.54 (0.04) | 0.46 (0.10) | 0.66 (0.01) | |
| 1 HA_C/ON | 0.98 (<0.01) | 0.98 (<0.01) | −0.25 (0.39) | −0.04 (0.96) | −0.01 (0.96) | 0.96 (<0.01) | 0.77 (<0.01) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lohr, D.; Gruda, N.S.; Meinken, E. Estimating Nitrogen Release from Organic Fertilizers for Soilless Production by Analysis of C and N Pools. Horticulturae 2023, 9, 767. https://doi.org/10.3390/horticulturae9070767
Lohr D, Gruda NS, Meinken E. Estimating Nitrogen Release from Organic Fertilizers for Soilless Production by Analysis of C and N Pools. Horticulturae. 2023; 9(7):767. https://doi.org/10.3390/horticulturae9070767
Chicago/Turabian StyleLohr, Dieter, Nazim S. Gruda, and Elke Meinken. 2023. "Estimating Nitrogen Release from Organic Fertilizers for Soilless Production by Analysis of C and N Pools" Horticulturae 9, no. 7: 767. https://doi.org/10.3390/horticulturae9070767
APA StyleLohr, D., Gruda, N. S., & Meinken, E. (2023). Estimating Nitrogen Release from Organic Fertilizers for Soilless Production by Analysis of C and N Pools. Horticulturae, 9(7), 767. https://doi.org/10.3390/horticulturae9070767







