The Influence of Viscosity on Heat Dissipation under Conditions of the High-Frequency Oscillating Magnetic Field
Abstract
1. Introduction
= τ0∙σ, σ << 1.
2. Experimental Materials and Methods
Magnetic Fluids (MF) Based on MOGUL, ITO 100, and MIDEL Oil
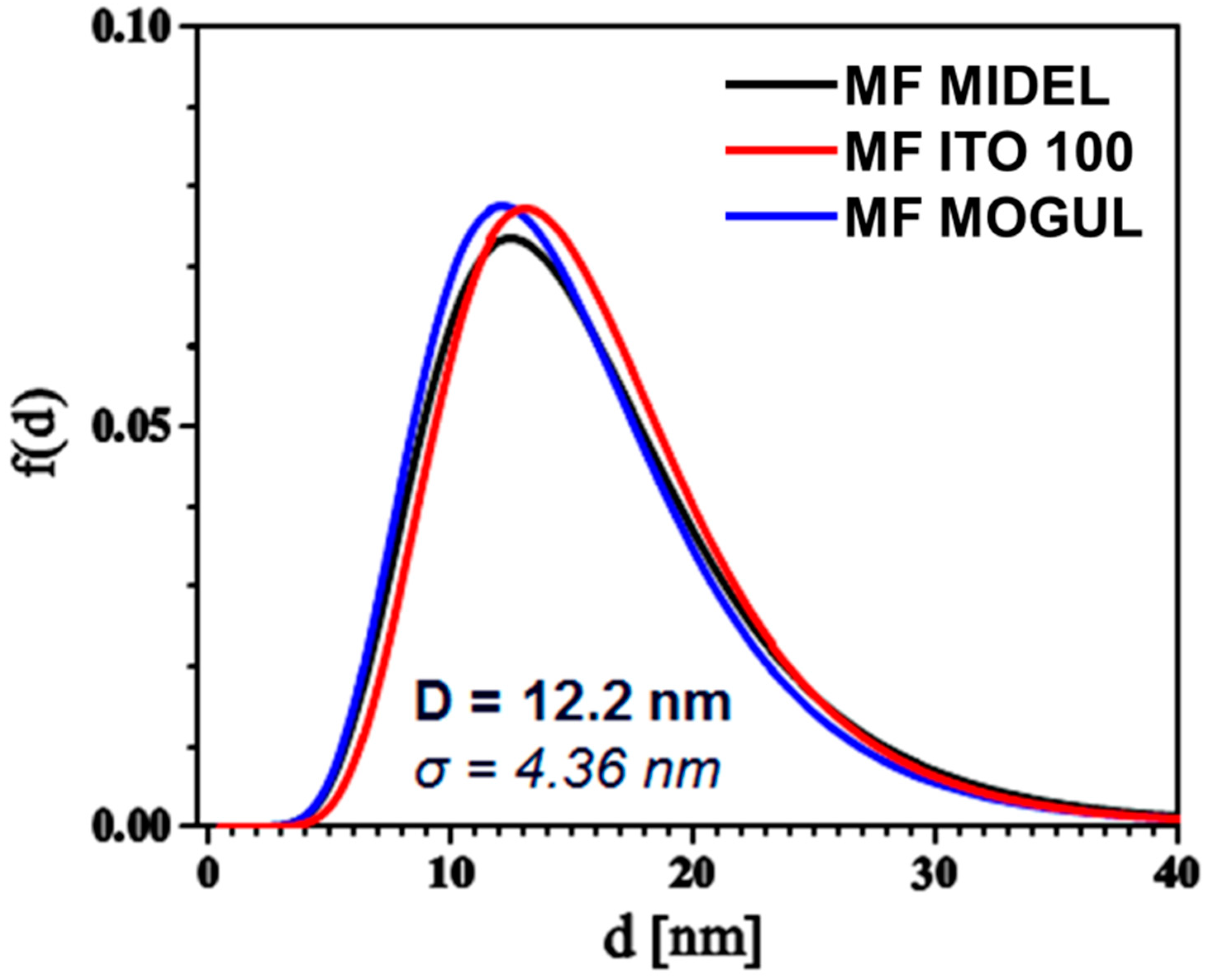
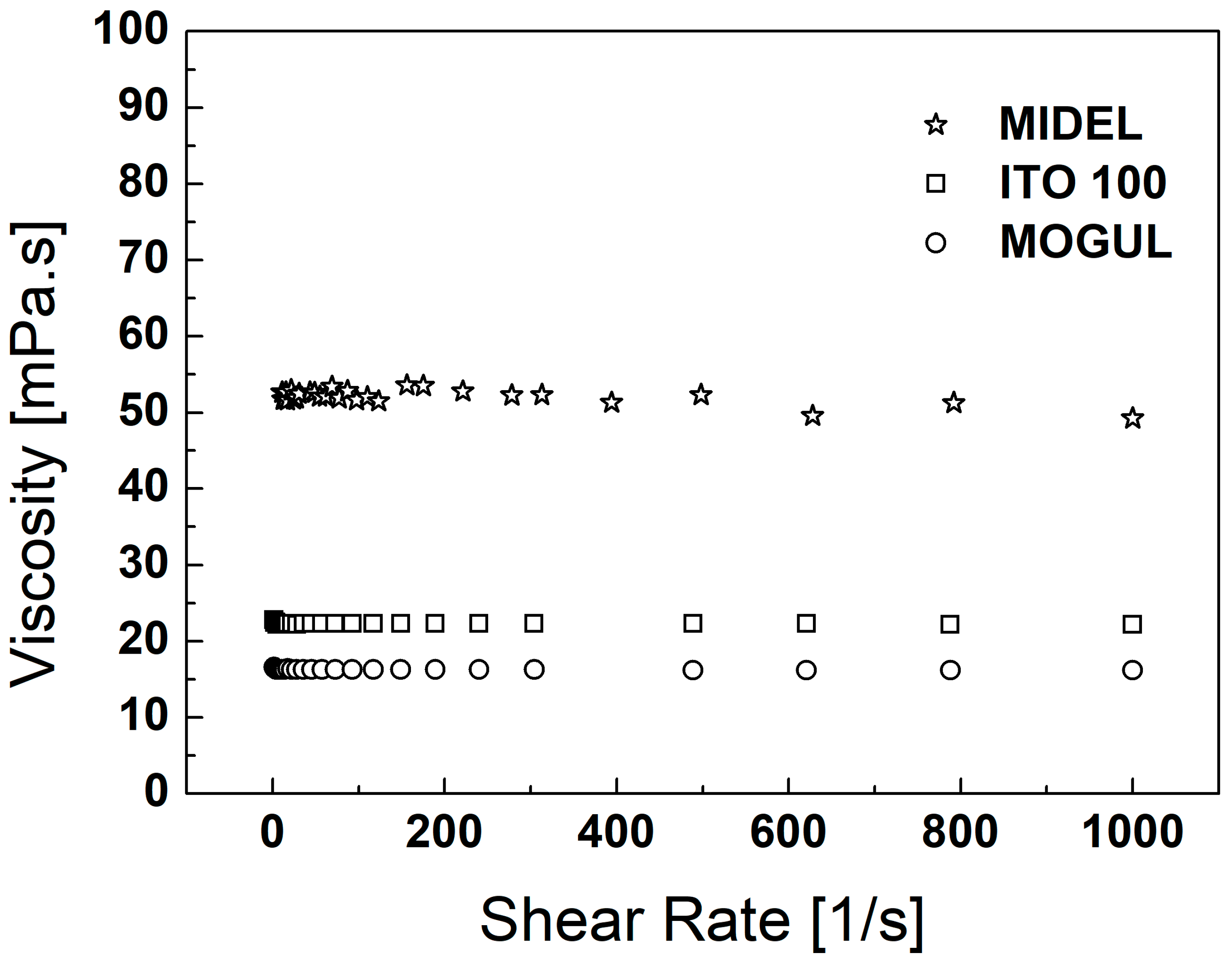
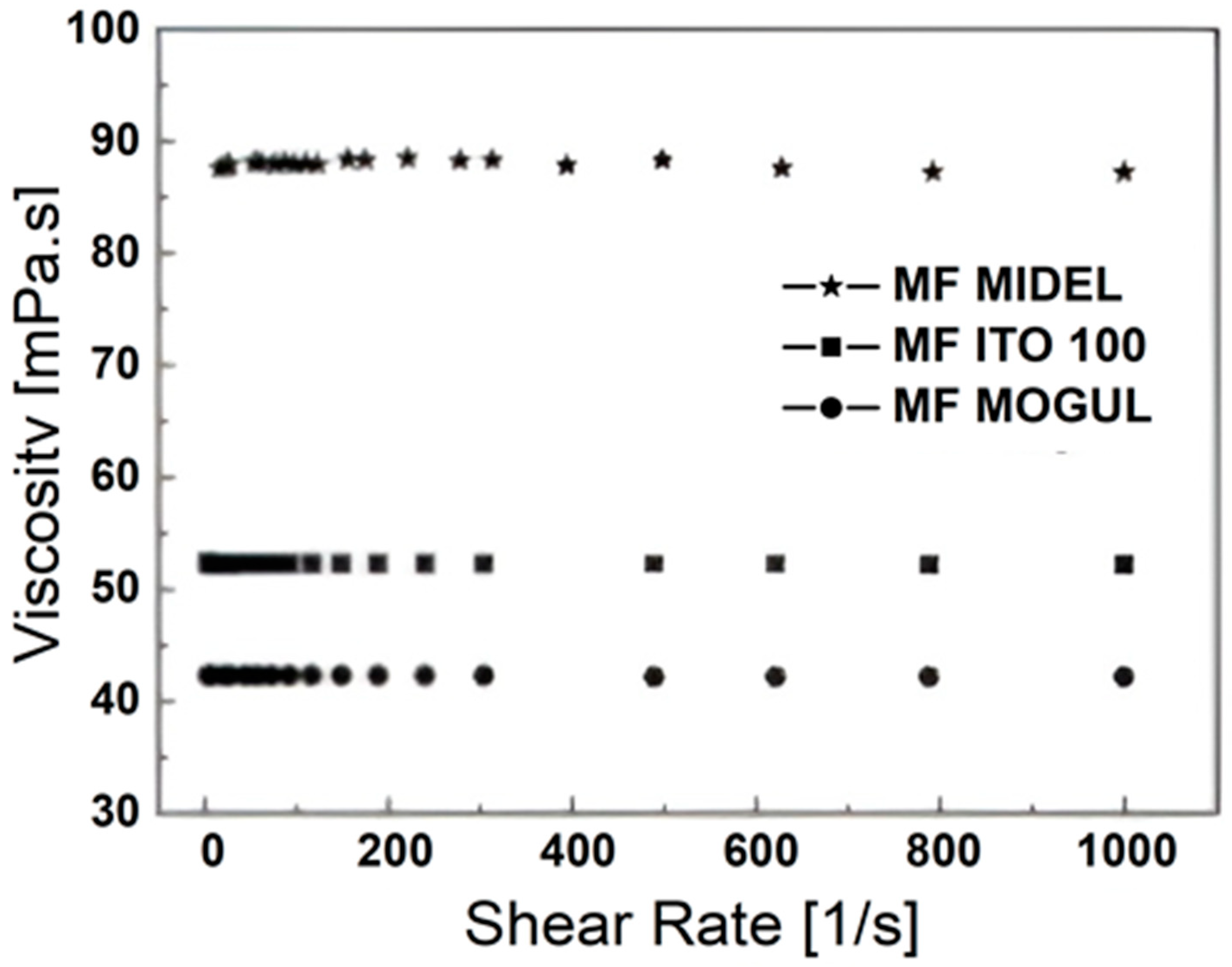
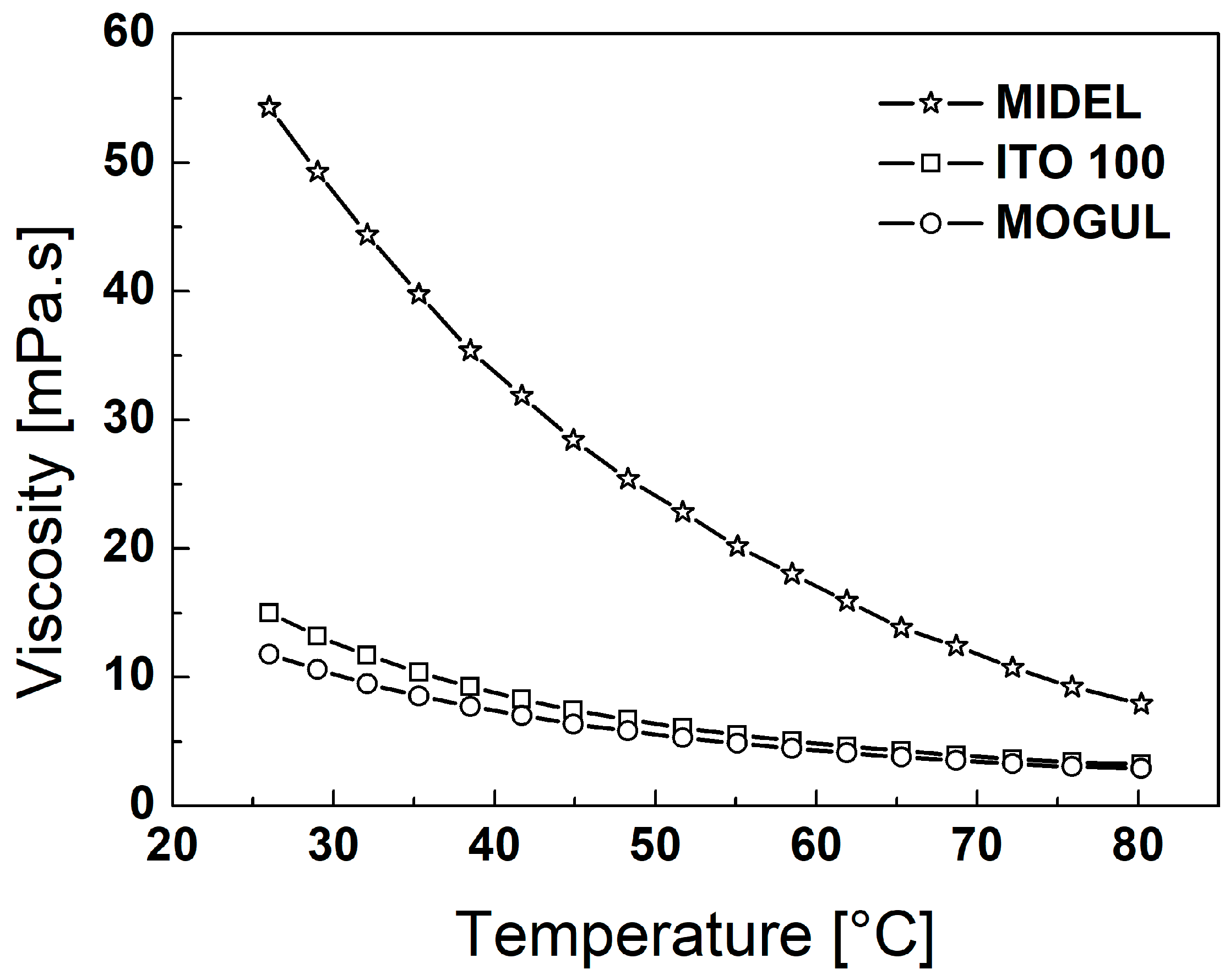
3. Particles, Oils, and Magnetic Fluid Parameters
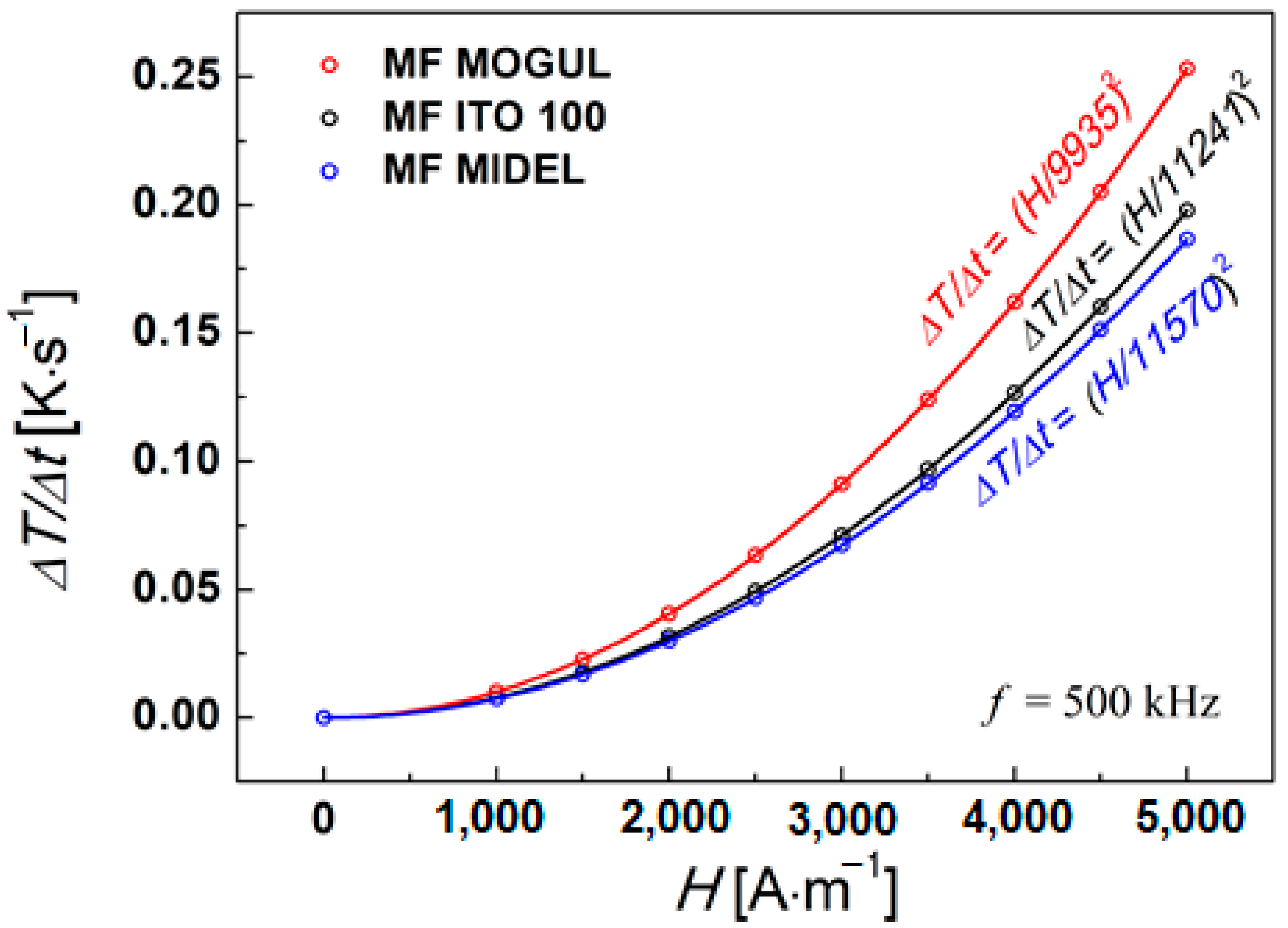
4. Hyperthermal Properties of Magnetic Fluids
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kole, M.; Khandekar, S. Engineering applications of ferrofluids: A review. J. Magn. Magn. Mater. 2021, 537, 168222. [Google Scholar] [CrossRef]
- Yao, J.; Li, D.; Chen, X.; Huang, C.; Xu, D. Damping performance of a novel ferrofluid dynamic vibration absorber. J. Fluids Struct. 2019, 90, 190–204. [Google Scholar] [CrossRef]
- Raj, K.; Moskowitz, B.; Casciari, R. Advances in ferrofluid technology. J. Magn. Magn. Mater. 1995, 149, 174–180. [Google Scholar] [CrossRef]
- Scherer, C.; Figueiredo Neto, A.M. Ferrofluids: Properties and applications. Braz. J. Phys. 2005, 35, 718–727. [Google Scholar] [CrossRef]
- Lee, M.Y.; Kim, H.J. Heat Transfer Characteristics of a Speaker Using Nano-Sized Ferrofluid. Entropy 2014, 16, 5891–5900. [Google Scholar] [CrossRef]
- Patel, J.; Parekh, K.; Upadhyay, R.V. Prevention of hot spot temperature in a distribution transformer using magnetic fluid as a coolant. Int. J. Therm. Sci. 2016, 103, 35–40. [Google Scholar] [CrossRef]
- Zanella, R.; Nore, C.; Bouillault, F.; Cappanera, L.; Tomas, I.; Mininger, X.; Guermond, J.L. Study of Magnetoconvection Impact on a Coil Cooling by Ferrofluid with a Spectral/Finite-Element Method. IEEE Trans. Magn. 2018, 54, 4600104. [Google Scholar] [CrossRef]
- Philip, J. Magnetic nanofluids (Ferrofluids): Recent advances, applications, challenges, and future directions. Adv. Colloid Interface Sci. 2023, 311, 102810. [Google Scholar] [CrossRef]
- Deatsch, A.E.; Evans, B.A. Heating efficiency in magnetic nanoparticle hyperthermia. J. Magn. Magn. Mater. 2014, 354, 163–172. [Google Scholar] [CrossRef]
- Rosensweig, R.E. Heating magnetic fluid with alternating magnetic field. J. Magn. Magn. Mater. 2002, 252, 370–374. [Google Scholar] [CrossRef]
- Hergt, R.; Dutz, S.; Uller, R.; Zeisberger, M. Magnetic particle hyperthermia: Nanoparticle magnetism and materials development for cancer therapy. J. Phys. Condens. Matter. 2006, 18, 2919–2934. [Google Scholar] [CrossRef]
- Fannin, P.C. Magnetic spectroscopy as an aide in understanding magnetic fluids. J. Magn. Magn. Mater. 2002, 252, 59–64. [Google Scholar] [CrossRef]
- Wildeboer, R.R.; Southern, P.; Pankhurst, Q.A. On the reliable measurement of specific absorption rates and intrinsic loss parameters in magnetic hyperthermia materials. J. Phys. D Appl. Phys. 2014, 47, 495003. [Google Scholar] [CrossRef]
- Molcan, M.; Kaczmarek, K.; Kubovcikova, M.; Gojzewski, H.; Kovac, J.; Timko, M.; Józefczak, A. Magnetic hyperthermia study of magnetosome chain systems in tissue-mimicking phantom. J. Mol. Liq. 2020, 320, 114470. [Google Scholar] [CrossRef]
- Garaio, E.; Sandre, O.; Collantes, J.M.; Garcia, J.A.; Mornet, S.; Plazaola, F. Specific absorption rate dependence on temperature in magnetic field hyperthermia measured by dynamic hysteresis losses (ac magnetometry). Nanotechnology 2015, 26, 015704. [Google Scholar] [CrossRef]
- Skumiel, A.; Hornowski, T.; Józefczak, A. Heating characteristics of transformer oil-based magnetic fluids of different magnetic particle concentrations. Int. J. Thermophys. 2011, 32, 876–885. [Google Scholar] [CrossRef][Green Version]
- Skumiel, A.; Kaczmarek, K.; Flak, D.; Rajnak, M.; Antal, I.; Brząkała, H. The influence of magnetic nanoparticle concentration with dextran polymers in agar gel on heating efficiency in magnetic hyperthermia. J. Mol. Liq. 2020, 304, 112734. [Google Scholar] [CrossRef]
- Musiał, J.; Skumiel, A.; Bielas, R. Study of the calorimetric effect in ferrogels subjected to the high-frequency rotating magnetic field. J. Magn. Magn. Mater. 2023, 588, 171462. [Google Scholar] [CrossRef]
- Chen, S.; Li, D. Control of Magnetic Particle Size in Ferrofluid and Its Effect on Rheological Properties. Chin. J. Mech. Eng. Engl. Ed. 2022, 35, 79. [Google Scholar] [CrossRef]
- Hergt, R.; Hiergeist, R.; Zeisberger, M.; Schüler, D.; Heyen, U.; Hilger, I.; Kaiser, W.A. Magnetic properties of bacterial magnetosomes as potential diagnostic and therapeutic tools. J. Magn. Magn. Mater. 2005, 293, 80–86. [Google Scholar] [CrossRef]
- Cabrera, D.; Camarero, J.; Ortega, D.; Teran, F.J. Influence of the aggregation, concentration, and viscosity on the nanomagnetism of iron oxide nanoparticle colloids for magnetic hyperthermia. J. Nanoparticle Res. 2015, 17, 121. [Google Scholar] [CrossRef]
- Ibarra, J.; Melendres, J.; Almada, M.; Burboa, M.G.; Taboada, P.; Juárez, J.; Valdez, M.A. Synthesis and characterization of magnetite/PLGA/chitosan nanoparticles. Mater. Res. Express 2015, 2, 095010. [Google Scholar] [CrossRef]
- Zhang, L.; He, R.; Gu, H.C. Oleic acid coating on the monodisperse magnetite nanoparticles. Appl. Surf. Sci. 2006, 253, 2611–2617. [Google Scholar] [CrossRef]
- Namduri, H.; Nasrazadani, S. Quantitative analysis of iron oxides using Fourier transform infrared spectrophotometry. Corros. Sci. 2008, 50, 2493–2497. [Google Scholar] [CrossRef]
- Yang, K.; Peng, H.; Wen, Y.; Li, N. Re-examination of characteristic FTIR spectrum of secondary layer in bilayer oleic acid-coated Fe3O4 nanoparticles. Appl. Surf. Sci. 2010, 256, 3093–3097. [Google Scholar] [CrossRef]
- Raşa, M. Magnetic properties and magneto-birefringence of magnetic fluids. Eur. Phys. J. E 2000, 2, 265–275. [Google Scholar] [CrossRef]
- Kubovcikova, M.; Sobotova, R.; Zavisova, V.; Antal, I.; Khmara, I.; Lisnichuk, M.; Bednarikova, Z.; Jurikova, A.; Strbak, O.; Vojtova, J.; et al. N-Acetylcysteine-Loaded Magnetic Nanoparticles for Magnetic Resonance Imaging. Int. J. Mol. Sci. 2023, 24, 11414. [Google Scholar] [CrossRef]
- Hadadian, Y.; Masoomi, H.; Dinari, A.; Ryu, C.; Hwang, S.; Kim, S.; Cho, B.K.; Lee, J.Y.; Yoon, J. From Low to High Saturation Magnetization in Magnetite Nanoparticles: The Crucial Role of the Molar Ratios between the Chemicals. ACS Omega 2022, 7, 15996–16012. [Google Scholar] [CrossRef]
- Daoush, W.M. Co-Precipitation and Magnetic Properties of Magnetite Nanoparticles for Potential Biomedical Applications. J. Nanomed. Res. 2017, 5, 00118. [Google Scholar] [CrossRef]
- Józefczak, A.; Hornowski, T.; Skumiel, A. Temperature dependence of particle size distribution in transformer oil-based ferrofluid. Int. J. Thermophys. 2011, 32, 795–806. [Google Scholar] [CrossRef]
- Nguyen, M.D.; Tran, H.V.; Xu, S.; Lee, T.R. Fe3O4 Nanoparticles: Structures, Synthesis, Magnetic Properties, Surface Functionalization, and Emerging Applications. Appl. Sci. 2021, 11, 11301. [Google Scholar] [CrossRef] [PubMed]
- Raikher, Y.L.; Stepanov, V.I. Physical aspects of magnetic hyperthermia: Low-frequency ac field absorption in a magnetic colloid. J. Magn. Magn. Mater. 2014, 368, 421–427. [Google Scholar] [CrossRef]




| ρoil [g∙cm−3] | ρMF [g∙cm−3] | MS [emu∙g−1] | ηoil [mPa∙s] | ηMF [mPa∙s] | |
|---|---|---|---|---|---|
| MIDEL | 0.975 | 1.202 | 26.10 | 55.48 | 85.51 |
| ITO 100 | 0.895 | 1.128 | 25.70 | 16.28 | 52.30 |
| MOGUL | 0.791 | 1.031 | 25.90 | 12.51 | 44.54 |
| Sample | Φ (Magnetic Volume Fraction) | a (H/a)2 | SAR (Specific Absorption Rate) f = 500 kHz | ||
|---|---|---|---|---|---|
| 5 kA·m−1 | 10 kA·m−1 | 10 kA·m−1 | |||
| % | W·g−1sample | W·g−1sample | W·g−1Fe3O4 | ||
| MF MOGUL | 6.6 | 9935 | 0.45 | 1.81 | 196.26 |
| MF ITO 100 | 6.6 | 11,241 | 0.39 | 1.56 | 169.84 |
| MF MIDEL | 6.6 | 11,570 | 0.35 | 1.42 | 154.68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Molcan, M.; Skumiel, A.; Tothova, J.; Paulovicova, K.; Kopcansky, P.; Timko, M. The Influence of Viscosity on Heat Dissipation under Conditions of the High-Frequency Oscillating Magnetic Field. Magnetochemistry 2024, 10, 2. https://doi.org/10.3390/magnetochemistry10010002
Molcan M, Skumiel A, Tothova J, Paulovicova K, Kopcansky P, Timko M. The Influence of Viscosity on Heat Dissipation under Conditions of the High-Frequency Oscillating Magnetic Field. Magnetochemistry. 2024; 10(1):2. https://doi.org/10.3390/magnetochemistry10010002
Chicago/Turabian StyleMolcan, Matus, Andrzej Skumiel, Jana Tothova, Katarina Paulovicova, Peter Kopcansky, and Milan Timko. 2024. "The Influence of Viscosity on Heat Dissipation under Conditions of the High-Frequency Oscillating Magnetic Field" Magnetochemistry 10, no. 1: 2. https://doi.org/10.3390/magnetochemistry10010002
APA StyleMolcan, M., Skumiel, A., Tothova, J., Paulovicova, K., Kopcansky, P., & Timko, M. (2024). The Influence of Viscosity on Heat Dissipation under Conditions of the High-Frequency Oscillating Magnetic Field. Magnetochemistry, 10(1), 2. https://doi.org/10.3390/magnetochemistry10010002






