A Magnet Splicing Method for Constructing a Three-Dimensional Self-Decoupled Magnetic Tactile Sensor
Abstract
:1. Introduction
2. Materials and Methods
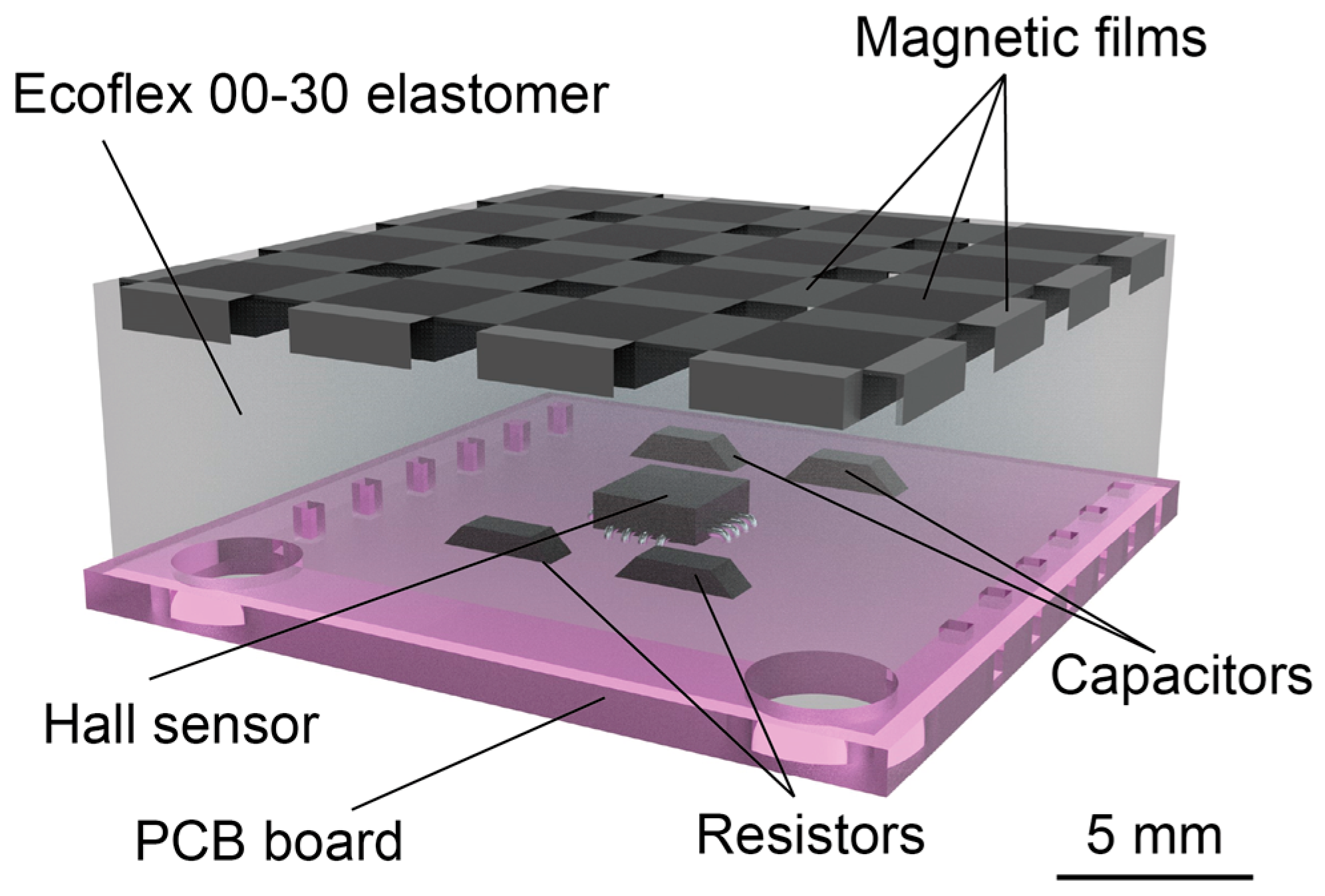
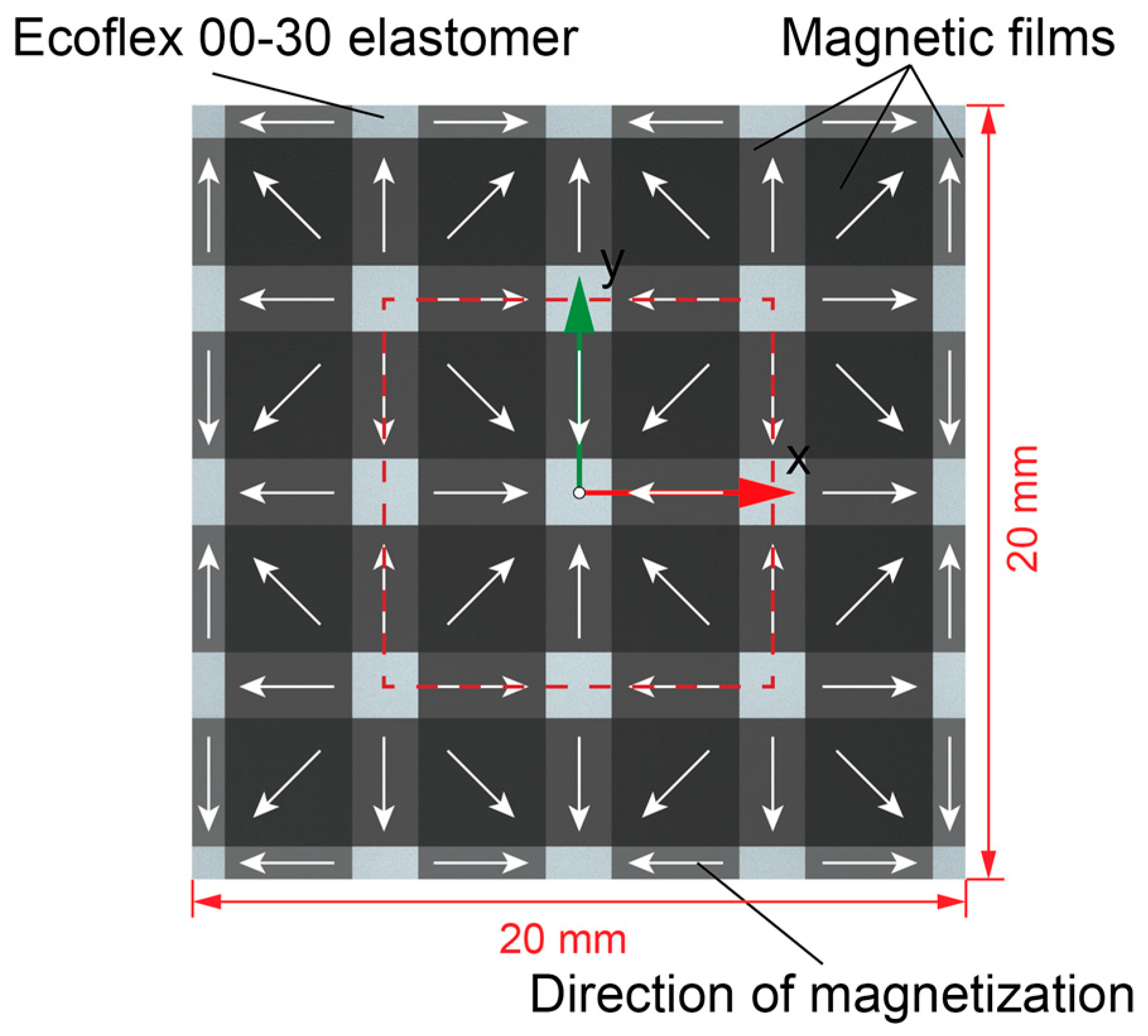
2.1. Structure and Mechanism
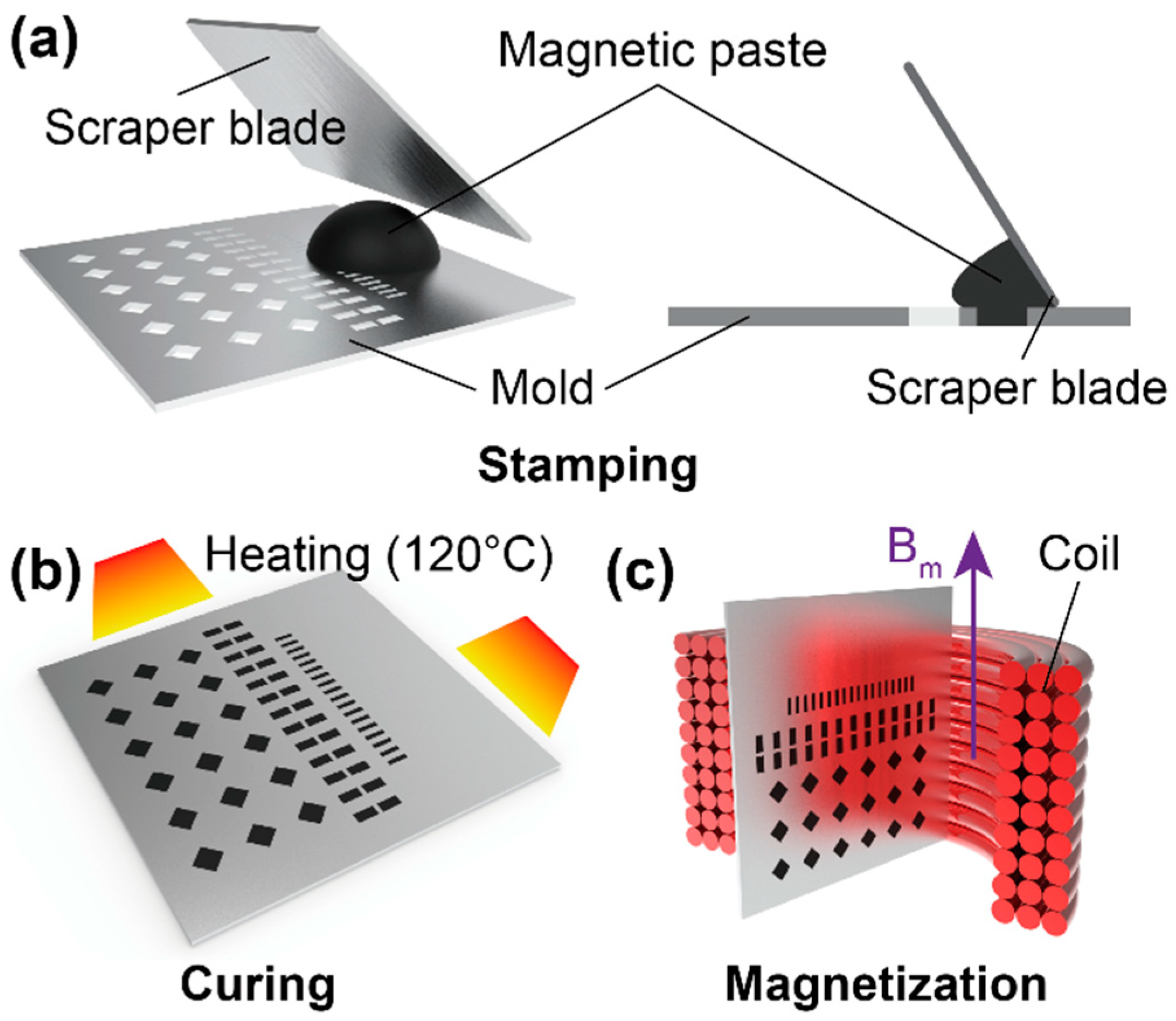
2.2. Materials and Fabrication
3. Results and Discussion
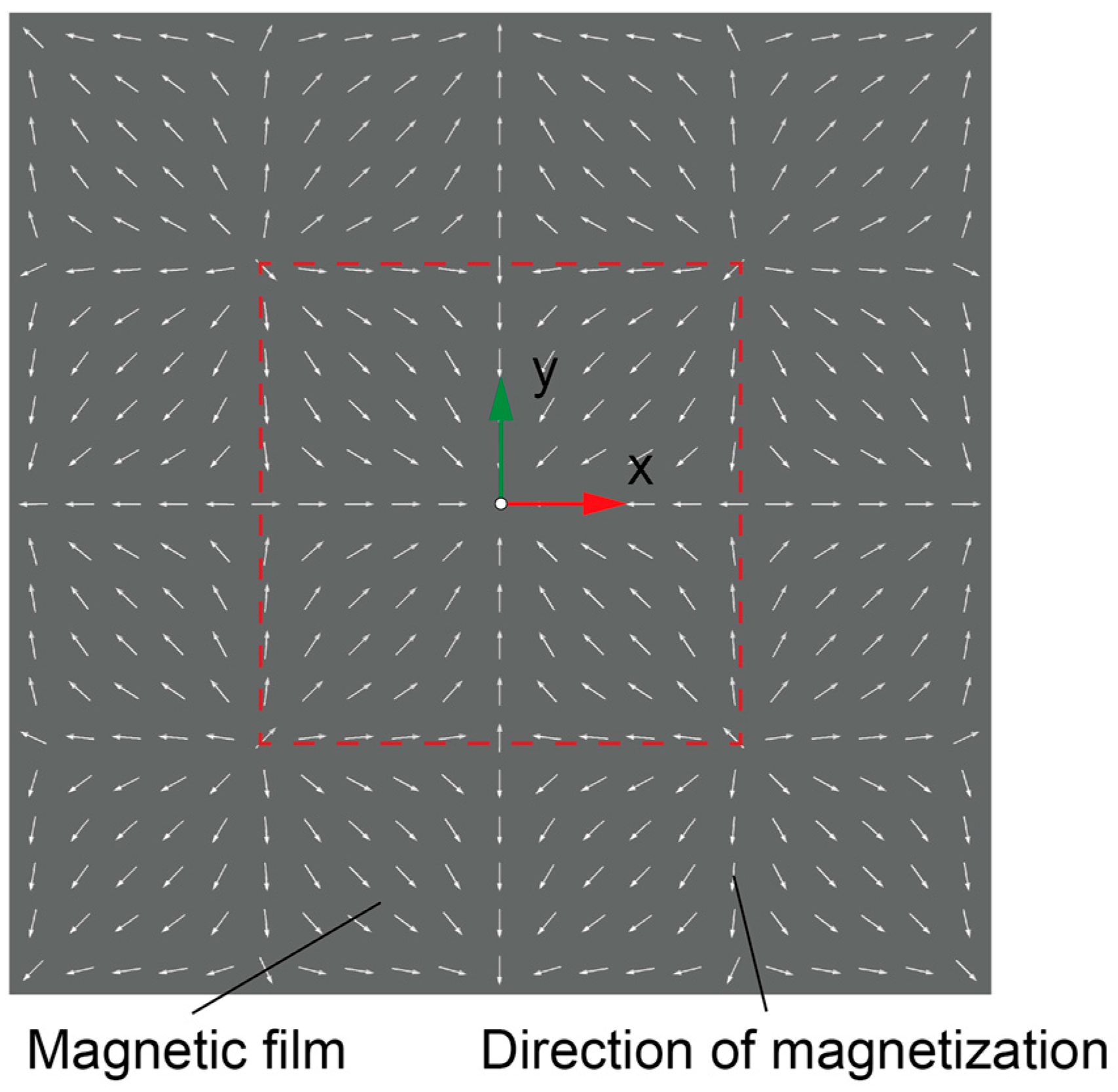
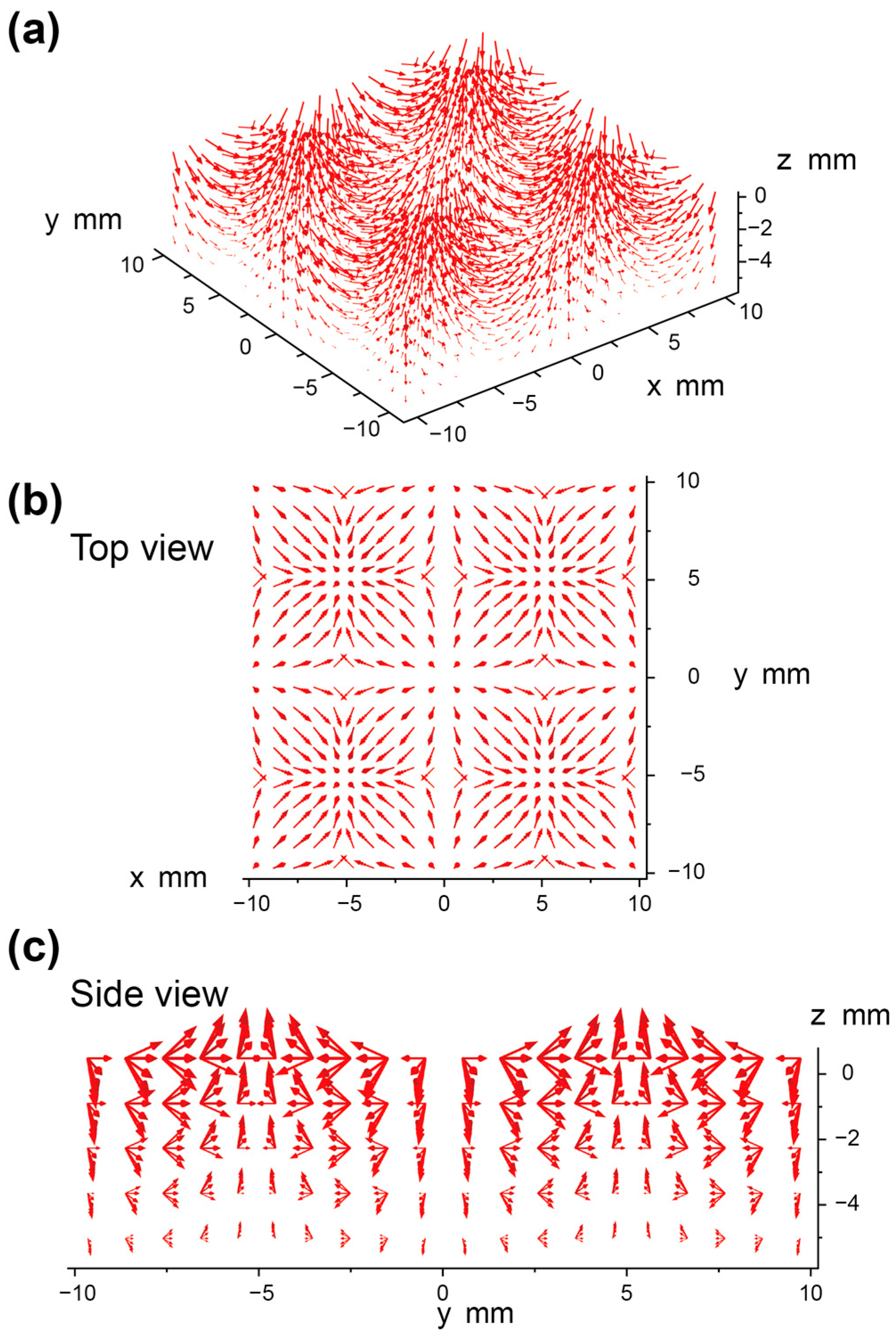
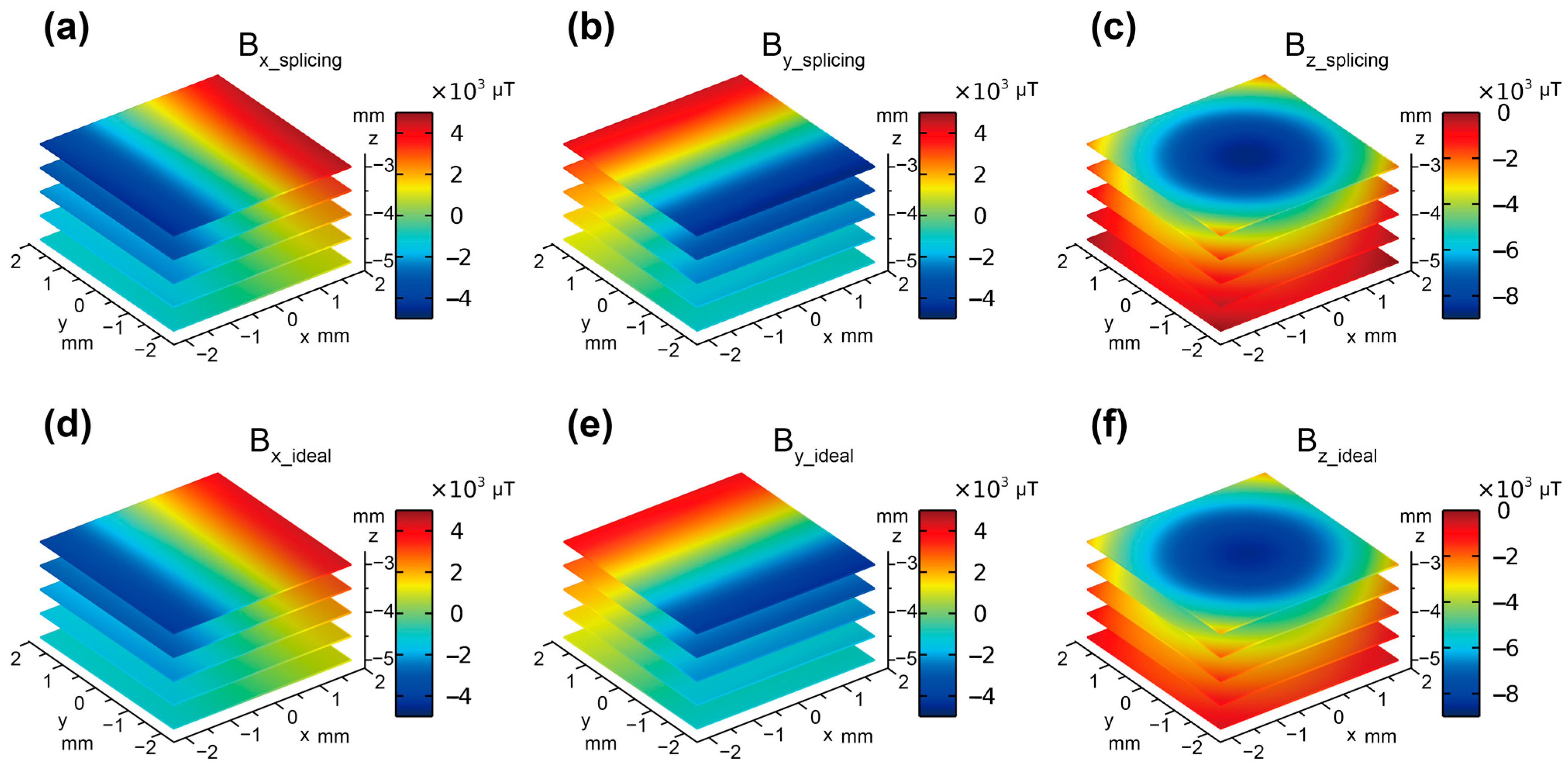
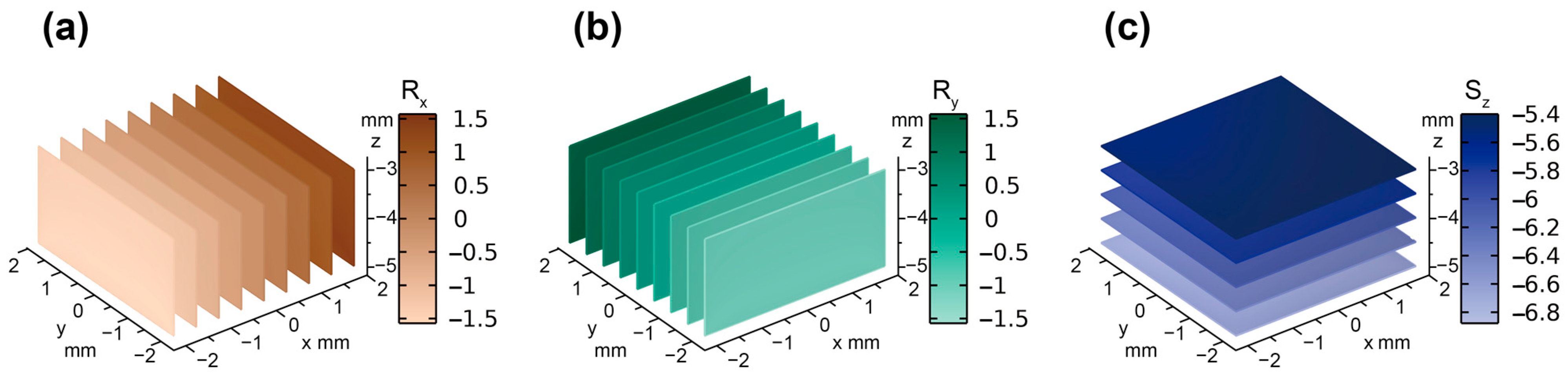
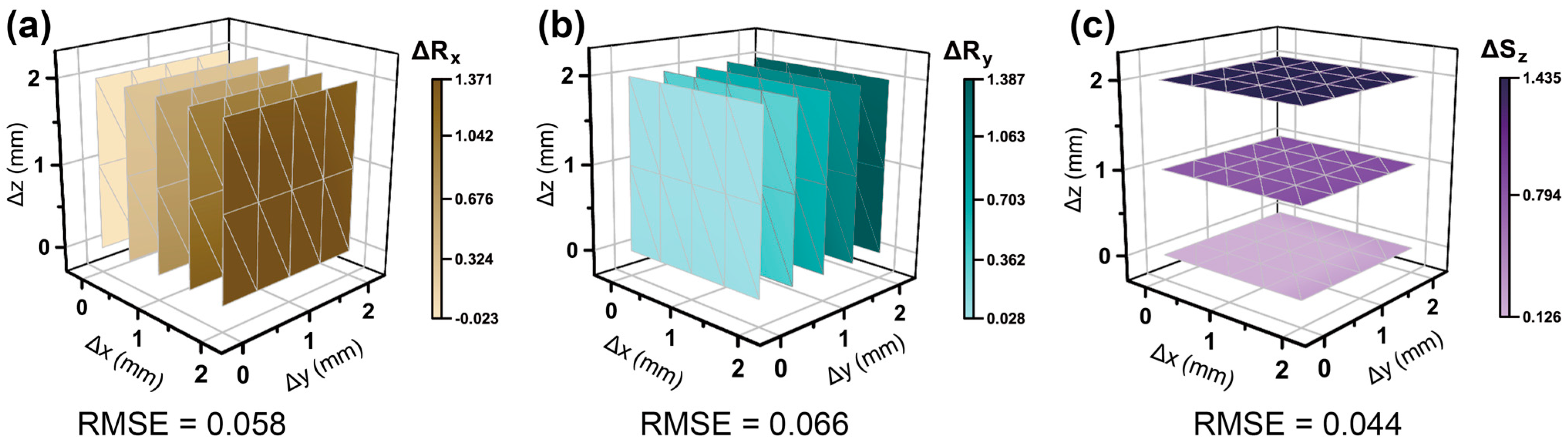
3.1. Simulation and Verification of the Spliced Magnetic Film
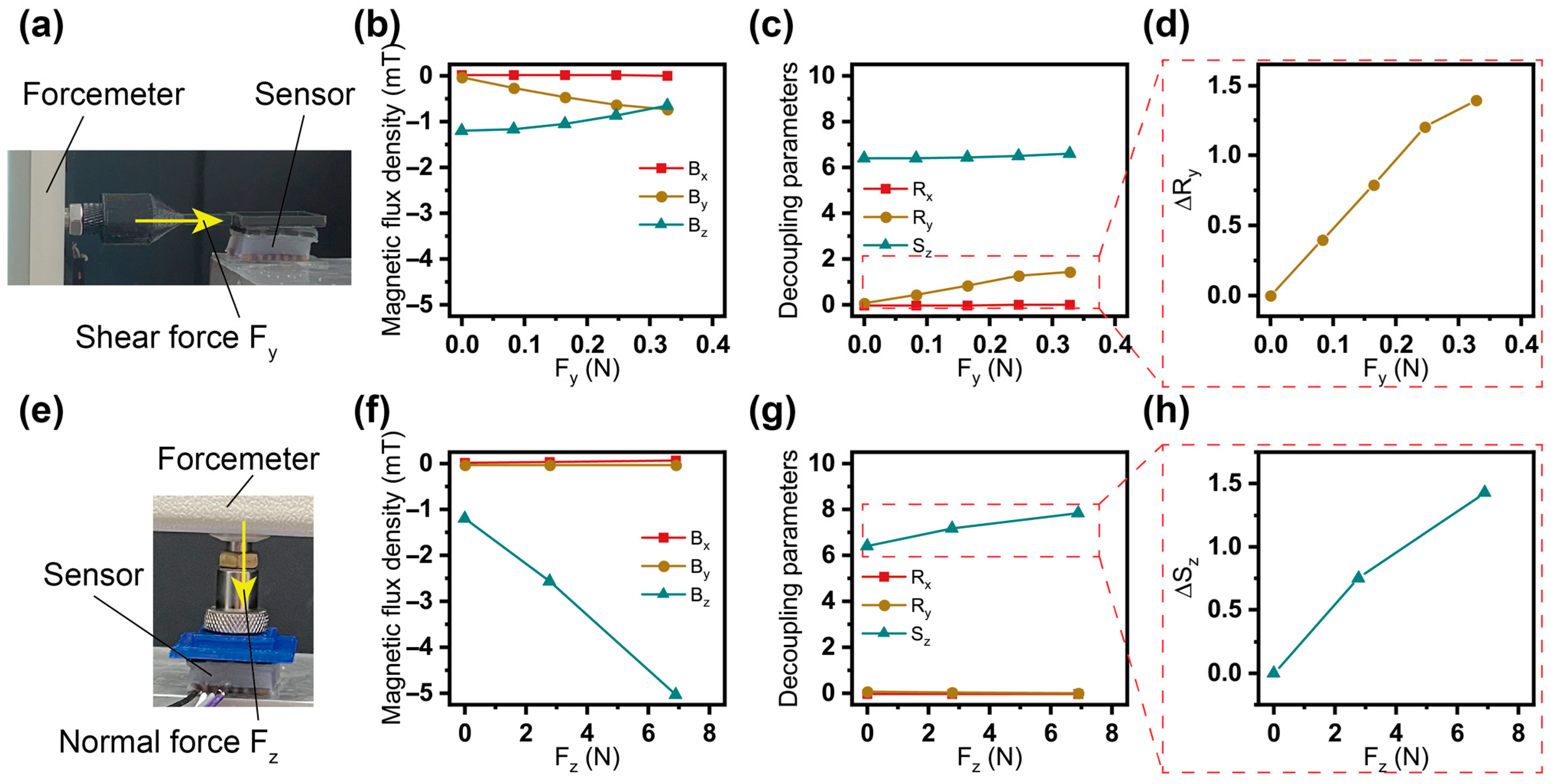
3.2. Decoupling Performance in Experiment
3.3. Force Sensing Experiment of the Tactile Sensor
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xie, Z.; Yuan, F.; Liu, J.; Tian, L.; Chen, B.; Fu, Z.; Mao, S.; Jin, T.; Wang, Y.; He, X.; et al. Octopus-inspired sensorized soft arm for environmental interaction. Sci. Robot. 2023, 8, eadh7852. [Google Scholar] [CrossRef] [PubMed]
- Yan, Y.; Hu, Z.; Yang, Z.; Yuan, W.; Song, C.; Pan, J.; Shen, Y. Soft magnetic skin for super-resolution tactile sensing with force self-decoupling. Sci. Robot. 2021, 6, eabc8801. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Duo, Y.; Liu, J.; Yuan, F.; Li, L.; Li, L.; Wang, G.; Chen, B.; Wang, S.; Yang, H.; et al. Touchless interactive teaching of soft robots through flexible bimodal sensory interfaces. Nat. Commun. 2022, 13, 5030. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Jia, H.; Zhou, J.; Huang, X.; Xu, L.; Jia, S.; Gao, Z.; Yao, K.; Li, D.; Zhang, B.; et al. Thin, soft, wearable system for continuous wireless monitoring of artery blood pressure. Nat. Commun. 2023, 14, 5009. [Google Scholar] [CrossRef] [PubMed]
- Gao, J.; Fan, Y.; Zhang, Q.; Luo, L.; Hu, X.; Li, Y.; Song, J.; Jiang, H.; Gao, X.; Zheng, L.; et al. Ultra-Robust and Extensible Fibrous Mechanical Sensors for Wearable Smart Healthcare. Adv. Mater. 2022, 34, 2107511. [Google Scholar] [CrossRef] [PubMed]
- Tee, B.C.; Chortos, A.; Berndt, A.; Nguyen, A.K.; Tom, A.; McGuire, A.; Lin, Z.C.; Tien, K.; Bae, W.G.; Wang, H.; et al. A skin-inspired organic digital mechanoreceptor. Science 2015, 350, 313–316. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, Y.; Zhou, Y.; Man, Q.; Hu, C.; Asghar, W.; Li, F.; Yu, Z.; Shang, J.; Liu, G.; et al. A skin-inspired tactile sensor for smart prosthetics. Sci. Robot. 2018, 3, eaat0429. [Google Scholar] [CrossRef]
- Johnson, K.O. The roles and functions of cutaneous mechanoreceptors. Curr. Opin. Neurobiol. 2001, 11, 455–461. [Google Scholar] [CrossRef]
- Abraira, V.E.; Ginty, D.D. The Sensory Neurons of Touch. Neuron 2013, 79, 618–639. [Google Scholar] [CrossRef]
- Wang, S.; Deng, W.; Yang, T.; Ao, Y.; Zhang, H.; Tian, G.; Deng, L.; Huang, H.; Huang, J.; Lan, B.; et al. Bioinspired MXene-Based Piezoresistive Sensor with Two-stage Enhancement for Motion Capture. Adv. Funct. Mater. 2023, 33, 2214503. [Google Scholar] [CrossRef]
- Sun, X.; Sun, J.; Li, T.; Zheng, S.; Wang, C.; Tan, W.; Zhang, J.; Liu, C.; Ma, T.; Qi, Z.; et al. Flexible Tactile Electronic Skin Sensor with 3D Force Detection Based on Porous CNTs/PDMS Nanocomposites. Nano-Micro Lett. 2019, 11, 57. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Yao, H.; Mo, J.; Chen, S.; Xie, Y.; Ma, S.; Chen, R.; Luo, T.; Ling, W.; Qin, L.; et al. Finger-inspired rigid-soft hybrid tactile sensor with superior sensitivity at high frequency. Nat. Commun. 2022, 13, 5076. [Google Scholar] [CrossRef] [PubMed]
- Zhou, P.; Zheng, Z.; Wang, B.; Guo, Y. Self-powered flexible piezoelectric sensors based on self-assembled 10 nm BaTiO3; nanocubes on glass fiber fabric. Nano Energy 2022, 99, 107400. [Google Scholar] [CrossRef]
- Bai, N.; Xue, Y.; Chen, S.; Shi, L.; Shi, J.; Zhang, Y.; Hou, X.; Cheng, Y.; Huang, K.; Wang, W.; et al. A robotic sensory system with high spatiotemporal resolution for texture recognition. Nat. Commun. 2023, 14, 7121. [Google Scholar] [CrossRef] [PubMed]
- Fu, C.; Tang, W.; Miao, Y.; Xu, A.; Nilghaz, A.; Xu, W.; Dong, K.; Su, B.; Xia, Z. Large-scalable fabrication of liquid metal-based double helix core-spun yarns for capacitive sensing, energy harvesting, and thermal management. Nano Energy 2023, 106, 108078. [Google Scholar] [CrossRef]
- Hou, X.; Zhang, L.; Su, Y.; Gao, G.; Liu, Y.; Na, Z.; Xu, Q.; Ding, T.; Xiao, L.; Li, L.; et al. A space crawling robotic bio-paw (SCRBP) enabled by triboelectric sensors for surface identification. Nano Energy 2023, 105, 108013. [Google Scholar] [CrossRef]
- Qu, X.; Liu, Z.; Tan, P.; Wang, C.; Liu, Y.; Feng, H.; Luo, D.; Li, Z.; Wang, Z.L. Artificial tactile perception smart finger for material identification based on triboelectric sensing. Sci. Adv. 2022, 8, eabq2521. [Google Scholar] [CrossRef]
- Wei, R.; He, J.; Ge, S.; Liu, H.; Ma, X.; Tao, J.; Cui, X.; Mo, X.; Li, Z.; Wang, C.; et al. Self-Powered All-Optical Tactile Sensing Platform for User-Interactive Interface. Adv. Mater. Technol. 2023, 8, 2200757. [Google Scholar] [CrossRef]
- Sferrazza, C.; D’Andrea, R. Sim-to-Real for High-Resolution Optical Tactile Sensing: From Images to Three-Dimensional Contact Force Distributions. Soft Robot. 2022, 9, 926–937. [Google Scholar] [CrossRef]
- Zhang, X.; Ai, J.; Ma, Z.; Du, Z.; Chen, D.; Zou, R.; Su, B. Magnetoelectric soft composites with a self-powered tactile sensing capacity. Nano Energy 2020, 69, 104391. [Google Scholar] [CrossRef]
- Ma, Z.; Ai, J.; Zhang, X.; Du, Z.; Wu, Z.; Wang, K.; Chen, D.; Su, B. Merkel’s Disks Bioinspired Self-Powered Flexible Magnetoelectric Sensors Toward the Robotic Arm’s Tactile Perceptual Functioning and Smart Learning. Adv. Intell. Syst. 2020, 2, 1900140. [Google Scholar] [CrossRef]
- Li, D.; Zhou, J.; Yao, K.; Liu, S.; He, J.; Su, J.; Qu, Q.; Gao, Y.; Song, Z.; Yiu, C.; et al. Touch IoT enabled by wireless self-sensing and haptic-reproducing electronic skin. Sci. Adv. 2022, 8, eade2450. [Google Scholar] [CrossRef] [PubMed]
- Le Signor, T.; Dupre, N.; Close, G.F. A Gradiometric Magnetic Force Sensor Immune to Stray Magnetic Fields for Robotic Hands and Grippers. IEEE Robot. Autom. Let. 2022, 7, 3070–3076. [Google Scholar] [CrossRef]
- Wang, H.; de Boer, G.; Kow, J.; Alazmani, A.; Ghajari, M.; Hewson, R.; Culmer, P. Design Methodology for Magnetic Field-Based Soft Tri-Axis Tactile Sensors. Sensors 2016, 16, 1356. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Zhu, H.; Chen, R.; Hu, S.; Jia, Z.; Yu, H.; Qu, S. Design of 3D Magnetic Tactile Sensors with High Sensing Accuracy Guided by the Theoretical Model. Adv. Intell. Syst. 2023, 5, 2200291. [Google Scholar] [CrossRef]
- Zhang, C.; Li, X.; Jiang, L.; Tang, D.; Xu, H.; Zhao, P.; Fu, J.; Zhou, Q.; Chen, Y. 3D Printing of Functional Magnetic Materials: From Design to Applications. Adv. Funct. Mater. 2021, 31, 2102777. [Google Scholar] [CrossRef]
- Hu, Z.; Zhang, C.; Sun, H.; Dai, H.; Tang, D.; Hu, H.; Li, T.; Fu, J.; Zhao, P. A microstructure enhancement method for hard magnetic particle chains based on magnetic field oscillation sieve. Mater. Des. 2024, 237, 112588. [Google Scholar] [CrossRef]
- Hu, Z.; Zhang, C.; Sun, H.; Ma, X.; Zhao, P. Length manipulation of hard magnetic particle chains under rotating magnetic fields. Sens. Actuators A Phys. 2023, 361, 114562. [Google Scholar] [CrossRef]
- Kim, Y.; Yuk, H.; Zhao, R.; Chester, S.A.; Zhao, X. Printing ferromagnetic domains for untethered fast-transforming soft materials. Nature 2018, 558, 274–279. [Google Scholar] [CrossRef]
- Lin, D.; Yang, F.; Gong, D.; Li, R. Bio-inspired magnetic-driven folded diaphragm for biomimetic robot. Nat. Commun. 2023, 14, 163. [Google Scholar] [CrossRef]
- Dai, H.; Zhang, C.; Pan, C.; Hu, H.; Ji, K.; Sun, H.; Lyu, C.; Tang, D.; Li, T.; Fu, J.; et al. Split-Type Magnetic Soft Tactile Sensor with 3D Force Decoupling. Adv. Mater. 2023, 2310145. [Google Scholar] [CrossRef] [PubMed]
| Parameter | Splicing Model | Ideal Model |
|---|---|---|
| Remanence () | 0.12 (T) | 0.12 (T) |
| Wavelength () | 10 (mm) | 10 (mm) |
| Film size | 20 × 20 (mm) | Infinite |
| Thickness (d) | 1 (mm) | 1 (mm) |
| Range of study | x: −2~2, y: −2~2, z: −5~−3 (mm) | x: −2~2, y: −2~2, z: −5~−3 (mm) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, H.; Wu, Z.; Meng, C.; Zhang, C.; Zhao, P. A Magnet Splicing Method for Constructing a Three-Dimensional Self-Decoupled Magnetic Tactile Sensor. Magnetochemistry 2024, 10, 6. https://doi.org/10.3390/magnetochemistry10010006
Dai H, Wu Z, Meng C, Zhang C, Zhao P. A Magnet Splicing Method for Constructing a Three-Dimensional Self-Decoupled Magnetic Tactile Sensor. Magnetochemistry. 2024; 10(1):6. https://doi.org/10.3390/magnetochemistry10010006
Chicago/Turabian StyleDai, Huangzhe, Zheyan Wu, Chenxian Meng, Chengqian Zhang, and Peng Zhao. 2024. "A Magnet Splicing Method for Constructing a Three-Dimensional Self-Decoupled Magnetic Tactile Sensor" Magnetochemistry 10, no. 1: 6. https://doi.org/10.3390/magnetochemistry10010006
APA StyleDai, H., Wu, Z., Meng, C., Zhang, C., & Zhao, P. (2024). A Magnet Splicing Method for Constructing a Three-Dimensional Self-Decoupled Magnetic Tactile Sensor. Magnetochemistry, 10(1), 6. https://doi.org/10.3390/magnetochemistry10010006








