Direct Observation of Short Large-Amplitude Magnetic Field Structures from Formation to Destruction
Abstract
:1. Introduction
2. Data
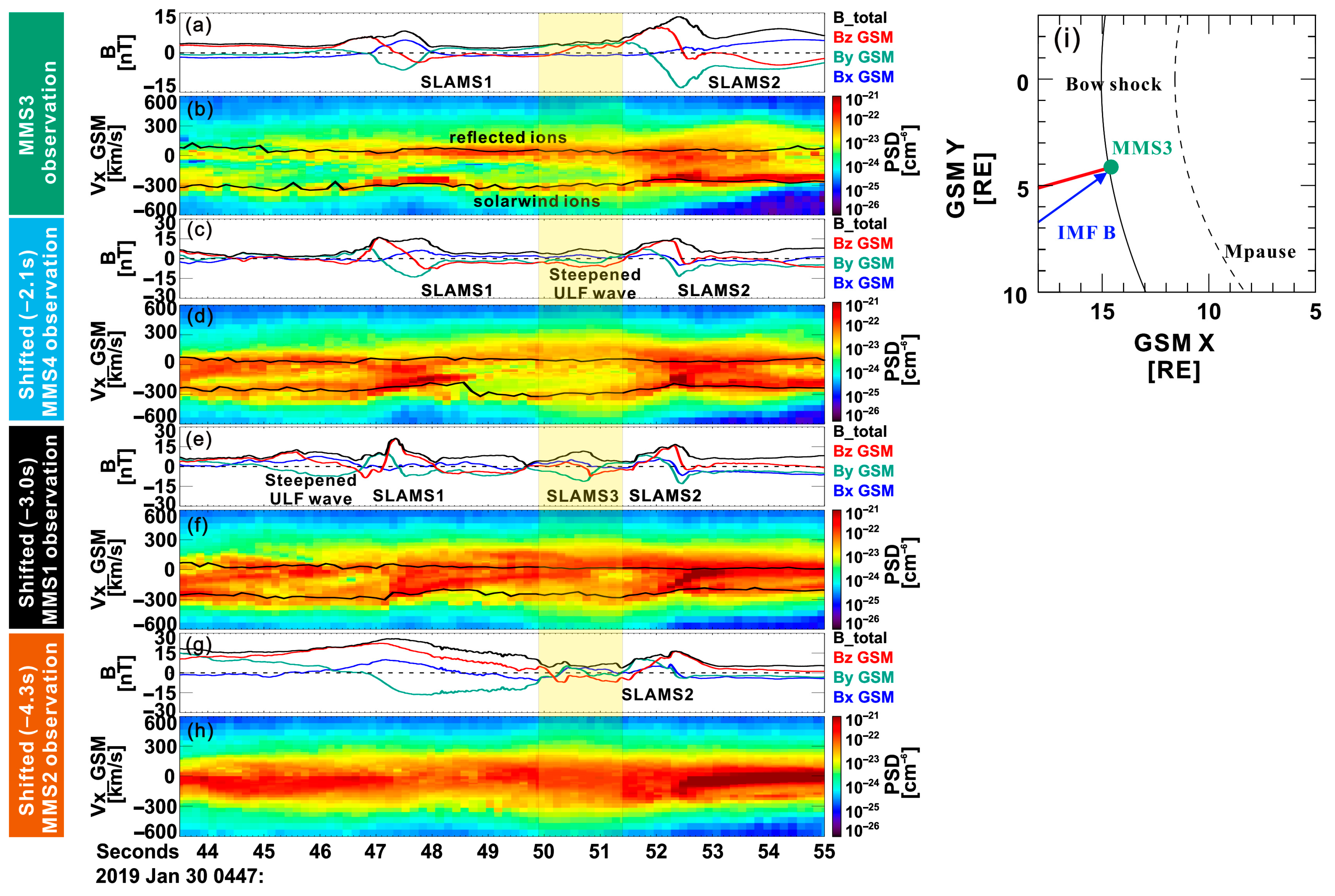
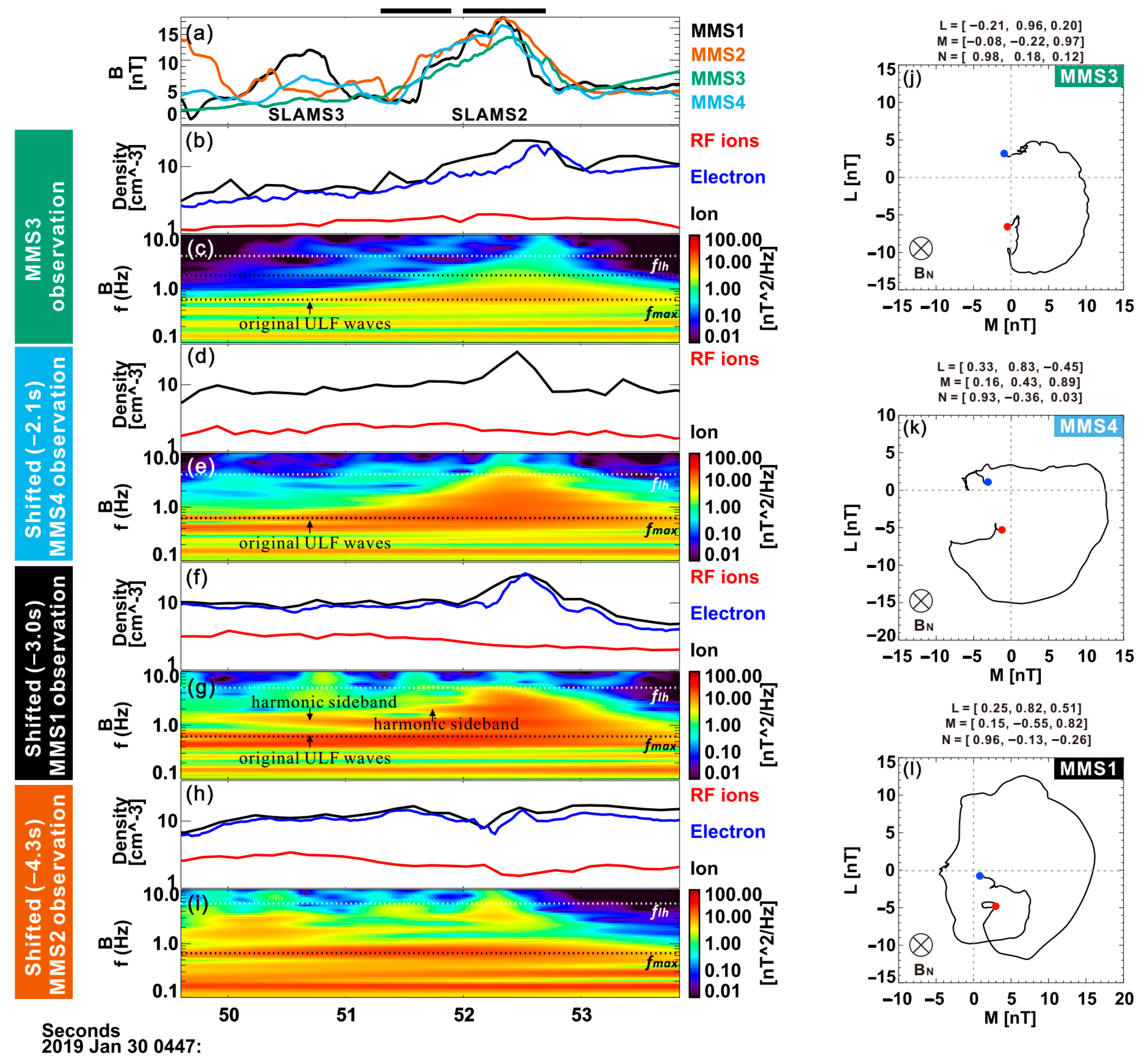
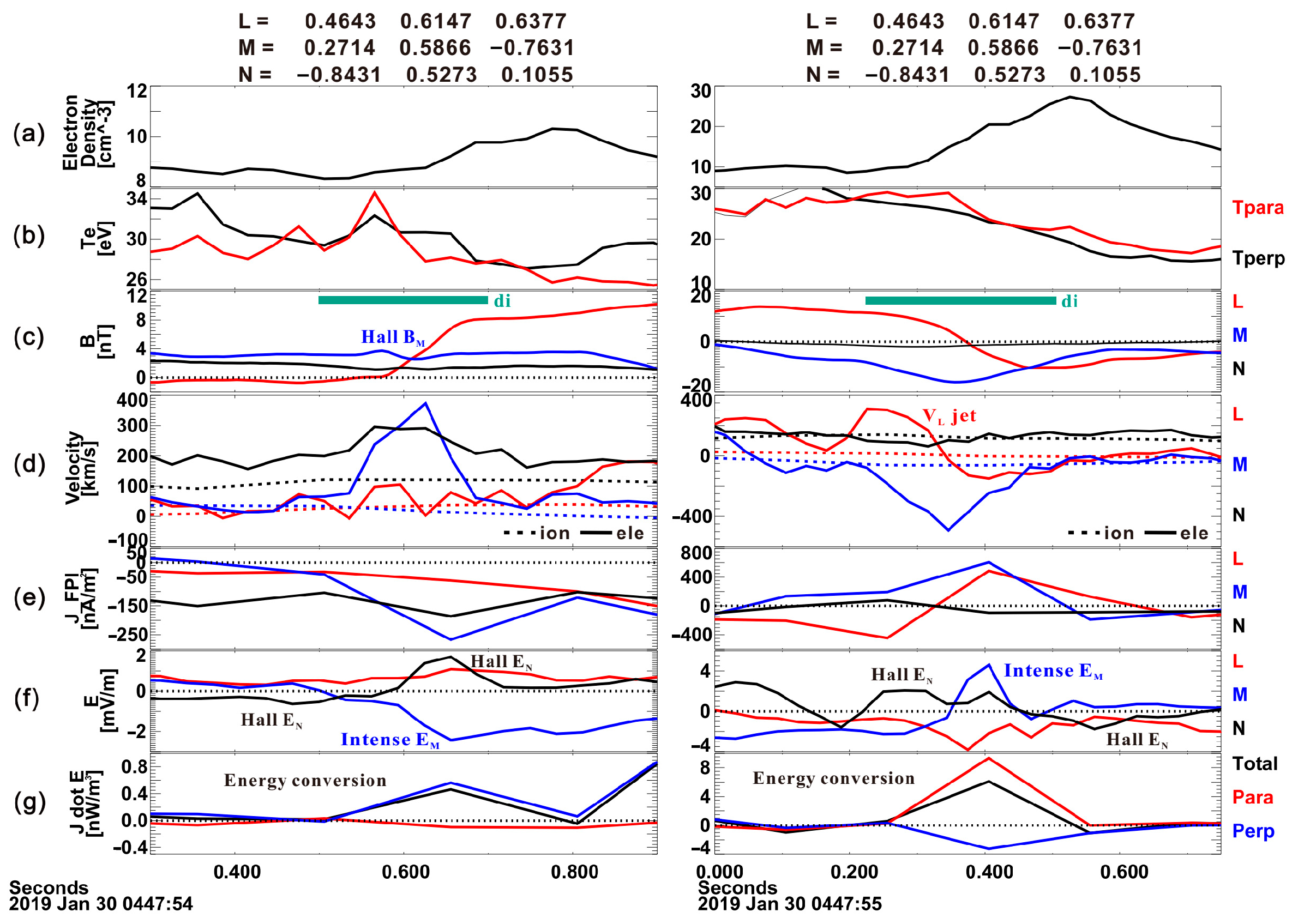
3. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Burgess, D.; Lucek, E.A.; Scholer, M.; Bale, S.D.; Balikhin, M.A.; Balogh, A.; Horbury, T.S.; Krasnoselskikh, V.V.; Kucharek, H.; Lembège, B.; et al. Quasi-parallel shock structure and processes. Space Sci. Rev. 2005, 118, 205–222. [Google Scholar] [CrossRef]
- Bale, S.D.; Balikhin, M.A.; Horbury, T.S.; Krasnoselskikh, V.V.; Kucharek, H.; Möbius, E.; Walker, S.N.; Balogh, A.; Burgess, D.; Lembège, B.; et al. Quasi-perpendicular shock structure and processes. Space Sci. Rev. 2005, 118, 161–203. [Google Scholar] [CrossRef]
- Zhang, H.; Zong, Q.G.; Connor, H.; Delamere, P.; Facskó, G.; Han, D.S.; Hasegawa, H.; Kallio, E.; Kis, A.; Le, G.; et al. Dayside Transient Phenomena and Their Impact on the Magnetosphere and Ionosphere. Space Sci. Rev. 2022, 218, 40. [Google Scholar] [CrossRef] [PubMed]
- Gary, S.P. Electromagnetic Ion Ion Instabilities and Their Consequences in Space Plasmas—A Review. Space Sci. Rev. 1991, 56, 373–415. [Google Scholar] [CrossRef]
- Hada, T.; Kennel, C.F.; Terasawa, T. Excitation of Compressional Waves and the Formation of Shocklets in the Earth’s Foreshock. J. Geophys. Res. Space Phys. 1987, 92, 4423–4435. [Google Scholar] [CrossRef]
- Omidi, N.; Winske, D. Steepening of Kinetic Magnetosonic Waves into Shocklets—Simulations and Consequences for Planetary Shocks and Comets. J. Geophys. Res. Space Phys. 1990, 95, 2281–2300. [Google Scholar] [CrossRef]
- Dubouloz, N.; Scholer, M. 2-Dimensional Simulations of Magnetic Pulsations Upstream of the Earth’s Bow Shock. J. Geophys. Res. Space Phys. 1995, 100, 9461–9474. [Google Scholar] [CrossRef]
- Onsager, T.G.; Winske, D.; Thomsen, M.F. Interaction of a Finite-Length Ion-Beam with a Background Plasma—Reflected Ions at the Quasi-Parallel Bow Shock. J. Geophys. Res. Space Phys. 1991, 96, 1775–1788. [Google Scholar] [CrossRef]
- Hoppe, M.M.; Russell, C.T.; Frank, L.A.; Eastman, T.E.; Greenstadt, E.W. Upstream Hydromagnetic-Waves and Their Association with Backstreaming Ion Populations—Isee-1 and Isee-2 Observations. J. Geophys. Res. Space Phys. 1981, 86, 4471–4492. [Google Scholar] [CrossRef]
- Lucek, E.A.; Horbury, T.S.; Balogh, A.; Dandouras, I.; Rème, H. Cluster observations of structures at quasi-parallel bow shocks. Ann. Geophys. 2004, 22, 2309–2313. [Google Scholar] [CrossRef]
- Lucek, E.A.; Horbury, T.S.; Dandouras, I.; Rème, H. Cluster observations of the Earth’s quasi-parallel bow shock. J. Geophys. Res. Space Phys. 2008, 113. [Google Scholar] [CrossRef]
- Mann, G.; Luhr, H.; Baumjohann, W. Statistical-Analysis of Short Large-Amplitude Magnetic-Field Structures in the Vicinity of the Quasi-Parallel Bow Shock. J. Geophys. Res. Space Phys. 1994, 99, 13315–13323. [Google Scholar] [CrossRef]
- Schwartz, S.J.; Burgess, D. Quasi-Parallel Shocks—A Patchwork of 3-Dimensional Structures. Geophys. Res. Lett. 1991, 18, 373–376. [Google Scholar] [CrossRef]
- Wilson, L.B. Low Frequency Waves at and Upstream of Collisionless Shocks. In Low-Frequency Waves in Space Plasmas; John Wiley & Sons: Hoboken, NJ, USA, 2016; pp. 269–291. [Google Scholar]
- Wilson, L.B.; Koval, A.; Sibeck, D.G.; Szabo, A.; Cattell, C.A.; Kasper, J.C.; Maruca, B.A.; Pulupa, M.; Salem, C.S.; Wilber, M. Shocklets, SLAMS, and field-aligned ion beams in the terrestrial foreshock. J. Geophys.Res. Space Phys. 2013, 118, 957–966. [Google Scholar] [CrossRef]
- Bai, S.C.; Shi, Q.Q.; Zhang, H.; Guo, R.L.; Shen, X.C.; Liu, T.Z.; Degeling, A.W.; Tian, A.M.; Bu, Y.D.; Zhang, S.; et al. Electron Dynamics and Whistler-Mode Waves Inside the Short Large-Amplitude Magnetic Field Structures. J. Geophys. Res. Space Phys. 2023, 128, e2023JA031816. [Google Scholar] [CrossRef]
- Bai, S.-C.; Shi, Q.; Shen, X.-C.; Tian, A.; Zhang, H.; Guo, R.; Wang, M.; Degeling, A.W.; Bu, Y.; Zhang, S.; et al. Whistler-Mode Waves Inside Short Large-Amplitude Magnetic Field Structures: Characteristics and Generation Mechanisms. J. Geophys. Res. Space Phys. 2024, 129, e2023JA032392. [Google Scholar] [CrossRef]
- Liu, T.Z.; Hao, Y.F.; Wilson, L.B.; Turner, D.L.; Zhang, H. Magnetospheric Multiscale Observations of Earth’s Oblique Bow Shock Reformation by Foreshock Ultralow-Frequency Waves. Geophys. Res. Lett. 2021, 48, e2020GL091184. [Google Scholar] [CrossRef]
- Johlander, A.; Battarbee, M.; Turc, L.; Ganse, U.; Pfau-Kempf, Y.; Grandin, M.; Suni, J.; Tarvus, V.; Bussov, M.; Zhou, H.Y.; et al. Quasi-Parallel Shock Reformation Seen by Magnetospheric Multiscale and Ion-Kinetic Simulations. Geophys. Res. Lett. 2022, 49, e2021GL096335. [Google Scholar] [CrossRef]
- Bessho, N.; Chen, L.J.; Wang, S.; Hesse, M.; Wilson, L.B. Magnetic Reconnection in a Quasi-Parallel Shock: Two-Dimensional Local Particle-in-Cell Simulation. Geophys. Res. Lett. 2019, 46, 9352–9361. [Google Scholar] [CrossRef]
- Bessho, N.; Chen, L.J.; Wang, S.; Hesse, M.; Wilson, L.B.; Ng, J. Magnetic reconnection and kinetic waves generated in the Earth’s quasi-parallel bow shock. Phys. Plasmas 2020, 27, 092901. [Google Scholar] [CrossRef]
- Gingell, I.; Schwartz, S.J.; Burgess, D.; Johlander, A.; Russell, C.T.; Burch, J.L.; Ergun, R.E.; Fuselier, S.; Gershman, D.J.; Giles, B.L.; et al. MMS Observations and Hybrid Simulations of Surface Ripples at a Marginally Quasi-Parallel Shock. J. Geophys. Res. Space Phys. 2017, 122, 11003–11017. [Google Scholar] [CrossRef]
- Gingell, I.; Schwartz, S.J.; Eastwood, J.P.; Burch, J.L.; Ergun, R.E.; Fuselier, S.; Gershman, D.J.; Giles, B.L.; Khotyaintsev, Y.V.; Lavraud, B.; et al. Observations of Magnetic Reconnection in the Transition Region of Quasi-Parallel Shocks. Geophys. Res. Lett. 2019, 46, 1177–1184. [Google Scholar] [CrossRef]
- Wang, S.; Chen, L.J.; Bessho, N.; Hesse, M.; Wilson, L.B.; Giles, B.; Moore, T.E.; Russell, C.T.; Torbert, R.B.; Burch, J.L. Observational Evidence of Magnetic Reconnection in the Terrestrial Bow Shock Transition Region. Geophys. Res. Lett. 2019, 46, 562–570. [Google Scholar] [CrossRef]
- Wang, S.; Chen, L.J.; Bessho, N.; Hesse, M.; Wilson, L.B.; Denton, R.; Ng, J.; Giles, B.; Torbert, R.; Burch, J. Ion-scale Current Structures in Short Large-amplitude Magnetic Structures. Astrophys. J. 2020, 898, 121. [Google Scholar] [CrossRef]
- Bai, S.C.; Shi, Q.Q.; Liu, T.Z.; Zhang, H.; Yue, C.; Sun, W.J.; Tian, A.M.; Degeling, A.W.; Bortnik, J.; Rae, I.J.; et al. Ion-Scale Flux Rope Observed inside a Hot Flow Anomaly. Geophys. Res. Lett. 2020, 47, e2019GL085933. [Google Scholar] [CrossRef]
- Liu, T.Z.; Lu, S.; Turner, D.L.; Gingell, I.; Angelopoulos, V.; Zhang, H.; Artemyev, A.; Burch, J.L. Magnetospheric Multiscale (MMS) Observations of Magnetic Reconnection in Foreshock Transients. J. Geophys. Res. Space Phys. 2020, 125, e2020JA027822. [Google Scholar] [CrossRef]
- Treumann, R.A. Fundamentals of collisionless shocks for astrophysical application, 1. Non-relativistic shocks. Astron. Astrophys. Rev. 2009, 17, 409–535. [Google Scholar] [CrossRef]
- Raptis, S.; Karlsson, T.; Plaschke, F.; Kullen, A.; Lindqvist, P.A. Classifying Magnetosheath Jets Using MMS: Statistical Properties. J. Geophys. Res. Space Phys. 2020, 125, e2019JA027754. [Google Scholar] [CrossRef]
- Karlsson, T.; Kullen, A.; Liljeblad, E.; Brenning, N.; Nilsson, H.; Gunell, H.; Hamrin, M. On the origin of magnetosheath plasmoids and their relation to magnetosheath jets. J. Geophys. Res. Space Phys. 2015, 120, 7390–7403. [Google Scholar] [CrossRef]
- Plaschke, F.; Hietala, H.; Archer, M.; Blanco-Cano, X.; Kajdic, P.; Karlsson, T.; Lee, S.H.; Omidi, N.; Palmroth, M.; Roytershteyn, V.; et al. Jets Downstream of Collisionless Shocks. Space Sci. Rev. 2018, 214, 81. [Google Scholar] [CrossRef]
- Wang, X.Y.; Lin, Y. Generation of nonlinear Alfven and magnetosonic waves by beam-plasma interaction. Phys. Plasmas 2003, 10, 3528–3538. [Google Scholar] [CrossRef]
- Winske, D.; Leroy, M.M. Diffuse Ions Produced by Electromagnetic Ion-Beam Instabilities. J. Geophys. Res. Space Phys. 1984, 89, 2673–2688. [Google Scholar] [CrossRef]
- Akimoto, K.; Winske, D.; Gary, S.P.; Thomsen, M.F. Nonlinear Evolution of Electromagnetic Ion-Beam Instabilities. J. Geophys. Res. Space Phys. 1993, 98, 1419–1433. [Google Scholar] [CrossRef]
- Gary, S.P.; Smith, C.W.; Lee, M.A.; Goldstein, M.L.; Forslund, D.W. Electromagnetic Ion-Beam Instabilities. Phys. Fluids 1984, 27, 1852–1862. [Google Scholar] [CrossRef]
- Le, G.; Russell, C.T. The Morphology of ULF Waves in the Earth’s Foreshock. In Solar Wind Sources of Magnetospheric Ultra-Low-Frequency Waves; John Wiley & Sons: Hoboken, NJ, USA, 1994; pp. 87–98. [Google Scholar]
- Scholer, M. Upstream waves, shocklets, short large-amplitude magnetic structures and the cyclic behavior of oblique quasi-parallel collisionless shocks. J. Geophys. Res. Space Phys. 1993, 98, 47–57. [Google Scholar] [CrossRef]
- Giacalone, J.; Schwartz, S.J.; Burgess, D. Observations of suprathermal ions in association with SLAMS. Geophys. Res. Lett. 1993, 20, 149–152. [Google Scholar] [CrossRef]
- Schwartz, S.J.; Burgess, D.; Wilkinson, W.P.; Kessel, R.L.; Dunlop, M.; Luhr, H. Observations of Short Large-Amplitude Magnetic-Structures at a Quasi-Parallel Shock. J. Geophys. Res. Space Phys. 1992, 97, 4209–4227. [Google Scholar] [CrossRef]
- Scholer, M.; Kucharek, H.; Shinohara, I. Short large-amplitude magnetic structures and whistler wave precursors in a full-particle quasi-parallel shock simulation. J. Geophys. Res. Space Phys. 2003, 108. [Google Scholar] [CrossRef]
- Tsubouchi, K.; Lembège, B. Full particle simulations of short large-amplitude magnetic structures (SLAMS) in quasi-parallel shocks. J. Geophys. Res. Space Phys. 2004, 109. [Google Scholar] [CrossRef]
- Chen, L.J.; Wang, S.; Ng, J.; Bessho, N.; Tang, J.M.; Fung, S.F.; Le, G.; Gershman, D.; Giles, B.; Russell, C.T.; et al. Solitary Magnetic Structures at Quasi-Parallel Collisionless Shocks: Formation. Geophys. Res. Lett. 2021, 48, e2020GL090800. [Google Scholar] [CrossRef]
- Burch, J.L.; Moore, T.E.; Torbert, R.B.; Giles, B.L. Magnetospheric Multiscale Overview and Science Objectives. Space Sci. Rev. 2016, 199, 5–21. [Google Scholar] [CrossRef]
- Russell, C.T.; Anderson, B.J.; Baumjohann, W.; Bromund, K.R.; Dearborn, D.; Fischer, D.; Le, G.; Leinweber, H.K.; Leneman, D.; Magnes, W.; et al. The Magnetospheric Multiscale Magnetometers. Space Sci. Rev. 2016, 199, 189–256. [Google Scholar] [CrossRef]
- Pollock, C.; Moore, T.; Jacques, A.; Burch, J.; Gliese, U.; Saito, Y.; Omoto, T.; Avanov, L.; Barrie, A.; Coffey, V.; et al. Fast Plasma Investigation for Magnetospheric Multiscale. Space Sci. Rev. 2016, 199, 331–406. [Google Scholar] [CrossRef]
- Lindqvist, P.A.; Olsson, G.; Torbert, R.B.; King, B.; Granoff, M.; Rau, D.; Needell, G.; Turco, S.; Dors, I.; Beckman, P.; et al. The Spin-Plane Double Probe Electric Field Instrument for MMS. Space Sci. Rev. 2016, 199, 137–165. [Google Scholar] [CrossRef]
- Ergun, R.E.; Tucker, S.; Westfall, J.; Goodrich, K.A.; Malaspina, D.M.; Summers, D.; Wallace, J.; Karlsson, M.; Mack, J.; Brennan, N.; et al. The Axial Double Probe and Fields Signal Processing for the MMS Mission. Space Sci. Rev. 2016, 199, 167–188. [Google Scholar] [CrossRef]
- Chao, J.K.; Wu, D.J.; Lin, C.H.; Yang, Y.H.; Wang, X.; Kesse, M.; Chen, S.H.; Lepping, R.P. Models for the size and shape of the Earth’s magnetopause and bow shock. Cospar Colloq. 2002, 12, 127–135. [Google Scholar]
- Sonnerup, B.U.Ö. Magnetic field reconnection. In Solar System Plasma Physics; Lanzerotti, L.J., Kennel, C.F., Parker, E.N., Eds.; North Holland: Amsterdam, The Netherlands, 1979; Volume 3. [Google Scholar]
- Sonnerup, B.U.Ö.; Scheible, M. Minimum and maximum variance analysis, in Analysis Methods for Multi-Spacecraft Data. In Analysis Methods for Multi-Spacecraft Data; Paschmann, G., Daly, P.W., Eds.; ESA Publications Division: Noordwijk, The Netherlands, 1998; pp. 185–220. [Google Scholar]
- Zahibo, N.; Slunyaev, A.; Talipova, T.; Pelinovsky, E.; Kurkin, A.; Polukhina, O. Strongly nonlinear steepening of long interfacial waves. Nonlinear Proc. Geophys. 2007, 14, 247–256. [Google Scholar] [CrossRef]
- Xie, H.S. BO: A unified tool for plasma waves and instabilities analysis. Comput. Phys. Commun. 2019, 244, 343–371. [Google Scholar] [CrossRef]
- Phan, T.D.; Eastwood, J.P.; Shay, M.A.; Drake, J.F.; Sonnerup, B.U.Ö.; Fujimoto, M.; Cassak, P.A.; Oieroset, M.; Burch, J.L.; Torbert, R.B.; et al. Electron magnetic reconnection without ion coupling in Earth’s turbulent magnetosheath. Nature 2018, 557, 202–206. [Google Scholar] [CrossRef]
- Lu, S.; Lu, Q.M.; Wang, R.S.; Pritchett, P.L.; Hubbert, M.; Qi, Y.; Huang, K.; Li, X.M.; Russell, C.T. Electron-Only Reconnection as a Transition From Quiet Current Sheet to Standard Reconnection in Earth’s Magnetotail: Particle-In-Cell Simulation and Application to MMS Data. Geophys. Res. Lett. 2022, 49, e2022GL098547. [Google Scholar] [CrossRef]
- Kennel, C.F.; Edmiston, J.P.; Hada, T. A Quarter Century of Collisionless Shock Research. In Collisionless Shocks in the Heliosphere: A Tutorial Review; American Geophysical Union: Washington, DC, USA, 1985; pp. 1–36. [Google Scholar]
- Muschietti, L.; Lembège, B. Two-stream instabilities from the lower-hybrid frequency to the electron cyclotron frequency: Application to the front of quasi-perpendicular shocks. Ann. Geophys. 2017, 35, 1093–1112. [Google Scholar] [CrossRef]
- Wu, C.S.; Zhou, Y.M.; Tsai, S.T.; Guo, S.C.; Winske, D.; Papadopoulos, K. A Kinetic Cross-Field Streaming Instability. Phys. Fluids 1983, 26, 1259–1267. [Google Scholar] [CrossRef]
- Mcbride, J.B.; Ott, E.; Boris, J.P.; Orens, J.H. Theory and Simulation of Turbulent Heating by Modified 2-Stream Instability. Phys. Fluids 1972, 15, 2367–2383. [Google Scholar] [CrossRef]
- Lemons, D.S.; Winske, D.; Gary, S.P. Non-Linear Theory and Computer-Simulation of Weibel Instability. Bull. Am. Phys. Soc. 1978, 23, 607. [Google Scholar]
- Angelopoulos, V.; Cruce, P.; Drozdov, A.; Grimes, E.W.; Hatzigeorgiu, N.; King, D.A.; Larson, D.; Lewis, J.W.; McTiernan, J.M.; Roberts, D.A.; et al. The Space Physics Environment Data Analysis System (SPEDAS). Space Sci. Rev. 2019, 215, 9. [Google Scholar] [CrossRef]


| Satellite | Ion | Density (1/cm−3) | Vth‖ (km/s) | Vthꓕ (km/s) | Vdrift‖ (km/s) | Vdriftꓕ (km/s) | δB/B0 from MMS | δB/B0 |
|---|---|---|---|---|---|---|---|---|
| MMS 3 | Solar wind ions (SW) | 0.7 | 30 | 50 | 200 | 190 | / | 0.93 |
| Reflected ions (rf) | 0.2 | 120 | 40 | 100 | −20 | |||
| Background ions | 0.02 | 20 | 20 | 20 | −20 | |||
| MMS 4 | Solar wind ions | 0.7 | 70 | 40 | −200 | 180 | 1.79 | 1.84 |
| Reflected ions | 1.2 | 80 | 120 | 80 | 80 | |||
| Background ions | 0.1 | 30 | 30 | 40 | 0 | |||
| MMS 1 | Solar wind ions | 0.7 | 60 | 40 | −160 | 10 | 2.81 | 3.21 |
| Reflected ions | 1.2 | 125 | 100 | −25 | 175 | |||
| Background ions | 0.12 | 25 | 25 | 20 | −25 | |||
| 2.5 | 175 | 120 | −105 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, S.-C.; Shi, Q.; Guo, R.; Degeling, A.W.; Zhang, H.; Tian, A.; Bu, Y. Direct Observation of Short Large-Amplitude Magnetic Field Structures from Formation to Destruction. Magnetochemistry 2024, 10, 54. https://doi.org/10.3390/magnetochemistry10080054
Bai S-C, Shi Q, Guo R, Degeling AW, Zhang H, Tian A, Bu Y. Direct Observation of Short Large-Amplitude Magnetic Field Structures from Formation to Destruction. Magnetochemistry. 2024; 10(8):54. https://doi.org/10.3390/magnetochemistry10080054
Chicago/Turabian StyleBai, Shi-Chen, Quanqi Shi, Ruilong Guo, Alexander W. Degeling, Hui Zhang, Anmin Tian, and Yude Bu. 2024. "Direct Observation of Short Large-Amplitude Magnetic Field Structures from Formation to Destruction" Magnetochemistry 10, no. 8: 54. https://doi.org/10.3390/magnetochemistry10080054
APA StyleBai, S.-C., Shi, Q., Guo, R., Degeling, A. W., Zhang, H., Tian, A., & Bu, Y. (2024). Direct Observation of Short Large-Amplitude Magnetic Field Structures from Formation to Destruction. Magnetochemistry, 10(8), 54. https://doi.org/10.3390/magnetochemistry10080054






