Ferromagnetic Multilayers: Magnetoresistance, Magnetic Anisotropy, and Beyond
Abstract
:1. Introduction
1.1. Giant Magnetoresistance Effect
1.2. Tunnel Magnetoresistance Effect
1.3. Colossal Magnetoresistance Effect
1.4. Spin Torque Transfer Effect
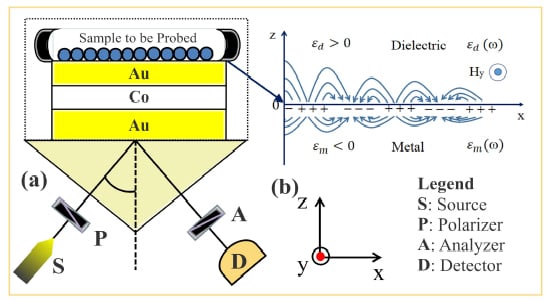
2. Experimental Methods
3. Theoretical Models
3.1. Electrical Conduction in Metals
3.1.1. Mott’s Two-Current Model Applied to Metals
3.2. Electrical Conduction in Multilayers
Mott’s Two-Current Model Applied to Multilayers
4. Potential Applications
5. Conclusions, Challenges, Potential Applications, and Future Prospects
Acknowledgments
Conflicts of Interest
References
- Baibich, M.N.; Broto, J.M.; Fert, A.; Dau, F.N.V.; Petroff, F.; Etienne, P.; Creuzet, G.; Friederich, A.; Chazelas, J. Giant Magnetoresistance of (001)Fe/(001)Cr Magnetic Superlattices. Phys. Rev. Lett. 1988, 61, 2472–2475. [Google Scholar] [CrossRef] [PubMed]
- Binasch, G.; Grünberg, P.; Saurenbach, F.; Zinn, W. Enhanced magnetoresistance in layered magnetic structures with antiferromagnetic interlayer exchange. Phys. Rev. B 1989, 39, 4828–4830. [Google Scholar] [CrossRef]
- Fullerton, E.; Conover, M.; Mattson, J.; Sowers, C.; Bader, S. 150 % magnetoresistance in sputtered Fe/Cr (100) superlattices. Appl. Phys. Lett. 1993, 63, 1699–1701. [Google Scholar] [CrossRef]
- Morrow, P.; Tang, X.T.; Parker, T.C.; Shima, M.; Wang, G.C. Magnetoresistance of oblique angle deposited multilayered Co/Cu nanocolumns measured by a scanning tunnelling microscope. J. Nanotechnol. 2008, 19, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Schwarzacher, W.; Lashmore, D.S. Giant magnetoresistance in electrodeposited films. IEEE Trans. Magn. 1996, 32, 3133–3153. [Google Scholar] [CrossRef]
- Locatelli, N.; Naletov, V.; Grollier, J.; de Loubens, G.; Cros, V.; Deranlot, C.; Ulysse, C.; Faini, G.; Klein, O.; Fert, A. Dynamics of two coupled vortices in a spin valve nanopillar excited by spin transfer torque. Appl. Phys. Lett. 2011, 98. [Google Scholar] [CrossRef]
- Rizal, C.; Moa, B.; Wingert, J.; Shpyrko, O.G. Magnetic anisotropy and magnetoresistance properties of Co/Au multilayers. IEEE Trans. Magn. 2015, 2. [Google Scholar] [CrossRef]
- Rizal, C.; Ueda, Y. Magnetoresistance and magnetic anisotropy properties of strain-induced Co/Ag multilayer films. IEEE Trans. Magn. 2009, 45, 2399–2402. [Google Scholar] [CrossRef]
- Shen, W.K.; Das, A.; Racine, M.; Cheng, R.; Judy, J.H.; Wang, J.P. Enhancement in magnetic anisotropy for hcp structured Co alloy thin films through Pt addition. IEEE Trans. Magn. 2006, 42, 2945–2947. [Google Scholar] [CrossRef]
- Ikeda, S.; Hayakawa, J.; Lee, Y.M.; Sasaki, R.; Meguro, T.; Matsukura, F.; Ohno, H. Dependence of tunnel magnetoresistance in MgO based magnetic tunnel junctions on Ar pressure during MgO sputtering. Jpn. J. Appl. Phys. 2005, 44. [Google Scholar] [CrossRef]
- Armelles, G.; Cebollada, A.; García-Martín, A.; González, M.U. Magnetoplasmonics: Magnetoplasmonics: Combining magnetic and plasmonic functionalities (Advanced Optical Materials 1/2013). Adv. Opt. Mat. 2013, 1. [Google Scholar] [CrossRef]
- Lodewijks, K.; Maccaferri, N.; Pakizeh, T.; Dumas, R.K.; Zubritskaya, I.; Åkerman, J.; Vavassori, P.; Dmitriev, A. Magnetoplasmonic design rules for active magnetooptics. Nano Lett. 2014, 14, 7207–7214. [Google Scholar] [CrossRef] [PubMed]
- Manera, M.G.; Ferreiro-Vila, E.; Garcia-Martin, J.M.; Garcia-Martin, A.; Rella, R. Enhanced antibody recognition with a magneto-optic surface plasmon resonance (MO-SPR) sensor. Biosens. Bioelectron. 2014, 58, 114–120. [Google Scholar] [CrossRef] [PubMed]
- Maksymov, I.S. Magneto-plasmonic nanoantennas: Basics and applications (Review). Reviews Phys. 2016, 1, 36–51. [Google Scholar] [CrossRef]
- Jain, P.K.; Xiao, Y.; Walsworth, R.; Cohen, A.E. Surface plasmon resonance enhanced magneto-optics (SuPREMO): Faraday rotation enhancement in gold-coated iron oxide nanocrystals. Nano Lett. 2009, 9, 1644–1650. [Google Scholar] [CrossRef] [PubMed]
- Sepúlveda, B.; Calle, A.; Lechuga, L.M.; Armelles, G. Highly sensitive detection of biomolecules with the magnetooptic surface plasmon resonance sensor. Opt. Lett. 2006, 31, 1085–1087. [Google Scholar] [CrossRef] [PubMed]
- Chin, J.Y.; Steinle, T.; Wehlus, T.; Dregely, D.; Weiss, T.; Belotelov, V.I.; Stritzker, B.; Giessen, H. Nonreciprocal plasmonics enables giant enhancement of thin film Faraday rotation. Nat. Commun. 2013, 4. [Google Scholar] [CrossRef] [PubMed]
- Hermann, C.; Kosobukin, V.; Lampel, G.; Peretti, J.; Safarov, V.; Bertrand, P. Surface-enhanced magneto-optics in metallic multilayer films. Phys. Rev. B 2001, 64. [Google Scholar] [CrossRef]
- Park, Y.; Fullerton, E.E.; Bader, S. Growth-induced uniaxial in-plane magnetic anisotropy for ultrathin Fe deposited on MgO (001) by oblique incidence molecular beam epitaxy. Appl. Phys. Lett. 1995, 66, 2140–2142. [Google Scholar] [CrossRef]
- Den Broeder, F.; Kuiper, D.; van de Mosselaer, A.; Hoving, W. Perpendicular magnetic anisotropy of CoAu multilayers induced by interface sharpening. Physi. Rev. Lett. 1988, 60. [Google Scholar] [CrossRef] [PubMed]
- Sporl, K.; Weller, D. Influence of annealing on structure and magnetic anisotropy of Au/Co multilayers. J. Magn. Magn. Mater. 1991, 101, 217–218. [Google Scholar] [CrossRef]
- Taniguchi, S.; Yamamoto, M. A note on a theory of the uniaxial ferromagnetic anisotropy induced by cold work or by magnetic annealing in cubic solid solutions. Jpn. Inst. Metals (Nippon Kinzoku Gakkaishi) 1954, 19, 269–281. [Google Scholar]
- Ueda, Y.; Sato, M. Magnetic anisotropy in single crystal nickel films electrodeposited on a (110) CuNi crystal surface. J. Appl. Phys. 1976, 47, 3380–3382. [Google Scholar] [CrossRef]
- Weller, D.; StÃűhr, J.; Nakajima, R.; Carl, A.; Samant, M.G.; Chappert, C.; MÃľgy, R.; Beauvillain, P.; Veillet, P.; Held, G.A. Microscopic origin of magnetic anisotropy in Au/Co/Au probed with X-ray magnetic circular dichroism. Phys. Rev. Lett. 1995, 75, 3752–3755. [Google Scholar] [CrossRef] [PubMed]
- Bardou, N.; Bartenlian, B.; Chappert, C.; Megy, R.; Veillet, P.; Renard, J.P.; Rousseaux, F.; Ravet, M.F.; Jamet, J.P.; Meyer, P. Magnetization reversal in patterned Co (0001) ultrathin films with perpendicular magnetic anisotropy. Phys. Rev. B 1996, 79, 5848–5850. [Google Scholar] [CrossRef]
- Cagnon, L.; Devolder, T.; Cortes, R.; Morrone, A.; Schmidt, J.E.; Chappert, C.; Allongue, P. Enhanced interface perpendicular magnetic anisotropy in electrodeposited Co/Au(111) layers. Phys. Rev. B 2001, 63, 104419–104423. [Google Scholar] [CrossRef]
- Chappert, C.; Bruno, P. Magnetic anisotropy in metallic ultrathin films and related experiments on Co films. J. Appl. Phys. 1988, 64, 5736–4741. [Google Scholar] [CrossRef]
- Ding, Y.; Judy, J.H.; Wang, J.P. Magneto-resistive read sensor with perpendicular magnetic anisotropy. IEEE Trans. Magn. 2005, 41, 707–712. [Google Scholar] [CrossRef]
- Khiraoui, S.E.; Sajieddine, M.; Hehn, M.; Robert, S.; Lenoble, O.; Bellouard, C.; Sahlaoui, M.; Benkirane, K. Magnetic studies of Fe/Cu multilayers. Phys. B Condens. Matter 2008, 403, 2509–2514. [Google Scholar] [CrossRef]
- Liu, Y.; Shan, Z.S.; Sellmyer, D.J. Nanostructure and magnetic anisotropy of Co/Au multilayers. J. Appl. Phys. 1997, 81, 5061–5063. [Google Scholar] [CrossRef]
- Murayama, A.; Hyomi, K.; Eickmann, J.; Falco, C.M. Strain dependence of the interface perpendicular magnetic anisotropy in epitaxial Co/Au/Cu(111) films. Phys. Rev. B 1999, 60, 15245–15250. [Google Scholar] [CrossRef]
- Pirota, K.R.; Vazquez, M. Arrays of electroplated multilayered Co/Cu nanowires with controlled magnetic anisotropy. Adv. Eng. Mater. 2005, 7, 1111–1113. [Google Scholar] [CrossRef]
- Den Broeder, F.; Hoving, W.; Bloemen, P. Magnetic anisotropy of multilayers. J. Magn. Magn. Mater. 1991, 93, 562–570. [Google Scholar] [CrossRef]
- Rizal, C.; Niraula, B.B. Ferromagnetic alloys: Magnetoresistance, microstructure, magnetism, and beyond (Review). J. Nano Electron. Phys. 2015, 7, 04068-1–04068-16. [Google Scholar]
- Rizal, C.; Wingert, J.; Fullerton, E.E. Perpendicular magnetic anisotropy and microstructure properties of Ta/Co (tCo)/Au (tAu) multilayers. In Proceedings of the Joint IEEE Magnetics and MMM Conferences, San Diego, CA, USA, 11–15 January 2016.
- Chikazumi, S.; Graham, C.D. Physics of Ferromagnetism, 2nd ed.; Oxford University Press: Oxford, UK, 1997; p. 655. [Google Scholar]
- Coey, J.M.D. Magnetism and Magnetic Materials, 1st ed.; Cambridge University Press: Cambridge, UK, 2010; p. 614. [Google Scholar]
- Cullity, B.D.; Graham, C.D. Introduction to Magnetic Materials, 2nd ed.; Wiley: Piscataway, NJ, USA; Hoboken, NJ, USA, 2009; p. 544. [Google Scholar]
- Chikazumi, S. Physics of Magnetism; Krieger: Malabar, FL, USA, 1978; Volume 153, p. 338. [Google Scholar]
- Rizal, C.; Gyawali, P.; Kshatry, I.; Pokharel, R.K. Strain-induced magnetoresistance and magnetic anisotropy of Co/Cu multilayers. J. Appl. Phys. 2012, 111. [Google Scholar] [CrossRef]
- Rizal, C. Study of magnetic anisotropy and magnetoresistance effects in ferromagnetic Co/Au multilayer films prepared by oblique incidence evaporation method. J. Magn. Magn. Mater. 2007, 310, e646–e648. [Google Scholar] [CrossRef]
- Thomson, W. On the electrodynamic qualities of metals: Effects of magnetization on the electric conductivity of Nickel and Iron. Proc. R. Soc. Lond. 1857, 8, 546–550. [Google Scholar] [CrossRef]
- McGuire, T.; Potter, R. Anisotropic magnetoresistance in ferromagnetic 3-d alloys. IEEE Trans. Magn. 1975, 11, 1018–1038. [Google Scholar] [CrossRef]
- Florczak, J.M.; Dahlberg, E.D.; Fullerton, E.E.; Schuller, I.K. Magnetotransport properties of Fe/Cu multilayer films. J. Appl. Phys. 1991, 70, 5836. [Google Scholar] [CrossRef]
- Fullerton, E.E.; Schuller, I.K. The 2007 Nobel Prize in physics: Magnetism and transport at the nanoscale. ACS Nano 2007, 1, 384–389. [Google Scholar] [CrossRef] [PubMed]
- Parkin, S.S.P. Giant magnetoresistance in magnetic nanostructures. Annu. Rev. Mater. Sci. 1995, 25, 357–388. [Google Scholar] [CrossRef]
- Ruderman, M.A.; Kittel, C. Indirect exchange coupling of nuclear magnetic moments by conduction electrons. Phys. Rev. 1954, 96. [Google Scholar] [CrossRef]
- Kasuya, T. A theory of metallic ferro-and antiferromagnetism on Zener’s model. Prog. Theor. Phys. 1956, 16, 45–57. [Google Scholar] [CrossRef]
- Yosida, K. Magnetic properties of Cu-Mn alloys. Phys. Rev. 1957, 106. [Google Scholar] [CrossRef]
- Bruno, P.; Chappert, C. Ruderman-Kittel theory of oscillatory interlayer exchange coupling. Phys. Rev. B 1992, 46. [Google Scholar] [CrossRef]
- Bruno, P.; Chappert, C. Oscillatory coupling between ferromagnetic layers separated by a nonmagnetic metal spacer. Phys. Rev. Lett. 1991, 67, 1602–1605. [Google Scholar] [CrossRef] [PubMed]
- Bakonyi, I.; Tóth-Kádár, E.; Cziráki, Á.; Tóth, J.; Kiss, L.; Ulhaq-Bouillet, C.; Pierron-Bohnes, V.; Dinia, A.; Arnold, B.; Wetzig, K. Preparation, structure, magnetic, and magnetotransport properties of electrodeposited Co (Ru)/Ru multilayers. J. Electrochem. Soc. 2002, 149, C469–C473. [Google Scholar] [CrossRef]
- Monchesky, T.; Heinrich, B.; Urban, R.; Myrtle, K.; Klaua, M.; Kirschner, J. Magnetoresistance and magnetic properties of Fe/Cu/GaS (100). Phys. Rev. B 1999, 60. [Google Scholar] [CrossRef]
- Sugiyama, T.; Nittono, O. Structure and giant magnetoresistance of Co/Ag granular alloy film fabricated by a multilayering method. Thin Solid Films 1998, 334, 206–208. [Google Scholar] [CrossRef]
- Suenaga, K.; Oomi, G.; Uwatoko, Y.; Saito, K.; Takanashi, K.; Fujimori, H. Study of strain and giant magnetoresistance of Co/Cu magnetic multilayers. Phys. Soc. Jpn. 2006, 75, 747151–747155. [Google Scholar]
- Rizal, C.; Gyawali, P.; Kshattry, I.; Ueda, Y.; Pokharel, R. Effect of strain on MR and magnetic properties of Co(tCo)/Ag nanostructures. In Proceedings of the 2011 IEEE Nanotechnology Materials and Devices Conference (NMDC), Jeju, Korea, 18–21 October 2011.
- Hyomi, K.; Murayama, A.; Oka, Y.; Falco, C.M. Misfit strain and magnetic anisotropies in ultrathin Co films hetero epitaxially grown on Au/Cu/Si(1 1 1). J. Cryst. Growth 2002, 235, 567–571. [Google Scholar] [CrossRef]
- Rizal, C.; Fullerton, E.E. Magnetic, Microstructure, and Plasma-Enhanced Magneto-Optic Properties of Ta/Au(tAu)/Co (tCo)/Au (tAu) Nanostructures. In Proceedings of the Material Research Society, San Francisco, CA, USA, 4 August 2016.
- Rizal, C. Magnetotransport properties of Co(tCo)/Cu(tCu) multilayer films. In Proceedings of the IEEE Joint Intermag-MMM Conference, Washington, DC, USA, 18–22 January 2010; p. 2.
- Yamada, A.; Houga, T.; Ueda, Y. Magnetism and magnetoresistance of Co/Cu multilayer films produced by pulse control electrodeposition method. J. Magn. Magn. Mater. 2002, 239, 272–275. [Google Scholar] [CrossRef]
- Ueda, Y.; Ikeda, S.; Hama, S.; Yamada, A. Magnetic properties and magnetoresistance of Fe/Cr multilayer films prepared by vapor deposition and electrodeposition. J. Magn. Magn. Mater. 1996, 156, 353–354. [Google Scholar] [CrossRef]
- Rizal, C.; Ueda, Y.; Pokharel, R.K. Magnetotransport properties of Co-Au granular alloys. Int. J. Appl. Phys. Math. 2011, 1, 161–166. [Google Scholar] [CrossRef]
- Bao, Z.L.; Kavanagh, K.L. Aligned Co nanodiscs by electrodeposition on GaAs. J. Cryst. Growth 2006, 287, 514–517. [Google Scholar]
- Rajasekaran, N.; Mohan, S.; Jagannathan, R. Giant magnetoresistance and ferromagnetic properties of DC and pulse electrodeposited CuCo alloys. J. Magn. Magn. Mater. 2012, 324, 2983–2988. [Google Scholar] [CrossRef]
- Bakonyi, I. Electrodeposited multilayer films with giant magnetoresistance (GMR): Progress and problems. Prog. Mater. Sci. 2010, 55, 107–245. [Google Scholar] [CrossRef]
- Brenner, A. Electrodeposition of Alloys Principle and Practice; Academic Press: New York, NY, USA, 1963. [Google Scholar]
- Puippe, J.C.; Leaman, F. Theory and Practice of Pulse Plating; The American Electroplaters and Surface Finishers Society: Orlando, FL, USA, 1986. [Google Scholar]
- Yuasa, S.; Nagahama, T.; Fukushima, A.; Suzuki, Y.; Ando, K. Giant room temperature magnetoresistance in single crystal Fe/MgO/Fe magnetic tunnel junctions. Nat. Mater. 2004, 3, 868–871. [Google Scholar] [CrossRef] [PubMed]
- Miyazaki, T.; Tezuka, N. Giant magnetic tunneling effect in Fe/Al2O3/Fe junction. J. Magn. Magn. Mater. 1995, 139, L231–L234. [Google Scholar] [CrossRef]
- Moodera, J.S.; Kinder, L.R.; Wong, T.M.; Meservey, R. Large magnetoresistance at room temperature in ferromagnetic thin film tunnel junctions. Phys. Rev. Lett. 1995, 74, 3273–3276. [Google Scholar] [CrossRef] [PubMed]
- Hayakawa, J.; Ikeda, S.; Lee, Y.M.; Matsukura, F.; Ohno, H. Effect of high annealing temperature on giant tunnel magnetoresistance ratio of CoFeB/MgO/CoFeB magnetic tunnel junctions. Appl. Phys. Lett. 2006. [Google Scholar] [CrossRef]
- Takanashi, K. Fundamentals of Magnetoresistance Effects. In Spintronics for Next Generation Innovative Devices; Wiley: New York, NY, USA, 2015; p. 1. [Google Scholar]
- Bowen, M.; Bibes, M.; Barthélémy, A.; Contour, J.P.; Anane, A.; Lemaıtre, Y.; Fert, A. Nearly total spin polarization in La2/3Sr1/3MnO3 from tunneling experiments. Appl. Phys. Lett. 2003, 82, 233–235. [Google Scholar] [CrossRef]
- Bratkovsky, A. Tunneling of electrons in conventional and half-metallic systems: Towards very large magnetoresistance. Phys. Rev. B 1997, 56. [Google Scholar] [CrossRef]
- Majumdar, S.; van Dijken, S. Pulsed laser deposition of La1−xSrxMnO3: Thin film properties and spintronic applications. J. Phys. D Appl. Phys. 2013, 47. [Google Scholar] [CrossRef]
- Greullet, F.; Snoeck, E.; Tiusan, C.; Hehn, M.; Lacour, D.; Lenoble, O.; Magen, C.; Calmels, L. Large inverse magnetoresistance in fully epitaxial Fe/Fe3O4/MgO/Co magnetic tunnel junctions. Appl. Phys. Lett. 2008, 92. [Google Scholar] [CrossRef]
- Ramirez, A. Colossal magnetoresistance. J. Phys. Condens. Matter 1997, 9. [Google Scholar] [CrossRef]
- Uehara, M.; Mori, S.; Chen, C.; Cheong, S.W. Percolative phase separation underlies colossal magnetoresistance in mixed valent manganites. Nature 1999, 399, 560–563. [Google Scholar]
- Almeida, T.M.D.; Piedade, M.S.; Sousa, L.A.; Germano, J.; Lopes, P.A.; Cardoso, F.A.; Freitas, P.P. On the modeling of new tunnel junction magnetoresistive biosensors. IEEE Trans. Instrum. Meas. 2010, 59, 92–100. [Google Scholar] [CrossRef]
- Coughlin, T. Thanks for the memories: Nonvolatile memory technology enables the age of spin [The art of storage]. IEEE Consum. Electron. Mag. 2014, 3, 85–92. [Google Scholar] [CrossRef]
- Andre, T.; Alam, S.M.; Gogl, D. Memory Device With Reduced on Chip Noise. U.S. Patent US20140104963 A1, 17 April 2014. [Google Scholar]
- Slonczewski, J.C. Current-driven excitation of magnetic multilayers. J. Magn. Magn. Mater. 1996, 159, L1–L7. [Google Scholar] [CrossRef]
- Berger, L. Emission of spin waves by a magnetic multilayer traversed by a current. Phys. Rev. B 1996, 54, 9353–9358. [Google Scholar] [CrossRef]
- Huai, Y.; Albert, F.; Nguyen, P.; Pakala, M.; Valet, T. Observation of spintransfer switching in deep submicron sized and low resistance magnetic tunnel junctions. Appl. Phys. Lett. 2004, 84. [Google Scholar] [CrossRef]
- Gallagher, W.J.; Parkin, S.S. Development of the magnetic tunnel junction MRAM at IBM: From first junctions to a 16 MBite MRAM demonstrator chip. IBM J. Res. Dev. 2006, 50, 5–23. [Google Scholar] [CrossRef]
- Rowlands, G.E.; Krivorotov, I.N. Magnetization dynamics in a dual freelayer spin-torque nano-oscillator. Phys. Rev. B 2012, 86. [Google Scholar] [CrossRef]
- Villard, P.; Ebels, U.; Houssameddine, D.; Katine, J.; Mauri, D.; Delaet, B.; Vincent, P.; Cyrille, M.C.; Viala, B.; Michel, J.P.; et al. A GHz spintronic-based RF oscillator. IEEE J. Solid State Circuits 2010, 45, 214–223. [Google Scholar] [CrossRef]
- Krishnan, K.M. Biomedical nanomagnetics: A spin through possibilities in imaging, diagnostics, and therapy. IEEE Trans. Magn. 2010, 46, 2523–2558. [Google Scholar] [CrossRef] [PubMed]
- Osterfeld, S.J.; Yu, H.; Gaster, R.S.; Caramuta, S.; Xu, L.; Han, S.J.; Hall, D.A.; Wilson, R.J.; Sun, S.; White, R.L.; et al. Multiplex protein assays based on real-time magnetic nanotag sensing. Proc. Natl. Acad. Sci. USA 2008, 105, 20637–20640. [Google Scholar] [CrossRef] [PubMed]
- Jing, Y.; He, S.; Kline, T.; Xu, Y.; Wang, J.P. High-magnetic-moment nanoparticles for biomedicine. In Proceedings of the IEEE Annual International Conference: Engineering in Medicine and Biology Society, San Diego, CA, USA, 2–6 September 2009; pp. 4483–4486.
- Wasa, K.; Kitabatake, M.; Adachi, H.; Makoto, H. Thin Film Materials Technology; William Andrew, Inc.: New York, NY, USA, 2004. [Google Scholar]
- Srolovitz, D. Shadowing effects on the microstructure of obliquely deposited films. J. Appl. Phys. 2002, 91, 1963–1972. [Google Scholar]
- Tang, F.; Liu, D.L.; Ye, D.; Zhao, Y.; Lu, T.; Wang, G.; Vijayaraghavan, A. Magnetic properties of Co nanocolumns fabricated by oblique angle deposition. J. Appl. Phys. 2003, 93, 4194–4200. [Google Scholar] [CrossRef]
- Takakura, W.; Ikeda, S.; Ueda, Y. Electrical resistance in Fe/Al2O3 multilayered films prepared by an electron beam evaporation method. Mater. Trans. 2001, 42, 881–885. [Google Scholar] [CrossRef]
- Ueda, Y.; Takahashi, M. Structure and magnetic properties in single-crystal iron film electrodeposited on a (110) copper crystal. J. Magn. Magn. Mater. 1988, 71, 212–218. [Google Scholar] [CrossRef]
- Chikazumi, S.; Oomura, T. On the origin of magnetic anisotropy induced by magnetic annealing. J. Phys. Soc. Jpn. 1955, 10, 842–849. [Google Scholar] [CrossRef]
- Yamada, A.; Shirota, M.; Houga, T.; Rizal, C.; Ueda, Y. Electric and magnetic properties of FeNi based particle and multilayer films produced by pulse control electrodeposition method. J. Jpn. Inst. Metals 2002, 66, 869–872. [Google Scholar]
- Rizal, C. Giant Magnetoresistance and Magnetic Properties of Ferromagnetic Hybrid Nanostructures. Ph.D. Thesis, The University of British Columbia, Vancouver, BC, Canada, 26 May 2012. [Google Scholar]
- Rizal, C.; Ueda, Y.; Karki, B.R. Magnetic properties of Fe/Cu multilayers prepared using pulsed current electrodeposition. J. Nano Electron. Phys. 2012, 4, 01001-1–01001-3. [Google Scholar]
- Gomez, E.; Torres, J.G.; Valles, E. Electrodeposition of CoAg films and compositional determination by electrochemical methods. Anal. Chim. Acta 2007, 60, 187–194. [Google Scholar] [CrossRef] [PubMed]
- Torres, J.G.; Peter, L.; Revesz, A.; Pogany, L.; Bakonyi, I. Preparation and giant magnetoresistance of electrodeposited CoAg/Ag multilayers. Thin Solid Films 2009, 517, 6081–6090. [Google Scholar] [CrossRef]
- Guan, M.; Podlaha, E.J. Electrodeposition of AuCo alloys and multilayers. J. Appl. Electrochem. 2007, 37. [Google Scholar] [CrossRef]
- Baskaran, I.; Narayanan, T.S.; Stephen, A. Pulsed electrodeposition of nanocrystalline CuNi alloy films and evaluation of their characteristic properties. Mater. Lett. 2006, 60, 1990–1995. [Google Scholar] [CrossRef]
- Kenane, S.; Voiron, J.; Benbrahim, N.; Chainet, E.; Robaut, F. Magnetic properties and giant magnetoresistance in electrodeposited CoAg granular films. J. Magn. Magn. Mater. 2006, 297, 99–106. [Google Scholar] [CrossRef]
- Houga, T.; Yamada, A.; Ueda, Y. Resistivity and magnetism of Co/Cu films produced by computer controlled pulse electrodeposition. J. Jpn. Inst. Met. 2000, 64, 739–742. [Google Scholar]
- Ueda, Y.; Houga, T.; Zaman, H.; Yamada, A. Magnetoresistance effect of CoCu nanostructure prepared by electrodeposition method. J. Solid State Chem. 1999, 147, 274–280. [Google Scholar] [CrossRef]
- Houga, T.; Zaman, H.; Chikazawa, S.; Ueda, Y. Magnetism and magnetoresistance effect in the CoCu and CoAg films produced by pulse electrodeposition. In Proceedings of the IEEE International Magnetics Conference, Tokyo, Japan, 18–21 May 1999.
- Zaman, H.; Ikeda, S.; Ueda, Y. Magnetoresistance in CoAg multilayers and granular films produced by electrodeposition method. IEEE Trans. Magn. 1997, 33, 3517–3519. [Google Scholar] [CrossRef]
- Santos, E.; Abbate, M.; Fernandes, V.; Mattoso, N. Electronic structure of metastable Fe1−x Cox alloys produced by electrodeposition. Electrochem. Solid State Lett. 2003, 6, C85–C87. [Google Scholar] [CrossRef]
- Scheck, C.; Evans, P.; Schad, R.; Zangari, G.; Williams, J.; Isaacs-Smith, T.F. Structure and magnetic properties of electrodeposited Ni films on nGaAs(001). J. Phys. Condens. Matter 2002, 14. [Google Scholar] [CrossRef]
- Valizadeh, S.; Svedberg, E.B.; Leisner, P. Electrodeposition of compositionally modulated Au/Co alloy layers. J. Appl. Electrochem. 2002, 32, 97–104. [Google Scholar] [CrossRef]
- Rizal, C.; Yamada, A.; Hori, Y.; Ishida, S.; Matsuda, M.; Ueda, Y. Magnetic properties and magnetoresistance effect in Co/Au, Ag nanostructure films produced by pulse electrodeposition. Phys. Status Solidi C Conf. 2004, 1, 1756–1759. [Google Scholar] [CrossRef]
- Rizal, C.; Yamada, A.; Ueda, Y. Pulse electrodeposition of Co/Au multilayers and granular alloys. Jpn. J. Appl. Surf. Finish. 2004, 55, 83–84. [Google Scholar] [CrossRef]
- Yamada, A.; Rizal, C.; Murata, S.; Ueda, Y. Electric properties of NiCo based multilayer films produced by pulse control electrodeposition method. J. Surf. Finish. Soc. Jpn. 2004, 55, 151–152. [Google Scholar] [CrossRef]
- Rizal, C.; Ueda, Y. Magnetoresistance effect and magnetic properties of strain induced Co/Cu multilayer films. In Proceedings of the 3rd International Nanoelectronics Conference (INEC), Hong Kong, China, 3–8 January 2010; pp. 927–928.
- Geoghegan, D.S.; Hutten, A.; Muller, K.H.; Schultz, L. Magnetoresistance of melt spun gold cobalt. J. Magn. Magn. Mater. 1998, 177–181, 1478–1479. [Google Scholar] [CrossRef]
- Hutten, A.; Bernardi, J.; Friedrichs, S.; Thomas, G.; Balcells, L. Microstructural influence on magnetic properties and giant magnetoresistance of melt spun AuCo. Scr. Metall. Mater. 1995, 33, 1647–1666. [Google Scholar] [CrossRef]
- Ikeda, S.; Houga, T.; Takakura, W.; Ueda, Y. Magnetoresistance in (CoxFe1−x)(20)Cu80 granular alloys produced by mechanical alloying. Mater. Sci. Eng. A 1996, 217, 376–380. [Google Scholar] [CrossRef]
- Jones, B.A.; Hanna, C. Contribution of quantum-well states to the RKKY coupling in magnetic multilayers. Phys. Rev. Lett. 1993, 71. [Google Scholar] [CrossRef] [PubMed]
- Camley, R.E.; Barnaś, J. Theory of giant magnetoresistance effects in magnetic layered structures with antiferromagnetic coupling. Phys. Rev. Lett. 1989, 63. [Google Scholar] [CrossRef] [PubMed]
- Barnaś, J.; Bruynseraede, Y. Electronic transport in ultrathin magnetic multilayers. Phys. Rev. B 1996, 53, 5449–5460. [Google Scholar] [CrossRef]
- Valet, T.; Fert, A. Classical theory of perpendicular giant magnetoresistance in magnetic multilayers. J. Magn. Magn. Mater. 1993, 121, 378–382. [Google Scholar] [CrossRef]
- Levy, P.M.; Shi, Z.P.; Zhang, S.; Camblong, H.E.; Fry, J.L. Interlayer coupling and magnetoresistance of multilayered structures. J. Magn. Magn. Mater. 1993, 121, 357–361. [Google Scholar] [CrossRef]
- Camblong, H.E.; Levy, P.M. Novel results for quasiclassical linear transport in metallic multilayers. Phys. Rev. Lett. 1992, 69, 2835–2838. [Google Scholar] [CrossRef] [PubMed]
- Asano, Y.; Oguri, A.; Maekawa, S. Parallel and perpendicular transport in multilayered structures. Phys. Rev. B 1993, 48, 6192–6198. [Google Scholar] [CrossRef]
- Itoh, H.; Inoue, J.; Maekawa, S. Theory of giant magnetoresistance for parallel and perpendicular currents in magnetic multilayers. Phys. Rev. B 1995, 51, 342–352. [Google Scholar] [CrossRef]
- Todorov, T.; Tsymbal, E.Y.; Pettifor, D. Giant magnetoresistance: Comparison of band structure and interfacial-roughness contributions. Phys. Rev. B 1996, 54. [Google Scholar] [CrossRef]
- Schep, K.M.; Kelly, P.J.; Bauer, G.E. Giant magnetoresistance without defect scattering. Phys. Rev. Lett. 1995, 74, 586–589. [Google Scholar] [CrossRef] [PubMed]
- Oguchi, T. Fermi velocity effect on magnetoresistance in Fe/transition metal multilayers. J. Magn. Magn. Mater. 1993, 126, 519–520. [Google Scholar] [CrossRef]
- Binder, S.; Langhammer, J.; Calci, A.; Navratil, P.; Roth, R. Ab initio calculations of medium-mass nuclei with explicit chiral 3N interactions. Phys. Rev. C 2013, 87. [Google Scholar] [CrossRef]
- Butler, W.; Zhang, X.G.; Nicholson, D.; MacLaren, J. First-principles calculations of electrical conductivity and giant magnetoresistance of Co/Cu/Co spin valves. Phys. Rev. B 1995, 52, 13399–13410. [Google Scholar] [CrossRef]
- Tsymbal, E.Y.; Pettifor, D. Perspectives of giant magnetoresistance. Solid State Phys. 2001, 56, 113–237. [Google Scholar]
- Blaas, C.; Weinberger, P.; Szunyogh, L.; Levy, P.; Sommers, C. Ab initio calculations of magnetotransport for magnetic multilayers. Phys. Rev. B 1999, 60. [Google Scholar] [CrossRef]
- Hartmann, U. Springer Series in Surface Sciences; Springer: Berlin, Germany, 2000; p. 321. [Google Scholar]
- McFadyen, I.; Fullerton, E.; Carey, M. State-of-the-art magnetic hard disk drives. MRS Bull. 2006, 31, 379–383. [Google Scholar] [CrossRef]
- Grochowski, E. Emerging trends in data storage on magnetic hard disk drives. Available online: https://courses.cs.washington.edu/courses/cse590s/03au/grochowski-trends.pdf (accessed on 13 April 2016).
- Belleson, J.; Grochowski, E. The era of giant magnetoresistive heads. Available online: https://www1.hgst.com/hdd/technolo/gmr/gmr.htm (accessed on 13 April 2016).
- Pannetier, M.; Fermon, C.; Legoff, G.; Simola, J.; Kerr, E.; Welling, M.; Wijngaarden, R.J. Ultra-sensitive field sensors-an alternative to SQUIDs. IEEE Trans. Appl. Supercond. 2005, 15, 892–895. [Google Scholar] [CrossRef]
- Pannetier-Lecoeur, M.; Polovy, H.; Sergeeva-Chollet, N.; Cannies, G.; Fermon, C.; Parkkonen, L. Magnetocardiography with GMR-Based Sensors; IOP Publishing: Bristol, UK, 2011. [Google Scholar]
- Kotitz, R.; Matz, H.; Trahms, L.; Koch, H.; Weitschies, W.; Rheinlander, T.; Semmler, W.; Bunte, T. SQUID based remanence measurements for immunoassays. IEEE Trans. Appl. Supercond. 1997, 7, 3678–3681. [Google Scholar] [CrossRef]
- Baselt, D.R.; Lee, G.U.; Natesan, M.; Metzger, S.W.; Sheehan, P.E.; Colton, R.J. A biosensor based on magnetoresistance technology. Biosens. Bioelectron. 1998, 13, 731–739. [Google Scholar] [CrossRef]
- Edelstein, R.; Tamanaha, C.; Sheehan, P.; Miller, M.; Baselt, D.; Whitman, L.; Colton, R. The BARC biosensor applied to the detection of biological warfare agents. Biosens. Bioelectron. 2000, 14, 805–813. [Google Scholar] [CrossRef]
- Han, S.J.; Yu, H.; Murmann, B.; Pourmand, N.; Wang, S.X. A high-density magnetoresistive biosensor array with drift compensation mechanism. In Proceedings of the 2007 IEEE International Solid-State Circuits Conference (Digest of Technical Papers), San Francisco, CA, USA, 11–15 February 2007.
- Ferreira, H.; Feliciano, N.; Graham, D.; Freitas, P. Effect of spin valve sensor magnetostatic fields on nanobead detection for biochip applications. J. Appl. Phys. 2005, 97. [Google Scholar] [CrossRef]
- Boer, B.D.; Kahlman, J.; Jansen, T.; Duric, H.; Veen, J. An integrated and sensitive detection platform for magneto-resistive biosensors. Biosens. Bioelectron. 2007, 22, 2366–2370. [Google Scholar] [CrossRef] [PubMed]
- Koets, M.; der Wijk, T.V.; Eemeren, J.V.; Amerongen, A.V.; Prins, M. Rapid DNA multi-analyte immunoassay on a magnetoresistance biosensor. Biosens. Bioelectron. 2009, 24, 1893–1898. [Google Scholar] [CrossRef] [PubMed]
- Graham, D.L.; Ferreira, H.A.; Freitas, P.P. Magnetoresistive based biosensors and biochips. Trends Biotechnol. 2004, 22, 455–462. [Google Scholar] [CrossRef] [PubMed]
- Germano, J.; Martins, V.C.; Cardoso, F.A.; Almeida, T.M.; Sousa, L.; Freitas, P.P.; Piedade, M.S. A portable and autonomous magnetic detection platform for biosensing. Sensors 2009, 9, 4119–4137. [Google Scholar] [CrossRef] [PubMed]
- Reiss, G.; Brueckl, H.; Huetten, A.; Schotter, J.; Brzeska, M.; Panhorst, M.; Sudfeld, D.; Becker, A.; Kamp, P.B.; Puehler, A.; et al. Magnetoresistive sensors and magnetic nanoparticles for biotechnology. J. Mat. Res. 2005, 20, 3294–3302. [Google Scholar] [CrossRef]
- Schotter, J.; Kamp, P.B.; Becker, A.; PÃhler, A.; Reiss, G.; Bruckl, H. Comparison of a prototype magnetoresistive biosensor to standard fluorescent DNA detection. Biosens. Bioelectron. 2004, 19, 1149–1156. [Google Scholar] [CrossRef] [PubMed]
- Srinivasan, B.; Li, Y.; Jing, Y.; Xu, Y.H.; Yao, X.; Xing, C.; Wang, J.P. A detection system based on giant magnetoresistive sensors and high—Moment magnetic nanoparticles demonstrates zeptomole sensitivity: Potential for personalized medicine. Angew. Chem. Int. Ed. 2009, 48, 2764–2767. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Yu, H.; Akhras, M.S.; Han, S.J.; Osterfeld, S.; White, R.L.; Pourmand, N.; Wang, S.X. Giant magnetoresistive biochip for DNA detection and HPV genotyping. Biosens. Bioelectron. 2008, 24, 99–103. [Google Scholar] [CrossRef] [PubMed]
- Wang, H. Magnetic sensors for diagnostic medicine: CMOS based magnetic particle detectors for medical diagnosis applications. IEEE Microw. Mag. 2013, 14, 110–130. [Google Scholar] [CrossRef]
- Wang, S.X.; Li, G. Advances in giant magnetoresistance biosensors with magnetic nanoparticle tags: Review and outlook. IEEE Trans. Magn. 2008, 44, 1687–1702. [Google Scholar] [CrossRef]
- Reig, C.; Cubells-Beltrán, M.D.; Ramírez Muńoz, D. Magnetic field sensors based on giant magnetoresistance (GMR) technology: Applications in electrical current sensing. Sensors 2009, 9, 7919–7942. [Google Scholar] [CrossRef] [PubMed]
- Jogschies, L.; Klaas, D.; Kruppe, R.; Rittinger, J.; Taptimthong, P.; Wienecke, A.; Rissing, L.; Wurz, M.C. Recent developments of magnetoresistive sensors for industrial applications. Sensors 2015, 15, 28665–28689. [Google Scholar] [CrossRef] [PubMed]
- Van den Berg, H.; Coehoorn, R.; Gijs, M.; Grünberg, P.; Rasing, T.; Röll, K.; Hartmann, U. Magnetic Multilayers and Giant Magnetoresistance: Fundamentals and Industrial Applications; Springer Science & Business Media; Springer: New York, NY, USA, 2013; Volume 37. [Google Scholar]
- Jander, A.; Smith, C.; Schneider, R. Magnetoresistive sensors for nondestructive evaluation. In Proceedings of the Advanced Sensor Technologies for Nondestructive Evaluation and Structural Health Monitoring, San Diego, CA, USA, 6 March 2005.
- Tian, G.Y.; Sophian, A.; Taylor, D.; Rudlin, J. Multiple sensors on pulsed eddy-current detection for 3-D subsurface crack assessment. IEEE Sens. J. 2005, 5, 90–96. [Google Scholar] [CrossRef]
- Lang, Z.; Agurto, A.; Tian, G.; Sophian, A. A system identification based approach for pulsed eddy current non-destructive evaluation. Meas. Sci. Technol. 2007, 18, 2083–2091. [Google Scholar] [CrossRef]
- Simm, A.; Theodoulidis, T.; Poulakis, N.; Tian, G.Y. Investigation of the magnetic field response from eddy current inspection of defects. Int. J. Adv. Manuf. Technol. 2011, 54, 223–230. [Google Scholar] [CrossRef]
- Cui, Z.; Wang, X.; Li, Y.; Tian, G.Y. High sensitive magnetically actuated micromirrors for magnetic field measurement. Sens. Actuators A Phys. 2007, 138, 145–150. [Google Scholar] [CrossRef]
- McGary, P.D.; Tan, L.; Zou, J.; Stadler, B.J.; Downey, P.R.; Flatau, A.B. Magnetic nanowires for acoustic sensors. J. Appl. Phys. 2006, 99. [Google Scholar] [CrossRef]
- Xiong, Z.; Wu, D.; Vardeny, Z.V.; Shi, J. Giant magnetoresistance in organic spin valves. Nature 2004, 427, 821–824. [Google Scholar] [CrossRef] [PubMed]
- Choi, B.; Ho, J.; Arnup, G.; Freeman, M. Nonequilibrium domain pattern formation in mesoscopic magnetic thin film elements assisted by thermally excited spin fluctuations. Phys. Rev. Lett. 2005, 95. [Google Scholar] [CrossRef] [PubMed]
- Choi, B.; Rudge, J.; Girgis, E.; Kolthammer, J.; Hong, Y.; Lyle, A. Spin current pulse induced switching of vortex chirality in permalloy/Cu/Co nanopillars. Appl. Phys. Lett. 2007, 91. [Google Scholar] [CrossRef]
- Katine, J.; Fullerton, E.E. Device implications of spin transfer torques. J. Magn. Magn. Mater. 2008, 320, 1217–1226. [Google Scholar] [CrossRef]
- Courtland, R. Spin memory shows its might [News]. IEEE Spectr. 2014, 51, 15–16. [Google Scholar] [CrossRef]
- Deac, A.M.; Fukushima, A.; Kubota, H.; Maehara, H.; Suzuki, Y.; Yuasa, S.; Nagamine, Y.; Tsunekawa, K.; Djayaprawira, D.D.; Watanabe, N. Bias driven high power microwave emission from MgO-based tunnel magnetoresistance devices. Nat. Phys. 2008, 4, 803–809. [Google Scholar] [CrossRef]
- Schubert, M.; Tiwald, T.E.; Woollam, J.A. Explicit solutions for the optical properties of arbitrary magnetooptic materials in generalized ellipsometry. Appl. Opt. 1999, 38, 177–187. [Google Scholar] [CrossRef] [PubMed]
- Stockman, M.I. Nanoplasmonics: The physics behind the applications. Phys. Today 2011, 64, 39–44. [Google Scholar] [CrossRef]
- Kretschmann, E. The angular dependence and the polarisation of light emitted by surface plasmons on metals due to roughness. Opt. Commun. 1972, 5, 331–336. [Google Scholar] [CrossRef]
- Kretschmann, E. Die bestimmung der oberfa¨ca¨cchenrauhigkeit dunner schichten durch messung der winkelabha¨cngigkeit der streustrahlung von oberfla¨cchenplasmaschwingungen. Opt. Commun. 1974, 10, 353–356. [Google Scholar] [CrossRef]
- Alleyne, C.J.; Kirk, A.G.; McPhedran, R.C.; Nicorovici, N.A.P.; Maystre, D. Enhanced SPR sensitivity using periodic metallic structures. Opt. Express 2007, 15, 8163–8169. [Google Scholar] [CrossRef] [PubMed]
- Otto, A. Eine neue Methode der Anregung nichtstrahlender Oberfla¨chenplasmaschwingungen. Phys. Status Solidi (b) 1968. [Google Scholar] [CrossRef]
- Inoue, M.; Baryshev, A.; Goto, T.; Baek, S.; Mito, S.; Takagi, H.; Lim, P. Magnetophotonic crystals: Experimental realization and applications. In Magnetophotonics; Springer: New York, NY, USA, 2013; pp. 163–190. [Google Scholar]
- Rizal, C.; Moa, B.; Brolo, A.G. Recent progress in ferromagnetic multilayer-basesd magnetoplasmonic devices for potential biomedical applications. In Proceedings of the Canadian Medical and Biomedical Engineering Society Series, Vancouver, BC, Canada, 19–23 May 2014; pp. 1–4.
- Rizal, C.; Brolo, A.G. Magnetoplasmonics Properties of Co/Au Nanostructures. In Proceedings of the 58th Annual Conference on Magnetism and Magnetic Materials, Denver, CO, USA, 4–8 November 2013.
- Rizal, C.; Niraula, B.; Lee, H.W. Bio-magnetoplasmonics, Emerging Biomedical Technologies, and Beyond (Mini Review). J. Nanomed. Res. 2016, 3. [Google Scholar] [CrossRef]











| Co-Ag | Co-Cu | Co-Au | |||
|---|---|---|---|---|---|
| Constituents | g/L | Constituents | g/L | Constituents | g/L |
| CoSOHO | 5–16 | CoSOHO | 28–39 | CoSOHO | 1–10 |
| AgSOHO | 0.1–5.5 | CuSOHO | 15–25 | AuK(CN) | 15–25 |
| NaCHOHO | 76 | NaCHOHO | 76 | NaCHOHO | 76 |
| NaSOHO | 4 | NaCl | 2 | NaCl | 2 |
| Layer Number (L.N.) | Materials | t (nm) | ||
|---|---|---|---|---|
| 6 | Samples | 6 | − | |
| 5 | Au | 2 | − | |
| 4 | Co | 10 | ||
| 3 | Au | 35 | − | |
| 2 | Ti | 2 | − | |
| 1 | Substrate | 2000 | 02.29 | − |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rizal, C.; Moa, B.; Niraula, B.B. Ferromagnetic Multilayers: Magnetoresistance, Magnetic Anisotropy, and Beyond. Magnetochemistry 2016, 2, 22. https://doi.org/10.3390/magnetochemistry2020022
Rizal C, Moa B, Niraula BB. Ferromagnetic Multilayers: Magnetoresistance, Magnetic Anisotropy, and Beyond. Magnetochemistry. 2016; 2(2):22. https://doi.org/10.3390/magnetochemistry2020022
Chicago/Turabian StyleRizal, Conrad, Belaid Moa, and Boris B. Niraula. 2016. "Ferromagnetic Multilayers: Magnetoresistance, Magnetic Anisotropy, and Beyond" Magnetochemistry 2, no. 2: 22. https://doi.org/10.3390/magnetochemistry2020022
APA StyleRizal, C., Moa, B., & Niraula, B. B. (2016). Ferromagnetic Multilayers: Magnetoresistance, Magnetic Anisotropy, and Beyond. Magnetochemistry, 2(2), 22. https://doi.org/10.3390/magnetochemistry2020022