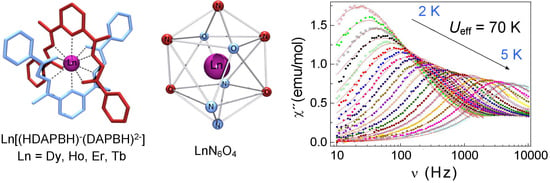
Ten-Coordinate Lanthanide [Ln(HL)(L)] Complexes (Ln = Dy, Ho, Er, Tb) with Pentadentate N3O2-Type Schiff-Base Ligands: Synthesis, Structure and Magnetism
Abstract
:1. Introduction
2. Results and Discussion
2.1. Synthetic Aspects
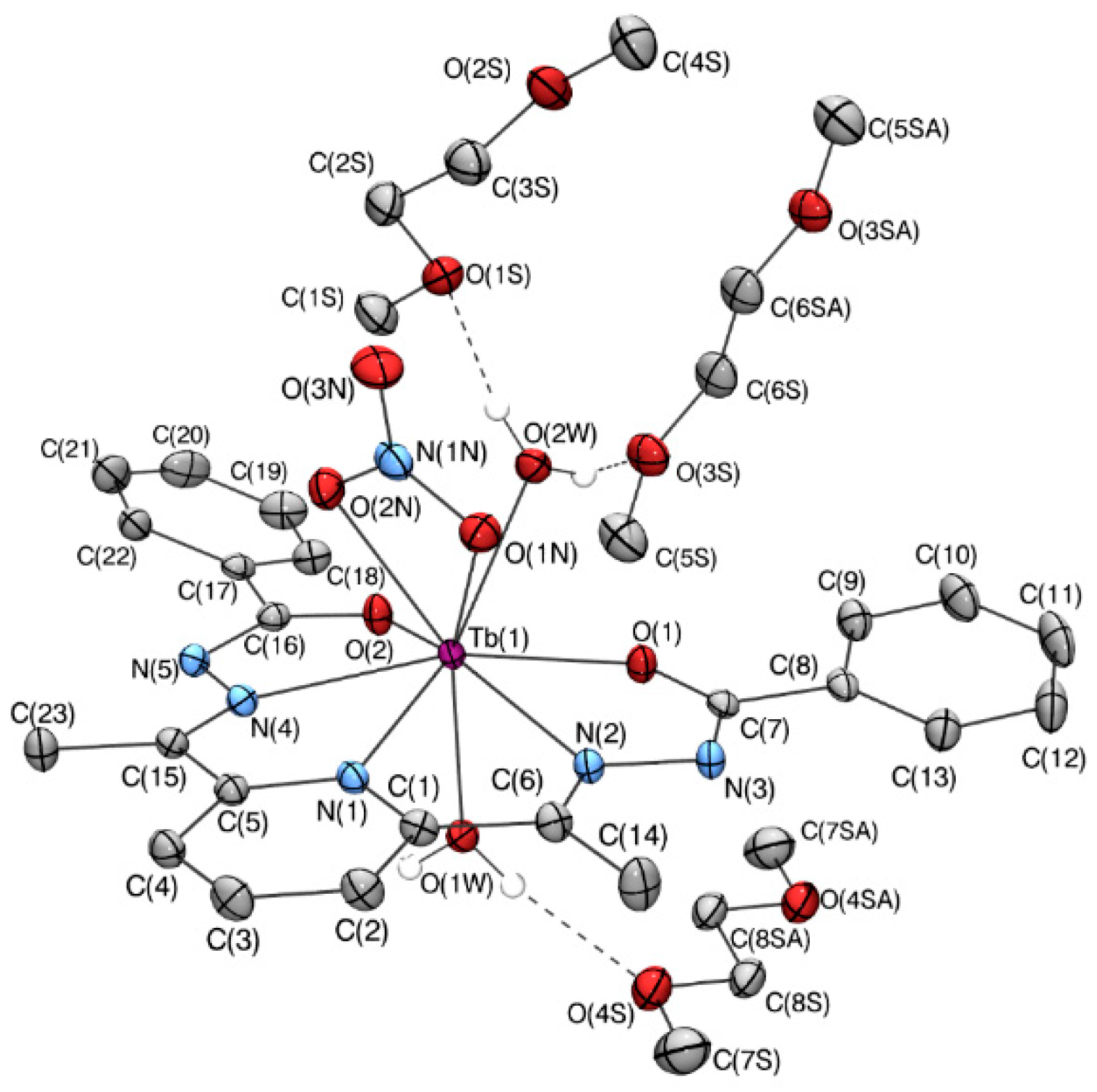
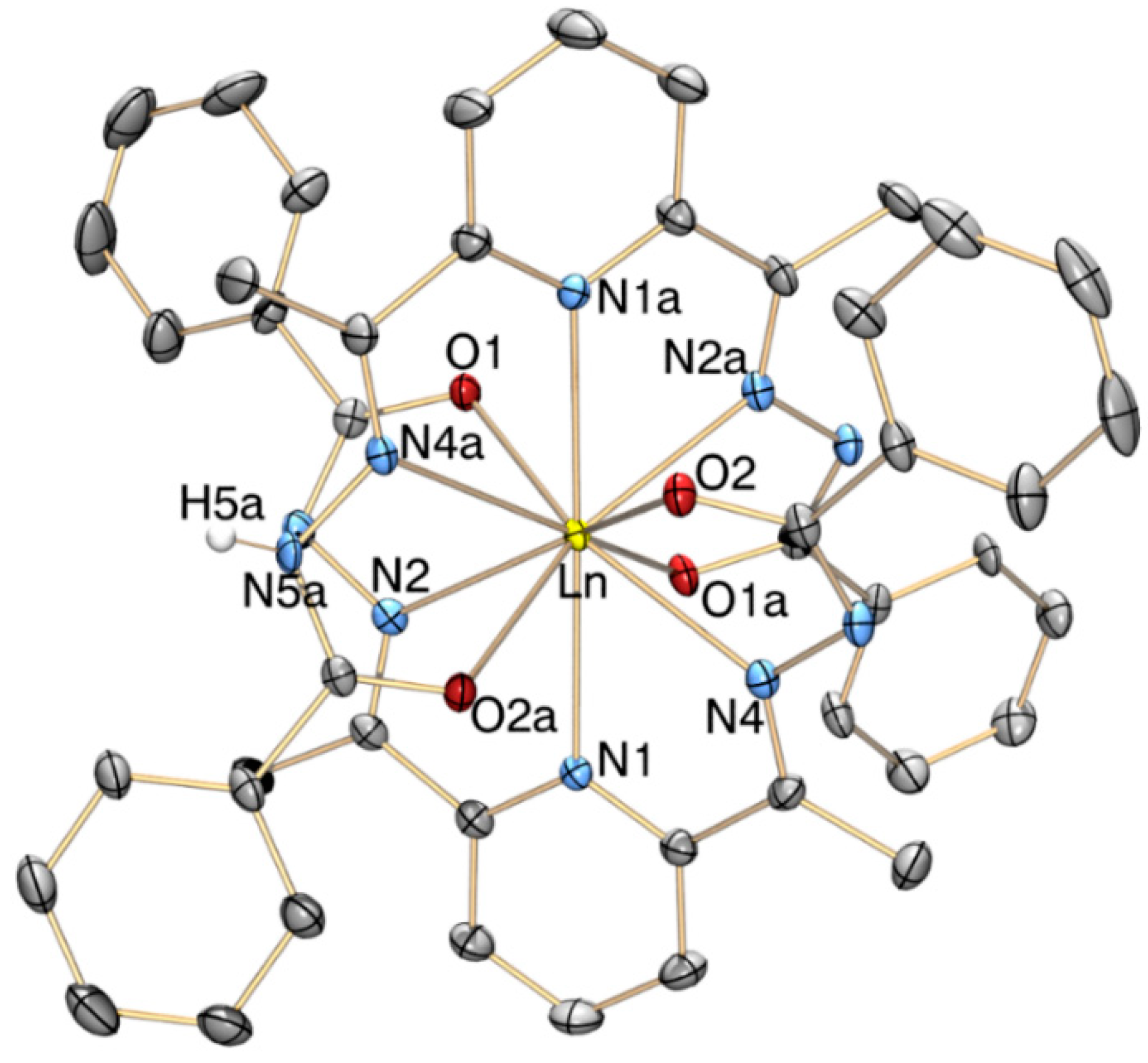
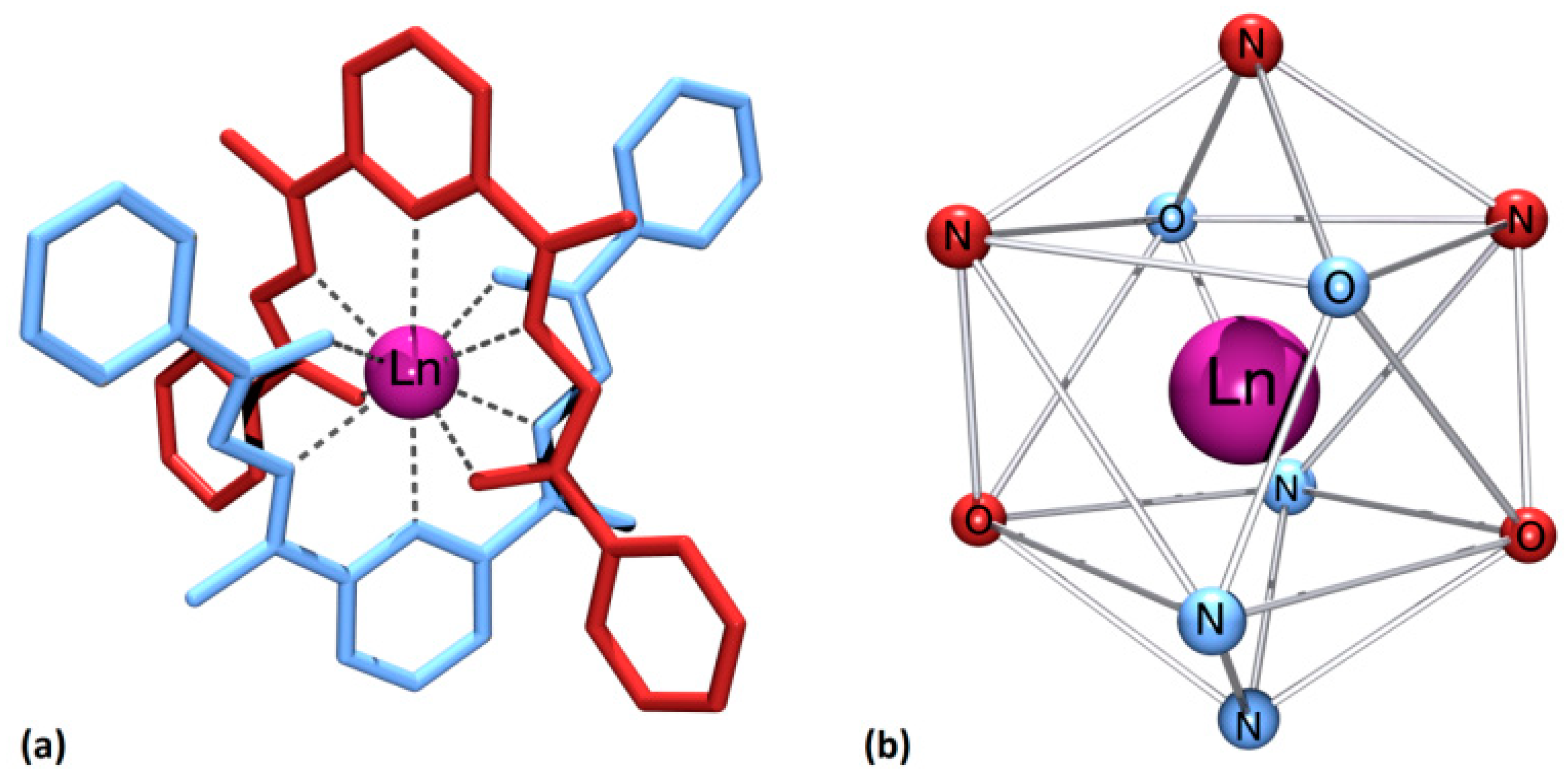
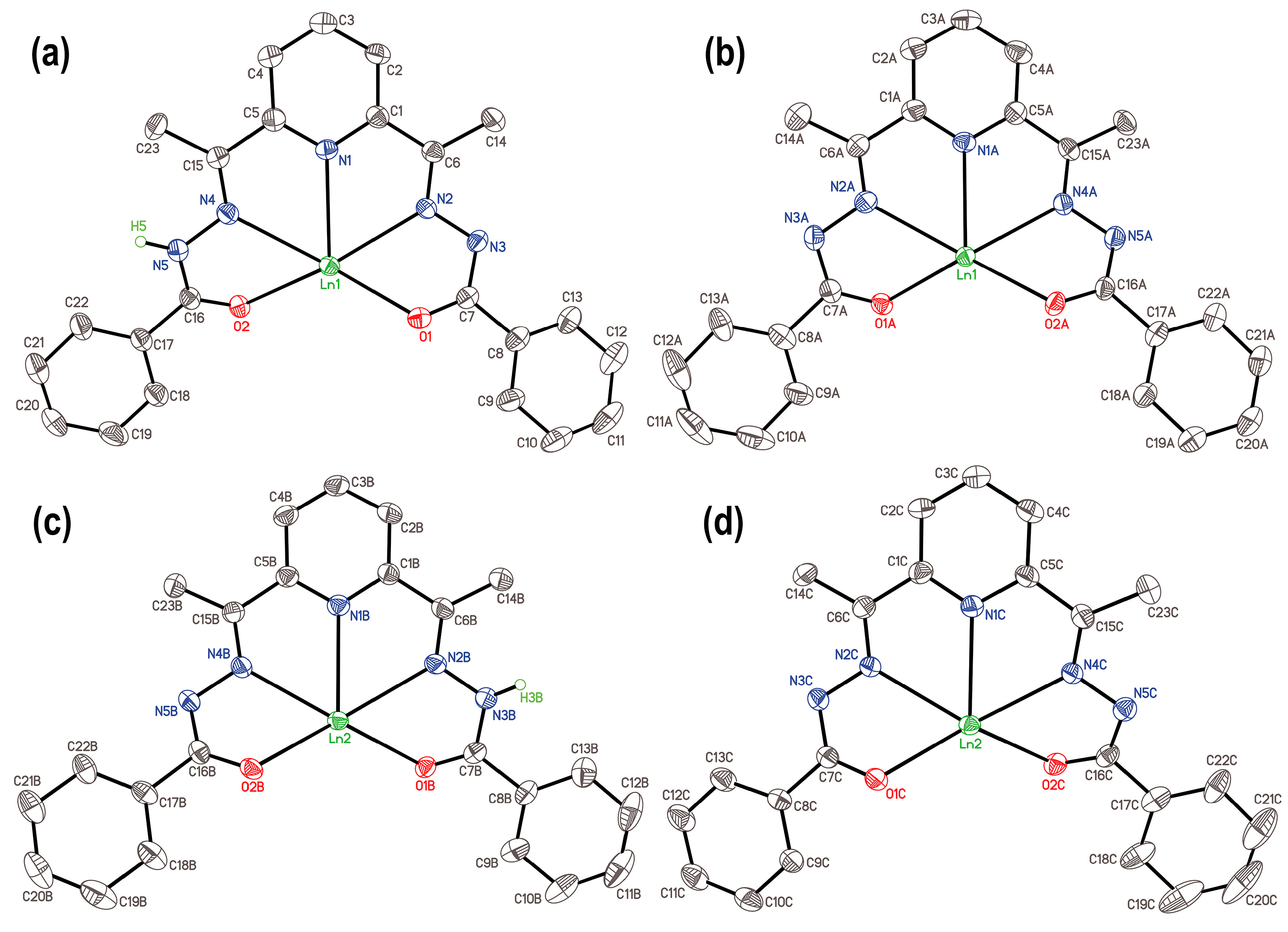
2.2. X-Ray Crystallography
2.3. Magnetism
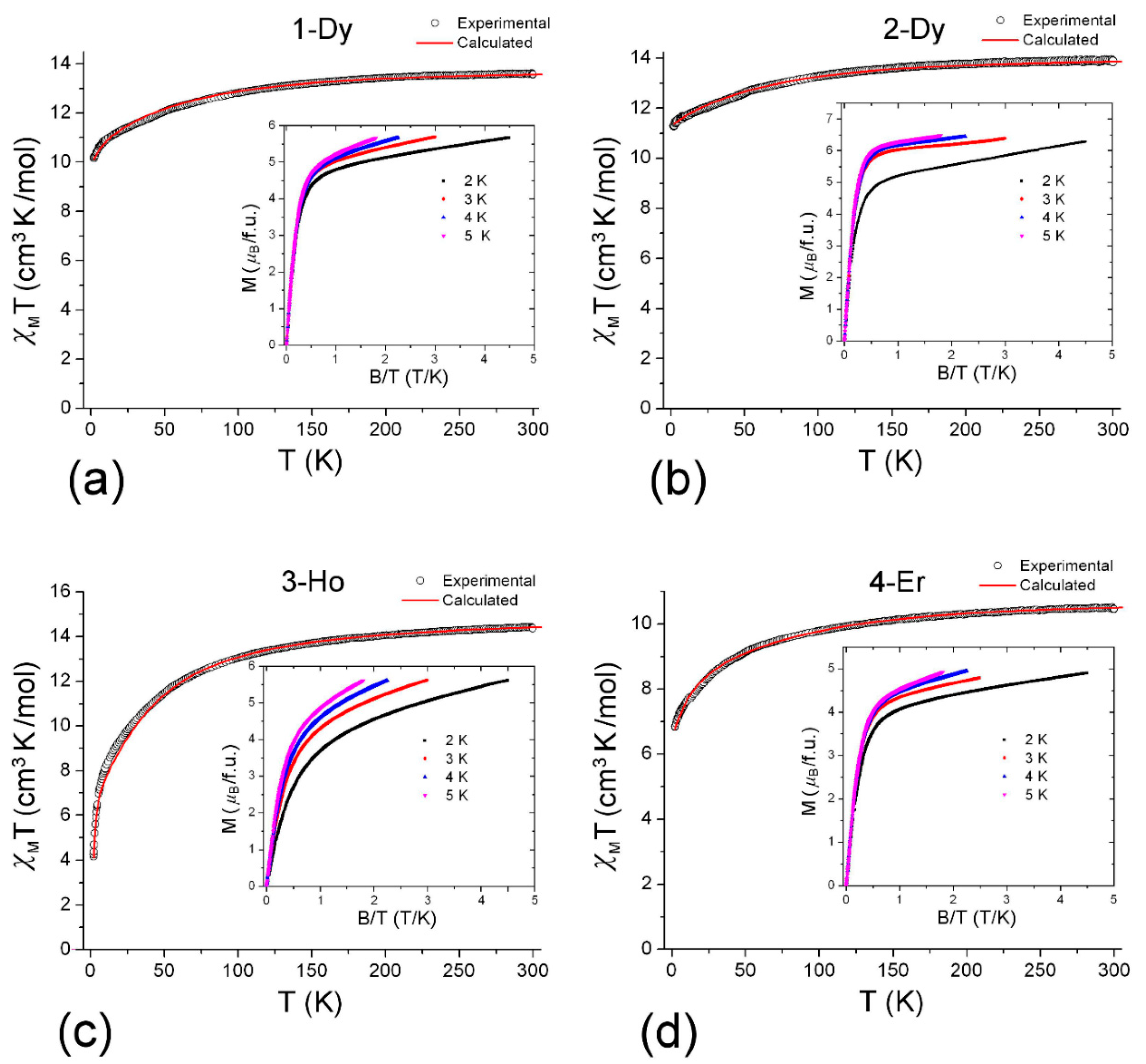
2.3.1. Static Magnetic Properties
2.3.2. Analysis of dc-Magnetic Data
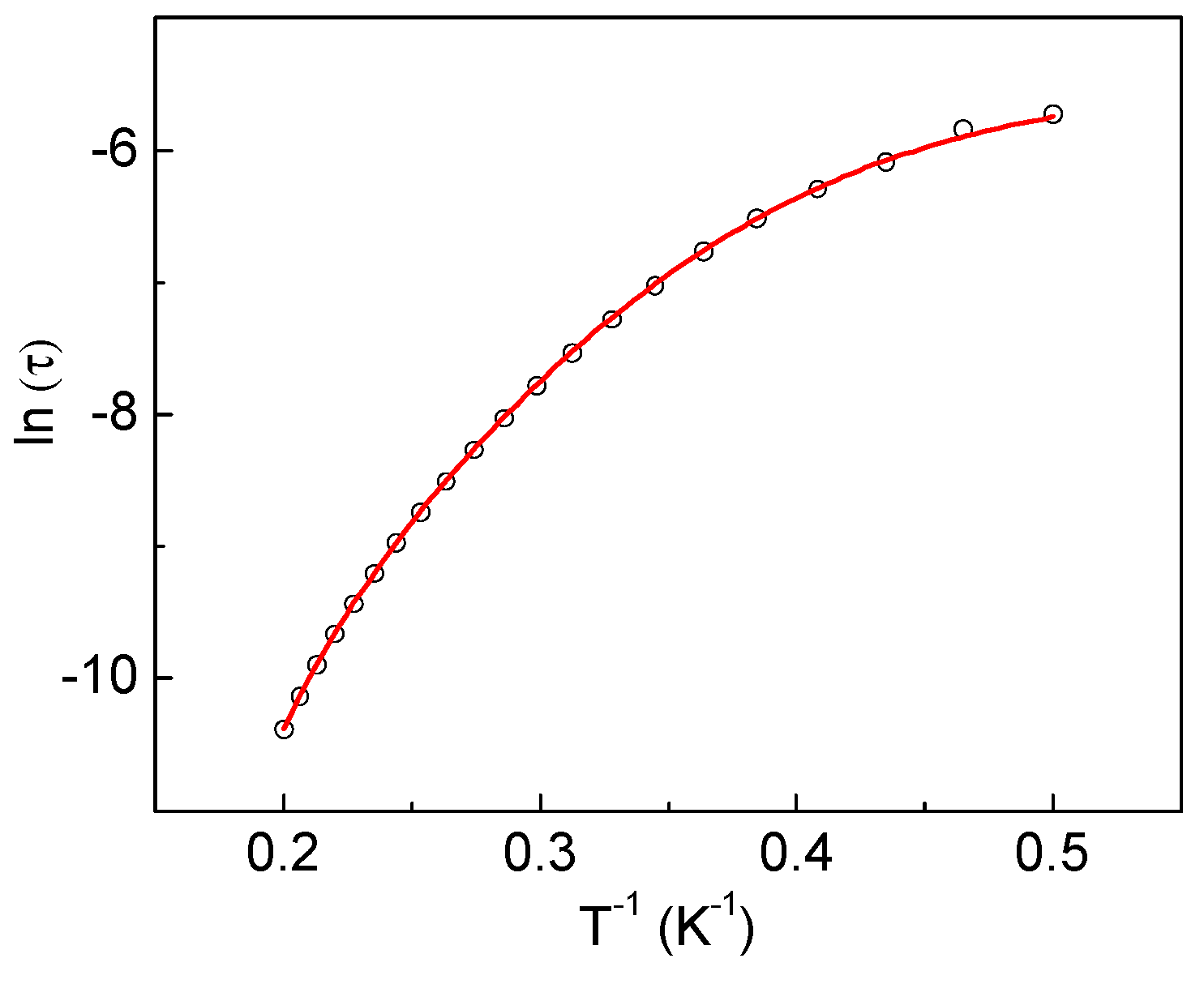
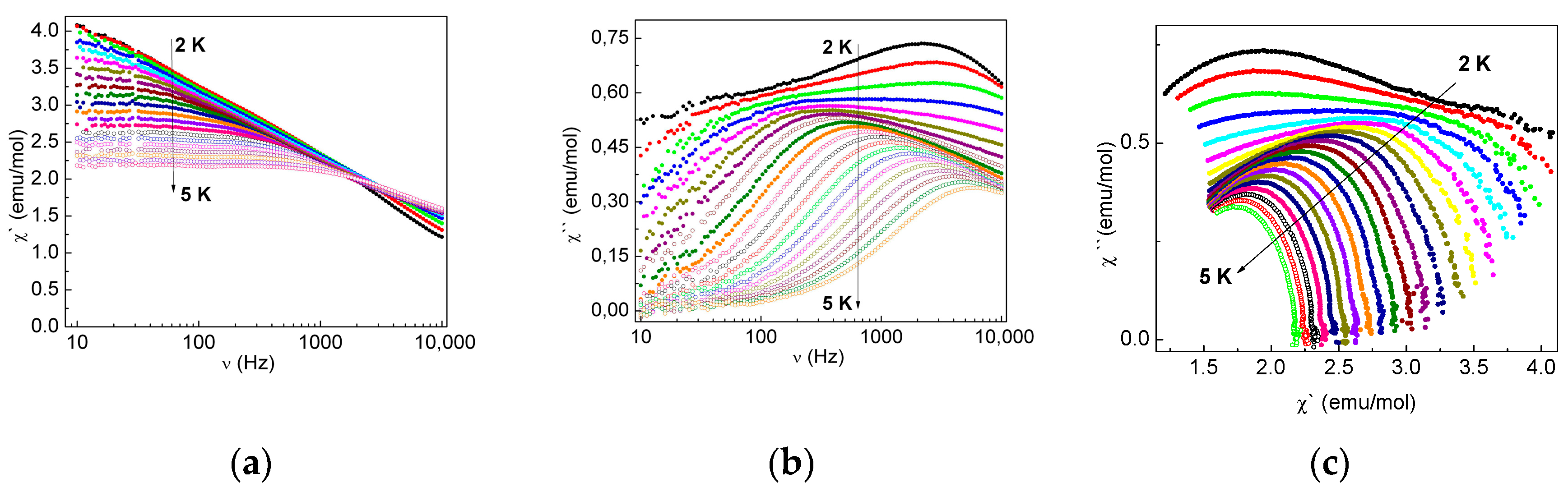
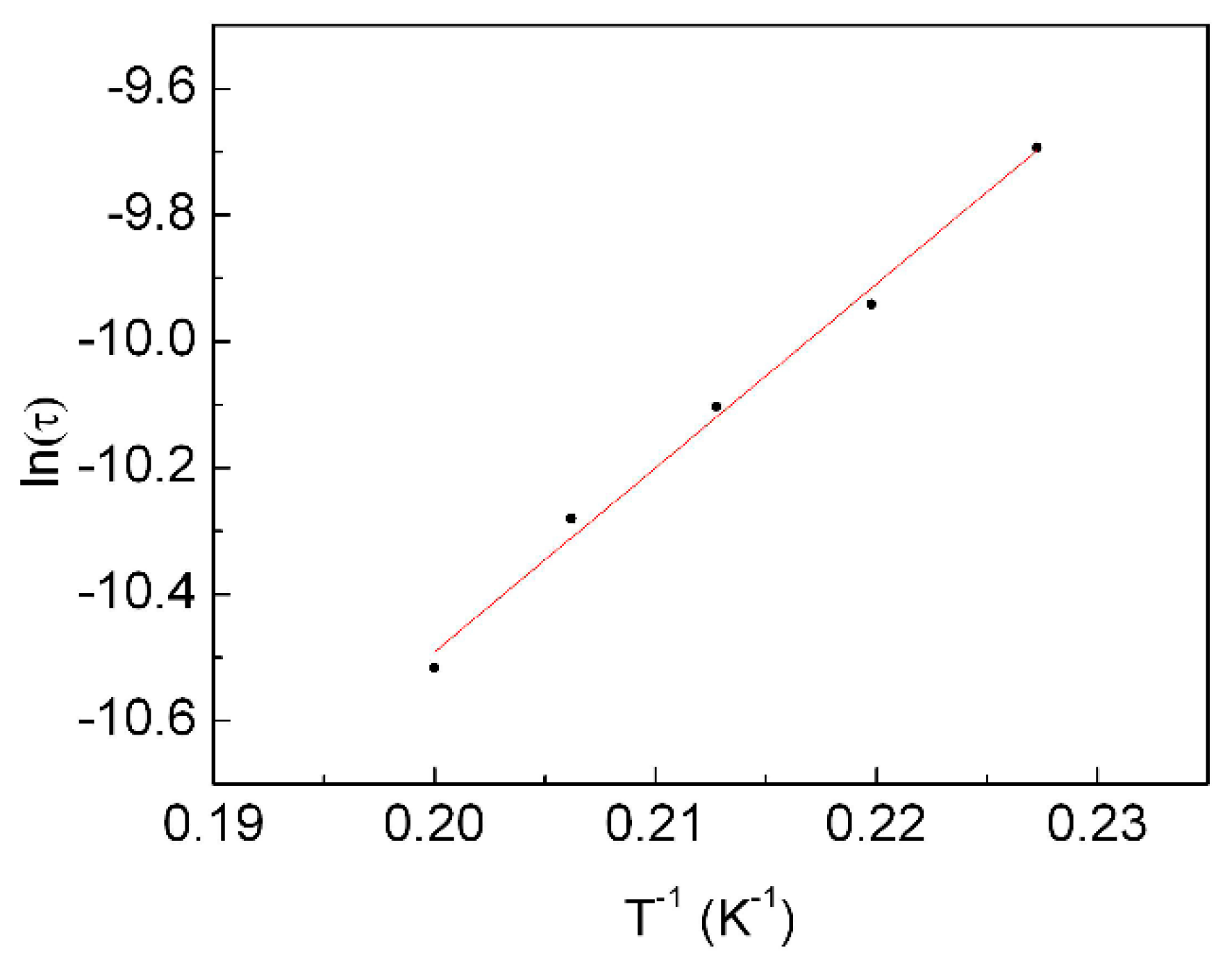
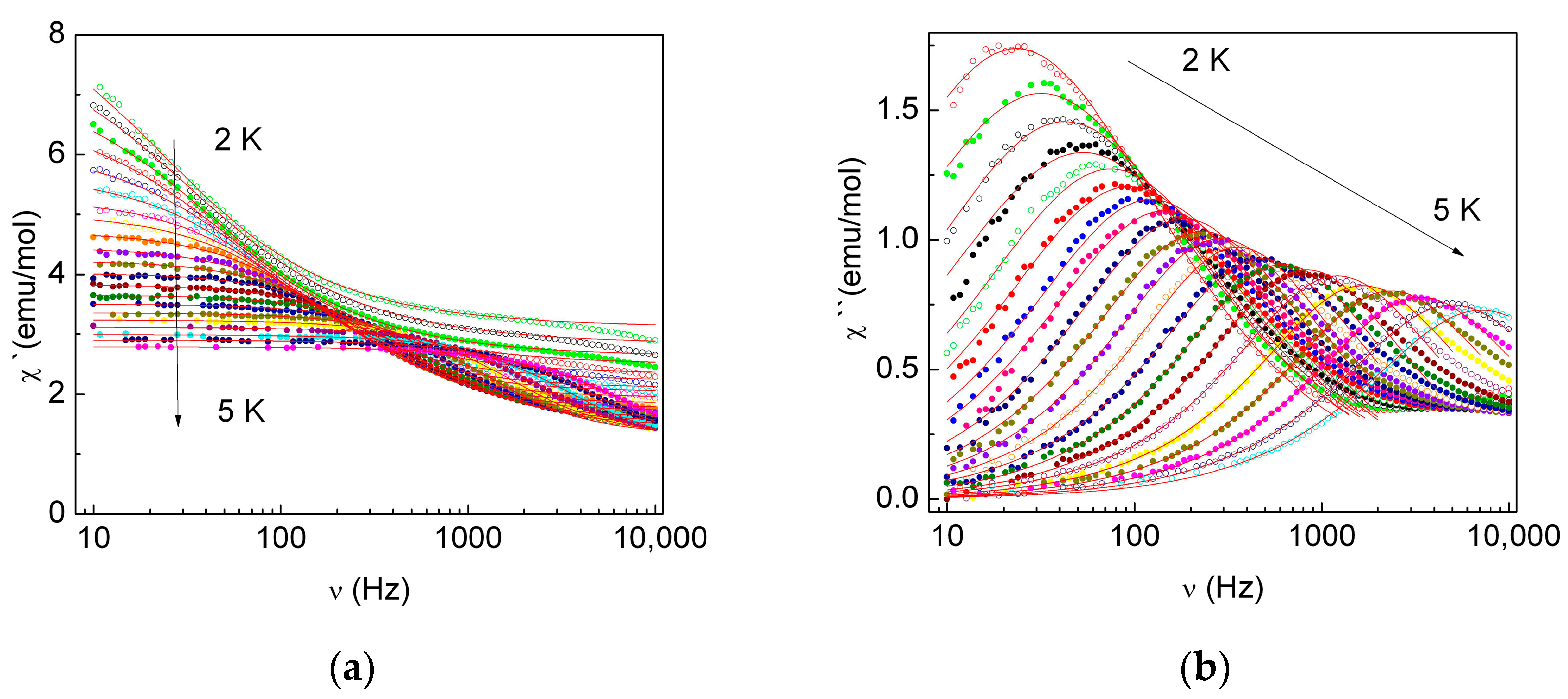
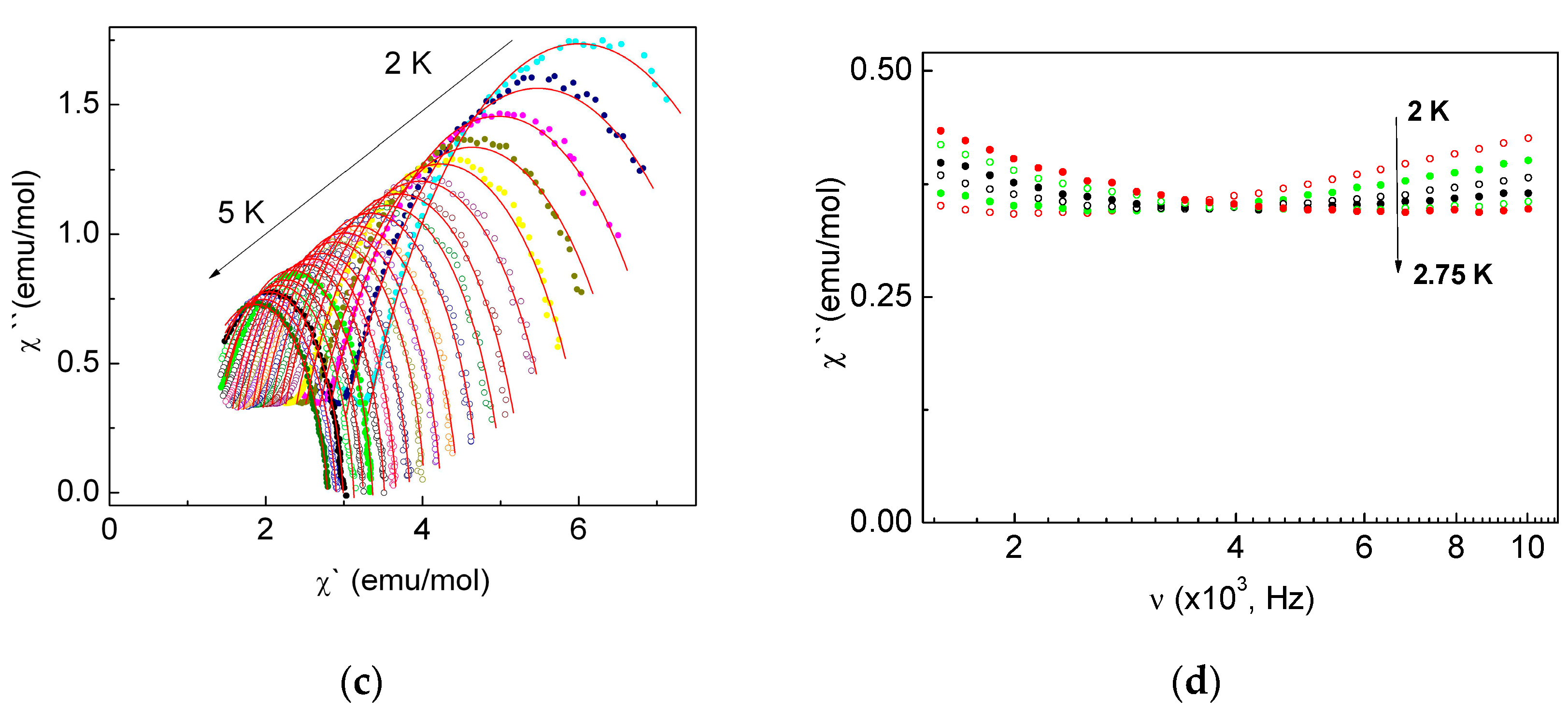
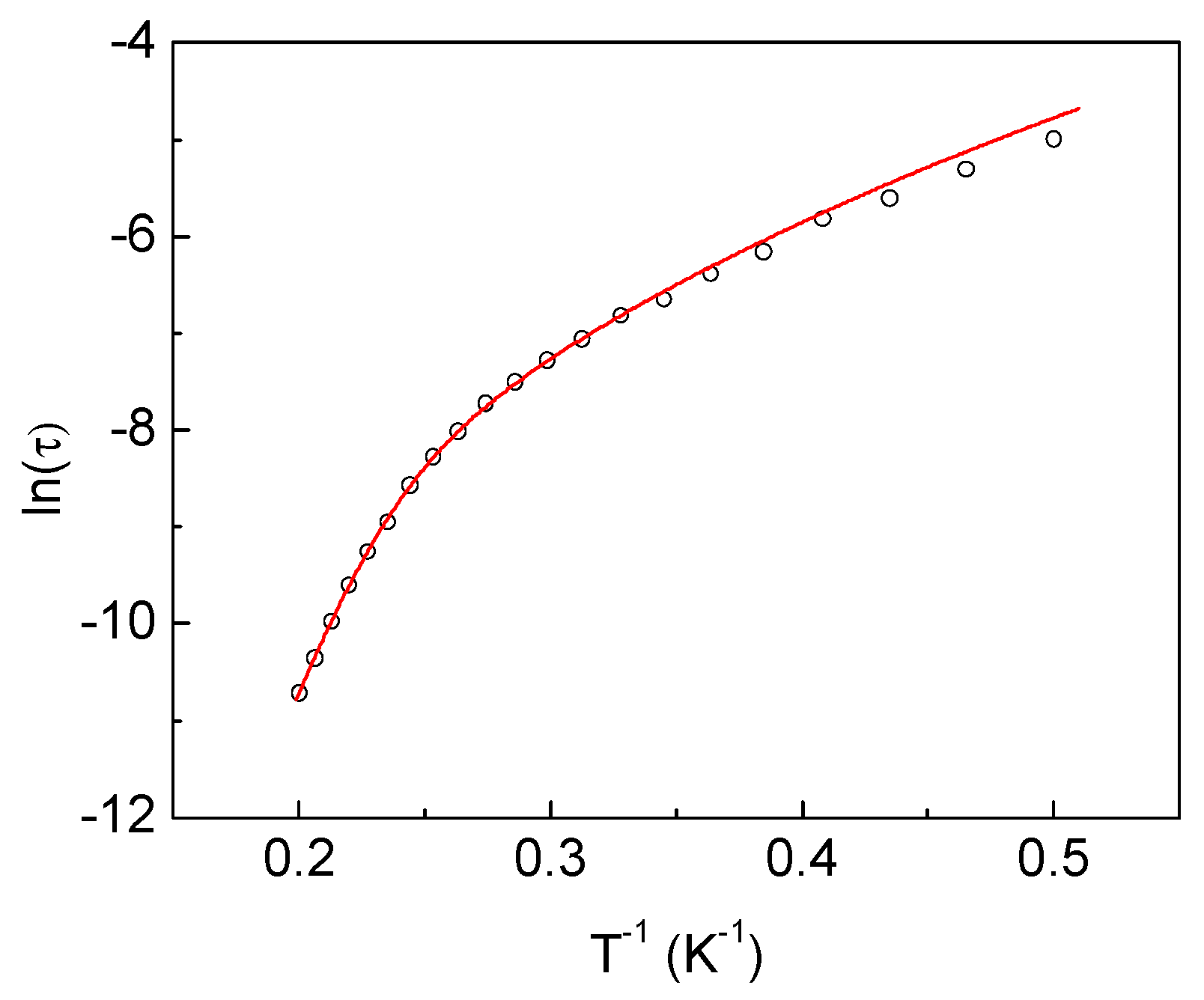
2.3.3. Dynamic Magnetic Properties
3. Materials and Methods
3.1. Synthetic Procedures
3.2. X-Ray Data Collection, Structure Solution and Refinement
3.3. Simulation of Static Magnetic Properties and CF Calculations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Sessoli, R.; Gatteschi, D.; Caneschi, A.; Novak, M.A. Magnetic bistability in a metal-ion cluster. Nature 1993, 365, 141–143. [Google Scholar] [CrossRef]
- Caneschi, A.; Gatteschi, D.; Sessoli, R.; Barra, A.L.; Brunel, L.C.; Guillot, M. Alternating current susceptibility, high field magnetization, and millimeter band EPR evidence for a ground S = 10 state in [Mn12O12(CH3COO)16(H2O)4].2 CH3COOH.4H2O. J. Am. Chem. Soc. 1991, 113, 5873–5874. [Google Scholar] [CrossRef]
- Gateschi, D.; Sessoli, R.; Villain, J. Molecular Nanomagnets; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Benelli, C.; Gatteschi, D. Introduction to Molecular Magnetism; Wiley-VCH: Weinheim, Germany, 2015. [Google Scholar]
- Leuenberger, M.N.; Loss, D. Quantum computing in molecular magnets. Nature 2001, 410, 789–793. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bogani, L.; Wernsdorfer, W. Molecular spintronics using single-molecule magnets. Nat. Mater. 2008, 7, 179–186. [Google Scholar] [CrossRef] [PubMed]
- Mannini, M.; Pineider, F.; Sainctavit, P.; Danieli, C.; Otero, E.; Sciancalepore, C.; Talarico, A.M.; Arrio, M.-A.; Cornia, A.; Gatteschi, D.; et al. Magnetic memory of a single-molecule quantum magnet wired to a gold surface. Nat. Mater. 2009, 8, 194–197. [Google Scholar] [CrossRef]
- Ishikawa, N.; Sugita, M.; Ishikawa, T.; Koshihara, S.Y.; Kaizu, Y. Lanthanide Double-Decker Complexes Functioning as Magnets at the Single-Molecular Level. J. Am. Chem. Soc. 2003, 125, 8694–8695. [Google Scholar] [CrossRef] [PubMed]
- Sessoli, R.; Powell, A.K. Strategies towards single molecule magnets based on lanthanide ions. Coord. Chem. Rev. 2009, 253, 2328–2341. [Google Scholar] [CrossRef]
- Sorace, L.; Benelli, C.; Gatteschi, D. Lanthanides in molecular magnetism: Old tools in a new field. Chem. Soc. Rev. 2011, 40, 3092–3104. [Google Scholar] [CrossRef]
- Woodruff, D.N.; Winpenny, R.E.P.; Layfield, R.A. Lanthanide Single-Molecule Magnets. Chem. Rev. 2013, 113, 5110–5148. [Google Scholar] [CrossRef]
- Nakano, M.; Oshio, H. Magnetic anisotropies in paramagnetic polynuclear metal complexes. Chem. Soc. Rev. 2011, 40, 3239–3248. [Google Scholar] [CrossRef]
- Tang, J.; Zhang, P. Lanthanide Single Molecular Magnets; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Jiang, S.-D.; Wang, B.-W.; Gao, S. Advances in Lanthanide Single-Ion Magnets. Struct. Bond. 2015, 164, 111–141. [Google Scholar]
- Habib, F.; Murugesu, M. Lessons learned from dinuclear lanthanide nano-magnets. Chem. Soc. Rev. 2013, 42, 3278–3288. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gregson, M.; Chilton, N.F.; Ariciu, A.-M.; Tuna, F.; Crowe, I.F.; Lewis, W.; Blake, A.J.; Collison, D.; McInnes, E.J.L.; Winpenny, R.E.P.; et al. A monometallic lanthanide bis(methanediide) single molecule magnet with a large energy barrier and complex spin relaxation behaviour. Chem. Sci. 2016, 7, 155–165. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Layfield, R.A.; Murugesu, M. (Eds.) Lanthanides and Actinides in Molecular Magnetism; Wiley-VCH: Weinheim, Germany, 2015. [Google Scholar]
- Wang, H.; Wang, B.-W.; Bian, Y.; Gao, S.; Jiang, J. Single-molecule magnetism of tetrapyrrole lanthanide compounds with sandwich multiple-decker structures. Coord. Chem. Rev. 2016, 306, 195–216. [Google Scholar] [CrossRef]
- Ishikawa, N.; Otsuka, S.; Kaizu, Y. The Effect of the f–f Interaction on the Dynamic Magnetism of a Coupled 4f8 System in a Dinuclear Terbium Complex with Phthalocyanines. Angew. Chem. Int. Ed. 2005, 44, 731–733. [Google Scholar] [CrossRef]
- Ishikawa, N.; Sugita, M.; Wernsdorfer, W. Quantum Tunneling of Magnetization in Lanthanide Single-Molecule Magnets: Bis(phthalocyaninato)terbium and Bis(phthalocyaninato)dysprosium Anions. Angew. Chem. Int. Ed. 2005, 44, 2931–2935. [Google Scholar] [CrossRef] [Green Version]
- Branzoli, F.; Carretta, P.; Filibian, M.; Zoppellaro, G.; Graf, M.J.; Galan-Mascaros, J.R.; Fuhr, O.; Brink, S.; Ruben, M. Spin Dynamics in the Negatively Charged Terbium (III) Bis-phthalocyaninato Complex. J. Am. Chem. Soc. 2009, 131, 4387–4396. [Google Scholar] [CrossRef]
- Jiang, S.-D.; Wang, B.-W.; Su, G.; Wang, Z.-M.; Gao, S. A Mononuclear Dysprosium Complex Featuring Single-Molecule-Magnet Behavior. Angew. Chem. Int. Ed. 2010, 49, 7448–7451. [Google Scholar] [CrossRef]
- Blagg, R.J.; Muryn, C.A.; McInnes, E.J.L.; Tuna, F.; Winpenny, R.E.P. Single Pyramid Magnets: Dy5 Pyramids with Slow Magnetic Relaxation to 40K. Angew. Chem. Int. Ed. 2011, 50, 6530–6533. [Google Scholar] [CrossRef]
- Liu, J.-L.; Chen, Y.-C.; Zheng, Y.-Z.; Lin, W.-Q.; Ungur, L.; Wernsdorfer, W.; Chibotaru, L.F.; Tong, M.-L. Switching the anisotropy barrier of a single-ion magnet by symmetry change from quasi-D5h to quasi-Oh. Chem. Sci. 2013, 4, 3310–3316. [Google Scholar] [CrossRef]
- Blagg, R.J.; Ungur, L.; Tuna, F.; Speak, J.; Comar, P.; Collison, D.; Wernsdorfer, W.; McInnes, E.J.L.; Chibotaru, L.F.; Winpenny, R.E.P. Magnetic relaxation pathways in lanthanide single-molecule magnets. Nat. Chem. 2013, 5, 673–678. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.-S.; Chilton, N.F.; Winpenny, R.E.P.; Zheng, Y.-Z. On Approaching the Limit of Molecular Magnetic Anisotropy: A Near-Perfect Pentagonal Bipyramidal Dysprosium(III) Single-Molecule Magnet. Angew. Chem. Int. Ed. 2016, 55, 16071–16074. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.-C.; Liu, J.-L.; Ungur, L.; Liu, J.; Li, Q.-W.; Wang, L.-F.; Ni, Z.-P.; Chibotaru, L.F.; Chen, X.-M.; Tong, M.-L. Symmetry-Supported Magnetic Blocking at 20 K in Pentagonal Bipyramidal Dy(III) Single-Ion Magnets. J. Am. Chem. Soc. 2016, 138, 2829–2837. [Google Scholar] [CrossRef]
- Liu, J.; Chen, Y.-C.; Liu, J.-L.; Vieru, V.; Ungur, L.; Jia, J.-H.; Chibotaru, L.F.; Lan, Y.; Wernsdorfer, W.; Gao, S.; et al. A Stable Pentagonal Bipyramidal Dy(III) Single-Ion Magnet with a Record Magnetization Reversal Barrier over 1000 K. J. Am. Chem. Soc. 2016, 138, 5441–5450. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Jung, J.; Zhang, P.; Guo, M.; Zhao, L.; Tang, J.; Le Guennic, B. Site-Resolved Two-Step Relaxation Process in an Asymmetric Dy2 Single-Molecule Magnet. Chem. Eur. J. 2016, 22, 1392–1398. [Google Scholar] [CrossRef] [PubMed]
- Ishikawa, N.; Sugita, M.; Wernsdorfer, W. Nuclear Spin Driven Quantum Tunneling of Magnetization in a New Lanthanide Single-Molecule Magnet: Bis(Phthalocyaninato)holmium Anion. J. Am. Chem. Soc. 2005, 127, 3650–3651. [Google Scholar] [CrossRef] [Green Version]
- Cardona-Serra, S.; Clemente-Juan, J.M.; Coronado, E.; Gaita-Ariño, A.; Camón, A.; Evangelisti, M.; Luis, F.; Martínez-Pérez, M.J.; Sesé, J. Lanthanoid Single-Ion Magnets Based on Polyoxometalates with a 5-fold Symmetry: The Series [LnP5W30O110]12– (Ln3+ = Tb, Dy, Ho, Er, Tm, and Yb). J. Am. Chem. Soc. 2012, 134, 14982–14990. [Google Scholar] [CrossRef]
- Chen, Y.-C.; Liu, J.-L.; Wernsdorfer, W.; Liu, D.; Chibotaru, L.F.; Chen, X.-M.; Tong, M.-L. Hyperfine-Interaction-Driven Suppression of Quantum Tunneling at Zero Field in a Holmium(III) Single-Ion Magnet. Angew. Chem. Int. Ed. 2017, 56, 4996–5000. [Google Scholar] [CrossRef]
- Jiang, S.-D.; Wang, B.-W.; Sun, H.-L.; Wang, Z.-M.; Gao, S. An Organometallic Single-Ion Magnet. J. Am. Chem. Soc. 2011, 133, 4730–4733. [Google Scholar] [CrossRef]
- Meihaus, K.R.; Long, J.R. Magnetic Blocking at 10 K and a Dipolar-Mediated Avalanche in Salts of the Bis(η8-cyclooctatetraenide) Complex [Er(COT)2]−. J. Am. Chem. Soc. 2013, 135, 17952–17957. [Google Scholar] [CrossRef]
- Ungur, L.; Le Roy, J.J.; Korobkov, I.; Murugesu, M.; Chibotaru, L.F. Fine-tuning the Local Symmetry to Attain Record Blocking Temperature and Magnetic Remanence in a Single-Ion Magnet. Angew. Chem. Int. Ed. 2014, 53, 4413–4417. [Google Scholar] [CrossRef] [PubMed]
- Le Roy, J.J.; Ungur, L.; Korobkov, I.; Chibotaru, L.F.; Murugesu, M. Coupling Strategies to Enhance Single-Molecule Magnet Properties of Erbium-Cyclooctatetraenyl Complexes. J. Am. Chem. Soc. 2014, 136, 8003–8010. [Google Scholar] [CrossRef] [PubMed]
- Bar, A.K.; Kalita, P.; Singh, M.K.; Rajaraman, G.; Chandrasekhar, V. Low-coordinate mononuclear lanthanide complexes as molecular nanomagnets. Coord. Chem. Rev. 2018, 367, 163–216. [Google Scholar] [CrossRef]
- Guo, F.-S.; Day, B.; Chen, Y.-C.; Tong, M.-L.; Mansikkamaki, A.; Layfield, R.A. A Dysprosium Metallocene Single-Molecule Magnet Functioning at the Axial Limit. Angew. Chem. Int. Ed. 2017, 56, 11445–11449. [Google Scholar] [CrossRef]
- Goodwin, C.A.P.; Ortu, F.; Reta, D.; Chilton, N.F.; Mills, D.P. Molecular magnetic hysteresis at 60 kelvin in dysprosocenium. Nature 2017, 548, 439–442. [Google Scholar] [CrossRef]
- Guo, F.S.; Day, B.M.; Chen, Y.C.; Tong, M.L.; Mansikkamäki, A.; Layfield, R.A. Magnetic hysteresis up to 80 kelvin in a dysprosium metallocene single-molecule magnet. Science 2018, 362, 1400–1403. [Google Scholar] [CrossRef] [Green Version]
- Gupta, S.K.; Rajeshkumar, T.; Rajaraman, G.; Murugavel, R. An air-stable Dy(III) single-ion magnet with high anisotropy barrier and blocking temperature. Chem. Sci. 2016, 7, 5181–5191. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.C.; Liu, J.L.; Lan, Y.; Zhong, Z.Q.; Mansikkamäki, A.; Ungur, L.; Li, Q.W.; Jia, J.H.; Chibotaru, L.F.; Han, J.B.; et al. Dynamic Magnetic and Optical Insight into a High Performance Pentagonal Bipyramidal DyIII Single-Ion Magnet. Chem. Eur. J. 2017, 23, 5708–5715. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.L.; Wu, J.Y.; Chen, Y.C.; Mereacre, V.; Powell, A.K.; Ungur, L.; Chibotaru, L.F.; Chen, X.M.; Tong, M.L. A Heterometallic FeII–DyIII Single-Molecule Magnet with a Record Anisotropy Barrier. Angew. Chem. Int. Ed. 2014, 53, 12966–12970. [Google Scholar] [CrossRef]
- Li, J.; Yuan, C.; Yang, L.; Kong, M.; Zhang, J.; Ge, J.Y.; Zhang, Y.Q.; Song, Y. Magnetic Anisotropy along a Series of Lanthanide Polyoxometalates with Pentagonal Bipyramidal Symmetry. Inorg. Chem. 2017, 56, 7835–7841. [Google Scholar] [CrossRef]
- Huang, X.C.; Zhang, M.; Wu, D.; Shao, D.; Zhao, X.H.; Huang, W.; Wang, X.Y. Single molecule magnet behavior observed in a 1-D dysprosium chain with quasi-D5h symmetry. Dalton Trans. 2015, 44, 20834–20838. [Google Scholar] [CrossRef] [PubMed]
- Ren, M.; Bao, S.S.; Wang, B.W.; Ferreira, R.A.S.; Zheng, L.M.; Carlos, L.D. Lanthanide phosphonates with pseudo-D5h local symmetry exhibiting magnetic and luminescence bifunctional properties. Inorg. Chem. Front. 2015, 2, 558–566. [Google Scholar] [CrossRef]
- Li, M.; Wu, H.; Yang, Q.; Ke, H.; Yin, B.; Shi, Q.; Wang, W.; Wei, Q.; Xie, G.; Chen, S. Experimental and Theoretical Interpretation on the Magnetic Behavior in a Series of Pentagonal-Bipyramidal DyIII Single-Ion Magnets. Chem. Eur. J. 2017, 23, 17775–17787. [Google Scholar] [CrossRef] [PubMed]
- Lisowski, J.; Sessler, J.L.; Lynch, V.; Mody, T.D. 1H NMR Spectroscopic Study of Paramagnetic Lanthanide(III) Texaphyrins. Effect of Axial Ligation. J. Am. Chem. Soc. 1995, 117, 2273–2285. [Google Scholar] [CrossRef]
- Magda, D.; Crofts, S.; Lin, A.; Miles, D.; Wright, M.; Sessler, J.L. Synthesis and Kinetic Properties of Ribozyme Analogues Prepared Using Phosphoramidite Derivatives of Dysprosium(III) Texaphyrin. J. Am. Chem. Soc. 1997, 119, 2293–2294. [Google Scholar] [CrossRef]
- Bar, A.K.; Kalita, P.; Sutter, J.P.; Chandrasekhar, V. Pentagonal-Bipyramid Ln(III) Complexes Exhibiting Single-Ion-Magnet Behavior: A Rational Synthetic Approach for a Rigid Equatorial Plane. Inorg. Chem. 2018, 57, 2398–2401. [Google Scholar] [CrossRef]
- Gavey, E.L.; Beldjoudi, Y.; Rawson, J.M.; Stamatatos, T.C.; Pilkington, M. Slow relaxation in the first penta-aza Dy(III) macrocyclic complex. Chem. Commun. 2014, 50, 3741–3743. [Google Scholar] [CrossRef]
- Gavey, E.L.; Pilkington, M. Employing Schiff-base macrocycles to probe the effect of ligand field on the relaxation dynamics of a family of DyIII SMMs. Polyhedron 2016, 108, 122–130. [Google Scholar] [CrossRef]
- Sasnovskaya, V.D.; Kopotkov, V.A.; Kazakova, A.V.; Talantsev, A.D.; Morgunov, R.B.; Simonov, S.V.; Zorina, L.V.; Mironov, V.S.; Yagubskii, E.B. Slow magnetic relaxation in mononuclear complexes of Tb, Dy, Ho and Er with the pentadentate (N3O2) Schiff-base dapsc ligand. New J. Chem. 2018, 42, 14883–14893. [Google Scholar] [CrossRef]
- Bazhenova, T.A.; Mironov, V.S.; Yakushev, I.A.; Svetogorov, R.D.; Maximova, O.V.; Manakin, Y.V.; Kornev, A.B.; Vasiliev, A.N.; Yagubskii, E.B. End-to-End Azido-Bridged Lanthanide Chain Complexes (Dy, Er, Gd, and Y) with a Pentadentate Schiff-Base [N3O2] Ligand: Synthesis, Structure, and Magnetism. Inorg. Chem. 2020, 59, 563–578. [Google Scholar] [CrossRef]
- Tamboura, F.B.; Haba, P.M.; Gaye, M.; Sall, A.S.; Barry, A.H.; Jouini, T. Structural studies of bis-(2,6-diacetylpyridine-bis-(phenylhydrazone)) and X-ray structure of its Y(III), Pr(III), Sm(III) and Er(III) complex. Polyhedron 2004, 23, 1191–1197. [Google Scholar] [CrossRef]
- Gao, X.-S.; Yao, X.J.C. Two new complexes of Lanthanide(III) ion with the N3O2-donor Schiff base ligand: Synthesis, crystal structure, and magnetic properties. J. Mol. Struct. 2016, 1126, 275–279. [Google Scholar] [CrossRef]
- Tamboura, F.B.; Diop, M.; Gaye, M.; Sall, A.S.; Barry, A.H.; Jouini, T. X-ray structure and spectroscopic properties of some lanthanides(III) complexes derived from 2,6-diacetylpyridine-bis(benzoylhydrazone). Inorg. Chem. Commun. 2003, 6, 1004–1010. [Google Scholar] [CrossRef]
- Farrugia, L.J. WinGX and ORTER for Windows: An update. J. Appl. Crystallogr. 2012, 45, 849–854. [Google Scholar] [CrossRef]
- Llunell, M.; Casanova, D.; Cirera, J.; Alemany, P.; Alvarez, S. SHAPE, version 2.1; Universitat de Barcelona: Barcelona, Spain, 2013; Available online: http://www.ee.ub.edu/index.php?option=com_jdownloads&view=viewcategories&Itemid=529 (accessed on 26 April 2013).
- Alvarez, S.; Alemany, P.; Casanova, D.; Cirera, J.; Llunell, M.; Avnir, D. Shape maps and polyhedral interconversion paths in transition metal chemistry. Coord. Chem. Rev. 2005, 249, 1693–1708. [Google Scholar] [CrossRef]
- Batchelor, L.J.; Cimatti, I.; Guillot, R.; Tuna, F.; Wernsdorfer, W.; Ungur, L.; Chibotaru, L.F.; Campbell, V.E.; Mallah, T. Chemical tuning of the magnetic relaxation in dysprosium(iii) mononuclear complexes. Dalton Trans. 2014, 43, 12146–12149. [Google Scholar] [CrossRef] [PubMed]
- Gamer, M.T.; Lan, Y.; Roesky, P.W.; Powell, A.K.; Clerac, R. Pentanuclear Dysprosium Hydroxy Cluster Showing Single-Molecule-Magnet Behavior. Inorg. Chem. 2008, 47, 6581–6583. [Google Scholar] [CrossRef]
- Layfield, R.A.; McDouall, J.J.W.; Sulway, S.A.; Tuna, F.; Collison, D.; Winpenny, R.E.P. Influence of the N-Bridging Ligand on Magnetic Relaxation in an Organometallic Dysprosium Single-Molecule Magnet. Chem. Eur. J. 2010, 16, 4442–4446. [Google Scholar] [CrossRef]
- Wybourne, G. Spectroscopic Properties of Rare Earths; Interscience: New York, NY, USA, 1965. [Google Scholar]
- Hüfner, S. Optical Spectra of Transparent Rare Earth Compounds; Academic: New York, NY, USA, 1978. [Google Scholar]
- Gorller-Walrand, C.; Binnemans, K. Rationalization of the crystal-field parametrization. In Handbook on the Physics and Chemistry of Rare Earths; Gschneidner, K.A., Jr., Eyring, L., Eds.; North-Holland: Amsterdam, The Netherlands, 1996; Volume 23, pp. 121–283. [Google Scholar]
- Carnall, W.T.; Fields, P.R.; Rajnak, K. Spectral Intensities of the Trivalent Lanthanides and Actinides in Solution. II. Pm3+, Sm3+, Eu3+, Gd3+, Tb3+, Dy3+, and Ho3+. J. Chem. Phys. 1968, 49, 4412–4423. [Google Scholar] [CrossRef]
- Carnall, W.T.; Goodman, G.L.; Rajnak, K.; Rana, R.S. A systematic analysis of the spectra of the lanthanides doped into single crystal LaF3. J. Chem. Phys. 1989, 90, 3443–3457. [Google Scholar] [CrossRef]
- Newman, D.J. The orbit-lattice interaction for lanthanide ions. I. Determination of empirical parameters. Aust. J. Phys. 1978, 31, 79–93. [Google Scholar] [CrossRef] [Green Version]
- Newman, D.J.; Ng, B. The superposition model of crystal fields. Rep. Prog. Phys. 1989, 52, 699–763. [Google Scholar] [CrossRef]
- Bungenstock, C.; Tröster, T.; Holzapfel, W.B. Effect of pressure on free-ion and crystal-field parameters of Pr3+ in LOCl (L = La, Pr, Gd). Phys. Rev. B 2000, 62, 7945–7955. [Google Scholar] [CrossRef]
- Gerloch, M.; McMeeking, R.F. Paramagnetic properties of unsymmetrical transition-metal complexes. J. Chem. Soc. Dalton Trans. 1975, 22, 2443–2451. [Google Scholar] [CrossRef]
- Mironov, V.S.; Li, L.E. Crystal field analysis of Pr3+ and Nd3+ ions in KR(WO4)2 (R = Y or Gd) potassium rare-earth tungstates. J. Alloys Compos. 1998, 279, 83–92. [Google Scholar] [CrossRef]
- Mironov, V.S.; Galyametdinov, Y.G.; Ceulemans, A.; Binnemans, K. On the magnetic anisotropy of lanthanide-containing metallomesogens. J. Chem. Phys. 2000, 113, 10293–10303. [Google Scholar] [CrossRef]
- Mironov, V.S.; Galyametdinov, Y.G.; Ceulemans, A.; Gorller-Walrand, C.; Binnemans, K. Room-temperature magnetic anisotropy of lanthanide complexes: A model study for various coordination polyhedra. J. Chem. Phys. 2002, 116, 4673–4685. [Google Scholar] [CrossRef]
- Chang, N.C.; Gruber, J.B.; Leavitt, R.P.; Morrison, C.A. Optical spectra, energy levels, and crystal-field analysis of tripositive rare earth ions in Y2O3. I. Kramers ions in C2 sites. J. Chem. Phys. 1982, 76, 3877–3889. [Google Scholar] [CrossRef]
- Cole, K.S.; Cole, R.H. Dispersion and Absorption in Dielectrics I. Alternating Current Characteristics. J. Chem. Phys. 1941, 9, 341–351. [Google Scholar] [CrossRef] [Green Version]
- Shrivastava, K.N. Theory of Spin–Lattice Relaxation. Phys. Status Solidi B 1983, 117, 437–458. [Google Scholar] [CrossRef]
- Guo, Y.-N.; Xu, G.-F.; Guo, Y.; Tang, J. Relaxation dynamics of dysprosium(III) single molecule magnets. Dalton Trans. 2011, 40, 9953–9963. [Google Scholar] [CrossRef]
- Gonidec, M.; Luis, F.; Vílchez, À.; Esquena, J.; Amabilino, D.B.; Veciana, J. A Liquid-Crystalline Single-Molecule Magnet with Variable Magnetic Properties. Angew. Chem. Int. Ed. 2010, 49, 1623–1626. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.-N.; Xu, G.-F.; Gamez, P.; Zhao, L.; Lin, S.-Y.; Deng, R.; Tang, J.; Zhang, H.-J. Two-Step Relaxation in a Linear Tetranuclear Dysprosium(III) Aggregate Showing Single-Molecule Magnet Behavior. J. Am. Chem. Soc. 2010, 132, 8538–8539. [Google Scholar] [CrossRef] [PubMed]
- Diaz-Ortega, I.F.; Herrera, J.M.; Aravena, D.; Ruiz, E.; Guta, T.; Rajaraman, G.; Nojiri, H.; Colacio, E. Designing a Dy2 Single-Molecule Magnet with Two Well-Differentiated Relaxation Processes by Using a Nonsymmetric Bis-bidentate Bipyrimidine-N-Oxide Ligand: A Comparison with Mononuclear Counterparts. Inorg. Chem. 2018, 57, 6362–6375. [Google Scholar] [CrossRef] [Green Version]
- Li, D.-P.; Wang, T.-W.; Li, C.-H.; Liu, D.-S.; Li, Y.-Z.; You, X.-Z. Single-ion magnets based on mononuclear lanthanide complexes with chiral Schiff base ligands [Ln(FTA)3L] (Ln = Sm, Eu, Gd, Tb and Dy). Chem. Commun. 2010, 46, 2929–2931. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Li, X.-L.; Wang, T.-W.; Song, Y.; You, X.-Z. Slow Relaxation Processes and Single-Ion Magnetic Behaviors in Dysprosium-Containing Complexes. Inorg. Chem. 2010, 49, 969–976. [Google Scholar] [CrossRef]
- Jiang, S.-D.; Liu, S.-S.; Zhou, L.-N.; Wang, B.-W.; Wang, Z.-M.; Gao, S. Series of Lanthanide Organometallic Single-Ion Magnets. Inorg. Chem. 2012, 51, 3079–3087. [Google Scholar] [CrossRef]
- Funes, A.V.; Carrella, L.; Rentschler, E.; Alborés, P. Exploring the Slow Relaxation of the Magnetization in CoIII-Decorated {DyIII2} Units. Chem. Eur. J. 2016, 22, 14308–14318. [Google Scholar] [CrossRef]
- Zhang, G.; Yu, Y.; Zhao, Y.; Xie, X.; Ding, C. Iron(III)/TEMPO-Catalyzed Synthesis of 2,5-Disubstituted 1,3,4-Oxadiazoles by Oxidative Cyclization under Mild Conditions. Synlett 2017, 28, 1373–1377. [Google Scholar]
- Murty, M.S.R.; Penthala, R.; Polepalli, S.; Jain, N. Synthesis and biological evaluation of novel resveratrol-oxadiazole hybrid heterocycles as potential antiproliferative agents. Med. Chem. Res. 2016, 25, 627–643. [Google Scholar] [CrossRef]
- Giordano, T.J.; Palenik, G.J.; Palenik, R.C.; Sullivan, D.A. Pentagonal-bipyramidal complexes. Synthesis and characterization of aqua(nitrato)[2,6-diacetylpyridine bis(benzoyl hydrazone)]cobalt(II) nitrate and diaqua[2,6-diacetylpyridine bis(benzoyl hydrazone)]nickel(II) nitrate dehydrate. Inorg. Chem. 1979, 18, 2445–2450. [Google Scholar] [CrossRef]
- Svetogorov, R.D.; Dorovatovskii, P.V.; Lazarenko, V.A. Belok/XSA Diffraction Beamline for Studying Crystalline Samples at Kurchatov Synchrotron Radiation Source. Cryst. Res. Technol. 2020, 55, 1900184. [Google Scholar] [CrossRef]
- Kabsch, W. XDS. Acta Crystallogr. Sect. D Biol. Crystallogr. 2010, 66, 125–132. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Spek, A.L. PLATON SQUEEZE: A tool for the calculation of the disordered solvent contribution to the calculated structure factors. Acta Cryst. 2015, C71, 9–18. [Google Scholar]
- Sheldrick, G.M. SHELXTL-97, version 5.10; Bruker AXS Inc.: Madison, WI, USA, 1997. [Google Scholar]
- Sheldrick, G.M. SHELXT—Integrated Space-Group and Crystal-Structure Determination. Acta Crystallogr. Sect. A Found. Adv. 2015, 71, 3–8. [Google Scholar] [CrossRef] [Green Version]


| 1-Dy | 2-Dy | 3-Ho | 4-Er | 5-Tb | |
|---|---|---|---|---|---|
| CCDC number | 1987371 | 1987372 | 1987373 | 1987374 | 1987375 |
| empirical formula | C46H42DyN10O5.50 | C52H54DyN10O9.50 | C48H45Cl2HoN10O5 | C50H45Cl12ErN10O5 | C31H43N6O11Tb |
| formula weight | 985.39 | 1133.55 | 1077.77 | 1458.62 | 834.63 |
| temperature, K | 120(2) | 120(2) | 100(2) | 120(2) | 120(2) |
| color, habit | yellow, block | yellow, block | yellow-green, prism | lemon, block | yellow, block |
| crystal size, mm | 0.232 × 0.208 × 0.208 | 0.320 × 0.210 × 0.190 | 0.180 × 0.100 × 0.080 | 0.435 × 0.431 × 0.220 | 0.325 × 0.285 × 0.242 |
| radiation source | fine-focus sealed tube | fine-focus sealed tube | synchrotron | fine-focus sealed tube | fine-focus sealed tube |
| wavelength, Å | 0.71073 | 0.71073 | 0.79272 | 0.71073 | 0.71073 |
| crystal system | Tetragonal | Triclinic | Monoclinic | Orthorhombic | Monoclinic |
| space group | P43 | P-1 | P21/c | P212121 | P21/n |
| a, Å | 14.0526(14) | 7.0262(2) | 20.115(4) | 11.5236(10) | 12.2369(8) |
| b, Å | 14.0526(14) | 13.4861(3) | 19.538(2) | 20.3299(17) | 19.6927(13) |
| c, Å | 46.815(5) | 31.4635(9) | 25.698(5) | 25.596(2) | 14.9627(10) |
| α, deg | 90 | 84.098(2) | 90 | 90 | 90 |
| β, deg | 90 | 74.746(2) | 104.258(16) | 90 | 106.0617(14) |
| γ, deg | 90 | 62.038(2) | 90 | 90 | 90 |
| V, Å3 | 9245(2) | 2437.9(4) | 9788(3) | 5996.5(9) | 3464.9(4) |
| Z | 8 | 2 | 8 | 4 | 4 |
| density (calcd), Mg/m3 | 1.416 | 1.544 | 1.463 | 1.616 | 1.600 |
| μ, mm−1 | 1.673 | 1.603 | 2.375 | 1.988 | 2.108 |
| F(000) | 3984 | 1156 | 4352 | 2908 | 1696 |
| θ range, deg | 1.690–28.000 | 1.242–29.000 | 1.165–28.500 | 1.880–28.999 | 2.017–28.998 |
| Index ranges | −18 ≤ h ≤ 17, −18 ≤ k ≤ 18, −61 ≤ l ≤ 57 | −16 ≤ h ≤ 17, −17 ≤ k ≤ 18, 0 ≤ l ≤ 23 | −24 ≤ h ≤ 24, −23 ≤ k ≤ 23, −30 ≤ l ≤ 30 | −15 ≤ h ≤ 15, −27 ≤ k ≤ 27, −34 ≤ l ≤ 34 | −16 ≤ h ≤ 16, −26 ≤ k ≤ 26, −20 ≤ l ≤ 20 |
| reflections collected | 63,809 | 31,974 | 211,750 | 71,924 | 33,909 |
| independent reflections | 21,755 (Rint =0.1051) | 12,799 (Rint = 0.0881) | 17,880 (Rint = 0.0785) | 15,895 (Rint = 0.0376) | 9218 (Rint = 0.0375) |
| R1/wR2 (I > 2σ(I)) | 0.0625/0.1229 | 0.0578/0.1357 | 0.0528/0.1493 | 0.0288/0.0713 | 0.0254/0.0535 |
| R1/wR2 (all data) | 0.0998/0.1397 | 0.0796/0.1571 | 0.0716/0.1601 | 0.0305/0.0721 | 0.0336/0.0572 |
| data/restraints/parameters | 21,755/21/1123 | 12,799/0/673 | 17,880/4/1206 | 15,895/14/744 | 9218/0/452 |
| goodness-of-fit on F2 | 0.992 | 1.122 | 1.270 | 1.176 | 1.031 |
| Tmin/Tmax | 0.5983/0.7461 | 0.6114/0.7460 | 0.0005/1.0000 | 0.5842/0.7461 | 0.5471/0.7460 |
| Δρmax/Δρmin, e·Å−3 | 1.726/−1.364 | 2.234/−2.266 | 1.809/−1.218 | 1.909/−1.385 | 0.784/−0.613 |
| 1-Dy(1) | 2-Dy | 3-Ho(1) | 4-Er | |
|---|---|---|---|---|
| Ln-N1 (pyridine) | 2.597(9) | 2.706(5) | 2.656(4) | 2.616(3) |
| Ln-N1A (pyridine) | 2.647(9) | 2.663(5) | 2.627(4) | 2.629(4) |
| Ln-N2 | 2.503(10) | 2.601(5) | 2.535(4) | 2.513(3) |
| Ln-N2A | 2.508(11) | 2.603(5) | 2.534(4) | 2.494(4) |
| Ln-N4 | 2.575(11) | 2.561(5) | 2.577(5) | 2.517(4) |
| Ln-N4A | 2.554(11) | 2.534(5) | 2.516(4) | 2.598(3) |
| Ln-O1 | 2.377(8) | 2.496(4) | 2.371(4) | 2.347(3) |
| Ln-O1A | 2.398(9) | 2.453(4) | 2.389(3) | 2.358(3) |
| Ln-O2 | 2.528(8) | 2.346(5) | 2.499(3) | 2.392(3) |
| Ln-O2A | 2.414(9) | 2.360(4) | 2.349(3) | 2.464(3) |
| Dihedral angle *, ° | 58.7(3) | 58.36(10) | 59.92(8) | 57.80(10) |
| 1-Dy, 6H15/2 | 2-Dy, 6H15/2 | 3-Ho, 5I8 | 4-Er, 4I15/2 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 23 | 39 | 0.6 | 23 |
| 65 | 77 | 85 | 75 |
| 109 | 116 | 92 | 197 |
| 210 | 197 | 117 | 234 |
| 253 | 267 | 132 | 284 |
| 295 | 312 | 162 | 328 |
| 345 | 358 | 187 | 390 |
| 227 | |||
| 250 | |||
| 282 | |||
| 330 | |||
| 339 | |||
| g-tensor components of the ground CF state | |||
| gx = 0.084 | gx = 0.082 | - | gx = 0.461 |
| gy = 1.096 | gy = 0.581 | gy = 1.037 | |
| gz = 17.981 | gz = 19.000 | gz = 14.884 | |
| g-tensor components of the first excited CF state | |||
| gx = 0.428 | gx = 0.306 | - | gx = 2.068 |
| gy = 0.620 | gy = 0.381 | gy = 4.896 | |
| gz = 16.210 | gz = 17.310 | gz = 11.618 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bazhenova, T.A.; Yakushev, I.A.; Lyssenko, K.A.; Maximova, O.V.; Mironov, V.S.; Manakin, Y.V.; Kornev, A.B.; Vasiliev, A.N.; Yagubskii, E.B. Ten-Coordinate Lanthanide [Ln(HL)(L)] Complexes (Ln = Dy, Ho, Er, Tb) with Pentadentate N3O2-Type Schiff-Base Ligands: Synthesis, Structure and Magnetism. Magnetochemistry 2020, 6, 60. https://doi.org/10.3390/magnetochemistry6040060
Bazhenova TA, Yakushev IA, Lyssenko KA, Maximova OV, Mironov VS, Manakin YV, Kornev AB, Vasiliev AN, Yagubskii EB. Ten-Coordinate Lanthanide [Ln(HL)(L)] Complexes (Ln = Dy, Ho, Er, Tb) with Pentadentate N3O2-Type Schiff-Base Ligands: Synthesis, Structure and Magnetism. Magnetochemistry. 2020; 6(4):60. https://doi.org/10.3390/magnetochemistry6040060
Chicago/Turabian StyleBazhenova, Tamara A., Ilya A. Yakushev, Konstantin A. Lyssenko, Olga V. Maximova, Vladimir S. Mironov, Yuriy V. Manakin, Alexey B. Kornev, Alexander N. Vasiliev, and Eduard B. Yagubskii. 2020. "Ten-Coordinate Lanthanide [Ln(HL)(L)] Complexes (Ln = Dy, Ho, Er, Tb) with Pentadentate N3O2-Type Schiff-Base Ligands: Synthesis, Structure and Magnetism" Magnetochemistry 6, no. 4: 60. https://doi.org/10.3390/magnetochemistry6040060
APA StyleBazhenova, T. A., Yakushev, I. A., Lyssenko, K. A., Maximova, O. V., Mironov, V. S., Manakin, Y. V., Kornev, A. B., Vasiliev, A. N., & Yagubskii, E. B. (2020). Ten-Coordinate Lanthanide [Ln(HL)(L)] Complexes (Ln = Dy, Ho, Er, Tb) with Pentadentate N3O2-Type Schiff-Base Ligands: Synthesis, Structure and Magnetism. Magnetochemistry, 6(4), 60. https://doi.org/10.3390/magnetochemistry6040060