Long-Term Converse Magnetoelectric Response of Actuated 1-3 Multiferroic Composite Structures
Abstract
:1. Introduction
1.1. Sample Preparation
1.2. Micrographic Analysis
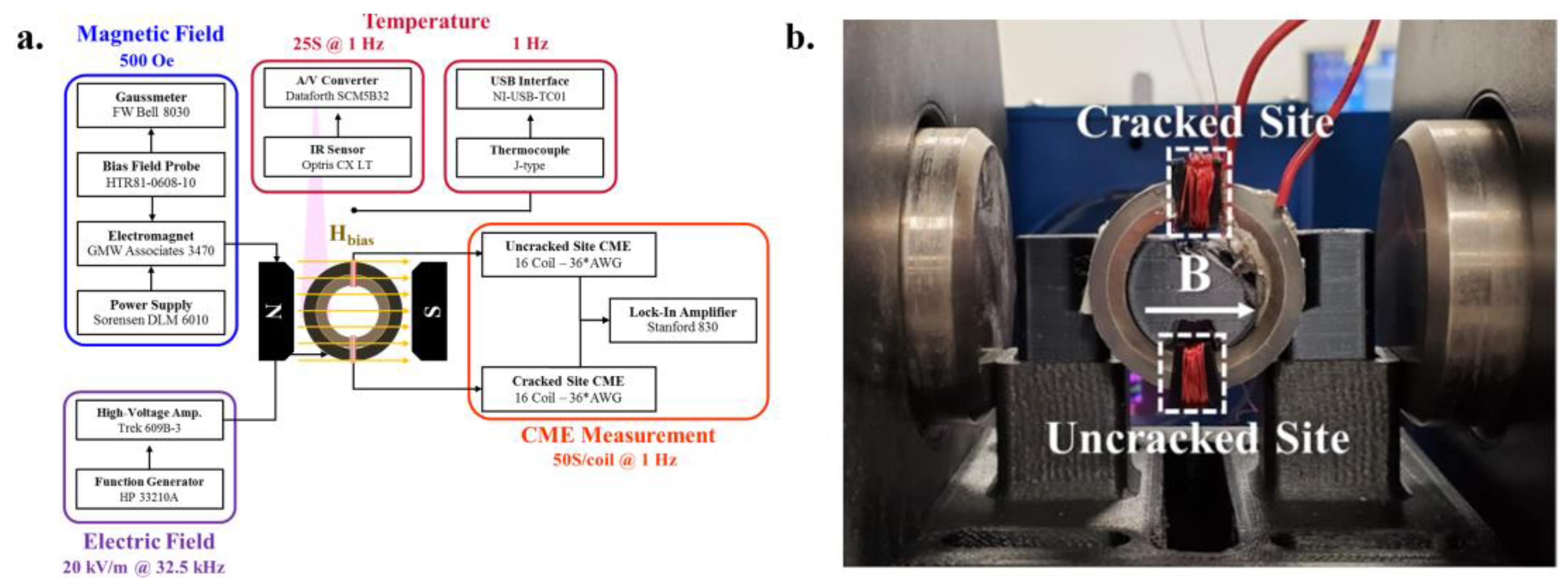
1.3. CME Measurement Setup
2. Results and Discussion
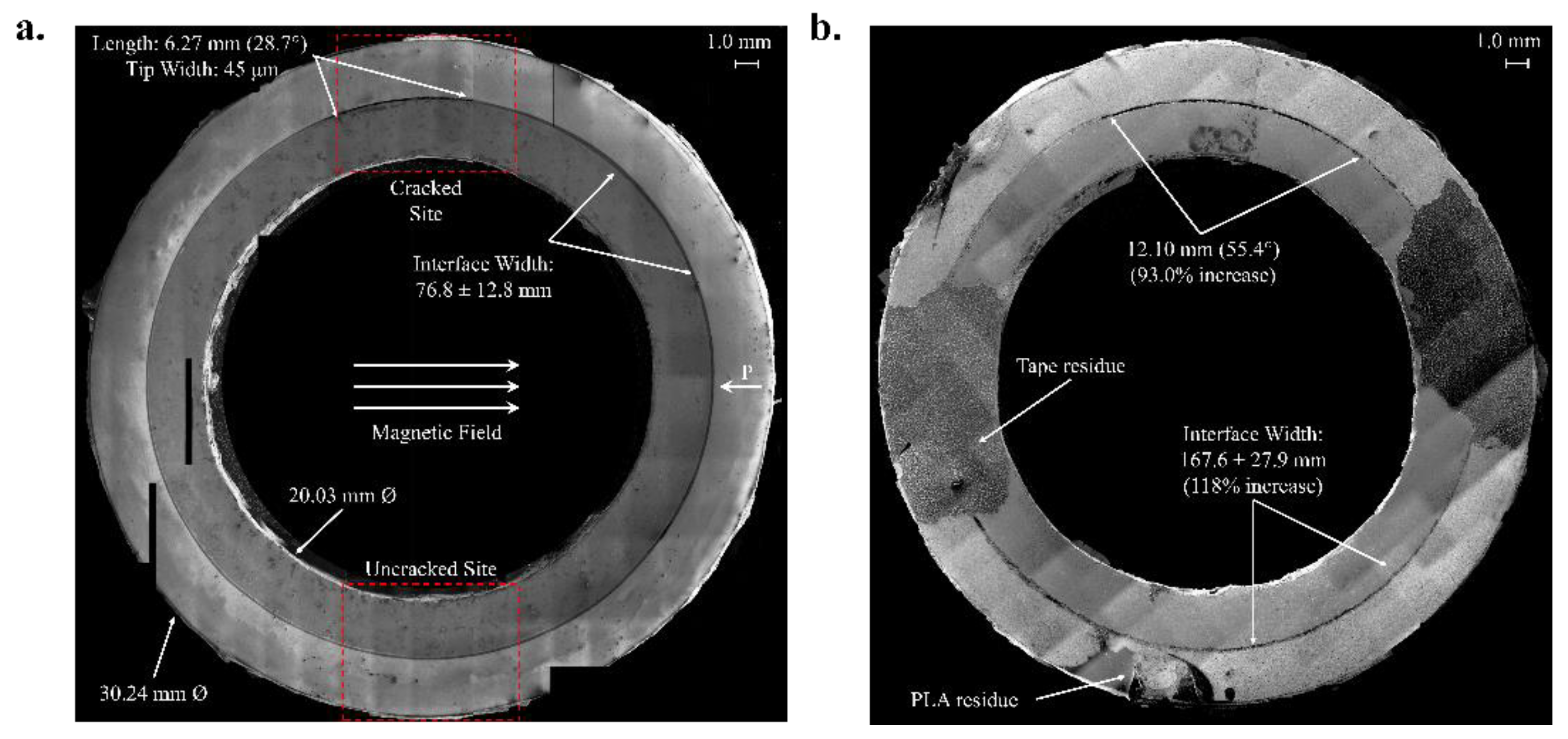
2.1. Results of the Micrographic Analysis
- The arc length of the predefined crack, which was the area of the most significant interface debonding at the location of the Teflon strip, increased to 12.10 mm from an initial length of 6.27 mm (Figure 5a), i.e., an increase of 93.0% from the initial crack length, corresponding to a total angle of 55.4°. The crack length nearly doubled due to the oscillatory nature of the loading, where the applied AC electric field resulted in cyclic strains that continuously loaded the samples and induced corresponding oscillatory magnetostriction in the inner Terfenol-D cylinder. In other words, the mechanical work provided by the generated piezoelectric strain and the induced piezomagnetic strain cyclically loaded the predefined crack to failure.
- Gross debonding was noticeable along the interfaces, particularly at the silver epoxy and Terfenol-D boundary. It is worthwhile to note that close examination of the tested sample confirmed that the debonding sites were a byproduct of the long-term testing.
- The quality of the bonding layer at the onset of testing was noted to be ‘excellent’ as the interface was free of voids or cracks, except for the predefined crack. However, the bonding layer quality noticeably degraded during testing, as evidenced in Figure 6 by the nucleation of voids and cracks within the bonding layer, which was attributed to the epoxy cohesion failure.
2.2. The CME Response
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ramesh, R.; Spaldin, N.A. Multiferroics: Progress and prospects in thin films. In Nanoscience and Technology: A Collection of Reviews from Nature Journals; World Scientific: Singapore, 2009; ISBN 9789814287005. [Google Scholar]
- Spaldin, N.A.; Fiebig, M. The renaissance of magnetoelectric multiferroics. Science 2005, 309, 391–392. [Google Scholar] [CrossRef] [PubMed]
- Spaldin, N.A.; Ramesh, R. Advances in magnetoelectric multiferroics. Nat. Mater. 2019, 18, 203–212. [Google Scholar] [CrossRef]
- Ramesh, R.; Spaldin, N.A. Multiferroics: Progress and prospects in thin films. Nat. Mater. 2007, 6, 20–29. [Google Scholar] [CrossRef]
- Nan, C.W.; Bichurin, M.I.; Dong, S.; Viehland, D.; Srinivasan, G. Multiferroic magnetoelectric composites: Historical perspective, status, and future directions. J. Appl. Phys. 2008, 103, 1. [Google Scholar] [CrossRef]
- Vopson, M.M. Fundamentals of Multiferroic Materials and Their Possible Applications. Crit. Rev. Solid State Mater. Sci. 2015, 40, 223–250. [Google Scholar] [CrossRef] [Green Version]
- Palneedi, H.; Annapureddy, V.; Priya, S.; Ryu, J. Status and perspectives of multiferroic magnetoelectric composite materials and applications. Actuators 2016, 5, 9. [Google Scholar] [CrossRef] [Green Version]
- Laughlin, D.E.; Willard, M.A.; McHenry, M.E. Magnetic Ordering: Some Structural Aspects. Phase Transform. Evol. Mater. 2000, 121–137. [Google Scholar]
- Wang, Y.; Hu, J.; Lin, Y.; Nan, C.W. Multiferroic magnetoelectric composite nanostructures. NPG Asia Mater. 2010, 2, 61–68. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Domann, J.P.; Liang, C.; Keller, S.; Carman, G.P. Sepulveda, Modeling Incoherent Strain Mediated Multiferroic Bennett Clocking. arXiv 2020, arXiv:2001.01405. [Google Scholar]
- Tressler, J.F.; Alkoy, S.; Newnham, R.E. Piezoelectric sensors and sensor materials. J. Electroceramics 1998, 2, 257–272. [Google Scholar] [CrossRef]
- Chavez, A.C.; Lopez, M.; Youssef, G. Converse magneto-electric coefficient of concentric multiferroic composite ring. J. Appl. Phys. 2016, 119, 233905. [Google Scholar] [CrossRef]
- Youssef, G.; Lopez, M.; Newacheck, S. On the effect of polarization direction on the converse magnetoelectric response of multiferroic composite rings. Smart Mater. Struct. 2017, 26, 037003. [Google Scholar] [CrossRef] [Green Version]
- Newacheck, S.; Webster, T.; Youssef, G. The effect of multidirectional bias magnetic fields on the converse magnetoelectric response of multiferroic concentric composite ring. Appl. Phys. Lett. 2018, 113, 172902. [Google Scholar] [CrossRef]
- Ge, X.H.; Ji, H.; Li, Y.; Chen, J.K.; Wang, Y.G. Diameter and sequence effects on magnetoelectric effect in FeCo/Pb(Zr,Ti)O3/Ni trilayered long cylindrical composite structures. J. Alloy. Compd. 2018, 752, 303–307. [Google Scholar] [CrossRef]
- Shen, H.Q.; Wang, Y.G.; Xie, D.; Cheng, J.H. Magnetoelectric effect in FeCo/PMN-PT/FeCo trilayers prepared by electroless deposition of FeCo on PMN-PT crystals with various orientations. J. Alloy. Compd. 2014, 610, 11–14. [Google Scholar] [CrossRef]
- Newacheck, S.; Youssef, G. Noncontact Spatiotemporal Strain Mapping of Composite Multiferroic Cylinders. Exp. Mech. 2020, 16, 857–868. [Google Scholar] [CrossRef]
- Newacheck, S.; Youssef, G. Wireless energy transfer based on strain-mediated composite multiferroics. Smart Mater. Struct. 2019, 29, 015014. [Google Scholar] [CrossRef]
- Youssef, G.; Newacheck, S.; Lopez, M. Mapping magnetoelastic response of terfenol-D ring structure. Appl. Phys. Lett. 2017, 110, 1–6. [Google Scholar] [CrossRef]
- TdVib LLC (Etrema) Terfenol-D. Available online: http://tdvib.com/terfenol-d/ (accessed on 20 May 2020).
- Rueden, C.T.; Schindelin, J.; Hiner, M.C.; DeZonia, B.E.; Walter, A.E.; Arena, E.T.; Eliceiri, K.W. ImageJ2: ImageJ for the next generation of scientific image data. BMC Bioinform. 2017, 18, 1–26. [Google Scholar] [CrossRef] [PubMed]
- Schindelin, J.; Arganda-Carreras, I.; Frise, E.; Kaynig, V.; Longair, M.; Pietzsch, T.; Preibisch, S.; Rueden, C.; Saalfeld, S.; Schmid, B.; et al. Fiji: An open-source platform for biological-image analysis. Nat. Methods 2012, 9, 676–682. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cardona, A.; Saalfeld, S.; Schindelin, J.; Arganda-Carreras, I.; Preibisch, S.; Longair, M.; Tomancak, P.; Hartenstein, V.; Douglas, R.J. TrakEM2 software for neural circuit reconstruction. PLoS ONE 2012, 7, e38011. [Google Scholar] [CrossRef] [Green Version]
- Saalfeld, S.; Fetter, R.; Cardona, A.; Tomancak, P. Elastic volume reconstruction from series of ultra-thin microscopy sections. Nat. Methods 2012, 9, 717–720. [Google Scholar] [CrossRef] [Green Version]
- Saalfeld, S.; Cardona, A.; Hartenstein, V.; Tomančák, P. As-rigid-as-possible mosaicking and serial section registration of large ssTEM datasets. Bioinformatics 2010, 26, i57–i63. [Google Scholar] [CrossRef] [PubMed]
- Cardona, A.; Douglas, R.J.; Preibisch, S.; Saalfeld, S. TrakEM2 User Manual. Available online: https://www.ini.uzh.ch/~acardona/trakem2_manual.html (accessed on 20 May 2020).
- Lopez, M.; Youssef, G. Converse magneto-electric coefficient of composite multiferroic rings. In Mechanics of Composite and Multi-Functional Materials; Springer International Publishing: New York, NY, USA, 2017; Volume 7, pp. 185–191. [Google Scholar]
- Youssef, G.; Somer, N.; Newacheck, S. Dynamic Magnetoelectric Response of Composite Multiferroics Cylinders. Smart Mater. Struct. 2020, 29, 035025. [Google Scholar] [CrossRef]
- Clark, A.E.; Teter, J.P.; Wun-Fogle, M. Characterization of Terfenol-D for magnetostrictive transducers. J. Acoust. Soc. Am. 1991, 89, 1448–1455. [Google Scholar] [CrossRef]
- Stampfli, R.; Youssef, G. Multiphysics Computational Analysis of Multiferroic Composite Ring Structures. Int. J. Mech. Sci. 2020, 17, 105573. [Google Scholar] [CrossRef]
- Dundurs, J. Edge-bonded dissimilar orthogonal elastic wedges under normal and shear loading. J. Appl. Mech. Trans. ASME 1964, 35, 460–466. [Google Scholar] [CrossRef] [Green Version]
- Schmauder, S.; Meyer, M. Correlation between Dundurs’ parameters and elastic constants. Z. Fuer Met. Res. Adv. Tech. 1992, 83, 524–527. [Google Scholar]
- Shaik, A.M.; Huynh, N.U.; Youssef, G. Micromechanical behavior of ultraviolet-exposed polyurea. Mech. Mater. 2020, 140, 103244. [Google Scholar] [CrossRef]
- Youssef, G.; Newacheck, S.; Yousuf, L.S. Insights into the displacement field in magnetoelectric composites. J. Intell. Mater. Syst. Struct. 2020, 31, 436–444. [Google Scholar] [CrossRef]
- Bichurin, M.I.; Viehland, D. Magnetoelectricity in Composites; CRC Press: Boca Raton, FL, USA, 2011; ISBN 9789814267830. [Google Scholar]
- Zheng, J.; Takahashi, S.; Yoshikawa, S.; Uchino, K.; De Vries, H. Heat Generation in Multilayer Piezoelectric Actuators. J. Am. Ceram. Soc. J. Amer. Ceram. Soc. 1996, 79, 3193–3198. [Google Scholar] [CrossRef]




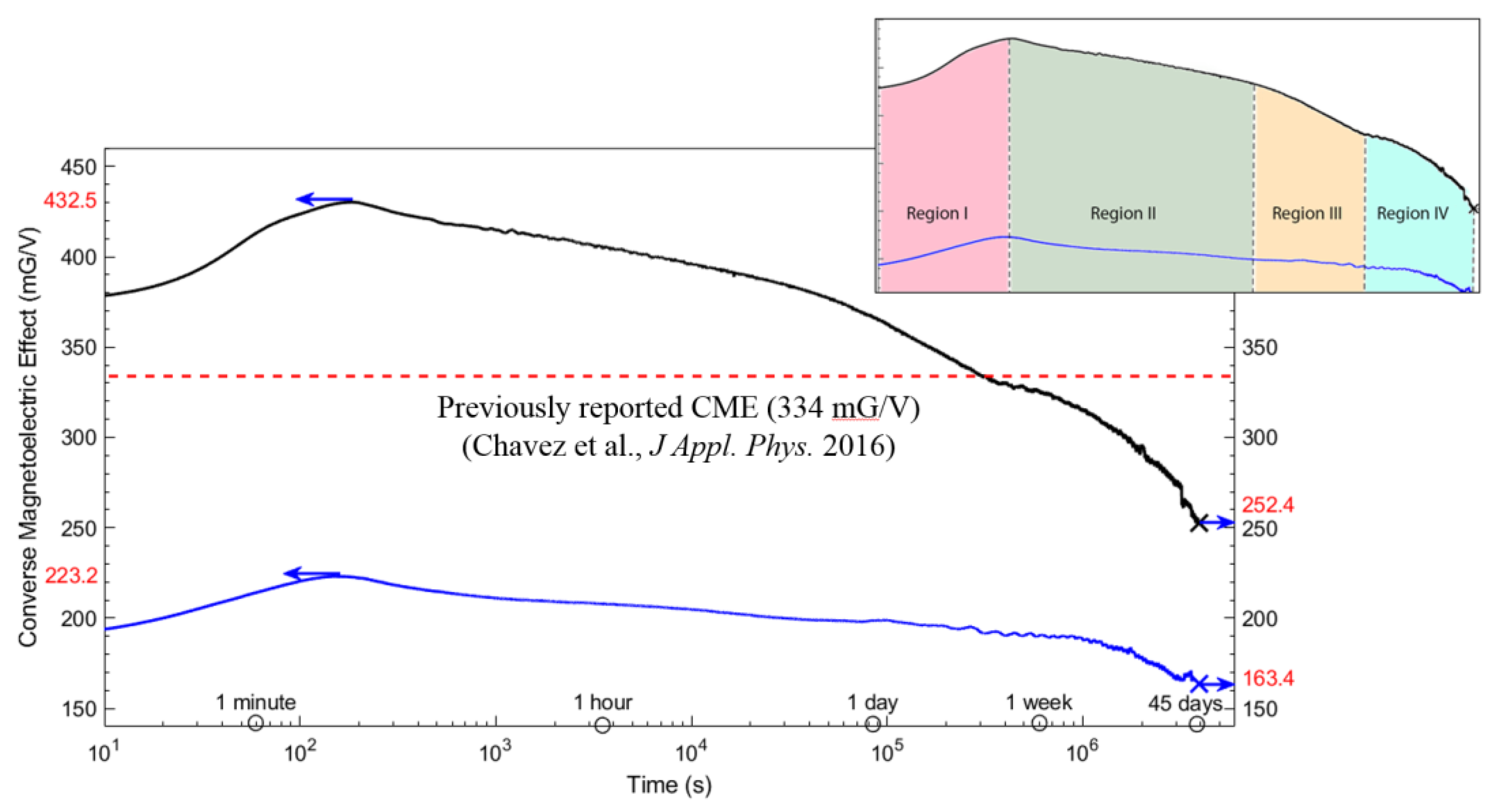
| Region | I | II | III | IV |
|---|---|---|---|---|
| Duration | 175 s (UC) 160 s (C) | 11 h | 3.6 days | 41 days |
| Uncracked CME (mG/V per decade) | 61.36 | −21.66 | −51.66 | −74.62 |
| Cracked CME (mG/V per decade) | 23.73 | −10.17 | −6.91 | −27.45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stampfli, R.; Huynh, N.U.; Youssef, G. Long-Term Converse Magnetoelectric Response of Actuated 1-3 Multiferroic Composite Structures. Magnetochemistry 2021, 7, 55. https://doi.org/10.3390/magnetochemistry7040055
Stampfli R, Huynh NU, Youssef G. Long-Term Converse Magnetoelectric Response of Actuated 1-3 Multiferroic Composite Structures. Magnetochemistry. 2021; 7(4):55. https://doi.org/10.3390/magnetochemistry7040055
Chicago/Turabian StyleStampfli, Ryan, Nha Uyen Huynh, and George Youssef. 2021. "Long-Term Converse Magnetoelectric Response of Actuated 1-3 Multiferroic Composite Structures" Magnetochemistry 7, no. 4: 55. https://doi.org/10.3390/magnetochemistry7040055
APA StyleStampfli, R., Huynh, N. U., & Youssef, G. (2021). Long-Term Converse Magnetoelectric Response of Actuated 1-3 Multiferroic Composite Structures. Magnetochemistry, 7(4), 55. https://doi.org/10.3390/magnetochemistry7040055






