Origin of Perovskite Multiferroicity and Magnetoelectric-Multiferroic Effects—The Role of Electronic Spin in Spontaneous Polarization of Crystals

Abstract

In this semi-review paper, we show that the multiferroic properties of perovskite ABO₃ crystals with B(dⁿ), n > 0, centers are fully controlled by the influence of the electronic spin on the local dipolar instability that triggers the spontaneous polarization of the crystal. Contrary to the widespread statements, the multiferroicity of these crystals does not emerge due to the addition of unpaired electrons (carrying magnetic moments) to the spontaneously polarizing crystal; the spin states themselves are an important part of the local electronic structure that determines the very possibility of the spontaneous polarization. This conclusion emerges from vibronic theory, in which the ferroelectricity is due to the cooperative interaction of the local dipolar distortions induced by the pseudo-Jahn-Teller effect (PJTE). The latter requires sufficiently strong vibronic coupling between ground and excited electronic states with opposite parity but the same spin multiplicity. The detailed electronic structure of the octahedral [B(dⁿ)O₆] center in the molecular orbital presentation shows how this requirement plays into the dependence of the possible perovskite magnetic, ferroelectric, and multiferroic properties on the number of d electrons, provided the criterion of the PJTE is obeyed. Revealed in detail, the role of the electronic spin in all these properties and their combination opens novel possibilities for their manipulation by means of external perturbations and exploration. In particular, it is shown that by employing the well-known spin-crossover phenomenon, a series of novel effects become possible, including magnetic-ferroelectric (multiferroic) crossover with electric-multiferroic, magnetic-ferroelectric, and magneto-electric effects, some of which have already been observed experimentally.

1. Introduction

Multiferroic perovskite ABO₃ crystals with coexisting magnetic and ferroelectric properties are presently well studied (see, e.g., in [1,2]), but for a long period of time, it was assumed that ferroelectricity takes place only when the B atom is in the d⁰ configuration (“the d⁰ mystery” [3]), as in the well-known ferroelectric BaTiO₃, with zero spin and no magnetism. It was conceived as if the spin is detrimental to the spontaneous polarization of the crystal. This misconception has been overcome more recently when a series of perovskite systems with dⁿ, n > 0, configurations of the B atom were shown to possess multiferroic properties [1,2].

The role of the number of electrons in the B(dⁿ) ion in multiferroic properties became more clarified when it was taken into account that the spontaneous polarization of such perovskite crystals is triggered by the local dipolar instability at the B centers, induced by the pseudo-Jahn-Teller effect (PJTE) [4,5]. This finding directly influences the possible dⁿ configurations, which could allow for ferroelectric properties in the presence of unpaired electrons, meaning multiferroicity [6,7]. Indeed, the PJTE in the [B(dⁿ)O₆] local center has no a priori limitations on the number of d electrons, but it has other limitations with regard to its spin state. Local dipolar (odd) distortions of this centrosymmetric unit take place when the PJTE, the vibronic coupling between its ground and excited electronic states (their mixing under the polar nuclear displacements), is sufficiently strong to overcome the local stiffness with regard to such displacements [4,5]. This, in turn, requires that the mixing local electronic states of this B center have opposite parity but the same spin multiplicity. The latter condition is essential: the vibronic coupling terms in the Hamiltonian have no spin operators (nuclear displacements directly affect the orbital motion of the electrons, but not their spin), and electronic states with different spin multiplicity are orthogonal. In this way, ferroelectricity and multiferroicity are interdependent and strongly dependent on the spin multiplicity of the ground and excited electronic states. Obviously, this also leads to a variety of possible magneto-electric-multiferroic effects.

In this semi-review paper, we show in more detail the micromechanisms of the PJTE-induced multiferroicity in perovskite crystals, especially the role of the electronic spin in their spontaneous polarization, and the spin classification of ferroelectric and multiferroic perovskites with electronic configurations B(dⁿ), n = 0, 1,…10 [6,7], as well as the occurring due to this effect novel properties in the interaction with external perturbations, including electric-multiferroic, magnetic-ferroelectric, and magneto-electric effects.

2. Electronic Structure and PJTE in Perovskite ABO₃ Crystals

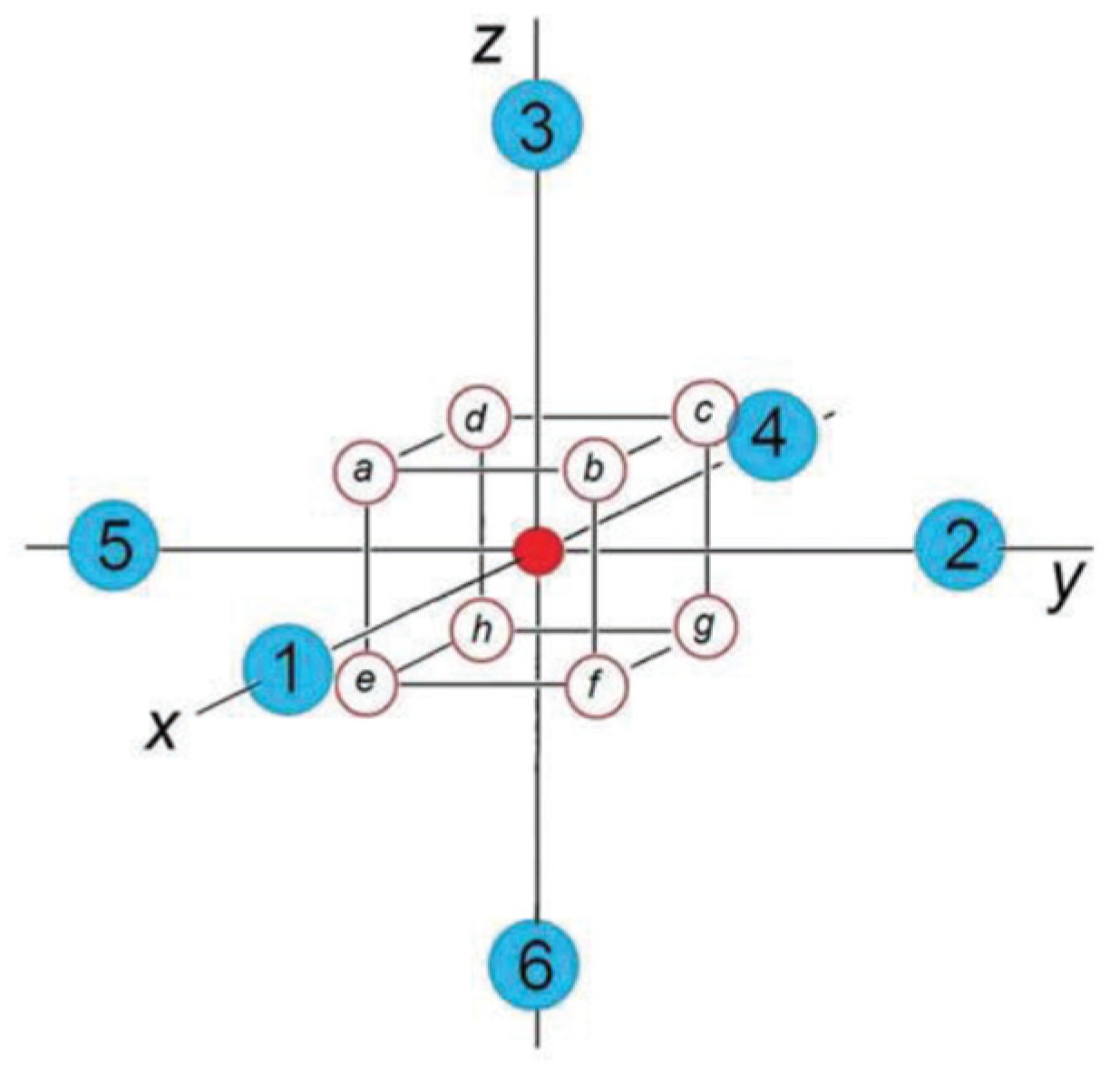
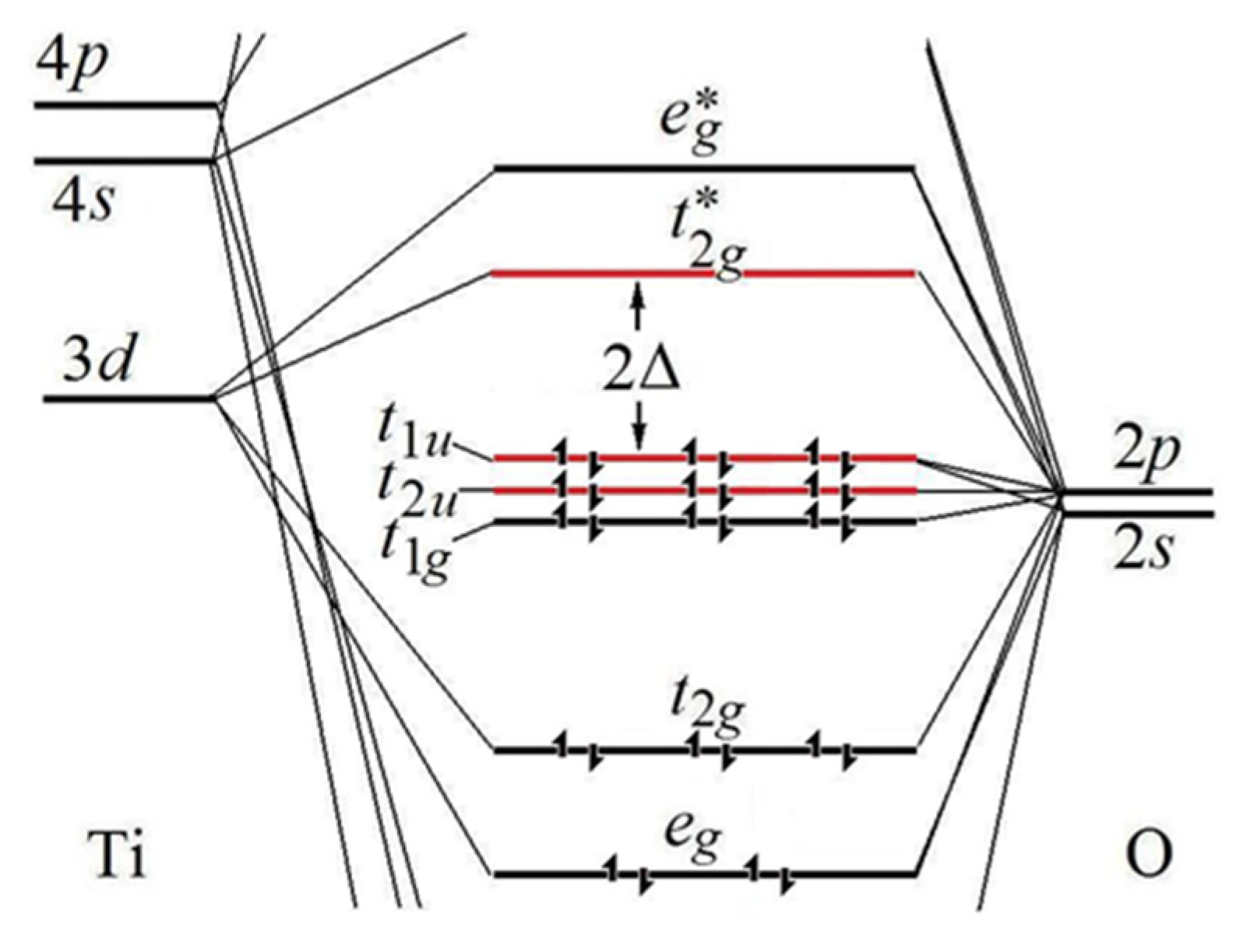
First, we address the central part of the perovskite crystal, the octahedral BO₆ center (Figure 1). Then, we refer to its detailed local electronic structure in terms of molecular orbitals (MO) to reveal its electronic states and spin multiplicity in a cluster presentation, taking into account their ionic state in the crystal. The general MO scheme for such a regular octahedral cluster with a B(dⁿ) transition metal as the central atom is shown in Figure 2 [8].

It shows the highest occupied (HOMO) and lowest unoccupied (LUMO) bonding, nonbonding, and antibonding MOs formed by the symmetry-adapted combinations of the valence s and p orbitals of the six oxygen atoms with the d orbitals of the central B atom, which transform as t_1u, t_2u, t_1g, t_2g, and e_g-irreducible representations of the octahedral symmetry group. This qualitative HOMO–LUMO scheme is general [8], but the relative energy level positions and their population with electrons is different for different B(dⁿ) centers; they determine a variety of physical and chemical properties of the system, including, as shown below, the ferroelectric and multiferroic properties. The local cluster consideration was extended to include the crystalline properties by involving the appropriate electronic and phonon bands instead of the local energy levels [9] (see below).

The population with electrons in Figure 2 is relevant to the particular d⁰ case of the [TiO₆]⁸⁻ center in the BaTiO₃ crystal [4,5]. It results in the ground state term ¹A_1g formed by the six fully occupied t_1u and t_2u (mostly oxygen 2p orbitals), and three LUMOs t_2g, mostly titanium 3d orbitals, a total of 9 MOs spanning the HOMO closed-shell (spin S = 0) electron configuration (t_1u)⁶ = (t_1u↓)³(t_1u↑)³ (the arrows denote the spin orientation). Its first excited state is produced by the lowest one-electron (t_1u↑)→(t_2g*↑) excitation, corresponding to the LUMO configuration (t_1u↓)³(t_1u↑)²(t_2g*↑)¹, yielding the odd-parity term ¹T_1u at the energy gap 2∆, that has the same spin S = 0. As shown below, this detailed local electronic structure based on the specific chemical bonding is most important in determining both the ferroelectric and multiferroic properties of crystals.

The next fundamental step is to involve the vibronic coupling theory leading to the PJTE-induced dipolar instability and ferroelectricity [4,5]. The electronic structure described above is obtained on the assumption that the local crystal cluster [BO₆] has an octahedral configuration with the B ion in the center and the oxygens in the regular octahedron positions. However, for some electronic structures, this arrangement does not correspond to the equilibrium geometry. Indeed, as mentioned above, the vibronic coupling may significantly change the nuclear dynamics, leading to spontaneous symmetry breaking with multi-minimum adiabatic potential energy surfaces (APESs), and lower symmetry in the minima. In the case under consideration, the important consequence of such symmetry breaking emerges in the form of the PJTE-induced dipolar distortion of the local [BO₆] cluster [4,5]. For the BaTiO₃ crystal, the vibronic coupling terms of the Hamiltonian, taken as perturbations, mix its noted above-ground ¹A_1g and first excited ¹T_1u terms along the polar t_1u-type normal displacement coordinates Q_x, Q_y, and Q_z. This PJTE (¹A_1g + ¹T_1u) ⊗ t_1u perturbation problem, involving all the 9 HOMO–LUMO active MOs, results in a 9$\times$9 secular equation. Its solution yields the following APES of the TiO₆⁸⁻ cluster, already obtained in the first paper on this subject [4]:

$$U\left(Q\right)=\frac{1}{2}{K}_0{Q}^2-2\left[\sqrt{{\Delta }^2+2F^2\left(Q^2-Q_x^2\right)}+\sqrt{{\Delta }^2+2F^2\left(Q^2-Q_y^2\right)}+\sqrt{{\Delta }^2+2F^2\left(Q^2-Q_z^2\right)}\right]$$

(1)

where Q² = Q_x² + Q_y² + Q_z², 2Δ is the energy gap between the mixing electronic states, K₀ is the primary force constant for the Q displacements (stiffness of the crystal without the vibronic coupling), and F is the vibronic coupling constant (H is the Hamiltonian),

$$F=\langle 2p_z\left(\mathrm{O}\right)\left|{\left(\frac{\partial H}{\partial Q_x}\right)}_0\right|3d_{xz}\left(\mathrm{Ti}\right)\rangle$$

(2)

In a recent, more rigorous treatment by the Green’s functions approach [9], the local PJTE in the cluster unit was appended with the bulk crystal properties by taking into account the interaction of the B ion with the whole crystal via its electronic and vibrational bands. It improved the results by yielding appropriately band-averaged parameters instead of the local cluster ones. (Note that the PJTE is not a second-order Jahn-Teller effect, as stated in some publications; for instance, in the case under consideration in this paper, as seen from the PJTE solution (1), the dependence of the APES on the low-symmetry distortions Q is far from being of just second order).

The three-dimensional APES (1) has a specific form. Under the condition where the surface (1) has a maximum (meaning instability) when the B ion is in the center of the octahedron, eight equivalent minima are placed along the four trigonal axes, in which the B ion is displaced toward three oxygen ions (away from the other three); 12 higher-in-energy equivalent saddle points along the six C_2v axes, at which the B ion is displaced toward two oxygen ions (at the top of the lowest barrier between two near-neighbor minima); and then six higher-in-energy equivalent saddle points, at which the B ion is displaced to one of the oxygen ions along the fourfold axes [4,5].

Δ < 8F²/K₀

(3)

For the case of BaTiO₃, all the main parameters of this APES were estimated [9] by employing two experimentally determined structural constants, the band-averaged energy gap 2Δ = 2.8 eV and the vibrational frequency at the bottom of the trigonal minimum ħω_e = 193 cm⁻¹. The estimated values of K₀, F, the positions of the minima Q_x = Q_y = Q_z = Q₀ and the first saddle points Q_x = Q_y = q₀, Q_z = 0, their PJTE stabilization energies, and the tunneling splitting δ₀ (a measure of the energy barrier between the near-neighbor minima of the APES) for this crystal are listed in

Table 1. Numerical values of the PJTE vibronic coupling and APES parameters of the Ti active centers in the BaTiO₃ crystal. E_PJT[111] is the PJTE stabilization energy at the trigonal minima; E_PJT[110] is the stabilization energy at the maximum of the barrier between two near-neighbor minima [9].

K0 (eV/Å2)	2Δ (eV)	F (eV/Å)	ħωe (cm−1)	Q0 (Å)	q0 (Å)	EPJT[111] (cm−1)	EPJT[110] (cm−1)	δ0 (cm−1)
55	2.8	3.42	193	0.14	0.16	−1250	−1130	35

. The order of magnitude of the APES minima depths in this case was first estimated in ESR experiments with probing ions [10] by substituting Ti⁴⁺ with the Mn⁴⁺ ion, which produces a very similar APES (Mn⁴⁺ is a “ferroelectric” ion, see below in

Table 2. Necessary conditions where ABO₃ perovskites with the B(dⁿ) electronic configuration possess both ferroelectric and magnetic properties simultaneously; EC = electronic configuration, GS = ground state, LUES = lowest odd-parity excited state, FE = ferroelectric, MM = magnetic, MF = multiferroic, LS = low-spin, HS = high-spin; IS = intermediate spin; LS* and HS* are two spin configurations of d³ in the one-electron excitation; (t_1u)⁶ = ${{(\mathrm{t}}_{1\mathrm{u}}\downarrow )}^3{{(\mathrm{t}}_{1\mathrm{u}}\uparrow )}^3$; (t_1u)⁵ = ${{(\mathrm{t}}_{1\mathrm{u}}\downarrow )}^2{{(\mathrm{t}}_{1\mathrm{u}}\uparrow )}^3$; (t_2g)⁶ = ${{(\mathrm{t}}_{2\mathrm{g}}\uparrow )}^3{{(\mathrm{t}}_{2\mathrm{g}}\uparrow )}^3$; (e_g)⁴ = (e_g↑ e_g↓) [6,7].

${\mathit{d}}^{\mathit{n}}$	$\mathit{E}\mathit{x}\mathit{a}\mathit{m}\mathit{p}\mathit{l}\mathit{e}$	HOMO EC, and GS TERM	LUMO EC, and LUES TERM	FE	MM	MF
$d^0$	Ti4+	${{(\mathrm{t}}_{1\mathrm{u}})}^6,{}^{1}A{}_{1g}$	${{(\mathrm{t}}_{1\mathrm{u}})}^5{{(\mathrm{t}}_{2\mathrm{g}}\uparrow )}^1,{}^{1}T{}_{1u}$	yes	no	no
$d^1$	Ti3+, V4+	${{(\mathrm{t}}_{1\mathrm{u}})}^6{{(\mathrm{t}}_{2\mathrm{g}}\uparrow )}^1,{}^{2}T{}_{2g}$	${{(\mathrm{t}}_{1\mathrm{u}})}^5{{(\mathrm{t}}_{2\mathrm{g}}\uparrow )}^2,{}^{4}T{}_{1u}$	no	yes	no
$d^2$	V3+, Cr4+	${{(\mathrm{t}}_{1\mathrm{u}})}^6{{(\mathrm{t}}_{2\mathrm{g}}\uparrow )}^2,{}^{3}T{}_{2g}$	${{(\mathrm{t}}_{1\mathrm{u}})}^5{{(\mathrm{t}}_{2\mathrm{g}}\uparrow )}^3,{}^{5}T{}_{1u}$	no	yes	no
$d^3$, LS	Cr3+, Mn4+	${{(\mathrm{t}}_{1\mathrm{u}})}^6{{(\mathrm{t}}_{2\mathrm{g}}\uparrow )}^3,{}^{4}A{}_{2g}$	${{(\mathrm{t}}_{1\mathrm{u}})}^5{{(\mathrm{t}}_{2\mathrm{g}}\uparrow )}^3{{(\mathrm{t}}_{2\mathrm{g}}\downarrow )}^1,{}^{4}T{}_{1u}$	yes	yes	yes
$d^3$, HS		${{(\mathrm{t}}_{1\mathrm{u}})}^6{{(\mathrm{t}}_{2\mathrm{g}}\uparrow )}^3,{}^{4}A{}_{2g}$	${{(\mathrm{t}}_{1\mathrm{u}})}^5{{(\mathrm{t}}_{2\mathrm{g}}\uparrow )}^3{{(\mathrm{e}}_{\mathrm{g}}\uparrow )}^1,{}^{6}T{}_{1u}$	no	yes	no
$d^4$, LS	Mn3+, Fe4+	${{(\mathrm{t}}_{1\mathrm{u}})}^6{{(\mathrm{t}}_{2\mathrm{g}}\uparrow )}^3{{(\mathrm{t}}_{2\mathrm{g}}\downarrow )}^1,{}^{3}T{}_{2g}$	${{(\mathrm{t}}_{1\mathrm{u}})}^5{{(\mathrm{t}}_{2\mathrm{g}}\uparrow )}^3{{(\mathrm{t}}_{2\mathrm{g}}\downarrow )}^2,{}^{3}T{}_{1u}$	yes	yes	yes
$d^4$, HS		${{(\mathrm{t}}_{1\mathrm{u}})}^6{{(\mathrm{t}}_{2\mathrm{g}}\uparrow )}^3{{(\mathrm{e}}_{\mathrm{g}}\uparrow )}^1,{}^{5}T{}_{2g}$	${{(\mathrm{t}}_{1\mathrm{u}})}^5{{(\mathrm{t}}_{2\mathrm{g}}\uparrow )}^3{{(\mathrm{e}}_{\mathrm{g}}\uparrow )}^2,{}^{7}T{}_{1u}$	no	yes	no
$d^5$, LS	Mn2+, Fe3+	${{(\mathrm{t}}_{1\mathrm{u}})}^6{{(\mathrm{t}}_{2\mathrm{g}}\uparrow )}^3{{(\mathrm{t}}_{2\mathrm{g}}\downarrow )}^2,{}^{2}T{}_{2g}$	${{(\mathrm{t}}_{1\mathrm{u}})}^5{{(\mathrm{t}}_{2\mathrm{g}})}^6,{}^{2}T{}_{1u}$	yes	yes	yes
$d^5$, HS		${{(\mathrm{t}}_{1\mathrm{u}})}^6{{(\mathrm{t}}_{2\mathrm{g}}\uparrow )}^3{{(\mathrm{e}}_{\mathrm{g}}\uparrow )}^2,{}^{6}A{}_{1g}$	${{(\mathrm{t}}_{1\mathrm{u}})}^5{{(\mathrm{t}}_{2\mathrm{g}})}^4{(e_g\uparrow )}^2,{}^{6}T{}_{1u}$	yes	yes	yes
$d^6$, LS	Fe2+, Co3+	${{(\mathrm{t}}_{1\mathrm{u}})}^6{{(\mathrm{t}}_{2\mathrm{g}})}^6,{}^{1}A{}_{1g}$	${{(\mathrm{t}}_{1\mathrm{u}})}^5{{(\mathrm{t}}_{2\mathrm{g}})}^6{(e_g\uparrow )}^1,{}^{3}T{}_{1u}$	no	no	no
$d^6$, IS1		${(t_{1u})}^6{{(\mathrm{t}}_{2\mathrm{g}})}^5{(e_g\uparrow )}^1,{}^{3}T{}_{1g}$	${{(\mathrm{t}}_{1\mathrm{u}})}^5{{(\mathrm{t}}_{2\mathrm{g}})}^6{(e_g\uparrow )}^1,{}^{3}T{}_{1u}$	yes	yes	yes
$d^6$, IS2		${(t_{1u})}^6{{(\mathrm{t}}_{2\mathrm{g}})}^5{(e_g\uparrow )}^1,{}^{3}T{}_{1g}$	${(t_{1u})}^5{{(\mathrm{t}}_{2\mathrm{g}})}^5{(e_g\uparrow )}^2,{}^{5}T{}_{1u}$	no	yes	no
$d^6$, HS		${{(\mathrm{t}}_{1\mathrm{u}})}^6{{(\mathrm{t}}_{2\mathrm{g}})}^4{{(\mathrm{e}}_{\mathrm{g}}\uparrow )}^2,{}^{5}T{}_{2g}$	${{(\mathrm{t}}_{1\mathrm{u}})}^5{{(\mathrm{t}}_{2\mathrm{g}})}^5{{(\mathrm{e}}_{\mathrm{g}}\uparrow )}^2,{}^{5}T{}_{1u}$	yes	yes	yes
$d^7$, LS	Co2+, Ni3+	${{(\mathrm{t}}_{1\mathrm{u}})}^6{{(\mathrm{t}}_{2\mathrm{g}})}^6{(e_g\uparrow )}^1,{}^{2}E{}_g$	${{(\mathrm{t}}_{1\mathrm{u}})}^5{{(\mathrm{t}}_{2\mathrm{g}})}^6{(e_g\uparrow )}^2,{}^{4}T{}_{1u}$	no	yes	no
$d^7$, HS		${{(\mathrm{t}}_{1\mathrm{u}})}^6{{(\mathrm{t}}_{2\mathrm{g}})}^5{(e_g\uparrow )}^2,{}^{4}T{}_{2g}$	${{(\mathrm{t}}_{1\mathrm{u}})}^5{{(\mathrm{t}}_{2\mathrm{g}})}^6{(e_g\uparrow )}^2,{}^{4}T{}_{1u}$	yes	yes	yes
$d^8$	Ni2+, Cu3+	${{(\mathrm{t}}_{1\mathrm{u}})}^6{{(\mathrm{t}}_{2\mathrm{g}})}^6{(e_g\uparrow )}^2,{}^{3}A{}_{1g}$	${{(\mathrm{t}}_{1\mathrm{u}})}^5{{(\mathrm{t}}_{2\mathrm{g}})}^6{(e_g)}^3,{}^{3}T{}_{1u}$	yes	yes	yes
$d^9$	Cu2+	${{(\mathrm{t}}_{1\mathrm{u}})}^6{{(\mathrm{t}}_{2\mathrm{g}})}^6{(e_g)}^3,{}^{2}E{}_g$	${{(\mathrm{t}}_{1\mathrm{u}})}^5{{(\mathrm{t}}_{2\mathrm{g}})}^6{(e_g)}^4,{}^{2}T{}_{1u}$	yes	yes	yes
$d^{10}$	Zn2+	${{(\mathrm{t}}_{1\mathrm{u}})}^6{{(\mathrm{t}}_{2\mathrm{g}})}^6{(e_g)}^4,{}^{1}A{}_g$	${{(\mathrm{t}}_{1\mathrm{u}})}^5{{(\mathrm{t}}_{2\mathrm{g}})}^6{(e_g)}^4{(ns\uparrow )}^1,{}^{3}T{}_{1u}$	no	no	no

), yielding approximate lifetimes in the minima (in s): 10⁻⁹ > τ >10⁻¹⁰. This is also seen in the NMR [11,12] and EXAFS [13,14] experiments, and confirmed in enumerable experimental works partly cited in [5].

The four phases of BaTiO₃ emerge directly from this APES by gradually populating the states in the minima with temperature and stepwise-overcoming its barriers [4,5]. Of particular interest is the prediction of disorder in the orthorhombic and tetragonal ferroelectric phases and in the cubic paraelectric phase, and order–disorder phase transitions between them, discussed in a series of publications (see in [5]).

3. Multiferroicity of ABO₃ Perovskites with B(dⁿ), n > 0, Configurations. The Role of High-Spin–Low-Spin Separation

As mentioned above, there is no multiferroicity in ABO₃ perovskites with B(d⁰) local centers, as in BaTiO₃ crystals, because there are no unpaired electrons to carry magnetic moments. The question then emerges, can we expect multiferroicity in perovskites with B(dⁿ), n > 0? The perovskite with the next, d¹ configuration is BaVO₃. This crystal is neither ferroelectric nor multiferroic; why? The existing theories that ignore the PJTE cannot answer this question directly, but it follows from the vibronic theory of ferroelectricity involving the PJTE [6].

Consider the electronic structure of the [B(d¹)O₆] local center of the perovskite in this case. Its MO energy level scheme remains (qualitatively) the same as in Figure 2, but their population with electrons is different from that of BaTiO₃ by adding one electron to its MO populations shown there. This leads to the HOMO electronic configuration (t_1u↓)³(t_1u↑)³(t_2g↑)¹, yielding the term ²T_2g, while, in the first excited state, the LUMO configuration (following Hund’s rule) is (t_1u↓)²(t_1u↑)³(t_2g↑)², forming the lowest odd-parity excited term ⁴T_1u. Thus, the two closest terms of different parity (which could be expected to produce the PJTE with dipolar instability) have different spin multiplicity, and hence, as mentioned above, they are not mixed by the vibronic coupling; the latter does not contain spin operators (nuclear displacements directly affect the orbitals of the electrons, but not their spin). There is still a theoretical possibility of a weak mixing of these two terms when the splitting of the higher-spin energy level and its wavefunction by spin-orbit interaction is taken into account. It yields a nonzero vibronic coupling constant F (see Equation (2)) of the order of λ/Δ, where λ is the spin-orbit coupling constant. This value is small in real crystals; squared in Equation (3), it reduces its right-hand side by at least an order of magnitude, thus making the condition of the PJTE with dipolar instability (and hence the ferroelectricity and multiferroicity) unfeasible. Similarly, the possible vibronic coupling of the [BO₆] ground state to higher-in-energy terms with appropriate parity and spin is not expected to lead to dipolar instability, because of their large Δ separation. Thus, B(d¹) perovskites are not expected to be ferroelectric and multiferroic.

Moving to the perovskite with B(d²) centers, and following the MO scheme of Figure 2, we notice that the electronic HOMO configuration of the ground state becomes (t_1u↓)³(t_1u↑)³(t_2g↑)² with the term ³T_2g, while the LUMO configuration (t_1u↓)³(t_1u↑)²(t_2g↑)³ yields the lowest excited term ⁵T_1u. Hence, again, the two close-in-energy ground and excited terms with opposite parity have different spin multiplicity, thus excluding the direct possibility of their PJTE mixing along dipolar distortions that lead to ferroelectric properties of the crystal. Similar to the d¹ case, no ferroelectricity and, hence, no multiferroicity are expected in perovskites with B(d²) centers under this mechanism.

The situation changes in the case of perovskites with B(d³) centers (such as in AMnO₃). In this case, following the MO scheme of Figure 2, the HOMO electronic configuration becomes (t_1u↓)³(t_1u↑)³(t_2g↑)³ with the ground state term ⁴A_1g. For its first excited state, there are two possibilities. First, if the MO t_2g-e_g separation (the 2Δ value in Figure 2) is not very large, the LUMO has the high-spin (HS) configuration (t_1u↓)²(t_1u↑)³(t_2g↑)³(e_g↑)¹, which, following Hund’s rule, yields the term ⁶T_1u with the lowest interelectron repulsion. However, if the gain in the latter is smaller than 2Δ, the LUMO configuration is (t_1u↓)²(t_1u↑)³(t_2g↑)³(t_2g↓)¹ with a lower spin (LS) and lowest odd-parity term ⁴T_1u. We see that, in this case, only the low-spin condition (strong crystal field, large 2Δ separation) yields a low-lying excited state of opposite parity that has the same spin. This, in turn, allows for the (⁴A_1g + ⁴T_1u)⊗t_1u PJTE, leading to dipolar instability and consequent ferroelectric properties. In the high-spin configuration, the two terms with the lowest separation have different spins and no PJTE coupling.

The theory of high-spin–low-spin (HS–LS) term separation in coordination systems is well known and widespread [8,15,16]. For d⁶ configurations in octahedral crystal fields, an intermediate spin (IS) arrangement is also possible. The parameter of these spin-term separations is the t_2g-e_g energy gap 2Δ mentioned above (Figure 2). It emerges from the crystal field theory as the splitting of the five atomic d electron states in the cubic crystal field of the environment [8]; the stronger the latter, the larger 2Δ is. Therefore, the two LS and HS spin configurations are often termed as the strong and weak crystal field cases, respectively. In the octahedral coordination of the [B(dⁿ)O₆] local centers in perovskites, the LS–HS separation takes place only for d³, d⁴, d⁵, d⁶, and d⁷ configurations, with the IS also possible for the d⁶ configuration.

Applying the PJTE theory to all possible B(dⁿ) containing perovskite crystals, their possible ferroelectric, magnetic, and multiferroic properties are revealed, as shown in Table 2 [6,7]. It indicates the electronic structure and spin states that may lead to the realization of the ferroelectricity (FE) and multiferroicity (MF), provided the main criterion of the PJTE in Equation (3) is obeyed quantitatively (which is hardly possible outside these Table 2 conditions).

We see that B ions with configurations d³(LS), d⁴(LS), d⁵(LS and HS), d⁶(HS and IS), d⁷(HS), d⁸, and d⁹ can, in principle, produce multiferroics, provided the criterion of instability (3) is satisfied, while configurations d⁰, d¹, d², d³(HS), d⁴(HS), d⁶(LS), d⁷(LS), and d¹⁰ are not expected to produce multiferroics under this mechanism of proper ferroelectricity. Experimentally observed perovskite multiferroics with such B ions, for example, Mn⁴⁺(d³), Cr³⁺(d³), Mn³⁺(d⁴), Fe³⁺(d⁵), Fe²⁺(d⁶), and Co²⁺(d⁷), fit well with these conclusions; there are no multiferroics with d⁰, d¹, d², and d¹⁰ configurations.

4. Spin-Crossover, Electric-Multiferroic, and Magnetoelectric Effects

The essential role revealed above of the electronic spin in the ferroelectric and multiferroic properties of perovskite crystals allows us to retrieve a gamma of possible new properties, streaming from the relatively easy ways to influence the spin state of the crystal centers. First, we involve the well-known spin-crossover (SCO) phenomenon, the change in the spin state of the system under external perturbations, including magnetic and electric fields, heat, stress, strain, optical excitation, etc. [15,16]. As follows from the data of Table 2, the change in the spin state leads to changes in the ferroelectric and multiferroic properties. In other words, the spin-crossover phenomenon may serve as a tool for a new phenomenon: magnetic-ferroelectric (multiferroic) crossover (MFCO) [6]. These coexisting magnetic, ferroelectric, and spin-crossover phenomena open a variety of new possibilities to manipulate the properties of the system with novel functionalities for materials science and applications. Below, we list some of them.

(1) Electric field-induced multiferroicity. For perovskite ABO₃ crystals with B(d³) and B(d⁴) centers (Cr³⁺, Mn⁴⁺, Mn³⁺, Fe⁴⁺, etc.) in the HS nonferroelectric state, an electric field that changes the spin under SCO conditions may transfer the system to the multiferroic LS state, thus realizing electric field-induced multiferroicity, accompanied by HS→LS demagnetization; alternatively, in their ferroelectric LS state, a magnetic field facilitates the LS→HS transition that destroys the ferroelectricity and multiferroicity.

(2) Electric magnetization or demagnetization. For B(d⁵) (Mn²⁺, Fe³⁺) perovskite ferroelectrics, under SCO conditions, if the ferroelectricity is (most probable) different in the two spin states, an electric field may change the spin state (electric magnetization or demagnetization); similarly, electric magnetization may take place for B(d⁶) and B(d⁷) perovskites in the LS state.

(3) Magnetoelectric effects. For B(d⁶) and B(d⁷) perovskites (Fe²⁺, Co³⁺, Co²⁺, Ni³⁺, etc.) in the nonferroelectric LS state under SCO conditions, magnetic fields facilitate the LS→HS transition that induces ferroelectricity and, hence, multiferroicity in a strong magnetoelectric effect (the d⁶ LS state is nonmagnetic).

(4) Multiferroic sensors. As mentioned above, the SCO phenomenon also takes place under stress, heat, light, and cooperative effects in crystals [15,16]; hence, these perturbations can be employed to manipulate the MFCO and all the consequent properties, including those listed above, the corresponding perovskite crystals thus serving as sensors. The dependence of the MFCO on pressure adds a ferroelastic order to the magnetic and ferroelectric ones.

(5) Magnetic bistability. Transition metal systems with SCO properties were tried multiply as units of magnetic bistability, but they failed in practice because of the fast relaxation (short lifetime) of the higher-in-energy spin state [15,16]. By choosing a system in the MFCO condition, outlined above, one can increase the lifetime of the excited dipolar (multiferroic) state by applying an external electric field.

(6) The listed magneto-electric-dipolar effects are of local origin. As controlled by the PJTE, which is of local origin, these effects do not necessarily require bulk samples with strong cooperative interactions, meaning that, in principle, they may take place in separate molecular systems, clusters, thin films, quantum dots, qubits, etc. provided the conditions of Table 2 and the criterion of the PJTE instability (3) are obeyed.

In addition to the examples mentioned above that confirm the (outlined by the PJTE theory) necessary conditions of multiferroicity, several papers [17,18,19,20,21] also reported observing the predicted magnetic-ferroelectric spin-crossover effect, while in Ref. [20], it is shown that in BiCoO₃, the ferroelectric polarization is greatly enhanced when the Co³⁺ ion is in the high-spin state, as compared to the nonmagnetic state with the Co³⁺ ion in the low-spin configuration. They also demonstrated the predicted electric magnetization (see above) [6], when, by means of electric field-induced polarization, the spin state changes from low-spin (S = 0) to high-spin (S = 2). The authors concluded that, contrary to the widespread belief, “unpaired electron spins actually drive ferroelectricity, rather than inhibit it, which represents a shift in the understanding of how ferroelectricity and magnetism interact in perovskite oxides” [20]. The PJTE theory elucidates the mechanism of all these effects.

5. Conclusions

Since its discovery and until recently, it was assumed that ferroelectricity is a macroscopic crystalline effect, with the widespread theories stating that the spontaneous polarization is due to the compensation of the ion repulsions in the local dipolar displacements with the cooperative dipole-dipole attractions in the bulk crystal. In contrast to this theory, the more recent micro theory of ferroelectricity and multiferroicity, reflected above in this paper, is based on the consideration of the detailed local electronic structure of the crystalline centers and its specific changes under nuclear displacements, the vibronic coupling. It yields the PJTE, which produces the local dipolar instability, the spontaneous polarization of the crystal being a consequence of the ordering of the local dipoles [4,5]. In this vibronic theory, the ferroelectricity and multiferroicity are thus essentially of local origin and depend directly on the microscopic electronic structure of the crystal centers. The PJTE has its own limiting conditions, which determine the limitations in electronic structure that may lead to ferroelectricity and multiferroicity.

In view of the multiferroic properties under consideration that require the presence of nonzero magnetic moments along the ferroelectric properties, this paper accentuates the role of the electronic spin states in the spontaneous polarization of the crystal. It follows directly from the limitations of the local PJTE, a product of vibronic mixing of appropriate local ground and excited electronic states, which is nonzero only when they have the same spin multiplicity. Moreover, because of this strong dependence of the multiferroic properties of the crystal on the electronic structure and the spin of its centers, a variety of novel possibilities to influence the crystal properties occurs. It is shown that the well-known spin-crossover phenomenon may be instrumental in realizing a series of these novel properties in the interaction of such crystals with external perturbations, including magnetic field-induced ferroelectricity and electric field-induced magnetic moments, as well as other magneto-ferroelectric crossover phenomena and magnetoelectric effects, some of them already realized experimentally.