Experimental and Numerical Analysis of the Assisted Abrasive Flow of Magnetic Particles on the Polishing of Fuel Injection Nozzles
Abstract
:1. Introduction
2. Materials and Methods
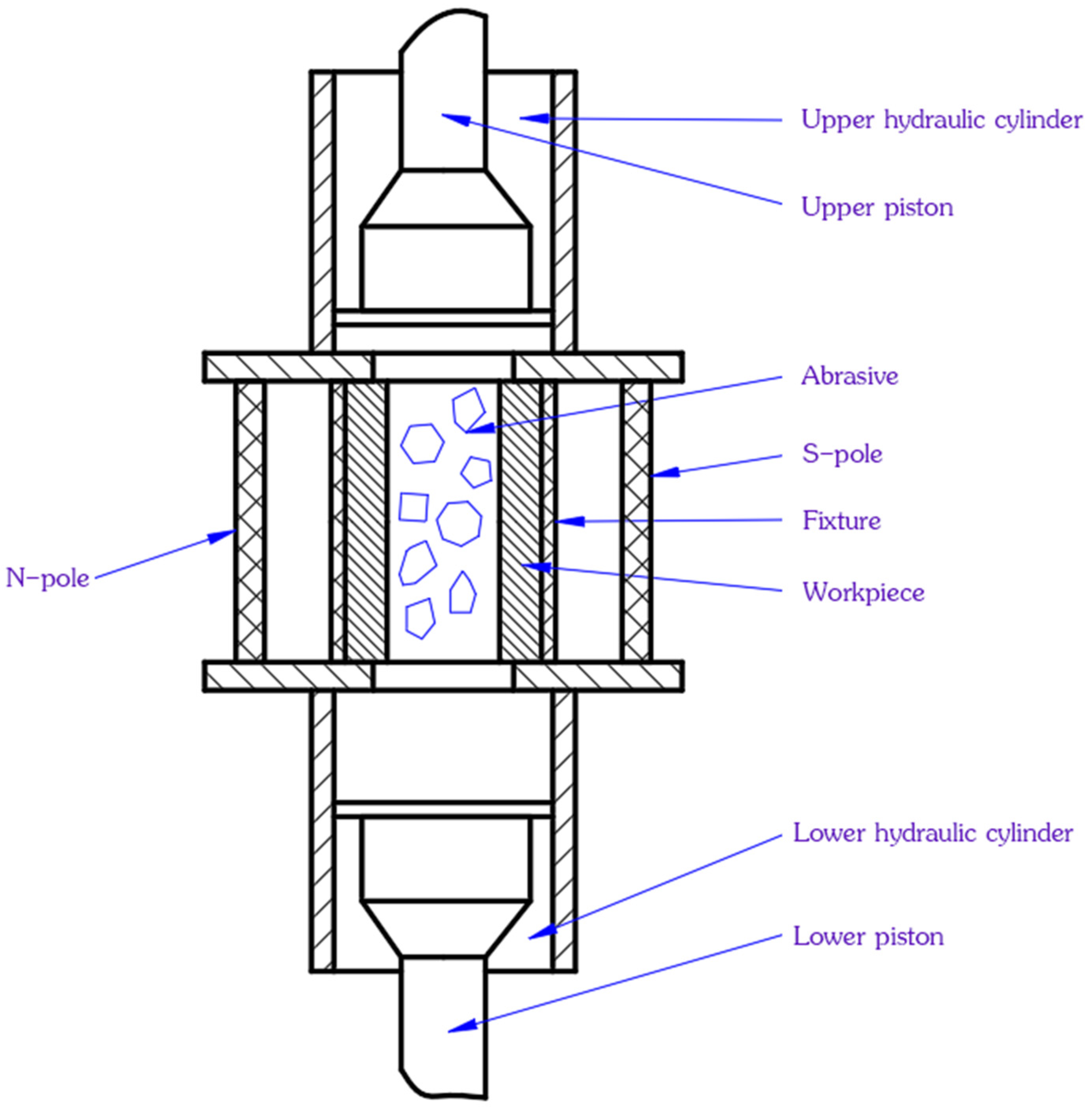
2.1. Principle Analysis of Abrasive Flow Processing Technology Containing Magnetic Particles
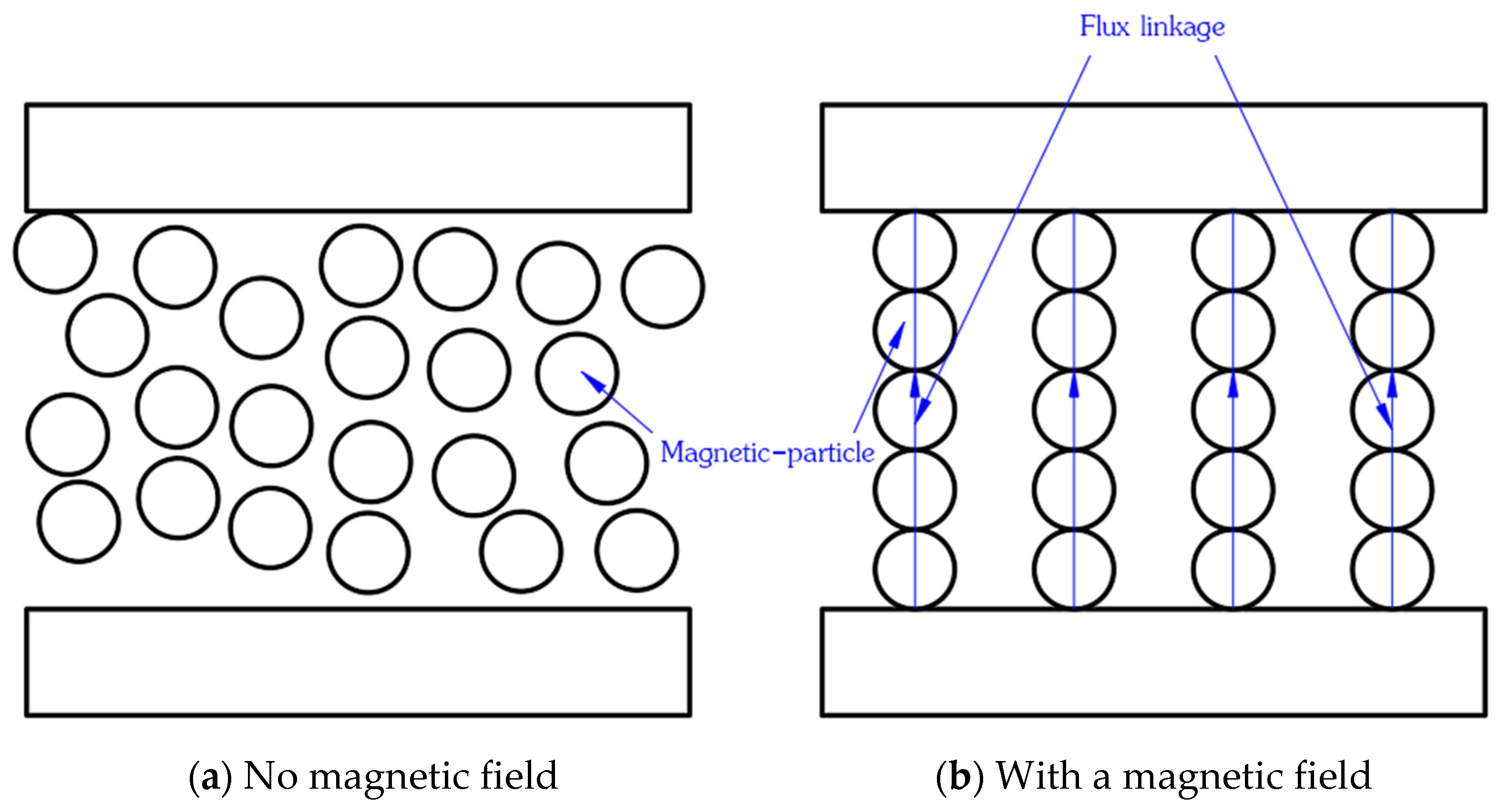
2.2. Three-Dimensional Magnetostatic Analysis Theory of Abrasive Flow Processing Technology Containing Magnetic Particles
3. Numerical Analysis of the Abrasive Flow Machining Nozzle with Magnetic Particles
3.1. Modeling and Parameter Setting of Five-Hole Nozzle
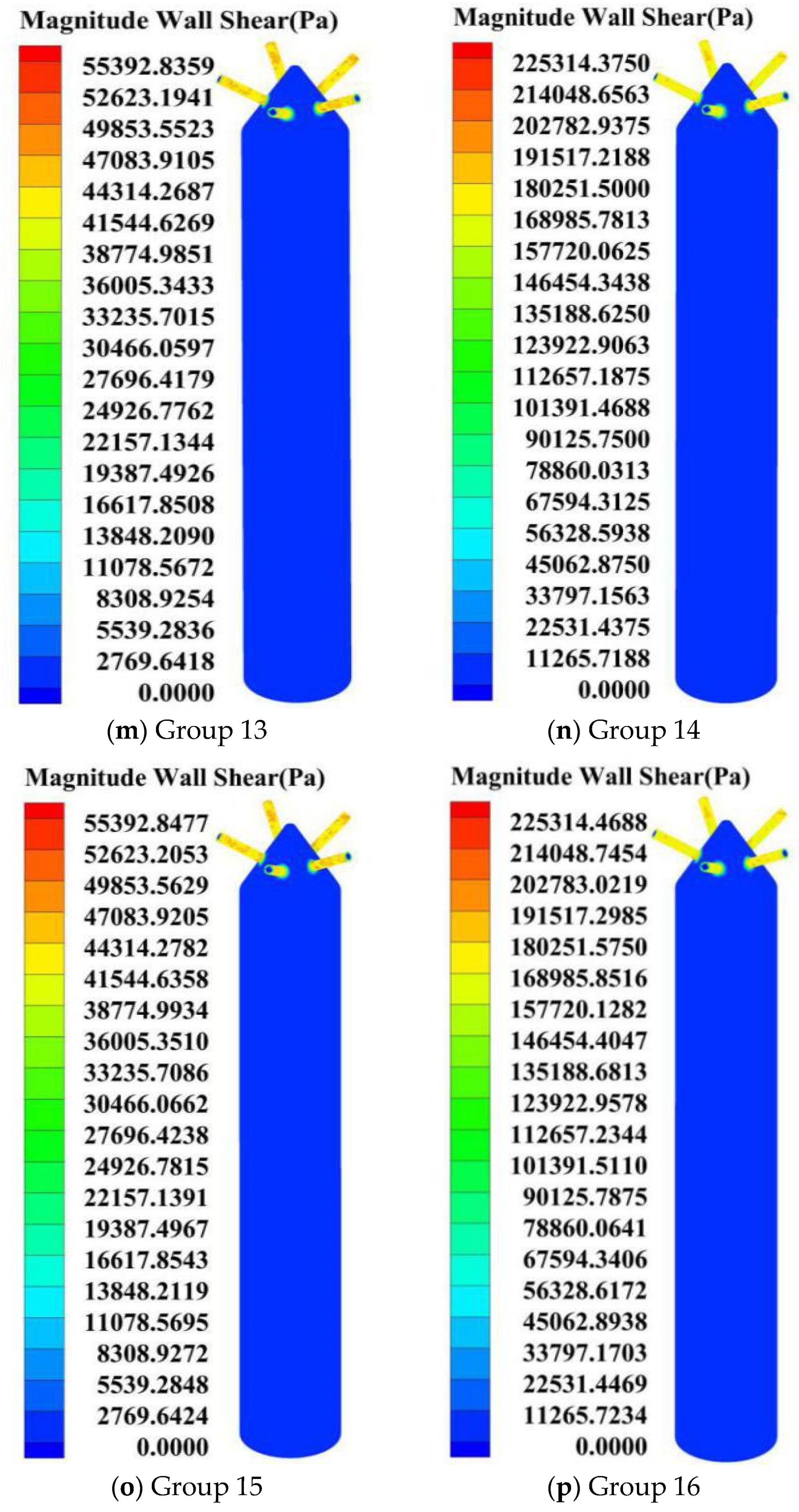
3.2. Analysis of Wall Shear Force Nephogram of Five-Hole Nozzle with Different Machining Parameters
4. Experimental Study of Solid–Liquid Two-Phase Magnetic Fluid Precision Polishing for Five-Hole Nozzle
4.1. Selection of a Five-Hole Nozzle
4.2. Selection of Test Parameters
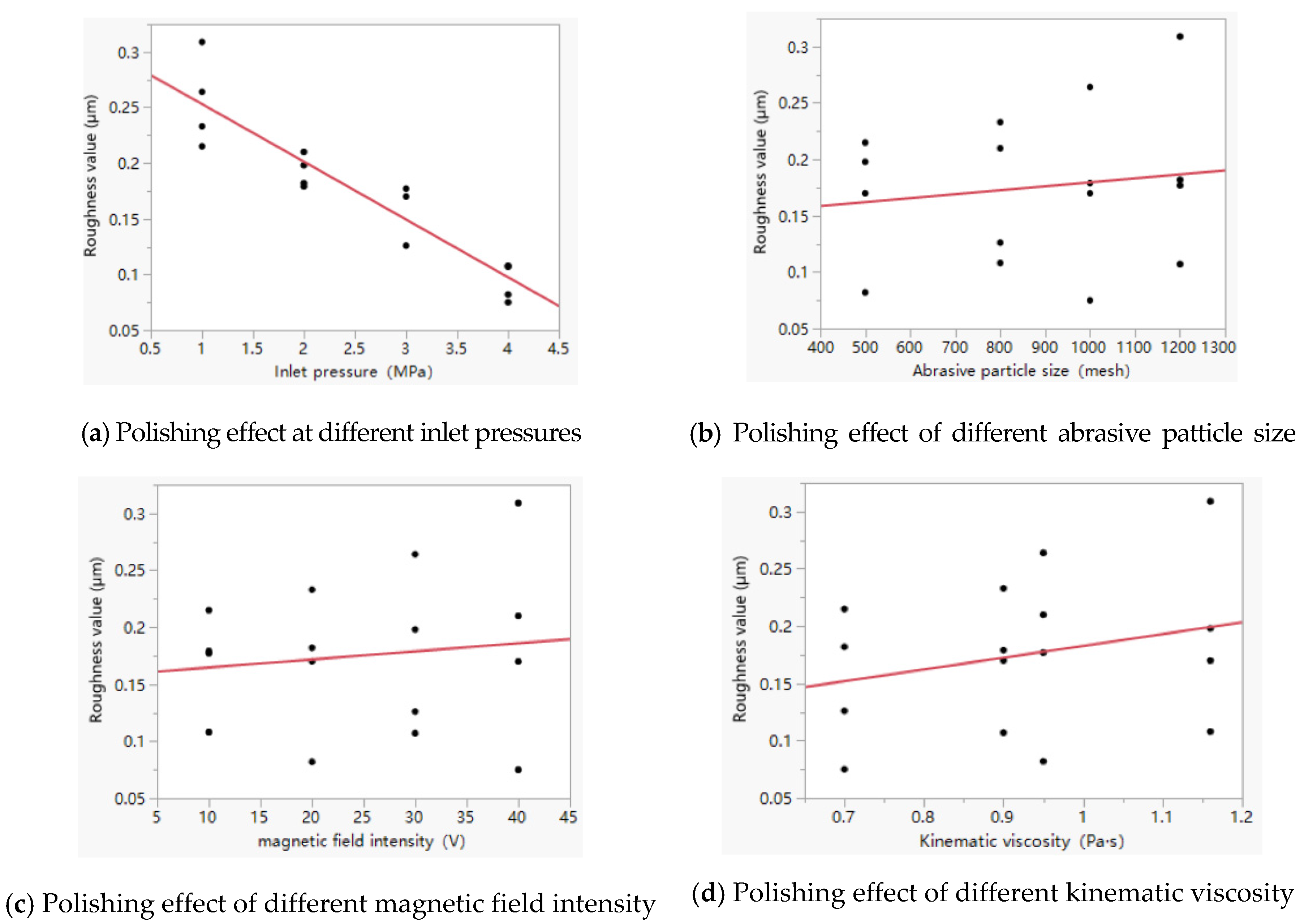
4.3. Profile Detection and Data Analysis of Optical Profilometer
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, J.; Jiang, E.; Qi, H.; Ji, S.; Chen, Z. A novel polishing method for single-crystal silicon using the cavitation rotary abrasive flow. Precis. Eng. 2020, 61, 72–81. [Google Scholar] [CrossRef]
- Wei, H.; Peng, C.; Gao, H.; Wang, X.; Wang, X. On establishment and validation of a new predictive model for material removal in abrasive flow machining. Int. J. Mach. Tools Manuf. 2019, 138, 66–79. [Google Scholar] [CrossRef]
- Wang, T.; Chen, D.; Zhang, W.; An, L. Study on key parameters of a new abrasive flow machining (AFM) process for surface finishing. Int. J. Adv. Manuf. Technol. 2019, 101, 39–54. [Google Scholar] [CrossRef]
- Sudhakara, D.; Suresh, S.; Vinod, B. Experimental Study on Abrasive Flow Machining (AFM): New Approach for Investigation on Nano-SiC in the Improvement of Material Removal and Surface Finishing. J. Bio-Tribo-Corr. 2020, 6, 24–35. [Google Scholar] [CrossRef]
- Li, J.-Y.; Zhou, Z.; Wei, L.; Zhang, X.; Xu, Y. Quality influence and process parameter optimization of T-pipe in abrasive flow finishing. Adv. Mech. Eng. 2017, 9, 2179–2187. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Yang, L.; Liu, W.; Zhang, X.; Sun, F. Experimental research into technology of abrsive flow maching non-linear tube runner. Adv. Mech. Eng. 2017, 6, 1283–1287. [Google Scholar]
- Li, J.; Yang, Z.; Liu, W.; Cai, W.; Qiao, Z. Numerical thermodynamic analysis of two-phase solid-liquid abrasive flow polishing in u-type tube. Adv. Mech. Eng. 2014, 8, 1–17. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, X.; Zang, X.; Li, J.-Y.; Su, N. Study on whole factorial experiment of polishing the micro-hole in non-linear tubes by abrasive flow. Adv. Mech. Eng. 2018, 10, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Singh, S.; Sankar, M.R.; Jain, V.K. Simulation and experimental investigations into abrasive flow nanofinishing of surgical stainless steel tubes. Mach. Sci. Technol. 2018, 22, 454–475. [Google Scholar] [CrossRef]
- Singh, S.; Kumar, D.; Sankar, M.R.; Jain, V.K. Viscoelastic medium modeling and surface roughness simulation of microholes finished by abrasive flow finishing process. Int. J. Adv. Manuf. Technol. 2019, 100, 1165–1182. [Google Scholar] [CrossRef]
- Venkatesh, G.; Sharma, A.K.; Kumar, P. On ultrasonic assisted abrasive flow finishing of bevel gears. Int. J. Mach. Tools Manuf. 2015, 89, 29–38. [Google Scholar] [CrossRef]
- Venkatesh, G.; Sharma, A.; Singh, N.; Kumar, P. Finishing of Bevel Gears using Abrasive Flow Machining. Procedia Eng. 2014, 97, 320–328. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Yin, K.; Zhu, L. Numerical simulation of swivel elbow erosion in reverse circulation drilling. J. Cent. South U Nat. Sci. 2013, 44, 5. [Google Scholar]
- Petare, A.C.; Mishra, A.; Palani, I.A.; Jain, N.K. Study of laser texturing assisted abrasive flow finishing for enhancing surface quality and microgeometry of spur gears. Int. J. Adv. Manuf. Technol. 2019, 101, 785–799. [Google Scholar] [CrossRef]
- Wang, N.; Liu, X.; Sun, S.; Krolczyk, G.; Li, Z.; Li, W. Microscopic characteristics of magnetorheological fluids subjected to magnetic fields. J. Magn. Magn. Mater. 2020, 501, 166443. [Google Scholar] [CrossRef]
- Kathiresan, S.; Mohan, B. Experimental analysis of magneto rheological abrasive flow finishing process on AISI stainless steel 316L. Mater. Manuf. Process. 2018, 33, 422–432. [Google Scholar] [CrossRef]
- Lee, J.W.; Hong, K.P.; Kwon, S.H.; Choi, H.J.; Cho, M.W. Suspension rheology and MR finishing characteristics of biopolymer-coated carbonyliron particles. Ind. Eng. Chem. Res. 2017, 56, 2416–2424. [Google Scholar] [CrossRef]
- Lee, J.W.; Hong, K.P.; Cho, M.W.; Kwon, S.H.; Choi, H.J. Polishing characteristics of optical glass using PMMA-coated carbonyl-iron-based MR fluid. Smart Mater. Struct. 2015, 24, 065002. [Google Scholar] [CrossRef]
- Fu, Y.; Gao, H.; Yan, Q.; Wang, X.; Wang, X. Rheological characterisation of abrasive media and finishing behaviours in abrasive flow machining. Int. J. Adv. Manuf. Technol. 2020, 107, 3569–3580. [Google Scholar] [CrossRef]
- Guo, M.; Luo, H.; Wang, C. Experimental Study on Magnetorheological Finishing Using Large Polishing Tool for Zirconia Ceramic Plane. Surf. Technol. 2018, 47, 28–34. [Google Scholar]
- Khan, D.A.; Jha, S. Synthesis of polishing fluid and novel approach for nanofinishing of copper using ball-end MR finishing process. Mater. Manuf. Process. 2017, 33, 1150–1159. [Google Scholar] [CrossRef]
- Khan, D.A.; Jha, S. Selection of optimum polishing fluid composition for ball end MR finishing (BEMRF) of copper. Int. J. Adv. Manuf. Technol. 2019, 100, 1093–1103. [Google Scholar] [CrossRef]
- Tian, T.; Nakano, M.; Li, W. Applications of shear thickening fluids: A review. Int. J. Hydromechatron. 2018, 1, 238–257. [Google Scholar] [CrossRef]








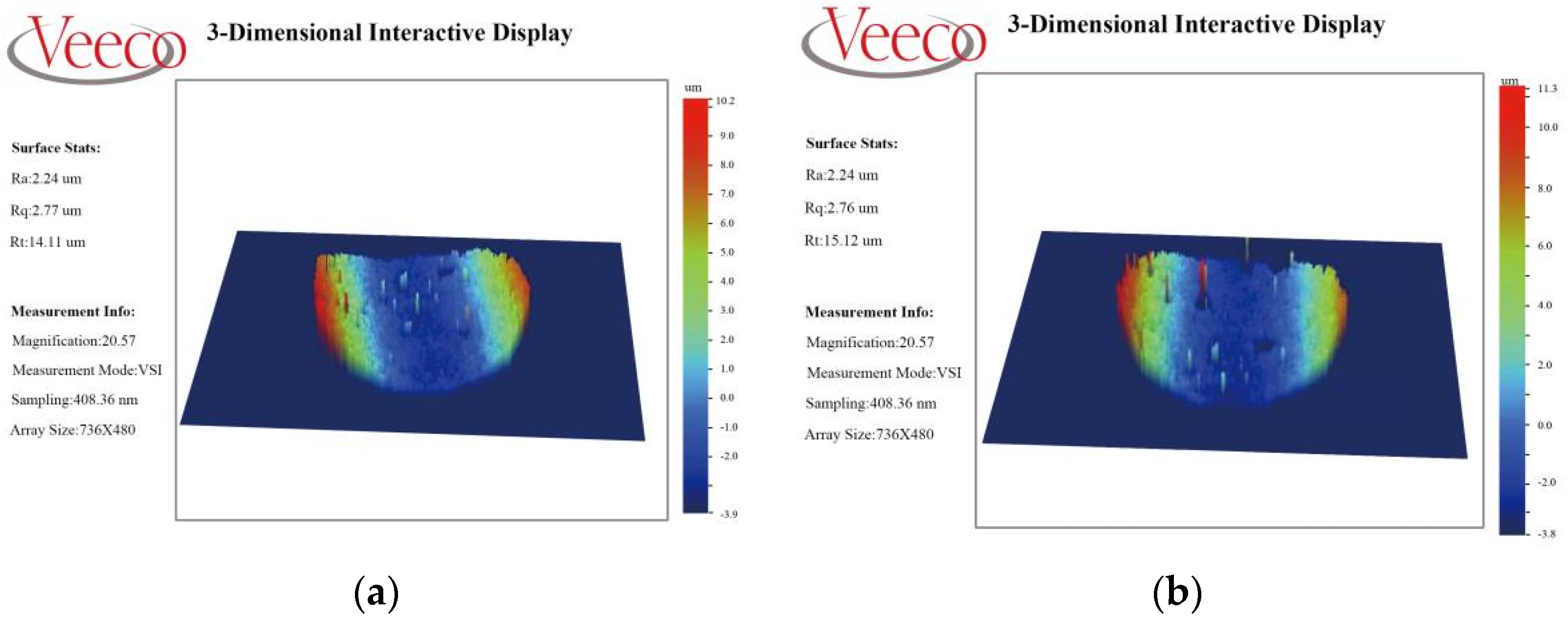


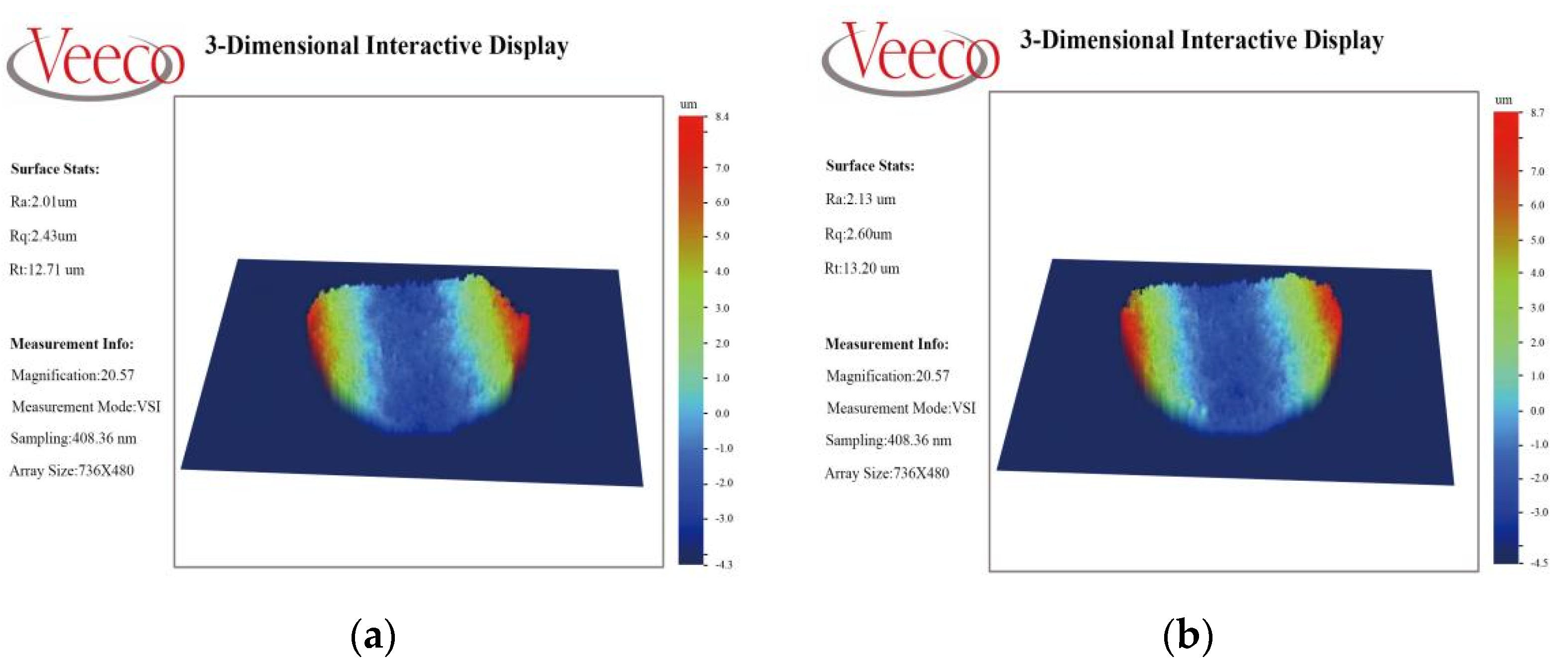

| Number of Groups | A (mesh) | B (Pa·s) | C (V) | D (MPa) |
|---|---|---|---|---|
| 1 | 500 | 0.7 | 0 | 1 |
| 2 | 500 | 0.7 | 0 | 4 |
| 3 | 500 | 0.7 | 40 | 1 |
| 4 | 500 | 0.7 | 40 | 4 |
| 5 | 500 | 1.16 | 0 | 1 |
| 6 | 500 | 1.16 | 0 | 4 |
| 7 | 500 | 1.16 | 40 | 1 |
| 8 | 500 | 1.16 | 40 | 4 |
| 9 | 1200 | 0.7 | 0 | 1 |
| 10 | 1200 | 0.7 | 0 | 4 |
| 11 | 1200 | 0.7 | 40 | 1 |
| 12 | 1200 | 0.7 | 40 | 4 |
| 13 | 1200 | 1.16 | 0 | 1 |
| 14 | 1200 | 1.16 | 0 | 4 |
| 15 | 1200 | 1.16 | 40 | 1 |
| 16 | 1200 | 1.16 | 40 | 4 |
| Contrast | Number of Groups | Wall Shear Force (Pa) | ||
|---|---|---|---|---|
| Difference in Macropore Area | Area Difference of Variable Caliber | Small Hole Area Difference | ||
| 1 | 1 | 8688.2684 | 78,194.4152 | 173,765.3672 |
| 2 | 310% | 310% | 310% | |
| 2 | 1 | 0.0004 | 0.0035 | 0.0078 |
| 3 | 0 | 0 | 0 | |
| 3 | 1 | 32.497 | 292.4737 | 649.9414 |
| 5 | 1.2% | 1.2% | 1.2% | |
| 4 | 1 | 0.3052 | 2.7475 | 6.1055 |
| 9 | 0 | 0 | 0 | |
| 5 | 2 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | |
| 6 | 2 | 223.3828 | 2010.4453 | 4467.6562 |
| 6 | 2% | 2% | 2% | |
| 7 | 2 | 27.3898 | 246.5086 | 547.7969 |
| 10 | 0.2% | 0.2% | 0.2% | |
| 8 | 3 | 8688.268 | 78,194.4117 | 173,765.3594 |
| 4 | 310% | 310% | 310% | |
| 9 | 3 | 32.497 | 292.4737 | 649.9440 |
| 7 | 1.2% | 1.2% | 1.2% | |
| 10 | 3 | 0.305 | 2.7457 | 6.1015 |
| 11 | 0 | 0 | 0 | |
| 11 | 4 | 223.382 | 2010.4383 | 4467.640 |
| 8 | 2% | 2% | 2% | |
| 12 | 4 | 27.3898 | 246.5086 | 547.7969 |
| 12 | 0.2% | 0.2% | 0.2% | |
| 13 | 5 | 8497.3826 | 76,476.4436 | 169,947.6521 |
| 6 | 307% | 307% | 307% | |
| 14 | 5 | 0.0004 | 0.0035 | 0.0078 |
| 7 | 0 | 0 | 0 | |
| 15 | 5 | 0.0928 | 0.8349 | 1.8555 |
| 13 | 0 | 0 | 0 | |
| Contrast | Number of Groups | Wall Shear Force (Pa) | ||
|---|---|---|---|---|
| Difference in Macropore Area | Area Difference of Variable Caliber | Small Hole Area Difference | ||
| 15 | 5 | 0.0928 | 0.8349 | 1.8555 |
| 13 | 0 | 0 | 0 | |
| 16 | 6 | 0.0008 | 0.007 | 0.0156 |
| 8 | 0 | 0 | 0 | |
| 17 | 6 | 1.3984 | 12.5859 | 27.9688 |
| 14 | 0 | 0 | 0 | |
| 18 | 7 | 8497.383 | 76,476.4471 | 169,947.6602 |
| 8 | 307% | 307% | 307% | |
| 19 | 7 | 0.0926 | 0.8331 | 1.8515 |
| 15 | 0 | 0 | 0 | |
| 20 | 8 | 1.3946 | 12.5507 | 27.8906 |
| 16 | 0 | 0 | 0 | |
| 21 | 9 | 8715.9634 | 78,443.6713 | 174,319.2696 |
| 10 | 311% | 311% | 311% | |
| 22 | 9 | 0.0006 | 0.0053 | 0.0118 |
| 11 | 0 | 0 | 0 | |
| 23 | 10 | 0 | 0 | 0 |
| 12 | 0 | 0 | 0 | |
| 24 | 10 | 252.171 | 2269.5398 | 5043.4219 |
| 14 | 2.2% | 2.2% | 2.2% | |
| 25 | 11 | 8715.9628 | 78,443.666 | 174,319.2578 |
| 12 | 311% | 311% | 311% | |
| 26 | 12 | 252.1664 | 2269.4976 | 5043.3281 |
| 16 | 2.2% | 2.2% | 2.2% | |
| 27 | 13 | 8496.077 | 76,464.6926 | 169,921.5391 |
| 14 | 307% | 307% | 307% | |
| 28 | 13 | 0.0006 | 0.0053 | 0.0118 |
| 15 | 0 | 0 | 0 | |
| 29 | 14 | 0.0046 | 0.0422 | 0.0938 |
| 16 | 0 | 0 | 0 | |
| 30 | 15 | 8496.081 | 76,464.7295 | 169,921.6211 |
| 16 | 307% | 307% | 307% | |
| Test Number | Inlet Pressure (MPa) | Magnetic Field Intensity (V) | Kinematic Viscosity (Pa·s) | Abrasive Particle Size (Mesh) |
|---|---|---|---|---|
| 01 | 1 | 10 | 0.70 | 500 |
| 02 | 1 | 20 | 0.90 | 800 |
| 03 | 1 | 30 | 0.95 | 1000 |
| 04 | 1 | 40 | 1.16 | 1200 |
| 05 | 2 | 10 | 0.90 | 1000 |
| 06 | 2 | 20 | 0.70 | 1200 |
| 07 | 2 | 30 | 1.16 | 500 |
| 08 | 2 | 40 | 0.95 | 800 |
| 09 | 3 | 10 | 0.95 | 1200 |
| 10 | 3 | 20 | 1.16 | 1000 |
| 11 | 3 | 30 | 0.70 | 800 |
| 12 | 3 | 40 | 0.90 | 500 |
| 13 | 4 | 10 | 1.16 | 800 |
| 14 | 4 | 20 | 0.95 | 500 |
| 15 | 4 | 30 | 0.90 | 1200 |
| 16 | 4 | 40 | 0.70 | 1000 |
| Test Number | Original Script | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 |
|---|---|---|---|---|---|---|---|---|---|
| Roughness (μm) | 0.336 | 0.215 | 0.233 | 0.264 | 0.309 | 0.179 | 0.182 | 0.198 | 0.210 |
| Test number | 09 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
| Roughness value (μm) | 0.177 | 0.170 | 0.126 | 0.170 | 0.108 | 0.082 | 0.107 | 0.075 |
| The Experimental Sequence | Inlet Pressure (MPa) | Magnetic Field Intensity (V) | Abrasive Particle Size (Mesh) | Roughness Value (μm) |
|---|---|---|---|---|
| 1 | 2 | 20 | 1200 | 0.182 |
| 2 | 4 | 20 | 800 | 0.870 |
| 3 | 2 | 40 | 800 | 0.210 |
| 4 | 4 | 40 | 800 | 0.069 |
| 5 | 4 | 40 | 1200 | 0.075 |
| 6 | 4 | 20 | 1200 | 0.112 |
| 7 | 2 | 40 | 1200 | 0.218 |
| 8 | 2 | 20 | 800 | 0.172 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G.; Li, J.; Zhu, S.; Zhu, X.; Qu, J.; Zhang, X. Experimental and Numerical Analysis of the Assisted Abrasive Flow of Magnetic Particles on the Polishing of Fuel Injection Nozzles. Magnetochemistry 2022, 8, 35. https://doi.org/10.3390/magnetochemistry8030035
Liu G, Li J, Zhu S, Zhu X, Qu J, Zhang X. Experimental and Numerical Analysis of the Assisted Abrasive Flow of Magnetic Particles on the Polishing of Fuel Injection Nozzles. Magnetochemistry. 2022; 8(3):35. https://doi.org/10.3390/magnetochemistry8030035
Chicago/Turabian StyleLiu, Guosong, Junye Li, Shangfu Zhu, Xu Zhu, Jiyong Qu, and Xinming Zhang. 2022. "Experimental and Numerical Analysis of the Assisted Abrasive Flow of Magnetic Particles on the Polishing of Fuel Injection Nozzles" Magnetochemistry 8, no. 3: 35. https://doi.org/10.3390/magnetochemistry8030035
APA StyleLiu, G., Li, J., Zhu, S., Zhu, X., Qu, J., & Zhang, X. (2022). Experimental and Numerical Analysis of the Assisted Abrasive Flow of Magnetic Particles on the Polishing of Fuel Injection Nozzles. Magnetochemistry, 8(3), 35. https://doi.org/10.3390/magnetochemistry8030035






