A Novel Method of Flow Curve Measurement for Magnetic Fluid Based on Plane Poiseuille Flow
Abstract
:1. Introduction
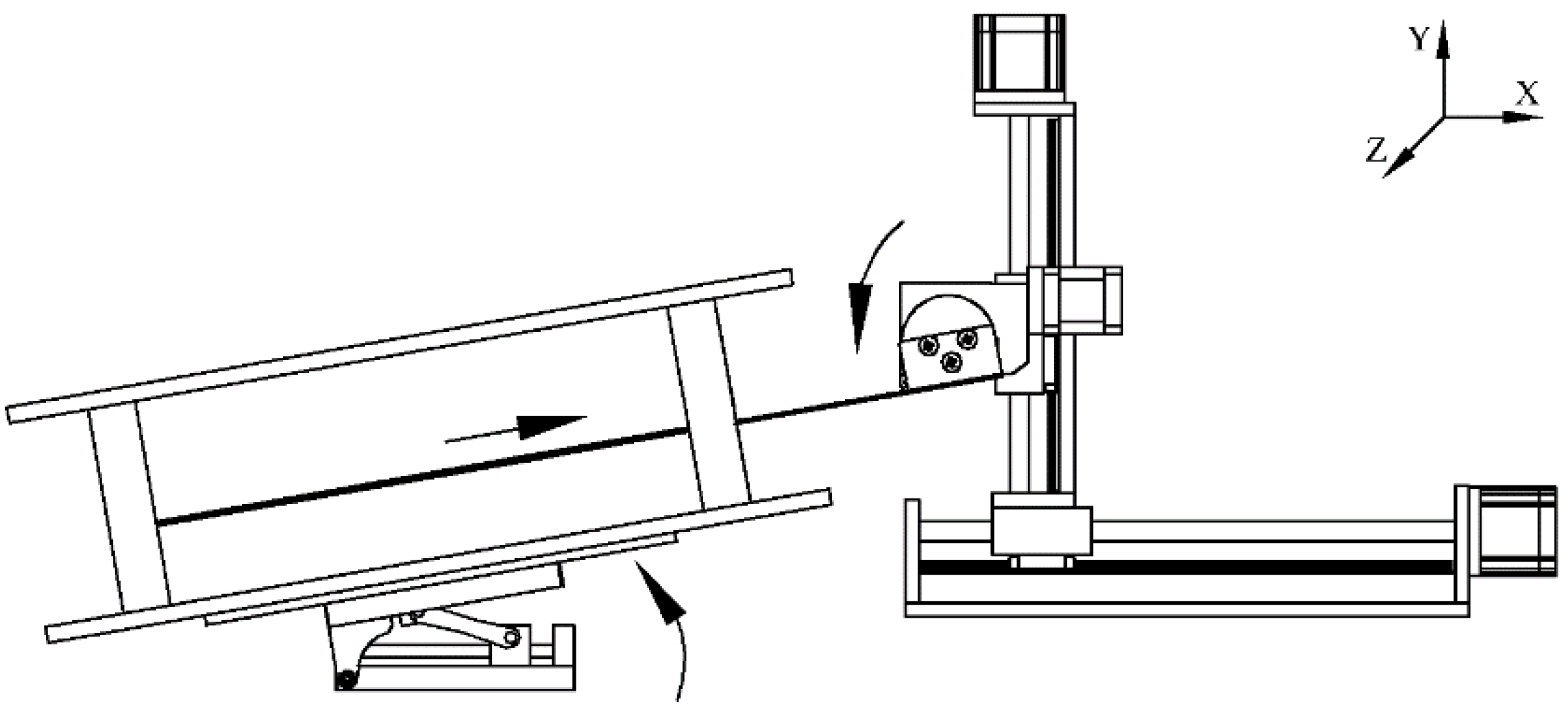
2. The Novel Measuring System
2.1. Components of the System
2.2. Rheological Model
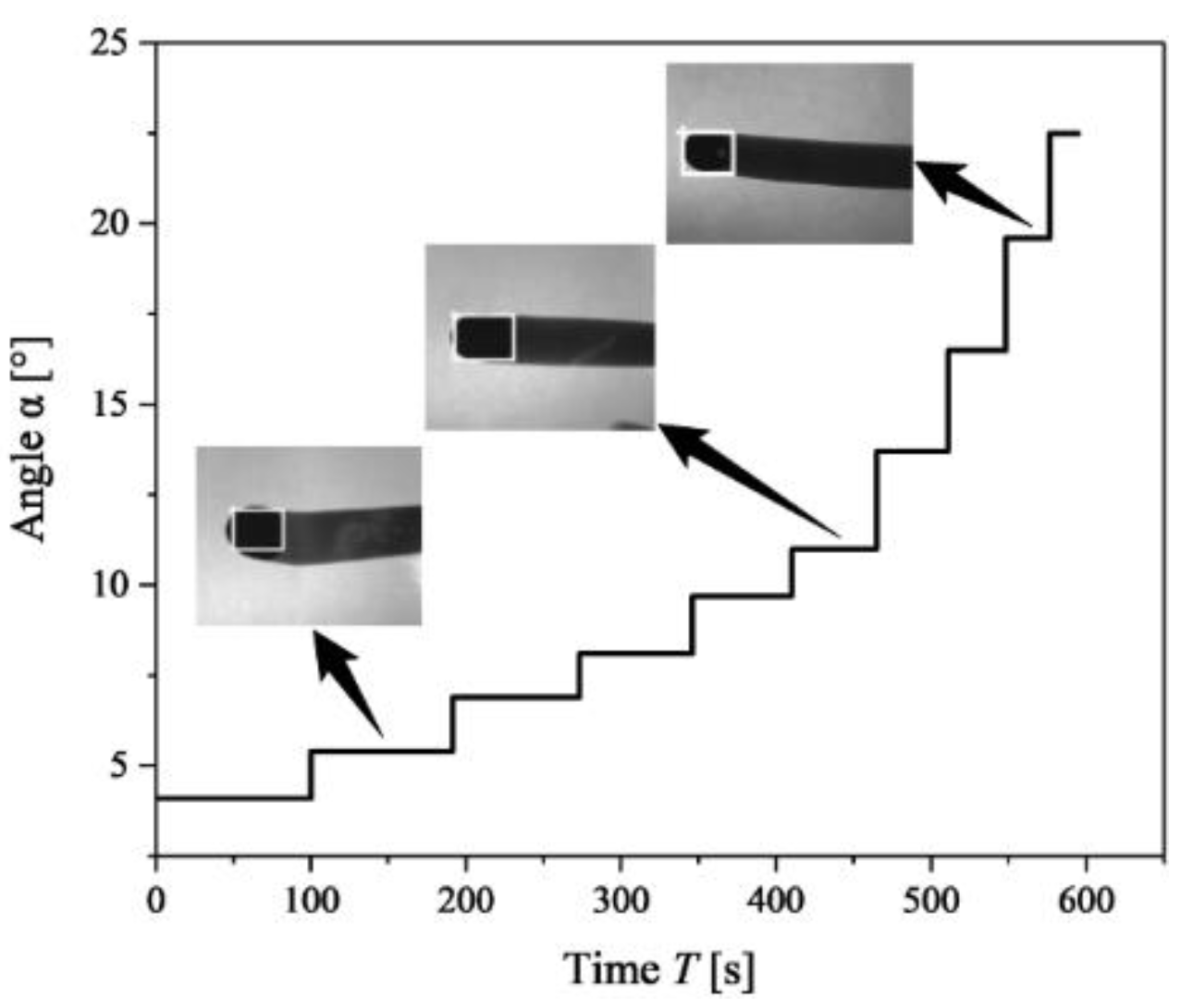
2.3. Measuring Procedure and Details
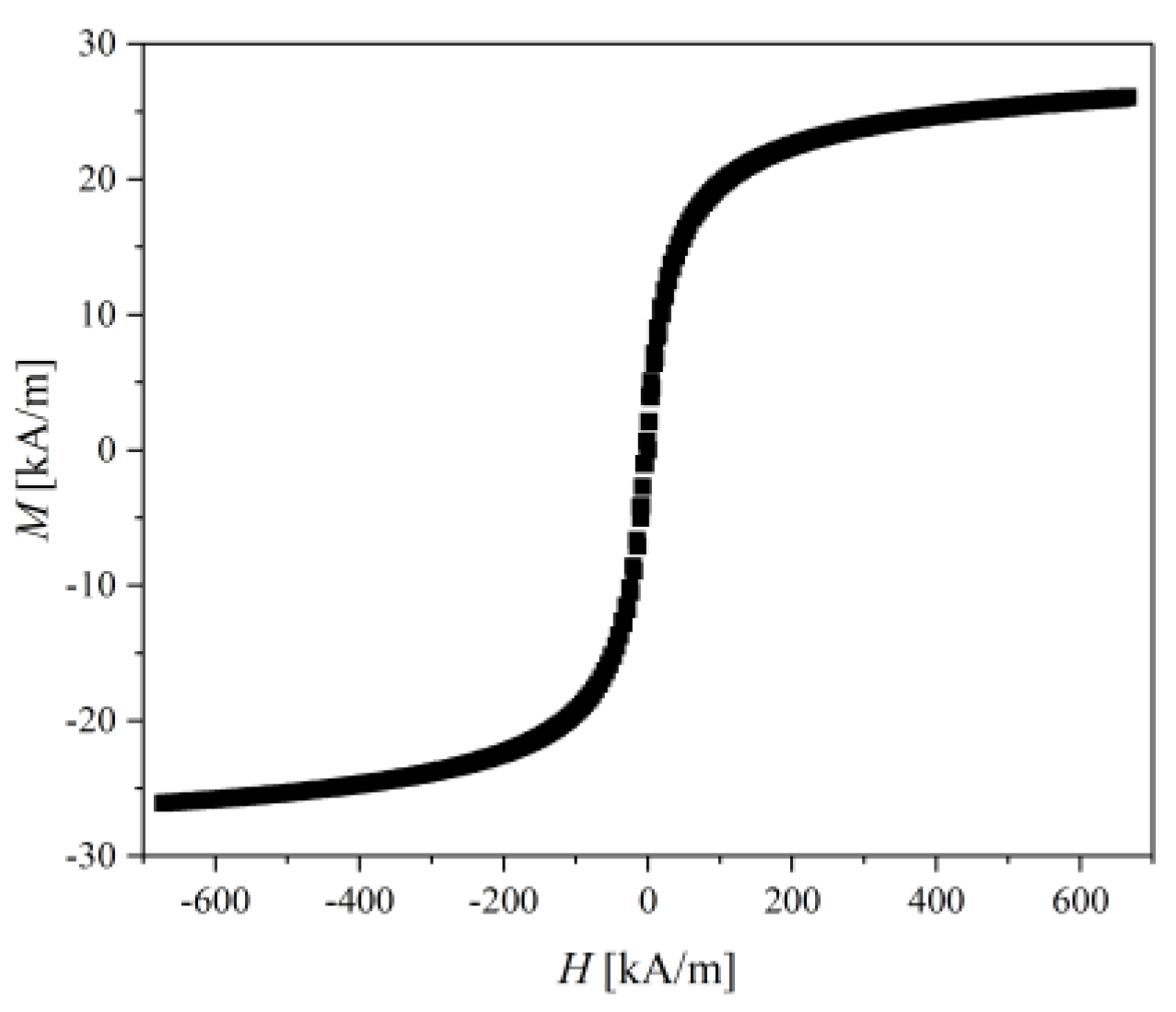
2.4. Materials
3. Results and Discussion
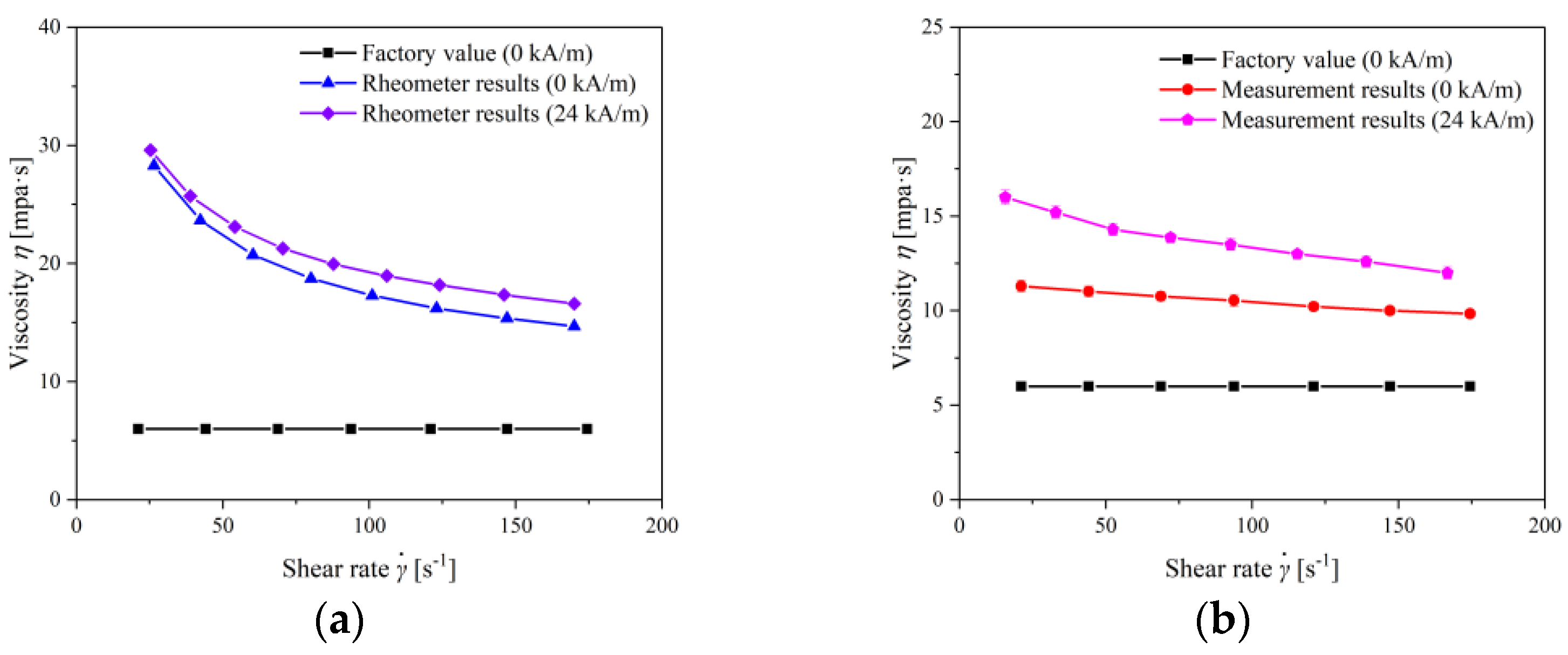
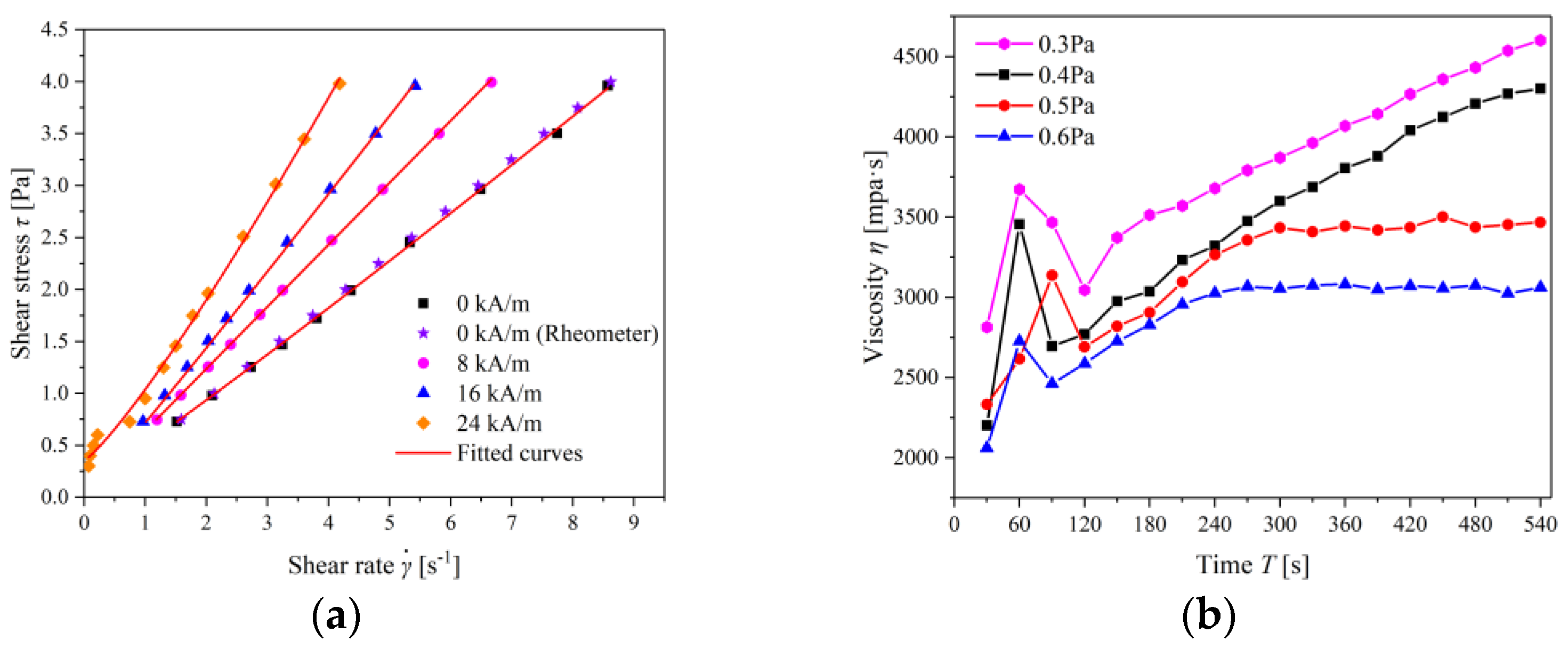
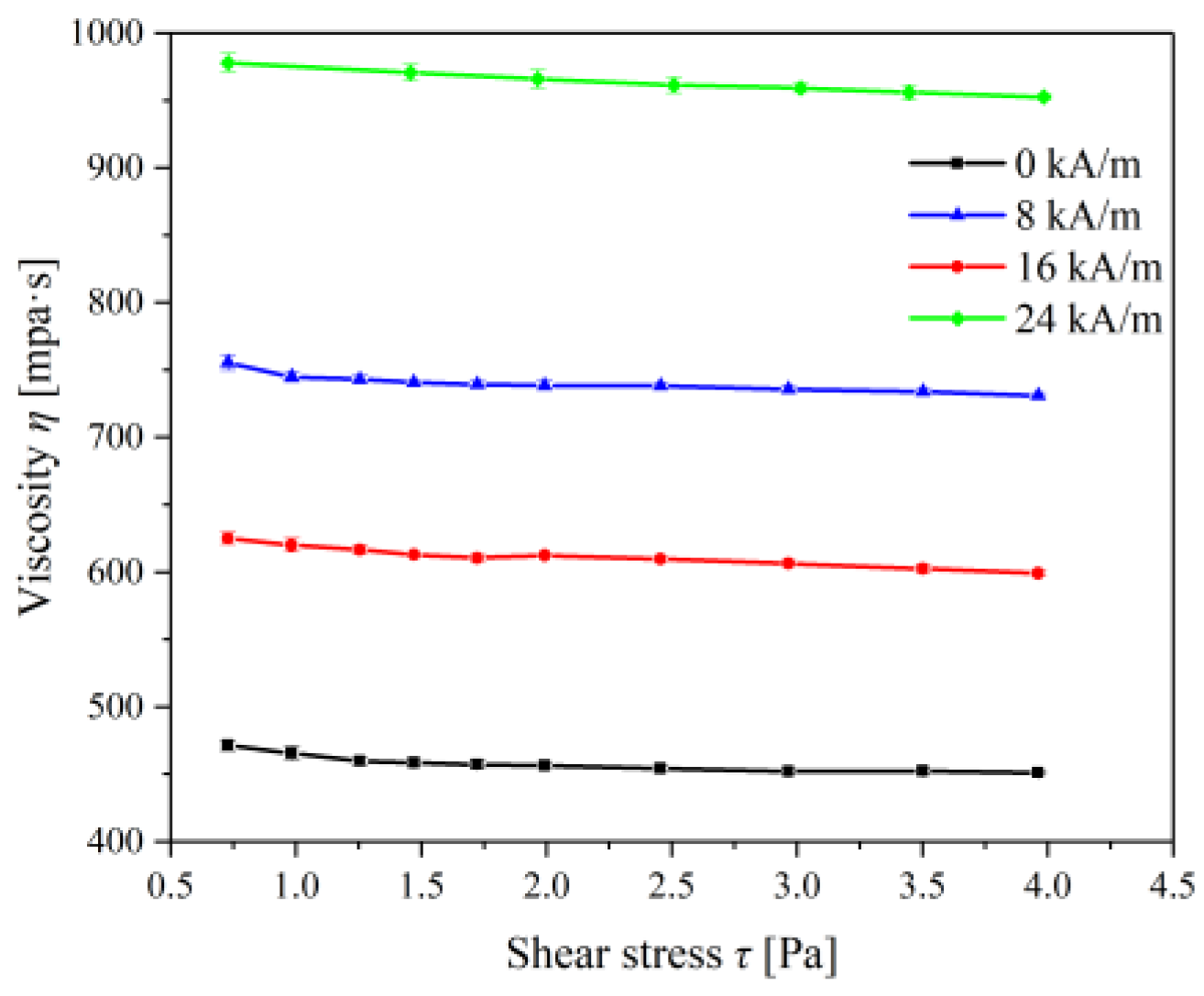
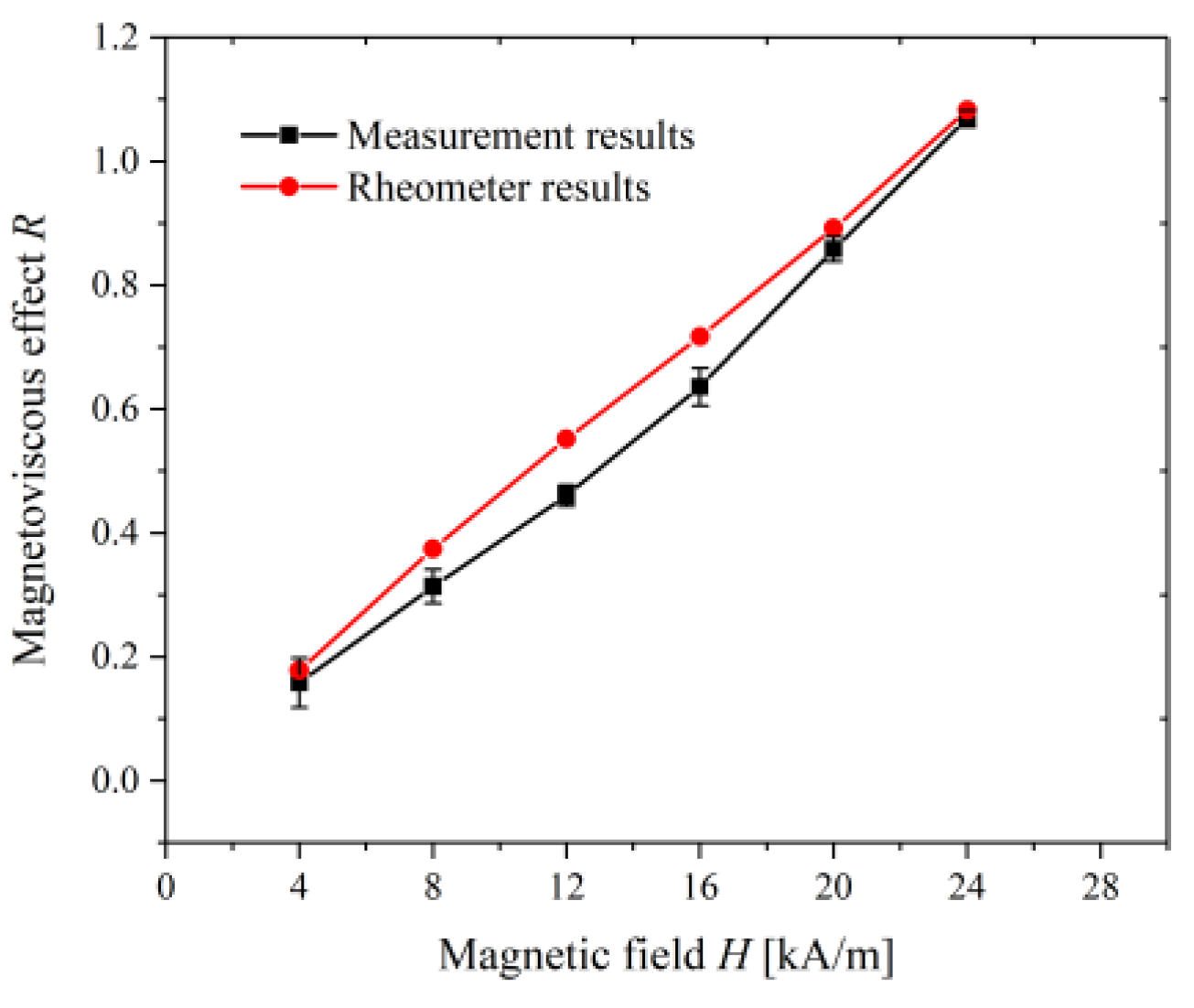
3.1. Commercial Magnetic Fluid Measurement
3.2. Lab-Made Magnetic Fluid Measurement
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, D. Theory and Application of Magnetic Fluid; Science Press: Beijing, China, 2003. [Google Scholar]
- Beik, J.; Abed, Z.; Ghoreishi, F.S.; Hosseini-Nami, S.; Mehrzadi, S.; Shakeri-Zadeh, A.; Kamrava, S.K. Nanotechnology in hyperthermia cancer therapy: From fundamental principles to advanced applications. J. Control. Release 2016, 235, 205–221. [Google Scholar] [CrossRef] [PubMed]
- Vasilakaki, M.; Chikina, I.; Shikin, V.B.; Ntallis, N.; Peddis, D.; Varlamov, A.A.; Trohidou, K.N. Towards high-performance electrochemical thermal energyharvester based on ferrofluids. Appl. Mater. Today 2020, 19, 100587. [Google Scholar] [CrossRef]
- Xu, M.; Dai, Q.; Huang, W.; Wang, X. Using magnetic fluids to improve the behavior of ball bearings under starved lubrication. Tribol. Int. 2020, 141, 105950. [Google Scholar] [CrossRef]
- Wang, W.; Timonen, J.V.; Carlson, A.; Drotlef, D.M.; Zhang, C.T.; Kolle, S.; Grinthal, A.; Wong, T.-S.; Hatton, B.; Kang, S.H.; et al. Multifunctional ferrofluid-infused surfaces with reconfigurable multiscale topography. Nature 2018, 559, 77–82. [Google Scholar] [CrossRef]
- Paul, G.; Chopkar, M.; Manna, I.; Das, P. Techniques for measuring the thermal conductivity of nanofluids: A review. Renew. Sustain. Energy Rev. 2010, 14, 1913–1924. [Google Scholar] [CrossRef]
- Shah, R.R.; Davis, T.P.; Glover, A.L.; Nikles, D.E.; Brazel, C.S. Impact of magnetic field parameters and iron oxide nanoparticle properties on heat generation for use in magnetic hyperthermia. J. Magn. Magn. Mater. 2015, 387, 96–106. [Google Scholar] [CrossRef]
- Li, Z.; Li, D.; Chen, Y.; Yang, Y.; Yao, J. Influence of Viscosity and Magnetoviscous Effect on the Performance of the Magnetic Fluid Seal in Water Environment. Tribol. Trans. 2017, 61, 367–375. [Google Scholar] [CrossRef]
- Bahiraei, M.; Hangi, M. Flow and heat transfer characteristics of magnetic nanofluids: A review. J. Magn. Magn. Mater. 2015, 374, 125–138. [Google Scholar] [CrossRef]
- Ellahi, R. The effects of MHD and temperature dependent viscosity on the flow of non-Newtonian nanofluid in a pipe: Analytical solutions. Appl. Math. Model. 2013, 37, 1451–1467. [Google Scholar] [CrossRef]
- Gu, H.; Tang, X.; Hong, R.; Feng, W.; Xie, H.; Chen, D.; Badami, D. Ubbelohde viscometer measurement of water-based Fe3O4 magnetic fluid prepared by coprecipitation. J. Magn. Magn. Mater. 2013, 348, 88–92. [Google Scholar] [CrossRef]
- Yang, C.; Bian, X.; Qin, J.; Zhao, X.; Zhang, K.; Bai, Y. An investigation of a viscosity-magnetic field hysteretic effect in nano-ferrofluid. J. Mol. Liq. 2014, 196, 357–362. [Google Scholar]
- Matsuno, Y.; Itoh, J. Estimation of the yield stress of a magnetic fluid from flow curves. J. Magn. Magn. Mater. 1995, 149, 22–25. [Google Scholar] [CrossRef]
- Ren, Z.S.; Zheng, D.; Hu, L.Y.; Huang, C.B. Design and Analysis of a Novel Magnetorheometer. Appl. Mech. Mater. 2012, 101–102, 154–157. [Google Scholar] [CrossRef]
- Li, Z.; Li, D.; Chen, Y.; Cui, H. Study on the thixotropic behaviors of ferrofluids. Soft Matter. 2018, 14, 3858–3869. [Google Scholar] [PubMed]
- Møller, P.C.F.; Mewis, J.; Bonn, D. Yield Stress and Thixotropy: On the Difficulty of Measuring Yield Stresses in Practice. Soft Matter 2006, 4, 274–283. [Google Scholar] [CrossRef] [PubMed]
- Barnes, H.A. The yield stress—A review or ‘παντα ρει’—Everything flows? J. Non-Newton. Fluid Mech. 1999, 81, 133–178. [Google Scholar]
- Zubarev, A.Y.; Iskakova, L.Y. Yield stress in thin layers of ferrofluids. Phys. A Stat. Mech. Its Appl. 2006, 365, 265–281. [Google Scholar] [CrossRef]
- Schramm, G. A Practical Approach to Rheology and Rheometry; Gebrueder Haake: Karlsruhe, Germany, 1994; pp. 74–76. [Google Scholar]
- Drenckhan, W.; Ritacco, H.; Saint-Jalmes, A.; Saugey, A.; McGuinness, P.; van der Net, A.; Langevin, D.; Weaire, D. Fluid dynamics of rivulet flow between plates. Phys. Fluids 2007, 19, 102101. [Google Scholar] [CrossRef]
- Song, F.Q.; Wang, J.D. Investigation of Influence of Wettability On Poiseuille Flow Via Molecular Dynamics Simulation. J. Hydrodyn. 2010, 22, 513–517. [Google Scholar] [CrossRef]
- Li, Z.; Li, D.; Hao, D.; Cheng, Y. Study on the creep and recovery behaviors of ferrofluids. Smart Mater. 2017, 26, 105022. [Google Scholar] [CrossRef]
- Martin, J.E.; Anderson, R.A. Chain model of electrorheology. J. Chem. Phys. 1996, 104, 4814. [Google Scholar] [CrossRef]
- Nowak, J.; Borin, D.; Haefner, S.; Richter, A.; Odenbach, S. Magnetoviscous effect in ferrofluids diluted with sheep blood. J. Magn. Magn. Mater. 2017, 442, 383–390. [Google Scholar] [CrossRef]
- Hall, W.F.; Busenberg, S.N. Viscosity of magnetic suspension. J. Chem. Phys. 1969, 51, 137. [Google Scholar] [CrossRef]
- Odenbach, S.; Störk, H. Shear dependence of field-induced contributions to the viscosity of magnetic fluids at low shear rates. J. Magn. Magn. Mater. 1998, 183, 188–194. [Google Scholar] [CrossRef]



| Nanoparticle Type | Saturation Magnetization (kA/m) | Viscosity @20 °C (mPa·s) | Density @20 °C (kg/m3) |
|---|---|---|---|
| EFH1 | 35 | 9 | 1.22 × 103 |
| Lab-made | 33 | 464 | 1.27 × 103 |
| Standard No. | Kinematical Viscosity @20 °C (mPa·s) | Density @20 °C (kg/m3) | Flash Point (°C) | Pour Point (°C) |
|---|---|---|---|---|
| L-AN46 | 327 | 0.92 × 103 | 220 | −28 |
| Magnetic Flux Density (kA/m) | k | n | Fitted Dynamic Yield Stress (Pa) |
|---|---|---|---|
| 0 | 0.3936 | 1.0578 | 0.1159 |
| 8 | 0.5992 | 0.9985 | 0.039 |
| 16 | 0.6798 | 1.0415 | 0.0377 |
| 24 | 0.6976 | 1.159 | 0.3567 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, J.; Hu, Y.; Su, B.; Li, Z.; Song, Z.; Li, D.; Cui, H.; Wang, D. A Novel Method of Flow Curve Measurement for Magnetic Fluid Based on Plane Poiseuille Flow. Magnetochemistry 2022, 8, 98. https://doi.org/10.3390/magnetochemistry8090098
Dong J, Hu Y, Su B, Li Z, Song Z, Li D, Cui H, Wang D. A Novel Method of Flow Curve Measurement for Magnetic Fluid Based on Plane Poiseuille Flow. Magnetochemistry. 2022; 8(9):98. https://doi.org/10.3390/magnetochemistry8090098
Chicago/Turabian StyleDong, Jiahao, Yifan Hu, Bingrui Su, Zhenkun Li, Zhongru Song, Decai Li, Hongchao Cui, and Deyi Wang. 2022. "A Novel Method of Flow Curve Measurement for Magnetic Fluid Based on Plane Poiseuille Flow" Magnetochemistry 8, no. 9: 98. https://doi.org/10.3390/magnetochemistry8090098
APA StyleDong, J., Hu, Y., Su, B., Li, Z., Song, Z., Li, D., Cui, H., & Wang, D. (2022). A Novel Method of Flow Curve Measurement for Magnetic Fluid Based on Plane Poiseuille Flow. Magnetochemistry, 8(9), 98. https://doi.org/10.3390/magnetochemistry8090098








