Effect of Electrode–Normal Magnetic Field on the Motion of Hydrogen Bubbles
Abstract
:1. Introduction
2. Material and Methods
3. Results and Discussion
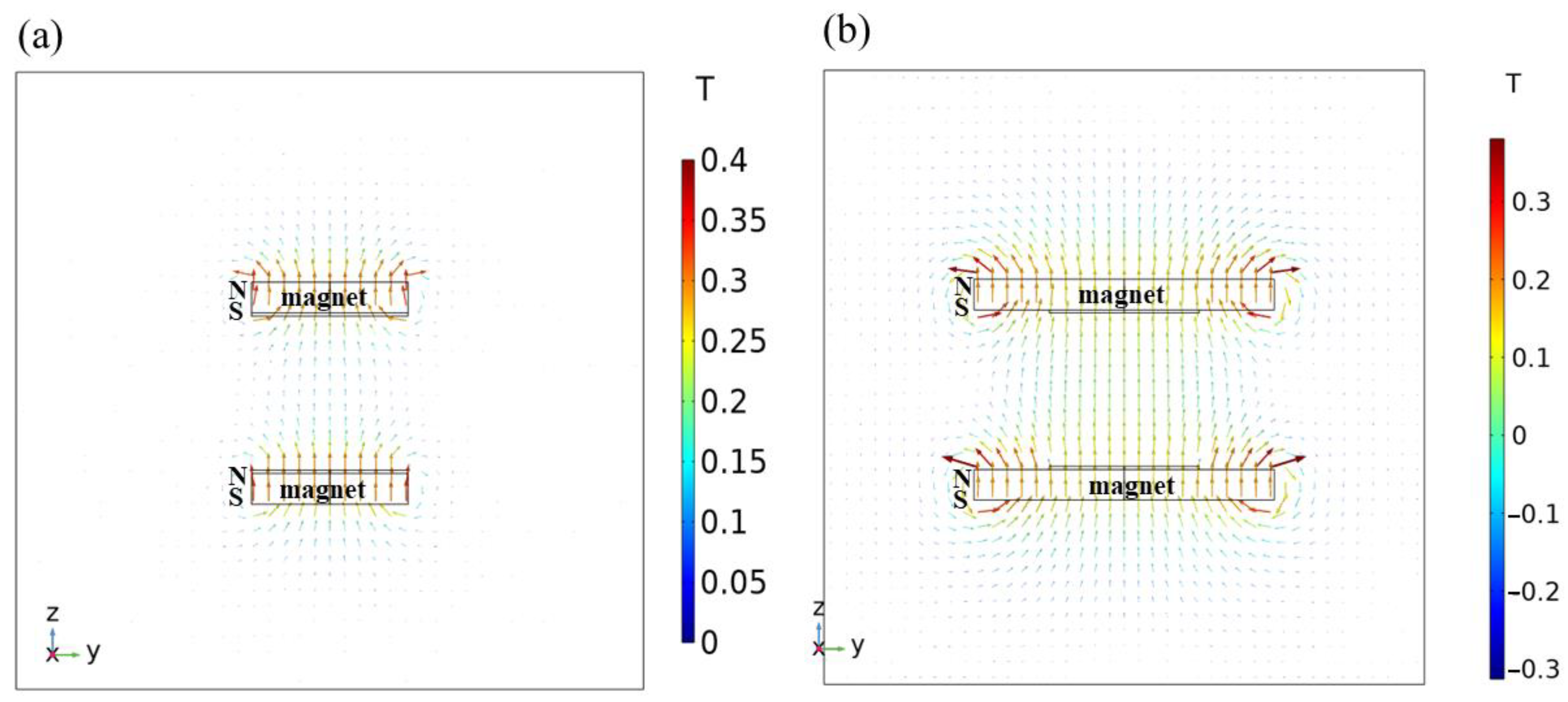
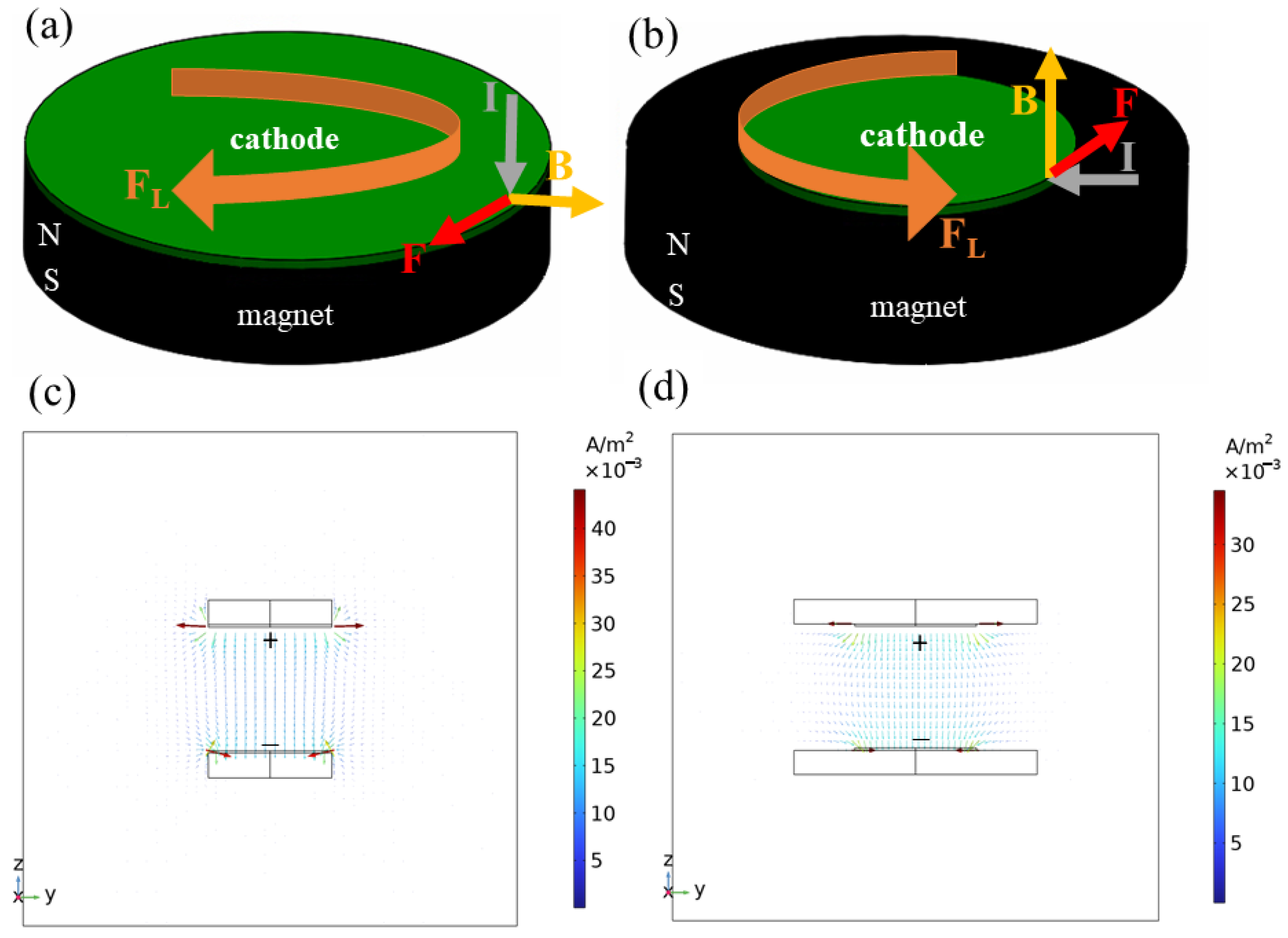
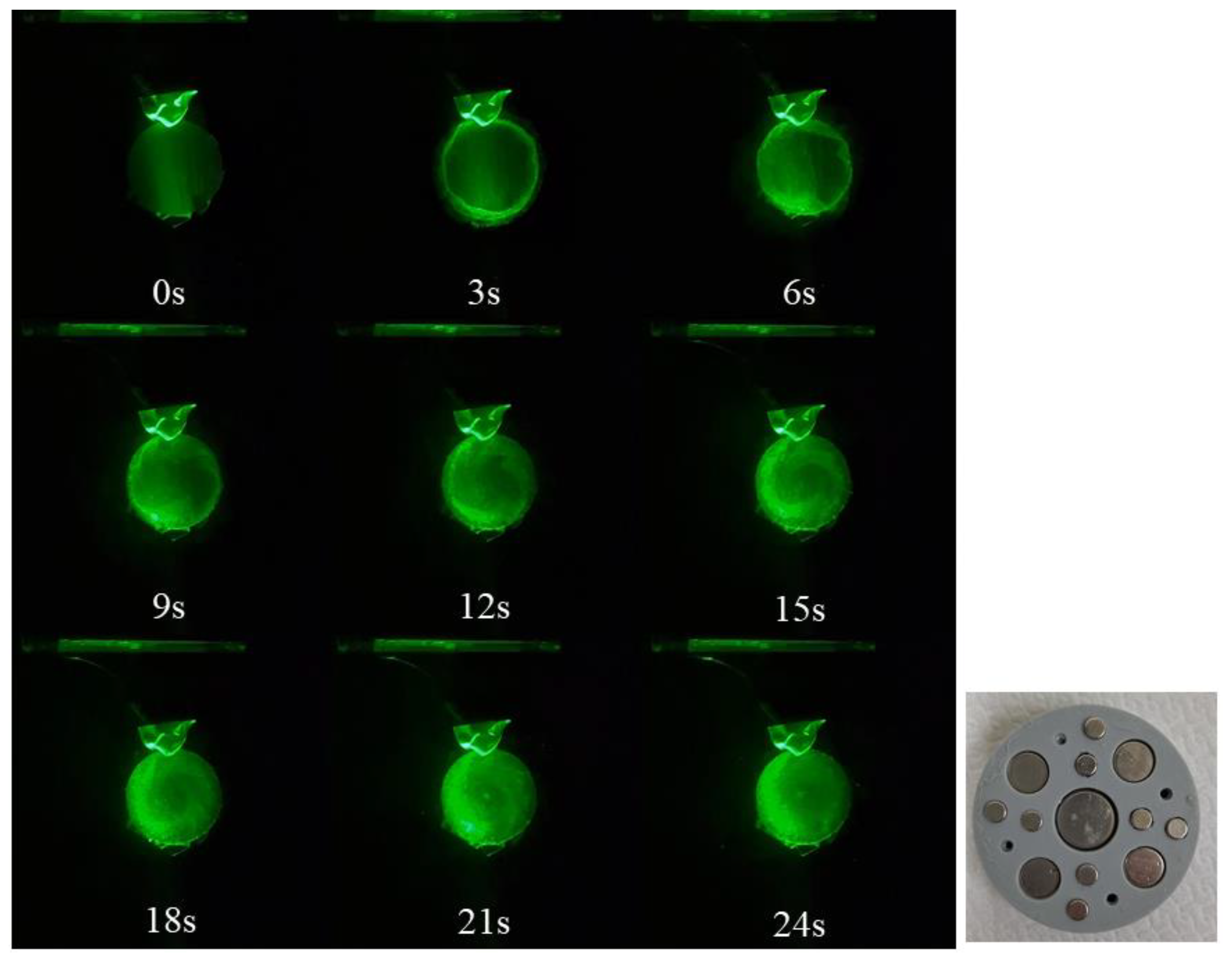
3.1. Influence of Magnet Edge and Electrode Edge on the Movement of the Gas Bubbles
3.2. Effect of Electrode Spacing on the Movement of Gas Bubbles
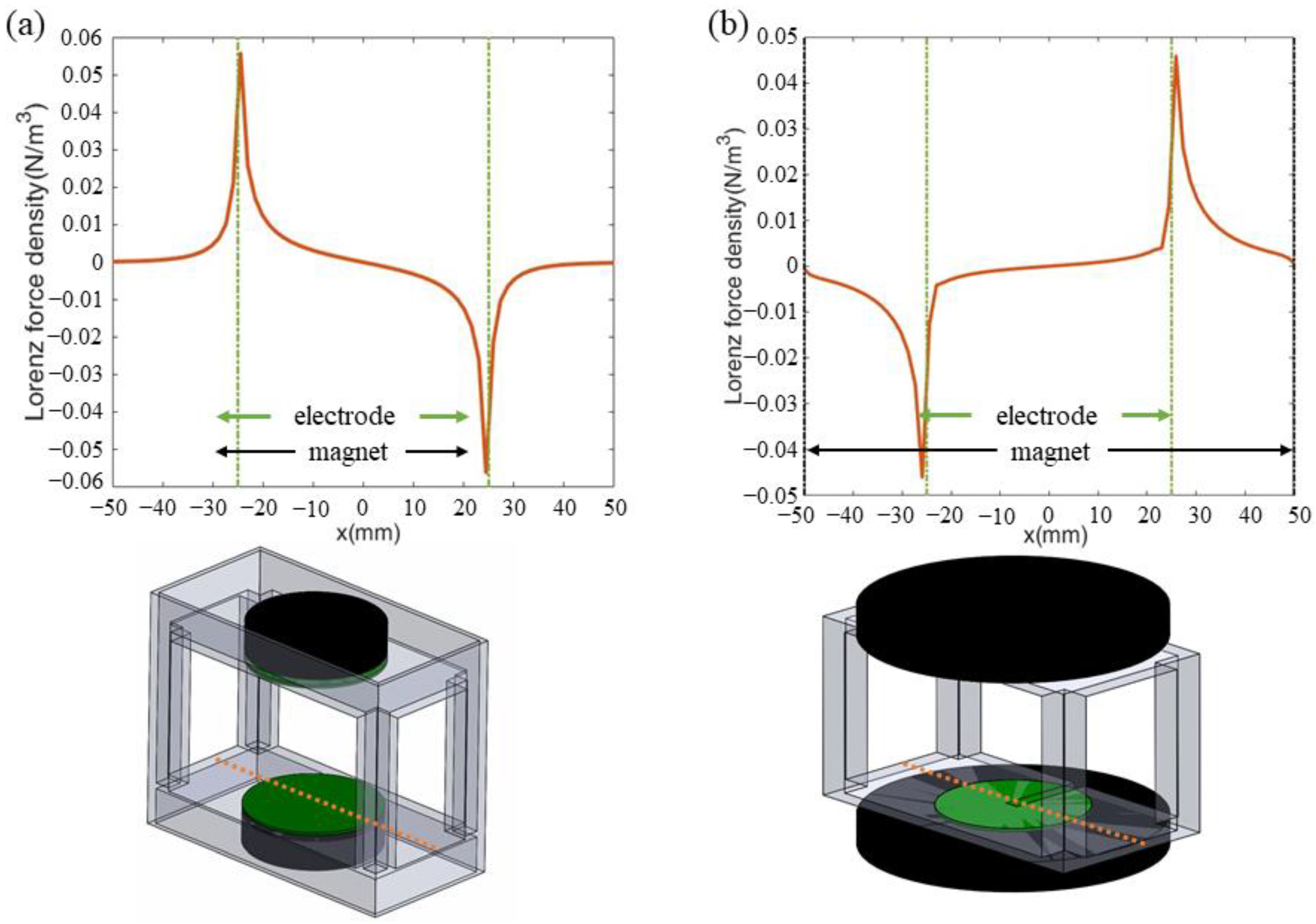
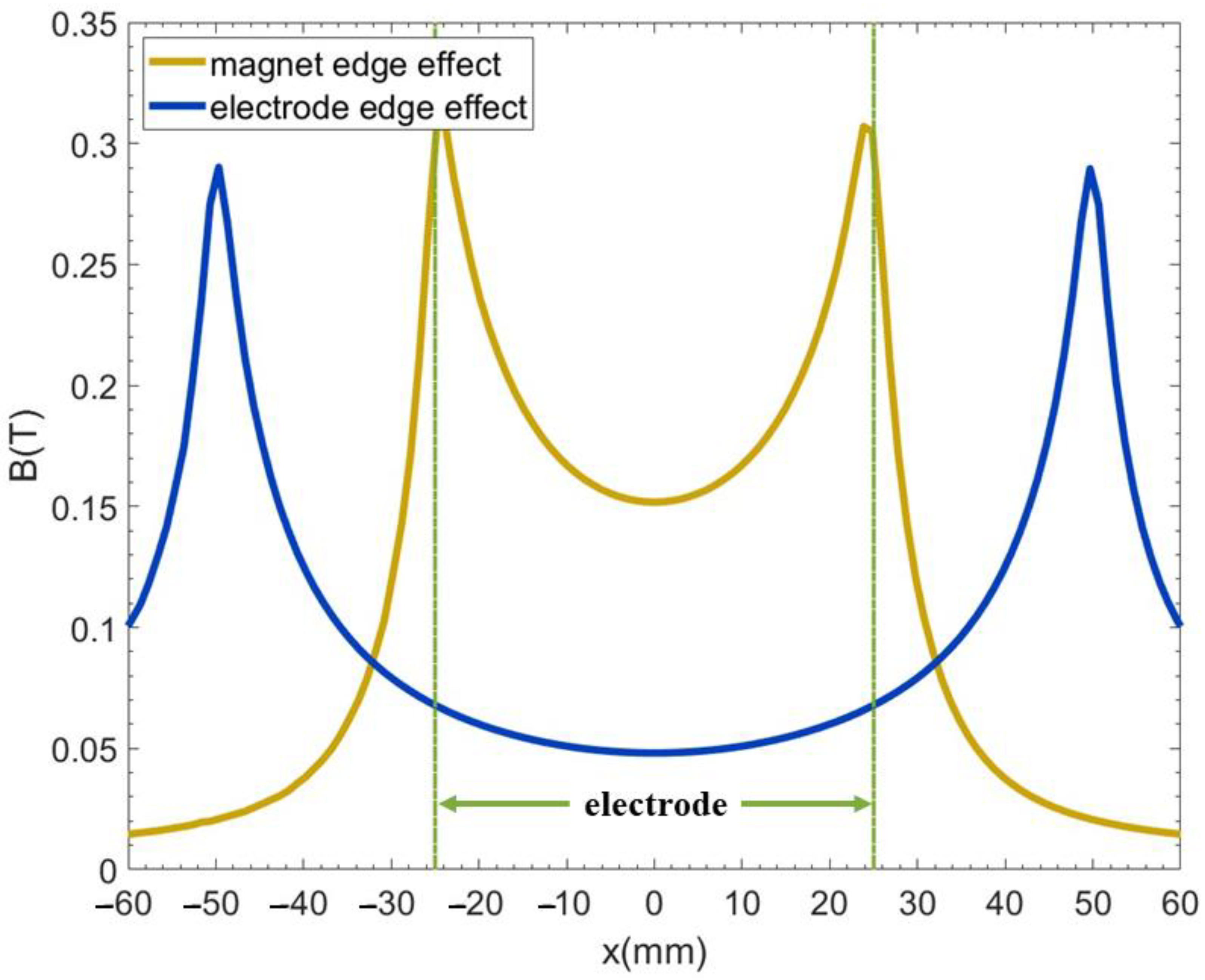
3.3. Impact of the Magnet and Electrode Edge Effect on the Lorentz Force on the Electrode Surface
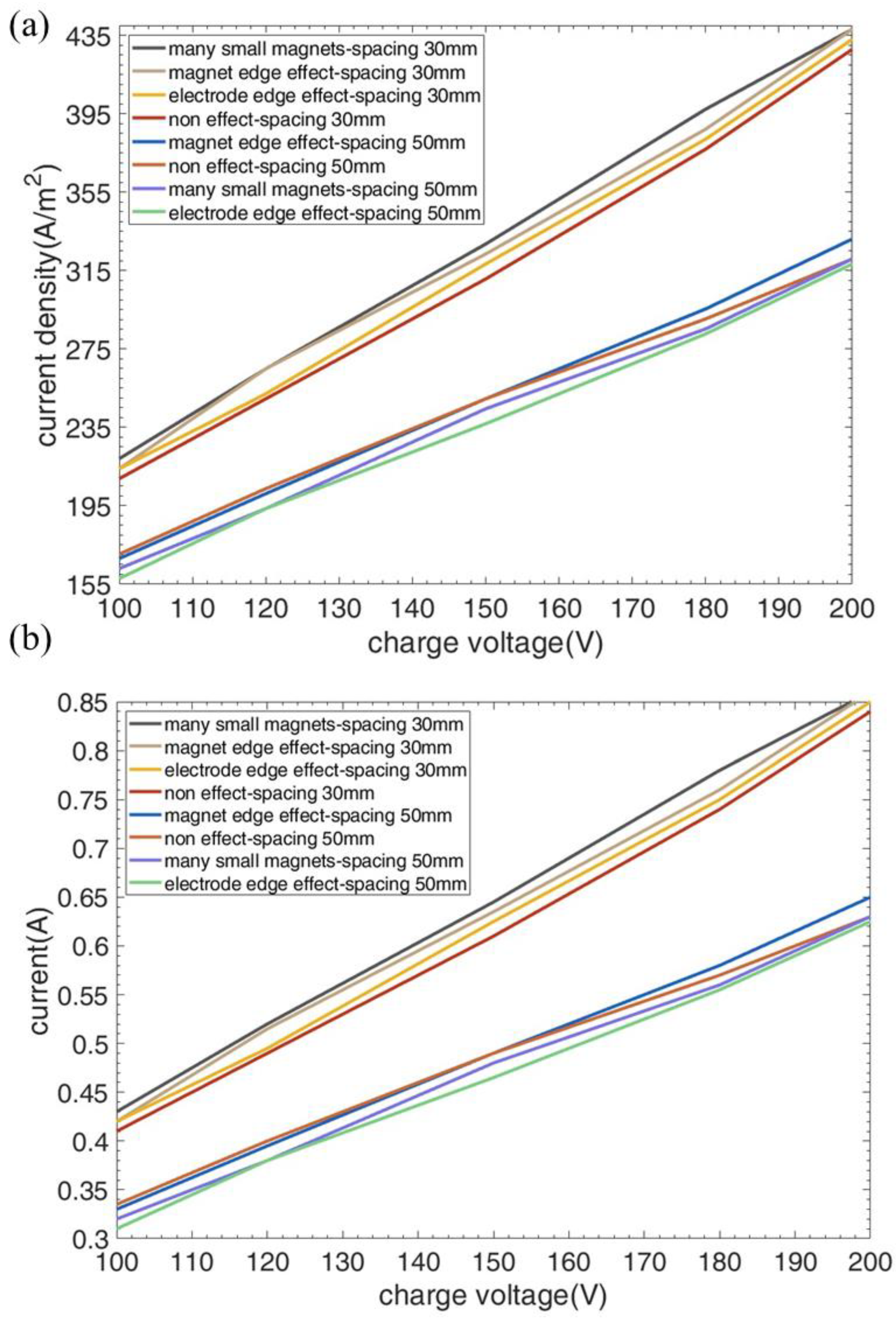
3.4. Comparison of Various Experimental Configurations for Improving Current Density Efficiency
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zeng, K.; Zhang, D. Recent Progress in Alkaline Water Electrolysis for Hydrogen Production and Applications. Prog. Energy Combust. Sci. 2010, 36, 307–326. [Google Scholar] [CrossRef]
- Kumar, S.S.; Himabindu, V. Hydrogen Production by PEM Water Electrolysis—A Review. Mater. Sci. Energy Technol. 2019, 2, 442–454. [Google Scholar]
- Ebbesen, S.D.; Mogensen, M. Electrolysis of Carbon Dioxide in Solid Oxide Electrolysis Cells. J. Power Sources 2009, 193, 349–358. [Google Scholar] [CrossRef]
- Nikolic, V.M.; Tasic, G.S.; Maksic, A.D.; Saponjic, D.P.; Miulovic, S.M.; Marceta Kaninski, M.P. Raising Efficiency of Hydrogen Generation from Alkaline Water Electrolysis—Energy Saving. Int. J. Hydrogen Energy 2010, 35, 12369–12373. [Google Scholar] [CrossRef]
- Manabe, A.; Kashiwase, M.; Hashimoto, T.; Hayashida, T.; Kato, A.; Hirao, K.; Shimomura, I.; Nagashima, I. Basic Study of Alkaline Water Electrolysis. Electrochim. Acta 2013, 100, 249–256. [Google Scholar] [CrossRef]
- ezzahra Chakik, F.; Kaddami, M.; Mikou, M. Effect of Operating Parameters on Hydrogen Production by Electrolysis of Water. Int. J. Hydrogen Energy 2017, 42, 25550–25557. [Google Scholar] [CrossRef]
- Saleh, M.M.; Weidner, J.W.; Ateya, B.G. Electrowinning of Non-Noble Metals with Simultaneous Hydrogen Evolution at Flow-Through Porous Electrodes: I. Theoretical. J. Electrochem. Soc. 1995, 142, 4113. [Google Scholar] [CrossRef]
- Liu, H.-B.; Xu, H.; Pan, L.-M.; Zhong, D.-H.; Liu, Y. Porous Electrode Improving Energy Efficiency under Electrode-Normal Magnetic Field in Water Electrolysis. Int. J. Hydrogen Energy 2019, 44, 22780–22786. [Google Scholar] [CrossRef]
- Liu, Y.; Pan, L.-M.; Liu, H.; Chen, T.; Yin, S.; Liu, M. Effects of Magnetic Field on Water Electrolysis Using Foam Electrodes. Int. J. Hydrogen Energy 2019, 44, 1352–1358. [Google Scholar] [CrossRef]
- Bidin, N.; Azni, S.R.; Islam, S.; Abdullah, M.; Ahmad, M.F.S.; Krishnan, G.; Johari, A.R.; Bakar, M.A.A.; Sahidan, N.S.; Musa, N.F. The Effect of Magnetic and Optic Field in Water Electrolysis. Int. J. Hydrogen Energy 2017, 42, 16325–16332. [Google Scholar] [CrossRef]
- Matsushima, H.; Fukunaka, Y.; Kuribayashi, K. Water Electrolysis under Microgravity Part II. Description of Gas Bubble Evolution Phenomena. Electrochim. Acta 2006, 51, 4190–4198. [Google Scholar] [CrossRef]
- Wang, M.; Wang, Z.; Guo, Z. Water Electrolysis Enhanced by Super Gravity Field for Hydrogen Production. Int. J. Hydrogen Energy 2010, 35, 3198–3205. [Google Scholar] [CrossRef]
- Iida, T.; Matsushima, H.; Fukunaka, Y. Water Electrolysis under a Magnetic Field. J. Electrochem. Soc. 2007, 154, E112. [Google Scholar] [CrossRef]
- Pletcher, D.; Li, X. Prospects for Alkaline Zero Gap Water Electrolysers for Hydrogen Production. Int. J. Hydrogen Energy 2011, 36, 15089–15104. [Google Scholar] [CrossRef]
- Hung, C.Y.; Li, S.D.; Wang, C.C.; Chen, C.Y. Influences of a Bipolar Membrane and an Ultrasonic Field on Alkaline Water Electrolysis. J. Membr. Sci. 2012, 389, 197–204. [Google Scholar] [CrossRef]
- Matsushima, H.; Kiuchi, D.; Fukunaka, Y. Measurement of Dissolved Hydrogen Supersaturation during Water Electrolysis in a Magnetic Field. Electrochim. Acta 2009, 54, 5858–5862. [Google Scholar] [CrossRef]
- Lin, M.Y.; Hourng, L.W.; Kuo, C.W. The Effect of Magnetic Force on Hydrogen Production Efficiency in Water Electrolysis. Int. J. Hydrogen Energy 2011, 37, 1311–1320. [Google Scholar] [CrossRef]
- Liu, Y.; Li, S.; Wu, H.; Shi, Y. The “tornado” Effect Induced by Magnetohydrodynamic Convection in an Electrolytic Cell with a Wire-Electrode. Int. J. Hydrogen Energy 2023, 33, 172–177. [Google Scholar] [CrossRef]
- Matsushima, H.; Iida, T.; Fukunaka, Y. Electrochimica Acta Gas Bubble Evolution on Transparent Electrode during Water Electrolysis in a Magnetic Field. Electrochim. Acta 2013, 100, 261–264. [Google Scholar] [CrossRef]
- Li, Y.H.; Chen, Y.J. The Effect of Magnetic Field on the Dynamics of Gas Bubbles in Water Electrolysis. Sci. Rep. 2021, 11, 9346. [Google Scholar] [CrossRef]
- Diao, Z.; Dunne, P.A.; Zangari, G.; Coey, J.M.D. Electrochemical Noise Analysis of the Effects of a Magnetic Field on Cathodic Hydrogen Evolution. Electrochem. Commun. 2009, 11, 740–743. [Google Scholar] [CrossRef]
- Chen, Y.J.; Li, Y.H.; Chen, C.Y. Studying the Effect of Electrode Material and Magnetic Field on Hydrogen Production Efficiency. Magnetochemistry 2022, 8, 53. [Google Scholar] [CrossRef]
- Kaya, M.Y.; Demir, N.; Albawabiji, M.S.; Tas, M. Investigation of alkaline water electrolysis performance for different cost effective electrodes under magnetic field. Int. J. Hydrogen Energy 2017, 42, 17583–17592. [Google Scholar] [CrossRef]
- Matsushima, H.; Iida, T.; Fukunaka, Y. Observation of bubble layer formed on hydrogen and oxygen gas-evolving electrode in a magnetic field. J. Solid State Electrochem. 2012, 16, 617–623. [Google Scholar] [CrossRef]
- Wang, M.Y.; Wang, Z.; Gong, X.Z.; Guo, Z.C. The intensification technologies to water electrolysis for hydrogen production-A review. Renew. Sustain. Energy Rev. 2014, 29, 573–588. [Google Scholar] [CrossRef]
- Koza, J.A.; Muhlenhoff, S.; Zabinski, P.; Nikrityuk, P.A.; Eckert, K.; Uhlemann, M.; Gebert, A.; Weier, T.; Schultz, L.; Odenbach, S. Hydrogen evolution under the influence of a magnetic field. Electrochim. Acta 2011, 56, 2665–2675. [Google Scholar] [CrossRef]
- Mohan, S.; Saravanan, G.; Bund, A. Role of magnetic forces in pulse electrochemical deposition of Ni nano Al2O3 composites. Electrochim. Acta 2012, 64, 94–99. [Google Scholar] [CrossRef]
- Monzon, L.M.A.; Coey, J.M.D. Magnetic fields in electrochemistry: The Lorentz force. A mini-review. Electrochem. Commun. 2014, 42, 38–41. [Google Scholar] [CrossRef]
- Scott, K. Process intensification: An electrochemical perspective. Renew. Sustain. Energy Rev. 2018, 81, 1406–1426. [Google Scholar] [CrossRef]
- Wang, K.; Pei, P.; Pei, Y.; Ma, Z.; Xu, H.; Chen, D. Magnetic field induced motion behavior of gas bubbles in liquid. Sci. Rep. 2016, 6, 21068. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.-J.; Li, Y.-H.; Chen, C.-Y. Effect of Electrode–Normal Magnetic Field on the Motion of Hydrogen Bubbles. Magnetochemistry 2023, 9, 233. https://doi.org/10.3390/magnetochemistry9120233
Chen Y-J, Li Y-H, Chen C-Y. Effect of Electrode–Normal Magnetic Field on the Motion of Hydrogen Bubbles. Magnetochemistry. 2023; 9(12):233. https://doi.org/10.3390/magnetochemistry9120233
Chicago/Turabian StyleChen, Yen-Ju, Yan-Hom Li, and Ching-Yao Chen. 2023. "Effect of Electrode–Normal Magnetic Field on the Motion of Hydrogen Bubbles" Magnetochemistry 9, no. 12: 233. https://doi.org/10.3390/magnetochemistry9120233
APA StyleChen, Y.-J., Li, Y.-H., & Chen, C.-Y. (2023). Effect of Electrode–Normal Magnetic Field on the Motion of Hydrogen Bubbles. Magnetochemistry, 9(12), 233. https://doi.org/10.3390/magnetochemistry9120233




