The Phase Space Density Evolution of Radiation Belt Electrons under the Action of Solar Wind Dynamic Pressure

Abstract

Earth’s radiation belt and ring current are donut-shaped regions of energetic and relativistic particles, trapped by the geomagnetic field. The strengthened solar wind dynamic pressure (P_dyn) can alter the structure of the geomagnetic field, which can bring about the dynamic variation of radiation belt and ring current. In the study, we firstly utilize group test particle simulations to investigate the phase space density (PSD) under the varying geomagnetic field modeled by the International Geomagnetic Reference Field (IGRF) and T96 magnetic field models from 19 December 2015 to 20 December 2015. Combining the observation of the Van Allen Probe, we find that the PSD of outer radiation belt electrons evolves towards different states under different levels of P_dyn. In the first stage, the P_dyn (~7.94 nPa) results in the obvious rise of electron anisotropy. In the second stage, there is a significant reduction in PSD for energetic electrons at all energy levels and pitch angles under the action of intense P_dyn (~22 nPa), which suggests that the magnetopause shadowing and outward radial diffusion play important roles in the second process. The result of the study can help us further understand the dynamic evolution of the radiation belt and ring current during a period of geomagnetic disturbance.

1. Introduction

The radiation belts are areas of magnetically trapped energetic/relativistic electrons and ions surrounding the Earth [1]. These particles can cause serious damage to the satellites and astronauts working in space [2]. In addition, energetic particles from the radiation belt can precipitate into the atmosphere and have a significant impact on the chemistry and composition of the Earth’s atmosphere [3,4]. For example, Rodger et al. (2010) show that the electron precipitation can lead to a large increase in odd nitrogen (NO_x) and odd hydrogen (HO_x), and when the electron precipitation been deposited into the polar winter atmosphere, it would have led to >20% in situ decreases in O₃ at 65–80 km altitudes through catalytic HO_x cycles [4]. Duderstadt et al. (2021) show that higher energy electron precipitation cause important contributions to atmospheric ionization and modeled NO_x concentrations in the mesosphere and upper stratosphere [5]. Studying the response of radiation belts electron flux to the solar wind dynamic pressure (P_dyn) can indirectly help us understand the potential chemical processes in the Earth’s atmosphere. In general, there are two distinct electron radiation belts, which are named inner and outer radiation belts. The inner belt is quite stable, which is centered at L~1.5 R_E. In addition, the outer radiation belt spans from L~3 R_E to L~8 R_E. The status of the outer radiation belt significantly changes on various timescales, and the electron flux of outer radiation belt is dependent on the dynamic imbalance between the electron acceleration and loss processes [6]. Since the magnetospheric compression contributed by strengthened P_dyn can change the structure of the geomagnetic field, it may result in obvious variation in electron phase space density (PSD) in the outer radiation belt. For example, the strengthened P_dyn can increase the anisotropy and perpendicular heating of the radiation belt electrons owing to the conservation of the first adiabatic invariant under the condition of strengthened P_dyn. On the other hand, the more obvious day-night azimuthal asymmetry of the Earth’s magnetic field due to enhanced P_dyn can bring about the drift shell splitting of radiation electrons [7]; the electrons with smaller equatorial pitch angle (PA) drift at smaller radial distances that those with larger equatorial PA [8,9]. This induces the drop out of radiation belts electrons with PA near 90° during geomagnetic disturbance, because they may move from closed to open drift shells. Therefore, the drift shell splitting may also lead to the decrease in PSD of radiation belt electrons.

We can see that the P_dyn plays important roles in both energization and loss of radiation belt electrons, its influence on electron PSD is very complex due to the competition of various mechanisms. Using multi-satellite simultaneous observations, Xiang et al. (2016) analyze the delay of the electron radiation belt during a more intense P_dyn pulse [10]. Zong et al. (2022) suggest that the ultra-low frequency waves related to solar wind pulses affect the evolution of the electron radiation belt [11]. Smirnov et al. (2022) present an empirical model of the equatorial electron pitch angle distributions in the outer radiation belt, the model can be used for converting the long-term data sets of electron fluxes to PSD in terms of adiabatic invariants [12].

Test particle simulation is a useful method to analyze the motion of the charged particle in the magnetosphere, especially under the condition of varying magnetic and electric fields. For example, using test particles simulation, Ukhorskiy et al. (2006) suggest that the evolution of the magnetic field is one of the principal factors governing the global behavior of the storm time electron belt [13], Saito et al. (2010) examine the drift loss of relativistic electrons by magnetopause shadowing and suggest that magnetopause shadowing actually causes the loss of the outer radiation belt [14], Califf et al. (2017) proved that the measured electric fields can account for the energization of electrons up to at least 500 keV in the slot region through inward radial transport [15]. Wang et al. (2017) observed that a convective electric field penetrating into the inner magnetosphere can produce zebra striped structures of ions and electrons, whose time evolution is determined by the total drift velocity of ions and electrons [16].

In this study, unlike most previous studies on test particles simulation, we use the IGRF (internal source field) and T96 (external source field, controlled by solar wind parameters) magnetic field models for magnetospheric magnetic field construction instead of using the ideal dipole magnetic field model [17]. Using the group test particle simulations, we simulated the adiabatic motion of radiation belt electrons under a case of very intense P_dyn on 19 December 2015, and further analyzed the PSD evolution of the outer radiation belt electrons near noon side. Combining the observation of Van Allen Probe, we find that the PSD of outer radiation belt electrons evolving towards different states under different levels of P_dyn, and the adiabatic motions of radiation belt electrons can roughly explain the variation of outer radiation belt electron PSD under P_dyn, although the whistler mode waves also play a little role in the electron with lower energies. These results can help us understand how PSD of radiation belt electrons responds to intense P_dyn.

2. Data and Methods

2.1. Instrument and Data

In this study, the differential flux of energetic electrons is measured by the Magnetic Electron Ion Spectrometer (MagEIS, NASA, Washington, DC, USA) onboard Van Allen Probe satellites [18]. The Van Allen Probe satellites, which are also called Radiation Belt Storm Probes (RBSP, NASA, USA), were launched on 30 August 2012. These satellites operate around the Earth with a perigee of 1.1 R_E and apogee of 5.8 R_E in the inner magnetosphere [19], so they provided a good opportunity to observe the evolution of the radiation belt. In addition, the 1 min resolution OMNI data (from the Space Physics Data Facility (SPDF) of NASA’s Goddard Space Flight Center, Greenbelt, MA, USA) are utilized to analyze the solar wind parameters, including the interplanetary magnetic field (IMF), P_dyn.

2.2. Event Observations

Figure 1a–c show the overview of solar wind parameters and geomagnetic indices for the event which occurred from 04:39:26 UT on 19 December 2015 to 07:30:47 UT on 20 December 2015. Following the sudden increase of P_dyn (from ~2 nPa to ~10 nPa) at 16:30 UT on 19 December 2015, the SYM−H increased from ~−8 nT to 20 nT, and a substorm is triggered (as shown in Figure 1a). At 18:07 UT on 19 December, the P_dyn rises sharply for the second time (from 8 nPa to 22 nPa), which also triggered a substorm. As shown in Figure 1a,b, during the time interval, there is a distinct enhancement of the SYM−H index, and the z-component of IMF basically shows a positive value. Figure 1d shows the calculated distance between the Geocenter and magnetopause under the subsolar position. A function form as below is used to model the subsolar point of magnetopause [20,21]:

$$R_0=12.544{\left({\mathrm{P}}_{\mathrm{dyn}}+{\mathrm{P}}_{\mathrm{mag}}\right)}^{-0.194}\left[1+0.305\times \frac{exp\left(0.0573\times B_z\right)-1}{exp\left(2.178\times B_z\right)+1}\right]$$

(1)

The calculation suggests that the two sudden enhancements of P_dyn obviously vary the position of magnetopause and intensities of magnetospheric magnetic field. As shown in Figure 1d, the subsolar point of magnetopause decreased from 10.8 R_E to 7.4 R_E while the first increase of P_dyn took place around 16:30 UT on 19 December 2015, and its position further decreased from 8.5 R_E to 6.6 R_E while the second increase of P_dyn around 18:07 UT on 19 December 2015.

The red and blue curves in Figure 1e indicate the magnetic local time (MLT, h) and L in RBSP-A orbit during the time interval. Figure 1f–i exhibits the electron differential flux with energies of 464.4 keV, 593 keV, 741.6 keV and 901.8 keV observed by RBSP-A, respectively. It implies that the fluxes and anisotropies of radiation belt electrons notably change under the contribution of strengthened P_dyn. Comparing with the PSDs of radiation belt electrons observed by RBSP-A during the first outbound orbit (indicated by the first black box while quiet P_dyn), the electron anisotropies with all energy levels RBSP-A during the second outbound orbit of RBSP-A (indicated by the second black box, affected by the first sudden increase of P_dyn) obviously increase. The differential fluxes of electrons with larger PA near 90° evidently raise, and the differential fluxes of electrons along the geomagnetic field line decrease. Interestingly, during the third outbound orbit of RBSP-A (indicated by the third black box, affected by the second sudden increase of P_dyn), the electron PSDs corresponding to all PAs and energy levels dramatically decrease, it seems that a huge amount of radiation belt electrons have been lost.

2.3. The Method of Test Particle Simulation

Then, we use group test particle simulations to analyze the evolution of radiation belt electron PSD under the action of intense P_dyn, and we simulate the particle drift motions about 40 minutes. Here, the first and second adiabatic invariants of electrons are considered conserved in the simulation. In order to exhibit the influence of intense P_dyn on the structure of the geomagnetic field, the tracing of geomagnetic field lines and corresponding field intensities are calculated by IGRF and T96 models. In order to reflect the change of the geomagnetic field from the quiet period to the disturbance period in the short time, we consider this change to be dynamic and approximately monotonic. The constructed magnetospheric magnetic field of the Earth is dynamically changed by the time-varying geomagnetic and solar wind parameters. In addition to varied magnetic fields, the motions of electrons are also contributed by the magnetospheric electric field, here we adopt stationary co-rotating electric field (E_r) and dynamic convection electric field (E_c) [22].

The E_r is expressed as follows:

$${\mathit{E}}_{\mathit{r}}=-\left({\omega }_E\times L\right)\times {\mathit{B}}_{\mathbf{0}}$$

(2)

where ω_E is the angular velocity of Earth’s rotation, B₀ is the magnetic fields in the magnetic equator.

The E_c is described by the Volland–Stern potential field [23,24,25]. This convective electric field model considers the influence of the solar wind on the magnetospheric electric field and is widely used. The potential field formula as follows:

$${\mathit{E}}_{\mathit{c}}=-\mathbf{\nabla }\Phi$$

(3)

where Φ is convection electric potential,

$$\Phi =\frac{0.12\times E_{sw}\times r^2\times \sin \left(\varphi \right)}{6.62\times {\mathrm{R}}_e} \left[V\right]$$

(4)

where E_sw is solar wind electric field, ϕ is geomagnetic longitude (ϕ = 0° corresponds to MLT = 0 h, ϕ = 90° corresponds to MLT = 6 h).

Using the above models, we calculate the motions of electrons as the combination of velocity due to gradient, curvature and E × B drifts [26,27]. The arbitrarily local velocity of gradient and curvature drift is expressed as:

$${\mathit{V}}_{\mathit{G}\mathit{C}}={\mathit{V}}_{\mathit{G}}+{\mathit{V}}_{\mathit{C}}=\frac{m}{q{B}^3}\left(\frac{v_{\perp }^2}{2}+v_{\parallel }^2\right)\mathit{B}\times {\mathbf{\nabla }}_{\perp }B+\frac{m{v}_{\parallel }^2}{q{B}^2}{\left(\mathbf{\nabla }\times \mathit{B}\right)}_{\perp }$$

(5)

where m as the relativistic mass $m=m_0\times \gamma$ (m₀ is rest mass; the Lorentz factor,$\gamma ={\left(1-{\left( v/c\right)}^2\right)}^{-\frac{1}{2}}$.

Then the bounce-averaged velocity of gradient and curvature drift is expressed as:

$$\langle {\mathit{V}}_0\rangle =\frac{1}{{\tau }_b}{{\displaystyle \int }}_0^{{\tau }_b}{V}_{GC}dt=\frac{2}{{\tau }_b}{{\displaystyle \int }}_{s_m^{\prime }}^{s_m}{V}_{GC}\frac{ds}{v_{\parallel }\left(\mathrm{s}\right)}$$

(6)

where τ_b indicates the bouncing period,

$${\tau }_b=2{{\displaystyle \int }}_{s_m^{\prime }}^{s_m}\frac{ds}{v_{\parallel }\left(s\right)}$$

(7)

Considering the contribution of magnetospheric electric field, the bounce-averaged velocity of the electron is assumed as:

$$\langle \mathit{V}\rangle =\langle {\mathit{V}}_{\mathbf{0}}\rangle +\frac{{\mathit{E}}_{\mathbf{0}}\times {\mathit{B}}_{\mathbf{0}}}{{\left|{\mathit{B}}_{\mathbf{0}}\right|}^2}$$

(8)

where E₀ and B₀ indicates the electric and magnetic fields in the magnetic equator, respectively.

As an example, the trajectories of radiation belt electrons under the condition of SYM−H = 12.47 nT, P_dyn = 7.94 nPa, B_ygsm = −3.56 nT, B_zgsm = 7.20 nT are shown in Figure 2. These electrons are emitted into the position with MLT ~0 h and L ~5 R_E. The blue (red) curve indicates the trajectory of electron with initial energy ~600 keV and PA ~10° (60°). It takes about 10 min for these electrons to drift from midnight to noon. In addition, we can see that the electrons with larger initial PA drift to higher L shells on the dayside. As the adiabatic invariant conservation during the drift process, the electron with initial energy ~600 keV and PA ~10° evolves to one with energy ~280 keV and PA ~15° while it drifts to noon. On the other hand, the electron with initial energy ~600 keV and PA ~60° evolves to one with energy ~512 keV and PA ~85° while it drifts to noon. We can see that both the energies and PA of radiation belt electrons significantly change due to intense P_dyn driven distortion of the geomagnetic field.

By simulating the simulated magnetic field from IGRF and T96 magnetic field models under different geomagnetic conditions, we find that there is a difference between the simulated geomagnetic field and observed values under strong P_dyn. In order to match the magnetic field intensity data observed by RBSP-A, we made some simple modifications for the input parameters of the T96 model. For the event from 14:00 UT to 18:05 UT on 19 December 2015, the real time SYM−H, B_ygsm, B_zgsm, and three times P_dyn are used as input parameters for the T96 model. The observed and modeled magnetic field intensities along the trajectory of RBSP-A are shown in Figure 3. The black curve displays the magnetic field intensities (B_A2) observed by RBSP-A during the second outbound orbit, the blue discrete circles display the magnetic field intensities (B_mo) simulated by inputting the original geomagnetic parameters, and the red discrete circles display the magnetic field intensities (B_mc) simulated by inputting three times the P_dyn. We can see that the B_A2 is much larger than B_mo, which is obtained with input from the original geomagnetic parameters. On the other hand, the B_mc is basically consistent with the observed magnetic field. So, the SYM−H, B_ygsm, B_zgsm, and three times P_dyn are used as input parameters of the T96 model in the following simulation.

In order to investigate the mechanism of PSD evolution, we used group test particle simulations to simulate the variation of electron PSD under the action of intense P_dyn on 19 December 2015. We consider the distribution of flux is uniform over the MLT during quiet periods of geomagnetic. In order to obtain the initial electron flux distribution function (during quiet period of P_dyn), the observed differential flux of energetic electrons (at each energy channel measured by RBSP-A) from ~6:20 UT to ~9:10 UT (while the P_dyn is relatively low, the first outbound orbit indicated in Figure 1) as a function of L shell is fitted with the summation of several Maxwellian functions. Then, the fitted flux distribution is interpolated at 1 keV steps (from 400 keV to 900 keV). The distribution achieved by the above method is considered as the initial energetic electron distribution. Moreover, the initial electron flux is assumed to be the same at different MLTs. Then the test particles are emitted into the time-varying magnetic and electric fields. If the particles drift out of the model magnetopause, the particles are considered as a loss.

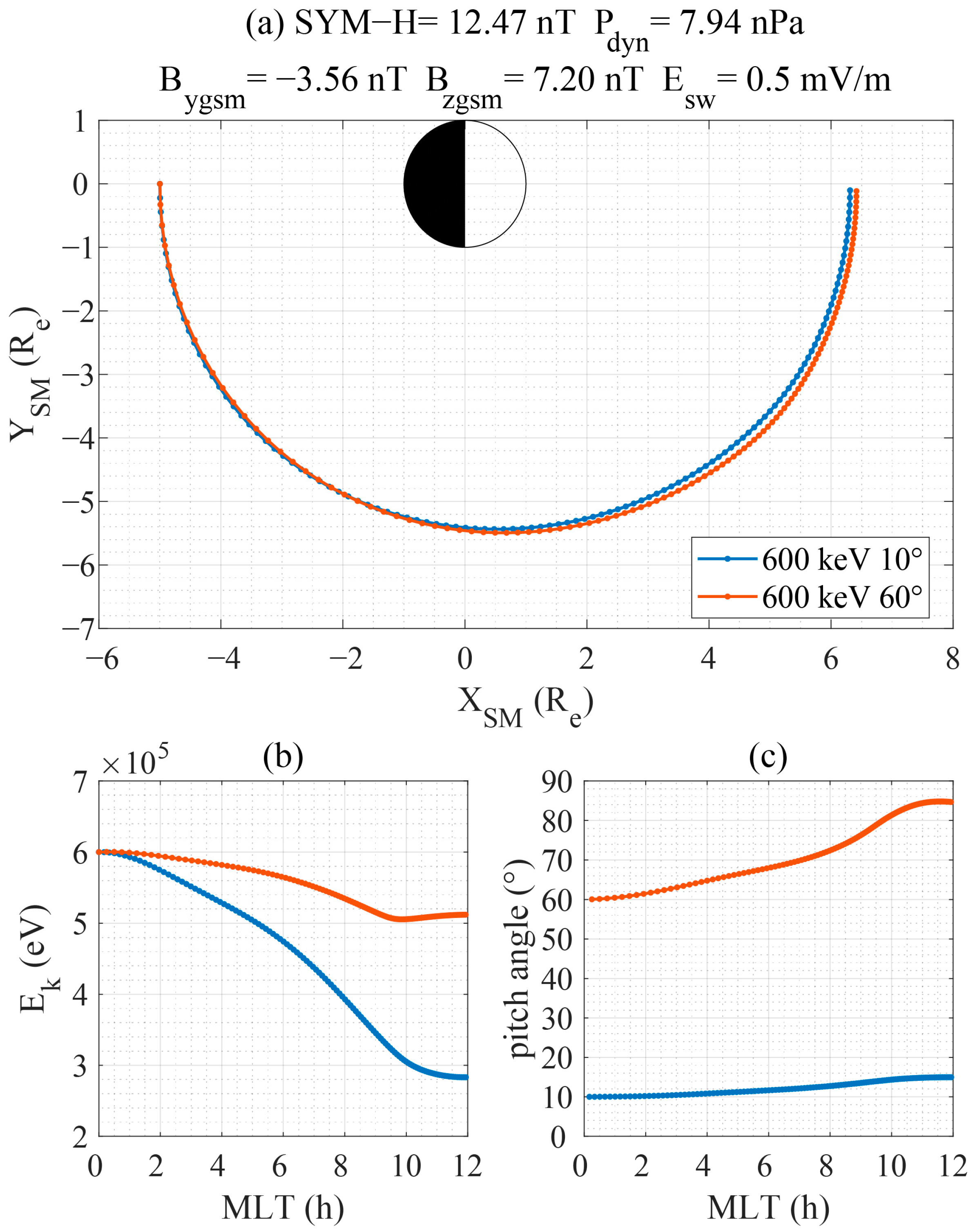
3. Results

Figure 4 shows the evolution of equatorial electron PSD (averaged from L ~5.4 R_E to L ~5.8 R_E) in the outer radiation belt as functions of PA and energy. Figure 4a shows the PSD (with energy from 450 to 770 keV, and PA from 0° to 90°) observed by RBSP-A during the first outbound orbit from 7:50 UT to 8:50 UT on 19 December 2015. It seems that the electrons with all energy levels display anisotropic distribution. Figure 4b shows the PSD observed by RBSP-A during the second outbound orbit from 16:20 UT to 17:15 UT on 19 December 2015. We can see that more electrons gather around PA ~90°, especially for the electrons in higher energy levels. On the other hand, the PSD of electrons with lower PAs is lower. Figure 4c shows the result of equatorial PSD from group test particle simulations under the action of realistic P_dyn from 16:10 UT to 16:40 UT. In the simulated model, the motions of electrons are assumed as adiabatic. It implies that the adiabatic motions of group test particles affected by intense P_dyn can roughly match the evolution of electron PSD from observation. Both the observation and simulation suggest that the anisotropies of electrons obviously increase.

In order to explain it better, Figure 4d shows the anisotropy A_T as a function of energy from observations and test particle simulations. For electrons with energies of several hundreds keV, the relativistic effect needs to be considered, in this condition, the thermal pressure tensor ($P$) can be defined by the following formula [28,29,30,31]:

$$P_{ij}=\int v_i{p}_{j}f\left(\mathit{p}\right)d^3\mathit{p}=\int \mathsf{\gamma }{m}_0{v}_i{v}_{j}f\left(\mathit{v}\right)d^3\mathit{v};i,j\in \left(x,y,z\right)$$

(9)

where the Lorentz factor $\gamma ={\left(1-{\left( v/c\right)}^2\right)}^{-\frac{1}{2}}$; $f\left(\mathit{p}\right)$ is a function of the PSD associated with the momentum $\mathit{p}$, and $P_{zz}=P_{\parallel }; P_{xx,yy}=P_{\perp };P_{\mathrm{ij},\mathrm{i}\ne \mathrm{j}}=0$; $f\left(\mathit{v}\right)$ is a function of the PSD associated with the particle velocity $\mathit{v}$.

Combining the relationship between the thermal pressure tensor ($\mathit{P}$) and the temperature, $\mathit{P}=n{k}_B\mathit{T}; P_{\parallel }=n{k}_B{T}_{\parallel }; P_{\perp }=n{k}_B{T}_{\perp }$ [28], where $n$ is the hot plasma number density, the parallel and perpendicular temperatures can be defined per the following formulas:

$$T_{\parallel }=\frac{P_{\parallel }}{n{k}_B}=\frac{m_0}{n{k}_B}\int \mathsf{\gamma }{v}_{\parallel }{}^{2}f\left(\mathit{v}\right)d^3\mathit{v}$$

(10)

$$T_{\perp }=\frac{P_{\perp }}{n{k}_B}=\frac{m_0}{2n{k}_B}\int \mathsf{\gamma }{v}_{\perp }{}^{2}f\left(\mathit{v}\right)d^3\mathit{v}$$

(11)

The anisotropy can be defined as the following formula:

$$A_T=\frac{T_{\perp }}{T_{\parallel }}-1=\frac{\frac{m_0}{2n{k}_B}\int \mathsf{\gamma }{v}_{\perp }{}^{2}f\left(\mathit{v}\right)d^3\mathit{v}}{\frac{m_0}{n{k}_B}\int \mathsf{\gamma }{v}_{\parallel }{}^{2}f\left(\mathit{v}\right)d^3\mathit{v}}-1=\frac{\int \mathsf{\gamma }{v}_{\perp }{}^{2}f\left(\mathit{v}\right)d^3\mathit{v}}{2\int \mathsf{\gamma }{v}_{\parallel }{}^{2}f\left(\mathit{v}\right)d^3\mathit{v}}-1$$

(12)

According to the Equation (12), when the PSD distribution of particle is isotropic, $A_T=0$.

The blue curve in Figure 4d indicates the averaged anisotropies of electron PSD in the outer radiation belt (averaged PSD from L ~5.4 R_E to L ~5.8 R_E) calculated from the observation from RBSP-A during the first outbound orbit from 7:50 UT to 8:50 UT on 19 December 2015. There is a slight upward trend of anisotropy with the increase in electron energy levels. The anisotropy for the electrons with energy ~464 keV is 0.18, and it is 0.21 for the electrons with energy ~742 keV. The red curve indicates the averaged anisotropies calculated from the observation of RBSP-A during the second outbound orbit from 16:20 UT to 17:15 UT on 19 December 2015, and the yellow curve indicates the corresponding anisotropies calculated from the test particle simulation result. Both observation and simulation results suggest that the anisotropies obviously increase. The enhancement of anisotropies is more notable for the electrons with higher energy levels, for example, the anisotropies of the electron with energy ~742 keV for both observation and simulation reach >0.7. Two mechanisms verified by the test particle simulation can explain the enhancement of anisotropy: (1) the enhanced magnetospheric compression due to strong P_dyn causes the perpendicular heating owing to conservation of the first adiabatic [32,33], (2) the enhanced z component of the magnetic field can cause the particles with high initial equatorial PA and mirror at high latitudes without passing through the equator, which is called as Shabansky orbits [34]. These also cause the enhancement of electron anisotropy near the geomagnetic equator.

Moreover, the anisotropies calculated from observation is slightly higher than that calculated from simulation result at lower energy channels (~462 keV to ~514 keV), it maybe because that electron PA scattering driven by whistler mode waves can transport the energetic electrons into the loss cone [35]. For example, chorus waves can cause efficient pitch angle scattering of electrons of 10 keV~1 MeV near the loss cone at a rate of the order of 10⁻³ s⁻¹ [10]. However, the process of wave particle interaction is not considered in our simulation.

While 18:07 UT on 19 December 2015, the P_dyn further increase based on the previous. The P_dyn reaches a very high level, about 22 nPa. Following the further enhancement of P_dyn, the position of magnetopause reduces to 6.69 R_E. From 18:07 UT to 22:35 UT, the RBSP-A operates with the inbound orbit (from apogee to perigee) on the afternoon side, so it hardly observes the variation in electron PSD in the outer radiation belt during the time interval. However, during the next outbound from 00:10 UT to 03:10 UT on 20 December, RBSP-A detected obvious dissipation with all PAs and energies (as shown in Figure 1), which maybe owing to the further enhancement of the compressed geomagnetic field and the reduction of magnetopause position.

Similar to Figure 4, the high-energy electron PSD evolution for L = 5.4 R_E to 5.8 R_E is shown in Figure 5 for the second P_dyn enhancement. Figure 5a displays the PSD observed by RBSP-A during the orbit from 16:20 UT to 17:15 UT on 19 December. Figure 5b shows the PSD observed by RBSP-A during the third outbound orbit from 01:38 UT to 02:30 UT on 19 December 2015. We can see that the PSD of electrons with energies from 450 keV to 770 keV is reduced more than three times. Figure 5c shows the result of equatorial PSD from group test particle simulations under the action of realistic P_dyn. In the simulated model, the motions of electrons are assumed adiabatic. It implies that the adiabatic motions of group test particles affected by intense P_dyn can roughly match the evolution of electron PSD from observation. Under the action of intense P_dyn, the electrons drift towards higher L shells on the dayside. Since the position of magnetopause decreased to 6.69 R_E, a large number of electrons drift outside the magnetopause and loss into the interplanetary space. Figure 5d shows the variation in the anisotropy during this process. Compared to the variation during the second orbit, the electron PSD during the third orbit shows a significant reduction in the value of anisotropy at all energy levels. In addition, it seems that the higher the energy levels, the greater the decrease. The results of the test particle simulations show the same phenomenon.

4. Discussion

The evolution of energetic electrons in the inner magnetosphere is influenced by many mechanisms [36,37,38], including plasma sheet electron injections, wave-particle interactions, outward transport, magnetopause shadowing and changes in the structure of the geomagnetic field [39,40,41,42,43]. For radiation belt electrons, non-adiabatic processes are primarily associated with energy and momentum transfer during interactions with various magnetospheric waves [44,45,46,47]. In some previous studies on the wave-particle interaction of inner magnetospheric particles, for example, using multi-satellite simultaneous observations, Turner et al. (2014) show direct evidence of the competitive nature of different wave-particle interactions controlling the electron radiation belt relativistic electron fluxes [38].

Although non-adiabatic processes are very important and may play leading roles in radiation belt evolution in a lot of conditions. In this study, we mainly analyze the adiabatic processes in the condition that the structure of magnetospheric magnetic fields obviously change in a short time interval. As the strengthened P_dyn alters the structure of the geomagnetic field, this can change the drift shells, energy and PA of charged particles. This can result in acceleration and heating of electrons. In addition, the compression of geomagnetic field under the action of P_dyn can lead to the outward radial diffusion of energetic particles, especially for the energetic particles with high PAs. These energetic particles may drift outside the magnetopause and loss into the interplanetary space. Ni et al. (2016) suggests that the occurrence rate of outer-zone relativistic electron butterfly distribution is closely related to the intensity of P_dyn, because the intense P_dyn can lead to obvious loss of relativistic electrons with PAs near 90° [48].

In the study, using the method of group test particle simulations, an example from 04:39:26 UT on 19 December 2015 to 07:30:47 UT on 20 December 2015 is analyzed to investigate the adiabatic evolution process of energetic electrons (from 450 keV to 770 keV) in the inner magnetosphere under the action of strong P_dyn. During this event, we focused on the two enhancements in the P_dyn. The P_dyn enhancement leads to the earthward compression of the magnetopause, and the structure of geomagnetic field is obviously changed. Fortunately, the apogee of the RBSP-A was located at L ~5.9 R_E and MLT ~12 h, it provides a good opportunity to observe the evolution of relativistic electron PSD in the outer radiation belt. The result suggests that there is a significant difference in the particle PSD evolution under the two P_dyn enhancements.

In the first stage, the P_dyn (~7.94 nPa) results in the obvious change in PSD and enhanced anisotropy. The PSD of high PA electrons is enhanced, while the PSD of low PA electrons is reduced, and the higher the energy levels, the larger rise of anisotropy. By performing group test particle simulations during the first stage, we find that with the conservation of the first adiabatic invariant, the enhanced magnetic field causes the acceleration of the electron in the vertical direction. Furthermore, the enhanced z component of magnetic field can cause the Shabansky orbits of electrons. These can lead to a significant rise of anisotropy.

In the second stage, there is a significant reduction in PSD for energetic electrons at all energy levels and PAs under the action of intense P_dyn (~22 nPa). The P_dyn is three times higher than the first, resulting in too much earthward compression of the magnetopause. A large number of electrons move from closed to open drift shells and loss into interplanetary. In addition, the electrons with smaller equatorial PA drift at smaller L shells than those with larger equatorial PA. As a result, a more significant reduction in electron PSD with high PAs is observed, which leads to a reduction in electron anisotropy.

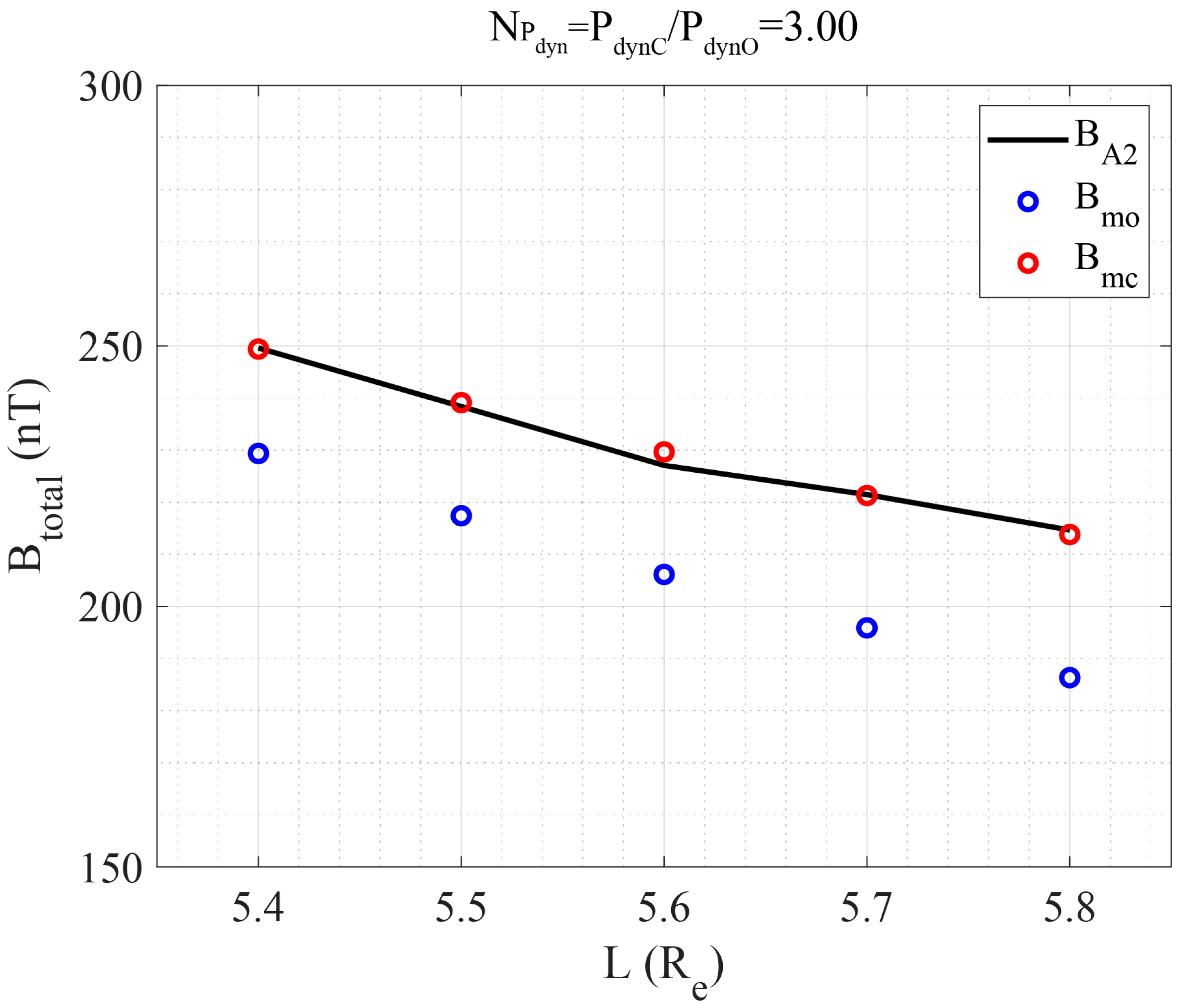
It implies that the particle acceleration mechanism plays a dominant role in the first stage under the action of enhanced P_dyn. On the other hand, the particle loss mechanism plays a dominant role in the second stage. The group test particle simulations of the electron adiabatic process well reproduce the observed PSD evolution.

5. Conclusions

The present study is dedicated to investigate the behaviors of the outer radiation belt electron PSD in response to two intense P_dyn enhancements on 19 December 2015. The PSD observed by RBSP-A and modeled by the group test particle simulations show that the evolution of the electron flux in the Earth’s outer radiation belt is strongly related to the structure of the inner magnetosphere magnetic field. The main conclusions are summarized as follows:

• The electron PSD in the outer radiation belt is sensitive to the change of the geomagnetic field structure, which is controlled by solar wind. The RBSP-A observations on 16:20 UT 19 December 2015 demonstrate that the sharp increase of P_dyn leads to the electron flux in the energy range of 464–901 keV enhance by about 0.3 orders of magnitude within 10 min;
• Under the action of medium P_dyn enhancement (~8 nPa), the electron PSD at high PAs and the energetic electron A_T obviously increases. The increase is more obvious for electrons with higher energy levels;
• Under the action of very intense P_dyn (~22 nPa), the electron PSD at all energy and PAs reduce. The anisotropy also decreases by about 0.25, which is related to the magnetopause shadowing effect.