Superconductivity and Fermi Surface Studies of β″-(BEDT-TTF)2[(H2O)(NH4)2Cr(C2O4)3]·18-Crown-6
Abstract
:1. Introduction
2. Materials and Methods
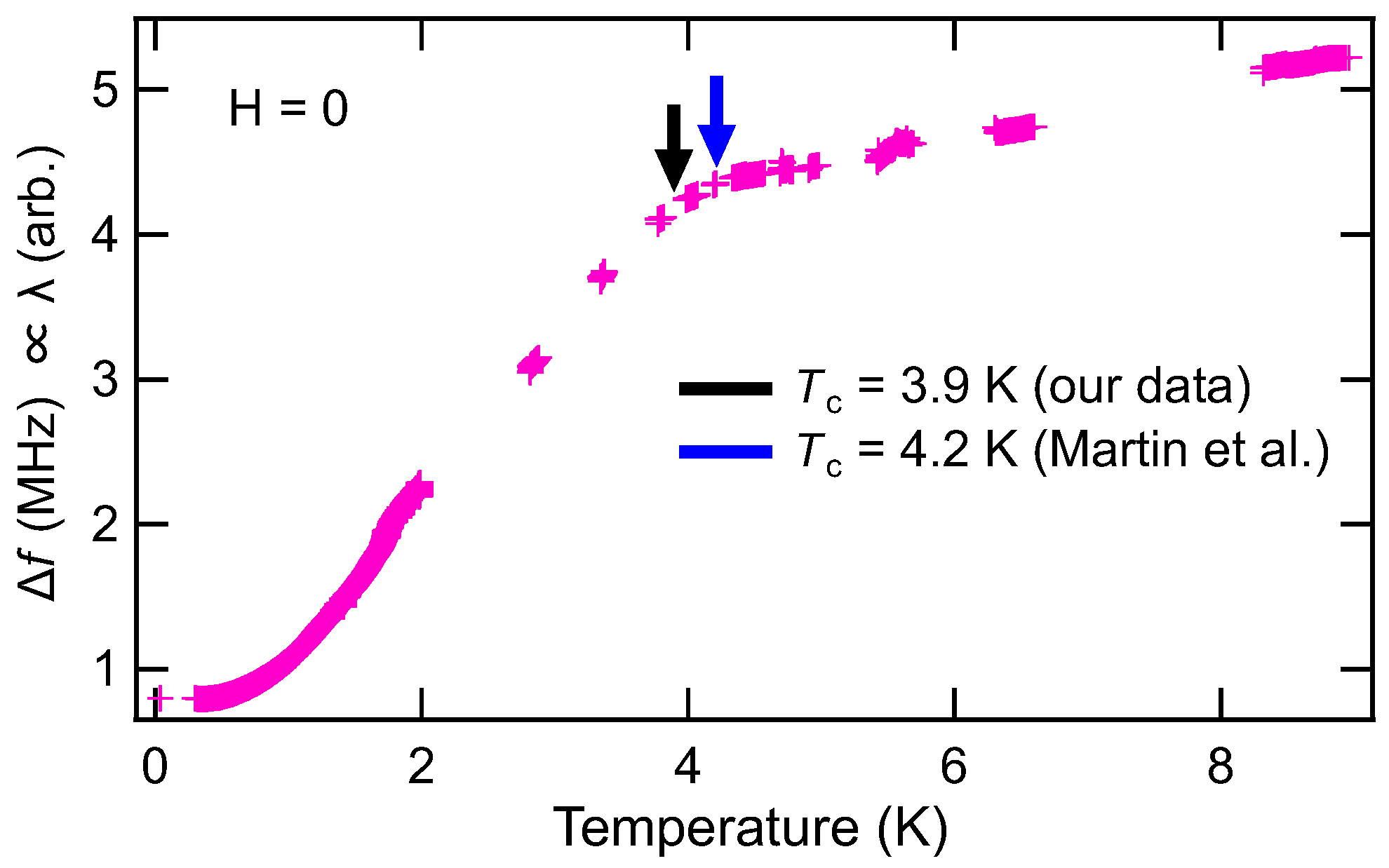
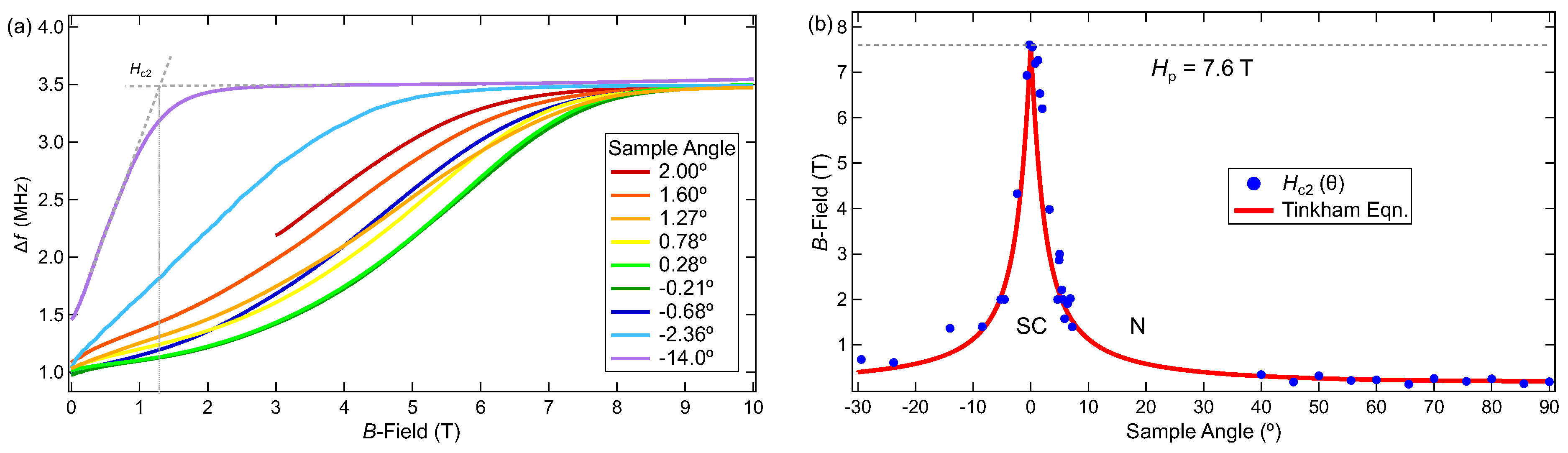
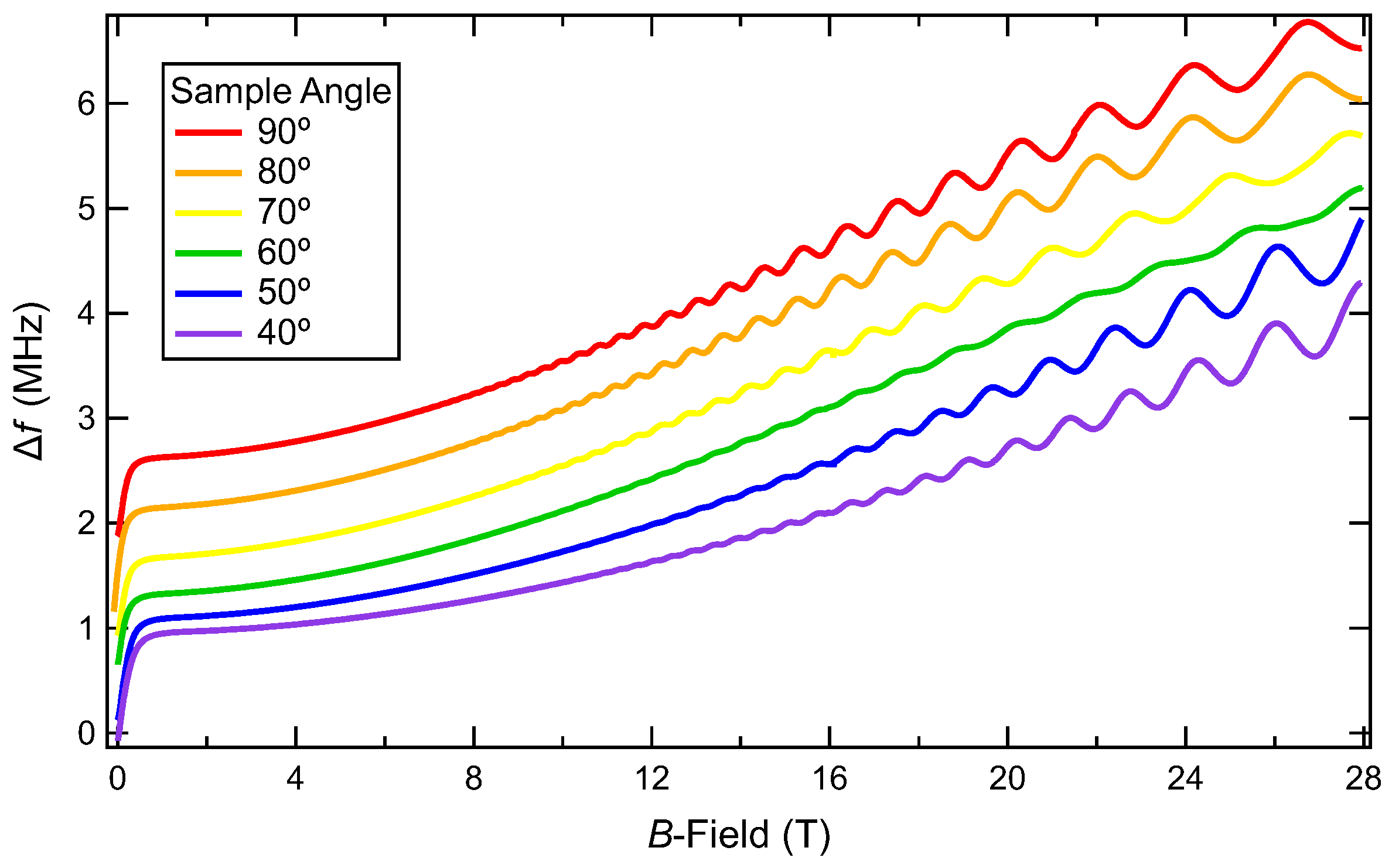
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ishiguro, T.; Yamaji, K.; Saito, G. Organic Superconductors; Springer Series in Solid-State Sciences; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Singleton, J.; Mielke, C. Quasi-two-dimensional organic superconductors: A review. Contemp. Phys. 2002, 43, 63–96. [Google Scholar] [CrossRef] [Green Version]
- Lebed, A. The Physics of Organic Superconductors and Conductors; Springer Series in Materials Sciences; Springer: Berlin/Heidelberg, Germany, 2008; Volume 110. [Google Scholar]
- Martin, L.; Lopez, J.R.; Akutsu, H.; Nakazawa, Y.; Imajo, S. Bulk Kosterlitz–Thouless Type Molecular Superconductor β″-(BEDT-TTF)2[(H2O)(NH4)2Cr(C2O4)3]·18-crown-6. Inorg. Chem. 2017, 56, 14045–14052. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Urayama, H.; Yamochi, H.; Saito, G.; Nozawa, K. A new ambient pressure organic superconductor based on BEDT-TTF with Tc higher than 10 K (Tc= 10.4 K). Chem. Lett. 1988, 17, 55–58. [Google Scholar] [CrossRef]
- Wosnitza, J.; Wanka, S.; Hagel, J.; Häussler, R.; Löhneysen, H.V.; Schlueter, J.A.; Geiser, U.; Nixon, P.G.; Winter, R.W.; Gard, G.L. Shubnikov—De Haas effect in the superconducting state of an organic superconductor. Phys. Rev. B 2000, 62, R11973–R11976. [Google Scholar] [CrossRef] [Green Version]
- Coffey, T.; Martin, C.; Agosta, C.C.; Kinoshota, T.; Tokumoto, M. Bulk two-dimensional Pauli-limited superconductor. Phys. Rev. B 2010, 82, 212502. [Google Scholar] [CrossRef] [Green Version]
- Agosta, C.C. Inhomogeneous Superconductivity in Organic and Related Superconductors. Crystals 2018, 8, 285. [Google Scholar] [CrossRef] [Green Version]
- Mansky, P.; Danner, G.; Chaikin, P. Vortex pinning and lock-in effect in a layered superconductor with large in-plane anisotropy. Phys. Rev. B (Condens. Matter) 1995, 52, 7554–7563. [Google Scholar] [CrossRef] [PubMed]
- Fulde, P.; Ferrell, R.A. Superconductivity in a Strong Spin-Exchange Field. Phys. Rev. 1964, 135, A550–A563. [Google Scholar] [CrossRef]
- Larkin, A.I.; Ovchinnikov, Y.N. Inhomogeneous State of Superconductors. Sov. Phys. JETP 1965, 20, 762. [Google Scholar]
- Maki, K. Effect of Pauli Paramagnetism on Magnetic Properties of High-Field Superconductors. Phys. Rev. 1966, 148, 362–369. [Google Scholar] [CrossRef]
- Mansky, P.A.; Chaikin, P.M.; Haddon, R.C. Evidence for Josephson vortices in κ-(BEDT-TTF)2Cu(NCS)2. Phys. Rev. B 1994, 50, 15929–15944. [Google Scholar] [CrossRef]
- Van Degrift, C.T. Tunnel diode oscillator for 0.001 ppm measurements at low temperatures. Rev. Sci. Instrum. 1975, 46, 599. [Google Scholar] [CrossRef]
- Schneider, T.; Schmidt, A. Dimensional crossover in the upper critical field of layered superconductors. Phys. Rev. B 1993, 47, 5915–5921. [Google Scholar] [CrossRef] [PubMed]
- Shoenberg, D. Magnetic Oscillations in Metals; Cambridge University Press: Cambridge, UK, 1984. [Google Scholar]
- McKenzie, R.H. Wilson’s ratio and the spin splitting of magnetic oscillations in quasi-two-dimensional metals. arXiv 1999, arXiv:9905044. [Google Scholar]
- Taylor, O.J.; Carrington, A.; Schlueter, J.A. Specific-Heat Measurements of the Gap Structure of the Organic Superconductors κ-(BEDT-TTF)2-Cu[N(CN)2]Br and κ-(ET)2Cu(NCS)2. Phys. Rev. Lett. 2007, 99, 057001. [Google Scholar] [CrossRef] [Green Version]
- Mihut, I.; Agosta, C.; Martin, C.; Mielke, C.; Coffey, T. Incoherent Bragg reflection and Fermi-surface hot spots in a quasi-two-dimensional metal. Phys. Rev. B 2006, 73, 125118. [Google Scholar] [CrossRef]
- Müller, J.; Lang, M.; Helfrich, R.; Steglich, F.; Sasaki, T. High-resolution ac-calorimetry studies of the quasi-two-dimensional organic superconductor κ-(BEDT-TTF)2Cu(NCS)2. Phys. Rev. B 2002, 65, 140509. [Google Scholar] [CrossRef] [Green Version]
- Zuo, F.; Su, X.; Zhang, P.; Brooks, J.S.; Wosnitza, J.; Schlueter, J.A.; Williams, J.M.; Nixon, P.G.; Winter, R.W.; Gard, G.L. Anomalous low-temperature and high-field magnetoresistance in the organic superconductor β″-(BEDT-TTF)2SF5CH2CF2SO3. Phys. Rev. B 1999, 60, 6296–6299. [Google Scholar] [CrossRef] [Green Version]
- Sugiura, S.; Terashima, T.; Uji, S.; Yasuzuka, S.; Schlueter, J.A. Josephson vortex dynamics and Fulde-Ferrell-Larkin-Ovchinnikov superconductivity in the layered organic superconductor β″-(BEDT-TTF)2SF5CH2CF2SO3. Phys. Rev. B 2019, 100, 014515. [Google Scholar] [CrossRef]
- Coniglio, W.A.; Winter, L.E.; Cho, K.; Agosta, C.C.; Fravel, B.; Montgomery, L.K. Superconducting phase diagram and FFLO signature in λ-(BETS)2GaCl4 from rf penetration depth measurements. Phys. Rev. B 2011, 83, 224507. [Google Scholar] [CrossRef] [Green Version]
- Tanatar, M.A.; Ishiguro, T.; Tanaka, H.; Kobayashi, H. Magnetic field-temperature phase diagram of the quasi-two-dimensional organic superconductor λ-(BETS)2GaCl4 studied via thermal conductivity. Phys. Rev. B 2002, 66, 134503. [Google Scholar] [CrossRef] [Green Version]
- Mielke, C.; Singleton, J.; Nam, M.S.; Harrison, N.; Agosta, C.C.; Fravel, B.; Montgomery, L.K. Superconducting properties and Fermi-surface topology of the quasi-two-dimensional organic superconductor λ-(BETS)2GaCl4 (BETS=; bis(ethylene-dithio)tetraselenafulvalene). J. Phys. Condens. Matter 2001, 13, 8325–8345. [Google Scholar] [CrossRef] [Green Version]
- Wanka, S.; Beckmann, D.; Wosnitza, J.; Balthes, E.; Schweitzer, D.; Strunz, W.; Keller, H.J. Critical fields and mixed-state properties of the layered organic superconductor κ-(BEDT-TTF)2I3. Phys. Rev. B 1996, 53, 9301–9309. [Google Scholar] [CrossRef] [PubMed]
- Wosnitza, J.; Liu, X.; Schweitzer, D.; Keller, H.J. Specific heat of the organic superconductor κ-(BEDT-TTF)2I3. Phys. Rev. B 1994, 50, 12747–12751. [Google Scholar] [CrossRef] [PubMed]
- Harrison, N.; Mielke, C.H.; Rickel, D.G.; Wosnitza, J.; Qualls, J.S.; Brooks, J.S.; Balthes, E.; Schweitzer, D.; Heinen, I.; Strunz, W. Quasi-two-dimensional spin-split Fermi-liquid behavior of κ-(BEDT-TTF)2I3 in strong magnetic fields. Phys. Rev. B 1998, 58, 10248–10255. [Google Scholar] [CrossRef]
- Wang, H.; Carlson, K.; Geiser, U.; Kwok, W.; Vashon, M.; Thompson, J.; Larsen, N.; McCabe, G.; Hulscher, R.; Williams, J. A New Ambient Pressure Organic Superconductor: (BEDT-TTF)2(NH4)Hg(SCN)4. Physica C 1990, 166, 57–61. [Google Scholar] [CrossRef]
- Brooks, J.S.; Chen, X.; Klepper, S.J.; Valfells, S.; Athas, G.J.; Tanaka, Y.; Kinoshita, T.; Kinoshita, N.; Tokumoto, M.; Anzai, H.; et al. Pressure effects on the electronic structure and low-temperature states in the α-(BEDT-TTF)2MHg(SCN)4 organic-conductor family (M=K, Rb, Tl, NH4). Phys. Rev. B 1995, 52, 14457–14478. [Google Scholar] [CrossRef]
- Padamsee, H.; Neighbor, J.; Shiffman, C. Quasiparticle phenomenology for thermodynamics of strong-coupling superconductors. J. Low Temp. Phys. 1973, 12, 387–411. [Google Scholar] [CrossRef]
- Johnston, D.C. Elaboration of the α-model derived from the BCS theory of superconductivity. Supercond. Sci. Technol. 2013, 26, 115011. [Google Scholar] [CrossRef] [Green Version]
- Werthamer, N.R.; Helfand, E.; Hohenberg, P.C. Temperature and Purity Dependence of the Superconducting Critical Field, Hc2. III. Electron Spin and Spin-Orbit Effects. Phys. Rev. 1966, 147, 295–302. [Google Scholar] [CrossRef]
- Klemm, R.A.; Luther, A.; Beasley, M.R. Theory of the upper critical field in layered superconductors. Phys. Rev. B 1975, 12, 877–891. [Google Scholar] [CrossRef]
- Kotliar, G.; Varma, C.M. Low-Temperature Upper-Critical-Field Anomalies in Clean Superconductors. Phys. Rev. Lett. 1996, 77, 2296–2299. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ovchinnikov, Y.N.; Kresin, V.Z. Critical magnetic field in layered superconductors. Phys. Rev. B 1995, 52, 3075–3078. [Google Scholar] [CrossRef] [PubMed]
- Agosta, C.; Ivanov, S.; Bayindir, Z.; Coffey, T.; Kushch, N.; Yagubskii, E.; Burgin, T.; Montgomery, L. The anomalous superconducting phase diagram of (BEDO-TTF)2ReO4·H2O. Synth. Met. 1999, 103, 1795–1796. [Google Scholar] [CrossRef]
- Wosnitza, J.; Crabtree, G.W.; Wang, H.H.; Geiser, U.; Williams, J.M.; Carlson, K.D. de Haas–van Alphen studies of the organic superconductors α-(ET)2(NH4)Hg(SCN)4 and κ-(ET)2Cu(NCS)2 [with ET = bis(ethelenedithio)-tetrathiafulvalene]. Phys. Rev. B 1992, 45, 3018–3025. [Google Scholar] [CrossRef] [PubMed]

| Crystal Name [Citations] | (K) | (T) | (T) | (T) | (T) | (Å) | (Å) | |
|---|---|---|---|---|---|---|---|---|
| -(ET)Cu(NCS) [18,19,20] | 9.6 | 28 | 6 | 17.6 | 21.6 | 3.5 | 900 | 74 |
| -(ET)SFCHCFSO [6,21,22] | 4.5 | 11 | 1.6 | 2.07 | 9.2 | 2.0 | 520 | 122 |
| -(BETS)GaCl [23,24,25] | 4.3 | 11 | 2.9 | 1.6 | 8.3 | 3.6 | 170 | 107 |
| (ET)Cr [4] | 4.1 | 7.6 | 0.4 | 0.49 | 7.6 | 1.4 | 367 | 286 |
| -(ET)I [26,27,28] | 3.5 | 6.7 | 0.2 | 1.37 | 5.7 | 3.9 | 953 | 410 |
| -(ET)NHHg(SCN) [7,29,30] | 0.96 | 2.1 | 0.12 | 0.05 | 2.1 | 2.5 | 663 | 605 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laramee, B.; Ghimire, R.; Graf, D.; Martin, L.; Blundell, T.J.; Agosta, C.C. Superconductivity and Fermi Surface Studies of β″-(BEDT-TTF)2[(H2O)(NH4)2Cr(C2O4)3]·18-Crown-6. Magnetochemistry 2023, 9, 64. https://doi.org/10.3390/magnetochemistry9030064
Laramee B, Ghimire R, Graf D, Martin L, Blundell TJ, Agosta CC. Superconductivity and Fermi Surface Studies of β″-(BEDT-TTF)2[(H2O)(NH4)2Cr(C2O4)3]·18-Crown-6. Magnetochemistry. 2023; 9(3):64. https://doi.org/10.3390/magnetochemistry9030064
Chicago/Turabian StyleLaramee, Brett, Raju Ghimire, David Graf, Lee Martin, Toby J. Blundell, and Charles C. Agosta. 2023. "Superconductivity and Fermi Surface Studies of β″-(BEDT-TTF)2[(H2O)(NH4)2Cr(C2O4)3]·18-Crown-6" Magnetochemistry 9, no. 3: 64. https://doi.org/10.3390/magnetochemistry9030064
APA StyleLaramee, B., Ghimire, R., Graf, D., Martin, L., Blundell, T. J., & Agosta, C. C. (2023). Superconductivity and Fermi Surface Studies of β″-(BEDT-TTF)2[(H2O)(NH4)2Cr(C2O4)3]·18-Crown-6. Magnetochemistry, 9(3), 64. https://doi.org/10.3390/magnetochemistry9030064








