Magnetic Properties of the Fe2B Alloy Doped with Transition Metal Elements
Abstract
:1. Introduction
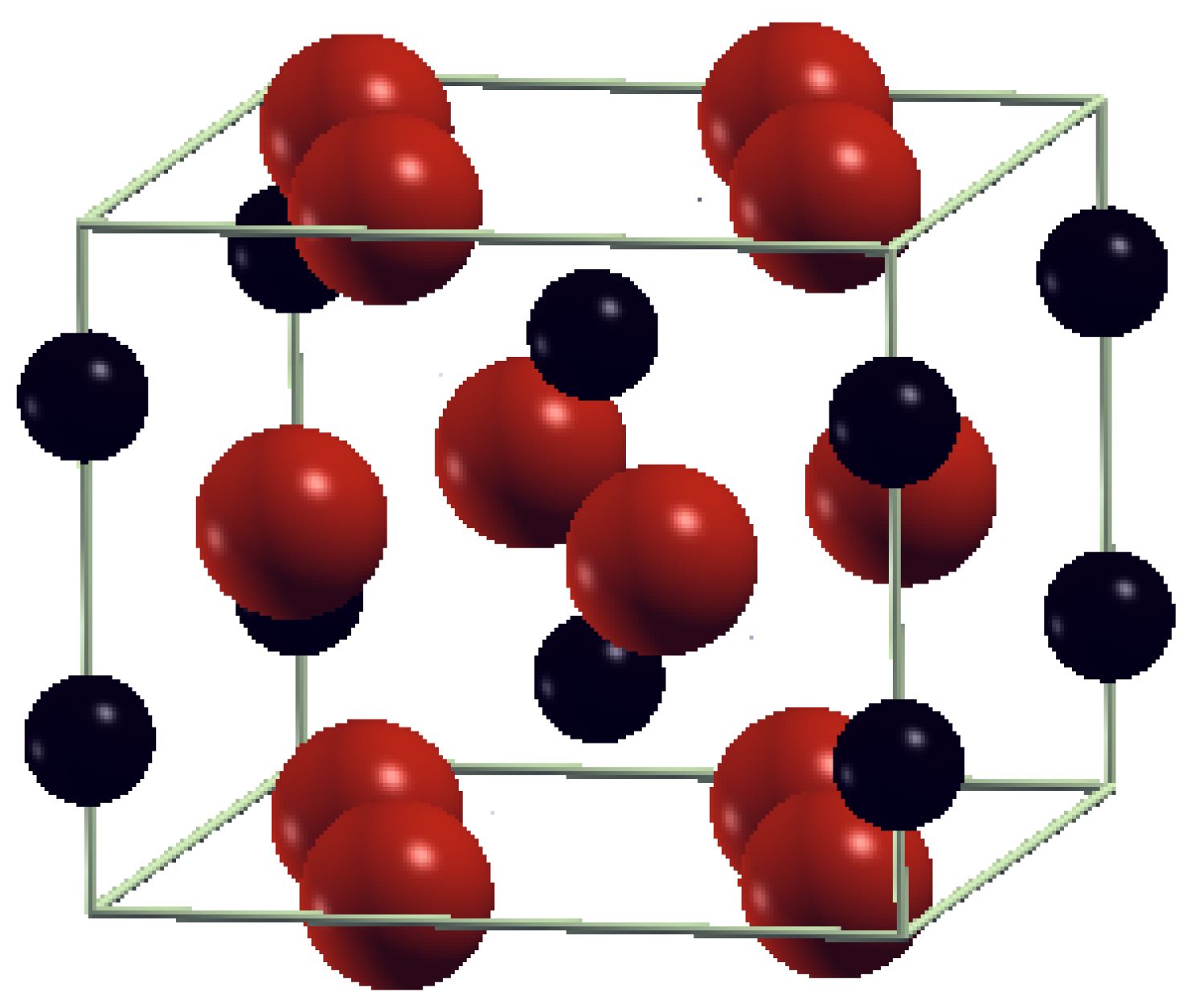
2. Materials and Methods
3. Results and Discussions
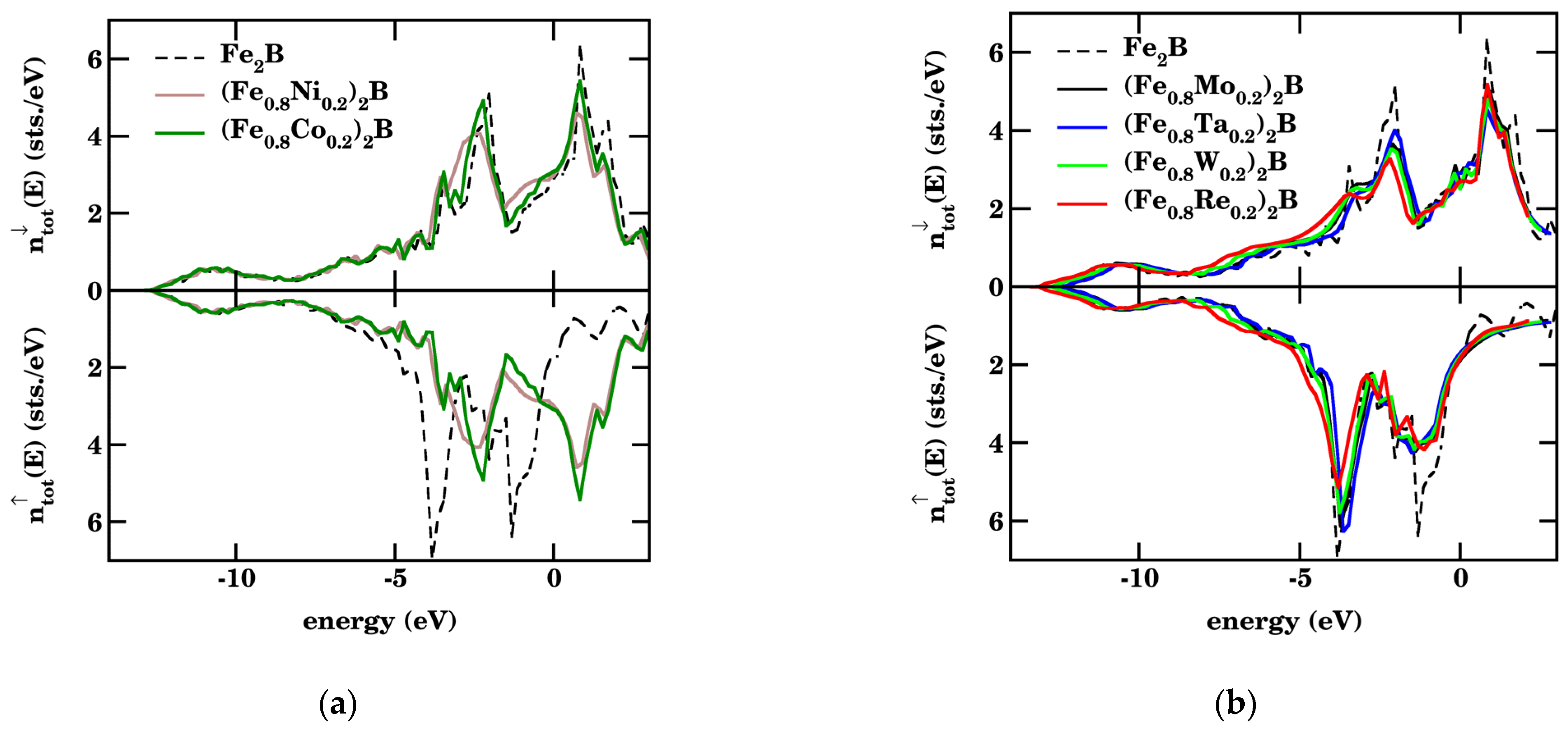
3.1. Density of States Calculations
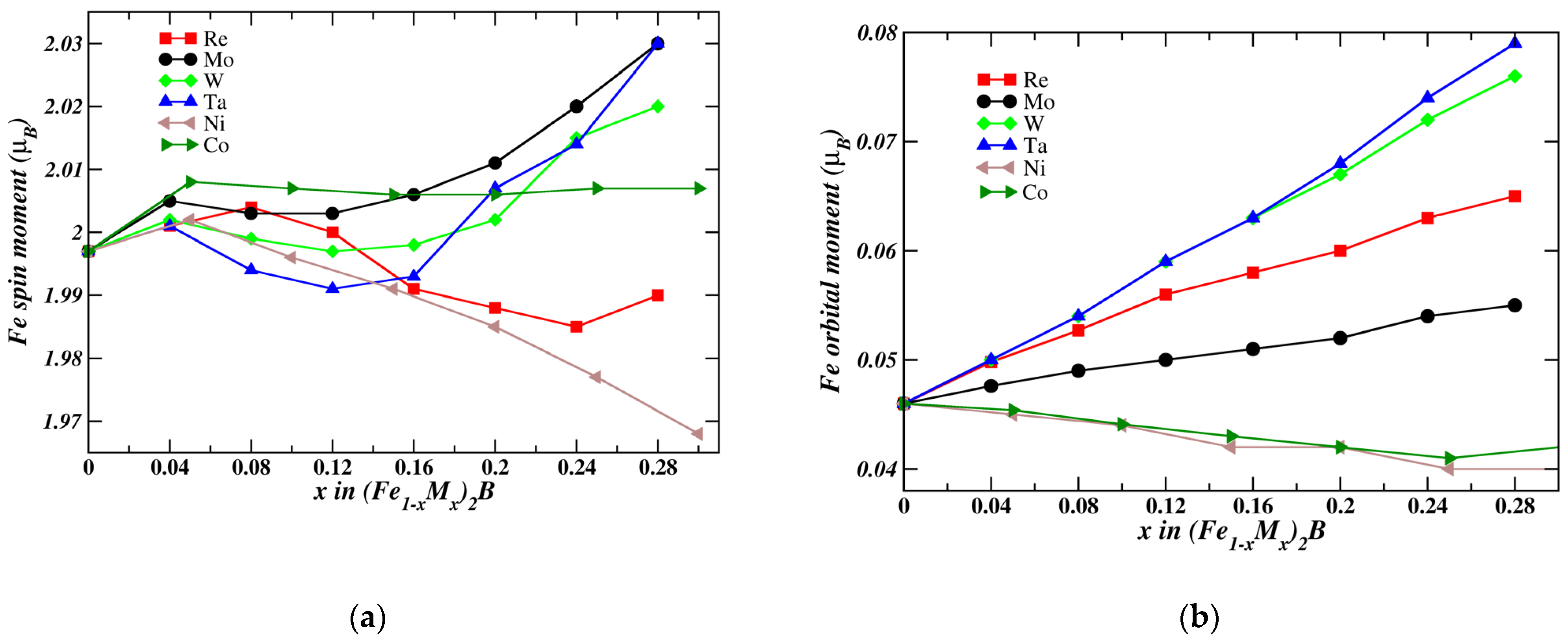
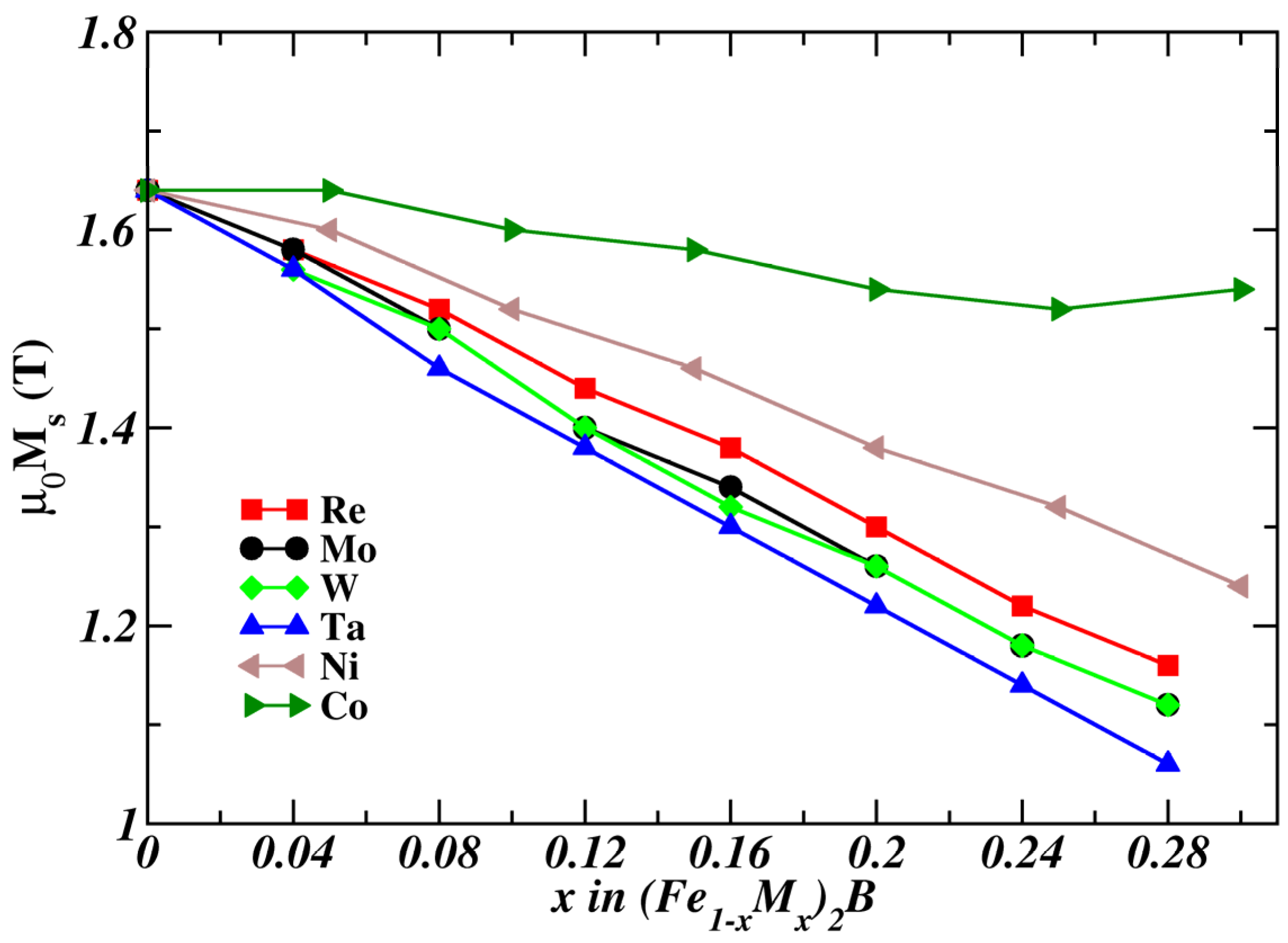
3.2. Magnetic Moments
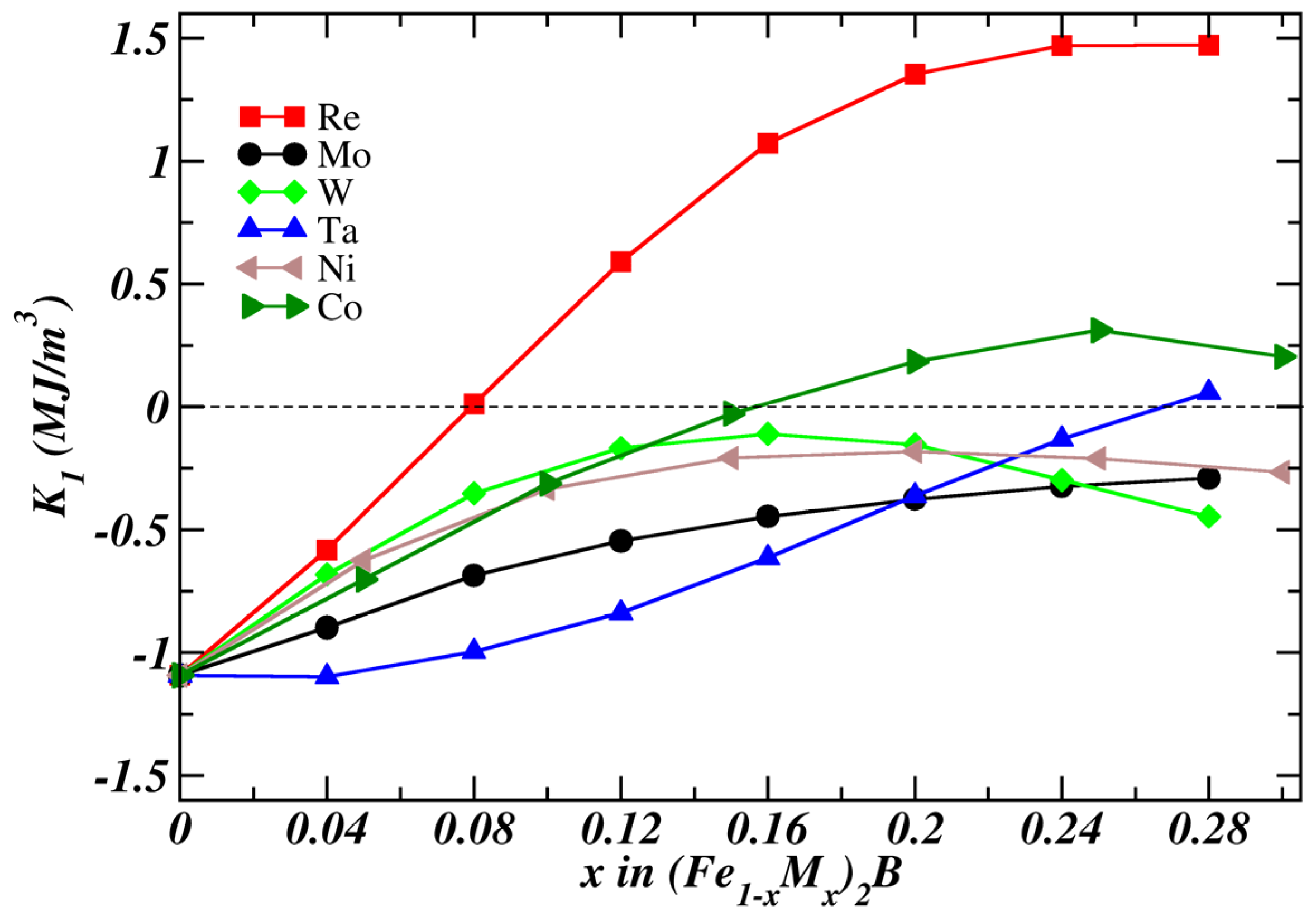
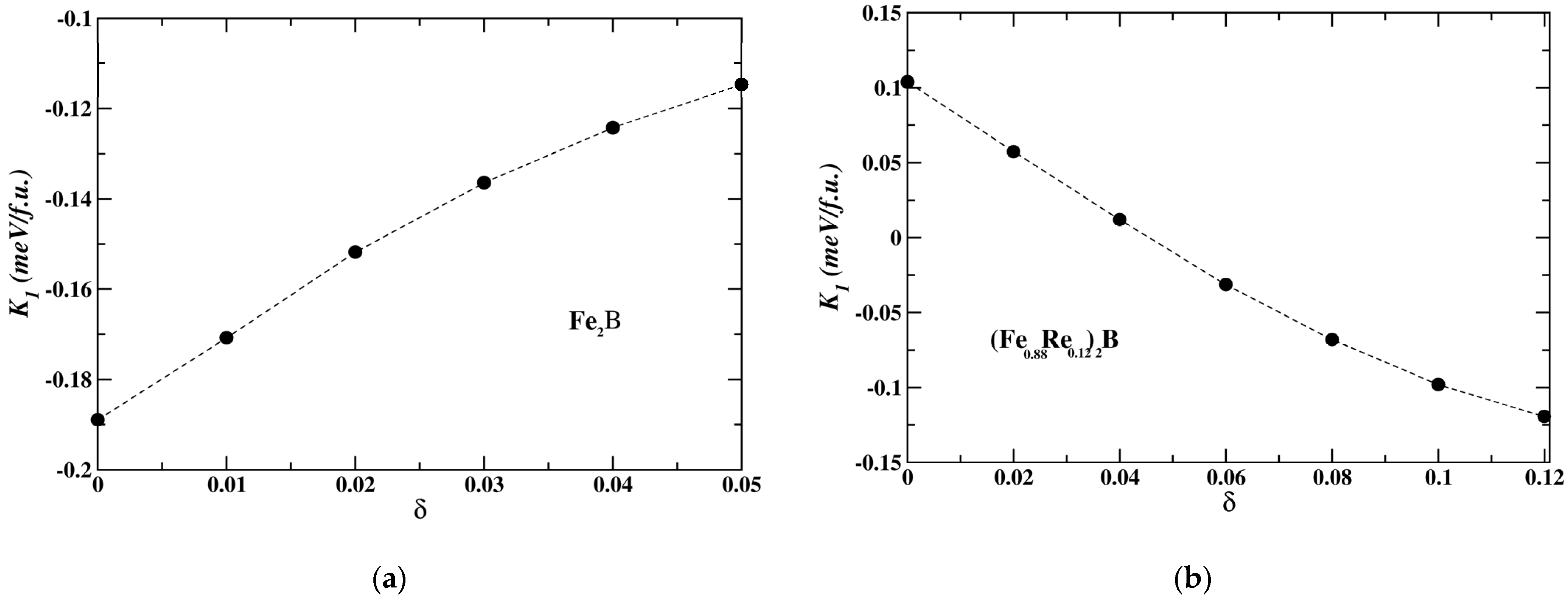
3.3. The Magnetocrystalline Anisotropy Energy (MAE)
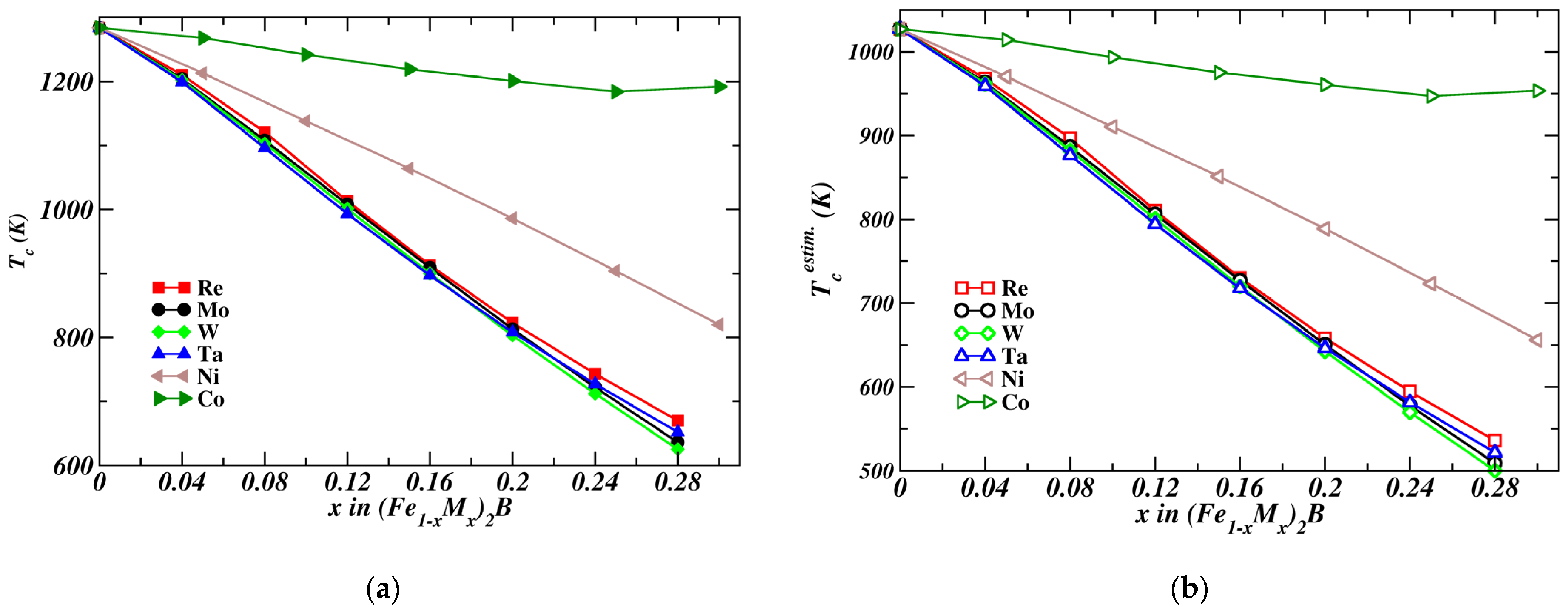
3.4. The Curie Temperatures
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kapfenberger, C.; Albert, B.; Pöttgen, R.; Huppertz, H. Structure refinements of iron borides Fe2B and FeB. Z. Kristallogr. 2006, 221, 477–481. [Google Scholar] [CrossRef]
- Aronsson, B. Borides Part A: Basic Factors. In Modern Materials; Hausner, H.H., Ed.; Elsevier: Amsterdam, The Netherlands, 1960; Volume 2, pp. 143–190. [Google Scholar] [CrossRef]
- Umegaki, T.; Yan, J.; Zhang, X.; Shioyama, H.; Kuriyama, N.; Xu, Q. Preparation and catalysis of poly(N-vinyl-2-pyrrolidone) (PVP) stabilized nickel catalyst for hydrolytic dehydrogenation of ammonia borane. Int. J. Hydrogen Energy 2009, 34, 3816–3822. [Google Scholar] [CrossRef]
- Abrenica, G.H.A.; Ocon, J.D.; Lee, J. Dip-coating synthesis of high-surface area nanostructured FeB for direct usage as anode in metal/metalloid-air battery. Curr. Appl. Phys. 2016, 16, 1075–1080. [Google Scholar] [CrossRef]
- Hamayun, M.A.; Abramchuk, M.; Alnasir, H.; Khan, M.; Pak, C.; Lenhert, S.; Ghazanfari, L.; Shatruk, M.; Manzoor, S. Magnetic and magnetothermal studies of iron boride (FeB) nanoparticles. J. Magn. Magn. Mater. 2018, 451, 407–413. [Google Scholar] [CrossRef]
- Wang, D.; Ma, L.; Li, L.; Xu, X.L.; Guo, Y.B.; Zhao, S.Q. Characterization of Polycrystalline Fe2B Compound with High Saturation Magnetization. J. Supercond. Nov. Magn. 2017, 31, 431–435. [Google Scholar] [CrossRef]
- Jian, H.; Skokov, K.P.; Kuz’Min, M.D.; Radulov, I.; Gutfleisch, O. Magnetic Properties of (Fe,Co)2B Alloys With Easy-Axis Anisotropy. IEEE Trans. Magn. 2014, 50, 2104504. [Google Scholar] [CrossRef]
- Iga, A.; Tawara, Y.; Yanase, A. Magnetocrystalline Anisotropy of Fe2B. J. Phys. Soc. Jpn. 1966, 21, 404. [Google Scholar] [CrossRef]
- Kuz’min, M.D.; Skokov, K.; Jian, H.; Radulov, I.; Gutfleisch, O. Towards high-performance permanent magnets without rare earths. J. Phys. Condens. Matter 2014, 26, 64205. [Google Scholar] [CrossRef]
- Skomski, R.; Coey, J. Magnetic anisotropy—How much is enough for a permanent magnet? Scr. Mater. 2016, 112, 3–8. [Google Scholar] [CrossRef]
- Skomski, R.; Kashyap, A.; Solanki, A.; Enders, A.; Sellmyer, D.J. Magnetic anisotropy in itinerant magnets. J. Appl. Phys. 2010, 107, 09A735. [Google Scholar] [CrossRef]
- Edström, A.; Werwiński, M.; Iuşan, D.; Rusz, J.; Eriksson, O.; Skokov, K.P.; Radulov, I.A.; Ener, S.; Kuz’Min, M.D.; Hong, J.; et al. Magnetic properties of(Fe1−xCox)2Balloys and the effect of doping by5delements. Phys. Rev. B 2015, 92, 174413. [Google Scholar] [CrossRef]
- Ebert, H.; Ködderitzsch, D.; Minar, J. Calculating condensed matter properties using the KKR-Green’s function method—Recent developments and applications. Rep. Prog. Phys. 2011, 74, 096501. [Google Scholar] [CrossRef]
- Faulkner, J.S.; Stocks, G.M. Calculating properties with the coherent-potential approximation. Phys. Rev. B 1980, 21, 3222–3244. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Staunton, J.B.; Szunyogh, L.; Buruzs, A.; Gyorffy, B.L.; Ostanin, S.; Udvardi, L. Temperature dependence of magnetic anisotropy: An ab initio approach. Phys. Rev. B 2006, 74, 144411. [Google Scholar] [CrossRef]
- Mankovsky, S.; Polesya, S.; Bornemann, S.; Minar, J.; Hoffmann, F.; Back, C.; Ebert, H. Spin-orbit coupling effect in (Ga,Mn)As films: Anisotropic exchange interactions and magnetocrystalline anisotropy. Phys. Rev. B 2011, 84, 201201. [Google Scholar] [CrossRef]
- Liechtenstein, A.; Katsnelson, M.; Antropov, V.; Gubanov, V. Local spin density functional approach to the theory of exchange interactions in ferromagnetic metals and alloys. J. Magn. Magn. Mater. 1987, 67, 65–74. [Google Scholar] [CrossRef]
- Nieves, P.; Arapan, S.; Maudes-Raedo, J.; Marticorena-Sánchez, R.; Del Brío, N.; Kovacs, A.; Echevarria-Bonet, C.; Salazar, D.; Weischenberg, J.; Zhang, H.; et al. Database of novel magnetic materials for high-performance permanent magnet development. Comput. Mater. Sci. 2019, 168, 188–202. [Google Scholar] [CrossRef]
- Kokalj, A. XCrySDen—A new program for displaying crystalline structures and electron densities. J. Mol. Graph. Model. 1999, 17, 176–179. [Google Scholar] [CrossRef]
- Ener, S.; Fries, M.; Hammerath, F.; Opahle, I.; Simon, E.; Fritsch, P.; Wurmehl, S.; Zhang, H.; Gutfleisch, O. Magnetic and magnetocaloric properties of the Co2-xMn B system by experiment and density functional theory. Acta Mater. 2018, 165, 270–277. [Google Scholar] [CrossRef]
- Neov, D.; Slavov, L.; Donkov, A.; Mirzayev, M.; Popov, E.; Demir, E.; Siemek, K.; Djourelov, N.; Turchenko, V.; Sharipov, Z.; et al. Structural study of W2B obtained via mechanical alloying of W, B4C, TiC and graphite before and after He ions irradiation. Nucl. Mater. Energy 2022, 31, 101201. [Google Scholar] [CrossRef]
- Havinga, E.; Damsma, H.; Hokkeling, P. Compounds and pseudo-binary alloys with the CuAl2(C16)-type structure I. Preparation and X-ray results. J. Less Common Met. 1972, 27, 169–186. [Google Scholar] [CrossRef]
- Akopov, G.; Yeung, M.T.; Kaner, R.B. Rediscovering the Crystal Chemistry of Borides. Adv. Mater. 2017, 29, 1604506. [Google Scholar] [CrossRef] [PubMed]
- Villars, P.; Calvert, L.D. Pearson’s Handbook of Crystallographic Data for Intermetallic Phases, 2nd ed.; ASM international: Novelty, OH, USA, 1991; Volume 3, p. 1615. [Google Scholar]
- Coene, W.; Hakkens, F.; Coehoorn, R.; de Mooij, D.; de Waard, C.; Fidler, J.; Grössinger, R. Magnetocrystalline anisotropy of Fe3B, Fe2B and Fe1.4Co0.6B as studied by Lorentz electron microscopy, singular point detection and magnetization measurements. J. Magn. Magn. Mater. 1991, 96, 189–196. [Google Scholar] [CrossRef]
- Takacs, L.; Cadeville, M.C.; Vincze, I. Mossbauer study of the intermetallic compounds (Fe1−xCox)2B and (Fe1−xCox)B. J. Phys. F Met. Phys. 1975, 5, 800–811. [Google Scholar] [CrossRef]
- Lawrence, R.A.; Donaldson, S.J.; Probert, M.I.J. Magnetic Transition State Searching: Beyond the Static Ion Approximation. Magnetochemistry 2023, 9, 42. [Google Scholar] [CrossRef]
- Sato, K.; Bergqvist, L.; Kudrnovsky, J.; Dederichs, P.H.; Eriksson, O.; Turek, I.; Sanyal, B.; Bouzerar, G.; Katayama-Yoshida, H.; Dinh, V.; et al. First-principles theory of dilute magnetic semiconductors. Rev. Mod. Phys. 2010, 82, 1633–1690. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benea, D.; Pop, V. Magnetic Properties of the Fe2B Alloy Doped with Transition Metal Elements. Magnetochemistry 2023, 9, 109. https://doi.org/10.3390/magnetochemistry9040109
Benea D, Pop V. Magnetic Properties of the Fe2B Alloy Doped with Transition Metal Elements. Magnetochemistry. 2023; 9(4):109. https://doi.org/10.3390/magnetochemistry9040109
Chicago/Turabian StyleBenea, Diana, and Viorel Pop. 2023. "Magnetic Properties of the Fe2B Alloy Doped with Transition Metal Elements" Magnetochemistry 9, no. 4: 109. https://doi.org/10.3390/magnetochemistry9040109
APA StyleBenea, D., & Pop, V. (2023). Magnetic Properties of the Fe2B Alloy Doped with Transition Metal Elements. Magnetochemistry, 9(4), 109. https://doi.org/10.3390/magnetochemistry9040109





