An Effect of Fe3+ Ion Substitution for Cr3+ in the Octahedral Sites of FeCr2O4 Multiferroic Spinel: Mössbauer Spectroscopy Study
Abstract
:1. Introduction
2. Experimental Part
3. Results and Discussion
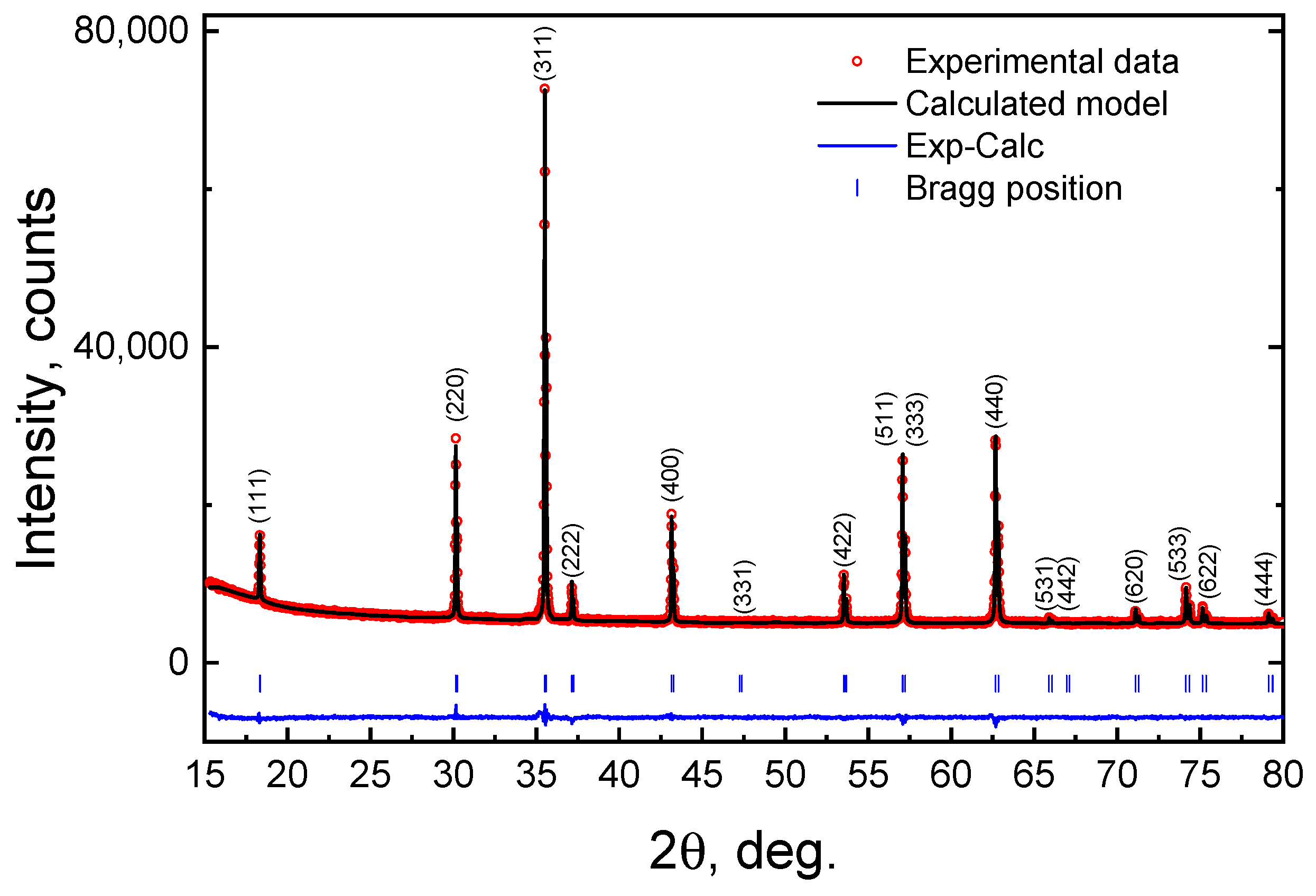
3.1. Powder X-ray Diffraction
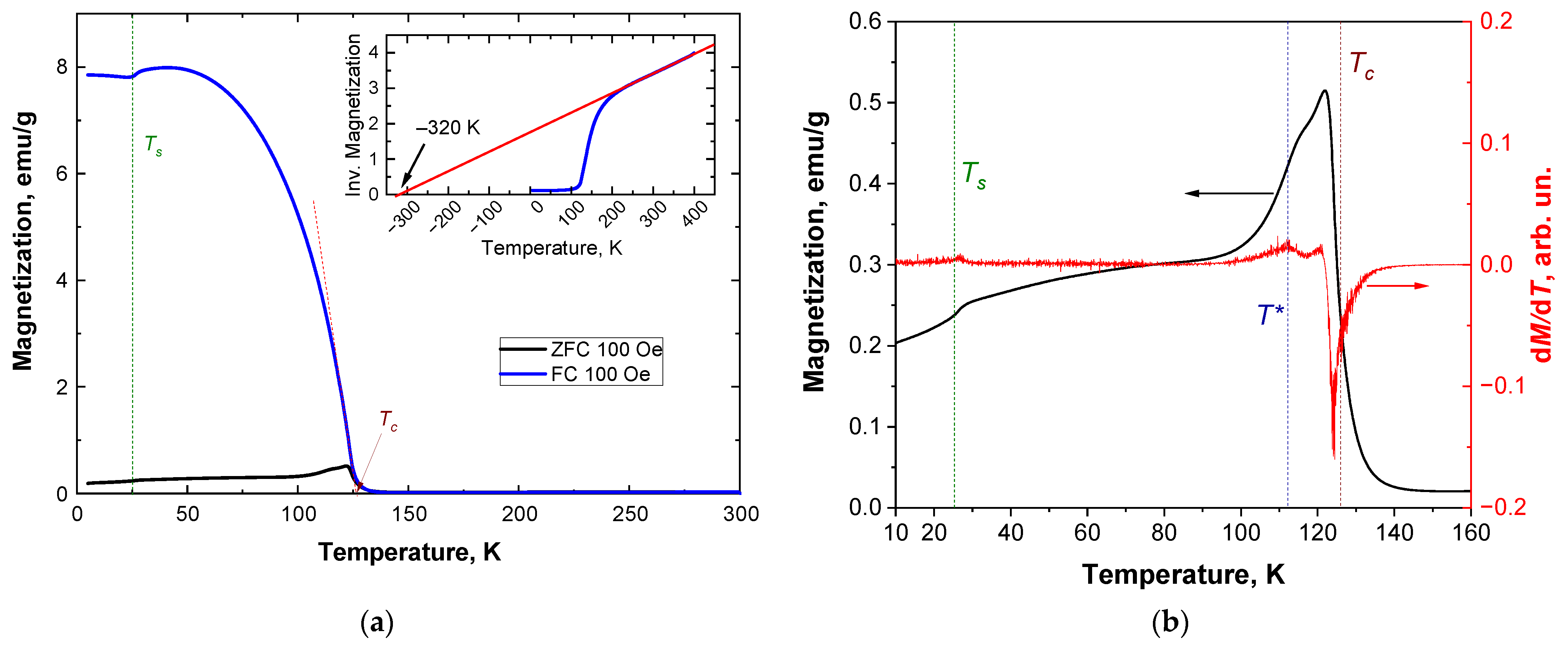
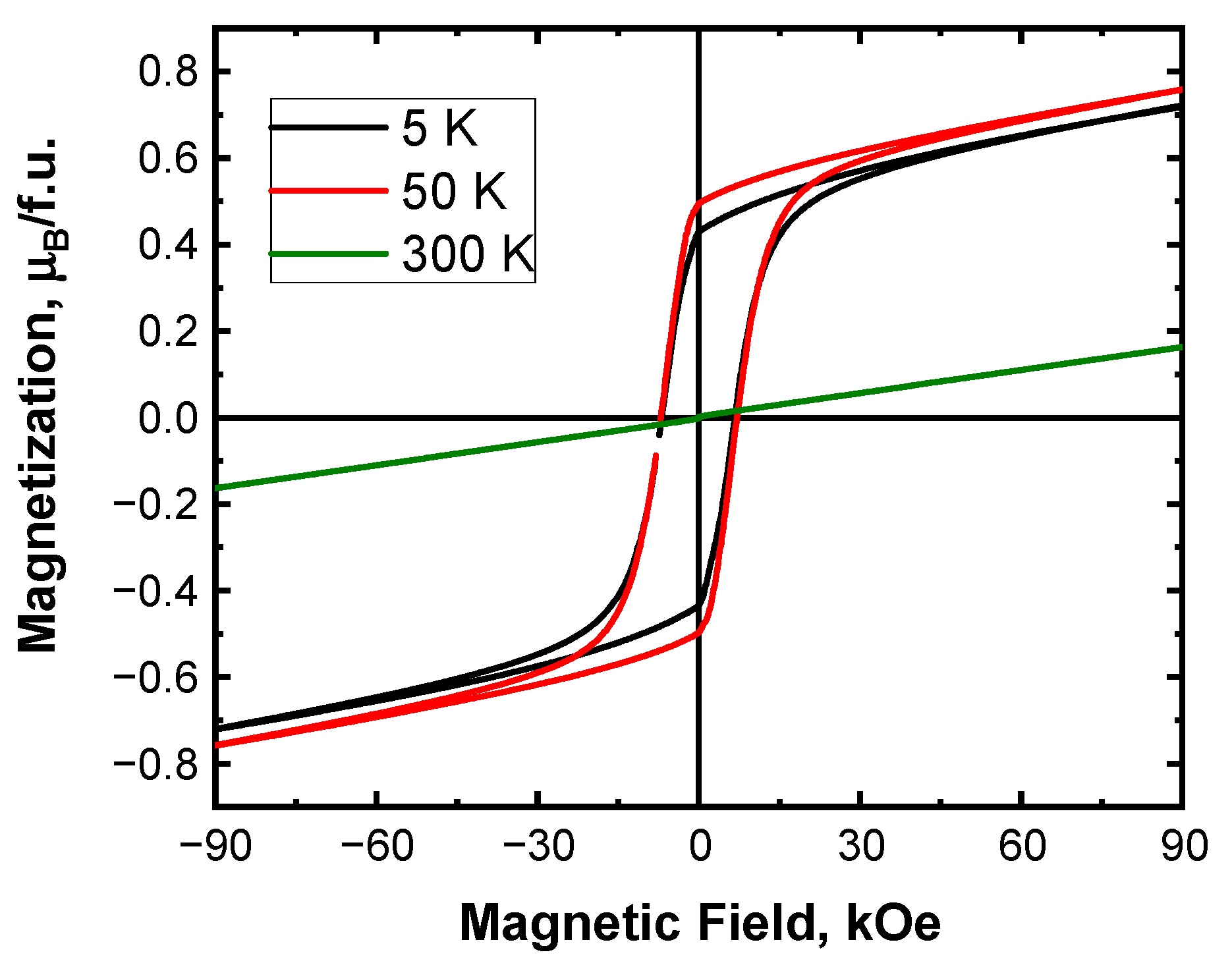
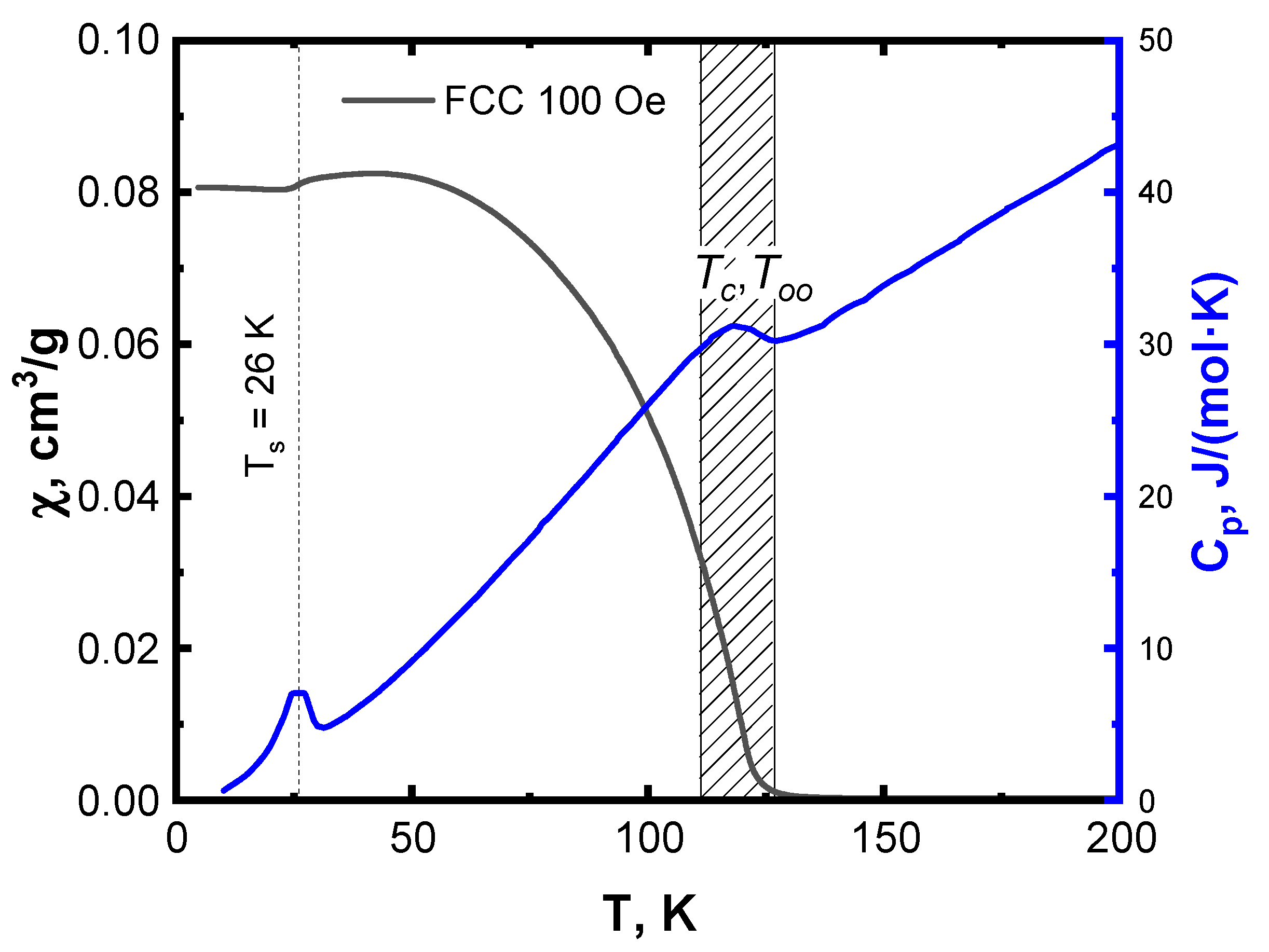
3.2. Magnetic Properties
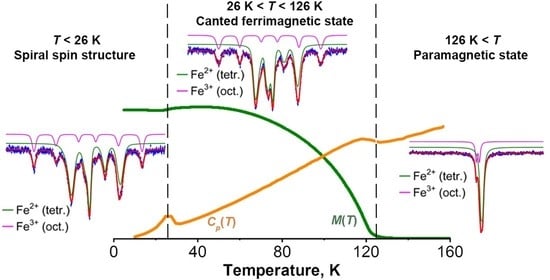
3.3. Specific Heat Studies
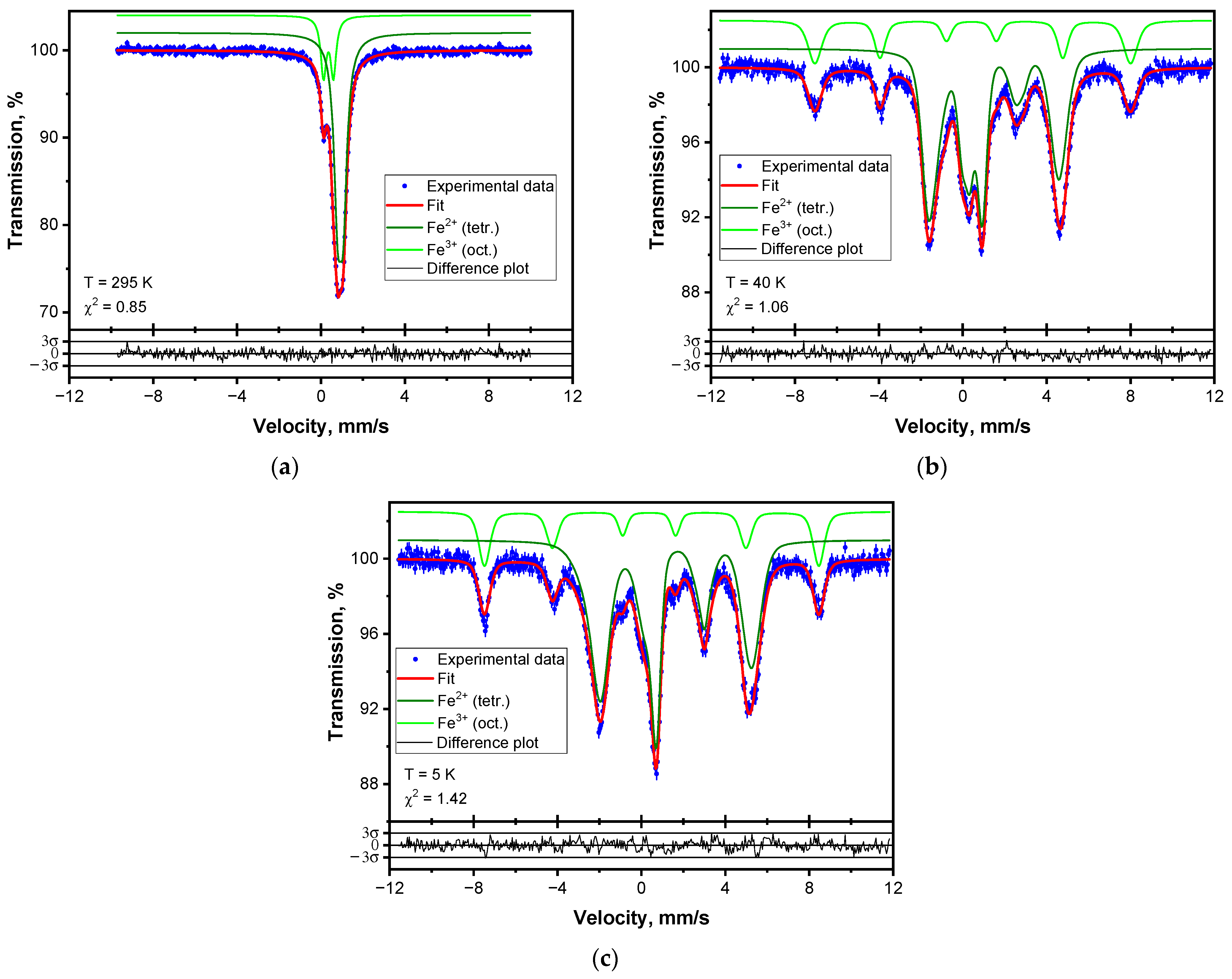
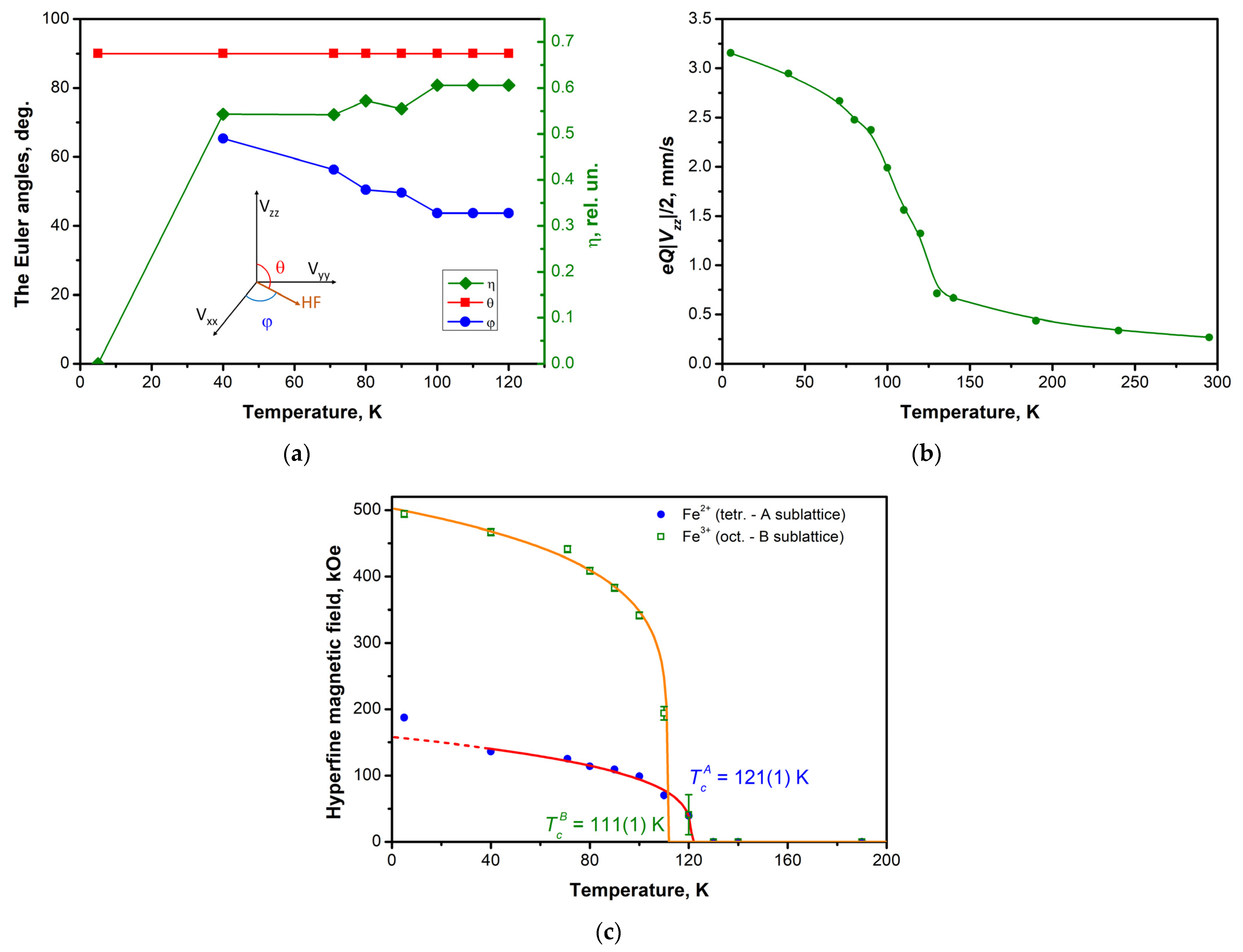
3.4. Mössbauer Effect Studies
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tsurkan, V.; von Nidda, H.-A.K.; Deisenhofer, J.; Lunkenheimer, P.; Loidl, A. On the Complexity of Spinels: Magnetic, Electronic, and Polar Ground States. Phys. Rep. 2021, 926, 1–86. [Google Scholar] [CrossRef]
- Yusupov, R.V.; Cherosov, M.A.; Gabbasov, B.F.; Vasin, K.V.; Batulin, R.G.; Kiyamov, A.G.; Eremin, M.V. Magnetic Irreversibilities and Nonreciprocity of the Microwave Absorption of FeCr2O4 Spinel. JETP Lett. 2022, 115, 167–173. [Google Scholar] [CrossRef]
- Batulin, R.; Cherosov, M.; Kiiamov, A.; Zinnatullin, A.; Vagizov, F.; Tayurskii, D.; Yusupov, R. Synthesis and Single Crystal Growth by Floating Zone Technique of FeCr2O4 Multiferroic Spinel: Its Structure, Composition, and Magnetic Properties. Magnetochemistry 2022, 8, 86. [Google Scholar] [CrossRef]
- Singh, K.; Maignan, A.; Simon, C.; Martin, C. FeCr2O4 and CoCr2O4 Spinels: Multiferroicity in the Collinear Magnetic State? Appl. Phys. Lett. 2011, 99, 172903. [Google Scholar] [CrossRef]
- Khomskii, D. Classifying Multiferroics: Mechanisms and Effects. Physics 2009, 2, 20. [Google Scholar] [CrossRef] [Green Version]
- Wang, J. (Ed.) Multiferroic Materials: Properties, Techniques, and Applications; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar] [CrossRef]
- Cano, A.; Meier, D.; Trassin, M. (Eds.) Multiferroics: Fundamentals and Applications; De Gruyter: Berlin/Boston, MA, USA, 2021. [Google Scholar] [CrossRef]
- Francombe, M.H. Lattice Changes in Spinel-Type Iron Chromites. J. Phys. Chem. Solids 1957, 3, 37–43. [Google Scholar] [CrossRef]
- Robbins, M.; Wertheim, G.K.; Sherwood, R.C.; Buchanan, D.N.E. Magnetic Properties and Site Distributions in the System FeCr2O4-Fe3O4(Fe2+Cr2−xFex3+O4. J. Phys. Chem. Solids 1971, 32, 717–729. [Google Scholar] [CrossRef]
- Levinstein, H.J.; Robbins, M.; Capio, C. A Crystallographic Study of the System FeCr2O4 Fe3O4 (Fe2+Fe3+xCr2−xO4). Mater. Res. Bull. 1972, 7, 27–34. [Google Scholar] [CrossRef]
- Ma, J.; Garlea, V.O.; Rondinone, A.; Aczel, A.A.; Calder, S.; dela Cruz, C.; Sinclair, R.; Tian, W.; Chi, S.; Kiswandhi, A.; et al. Magnetic and Structural Phase Transitions in the Spinel Compound Fe1+xCr2−xO4. Phys. Rev. B 2014, 89, 134106. [Google Scholar] [CrossRef] [Green Version]
- Kose, K.; Iida, S. Interacting Phase Transitions in Fe1+xCr2−xO4 (0 ≤ x ≤ 0.4). J. Appl. Phys. 1984, 55, 2321–2323. [Google Scholar] [CrossRef]
- Brown, R.A.; Bevan, S.C. The Thermal Decomposition of Ferrous Oxalate Dihydrate. J. Inorg. Nucl. Chem. 1966, 28, 387–391. [Google Scholar] [CrossRef]
- Mohamed, M.A.; Galwey, A.K. A Kinetic and Mechanistic Study of the Isothermal Decomposition of Ferrous Oxalate Dihydrate. Thermochim. Acta 1993, 213, 269–278. [Google Scholar] [CrossRef]
- Hermanek, M.; Zboril, R.; Mashlan, M.; Machala, L.; Schneeweiss, O. Thermal Behaviour of Iron(II) Oxalate Dihydrate in the Atmosphere of Its Conversion Gases. J. Mater. Chem. 2006, 16, 1273. [Google Scholar] [CrossRef]
- Matsnev, M.E.; Rusakov, V.S. SpectrRelax: An Application for Mössbauer Spectra Modeling and Fitting. AIP Conf. Proc. 2012, 1489, 178–185. [Google Scholar] [CrossRef]
- Rodríguez-Carvajal, J. Recent Advances in Magnetic Structure Determination by Neutron Powder Diffraction. Phys. B Condens. Matter 1993, 192, 55–69. [Google Scholar] [CrossRef]
- Lacroix, C.; Mendels, P.; Mila, F. (Eds.) Introduction to Frustrated Magnetism; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef] [Green Version]
- Joy, P.A.; Date, S.K. Comparison of the Zero-Field-Cooled Magnetization Behavior of Some Ferromagnetic and Ferrimagnetic Systems. J. Magn. Magn. Mater. 2000, 218, 229–237. [Google Scholar] [CrossRef]
- Lotgering, F.K. On the ferrimagnetism of some sulphides and oxides. Philips Res. Rep. 1956, 11, 190–249. [Google Scholar]
- Jacobs, I.S. High Field Magnetization Study of Ferrimagnetic Arrangements in Chromite Spinels. J. Phys. Chem. Solids 1960, 15, 54–65. [Google Scholar] [CrossRef]
- Goldanskii, V.I.; Herber, R.H. Chemical Applications of Mossbauer Spectroscopy; Academic Press: San Diego, CA, USA, 1968. [Google Scholar]
- Chen, Y.-L.; Yang, D.-P. Mössbauer Effect in Lattice Dynamics; Wiley-VCH: Weinheim, Germany, 2007. [Google Scholar]
- Kaul, S.N. Static Critical Phenomena in Ferromagnets with Quenched Disorder. J. Magn. Magn. Mater. 1985, 53, 5–53. [Google Scholar] [CrossRef]
- Hartmann-Boutron, F.; Imbert, P. Mössbauer Study of the Electronic and Magnetic Properties of Fe2+ Ions in Some Spinel-Type Compounds. J. Appl. Phys. 1968, 39, 775–785. [Google Scholar] [CrossRef]
- Reimers, J.N.; Greedan, J.E.; Björgvinsson, M. Critical Properties of Highly Frustrated Pyrochlore Antiferromagnets. Phys. Rev. B 1992, 45, 7295–7306. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zinnatullin, A.L.; Cherosov, M.A.; Batulin, R.G.; Vagizov, F.G.; Yusupov, R.V. An Effect of Fe3+ Ion Substitution for Cr3+ in the Octahedral Sites of FeCr2O4 Multiferroic Spinel: Mössbauer Spectroscopy Study. Magnetochemistry 2023, 9, 98. https://doi.org/10.3390/magnetochemistry9040098
Zinnatullin AL, Cherosov MA, Batulin RG, Vagizov FG, Yusupov RV. An Effect of Fe3+ Ion Substitution for Cr3+ in the Octahedral Sites of FeCr2O4 Multiferroic Spinel: Mössbauer Spectroscopy Study. Magnetochemistry. 2023; 9(4):98. https://doi.org/10.3390/magnetochemistry9040098
Chicago/Turabian StyleZinnatullin, Almaz L., Mikhail A. Cherosov, Ruslan G. Batulin, Farit G. Vagizov, and Roman V. Yusupov. 2023. "An Effect of Fe3+ Ion Substitution for Cr3+ in the Octahedral Sites of FeCr2O4 Multiferroic Spinel: Mössbauer Spectroscopy Study" Magnetochemistry 9, no. 4: 98. https://doi.org/10.3390/magnetochemistry9040098
APA StyleZinnatullin, A. L., Cherosov, M. A., Batulin, R. G., Vagizov, F. G., & Yusupov, R. V. (2023). An Effect of Fe3+ Ion Substitution for Cr3+ in the Octahedral Sites of FeCr2O4 Multiferroic Spinel: Mössbauer Spectroscopy Study. Magnetochemistry, 9(4), 98. https://doi.org/10.3390/magnetochemistry9040098