Spin-Topological Electronic Valve in Ni/hBN–Graphene–hBN/Ni Magnetic Junction
Abstract
:1. Introduction
2. Computational Methods
3. Results and Discussion
3.1. Total Energy and Its Correlation to Van Der Waals Interaction
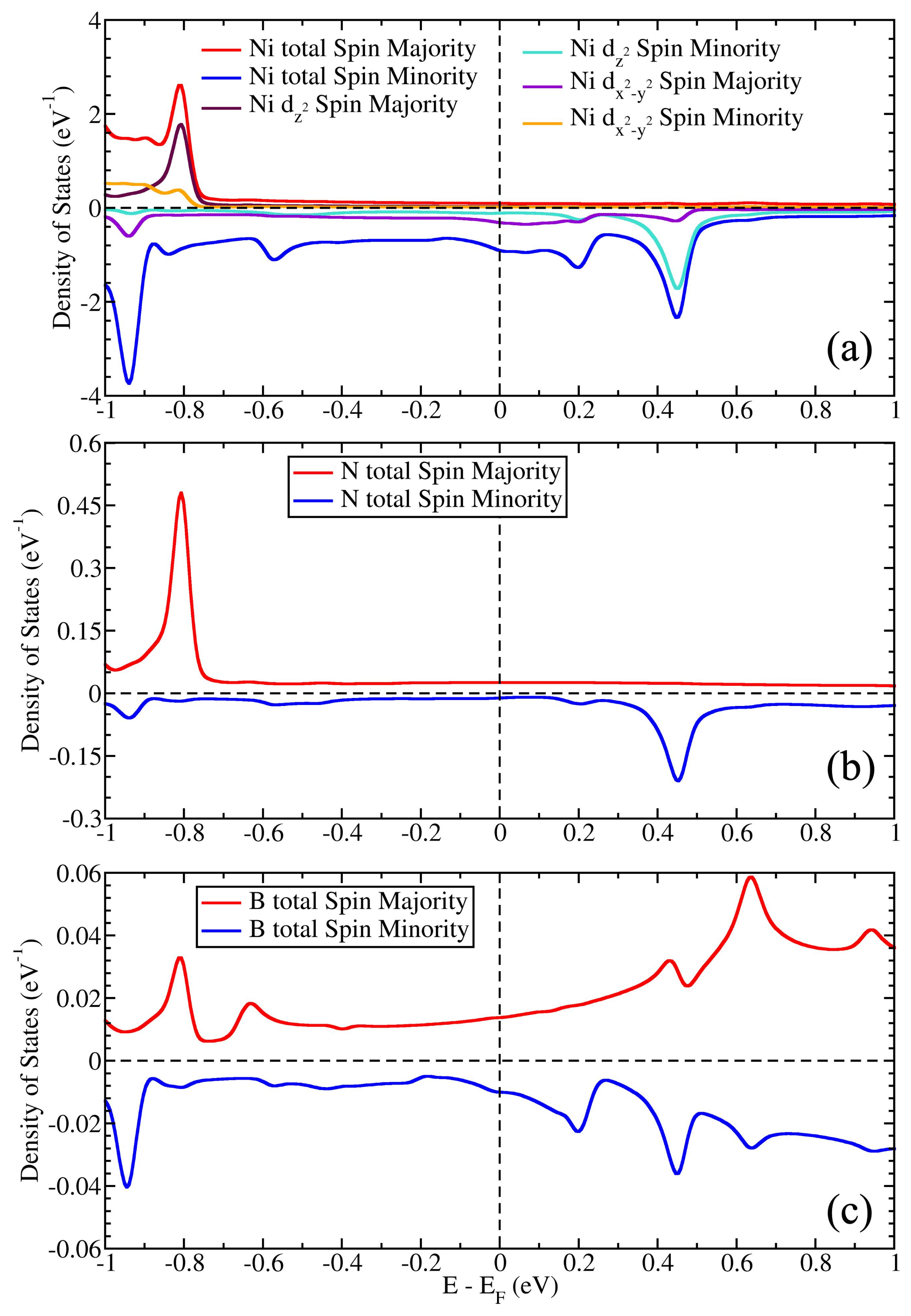
3.2. Magnetic Properties and Induced Magnetic Moments on Graphene
3.3. A Controllable Dirac Cone of Graphene due to a Tunable Pseudospin Term of Graphene
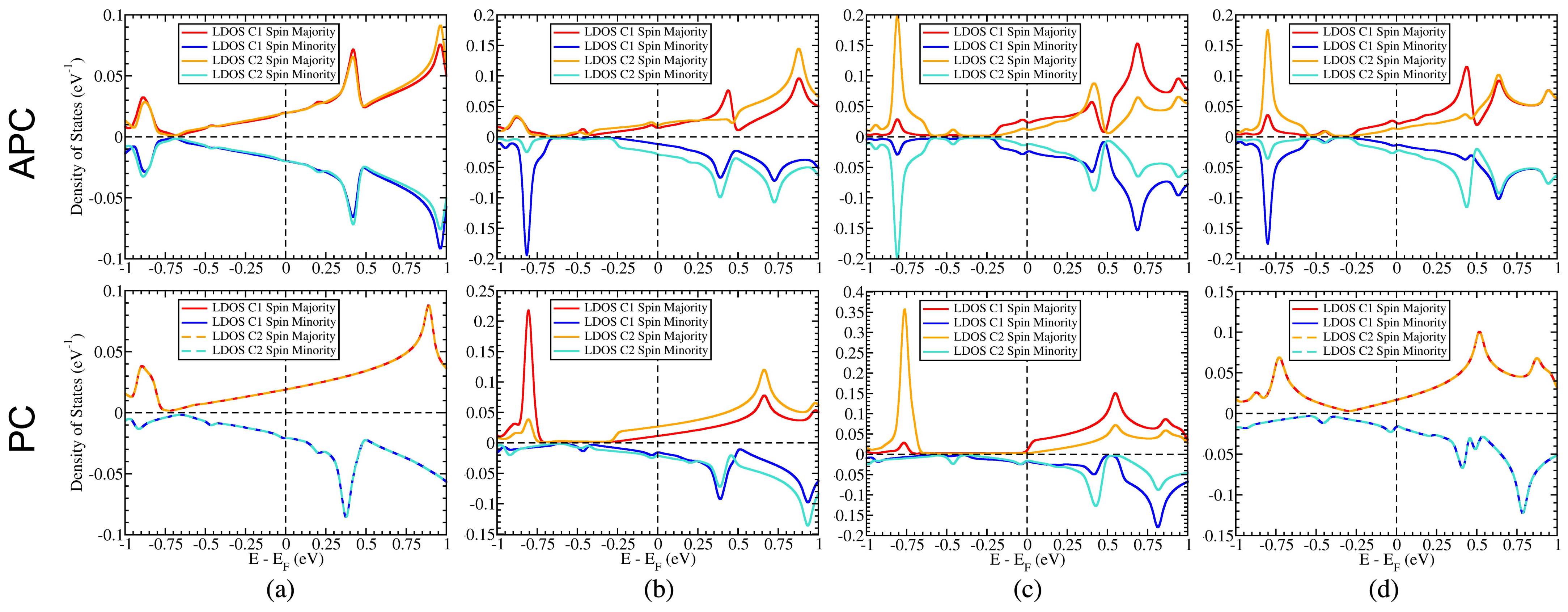
3.4. The Influence of the Surface State of Ni Works Directly on C Atoms in the Gapped Dirac Cone
3.5. Controllable Mass-Gapped Dirac Cone through the Ni Surface State Influence on C Atoms
3.6. Possible Application on the Spin-Topological Electronic Valve
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef] [PubMed]
- Morozov, S.V.; Novoselov, K.S.; Katsnelson, M.I.; Schedin, F.; Elias, D.C.; Jaszczak, J.A.; Geim, A.K. Giant Intrinsic Carrier Mobilities in Graphene and Its Bilayer. Phys. Rev. Lett. 2008, 100, 016602. [Google Scholar] [CrossRef]
- Schedin, F.; Geim, A.K.; Morozov, S.V.; Hill, E.W.; Blake, P.; Katsnelson, M.I.; Novoselov, K.S. Detection of individual gas molecules adsorbed on graphene. Nat. Mater. 2007, 6, 652–655. [Google Scholar] [CrossRef]
- Schultz, B.J.; Jaye, C.; Lysaght, P.S.; Fischer, D.A.; Prendergast, D.; Banerjee, S. On chemical bonding and electronic structure of graphene–metal contacts. Chem. Sci. 2013, 4, 494–502. [Google Scholar] [CrossRef]
- Abtew, T.; Shih, B.C.; Banerjee, S.; Zhang, P. Graphene–ferromagnet interfaces: Hybridization, magnetization and charge transfer. Nanoscale 2013, 5, 1902–1909. [Google Scholar] [CrossRef] [PubMed]
- Weser, M.; Rehder, Y.; Horn, K.; Sicot, M.; Fonin, M.; Preobrajenski, A.B.; Voloshina, E.N.; Goering, E.; Dedkov, Y.S. Induced magnetism of carbon atoms at the graphene/Ni(111) interface. Appl. Phys. Lett. 2010, 96, 012504. [Google Scholar] [CrossRef]
- Joshi, N.; Ballav, N.; Ghosh, P. Hydrogen-induced reversal of spin alignment in graphene supported on Ni(111) surface. Phys. Rev. B 2012, 86, 121411. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef]
- Morishita, N.; Sunnardianto, G.K.; Miyao, S.; Kusakabe, K. Theoretical Analysis of Pseudodegenerate Zero-Energy Modes in Vacancy-Centered Hexagonal Armchair Nanographene. J. Phys. Soc. Jpn. 2016, 85, 084703. [Google Scholar] [CrossRef]
- Dahal, A.; Batzill, M. Graphene–nickel interfaces: A review. Nanoscale 2014, 6, 2548–2562. [Google Scholar] [CrossRef] [PubMed]
- Cho, Y.; Choi, Y.C.; Kim, K.S. Graphene Spin-Valve Device Grown Epitaxially on the Ni(111) Substrate: A First Principles Study. J. Phys. Chem. C 2011, 115, 6019–6023. [Google Scholar] [CrossRef]
- Sato, R.; Hiraiwa, T.; Inoue, J.; Honda, S.; Itoh, H. Magnetoresistance in fcc Ni/graphene/fcc Ni(111) junctions. Phys. Rev. B 2012, 85, 094420. [Google Scholar] [CrossRef]
- Liu, H.; Kondo, H.; Ohno, T. Spintronic Transport in Armchair Graphene Nanoribbon with Ferromagnetic Electrodes: Half-Metallic Properties. Nanoscale Res. Lett. 2016, 11, 456. [Google Scholar] [CrossRef]
- Martin, M.B.; Dlubak, B.; Weatherup, R.S.; Piquemal-Banci, M.; Yang, H.; Blume, R.; Schloegl, R.; Collin, S.; Petroff, F.; Hofmann, S.; et al. Protecting nickel with graphene spin-filtering membranes: A single layer is enough. Appl. Phys. Lett. 2015, 107, 012408. [Google Scholar] [CrossRef]
- Asshoff, P.U.; Sambricio, J.L.; Rooney, A.P.; Slizovskiy, S.; Mishchenko, A.; Rakowski, A.M.; Hill, E.W.; Geim, A.K.; Haigh, S.J.; Fal’ko, V.I.; et al. Magnetoresistance of vertical Co-graphene-NiFe junctions controlled by charge transfer and proximity-induced spin splitting in graphene. 2D Mater. 2017, 4, 031004. [Google Scholar] [CrossRef]
- Entani, S.; Seki, T.; Sakuraba, Y.; Yamamoto, T.; Takahashi, S.; Naramoto, H.; Takanashi, K.; Sakai, S. Magnetoresistance effect in Fe20Ni80/graphene/Fe20Ni80 vertical spin valves. Appl. Phys. Lett. 2016, 109, 082406. [Google Scholar] [CrossRef]
- Mohiuddin, T.M.G.; Hill, E.; Elias, D.; Zhukov, A.; Novoselov, K.; Geim, A. Graphene in Multilayered CPP Spin Valves. IEEE Trans. Magn. 2008, 44, 2624–2627. [Google Scholar] [CrossRef]
- Iqbal, M.Z.; Iqbal, M.W.; Lee, J.H.; Kim, Y.S.; Chun, S.H.; Eom, J. Spin valve effect of NiFe/graphene/NiFe junctions. Nano Res. 2013, 6, 373–380. [Google Scholar] [CrossRef]
- Iqbal, M.Z.; Iqbal, M.W.; Jin, X.; Hwang, C.; Eom, J. Interlayer dependent polarity of magnetoresistance in graphene spin valves. J. Mater. Chem. C 2015, 3, 298–302. [Google Scholar] [CrossRef]
- Chen, J.J.; Meng, J.; Zhou, Y.B.; Wu, H.C.; Bie, Y.Q.; Liao, Z.M.; Yu, D.P. Layer-by-layer assembly of vertically conducting graphene devices. Nat. Commun. 2013, 4, 1921. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Li, T.; Guo, X. Vertical Graphene Spin Valves Based on La2/3Sr1/3MnO3 Electrodes. ACS Appl. Mater. Interfaces 2014, 6, 1187–1192. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Xue, L.; Abruña, H.D.; Ralph, D.C. Magnetic tunnel junctions with single-layer-graphene tunnel barriers. Phys. Rev. B 2014, 89, 184418. [Google Scholar] [CrossRef]
- Mandal, S.; Saha, S.K. Ni/graphene/Ni nanostructures for spintronic applications. Nanoscale 2012, 4, 986–990. [Google Scholar] [CrossRef]
- Wicaksono, Y.; Teranishi, S.; Nishiguchi, K.; Kusakabe, K. Tunable induced magnetic moment and in-plane conductance of graphene in Ni/graphene/Ni nano-spin-valve-like structure: A first principles study. Carbon 2019, 143, 828–836. [Google Scholar] [CrossRef]
- Wicaksono, Y.; Harfah, H.; Sunnardianto, G.K.; Majidi, M.A.; Kusakabe, K. Colossal in-plane magnetoresistance ratio of graphene sandwiched with Ni nanostructures. RSC Adv. 2022, 12, 13985–13991. [Google Scholar] [CrossRef]
- Harfah, H.; Wicaksono, Y.; Sunnardianto, G.K.; Majidi, M.A.; Kusakabe, K. High magnetoresistance of a hexagonal boron nitride–graphene heterostructure-based MTJ through excited-electron transmission. Nanoscale Adv. 2022, 4, 117–124. [Google Scholar] [CrossRef]
- Pezo, A.; Zanolli, Z.; Wittemeier, N.; Ordejón, P.; Fazzio, A.; Roche, S.; Garcia, J.H. Manipulation of spin transport in graphene/transition metal dichalcogenide heterobilayers upon twisting. 2D Mater. 2021, 9, 015008. [Google Scholar] [CrossRef]
- Zollner, K.; Fabian, J. Engineering Proximity Exchange by Twisting: Reversal of Ferromagnetic and Emergence of Antiferromagnetic Dirac Bands in Graphene/Cr2Ge2Te6. Phys. Rev. Lett. 2022, 128, 106401. [Google Scholar] [CrossRef]
- Eliseev, E.A.; Morozovska, A.N.; Strikha, M.V. Strain Engineering of Ferromagnetic-Graphene-Ferroelectric Nanostructures. Phys. Rev. Appl. 2020, 14, 024081. [Google Scholar] [CrossRef]
- Harfah, H.; Wicaksono, Y.; Majidi, M.A.; Kusakabe, K. Spin-Current Control by Induced Electric Polarization Reversal in Ni/hBN/Ni: A Cross-Correlation Material. ACS Appl. Electron. Mater. 2020, 2, 1689–1699. [Google Scholar] [CrossRef]
- Wicaksono, Y. Theoretical Study of Gap Opening/Closing Control of Dirac Cone Using Spin-dependent Potentials in Graphene-based Magnetic Junctions. Ph.D. Thesis, Osaka University, Osaka, Japan, 2022. Available online: https://ir.library.osaka-u.ac.jp/repo/ouka/all/89505/32918_Dissertation.pdf (accessed on 21 March 2023).
- Sánchez-Portal, D.; Ordejón, P.; Artacho, E.; Soler, J.M. Density-functional method for very large systems with LCAO basis sets. Int. J. Quantum Chem. 1997, 65, 453–461. [Google Scholar] [CrossRef]
- Soler, J.M.; Artacho, E.; Gale, J.D.; García, A.; Junquera, J.; Ordejón, P.; Sánchez-Portal, D. The SIESTA method for ab initio order-N materials simulation. J. Physics: Condens. Matter 2002, 14, 2745–2779. [Google Scholar] [CrossRef]
- Troullier, N.; Martins, J. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 1991, 43, 1993–2006. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef]
- Ozaki, T.; Kino, H. Numerical atomic basis orbitals from H to Kr. Phys. Rev. B 2004, 69, 195113. [Google Scholar] [CrossRef]
- Ozaki, T. Variationally optimized atomic orbitals for large-scale electronic structures. Phys. Rev. B 2003, 67, 155108. [Google Scholar] [CrossRef]
- Sánchez-Portal, D.; Artacho, E.; Soler, J. Analysis of atomic orbital basis sets from the projection of plane-wave results. J. Phys. Condens. Matter 1996, 8, 3859–3880. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- Ambrosetti, A.; Ferri, N.; DiStasio, R.A.; Tkatchenko, A. Wavelike charge density fluctuations and van der Waals interactions at the nanoscale. Science 2016, 351, 1171–1176. [Google Scholar] [CrossRef]
- Ambrosetti, A.; Silvestrelli, P.L.; Tkatchenko, A. Physical adsorption at the nanoscale: Towards controllable scaling of the substrate-adsorbate van der Waals interaction. Phys. Rev. B 2017, 95, 235417. [Google Scholar] [CrossRef]
- Dobson, J.F.; White, A.; Rubio, A. Asymptotics of the Dispersion Interaction: Analytic Benchmarks for van der Waals Energy Functionals. Phys. Rev. Lett. 2006, 96, 073201. [Google Scholar] [CrossRef]
- Ambrosetti, A.; Silvestrelli, P.L. Hidden by graphene—Towards effective screening of interface van der Waals interactions via monolayer coating. Carbon 2018, 139, 486–491. [Google Scholar] [CrossRef]
- Ambrosetti, A.; Silvestrelli, P.L. Faraday-like Screening by Two-Dimensional Nanomaterials: A Scale-Dependent Tunable Effect. J. Phys. Chem. Lett. 2019, 10, 2044–2050. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Reimers, J.R.; Dobson, J.F.; Gould, T. Faraday cage screening reveals intrinsic aspects of the van der Waals attraction. Proc. Natl. Acad. Sci. USA 2018, 115, E10295–E10302. [Google Scholar] [CrossRef] [PubMed]
- Ambrosetti, A.; Silvestrelli, P.L. Communication: Enhanced chemical reactivity of graphene on a Ni(111) substrate. J. Chem. Phys. 2016, 144, 111101. [Google Scholar] [CrossRef] [PubMed]
- Quhe, R.; Zheng, J.; Luo, G.; Liu, Q.; Qin, R.; Zhou, J.; Yu, D.; Nagase, S.; Mei, W.N.; Gao, Z.; et al. Tunable and sizable band gap of single-layer graphene sandwiched between hexagonal boron nitride. NPG Asia Mater. 2012, 4, e6. [Google Scholar] [CrossRef]
- Wasserman, E.; Murray, R.W.; Yager, W.A.; Trozzolo, A.M.; Smolinsky, G. Quintet ground states of m-dicarbene and m-dinitrene compounds. J. Am. Chem. Soc. 1967, 89, 5076–5078. [Google Scholar] [CrossRef]
- Ando, T. Exotic electronic and transport properties of graphene. Phys. Low-Dimens. Syst. Nanostruct. 2007, 40, 213–227. [Google Scholar] [CrossRef]
- Zhou, S.Y.; Gweon, G.H.; Fedorov, A.V.; First, P.N.; de Heer, W.A.; Lee, D.H.; Guinea, F.; Castro Neto, A.H.; Lanzara, A. Substrate-induced bandgap opening in epitaxial graphene. Nat. Mater. 2007, 6, 770–775. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Y.B.; Yin, J.; Tóvári, E.; Yang, Y.; Lin, L.; Holwill, M.; Birkbeck, J.; Perello, D.J.; Xu, S.; et al. Composite super-moirélattices in double-aligned graphene heterostructures. Sci. Adv. 2022, 5, eaay8897. [Google Scholar] [CrossRef] [PubMed]
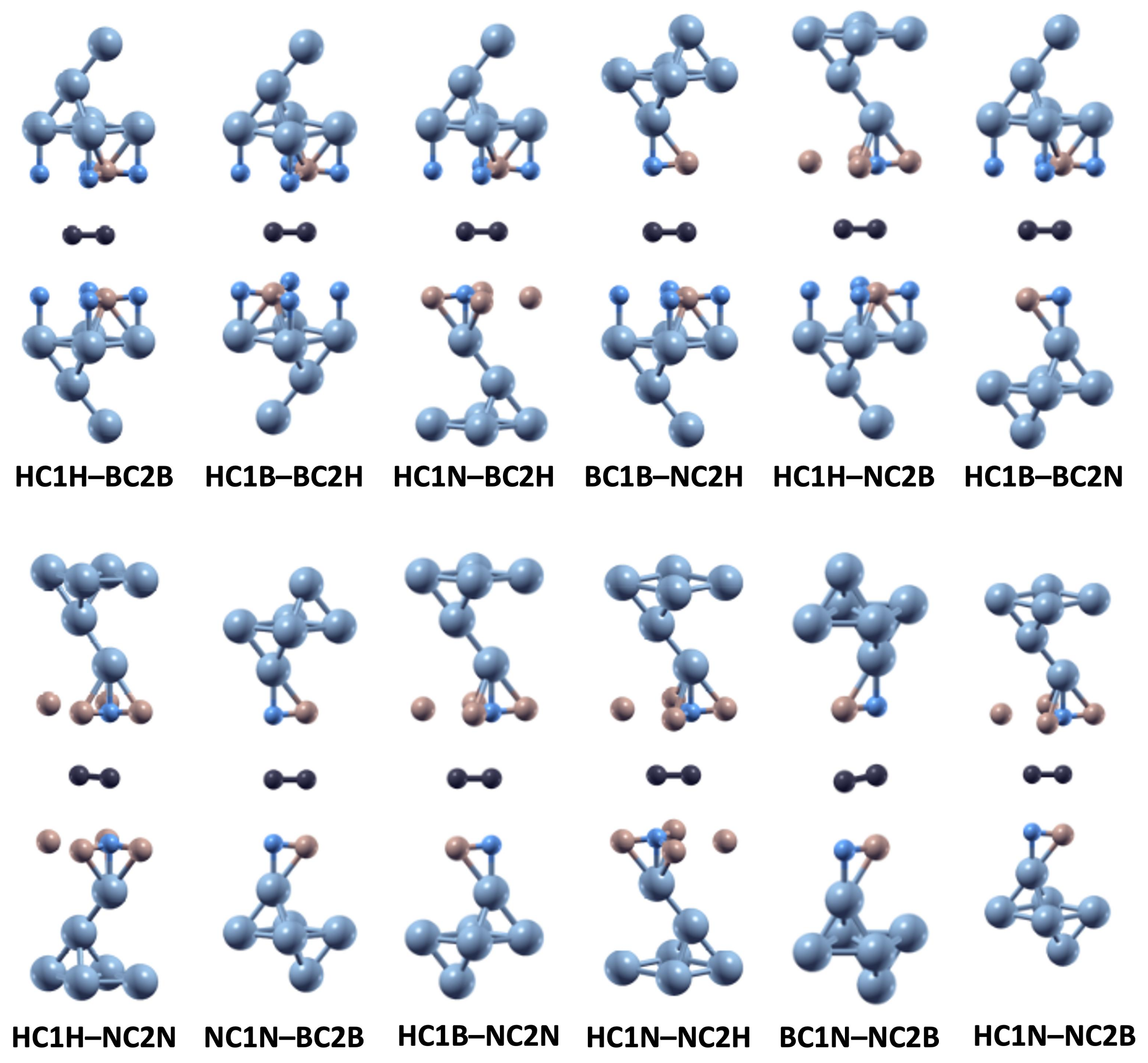
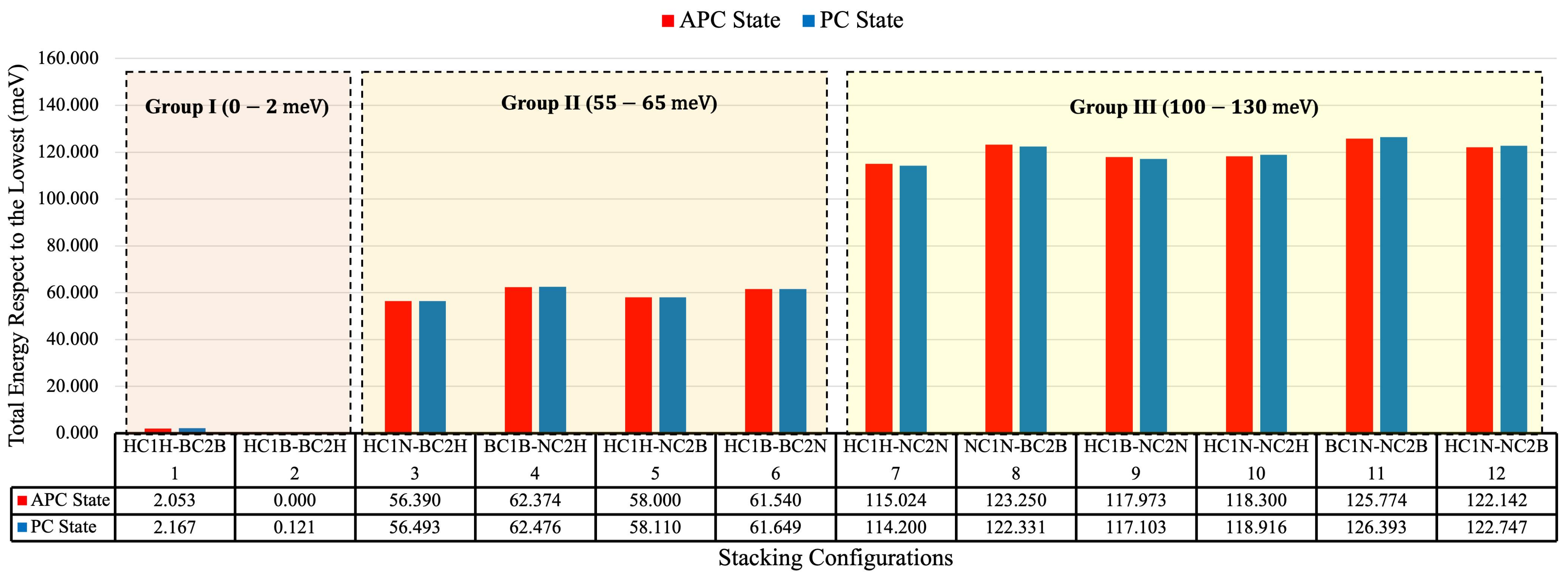


| No. | Stacking Arrangement Name | Interlayer Distance (Å) | |||
|---|---|---|---|---|---|
| N-Gr | B-Gr | ||||
| Upper | Lower | Upper | Lower | ||
| 1 | HC1H–BC2B | 2.71 | 2.71 | 2.85 | 2.85 |
| 2 | HC1B–BC2H | 2.71 | 2.71 | 2.85 | 2.85 |
| 3 | HC1N–BC2H | 2.74 | 2.76 | 2.88 | 2.90 |
| 4 | BC1B–NC2H | 2.77 | 2.76 | 2.91 | 2.89 |
| 5 | HC1H–NC2B | 2.76 | 2.75 | 2.90 | 2.88 |
| 6 | HC1B–BC2N | 2.76 | 2.78 | 2.89 | 2.92 |
| 7 | HC1H–NC2N | 2.79 | 2.79 | 2.93 | 2.93 |
| 8 | NC1N–BC2B | 2.81 | 2.81 | 2.95 | 2.95 |
| 9 | HC1B–NC2N | 2.80 | 2.81 | 2.94 | 2.94 |
| 10 | HC1N–NC2H | 2.80 | 2.80 | 2.94 | 2.94 |
| 11 | BC1N–NC2B | 2.83 | 2.83 | 2.96 | 2.96 |
| 12 | HC1N–NC2B | 2.81 | 2.82 | 2.95 | 2.95 |
| No. | Stacking Arrangement Name | Magnetic Moment () | |||
|---|---|---|---|---|---|
| APC | PC | ||||
| C1 | C2 | C1 | C2 | ||
| 1 | HC1H–BC2B | 0.000 | 0.000 | 0.002 | 0.003 |
| 2 | HC1B–BC2H | 0.001 | −0.001 | 0.002 | 0.002 |
| 3 | HC1N–BC2H | −0.006 | 0.005 | −0.004 | 0.006 |
| 4 | BC1B–NC2H | −0.005 | 0.006 | 0.006 | −0.003 |
| 5 | HC1H–NC2B | −0.004 | 0.005 | 0.007 | −0.002 |
| 6 | HC1B–BC2N | 0.004 | −0.004 | 0.007 | −0.002 |
| 7 | HC1H–NC2N | 0.000 | 0.000 | −0.011 | 0.015 |
| 8 | NC1N–BC2B | 0.000 | 0.000 | −0.014 | 0.015 |
| 9 | HC1B–NC2N | 0.000 | 0.001 | 0.015 | −0.012 |
| 10 | HC1N–NC2H | 0.012 | −0.012 | 0.002 | 0.002 |
| 11 | BC1N–NC2B | −0.010 | 0.010 | 0.003 | 0.003 |
| 12 | HC1N–NC2B | −0.011 | 0.011 | 0.002 | 0.002 |
| No. | Atom Name | Mulliken Partial Atomic Charge | |||
|---|---|---|---|---|---|
| HC1B–BC2H | BC1B–NC2H | ||||
| Spin UP | Spin DOWN | Spin UP | Spin DOWN | ||
| 1 | Upper B | 1.914 | 1.935 | 1.917 | 1.938 |
| 2 | Upper N | 2.193 | 2.169 | 2.187 | 2.161 |
| 3 | C1 | 1.981 | 1.979 | 1.997 | 1.991 |
| 4 | C2 | 1.981 | 1.979 | 1.969 | 1.972 |
| 5 | Lower N | 2.193 | 2.169 | 2.193 | 2.168 |
| 6 | Lower B | 1.914 | 1.935 | 1.915 | 1.936 |
| No. | Stacking Arrangement Name | Integrated SPIN-charge Density () of -Orbital | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| APC | PC | ||||||||||||
| C1 | C2 | C1-C2 | C1 | C2 | C1-C2 | ||||||||
| ↑ | ↓ | ↑ | ↓ | ↑ | ↓ | ↑ | ↓ | ↑ | ↓ | ↑ | ↓ | ||
| 1 | HC1H–BC2B | 0.456 | 0.456 | 0.460 | 0.460 | −0.004 | −0.004 | 0.457 | 0.456 | 0.461 | 0.461 | −0.004 | 0.003 |
| 2 | HC1B–BC2H | 0.458 | 0.459 | 0.459 | 0.458 | −0.001 | 0.001 | 0.459 | 0.458 | 0.459 | 0.459 | 0.000 | 0.000 |
| 3 | HC1N–BC2H | 0.451 | 0.457 | 0.468 | 0.463 | −0.017 | −0.006 | 0.453 | 0.456 | 0.468 | 0.463 | −0.015 | −0.007 |
| 4 | HC1H–NC2N | 0.449 | 0.449 | 0.474 | 0.474 | −0.025 | −0.025 | 0.443 | 0.454 | 0.482 | 0.467 | −0.039 | −0.013 |
| 5 | BC1N–NC2B | 0.455 | 0.464 | 0.464 | 0.455 | −0.009 | 0.009 | 0.461 | 0.459 | 0.460 | 0.459 | 0.001 | 0.000 |
| No. | Interchanging Stacking Configuration | In-Plane Conductance Difference Ratio |
|---|---|---|
| 1 | HC1B-BC2H ↔ BC1B-NC2H | 42% |
| 2 | BC1B-NC2H ↔ BC1N-NC2B | 66% |
| 3 | HC1B-BC2H ↔ BC1N-NC2B | 80% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wicaksono, Y.; Harfah, H.; Sunnardianto, G.K.; Majidi, M.A.; Kusakabe, K. Spin-Topological Electronic Valve in Ni/hBN–Graphene–hBN/Ni Magnetic Junction. Magnetochemistry 2023, 9, 113. https://doi.org/10.3390/magnetochemistry9050113
Wicaksono Y, Harfah H, Sunnardianto GK, Majidi MA, Kusakabe K. Spin-Topological Electronic Valve in Ni/hBN–Graphene–hBN/Ni Magnetic Junction. Magnetochemistry. 2023; 9(5):113. https://doi.org/10.3390/magnetochemistry9050113
Chicago/Turabian StyleWicaksono, Yusuf, Halimah Harfah, Gagus Ketut Sunnardianto, Muhammad Aziz Majidi, and Koichi Kusakabe. 2023. "Spin-Topological Electronic Valve in Ni/hBN–Graphene–hBN/Ni Magnetic Junction" Magnetochemistry 9, no. 5: 113. https://doi.org/10.3390/magnetochemistry9050113
APA StyleWicaksono, Y., Harfah, H., Sunnardianto, G. K., Majidi, M. A., & Kusakabe, K. (2023). Spin-Topological Electronic Valve in Ni/hBN–Graphene–hBN/Ni Magnetic Junction. Magnetochemistry, 9(5), 113. https://doi.org/10.3390/magnetochemistry9050113







