A Cu12 Metallacycle Assembled from Four C3-Symmetric Spin Frustrated Triangular Units
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials and General Information
Synthesis of [{Cu3L(µ-N3)}4(Py)14]·2Py·4[CH3OH]·0.8[H2O] (Cu12)
2.2. Crystallography
2.3. Magnetic Measurements
2.4. Theoretical Calculations
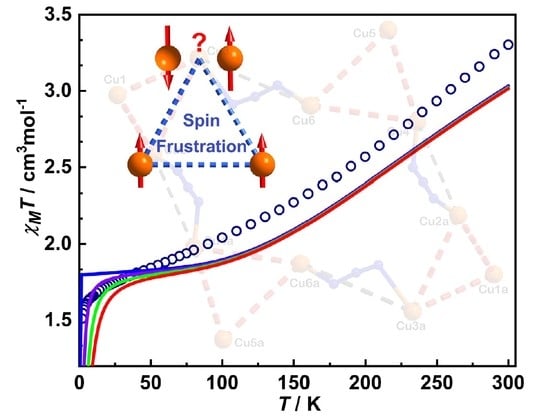
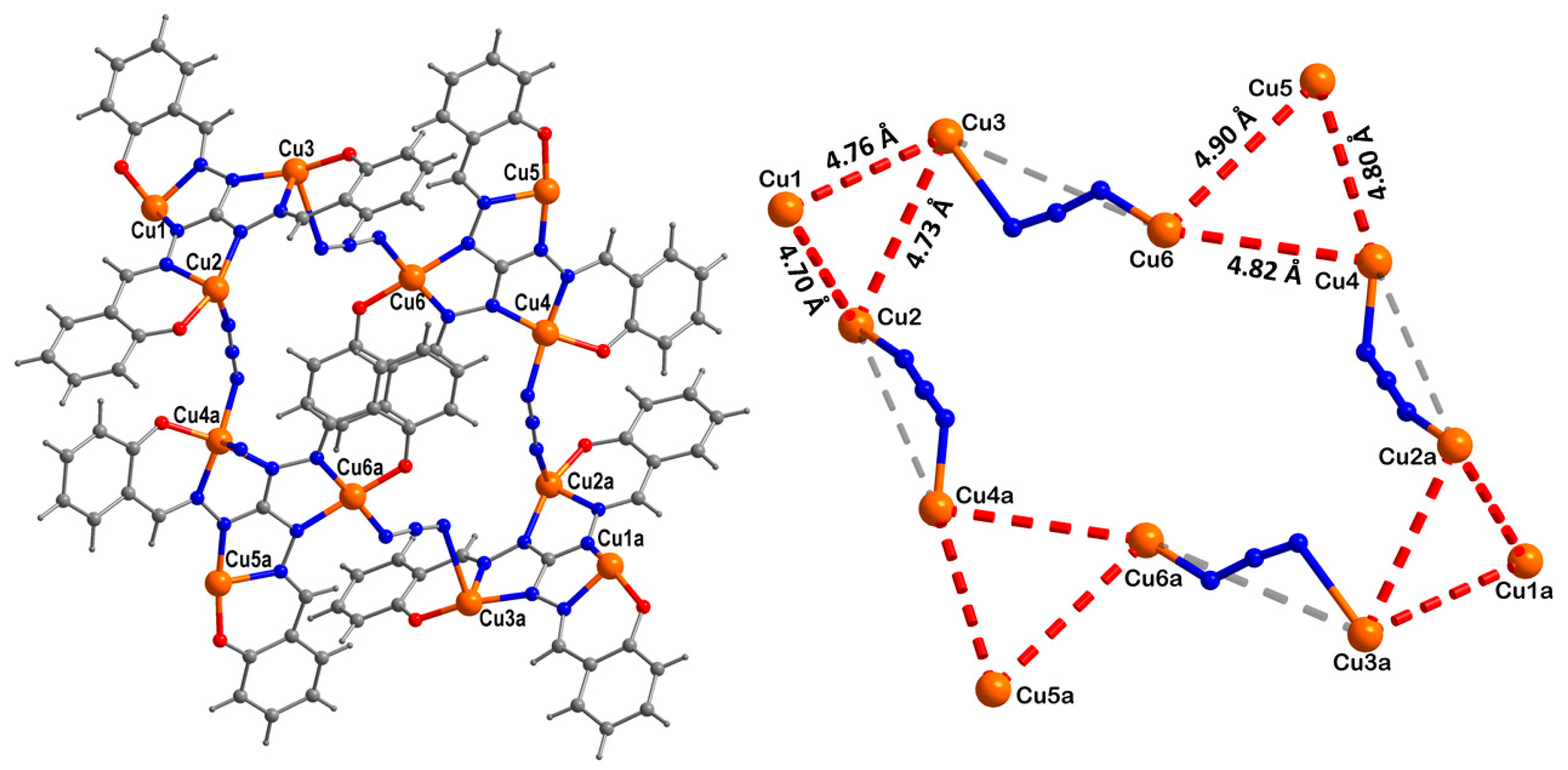
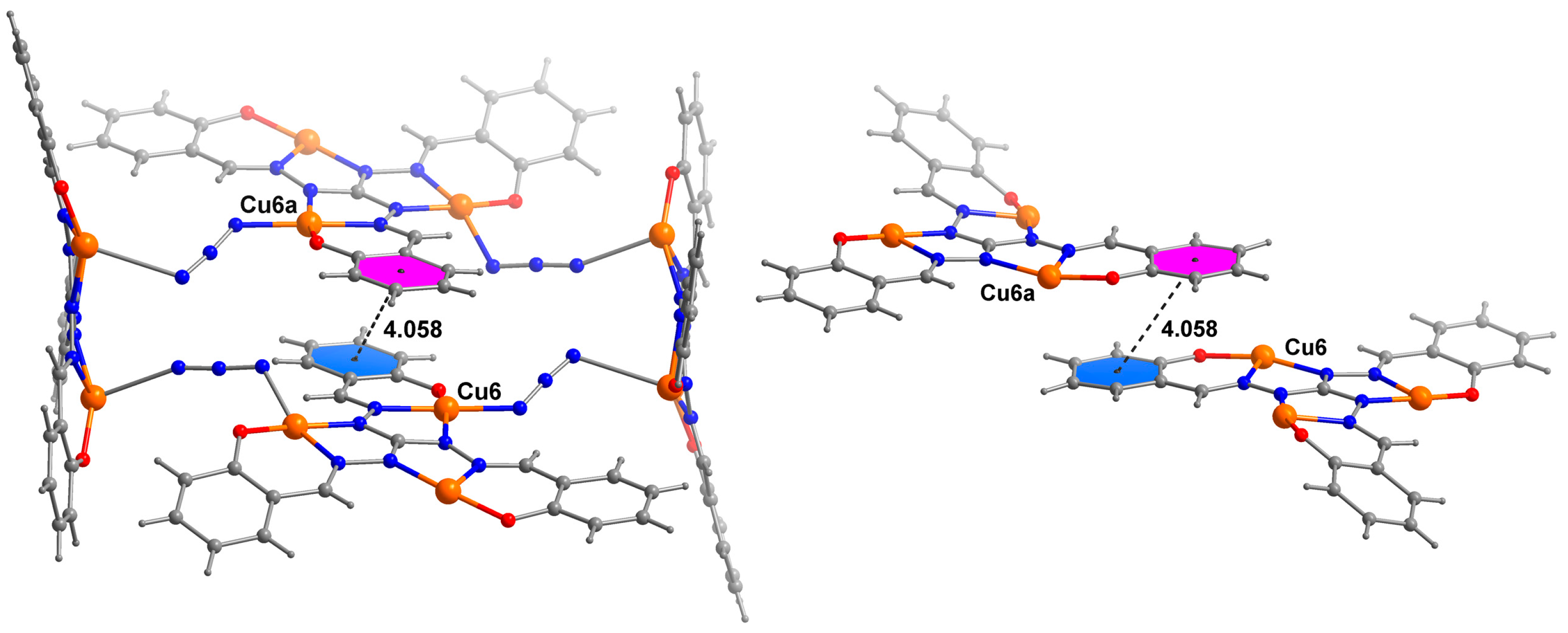
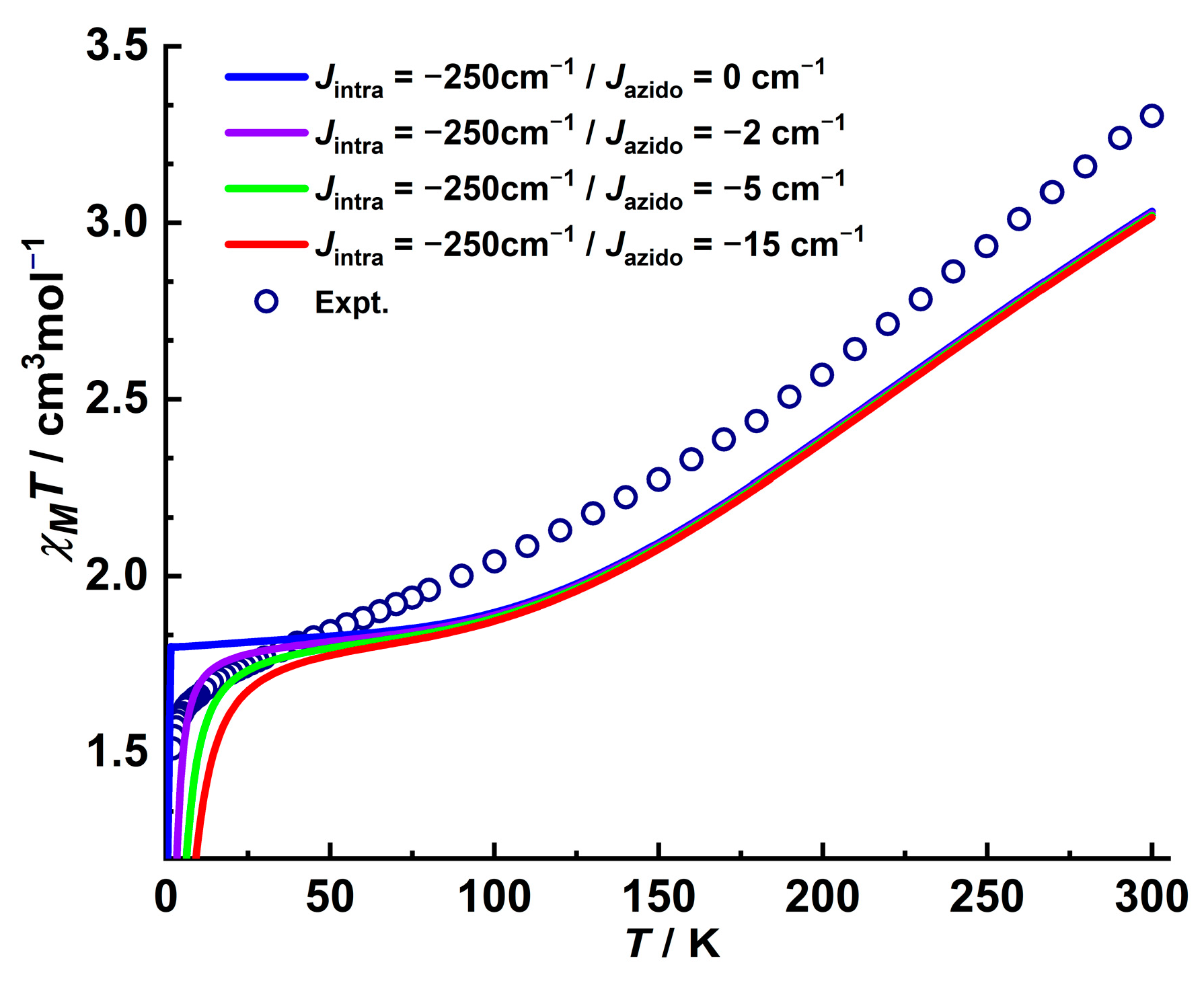
3. Results and Discussions
3.1. Crystal Structure of Cu12
3.2. Magnetic Properties
3.3. Theoretical Calculations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Leininger, S.; Olenyuk, B.; Stang, P.J. Self-Assembly of Discrete Cyclic Nanostructures Mediated by Transition Metals. Chem. Rev. 2000, 100, 853–908. [Google Scholar] [CrossRef]
- Müller, I.M.; Robson, R. A New Class of Easily Obtained Carbonate-Related μ3-Ligands and a Protein-Sized Doughnut-Shaped Coordination Oligomer. Angew. Chem. Int. Ed. 2000, 39, 4357–4359. [Google Scholar] [CrossRef]
- Buccella, D.; Lim, M.H.; Morrow, J.R. Metals in Biology: From Metallomics to Trafficking. Inorg. Chem. 2019, 58, 13505–13508. [Google Scholar] [CrossRef]
- Holm, R.H.; Kennepohl, P.; Solomon, E.I. Structural and functional aspects of metal sites in biology. Chem. Rev. 1996, 96, 2239–2314. [Google Scholar] [CrossRef] [PubMed]
- Brown, A.C.; Suess, D.L.M. An Open-Cuboidal [Fe3S4] Cluster Characterized in Both Biologically Relevant Redox States. J. Am. Chem. Soc. 2023, 145, 2075–2080. [Google Scholar] [CrossRef] [PubMed]
- Manicke, N.; Hoof, S.; Keck, M.; Braun-Cula, B.; Feist, M.; Limberg, C. A Hexanuclear Iron(II) Layer with Two Square-Planar FeO4 Units Spanned by Tetrasiloxide Ligands: Mimicking of Minerals and Catalysts. Inorg. Chem. 2017, 56, 8554–8561. [Google Scholar] [CrossRef]
- Nesterov, D.S.; Nesterova, O.V.; Pombeiro, A.J.L. Homo- and heterometallic polynuclear transition metal catalysts for alkane C-H bonds oxidative functionalization: Recent advances. Coord. Chem. Rev. 2018, 355, 199–222. [Google Scholar] [CrossRef]
- Doroshenko, I.; Babiak, M.; Buchholz, A.; Tucek, J.; Plass, W.; Pinkas, J. Hexanuclear iron(III) alpha-aminophosphonate: Synthesis, structure, and magnetic properties of a molecular wheel. New J. Chem. 2018, 42, 1931–1938. [Google Scholar] [CrossRef]
- Doroshenko, I.; Babiak, M.; Buchholz, A.; Görls, H.; Plass, W.; Pinkas, J. New molecular heptanuclear cobalt phosphonates: Synthesis, structures and magnetic properties. New J. Chem. 2018, 42, 9568–9577. [Google Scholar] [CrossRef]
- Kostakis, G.E.; Perlepes, S.P.; Blatov, V.A.; Proserpio, D.M.; Powell, A.K. High-nuclearity cobalt coordination clusters: Synthetic, topological and magnetic aspects. Coord. Chem. Rev. 2012, 256, 1246–1278. [Google Scholar] [CrossRef]
- Frost, J.M.; Harriman, K.L.M.; Murugesu, M. The rise of 3-d single-ion magnets in molecular magnetism: Towards materials from molecules? Chem. Sci. 2016, 7, 2470–2491. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Mrozek, J.; Ullah, A.; Duan, Y.; Baldoví, J.J.; Coronado, E.; Gaita-Ariño, A.; Ardavan, A. Quantum coherent spin–electric control in a molecular nanomagnet at clock transitions. NatPh 2021, 17, 1205–1209. [Google Scholar] [CrossRef]
- Boudalis, A.K. Half-Integer Spin Triangles: Old Dogs, New Tricks. Chem. Eur. J. 2021, 27, 7022–7042. [Google Scholar] [CrossRef] [PubMed]
- Cañón-Mancisidor, W.; Hermosilla-Ibáñez, P.; Spodine, E.; Paredes-García, V.; Gómez-García, C.J.; Espallargas, G.M.; Venegas-Yazigi, D. Slow Relaxation of the Magnetization on Frustrated Triangular FeIII Units with S = 1/2 Ground State: The Effect of the Highly Ordered Crystal Lattice and the Counteranions. Cryst. Growth Des. 2021, 21, 6213–6222. [Google Scholar] [CrossRef]
- Gangu, K.K.; Maddila, S.; Mukkamala, S.B.; Jonnalagadda, S.B. A review on contemporary Metal-Organic Framework materials. Inorg. Chim. Acta 2016, 446, 61–74. [Google Scholar] [CrossRef]
- Chen, T.-H.; Popov, I.; Kaveevivitchai, W.; Miljanic, O.S. Metal-Organic Frameworks: Rise of the Ligands. Chem. Mater. 2014, 26, 4322–4325. [Google Scholar] [CrossRef]
- Moulton, B.; Zaworotko, M.J. From molecules to crystal engineering: Supramolecular isomerism and polymorphism in network solids. Chem. Rev. 2001, 101, 1629–1658. [Google Scholar] [CrossRef]
- Kitagawa, S.; Kitaura, R.; Noro, S.-i. Functional Porous Coordination Polymers. Angew. Chem. Int. Ed. 2004, 43, 2334–2375. [Google Scholar] [CrossRef]
- Akintola, O.; Hornig, D.; Buchholz, A.; Görls, H.; Plass, W. Solvent-dependent selective cation exchange in anionic frameworks based on cobalt(II) and triphenylamine linkers: Reactor-dependent synthesis and sorption properties. Dalton Trans. 2017, 46, 8037–8050. [Google Scholar] [CrossRef]
- Akintola, O.; Ziegenbalg, S.; Buchholz, A.; Görls, H.; Plass, W. A robust anionic pillared-layer framework with triphenylamine-based linkers: Ion exchange and counterion-dependent sorption properties. CrystEngComm 2017, 19, 2723–2732. [Google Scholar] [CrossRef]
- Conerney, B.; Jensen, P.; Kruger, P.E.; MacGloinn, C. The ‘Trinity’ helix: Synthesis and structural characterisation of a C3-symmetric tris-bidentate ligand and its coordination to Ag(I). Chem. Commun. 2003, 11, 1274–1275. [Google Scholar] [CrossRef] [PubMed]
- Kisets, I.; Gelman, D. Carbometalated Complexes Possessing Tripodal Pseudo-C3-Symmetric Triptycene-Based Ligands. Organometallics 2018, 37, 526–529. [Google Scholar] [CrossRef]
- Lusby, P.J.; Müller, P.; Pike, S.J.; Slawin, A.M.Z. Stimuli-Responsive Reversible Assembly of 2D and 3D Metallosupramolecular Architectures. J. Am. Chem. Soc. 2009, 131, 16398–16400. [Google Scholar] [CrossRef]
- Liu, Y.; Xuan, W.; Zhang, H.; Cui, Y. Chirality- and Threefold-Symmetry-Directed Assembly of Homochiral Octupolar Metal−Organoboron Frameworks. Inorg. Chem. 2009, 48, 10018–10023. [Google Scholar] [CrossRef] [PubMed]
- Müller, I.M.; Möller, D. A New Ligand for the Formation of Triangular Building Blocks in Supramolecular Chemistry. Eur. J. Inorg. Chem. 2005, 2005, 257–263. [Google Scholar] [CrossRef]
- Müller, I.M.; Spillmann, S.; Franck, H.; Pietschnig, R. Rational Design of the First Closed Coordination Capsule with Octahedral Outer Shape. Chem. Eur. J. 2004, 10, 2207–2213. [Google Scholar] [CrossRef]
- Müller, I.M.; Möller, D.; Föcker, K. From a Monomer to a Protein-Sized, Doughnut-Shaped Coordination Oligomer—The Influence of Side Chains of C3-Symmetric Ligands in Supramolecular Chemistry. Chem. Eur. J. 2005, 11, 3318–3324. [Google Scholar] [CrossRef]
- Müller, I.M.; Robson, R.; Separovic, F. A metallosupramolecular capsule with the topology of the tetrahedron, 33, assembled from four guanidine-based ligands and twelve cadmium centers. Angew. Chem. Int. Ed. 2001, 40, 4385–4386. [Google Scholar] [CrossRef]
- Oppel, I.M.; Föcker, K. Rational design of a double-walled tetrahedron containing two different C3-symmetric ligands. Angew. Chem. Int. Ed. 2008, 47, 402–405. [Google Scholar] [CrossRef]
- Plass, W. Structural variety and magnetic properties of polynuclear assemblies based on 2-aminoglucose and tritopic triaminoguanidine ligands. Coord. Chem. Rev. 2009, 253, 2286–2295. [Google Scholar] [CrossRef]
- Böhme, M.; Ion, A.E.; Kintzel, B.; Buchholz, A.; Görls, H.; Plass, W. Pentanucletear Nickel(II) Complex with two Vertex-Shared Triaminoguanidine Fragments and Symmetric Capping Ligand. Z. Anorg. Allg. Chem. 2020, 646, 999–1009. [Google Scholar] [CrossRef]
- Zharkouskaya, A.; Görls, H.; Vaughan, G.; Plass, W. A new three-dimensional Cu(II) coordination polymer with triaminoguanidin building blocks. Inorg. Chem. Commun. 2005, 8, 1145–1148. [Google Scholar] [CrossRef]
- Zharkouskaya, A.; Buchholz, A.; Plass, W. A new coordination polymer architecture with (10,3)-a network containing chiral hydrophilic 3-D channels. Eur. J. Inorg. Chem. 2005, 2005, 4875–4879. [Google Scholar] [CrossRef]
- Plaul, D.; Böhme, M.; Ostrovsky, S.; Tomkowicz, Z.; Görls, H.; Haase, W.; Plass, W. Modeling Spin Interactions in a Triangular Cobalt(II) Complex with Triaminoguanidine Ligand Framework: Synthesis, Structure, and Magnetic Properties. Inorg. Chem. 2018, 57, 106–119. [Google Scholar] [CrossRef]
- Böhme, M.; Schuch, D.; Buchholz, A.; Görls, H.; Plass, W. Spin Interactions and Magnetic Anisotropy in a Triangular Nickel(II) Complex with Triaminoguanidine Ligand Framework. Z. Anorg. Allg. Chem. 2020, 646, 166–174. [Google Scholar] [CrossRef]
- Hamblin, J.; Tuna, F.; Bunce, S.; Childs, L.J.; Jackson, A.; Errington, W.; Alcock, N.W.; Nierengarten, H.; Van Dorsselaer, A.; Leize-Wagner, E.; et al. Supramolecular Circular Helicates Formed by Destabilisation of Supramolecular Dimers. Chem. Eur. J. 2007, 13, 9286–9296. [Google Scholar] [CrossRef]
- Kintzel, B.; Böhme, M.; Plaul, D.; Görls, H.; Yeche, N.; Seewald, F.; Klauss, H.-H.; Zvyagin, A.A.; Kampert, E.; Herrmannsdörfer, T.; et al. A Trinuclear High-Spin Iron(III) Complex with a Geometrically Frustrated Spin Ground State Featuring Negligible Magnetic Anisotropy and Antisymmetric Exchange. Inorg. Chem. 2023, 62, 3420–3430. [Google Scholar] [CrossRef]
- Spielberg, E.T.; Gilb, A.; Plaul, D.; Geibig, D.; Hornig, D.; Schuch, D.; Buchholz, A.; Ardavan, A.; Plass, W. A Spin-Frustrated Trinuclear Copper Complex Based on Triaminoguanidine with an Energetically Well-Separated Degenerate Ground State. Inorg. Chem. 2015, 54, 3432–3438. [Google Scholar] [CrossRef]
- Kintzel, B.; Böhme, M.; Liu, J.; Burkhardt, A.; Mrozek, J.; Buchholz, A.; Ardavan, A.; Plass, W. Molecular electronic spin qubits from a spin-frustrated trinuclear copper complex. Chem. Commun. 2018, 54, 12934–12937. [Google Scholar] [CrossRef]
- Liu, J.; Mrozek, J.; Myers, W.K.; Timco, G.A.; Winpenny, R.E.P.; Kintzel, B.; Plass, W.; Ardavan, A. Electric Field Control of Spins in Molecular Magnets. Phys. Rev. Lett. 2019, 122, 037202. [Google Scholar] [CrossRef]
- Ali, B.; Gendron, F.; Li, X.-L.; Le Guennic, B.; Tang, J. Cis and Trans Linkage of Spin Frustrated Copper Triangles Creating Cu6 Clusters. Chem. Sq. 2020, 4, 4. [Google Scholar] [CrossRef]
- Müller, I.M.; Möller, D.; Schalley, C.A. Rational design of tightly closed coordination tetrahedra that are stable in the solid state, in solution, and in the gas phase. Angew. Chem. Int. Ed. 2005, 44, 480–484. [Google Scholar] [CrossRef]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. Sect. C Struct. Chem. 2015, 71, 3–8. [Google Scholar] [CrossRef] [PubMed]
- Sheldrick, G.M. SHELXT—Integrated space-group and crystal-structure determination. Acta Crystallogr. Sect. A Found. Adv. 2015, 71, 3–8. [Google Scholar] [CrossRef] [PubMed]
- Bain, G.A.; Berry, J.F. Diamagnetic Corrections and Pascal’s Constants. J. Chem. Educ. 2008, 85, 532. [Google Scholar] [CrossRef]
- Roos, B.O.; Taylor, P.R.; Sigbahn, P.E.M. A complete active space SCF method (CASSCF) using a density matrix formulated super-CI approach. Chem. Phys. 1980, 48, 157–173. [Google Scholar] [CrossRef]
- Fdez. Galván, I.; Vacher, M.; Alavi, A.; Angeli, C.; Aquilante, F.; Autschbach, J.; Bao, J.J.; Bokarev, S.I.; Bogdanov, N.A.; Carlson, R.K.; et al. OpenMolcas: From Source Code to Insight. J. Chem. Theory Comput. 2019, 15, 5925–5964. [Google Scholar] [CrossRef]
- Roos, B.O.; Lindh, R.; Malmqvist, P.-Å.; Veryazov, V.; Widmark, P.-O. Main Group Atoms and Dimers Studied with a New Relativistic ANO Basis Set. J. Phys. Chem. A 2004, 108, 2851–2858. [Google Scholar] [CrossRef]
- Widmark, P.-O.; Malmqvist, P.-Å.; Roos, B.O. Density matrix averaged atomic natural orbital (ANO) basis sets for correlated molecular wave functions. Theor. Chim. Acta 1990, 77, 291–306. [Google Scholar] [CrossRef]
- Douglas, M.; Kroll, N.M. Quantum electrodynamical corrections to the fine structure of helium. Ann. Phys.-N. Y. 1974, 82, 89–155. [Google Scholar] [CrossRef]
- Hess, B.A. Applicability of the no-pair equation with free-particle projection operators to atomic and molecular structure calculations. Phys. Rev. A 1985, 32, 756–763. [Google Scholar] [CrossRef] [PubMed]
- Hess, B.A. Relativistic electronic-structure calculations employing a two-component no-pair formalism with external-field projection operators. Phys. Rev. A 1986, 33, 3742–3748. [Google Scholar] [CrossRef] [PubMed]
- Malmqvist, P.Å.; Roos, B.O.; Schimmelpfennig, B. The restricted active space (RAS) state interaction approach with spin–orbit coupling. Chem. Phys. Lett. 2002, 357, 230–240. [Google Scholar] [CrossRef]
- Bolvin, H. An Alternative Approach to the g-Matrix: Theory and Applications. Chemphyschem 2006, 7, 1575–1589. [Google Scholar] [CrossRef] [PubMed]
- Chibotaru, L.F.; Ungur, L. Ab initio calculation of anisotropic magnetic properties of complexes. I. Unique definition of pseudospin Hamiltonians and their derivation. J. Chem. Phys. 2012, 137, 064112. [Google Scholar] [CrossRef] [PubMed]
- Fonseca Guerra, C.; Snijders, J.G.; te Velde, G.; Baerends, E.J. Towards an order-N DFT method. Theor. Chem. Acc. 1998, 99, 391–403. [Google Scholar] [CrossRef]
- te Velde, G.; Bickelhaupt, F.M.; Baerends, E.J.; Fonseca Guerra, C.; van Gisbergen, S.J.A.; Snijders, J.G.; Ziegler, T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. [Google Scholar] [CrossRef]
- Baerends, A.J.A.; Atkins, E.J.Z.T.; Bashford, J.; Baseggio, D.; Bérces, O.; Bo, A.B.F.M.; Boerritger, C.; Cavallo, P.M.; Daul, L.; Chong, C.; et al. ADF2017, SCM, Theoretical Chemistry; Vrije Universiteit: Amsterdam, The Netherlands, 2017; Available online: https://www.scm.com (accessed on 1 January 2022).
- van Lenthe, E.; Baerends, E.J.; Snijders, J.G. Relativistic regular two-component Hamiltonians. J. Chem. Phys. 1993, 99, 4597–4610. [Google Scholar] [CrossRef]
- Ernzerhof, M.; Scuseria, G.E. Assessment of the Perdew–Burke–Ernzerhof exchange-correlation functional. J. Chem. Phys. 1999, 110, 5029–5036. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Salomon, O.; Reiher, M.; Hess, B.A. Assertion and validation of the performance of the B3LYP⋆ functional for the first transition metal row and the G2 test set. J. Chem. Phys. 2002, 117, 4729–4737. [Google Scholar] [CrossRef]
- Van Lenthe, E.; Baerends, E.J. Optimized Slater-type basis sets for the elements 1–118. J. Comput. Chem. 2003, 24, 1142–1156. [Google Scholar] [CrossRef] [PubMed]
- Noodleman, L. Valence bond description of antiferromagnetic coupling in transition metal dimers. J. Chem. Phys. 1981, 74, 5737–5743. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Fukui, H.; Fueno, T. Molecular Orbital (Mo) Theory for Magnetically Interacting Organic Compounds. Ab-Initio Mo Calculatins of The Effective Exchange Integrals for Cyclophane-Type Carbene Dimers. Chem. Lett. 1986, 15, 625–628. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Takahara, Y.; Fueno, T.; Houk, K.N. Extended Hartree-Fock (EHF) theory of chemical reactions. Theor. Chim. Acta 1988, 73, 337–364. [Google Scholar] [CrossRef]
- Fabrizi de Biani, F.; Ruiz, E.; Cano, J.; Novoa, J.J.; Alvarez, S. Magnetic Coupling in End-to-End Azido-Bridged Copper and Nickel Binuclear Complexes: A Theoretical Study. Inorg. Chem. 2000, 39, 3221–3229. [Google Scholar] [CrossRef]
- Cabrero, J.; de Graaf, C.; Bordas, E.; Caballol, R.; Malrieu, J.-P. Role of the Coordination of the Azido Bridge in the Magnetic Coupling of Copper(II) Binuclear Complexes. Chem. Eur. J. 2003, 9, 2307–2315. [Google Scholar] [CrossRef] [PubMed]
- Chastanet, G.; Guennic, B.L.; Aronica, C.; Pilet, G.; Luneau, D.; Bonnet, M.-L.; Robert, V. Tuning magnetic exchange using the versatile azide ligand. Inorg. Chim. Acta 2008, 361, 3847–3855. [Google Scholar] [CrossRef]
- Le Guennic, B.; Robert, V. From magnetic molecules to magnetic solids: An ab initio expertise. C R Chim. 2008, 11, 650–664. [Google Scholar] [CrossRef]
- Casanova, D.; Llunell, M.; Alemany, P.; Alvarez, S. The Rich Stereochemistry of Eight-Vertex Polyhedra: A Continuous Shape Measures Study. Chem. Eur. J. 2005, 11, 1479–1494. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, B.; David, G.; Gendron, F.; Li, X.-L.; Cador, O.; Plass, W.; Le Guennic, B.; Tang, J. A Cu12 Metallacycle Assembled from Four C3-Symmetric Spin Frustrated Triangular Units. Magnetochemistry 2023, 9, 122. https://doi.org/10.3390/magnetochemistry9050122
Ali B, David G, Gendron F, Li X-L, Cador O, Plass W, Le Guennic B, Tang J. A Cu12 Metallacycle Assembled from Four C3-Symmetric Spin Frustrated Triangular Units. Magnetochemistry. 2023; 9(5):122. https://doi.org/10.3390/magnetochemistry9050122
Chicago/Turabian StyleAli, Basharat, Grégoire David, Frédéric Gendron, Xiao-Lei Li, Olivier Cador, Winfried Plass, Boris Le Guennic, and Jinkui Tang. 2023. "A Cu12 Metallacycle Assembled from Four C3-Symmetric Spin Frustrated Triangular Units" Magnetochemistry 9, no. 5: 122. https://doi.org/10.3390/magnetochemistry9050122
APA StyleAli, B., David, G., Gendron, F., Li, X. -L., Cador, O., Plass, W., Le Guennic, B., & Tang, J. (2023). A Cu12 Metallacycle Assembled from Four C3-Symmetric Spin Frustrated Triangular Units. Magnetochemistry, 9(5), 122. https://doi.org/10.3390/magnetochemistry9050122