Abstract
As society becomes more reliant on Lithium-ion (Li-ion) batteries, state-of-health (SOH) estimation will need to become more accurate and reliable. Therefore, SOH modelling is in the process of shifting from using simple and continuous charge/discharge profiles to more dynamic profiles constructed to mimic real operation when ageing the Li-ion batteries. However, in most cases, when ageing the batteries, the same exact profile is just repeated until the battery reaches its end of life. Using data from batteries aged in this fashion to create a model, there is a very real possibility that the model will rely on the built-in repetitiveness of the profile. Therefore, this work will examine the dependence of the performance of a multiple linear regression on the number of charges used to train the model, and their location within the profile used to age the batteries. The investigation shows that it is possible to train models using randomly selected partial charges while still reaching errors as low as 0.5%. Furthermore, it shows that only one randomly sampled partial charge is needed to achieve errors smaller than 1%. Lastly, as the number of randomly sampled partial charges used to train the model increases, the dependence on particular partial charges tends to decrease.
1. Introduction
Society’s reliance on Lithium-ion (Li-ion) batteries is going to increase with the increased focus on electrification of the transportation sector and the shift to more volatile renewable energy sources. However, Li-ion batteries degrade over time, decreasing their available capacity and increasing their resistance, leading to decreasing acceleration and range in electric vehicles (EVs). Thus, determining a battery’s level of degradation, called its state of health (SOH), is important to both the safe operation and maintenance of the battery as well as the application in which the battery is operated.
Methods used to estimate the SOH of Li-ion batteries fall into one of three categories, physics-driven models, data-driven models, and hybrid models combining aspects of data-driven and physics-driven methods. The physics-driven methods aim to model the internal states and processes of the battery using physics, chemistry, and electrical circuits [1,2,3,4,5,6]. While they can be very accurate when tailored to a specific battery, they tend to be very computationally complicated and inaccurate if applied to different batteries. This is partly the reason for the rise in the use of data-driven methods. Of these methods, the most common include multiple linear regression (MLR) [7], support vector regression (SVR) [8,9,10,11], Gaussian process regression (GPR) [12,13,14,15,16,17,18], and neural networks (NN) [19,20,21,22,23]. It has been shown that if enough data are available, then these methods can be used to predict the SOH with very small errors. The main disadvantage of these methods is that they require lots of data and that most are very complex or essentially black-box methods. This has led to the development of hybrid methods combining data- and physics-driven methods [24,25,26]. These are usually divided into two types: the first uses data-driven methods to parameterise physics-driven methods, while the second uses physics to constrain the data-driven methods [25]. Both approaches are relatively new in the field of SOH estimation but have been applied to great effect in other areas of research.
Historically, data-driven SOH estimation models have been built using data created in extensive laboratory experiments. These data have typically been created by isolating a single stress factor at a time and observing its effect on the degradation of the battery. Furthermore, the charge/discharge pattern has tended to be continuous charging and discharging. However, it has been shown that the degradation of the battery is heavily influenced by its operation (and the order of this operation). Thus, it follows that for models to achieve good performance in actual operation, when the data are created using continuous charge/discharge, the number of conditions (or combinations of conditions) needs to be exhaustive. This is not only time- and resource-demanding but is also limited to the particular type of battery examined (i.e., the materials used to construct it, the manufacturer making it, and the version/generation for this manufacturer). Therefore, the field has, in recent years, started moving from creating models based on batteries subjected to these very simple continuous charge/discharge patterns, to batteries aged using more domain-specific operation profiles [27,28]. These profiles tend to be more dynamic and a better representation of the degradation behaviour in the specific context but are also harder to manage as they are more complex and tend to be sparser (in that there will be fewer complete charges or discharges).
With that said, in the case of the dynamic operation profiles in EVs, information about the battery charge capacity can be extracted every time the vehicle is charged, as the current is relatively consistent. Nevertheless, these charges are not complete, as the vehicle will never be entirely depleted, which would leave the operator of the vehicle stranded, resulting in only partial charges. Previous work on battery SOH estimation using partial charges has shown that information extracted from these can be used to predict the complete capacity of the battery with errors below 1%. However, these methods tend to rely on either extracting information from sub-sequences of the complete charge curve [29], which cannot be accessed in operation, extracting information from many partial charges [30], which makes the model either reliant on the number of partial charges needed to make predictions, or domain adaptation [30,31,32,33], which, in a lot of cases, requires fine-tuning. Furthermore, building and evaluating methods based on consistent profiles, even if they are dynamic, will lead to overfitting these methods to the data (including the profile) used to train them. Therefore, this work aims to examine the effect of the number of partial charges used to train the SOH estimation models and if a dependence on the location of a partial charge within a mission profile can be detected.
The remainder of the paper is organised as follows: the experimental data used to train the models are introduced in Section 2.1. This is followed by a more precise definition of the partial charges and the features extracted from these partial charges are presented in Section 2.2, after which Section 2.3 and Section 2.4 contain a short explanation of the state-of-health estimation model and feature selection used in this paper. The approaches used to study the sensitivity to, and importance of, the partial charges are found in Section 2.5. The results of the modelling, sensitivity, and importance are presented in Section 3. Lastly, conclusions are found in Section 4.
2. Materials and Methods
2.1. Forklifts and Realistic Load Profiles
Three Li-ion LFP battery cells were aged using a realistic forklift load profile of approximately two weeks. This profile was distilled from four months of field operation. The current and SOC of the resulting two-week profile is shown in Figure 1. Furthermore, to accelerate the ageing of the three cells, they were subjected to high temperatures during operation of 45, 40, and 35 °C, respectively.
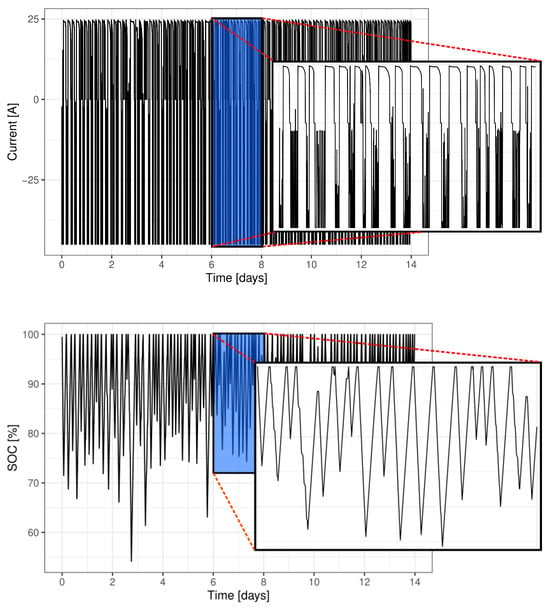
Figure 1.
The current and SOC of the two-week forklift profile used to age the Li-ion LFP cells.
At the end of every round of ageing (i.e., at the end of the two weeks of operation using the forklift profile), a reference performance test (RPT) is performed (at 25 °C) to assess the health of the battery (i.e., the capacity and resistance is measured). This two-step process was repeated until the cell aged at 45 °C reached end of life (80% of its initial capacity measurement). The resulting capacities obtained for each of the three cells can be seen in Figure 2. A more thorough introduction and description of the data used can be found in [28], and the data can be accessed at [34].
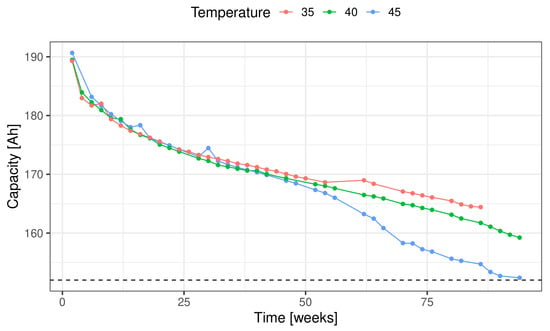
Figure 2.
The capacity measured during the RPT performed at the end of every round of ageing for each of the three cells.
2.2. Partial Charges
In most applications, obtaining an accurate measurement of the capacity is not possible during operation, as the cell will never be completely discharged (this is also illustrated by the SOC profile found in the right-hand panel of Figure 1). Thus, between two reference measurements, it is only possible to observe partial charges of the cell. The forklift profile, shown in Figure 1, contains more than 110 of these partial charges (depending slightly on the criteria used to determine the partial charges).
This can be incorporated into the model; given an appropriately chosen voltage interval, it is possible to relate the current accumulated within the interval during charging, , to the total capacity of the battery, Q, as shown in previous work [29,35]. A sketch of the general idea is shown in Figure 3; given a voltage interval from to , the amount of charge within the interval can be related to the total capacity of the cell. This idea has also been extended to other features extracted from the current, voltage, and temperature [30]. Given a sequence, , of length N, the following features are extracted as follows:
- Initial value of the sequence.
- Summation of the entire sequence, found as:
- Average value of the sequence, a measure of it centre, found as:
- Standard deviation (SD) of the sequence, a measure of squared deviation around the average, found as:
- Skewness of the sequence, a measure of asymmetry, found as:
- Kurtosis of the sequence, a measure of the tails of the distribution (when compared to the tails of a normal distribution), found as:
- Mean absolute deviation (MAD) of the sequence, a measure of absolute deviation around the average, found as:
- Largest difference of the sequence, a measure of the largest absolute difference, found as:
- Total difference of the sequence, a measure of the difference between the beginning and end, found as:
- Fuzzy entropy of the sequence, a measure of similarity of sequence, comparing repetitions in sub-sequences of size m and with sub-sequences of size simultaneously. A more thorough introduction can be found in [36].
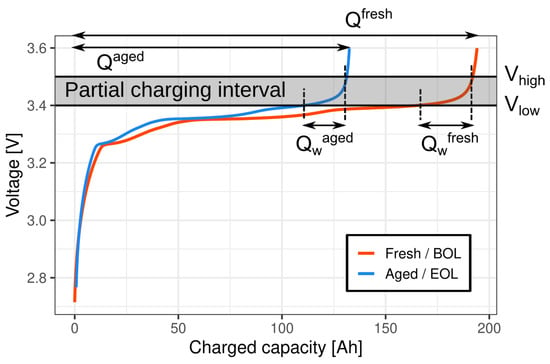
Figure 3.
A sketch of the partial charging concept. The charge measured within the voltage interval , denoted , changes as the battery ages, and can thus be compared to the total capacity of the cell Q.
Because the profile contains multiple partial charges, these features can be extracted multiple times between two consecutive RPT capacity measurements and are used to predict the reference capacity measured at the end of the two-week profile, as highlighted in Figure 4. The features extracted from the d’th partial charge in the n’th round of ageing will be denoted . An overview of what features are extracted for each type of signal (i.e., current, voltage, temperature, etc.) is marked with a cross (×) in Table 1. Note: the average is the only feature extracted from the temperature because the ambient temperature is kept very stable throughout the ageing process (for each cell). Furthermore, the fuzzy entropy is only extracted from the voltage, as it is very computationally intensive to extract. Lastly, the FEC at the beginning of each partial charge is also extracted (called the initial value of the current in Table 1.
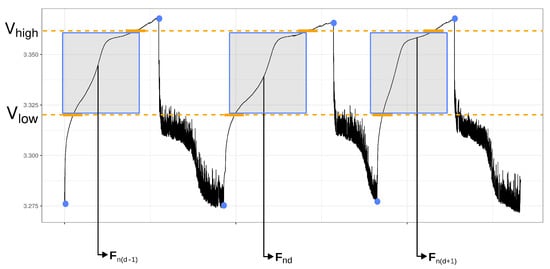
Figure 4.
The partial charging interval applied to a dynamic load profile.

Table 1.
The features extracted from each of the three measurement sequences. The features initially extracted from each sequence are marked by a cross (×). The features kept for further modelling after analysing the pairwise Pearson correlations are marked with a circle (◯).
The pair-wise Pearson correlations between the features and the logarithm of the capacity are shown in Figure 5. The figure shows that the pair-wise Pearson correlation between some features is very high. Because the model used to construct a relationship between features and capacity is multiple linear regression, a large correlation between features, called multicollinearity, can result in instabilities when training the model (due to linear dependence in columns of the matrix containing the features, i.e., the design matrix). Therefore, if a pair of features has a Pearson correlation above 0.8, then the feature with the smallest Pearson correlation to the logarithm of the capacity is eliminated from further consideration. The remaining features are marked with a circle (◯) in Table 1. Note: features are not excluded based on their Pearson correlation with the logarithm of the capacity, as interaction will be allowed in the multiple linear regression model.
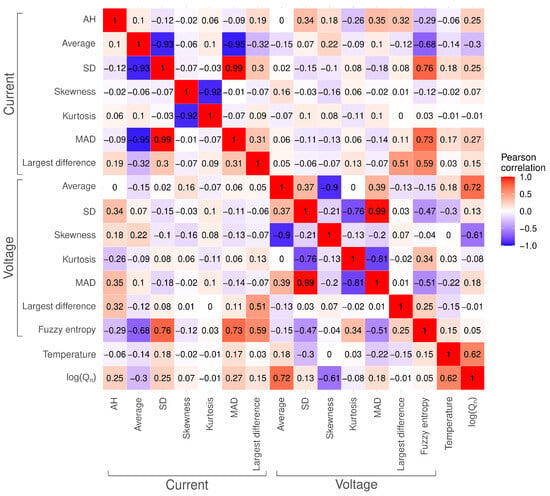
Figure 5.
Pearson correlation between the features and the logarithm of the capacity.
2.3. State-of-Health Modelling
The SOH prediction model used in this paper will be based on multiple linear regression (MLR). MLR maps the features extracted from each partial charge passing through the voltage interval, and the measured capacity at the end of every round of ageing using an affine transformation. MLR was chosen as it is simple, while still having the ability to achieve errors less than 0.5%. Furthermore, the focus is not on the choice of model but on investigating the sensitivity in both the amount of data and the dependence on where these data are extracted from on the performance of the model.
MLR defines a parametric relationship between the logarithm of the capacity, , and a vector containing all the extracted features, , as follows:
where p is the total number of extracted features, is the intercept, is the slope corresponding to feature i, is the interaction between features i and j, and is a random variable with mean 0 and variance accounting for noise.
The rounds of ageing are randomly split into two parts, a training set and validation set. Using the notation above, the complete set of parameters is then trained using the training set by ordinary least squares (OLS).
2.4. Step-Wise Feature Selection by Leave-One-Out Cross-Validation
In an effort to avoid overfitting, and produce simpler models, leave-one-out cross-validation (LOOCV) will be used on the training set to find the combination of features minimising the out-of-sample error. The LOOCV was chosen, as it can be calculated by training the model once using the entire training set. Given a vector of N capacity measurements, , a matrix of corresponding features F, and a vector of parameters, , trained using and F, then the LOOCV is found as:
where is a vector containing the features of the n’th round of ageing and d’th partial charge, and is the diagonal entry of the hat matrix, i.e., , corresponding to n’th round of ageing and d’th partial charge.
Step-wise selection, in both directions, using LOOCV as the measure of out-of-sample error, is employed to reduce the number of parameters in the model. That is, parameters, main effects and interactions (without breaking the hierarchical principle) are allowed to enter and leave the model if it reduces the LOOCV.
2.5. Sensitivity and Importance of Partial Charges
Firstly, in order to investigate the sensitivity in the number of partial charges on the performance of the model, a sequence of limits, , will be successively imposed to restrict the number of partial charges from each round of ageing used to train the model.
Secondly, to explore the importance of each partial charge—more specifically, its location within the two-week ageing period—three approaches will be compared when selecting partial charges for training:
- (1)
- Using the first L partial charges, i.e., the partial charges closest to the beginning of the round of ageing (and the previous reference measurement).
- (2)
- Using the last L partial charges, i.e., the partial charges closest to the end of the round of ageing (and the next reference measurement).
- (3)
- Using L partial charges selected at random with replacement, i.e., a partial charge can be used multiple times.
The first two approaches are introduced as reference methods, as these would be the most logical approach when implementing this model in an actual application. That is, the system either only has to store the features extracted from the first L, or the previous L, partial charges. The third approach will be used to explore the dependence of the model on particular partial charges. This is possible because the partial charges are chosen at random with replacement, which is equivalent to a type of bootstrapping called m-out-of-n bootstrapping [37]. As a consequence, the out-of-bag error (i.e., the error on the observations not used to train the model) can be evaluated, giving insight into the importance of each partial charge to the model. In each repetition, the root mean square error (RMSE) will be found for each partial charge not used to train the model, the out-of-bag RMSE, and averaged across repetitions. Furthermore, as the training process is also repeated in the third approach, it will be possible to examine the prevalence of each feature in the model, i.e., how often a feature is included in the across the 25 repetitions.
3. Results
The mean absolute percentage error (MAPE) for all three selection approaches introduced in Section 2.5 as a function of the number of partial charges used during the training of the models is shown in Figure 6. The results of the models using the first L partial charges, the last L partial charges, and the 25 repetitions of L randomly sampled partial charges are shown in red, green, and blue, respectively. The figure shows that whether using the first or last L partial charges behaves like expected, they are both decreasing as the number of partial charges increases and it is easier to create a model with good performance using partial charges from closer to the RPT measurement. What is surprising is the average performance of the random sampling approach starts around 0.6–0.7% error using a single randomly chosen partial charge and ends below 0.5%; for comparison, it takes 15 and 20 partial charges for the other two selection approaches to reach an MAPE similar to the starting MAPE of the random approach. However, it is worth noting that as the number of partial charges increases, the three methods converge.
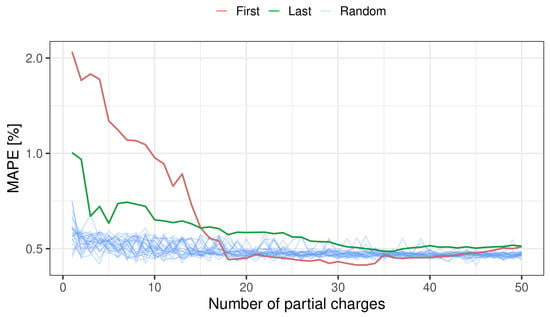
Figure 6.
The validation MAPE of the three partial charge selection approaches against the number of partial charges, from each round ageing, used to train the model.
The predictions for each model trained under all three selection approaches of partial charge locations are found in the first, second, and third rows of Figure 7, respectively. The figure shows the measured and predicted capacity against the full equivalent cycles (FEC), coloured by the number of partial charges from each round of ageing used to train the models. Furthermore, the measured capacity used for training and validation are shown as circles and triangles, respectively. In general, the panels show that as the number of partial charges used to train the models increases, the predicted capacity slowly tends toward the measured capacity. This is completely in line with what should be expected by examining Figure 6. Visually comparing the panels of the first and second approach (i.e., the first and second row, respectively), it looks like the former requires more partial charges than the latter. This makes intuitive sense, as the last partial charges are going to be closer to the reference measurement the model is trying to predict. This is again supported by the results found in Figure 6. The third row mostly corresponds with what was expected when looking at Figure 6. The exception is the panel of the results at 45 °C, showing a couple of rounds yielding large deviations between the predicted and measured capacity for small values of L. While this is not entirely surprising, these deviations seem quite isolated (compared to the first and second approaches), but decrease as the number of partial charges increases. It is also worth noting that these deviations occur for rounds used to train the model and are, therefore, not affecting the validation MAPE seen in Figure 6.
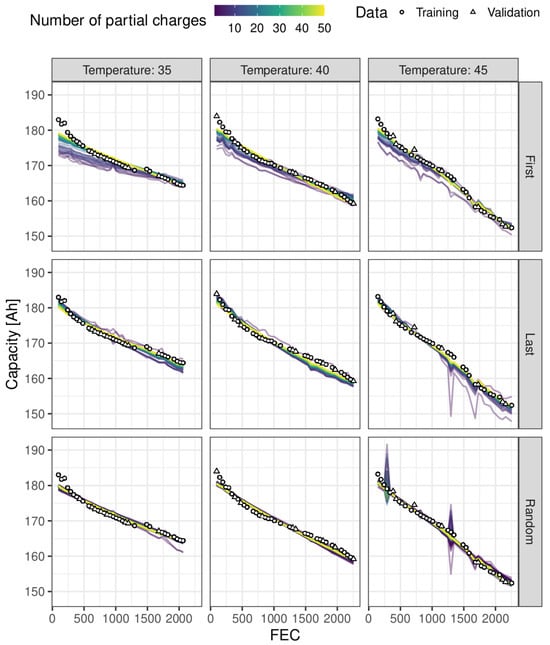
Figure 7.
The capacity against FEC, showing data used for training and validation as circles and triangles, respectively. The predictions of the MLR models, coloured by the number of partial charges, from each round, used to train the models, for both approaches are shown in the first and second row, respectively.
Figure 8 shows the average out-of-bag RMSE for each partial charge against the location of the partial charge in the two-week profile to examine its effect on model prediction. The resulting figure should be interpreted as the RMSE when the partial charge is not used to train the model. When the temperature is 35 and 40 °C, the out-of-bag RMSE is very low even when the number of partial charges used to train the model is relatively small. Furthermore, the out-of-bag RMSE decreases as the number of partial charges increases, thereby decreasing the reliance on a particular partial charge. However, while the same is mostly true at 45 °C, there do seem to be specific partial charges, which have a large effect on the performance of the model. This aligns with what was found in Figure 7. That is, the large deviations seen in Figure 7 are a direct consequence of over-reliance on these particular partial charges not being included in the training set (and vice versa).
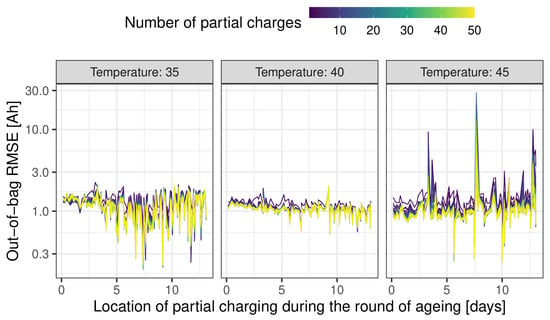
Figure 8.
The RMSE of the out-of-bag observations against the position of the partial charge in the two-week profile, coloured by the number of partial charges, from each round, to train the model.
Lastly, a heatmap of the prevalence of each feature is shown in Figure 9. The figure shows that the two most important features are FEC and temperature with a prevalence of 100% even using a single partial charge. Furthermore, as the number of partial charges used to create the model increases, the prevalence of the average and MAD of the voltage also increases, hitting a 100% prevalence at two and five partial charges, respectively. This is in line with the heatmap of Pearson correlation in Figure 5, as they are the two voltage features with the highest Pearson correlation (of those remaining after exclusion based on large pairwise Pearson correlation). The current features seem to be chosen less often in the beginning stages, but as the number of partial charges increases (increasing the degrees of freedom in the data), the average current and the skewness of the current become more prevalent. It follows that the voltage and current within the defined partial voltage interval can be represented by their first three central moments.
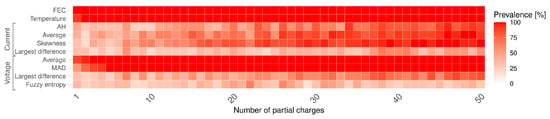
Figure 9.
The prevalence of each feature against the number of partial charges taken across the 25 bootstrap repetition.
4. Conclusions
The results show that if it is only possible to extract, or measure, a few partial charges between two reference measurements, then it is better for these to be sampled at random, rather than those found at either the beginning or the end of the round of ageing. This result is quite surprising, not just because the validation MAPE is smaller, but also for how long the random approach (for all repetitions!) outperformed the two other approaches. However, as is to be expected, when the number of available partial charges increases, the models built using a more consistent set of partial charges had superior performance. This could indicate that time (or the location of the partial charge within the round of ageing) is implicitly built into the model. While the dependence could be exploited, it is going to be difficult to determine whether or not this dependence is just an artefact of repeating the same profile in every round of ageing. Furthermore, while the reason for the difference between the non-random and random approaches is not entirely clear, the random sampling approach does seem to benefit in a couple of ways: (1) features extracted from partial charges in close proximity within the two-week profile seem to be more highly correlated, which can lead to instabilities when training an MLR, and (2) the partial charges are sampled entirely at random between reference measurements. It follows that the random sampling approach will create models covering more of the sample space, even with a very small number of partial charges. The two points combined mean that when using the random sampling approach the diversity of the data used to train the models is much larger when compared to the other two approaches, especially for a relatively small number of partial charges. This makes the random sampling approach much more robust to new information.
Further investigations into the dependence of particular partial charges for models built using the random sampling approach showed that while there can be some dependence when the model relies on a very small number of partial charges, it mostly disappears as the number of partial charges increases, at least for 35 and 40 °C. This dependence never seems to disappear entirely at 45 °C, which still exhibits some dependence on partial charges even as they increase in number. The reason is, again, not entirely clear. However, a likely hypothesis is that the battery aged at 45 °C degrades at a much higher rate and has points at which this degradation accelerates (e.g., around 50–55 weeks in Figure 7). Furthermore, this idea also extends to the amount of degradation within the two-week profile itself. That is, the difference between the capacity at the beginning and the end of the two-week profile is larger at 45 °C than at 35 and 40 °C. This results in a bigger discrepancy between the features extracted at the beginning and end of the profile.
Lastly, the prevalence of each of the features used to create the models built using the random sampling approach was explored. This investigation showed that the extracting FEC, temperature, and the first three central moments (i.e., average, variance, and skewness) are enough to create models with errors as low as 0.5%. This greatly simplifies the feature extraction process as these types of features can be extracted in an online fashion as the current, voltage, and temperature are measured.
Author Contributions
Conceptualization, S.B.V. and D.-I.S.; methodology, S.B.V. and D.-I.S.; software, S.B.V.; validation, S.B.V.; investigation, S.B.V. and D.-I.S.; resources, D.-I.S.; data curation, D.-I.S.; writing—original draft preparation, S.B.V. and D.-I.S.; writing—review and editing, S.B.V. and D.-I.S.; visualization, S.B.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author. Furthermore, data used in this article are publicly available [28].
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Prasad, G.; Rahn, C. Model based identification of aging parameters in lithium ion batteries. Power Sources 2013, 232, 79–85. [Google Scholar] [CrossRef]
- Zheng, L.; Zhang, L.; Zhu, J.; Wang, G.; Jiang, J. Co-estimation of state-of-charge, capacity and resistance for lithium-ion batteries based on a high-fidelity electrochemical model. Appl. Energy 2016, 180, 424–434. [Google Scholar] [CrossRef]
- Andre, D.; Meiler, M.; Steiner, K.; Walz, H.; Soczka-Guth, T.; Sauer, D.U. Characterization of high-power lithium-ion batteries by electrochemical impedance spectroscopy. II: Modelling. J. Power Sources 2011, 196, 5349–5356. [Google Scholar] [CrossRef]
- Chen, M.; Rincon-Mora, G.A. Accurate electrical battery model capable of predicting runtime and I-V performance. IEEE Trans. Energy Convers. 2006, 21, 504–511. [Google Scholar] [CrossRef]
- Hentunen, A.; Lehmuspelto, T.; Suomela, J. Time-Domain Parameter Extraction Method for Thevenin-Equivalent Circuit Battery Models. IEEE Trans. Energy Convers. 2014, 29, 558–566. [Google Scholar] [CrossRef]
- Stroe, D.I.; Swierczynski, M.; Stroe, A.I.; Knudsen Kær, S. Generalized Characterization Methodology for Performance Modelling of Lithium-Ion Batteries. Batteries 2016, 2, 37. [Google Scholar] [CrossRef]
- Vilsen, S.B.; Stroe, D.I. Battery state-of-health modelling by multiple linear regression. J. Clean. Prod. 2021, 290, 125700. [Google Scholar] [CrossRef]
- Klass, V.; Behm, M.; Lindbergh, G. A support vector machine-based state-of-health estimation method for lithium-ion batteries under electric vehicle operation. J. Power Sources 2014, 270, 262–272. [Google Scholar] [CrossRef]
- Patil, M.; Tagade, P.; Hariharan, K.; Kolake, S.; Song, T.; Yeo, T.; Doo, S. A novel multistage Support Vector Machine based approach for Li ion battery remaining useful life estimation. Appl. Energy 2015, 159, 285–297. [Google Scholar] [CrossRef]
- Zhao, Q.; Qin, X.; Zhao, H.; Feng, W. A novel prediction method based on the support vector regression for the remaining useful life of lithium-ion batteries. Microelectron. Reliab. 2018, 85, 99–108. [Google Scholar] [CrossRef]
- Shu, X.; Li, G.; Shen, J.; Lei, Z.; Chen, Z. A uniform estimation framework for state of health of lithium-ion batteries considering feature extraction and parameters optimization. Energy 2020, 204, 117957. [Google Scholar] [CrossRef]
- Liu, D.; Pang, J.; Zhou, J.; Peng, Y.; Pecht, M. Prognostics for state of health estimation of lithium-ion batteries based on combination Gaussian process functional regression. Microelectron. Reliab. 2013, 53, 832–839. [Google Scholar] [CrossRef]
- Richardson, R.; Osborne, M.; Howey, D. Gaussian process regression for forecasting battery state of health. J. Power Sources 2017, 357, 209–219. [Google Scholar] [CrossRef]
- Zhou, D.; Yin, H.; Fu, P.; Song, X.; Lu, W.; Yuan, L.; Fu, Z. Prognostics for State of Health of Lithium-Ion Batteries Based on Gaussian Process Regression. Math. Probl. Eng. 2018, 2018, 8358025. [Google Scholar] [CrossRef]
- Yu, J. State of health prediction of lithium-ion batteries: Multiscale logic regression and Gaussian process regression ensemble. Reliab. Eng. Syst. Saf. 2018, 174, 82–95. [Google Scholar] [CrossRef]
- Lyu, Z.; Gao, R. Li-ion battery state of health estimation through Gaussian process regression with Thevenin model. Int. J. Energy Res. 2020, 44, 10262–10281. [Google Scholar] [CrossRef]
- Jia, J.; Liang, J.; Shi, Y.; Wen, J.; Pang, X.; Zeng, J. SOH and RUL Prediction of Lithium-Ion Batteries Based on Gaussian Process Regression with Indirect Health Indicators. Energies 2020, 13, 375. [Google Scholar] [CrossRef]
- Feng, H.; Shi, G. SOH and RUL prediction of Li-ion batteries based on improved Gaussian process regression. J. Power Electron. 2021, 21, 1845–1854. [Google Scholar] [CrossRef]
- Yang, D.; Wang, Y.; Pan, R.; Chen, R.; Chen, Z. A neural network based state-of-health estimation of lithium-ion battery in electric vehicles. Energy Procedia 2017, 105, 2059–2064. [Google Scholar] [CrossRef]
- Kim, J.; Yu, J.; Kim, M.; Kim, K.; Han, S. Estimation of Li-ion State of Health based on Multilayer Perceptron as an EV Application. IFAC-Pap. 2018, 51, 392–397. [Google Scholar] [CrossRef]
- Chaoui, H.; Ibe-Ekeocha, C. State of Charge and State of Health Estimation for Lithium Batteries Using Recurrent Neural Networks. IEEE Trans. Veh. Technol. 2017, 66, 8773–8783. [Google Scholar] [CrossRef]
- You, G.; Park, S.; Oh, D. Diagnosis of electric vehicle batteries using recurrent neural networks. IEEE Trans. Ind. Electron. 2017, 64, 4885–4893. [Google Scholar] [CrossRef]
- Wu, Y.; Xue, Q.; Shen, J.; Lei, Z.; Chen, Z.; Liu, Y. State of Health Estimation for Lithium-Ion Batteries Based on Healthy Features and Long Short-Term Memory. IEEE Access 2020, 8, 28533–28547. [Google Scholar] [CrossRef]
- Bian, X.; Wei, Z.; Li, W.; Pou, J.; Sauer, D.U.; Liu, L. State-of-Health Estimation of Lithium-Ion Batteries by Fusing an Open Circuit Voltage Model and Incremental Capacity Analysis. IEEE Trans. Power Electron. 2022, 37, 2226–2236. [Google Scholar] [CrossRef]
- Guo, W.; Sun, Z.; Vilsen, S.B.; Meng, J.; Stroe, D.I. Review of “grey box” lifetime modeling for lithium-ion battery: Combining physics and data-driven methods. J. Energy Storage 2022, 56, 105992. [Google Scholar] [CrossRef]
- Guo, W.; Li, Y.; Sun, Z.; Vilsen, S.B.; Stroe, D.I. A digital twin to quantitatively understand aging mechanisms coupled effects of NMC battery using dynamic aging profiles. Energy Storage Mater. 2023, 63, 102965. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, J.; Lund, P.D.; Zhang, Y. Estimation and prediction of state of health of electric vehicle batteries using discrete incremental capacity analysis based on real driving data. Energy 2021, 225, 120160. [Google Scholar] [CrossRef]
- Vilsen, S.; Stroe, D. Dataset of lithium-ion battery degradation based on a forklift mission profile for state-of-health estimation and lifetime prediction. Data Brief 2024, 52, 109861. [Google Scholar] [CrossRef] [PubMed]
- Meng, J.; Cai, L.; Stroe, D.I.; Luo, G.; Sui, X.; Teodorescu, R. Lithium-ion battery state-of-health estimation in electric vehicle using optimized partial charging voltage profiles. Energy 2019, 185, 1054–1062. [Google Scholar] [CrossRef]
- Vilsen, S.B.; Stroe, D.I. Transfer Learning for Adapting Battery State-of-Health Estimation From Laboratory to Field Operation. IEEE Access 2022, 10, 26514–26528. [Google Scholar] [CrossRef]
- Tan, Y.; Zhao, G. Transfer Learning with Long Short-Term Memory Network for State-of-Health Prediction of Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 2020, 67, 8723–8731. [Google Scholar] [CrossRef]
- Kim, S.; Choi, Y.; Kim, K.; Choi, J. Forecasting state-of-health of lithium-ion batteries using variational long short-term memory with transfer learning. Energy Storage 2021, 41, 102893. [Google Scholar] [CrossRef]
- Che, Y.; Forest, F.; Zheng, Y.; Xu, L.; Teodorescu, R. Health Prediction for Lithium-Ion Batteries Under Unseen Working Conditions. IEEE Trans. Ind. Electron. 2024; early access. [Google Scholar] [CrossRef]
- Vilsen, S.; Stroe, D. Lithium-Ion Battery Degradation Dataset Based on a Realistic Forklift Operation Profile. Mendeley Data, V2. 2023. Available online: https://data.mendeley.com/datasets/yz4pttm73n/2 (accessed on 28 May 2024).
- Stroe, D.I.; Knap, V.; Schaltz, E. State-of-Health Estimation of Lithium-Ion Batteries Based on Partial Charging Voltage Profiles. ECS Trans. 2018, 85, 379. [Google Scholar] [CrossRef]
- Chen, W.; Wang, Z.; Xie, H.; Yu, W. Characterization of Surface EMG Signal Based on Fuzzy Entropy. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 266–272. [Google Scholar] [CrossRef]
- Alin, A.; Martin, M.; Beyaztas, U.; Pathak, P. Sufficient m-out-of-n (m/n) bootstrap. J. Stat. Comput. Simul. 2017, 87, 1742–1753. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).