Fault Diagnosis for Lithium-Ion Battery Pack Based on Relative Entropy and State of Charge Estimation
Abstract
:1. Introduction
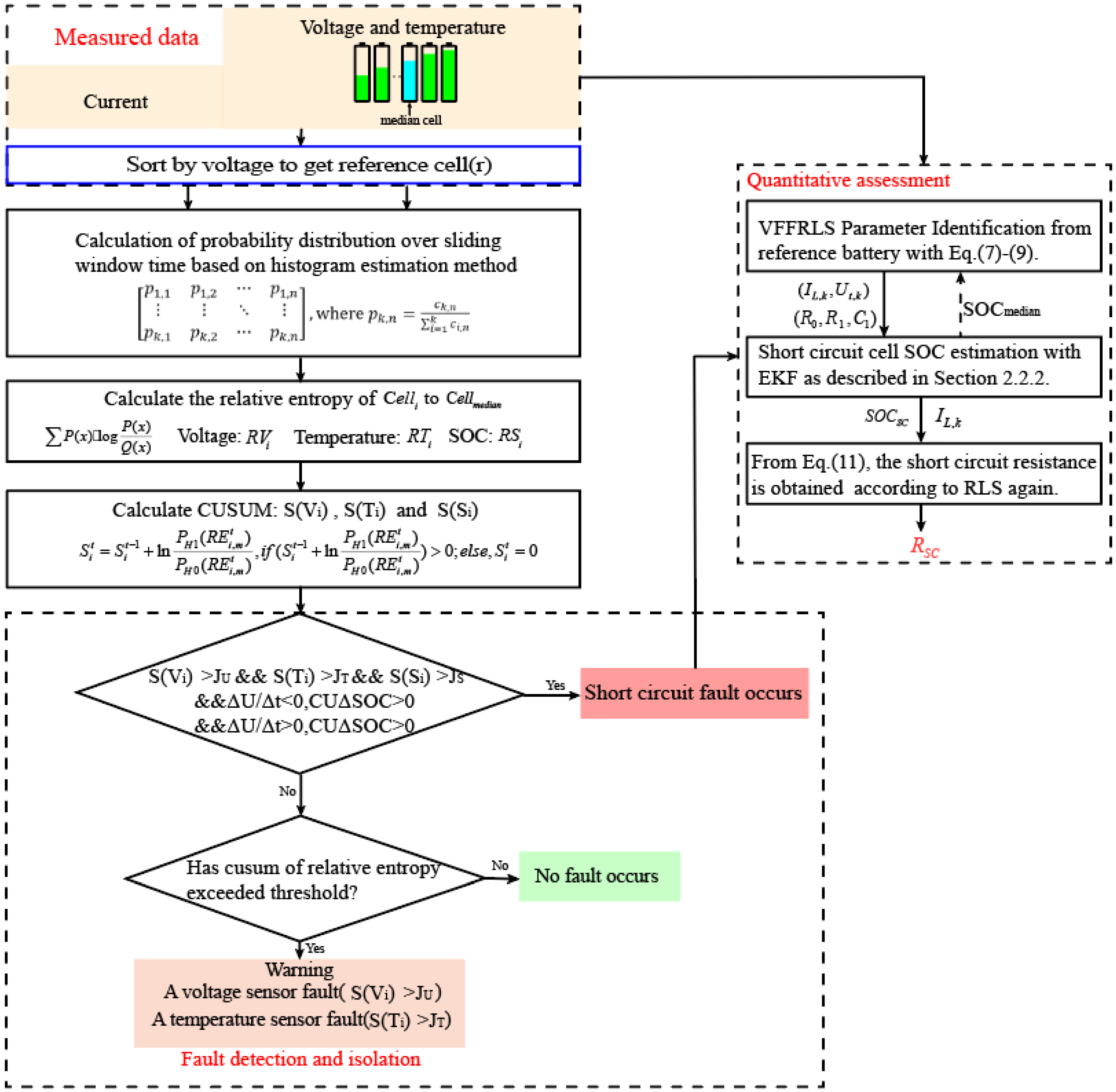
2. Methods
2.1. Description of Relative Entropy Method
2.1.1. Relative Entropy Calculation
2.1.2. Relative Entropy Evaluation
2.2. Quantitative Assessment Method of Short-Circuit Fault
2.2.1. Online Parameter Identification
2.2.2. Short-Circuit Resistance Estimation Based on SOC
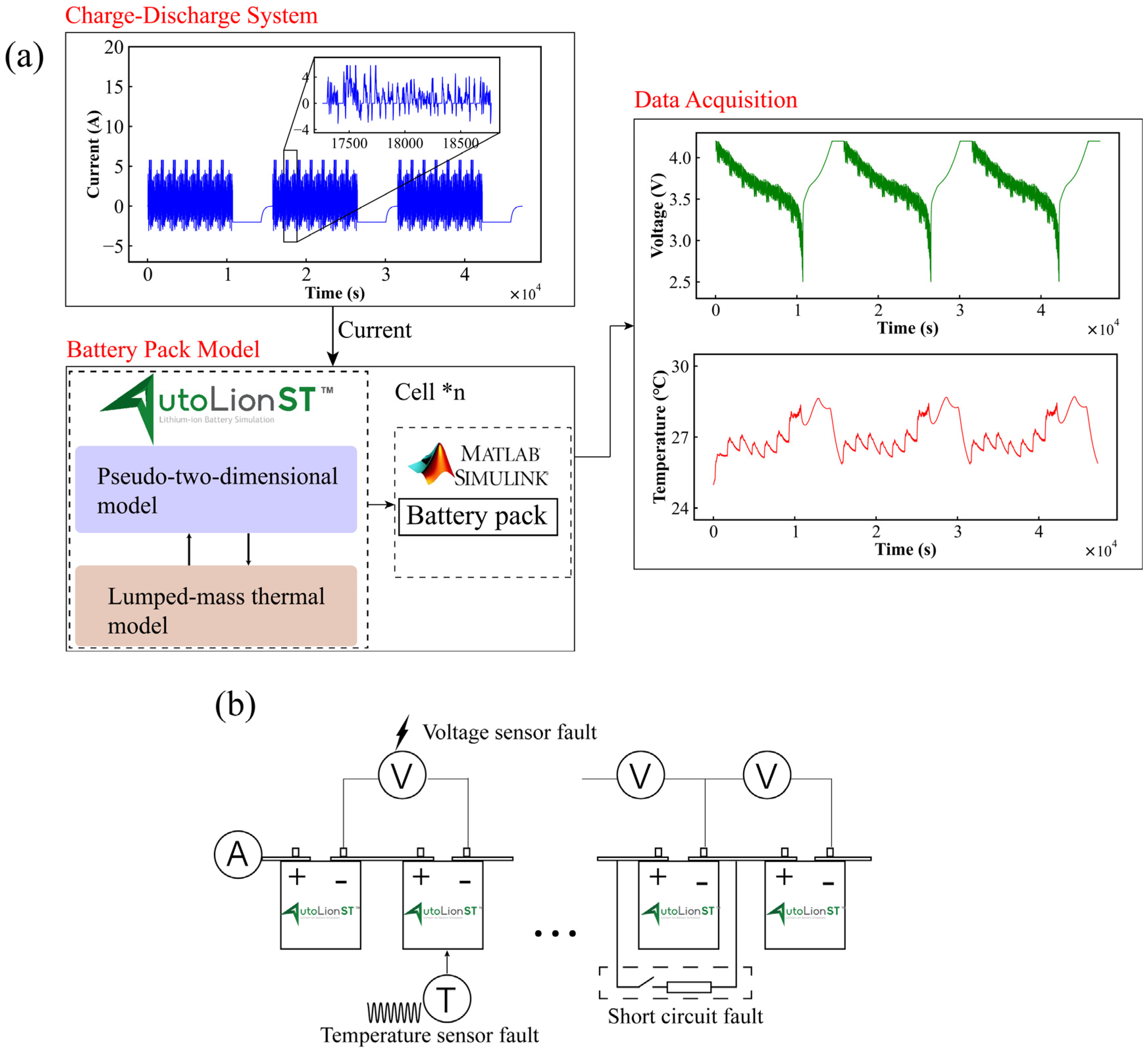
3. Results and Discussion
3.1. Data Preparation and Preprocessing
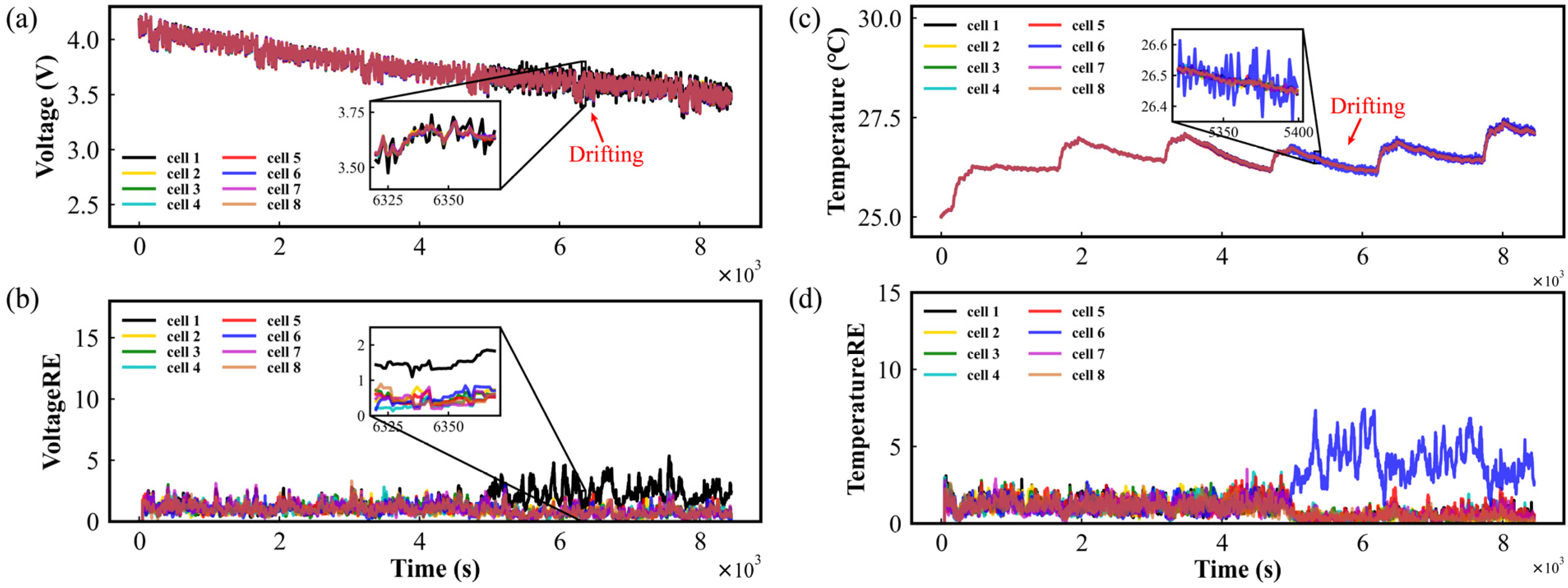
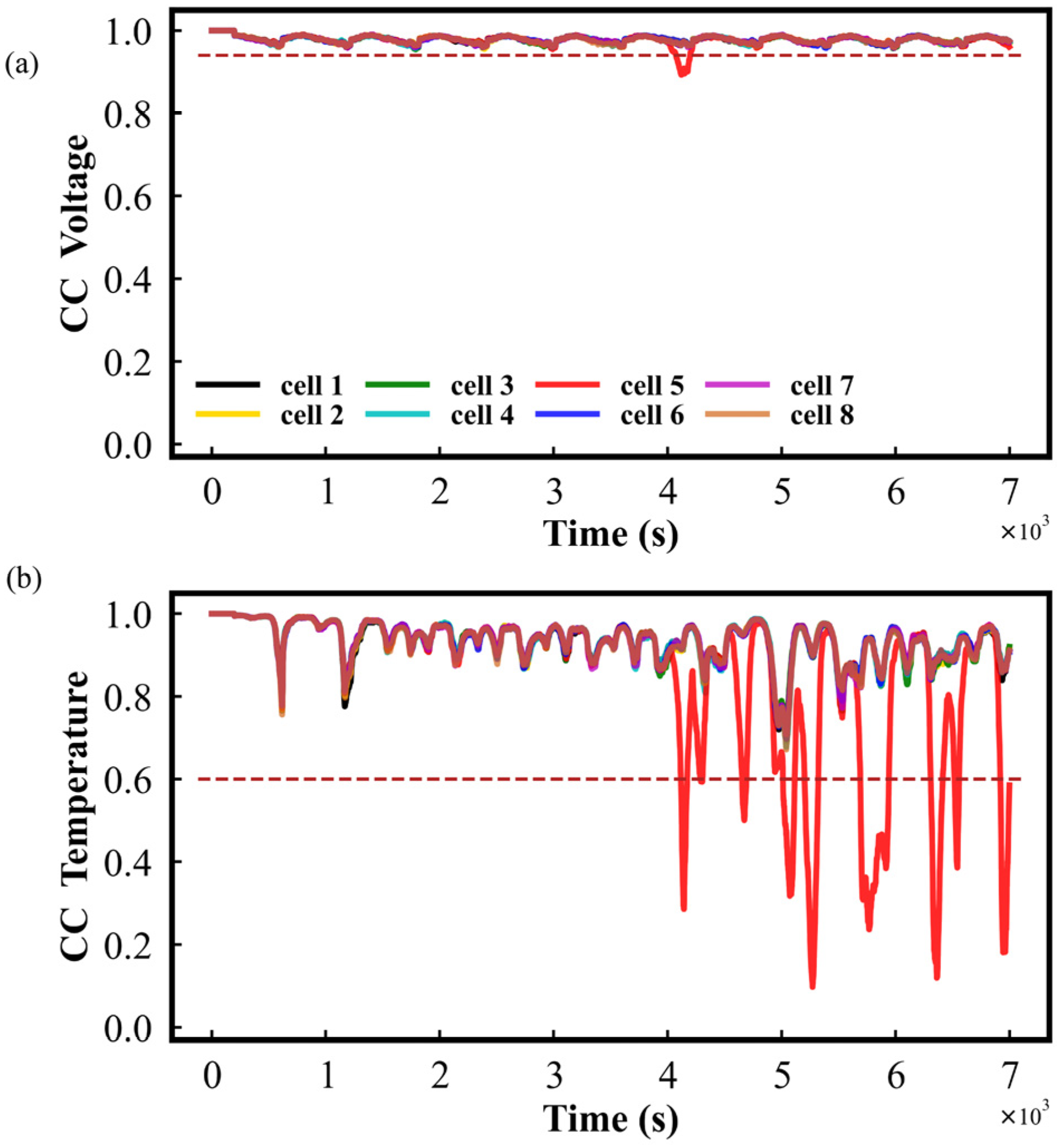
3.2. The Relative Entropy Calculation at Normal Condition
3.3. The Results of Fault Diagnosis under FUDS Conditions
3.3.1. The Results of Sensor Faults Diagnosis
3.3.2. The Results of Short-Circuit Fault Diagnosis
3.4. Method Comparison under US06 Condition
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xiong, R.; Sun, W.; Yu, Q.; Sun, F. Research progress, challenges and prospects of fault diagnosis on battery system of electric vehicles. Appl. Energy 2020, 279, 115855. [Google Scholar] [CrossRef]
- Qiao, D.; Wei, X.; Fan, W.; Jiang, B.; Lai, X.; Zheng, Y.; Tang, X.; Dai, H. Toward safe carbon-neutral transportation: Battery internal short circuit diagnosis based on cloud data for electric vehicles. Appl. Energy 2022, 317, 119168. [Google Scholar] [CrossRef]
- Yang, T.; Zheng, Y.; Liu, Y.; Luo, D.; Yu, A.; Chen, Z. Reviving low-temperature performance of lithium batteries by emerging electrolyte systems. Renewables 2023, 1, 2–20. [Google Scholar] [CrossRef]
- Pan, Y.; Feng, X.; Zhang, M.; Han, X.; Lu, L.; Ouyang, M. Internal short circuit detection for lithium-ion battery pack with parallel-series hybrid connections. J. Clean. Prod. 2020, 255, 120277. [Google Scholar] [CrossRef]
- Zhang, J.N.; Zhang, L.; Sun, F.C.; Wang, Z.P. An Overview on Thermal Safety Issues of Lithium-ion Batteries for Electric Vehicle Application. IEEE Access 2018, 6, 23848–23863. [Google Scholar] [CrossRef]
- Gan, N.F.; Sun, Z.Y.; Zhang, Z.S.; Xu, S.Q.; Liu, P.; Qin, Z.A. Data-Driven Fault Diagnosis of Lithium-Ion Battery Overdischarge in Electric Vehicles. IEEE Trans. Power Electron. 2022, 37, 4575–4588. [Google Scholar] [CrossRef]
- Seo, M.; Park, M.; Song, Y.; Kim, S.W. Online Detection of Soft Internal Short Circuit in Lithium-Ion Batteries at Various Standard Charging Ranges. IEEE Access 2020, 8, 70947–70959. [Google Scholar] [CrossRef]
- Ouyang, M.G.; Zhang, M.X.; Feng, X.N.; Lu, L.G.; Li, J.Q.; He, X.M.; Zheng, Y.J. Internal short circuit detection for battery pack using equivalent parameter and consistency method. J. Power Sources 2015, 294, 272–283. [Google Scholar] [CrossRef]
- Zhu, X.Q.; Wang, Z.P.; Wang, Y.T.; Wang, H.; Wang, C.; Tong, L.; Yi, M. Overcharge investigation of large format lithium-ion pouch cells with Li(Ni0.6Co0.2Mn0.2)O2 cathode for electric vehicles: Thermal runaway features and safety management method. Energy 2019, 169, 868–880. [Google Scholar] [CrossRef]
- Xiong, R.; Yu, Q.Q.; Shen, W.X.; Lin, C.; Sun, F.C. A Sensor Fault Diagnosis Method for a Lithium-Ion Battery Pack in Electric Vehicles. IEEE Trans. Power Electron. 2019, 34, 9709–9718. [Google Scholar] [CrossRef]
- Zhang, K.; Hu, X.S.; Liu, Y.G.; Lin, X.K.; Liu, W.X. Multi-fault Detection and Isolation for Lithium-Ion Battery Systems. IEEE Trans. Power Electron. 2022, 37, 971–989. [Google Scholar] [CrossRef]
- Gao, W.K.; Zheng, Y.J.; Ouyang, M.G.; Li, J.Q.; Lai, X.; Hu, X.S. Micro-Short-Circuit Diagnosis for Series-Connected Lithium-Ion Battery Packs Using Mean-Difference Model. IEEE Trans. Ind. Electron. 2019, 66, 2132–2142. [Google Scholar] [CrossRef]
- Hu, J.; He, H.W.; Wei, Z.B.; Li, Y. Disturbance-Immune and Aging-Robust Internal Short Circuit Diagnostic for Lithium-Ion Battery. IEEE Trans. Ind. Electron. 2022, 69, 1988–1999. [Google Scholar] [CrossRef]
- Liu, Z.T.; He, H.W. Sensor fault detection and isolation for a lithium-ion battery pack in electric vehicles using adaptive extended Kalman filter. Appl. Energy 2017, 185, 2033–2044. [Google Scholar] [CrossRef]
- Naha, A.; Khandelwal, A.; Agarwal, S.; Tagade, P.; Hariharan, K.S.; Kaushik, A.; Yadu, A.; Kolake, S.M.; Han, S.; Oh, B. Internal short circuit detection in Li-ion batteries using supervised machine learning. Sci. Rep. 2020, 10, 1301. [Google Scholar] [CrossRef] [PubMed]
- Kang, Y.Z.; Duan, B.; Zhou, Z.K.; Shang, Y.L.; Zhang, C.H. A multi-fault diagnostic method based on an interleaved voltage measurement topology for series connected battery packs. J. Power Sources 2019, 417, 132–144. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, P.; Wang, Z.P.; Zhang, L.; Hong, J.C. Fault and defect diagnosis of battery for electric vehicles based on big data analysis methods. Appl. Energy 2017, 207, 354–362. [Google Scholar] [CrossRef]
- Shang, Y.L.; Lu, G.P.; Kang, Y.Z.; Zhou, Z.K.; Duan, B.; Zhang, C.H. A multi-fault diagnosis method based on modified Sample Entropy for lithium-ion battery strings. J. Power Sources 2020, 446, 227275. [Google Scholar] [CrossRef]
- Wang, Z.P.; Hong, J.C.; Liu, P. Voltage fault diagnosis and prognosis of battery systems based on entropy and Z-score for electric vehicles. Appl. Energy 2017, 196, 289–302. [Google Scholar] [CrossRef]
- Chen, Z.H.; Xu, K.; Wei, J.W.; Dong, G.Z. Voltage fault detection for lithium-ion battery pack using local outlier factor. Measurement 2019, 146, 544–556. [Google Scholar] [CrossRef]
- Li, X.Y.; Wang, Z.P. A novel fault diagnosis method for lithium-Ion battery packs of electric vehicles. Measurement 2018, 116, 402–411. [Google Scholar] [CrossRef]
- Ma, G.; Xu, S.; Cheng, C. Fault detection of lithium-ion battery packs with a graph-based method. J. Energy Storage 2021, 43, 103209. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, Z.; Liu, P.; Zhang, Z.; Wang, S.; Dorrell, D.G. Relative Entropy based Lithium-ion Battery Pack Short Circuit Detection for Electric Vehicle. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 5061–5067. [Google Scholar] [CrossRef]
- Yao, L.; Wang, Z.P.; Ma, J. Fault detection of the connection of lithium-ion power batteries based on entropy for electric vehicles. J. Power Sources 2015, 293, 548–561. [Google Scholar] [CrossRef]
- Blanke, M.; Kinnaert, M.; Lunze, J.; Staroswiecki, M. Diagnosis and Fault-Tolerant Control, 3rd ed.; Springer: Berlin, Germany, 2016. [Google Scholar]
- Zheng, Y.; Shen, A.; Han, X.; Ouyang, M. Quantitative short circuit identification for single lithium-ion cell applications based on charge and discharge capacity estimation. J. Power Sources 2022, 517, 230716. [Google Scholar] [CrossRef]
- Kang, Y.Z.; Duan, B.; Zhou, Z.K.; Shang, Y.L.; Zhang, C.H. Online multi-fault detection and diagnosis for battery packs in electric vehicles. Appl. Energy 2020, 259, 114170. [Google Scholar] [CrossRef]
- Qiu, Y.S.; Cao, W.J.; Peng, P.; Jiang, F.M. A novel entropy-based fault diagnosis and inconsistency evaluation approach for lithium-ion battery energy storage systems. J. Energy Storage 2021, 41, 102852. [Google Scholar] [CrossRef]
- Xu, J.; Wang, H.T.; Shi, H.; Mei, X.S. Multi-scale short circuit resistance estimation method for series connected battery strings. Energy 2020, 202, 117647. [Google Scholar] [CrossRef]
- Gu, W.B.; Wang, C.Y. Thermal and electrochemical coupled modeling of a lithium-ion cell in lithium batteries. ECS Proc. 2000, 99, 748–762. [Google Scholar]
- Srinivasan, V.; Wang, C.Y. Analysis of electrochemical and thermal behavior of Li-ion cells. J. Electrochem. Soc. 2003, 150, A98–A106. [Google Scholar] [CrossRef]
- Smith, K.; Wang, C.Y. Power and thermal characterization of a lithium-ion battery pack for hybrid-electric vehicles. J. Power Sources 2006, 160, 662–673. [Google Scholar] [CrossRef]
- Fang, W.F.; Kwon, O.J.; Wang, C.Y. Electrochemical-thermal modeling of automotive Li-ion batteries and experimental validation using a three-electrode cell. Int. J. Energy Res. 2010, 34, 107–115. [Google Scholar] [CrossRef]
- USABC. Electric Vehicle Battery Test Procedures Manual. Revision 2, United States; U.S. Department of Energy Office of Scientific and Technical Information: Oak Ridge, TN, USA, 1996. [Google Scholar] [CrossRef]
- Feng, X.N.; Pan, Y.; He, X.M.; Wang, L.; Ouyang, M.G. Detecting the internal short circuit in large-format lithium-ion battery using model-based fault-diagnosis algorithm. J. Energy Storage 2018, 18, 26–39. [Google Scholar] [CrossRef]
- Xia, B.; Shang, Y.; Nguyen, T.; Mi, C. A correlation based fault detection method for short circuits in battery packs. J. Power Sources 2017, 337, 1–10. [Google Scholar] [CrossRef]



| Parameters (Units) | Value |
|---|---|
| Positive electrode material | NCM111 |
| Negative electrode material | GRAPHITE |
| Diameter × Height (mm) | 18.6 × 65.2 |
| Cell weight (g) | 43.39 |
| Nominal capacity (Ah) | 2.15@1 C |
| Nominal voltage (V) | 3.65 |
| Discharge cutoff voltage (V) | 2.5 |
| Charge cutoff voltage (V) | 4.2 |
| Fault Type | Cell No. | Fault Description | Fault Level | Trigger Time |
|---|---|---|---|---|
| Short-circuit | 5 | Resistance (Ω) | 5/10 | 4000 s |
| Voltage Sensor | 1 | Drift (V) | 0.02/0.05 | 5000 s |
| Temperature Sensor | 6 | Drift (°C) | 0.2/0.5 | 5000 s |
| Methods | FUDS | US06 | ||
|---|---|---|---|---|
| Proposed method | Fault type | Detection time (s) | Fault type | Detection time (s) |
| ISC (5 Ω) | 111 | ISC (5 Ω) | 77 | |
| ISC (10 Ω) | 200 | ISC (10 Ω) | 121 | |
| Correlation coefficient method | ISC (5 Ω) | 281 | ISC (5 Ω) | 89 |
| ISC (10 Ω) | 765 | ISC (10 Ω) | 298 | |
| Conditions | Short-Circuit Degree (Ω) | Standard Deviation Error (Ω) | Mean Absolute Error (Ω) |
|---|---|---|---|
| FUDS | 5 | 0.12 | 0.17 |
| 10 | 0.33 | 0.42 | |
| US06 | 5 | 0.13 | 0.21 |
| 10 | 0.37 | 0.51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, T.-E.; Chen, F.; Lei, H.-R.; Tang, X.; Feng, F. Fault Diagnosis for Lithium-Ion Battery Pack Based on Relative Entropy and State of Charge Estimation. Batteries 2024, 10, 217. https://doi.org/10.3390/batteries10070217
Fan T-E, Chen F, Lei H-R, Tang X, Feng F. Fault Diagnosis for Lithium-Ion Battery Pack Based on Relative Entropy and State of Charge Estimation. Batteries. 2024; 10(7):217. https://doi.org/10.3390/batteries10070217
Chicago/Turabian StyleFan, Tian-E, Fan Chen, Hao-Ran Lei, Xin Tang, and Fei Feng. 2024. "Fault Diagnosis for Lithium-Ion Battery Pack Based on Relative Entropy and State of Charge Estimation" Batteries 10, no. 7: 217. https://doi.org/10.3390/batteries10070217






