A Physics–Guided Machine Learning Approach for Capacity Fading Mechanism Detection and Fading Rate Prediction Using Early Cycle Data
Abstract
:1. Introduction
2. Data Generation
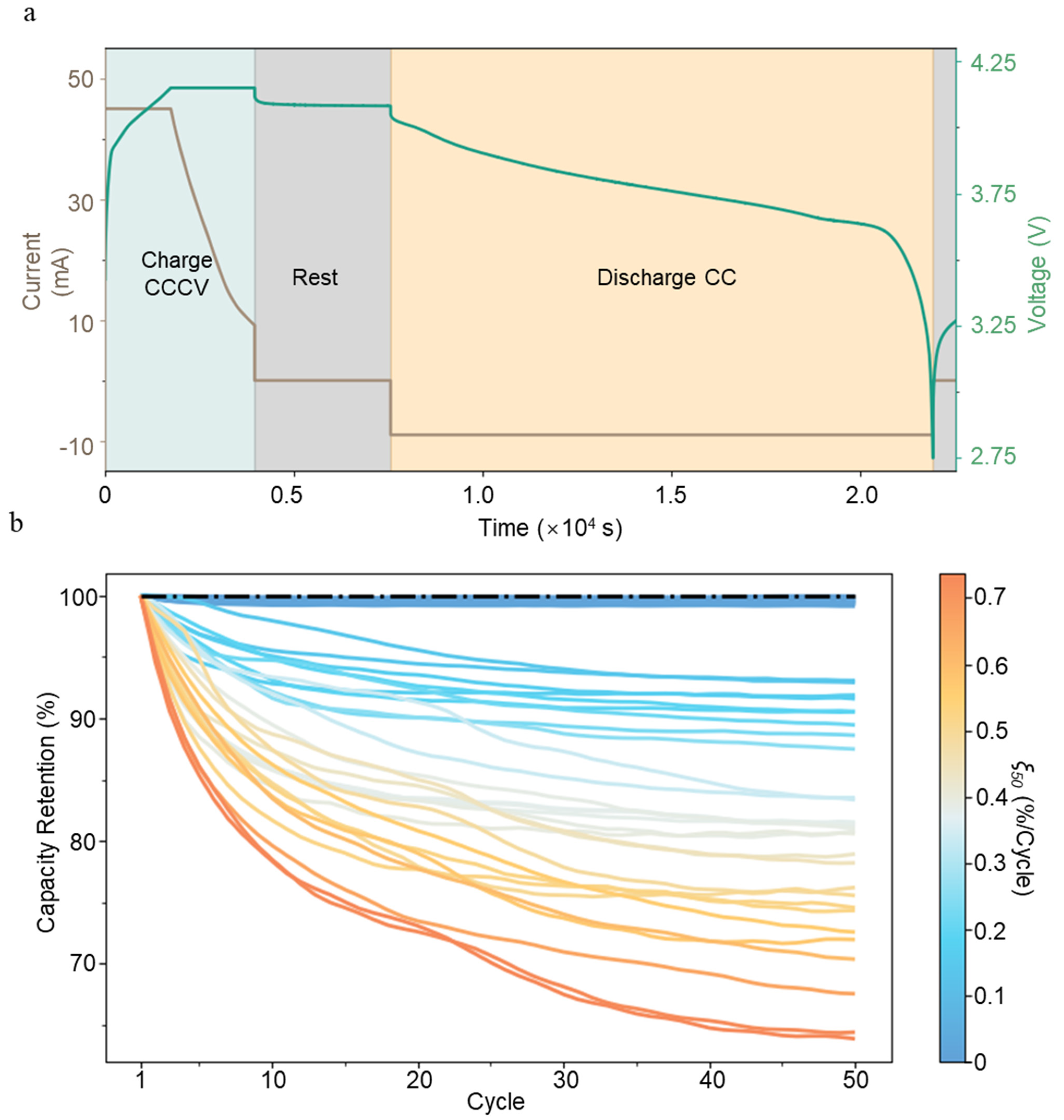
- The first data stream contains the voltage of the battery, V(t), during cycling (Figure 1a). The side reactions inside the battery, lithium deposits on the graphite anode, and the growth of the SEI cause the battery capacity to decay. Their effects are manifested in the shape of the V(t) curve. Therefore, the features from the V(t) and I(t) curves contain physical information about side reactions. For example, incremental capacity analysis can be conducted, and features such as peak location and peak area can be used to identify the fading mode [26]. Note that I(t) is predetermined as the input for battery cycling for constant current charge and discharge.
- The second data stream contains the discharging capacity C(N) and Faraday efficiency η(N) for each cycle (Figure 1b). N refers to the battery cycle number. C(N) is used to calculate the rate of capacity fading. The normalized capacity of each battery is shown in Figure 1b. Based on this data stream, the average capacity fading rate at the Nth cycle, , is calculated as follows:
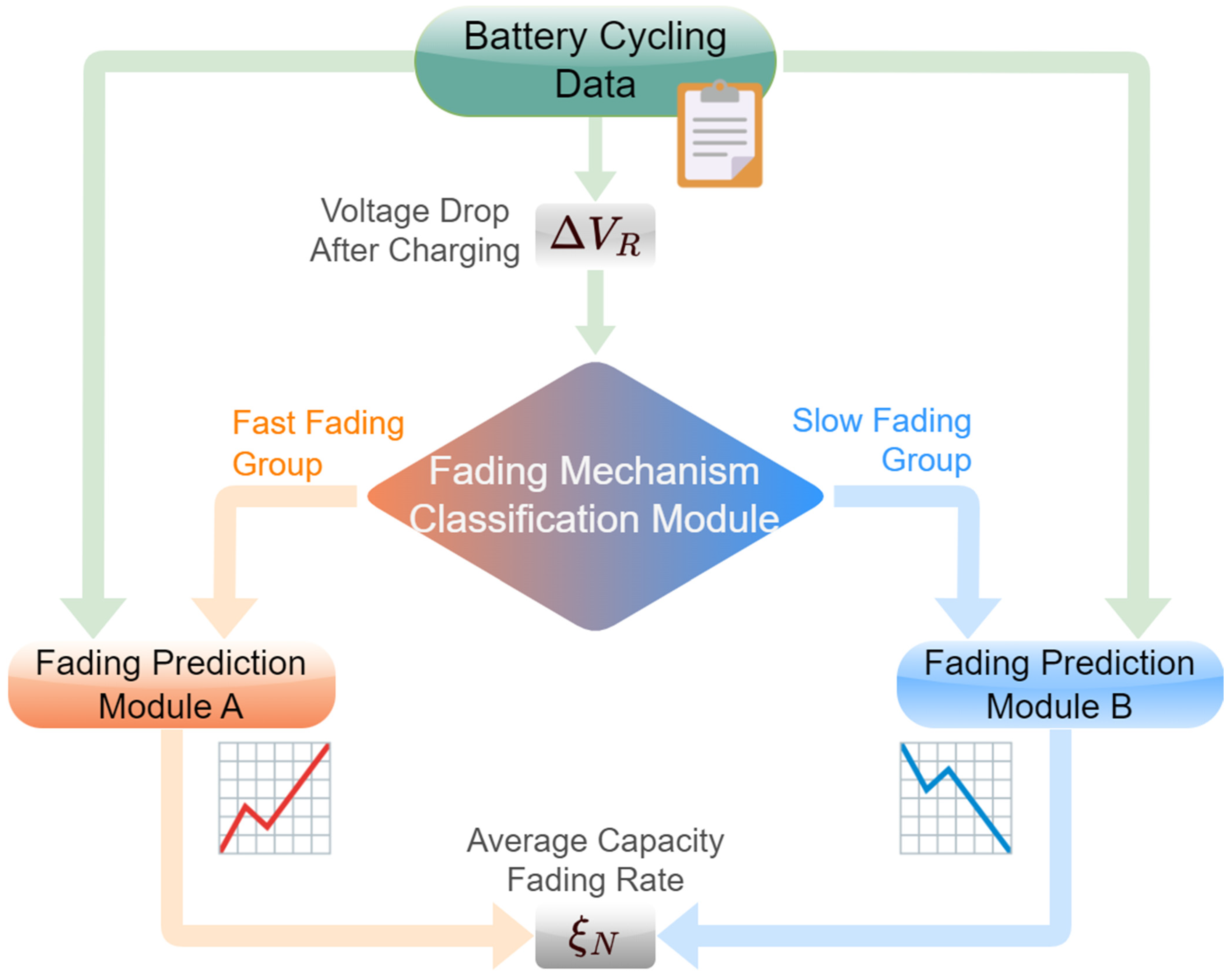
3. Model Framework
4. Machine–Learning Model Development
4.1. K–Mean Clustering
4.2. Linear Support Vector Regression
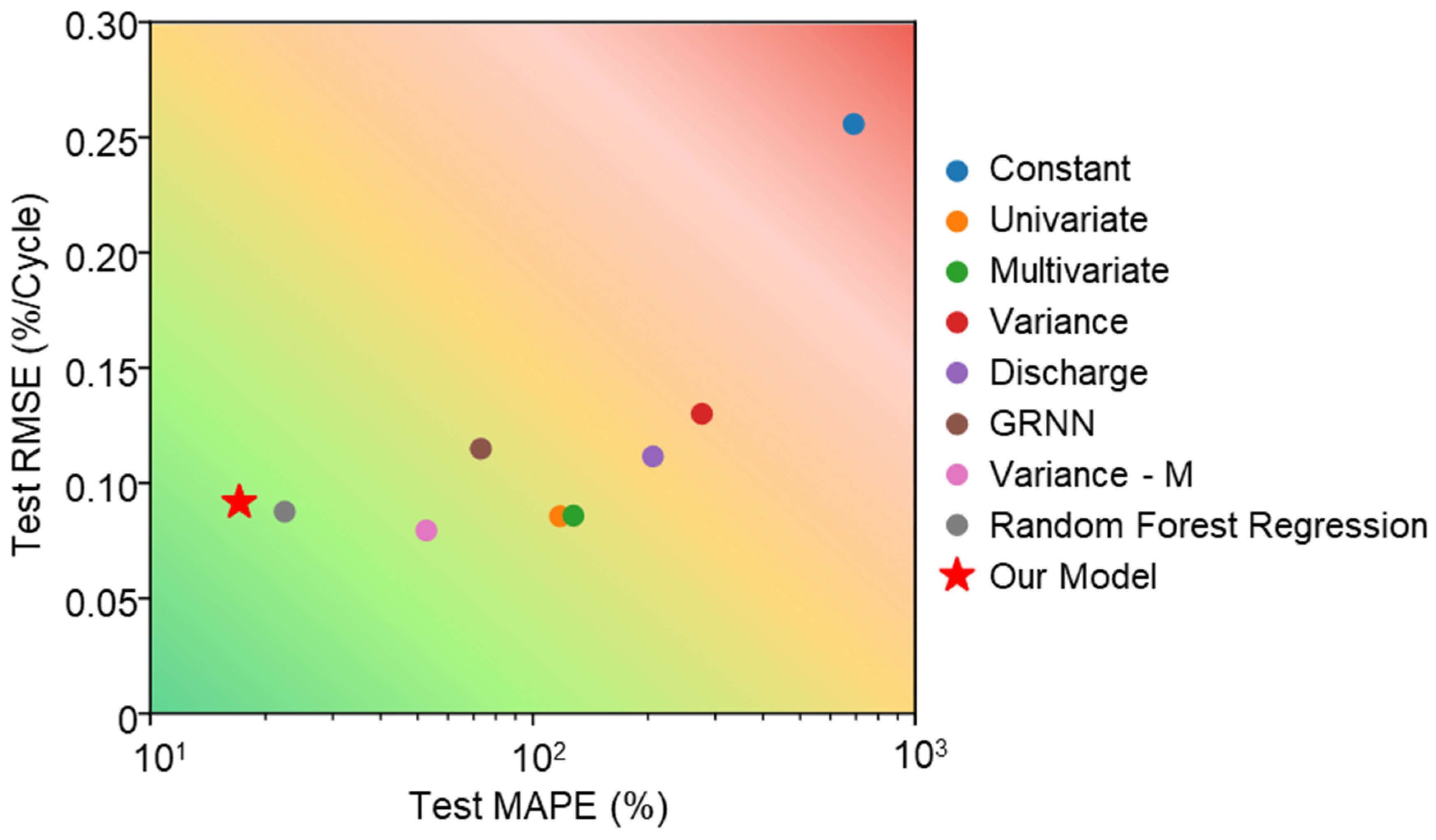
5. Results
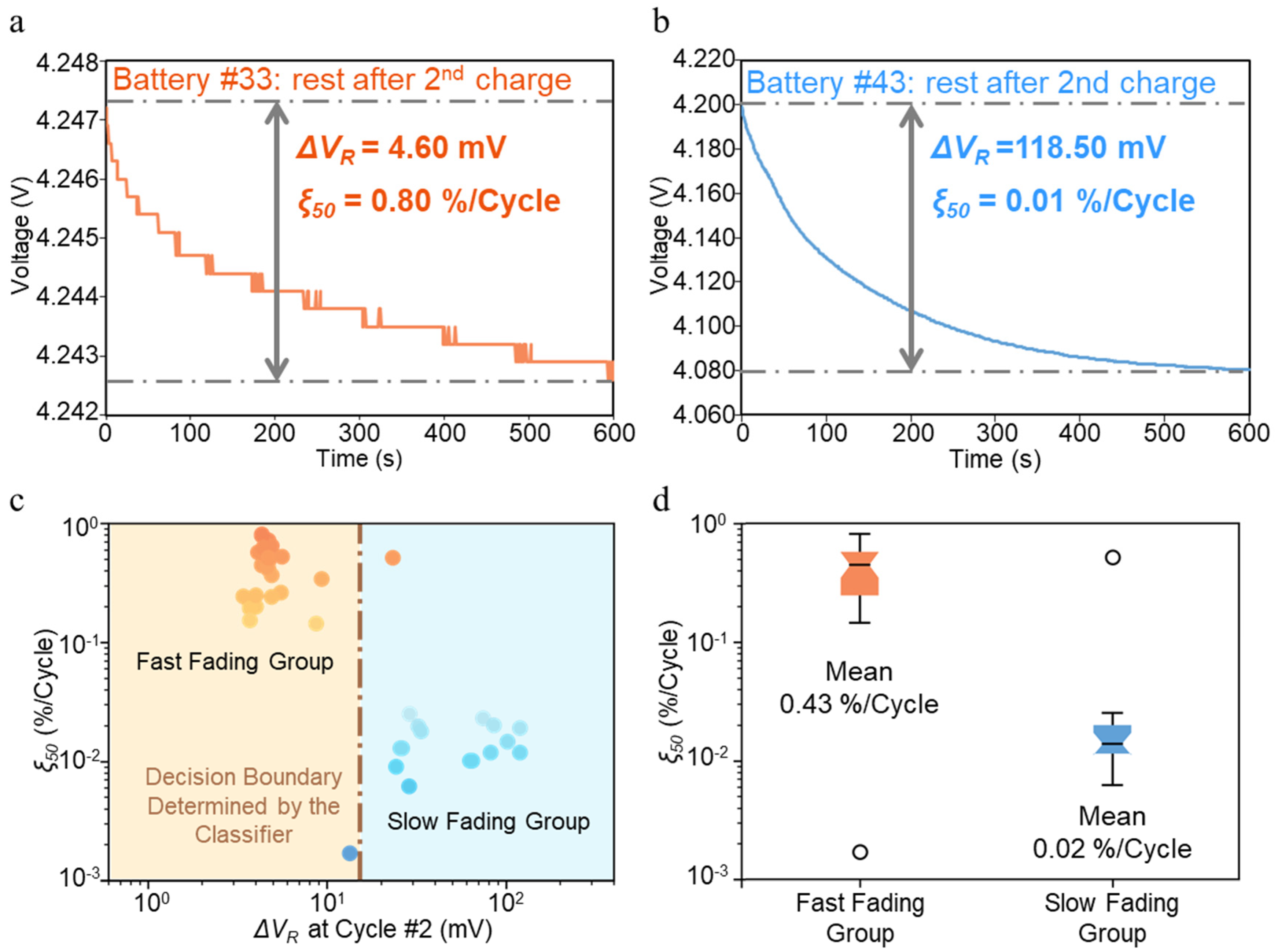
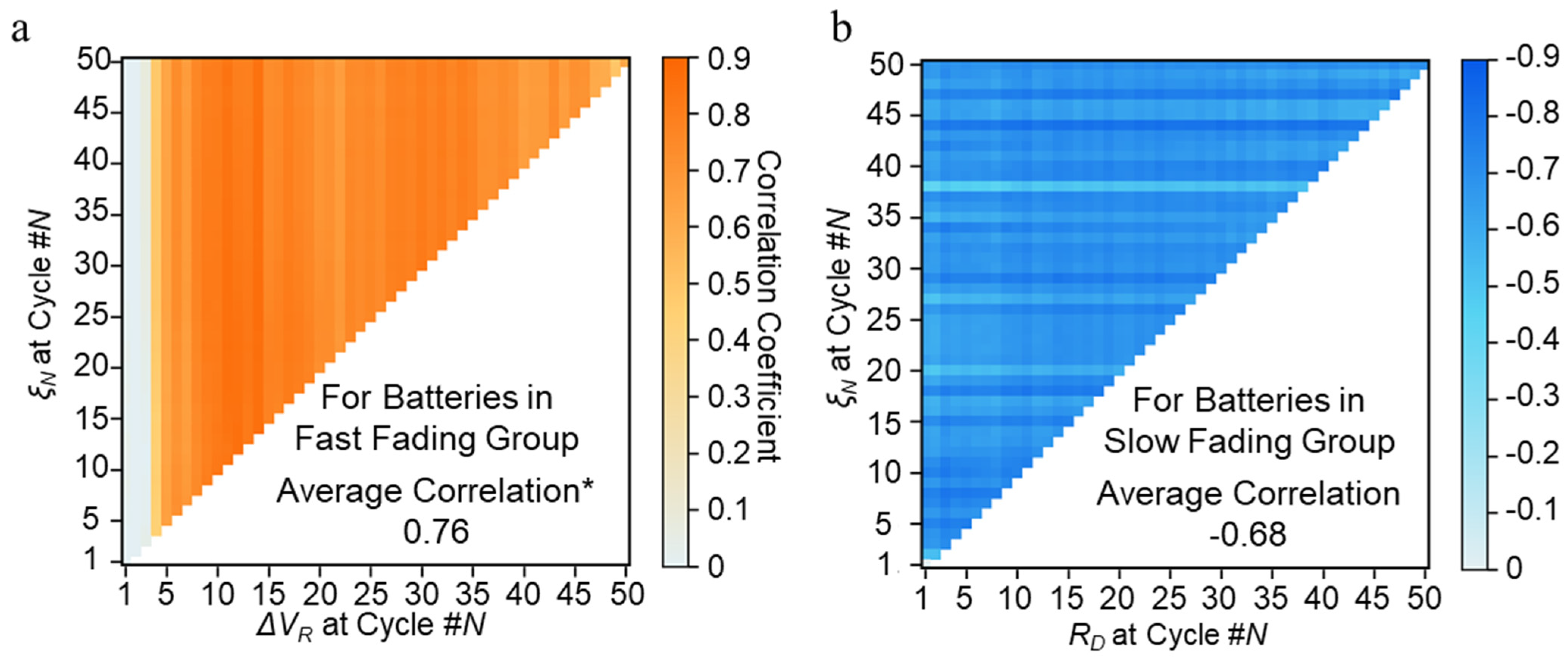
5.1. Fading Mechanism Classification
5.2. Capacity Fading Prediction
- (1)
- Discharge model. In [8], the authors proposed three models to predict battery lifetime. The model with six features, derived from first–100–cycle data, provided the best prediction result with an elastic net regression model. We reproduce these features using the first–5–cycle degradation data.
- (2)
- General Regression Neural Network (GRNN). In [14], based on the importance ranking of all features, four features derived from first–100–cycle data were selected and input into a GRNN model. However, the fourth feature, the increase in internal resistance, is not included in our dataset. Therefore, three features are reproduced with our dataset and fed into a GRNN model.
6. Discussion
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xiong, W.; Mo, Y.; Yan, C. Lithium–Ion Battery Parameters and State of Charge Joint Estimation Using Bias Compensation Least Squares and the Alternate Algorithm. Math. Probl. Eng. 2020, 2020, 1DUMMMY. [Google Scholar] [CrossRef]
- Schmalstieg, J.; Käbitz, S.; Ecker, M.; Sauer, D.U. A Holistic Aging Model for Li(NiMnCo)O2 Based 18650 Lithium–Ion Batteries. J. Power Sources 2014, 257, 325–334. [Google Scholar] [CrossRef]
- Broussely, M.; Herreyre, S.; Biensan, P.; Kasztejna, P.; Nechev, K.; Staniewicz, R.J. Aging Mechanism in Li Ion Cells and Calendar Life Predictions. J. Power Sources 2001, 97–98, 13–21. [Google Scholar] [CrossRef]
- Sulzer, V.; Marquis, S.G.; Timms, R.; Robinson, M.; Chapman, S.J. Python Battery Mathematical Modelling (PyBaMM). J. Open Res. Softw. 2021, 9, 1–8. [Google Scholar] [CrossRef]
- Yan, L.; Peng, J.; Gao, D.; Wu, Y.; Liu, Y.; Li, H.; Liu, W.; Huang, Z. A Hybrid Method with Cascaded Structure for Early–Stage Remaining Useful Life Prediction of Lithium–Ion Battery. Energy 2022, 243, 123038. [Google Scholar] [CrossRef]
- Tang, X.; Liu, K.; Wang, X.; Liu, B.; Gao, F.; Widanage, W.D. Real–Time Aging Trajectory Prediction Using a Base Model–Oriented Gradient–Correction Particle Filter for Lithium–Ion Batteries. J. Power Sources 2019, 440, 227118. [Google Scholar] [CrossRef]
- Xiong, W.; Xu, G.; Li, Y.; Zhang, F.; Ye, P.; Li, B. Early Prediction of Lithium–Ion Battery Cycle Life Based on Voltage–Capacity Discharge Curves. J. Energy Storage 2023, 62, 106790. [Google Scholar] [CrossRef]
- Severson, K.A.; Attia, P.M.; Jin, N.; Perkins, N.; Jiang, B.; Yang, Z.; Chen, M.H.; Aykol, M.; Herring, P.K.; Fraggedakis, D.; et al. Data–Driven Prediction of Battery Cycle Life before Capacity Degradation. Nat. Energy 2019, 4, 383–391, ISBN 4156001903. [Google Scholar] [CrossRef]
- Attia, P.M.; Severson, K.A.; Witmer, J.D. Statistical Learning for Accurate and Interpretable Battery Lifetime Prediction. J. Electrochem. Soc. 2021, 168, 090547. [Google Scholar] [CrossRef]
- Li, X.; Wang, Z.; Yan, J. Prognostic Health Condition for Lithium Battery Using the Partial Incremental Capacity and Gaussian Process Regression. J. Power Sources 2019, 421, 56–67. [Google Scholar] [CrossRef]
- Richardson, R.R.; Osborne, M.A.; Howey, D.A. Gaussian Process Regression for Forecasting Battery State of Health. J. Power Sources 2017, 357, 209–219. [Google Scholar] [CrossRef]
- Gao, D.; Huang, M. Prediction of Remaining Useful Life of Lithium–Ion Battery Based on Multi–Kernel Support Vector Machine with Particle Swarm Optimization. J. Power Electron. 2017, 17, 1288–1297. [Google Scholar] [CrossRef]
- Fei, Z.; Zhang, Z.; Yang, F.; Tsui, K.L.; Li, L. Early–Stage Lifetime Prediction for Lithium–Ion Batteries: A Deep Learning Framework Jointly Considering Machine–Learned and Handcrafted Data Features. J. Energy Storage 2022, 52, 104936. [Google Scholar] [CrossRef]
- Zhang, Y.; Peng, Z.; Guan, Y.; Wu, L. Prognostics of Battery Cycle Life in the Early–Cycle Stage Based on Hybrid Model. Energy 2021, 221, 119901. [Google Scholar] [CrossRef]
- Xu, F.; Yang, F.; Fei, Z.; Huang, Z.; Tsui, K.L. Life Prediction of Lithium–Ion Batteries Based on Stacked Denoising Autoencoders. Reliab. Eng. Syst. Saf. 2021, 208, 107396. [Google Scholar] [CrossRef]
- Yao, J.; Powell, K.; Gao, T. A two-stage deep learning framework for early-stage lifetime prediction for lithium-ion batteries with consideration of features from multiple cycles. Front. Energy Res. 2020, 10, 1059126. [Google Scholar]
- Hsu, C.W.; Xiong, R.; Chen, N.Y.; Li, J.; Tsou, N.T. Deep Neural Network Battery Life and Voltage Prediction by Using Data of One Cycle Only. Appl. Energy 2022, 306, 118134. [Google Scholar] [CrossRef]
- Aykol, M.; Gopal, C.B.; Anapolsky, A.; Herring, P.K.; van Vlijmen, B.; Berliner, M.D.; Bazant, M.Z.; Braatz, R.D.; Chueh, W.C.; Storey, B.D. Perspective—Combining Physics and Machine Learning to Predict Battery Lifetime. J. Electrochem. Soc. 2021, 168, 030525. [Google Scholar] [CrossRef]
- Thelen, A.; Lui, Y.H.; Shen, S.; Laflamme, S.; Hu, S.; Ye, H.; Hu, C. Integrating Physics–Based Modeling and Machine Learning for Degradation Diagnostics of Lithium–Ion Batteries. Energy Storage Mater. 2022, 50, 668–695. [Google Scholar] [CrossRef]
- Najera–Flores, D.A.; Hu, Z.; Chadha, M.; Todd, M.D. A Physics–Constrained Bayesian Neural Network for Battery Remaining Useful Life Prediction. Appl. Math. Model. 2023, 122, 42–59. [Google Scholar] [CrossRef]
- Shi, J.; Rivera, A.; Wu, D. Battery Health Management Using Physics–Informed Machine Learning: Online Degradation Modeling and Remaining Useful Life Prediction. Mech. Syst. Signal Process. 2022, 179, 109347. [Google Scholar] [CrossRef]
- Deng, Z.; Lin, X.; Cai, J.; Hu, X. Battery Health Estimation with Degradation Pattern Recognition and Transfer Learning. J. Power Sources 2022, 525, 231027. [Google Scholar] [CrossRef]
- Jiang, B.; Gent, W.E.; Mohr, F.; Ermon, S.; Chueh, W.C.; Richard, D.; Jiang, B.; Gent, W.E.; Mohr, F.; Das, S.; et al. Bayesian Learning for Rapid Prediction of Lithium–Ion Battery–Cycling Protocols of Lithium–Ion Battery–Cycling Protocols. Joule 2021, 5, 3187–3203. [Google Scholar] [CrossRef]
- Chen, B.R.; Kunz, M.R.; Tanim, T.R.; Dufek, E.J. A Machine Learning Framework for Early Detection of Lithium Plating Combining Multiple Physics–Based Electrochemical Signatures. Cell Reports Phys. Sci. 2021, 2, 100352. [Google Scholar] [CrossRef]
- Chen, B.R.; Walker, C.M.; Kim, S.; Kunz, M.R.; Tanim, T.R.; Dufek, E.J. Battery Aging Mode Identification across NMC Compositions and Designs Using Machine Learning. Joule 2022, 6, 2776–2793. [Google Scholar] [CrossRef]
- Ansean, D.; Garcia, V.M.; Gonzalez, M.; Blanco–Viejo, C.; Viera, J.C.; Pulido, Y.F.; Sanchez, L. Lithium–Ion Battery Degradation Indicators Via Incremental Capacity Analysis. IEEE Trans. Ind. Appl. 2019, 55, 2992–3002. [Google Scholar] [CrossRef]
- Ahmed, M.; Seraj, R.; Islam, S.M.S. The K–Means Algorithm: A Comprehensive Survey and Performance Evaluation. Electron. 2020, 9, 1295. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support–Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Drucker, H.; Surges, C.J.C.; Kaufman, L.; Smola, A.; Vapnik, V. Support Vector Regression Machines. Adv. Neural Inf. Process. Syst. 1997, 1, 155–161. [Google Scholar]
- Smola, A.J.; Schölkopf, B. A Tutorial on Support Vector Regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Pinson, M.B.; Bazant, M.Z. Theory of SEI Formation in Rechargeable Batteries: Capacity Fade, Accelerated Aging and Lifetime Prediction. J. Electrochem. Soc. 2013, 160, A243–A250. [Google Scholar] [CrossRef]
- Gao, T.; Han, Y.; Fraggedakis, D.; Das, S.; Zhou, T.; Yeh, C.N.; Xu, S.; Chueh, W.C.; Li, J.; Bazant, M.Z. Interplay of Lithium Intercalation and Plating on a Single Graphite Particle. Joule 2021, 5, 393–414. [Google Scholar] [CrossRef]
- Chowdhury, S.; Lin, Y.; Liaw, B.; Kerby, L. Evaluation of Tree Based Regression over Multiple Linear Regression for Non–Normally Distributed Data in Battery Performance. In Proceedings of the 2022 International Conference on Intelligent Data Science Technologies and Applications (IDSTA), San Antonio, TX, USA, 5–7 September 2022; pp. 17–25. [Google Scholar] [CrossRef]
- Tanim, T.R.; Paul, P.P.; Thampy, V.; Cao, C.; Steinrück, H.G.; Nelson Weker, J.; Toney, M.F.; Dufek, E.J.; Evans, M.C.; Jansen, A.N.; et al. Heterogeneous Behavior of Lithium Plating during Extreme Fast Charging. Cell Rep. Phys. Sci. 2020, 1, 100114. [Google Scholar] [CrossRef]
- Tanim, T.R.; Dufek, E.J.; Evans, M.; Dickerson, C.; Jansen, A.N.; Polzin, B.J.; Dunlop, A.R.; Trask, S.E.; Jackman, R.; Bloom, I.; et al. Extreme Fast Charge Challenges for Lithium–Ion Battery: Variability and Positive Electrode Issues. J. Electrochem. Soc. 2019, 166, A1926–A1938. [Google Scholar] [CrossRef]
- Gallagher, K.G.; Trask, S.E.; Bauer, C.; Woehrle, T.; Lux, S.F.; Tschech, M.; Lamp, P.; Polzin, B.J.; Ha, S.; Long, B.; et al. Optimizing Areal Capacities through Understanding the Limitations of Lithium–Ion Electrodes. J. Electrochem. Soc. 2016, 163, A138–A149. [Google Scholar] [CrossRef]
- Tomaszewska, A.; Chu, Z.; Feng, X.; O’Kane, S.; Liu, X.; Chen, J.; Ji, C.; Endler, E.; Li, R.; Liu, L.; et al. Lithium–Ion Battery Fast Charging: A Review. eTransportation 2019, 1, 100011. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, J.; Gao, Q.; Gao, T.; Jiang, B.; Powell, K.M. A Physics–Guided Machine Learning Approach for Capacity Fading Mechanism Detection and Fading Rate Prediction Using Early Cycle Data. Batteries 2024, 10, 283. https://doi.org/10.3390/batteries10080283
Yao J, Gao Q, Gao T, Jiang B, Powell KM. A Physics–Guided Machine Learning Approach for Capacity Fading Mechanism Detection and Fading Rate Prediction Using Early Cycle Data. Batteries. 2024; 10(8):283. https://doi.org/10.3390/batteries10080283
Chicago/Turabian StyleYao, Jiwei, Qiang Gao, Tao Gao, Benben Jiang, and Kody M. Powell. 2024. "A Physics–Guided Machine Learning Approach for Capacity Fading Mechanism Detection and Fading Rate Prediction Using Early Cycle Data" Batteries 10, no. 8: 283. https://doi.org/10.3390/batteries10080283
APA StyleYao, J., Gao, Q., Gao, T., Jiang, B., & Powell, K. M. (2024). A Physics–Guided Machine Learning Approach for Capacity Fading Mechanism Detection and Fading Rate Prediction Using Early Cycle Data. Batteries, 10(8), 283. https://doi.org/10.3390/batteries10080283







