Investigation of the Suitability of the DTV Method for the Online SoH Estimation of NMC Lithium-Ion Cells in Battery Management Systems
Abstract
:1. Introduction
2. Experimental Setup
2.1. Device Under Test
2.2. Testbench
2.3. Check-Up Definition
2.4. Test Matrix
2.4.1. Calendar Aging
2.4.2. Cyclic Aging
3. Model Development
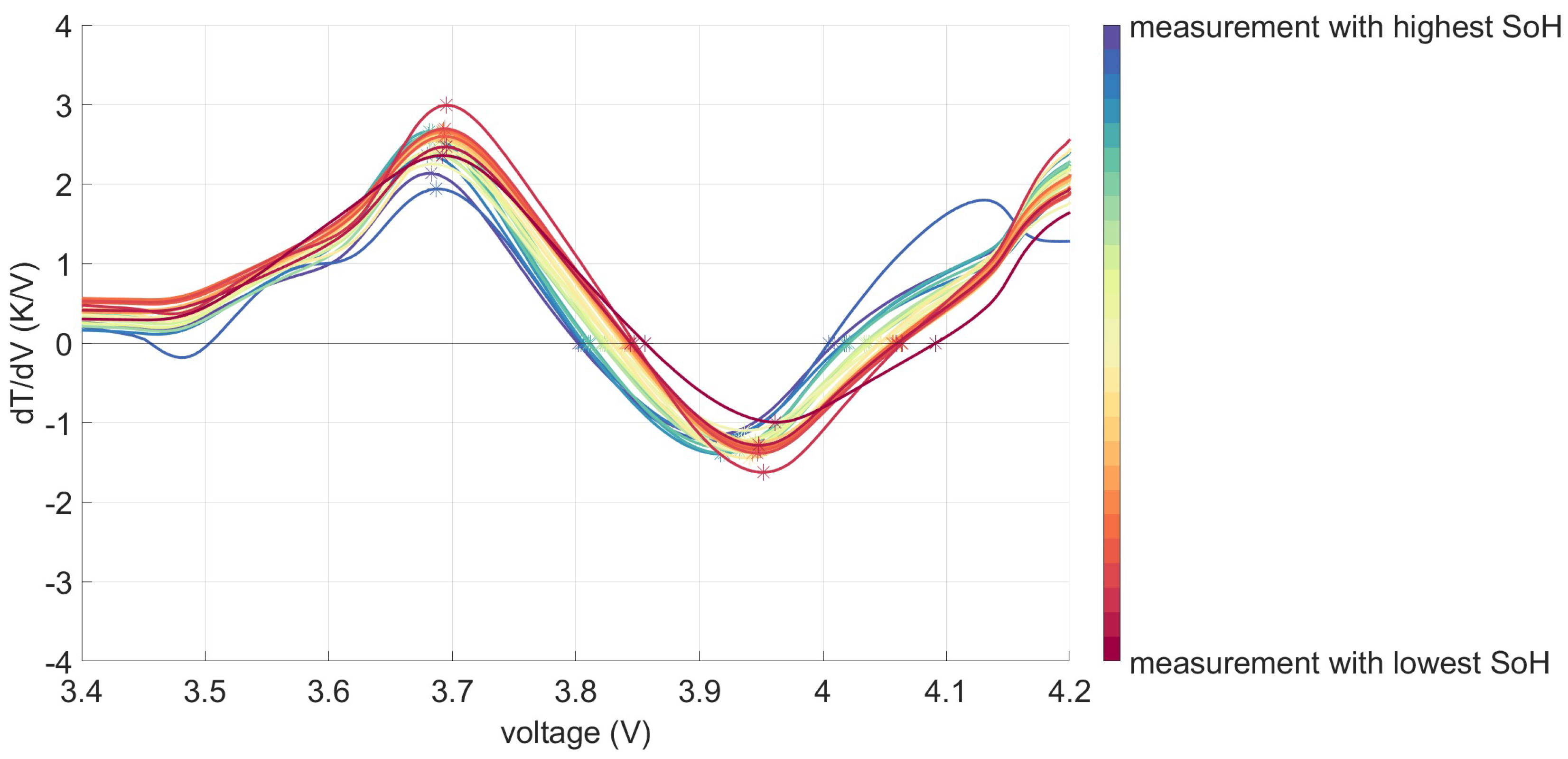
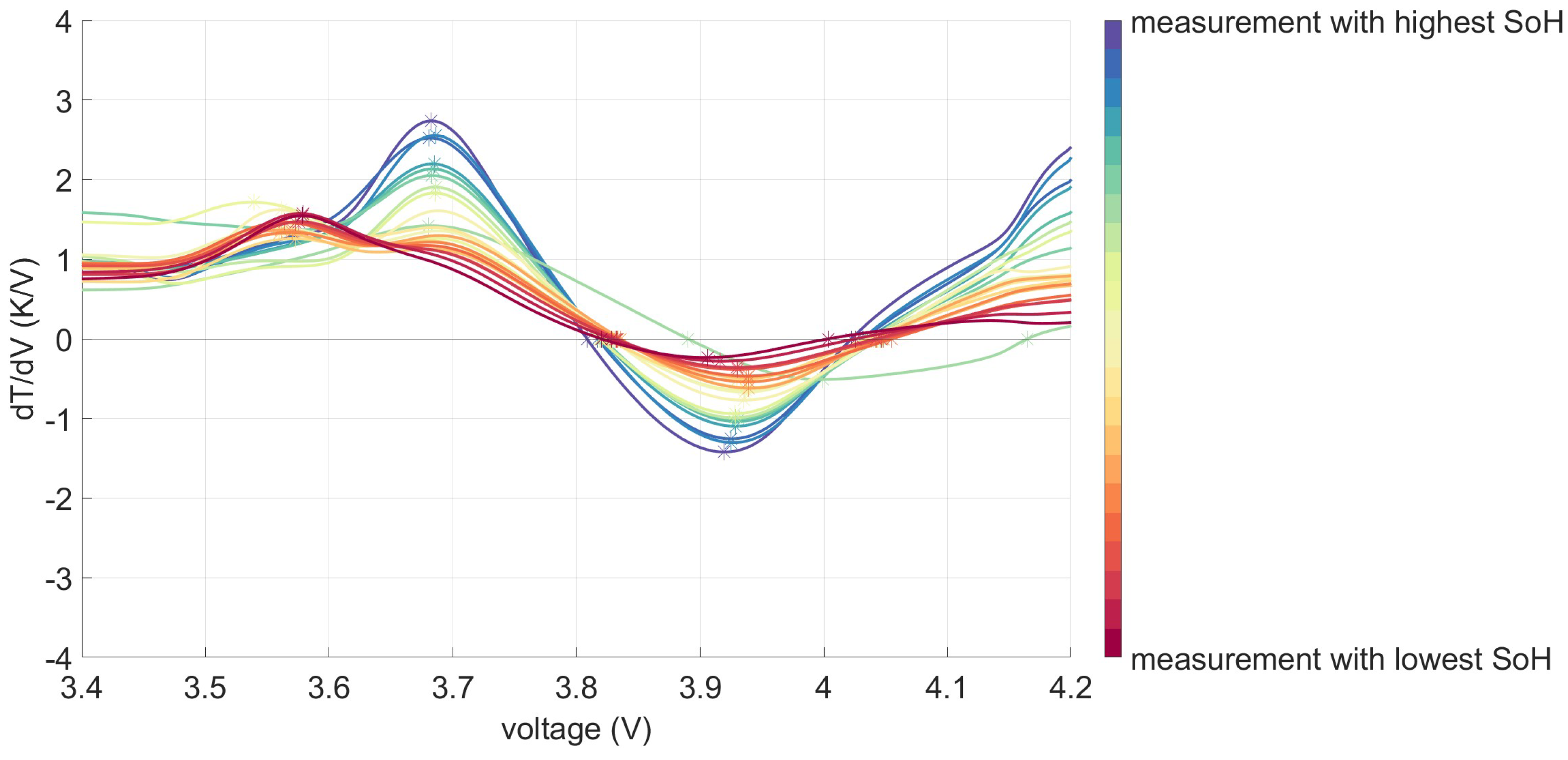
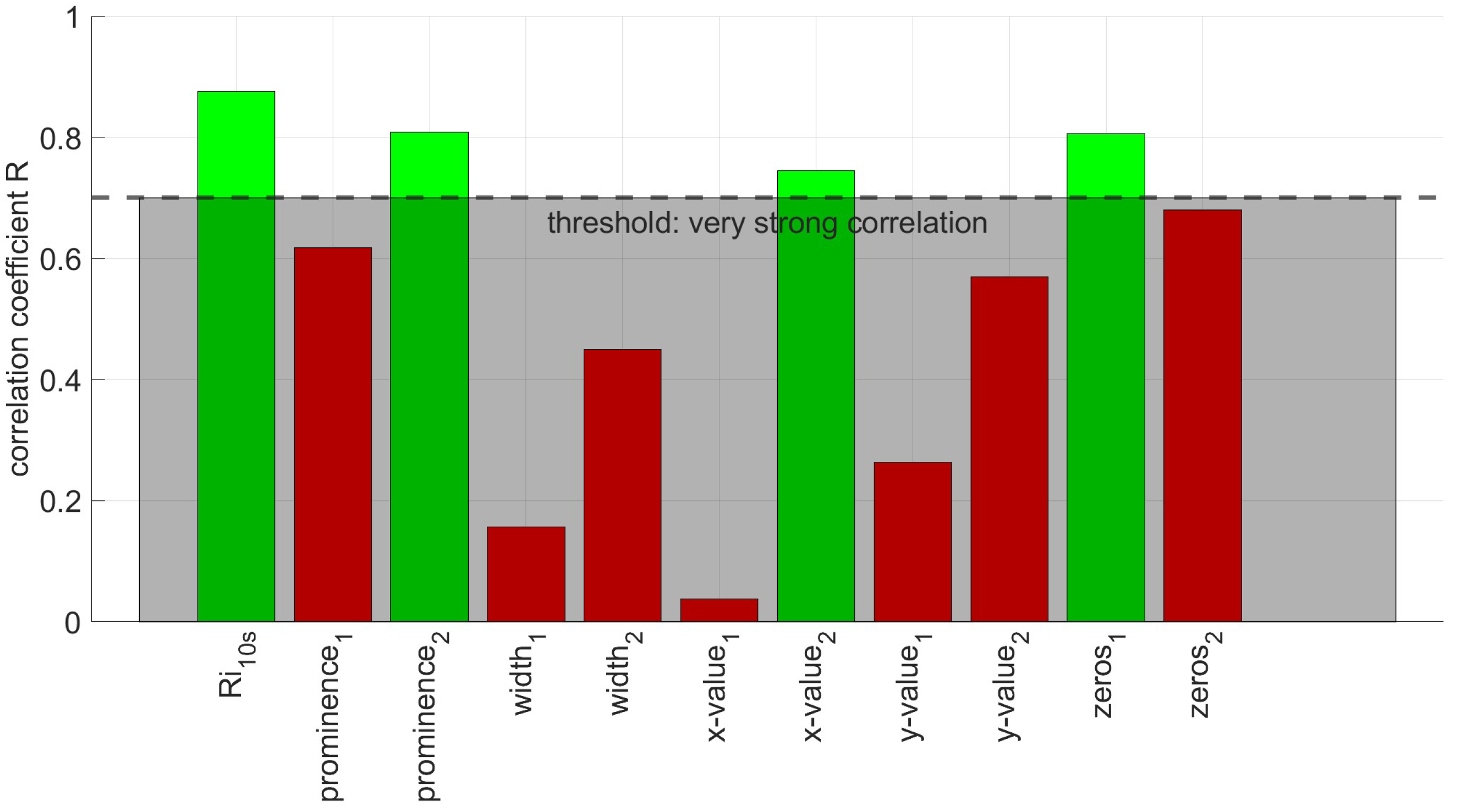
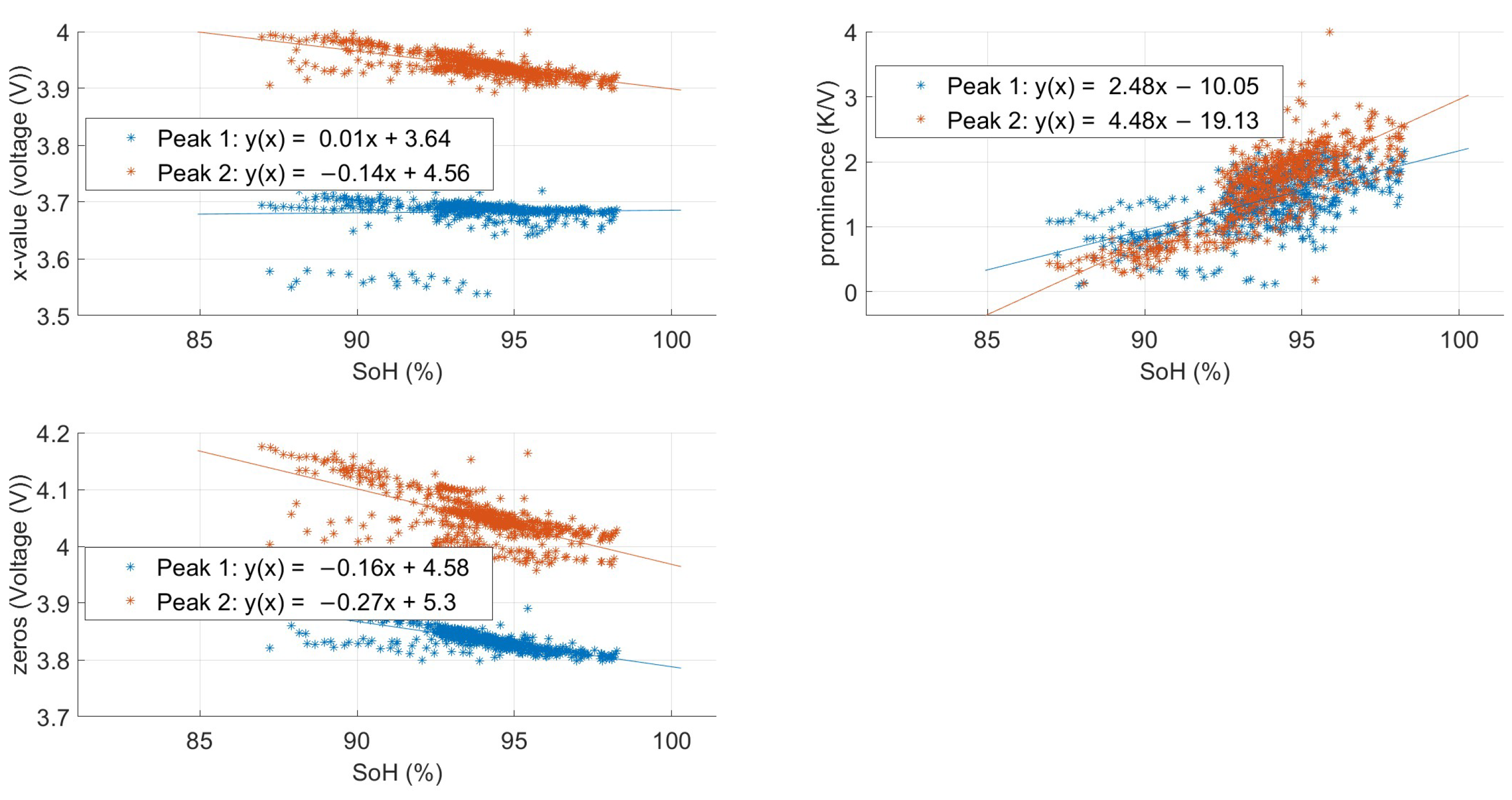
3.1. Distinctive Points
3.2. Model Structure
- DoD;
- Mid-SoC;
- Temperature;
- Charging current;
- Discharging current.
- SoC;
- Temperature.
4. Results
4.1. Analysis of the DTV Curves
4.2. Definition of the SoH Regression Line
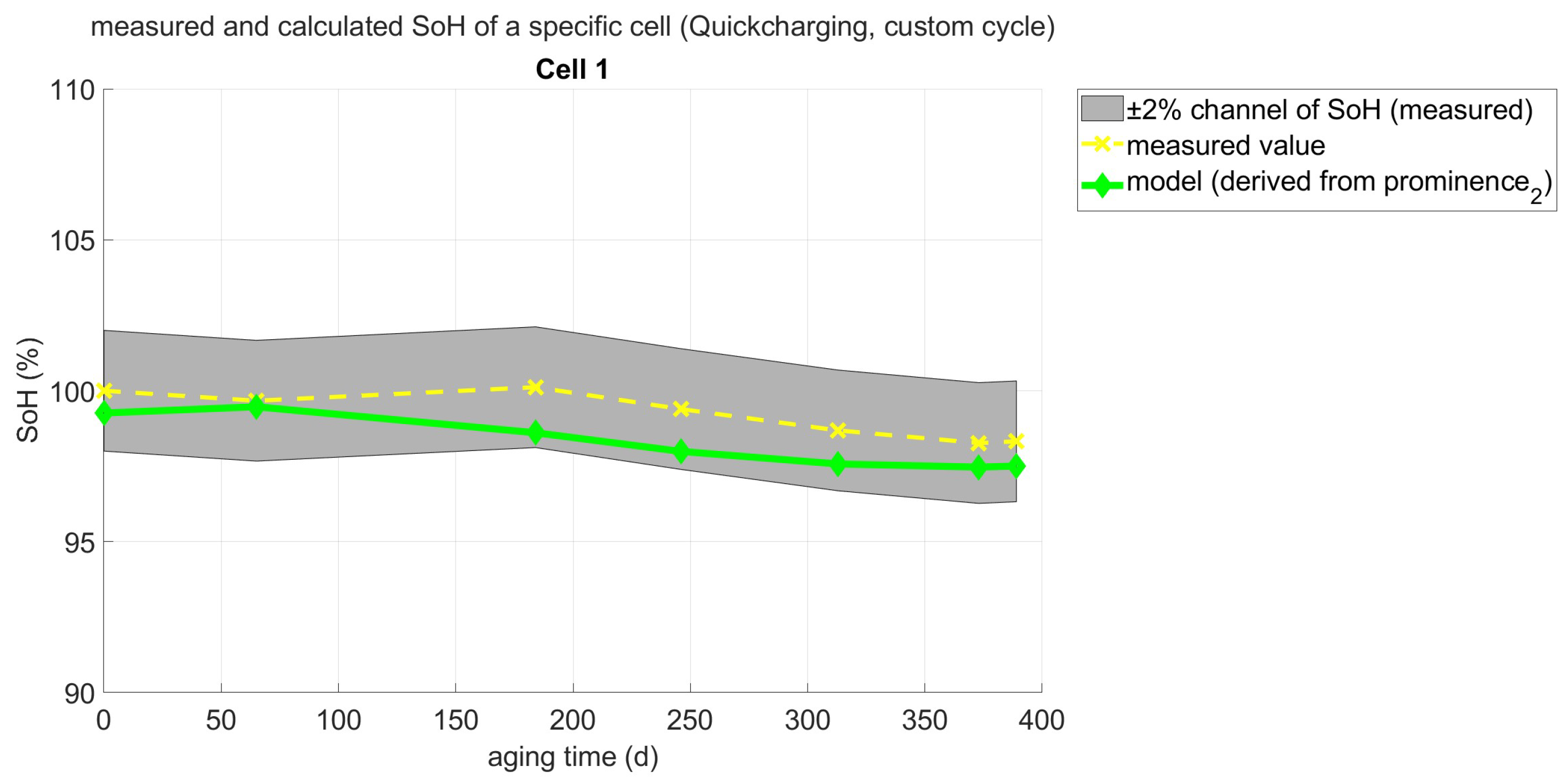
4.3. Validation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BMS | Battery Management System |
| BMU | Battery Management Unit |
| CU | Check-Up |
| DiPo | Distinctive Points |
| DOAJ | Directory of open access journals |
| DVA | Differential Voltage Analysis |
| DTV | Differential Thermal Voltammetry |
| EIS | Electrochemical Impedance Spectroscopy |
| LAM | Loss of Active Material |
| LFP | Lithium Iron Phosphate |
| LLI | Loss of Lithium Inventory |
| MDPI | Multidisciplinary Digital Publishing Institute |
| NMC | Nickel Manganese Cobalt |
| NTC | Negative Temperature Coefficient |
| OCV | Open Circuit Voltage |
| SoC | State of Charge |
| SoH | State of Health |
| SRCV | Slow Rate Cyclic Voltammetry |
References
- Kawamoto, R.; Mochizuki, H.; Moriguchi, Y.; Nakano, T.; Motohashi, M.; Sakai, Y.; Inaba, A. Estimation of CO2 Emissions of Internal Combustion Engine Vehicle and Battery Electric Vehicle Using LCA. Sustainability 2019, 11, 2690. [Google Scholar] [CrossRef]
- Bickert, S.; Kampker, A.; Greger, D. Developments of CO2-emissions and costs for small electric and combustion engine vehicles in Germany. Transp. Res. Part D Transp. Environ. 2015, 36, 138–151. [Google Scholar] [CrossRef]
- Mohtasham, J. Review Article-Renewable Energies. Energy Procedia 2015, 74, 1289–1297. [Google Scholar] [CrossRef]
- Nelson, V. Wind Energy; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar] [CrossRef]
- Lu, L.; Han, X.; Li, J.; Hua, J.; Ouyang, M. A review on the key issues for lithium-ion battery management in electric vehicles. J. Power Sources 2013, 226, 272–288. [Google Scholar] [CrossRef]
- Zhou, C.C.; Su, Z.; Gao, X.L.; Cao, R.; Yang, S.C.; Liu, X.H. Ultra-high-energy lithium-ion batteries enabled by aligned structured thick electrode design. Rare Met. 2022, 41, 14–20. [Google Scholar] [CrossRef]
- Lu, Q.; Jie, Y.; Meng, X.; Omar, A.; Mikhailova, D.; Cao, R.; Jiao, S.; Lu, Y.; Xu, Y. Carbon materials for stable Li metal anodes: Challenges, solutions, and outlook. Carbon Energy 2021, 3, 957–975. [Google Scholar] [CrossRef]
- Han, X.; Ouyang, M.; Lu, L.; Li, J.; Zheng, Y.; Li, Z. A comparative study of commercial lithium ion battery cycle life in electrical vehicle: Aging mechanism identification. J. Power Sources 2014, 251, 38–54. [Google Scholar] [CrossRef]
- Birkl, C.R.; Roberts, M.R.; McTurk, E.; Bruce, P.G.; Howey, D.A. Degradation diagnostics for lithium ion cells. J. Power Sources 2017, 341, 373–386. [Google Scholar] [CrossRef]
- Jossen, A.; Weydanz, W. Moderne Akkumulatoren Richtig Einsetzen, 2. überarbeitete Auflage von März 2019, revidierte Ausgabe ed.; MatrixMedia: Göttingen, Germany, 2021. [Google Scholar]
- Börger, A.; Wenzl, H. Batterien: Grundlagen, Systeme, Anwendungen; Wiley-VCH: Weinheim, Germany, 2022. [Google Scholar]
- Noura, N.; Boulon, L.; Jemeï, S. A Review of Battery State of Health Estimation Methods: Hybrid Electric Vehicle Challenges. World Electr. Veh. J. 2020, 11, 66. [Google Scholar] [CrossRef]
- Plett, G.L. Part 2. Sigma-point Kalman filtering for battery management systems of LiPB-based HEV battery packs: Simultaneous state and parameter estimation. J. Power Sources 2006, 161 Pt 2, 1369–1384. [Google Scholar] [CrossRef]
- Schmalstieg, J.; Käbitz, S.; Ecker, M.; Sauer, D.U. A holistic aging model for Li(NiMnCo)O2 based 18650 lithium-ion batteries. J. Power Sources 2014, 257, 325–334. [Google Scholar] [CrossRef]
- Li, Y.; Liu, K.; Foley, A.M.; Zülke, A.; Berecibar, M.; Nanini-Maury, E.; Van Mierlo, J.; Hoster, H.E. Data-driven health estimation and lifetime prediction of lithium-ion batteries: A review. Renew. Sustain. Energy Rev. 2019, 113, 109254. [Google Scholar] [CrossRef]
- Keil, P. Aging of Lithium-Ion Batteries in Electric Vehicles. Ph.D. Thesis, Technische Universität München, München, Germany, 2017. [Google Scholar]
- Merla, Y.; Wu, B.; Yufit, V.; Brandon, N.P.; Martinez-Botas, R.F.; Offer, G.J. Extending battery life: A low-cost practical diagnostic technique for lithium-ion batteries. J. Power Sources 2016, 331, 224–231. [Google Scholar] [CrossRef]
- Wu, B.; Yufit, V.; Merla, Y.; Martinez-Botas, R.F.; Brandon, N.P.; Offer, G.J. Differential thermal voltammetry for tracking of degradation in lithium-ion batteries. J. Power Sources 2015, 273, 495–501. [Google Scholar] [CrossRef]
- Asenbauer, J.; Eisenmann, T.; Kuenzel, M.; Kazzazi, A.; Chen, Z.; Bresser, D. The success story of graphite as a lithium-ion anode material—Fundamentals, remaining challenges, and recent developments including silicon (oxide) composites. Sustain. Energy Fuels 2020, 4, 5387–5416. [Google Scholar] [CrossRef]
- Anna Mitin. Identifizierung und Quantifizierung von Alterungsphänomenen in Lithium-Ionen-Batterien. Ph.D. Thesis, Technische Universität Carolo-Wilhelmina zu Braunschweig, Braunschweig, Germany, 2018.
- Lewerenz, M.; Marongiu, A.; Warnecke, A.; Sauer, D.U. Differential voltage analysis as a tool for analyzing inhomogeneous aging: A case study for LiFePO4|Graphite cylindrical cells. J. Power Sources 2017, 368, 57–67. [Google Scholar] [CrossRef]
- Shibagaki, T.; Merla, Y.; Offer, G.J. Tracking degradation in lithium iron phosphate batteries using differential thermal voltammetry. J. Power Sources 2018, 374, 188–195. [Google Scholar] [CrossRef]
- Merla, Y.; Wu, B.; Yufit, V.; Brandon, N.P.; Martinez-Botas, R.F.; Offer, G.J. Novel application of differential thermal voltammetry as an in-depth state-of-health diagnosis method for lithium-ion batteries. J. Power Sources 2016, 307, 308–319. [Google Scholar] [CrossRef]
- Prosser, R.; Offer, G.; Patel, Y. Lithium-Ion Diagnostics: The First Quantitative In-Operando Technique for Diagnosing Lithium Ion Battery Degradation Modes under Load with Realistic Thermal Boundary Conditions. J. Electrochem. Soc. 2021, 168, 030532. [Google Scholar] [CrossRef]
- Wang, Z.; Yuan, C.; Li, X. Lithium Battery State-of-Health Estimation via Differential Thermal Voltammetry With Gaussian Process Regression. IEEE Trans. Transp. Electrif. 2021, 7, 16–25. [Google Scholar] [CrossRef]
- Ma, B.; Yu, H.Q.; Wang, W.T.; Yang, X.B.; Zhang, L.S.; Xie, H.C.; Zhang, C.; Chen, S.Y.; Liu, X.H. State of health and remaining useful life prediction for lithium-ion batteries based on differential thermal voltammetry and a long and short memory neural network. Rare Met. 2023, 42, 885–901. [Google Scholar] [CrossRef]
- Zülke, A.; Li, Y.; Keil, P.; Burrell, R.; Belaisch, S.; Nagarathinam, M.; Mercer, M.P.; Hoster, H.E. High–Energy Nickel–Cobalt–Aluminium Oxide (NCA) Cells on Idle: Anode– versus Cathode–Driven Side Reactions. Batter. Supercaps 2021, 4, 934–947. [Google Scholar] [CrossRef]
- Lewerenz, M.; Dechent, P.; Endisch, C.; Sauer, D.U. Investigation of capacity and homogeneity recovery of commercial cells after cycle life tests. In Electrochemical Society Meeting Abstracts 235; The Electrochemical Society, Inc.: Pennington, NJ, USA, 2019. [Google Scholar]



| Type | Cylindrical |
| Format | 21700 |
| Length | 70.1 mm |
| Diameter | 21.1 mm |
| Weight | 68 g |
| Nominal Energy | 18.2 Wh |
| Lower Voltage Limit | 2.5 V |
| Upper Voltage Limit | 4.2 V |
| Nominal Voltage | 3.7 V |
| Max Current | 3 C |
| Temperature Range | −20 up to 60 °C |
| SoC/Temp. | 10 °C | 25 °C | 45 °C | 55 °C |
|---|---|---|---|---|
| 100% | − | X | X | − |
| 95% | X | X | X | X |
| 80% | − | X | X | X |
| 70% | − | X | − | − |
| 60% | X | X | X | X |
| 30% | − | X | X | X |
| DoD/mSoC | 20% | 50% | 60% | 70% |
|---|---|---|---|---|
| 100% | − | a | − | − |
| 80% | − | a | − | − |
| 60% | − | a, g | a | − |
| 20% | a | a, b, c, d, e, f, g | a | a |
| 10% | − | a | − | − |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neunzling, J.; Hainke, P.; Winter, H.; Henriques, D.; Fleckenstein, M.; Markus, T. Investigation of the Suitability of the DTV Method for the Online SoH Estimation of NMC Lithium-Ion Cells in Battery Management Systems. Batteries 2025, 11, 25. https://doi.org/10.3390/batteries11010025
Neunzling J, Hainke P, Winter H, Henriques D, Fleckenstein M, Markus T. Investigation of the Suitability of the DTV Method for the Online SoH Estimation of NMC Lithium-Ion Cells in Battery Management Systems. Batteries. 2025; 11(1):25. https://doi.org/10.3390/batteries11010025
Chicago/Turabian StyleNeunzling, Jan, Philipp Hainke, Hanno Winter, David Henriques, Matthias Fleckenstein, and Torsten Markus. 2025. "Investigation of the Suitability of the DTV Method for the Online SoH Estimation of NMC Lithium-Ion Cells in Battery Management Systems" Batteries 11, no. 1: 25. https://doi.org/10.3390/batteries11010025
APA StyleNeunzling, J., Hainke, P., Winter, H., Henriques, D., Fleckenstein, M., & Markus, T. (2025). Investigation of the Suitability of the DTV Method for the Online SoH Estimation of NMC Lithium-Ion Cells in Battery Management Systems. Batteries, 11(1), 25. https://doi.org/10.3390/batteries11010025






