Joint Adaptive Assessment of the State of Charge of Lithium Batteries at Varying Temperatures

Abstract

The fixed battery model parameters result in poor real-time state of charge (SOC) estimation, and the model-based estimation method of lithium battery SOC ignores the consequences of various working conditions and temperatures with the battery, resulting in low estimation accuracy. Based on multi-new information theories, this work proposes a joint evaluation method for lithium battery state of charge using adaptive extended Kalman filtering (AEKF) and variable forgetting factor recursive least squares (VFFRLS). Through testing at various temperatures and working conditions and a comparison with the conventional joint method, the efficacy of the algorithm presented in this study is confirmed. The findings demonstrate that the maximum root mean square error is kept at 1.57% and that the joint VFFRLS-AEKF technique suggested in this paper can effectively predict the lithium battery SOC. In contrast, the algorithm in this paper takes an average of less than 151 s to converge to within the 2% error range of the true value under various working conditions when the initial SOC value is set incorrectly. It also has good robustness and adaptability to adjust well to complex working conditions, which enhances the ability to predict energy consumption and the battery’s efficiency.

1. Introduction

Due to their low self-discharge rate, extended lifespan, a great deal of energy, and absence of memory effect, lithium batteries are the preferred batteries for mobile devices, electric cars, renewable energy storage systems, and other applications [1]. Therefore, accurate estimation of the state of charge (SOC) of lithium batteries plays an important role in improving the efficiency of battery use and extending the battery life.

Model-based, data-driven, experiment-based, and fusion-based SOC estimation techniques are available [2,3]. Data-driven SOC estimation techniques frequently make use of machine learning platforms, where sophisticated algorithms automatically learn network parameters and derive the relationship between battery parameters and SOC [4]. Neural networks and deep learning [5], Support Vector Machine (SVM) [6], and Extreme Learning Machine (ELM) [7] are machine learning techniques that are frequently utilized for SOC estimates. For example, Wang et al. [8] optimized the results of support vector machine parameters by analyzing the swarm intelligence optimization algorithm, Ma et al. [9] used the extreme learning machine (ELM) to predict SOC estimation errors and corrected the ansatz integration method for the SOC estimation results, and Qian et al. [10] combined fuzzy theory with neural networks and optimized the network structure by designing a fuzzy rule optimization algorithm. Data-based SOC estimation methods only need to use historical monitoring data to find and discover patterns, eliminating the tedious process of building physical models, but the method is highly dependent on the quality of the data.

Among the model-based techniques, the Kalman filtering algorithm [11] and the state observer method [12] are the most well-established and successful. One of the more sophisticated and successful techniques is the Kalman filtering algorithm. However, due to the nonlinear chemical reaction of lithium battery operation, many enhanced Kalman filtering algorithms have been developed, including the Cubature Kalman Filter (CKF) [13], Extended Kalman Filter (EKF) [14], and Unscented Kalman filter (UKF) [15]. Nevertheless, the covariance of UKF and CKF may change from positive to non-positive in non-Gaussian noise settings, which may cause their recursive calculations to lose convergence. At the same time, the EKF technique is more robust and does not require complex matrix breakdown calculations but is slightly less precise than the UKF and CKF methods [16]. Fan et al. [17] estimated the SOC of lithium batteries as early as 2017 by combining the EKF algorithm using the ampere-time analysis approach. Chen et al. [18] created an Internal Short Circuit (ISC) for the battery’s equivalent circuit model and employed the FFRLS technique to identify the model parameters before combining them with the EKF to estimate the SOC, with a maximum estimation error of 0.9%. The SOC prediction solution relying on the hybrid filtering algorithm of EKF and Median Filter was suggested by Zhao et al. [19]. This method not only provides an accurate estimate of the SOC but also establishes the basis for assessing the battery’s overall health.

However, a real system with unknown and changeable noise results in low estimating accuracy since the procedure noisy or observational noise of EKF is supposed to be with zero means. Tang et al. [20] therefore combined the EKF with the Sage–Husa adaptive algorithm to evaluate the SOC of a lithium-ion battery using the equivalent circuit model of a two-resistance capacitor. The results demonstrated that the combined approach has improved steady state and dynamic performance. Xia et al. [21] utilized FFRLS to complete the online recognition of battery model parameters and combined it with an Adaptive Extended Kalman Filter (AEKF) to realize SOC estimation. To achieve accurate noise estimation, a unique variable window Adaptive Extended Kalman Filter (CW-AEKF) technique was introduced by Du et al. [22]. It uses judgment to automatically adjust the ideal noise window length. The algorithm uses Levene’s test and variance ratio to identify variations in the dispersion of the error innovation series. For instance, Ma et al. [23] proposed the combination of both Convolutional Neural Network (CNN) and UKF to estimate SOC. To achieve the numerical analysis and state estimation of the parameters of the multifactor coupled model under the dynamic operating conditions of lithium batteries for electric vehicles, Liu et al. [24] looked into a novel multifactor fuzzy affiliation function self-adaptive Extended Kalman Filter (MFMF-AEKF) technology.

On the other hand, choosing the right battery model and identifying its parameters are crucial preconditions for precise SOC estimates, and the model’s performance is mostly determined by how well the parameter identification algorithm works. Least squares, filtering algorithms, group intelligence algorithms, statistical algorithms, and artificial intelligence algorithms are the primary categories of parameter identification algorithms. For example, by modifying the battery parameters, the Chaotic Firefly-Particle Filtering Method (CF-PF), which was suggested by Qiao et al. [25], is one of the filtering algorithms that can accurately reflect the dynamic features of lithium batteries in various aging phases in real-time. To develop a novel offline identification model for the lithium-ion battery parameter identification problem, Tang et al. [26] suggested the adaptive multi-context co-evolutionary parallel differential evolutionary algorithm (AMCC-PDE) for the population intelligent optimization method. In addition, some parameter identification algorithms based on statistics and artificial intelligence have appeared in recent years [27].

Nonetheless, numerous studies have demonstrated that the recursive least square (RLS) approach is the most effective way to identify the parameters of a lithium battery model and offers the following benefits: simplicity, broad applicability, robustness, and good dynamic features. But as the system’s data collection grows, the knowledge from the new data is progressively overtaken by the old data, making the algorithm incapable of making corrections; this is known as “data saturation” [28]. Although Li et al. [29] suggested forgetting factor re-cursive least squares (FFRLS) to circumvent this phenomenon, the fixed forgetting factor is unable to be adjusted to the rapidly evolving requirements of the lithium battery system. By applying the forgetting factor, the system can better utilize the information of the new data, lessen the system’s reliance on outdated data, and increase the precision of parameter identification. Quick shifts in demand. Many academics later built upon FFRLS and improved it in several ways. An enhanced Compressed Factor Particle Swarm Optimized Forgetting Factor Recursive Least Squares (CFPSO-FFRLS) approach was presented by Yang et al. [30] to maximize the forgetting factor along with finding more precise parameters. Ge et al. [31] suggested an enhanced FFRLS approach depending on flexible restrictions and parametric retracing, while Xiao et al. [32] presented an artificial fish schooling (AFS) approach proposed for improving the forgetting factor in FFRLS. The concept of adaptive parameter identification has also been proposed by some scholars. Sun et al. [33] proposed an RLS technique for Adaptive Forgetting Factor Recursive Least Squares (AFFRLS), which has been tested and found to perform better than the FFRLS algorithm in terms of speed and accuracy. By specifying the evaluation factor, the fuzzy control is used to achieve the linkage between the assessment factor as well as the correction number of the forgetting factor, to realize the responsive modification of the forgetting factor, Shrivastava et al. [34] and Shi et al. [35] also presented an enhanced recursive least squares algorithm built on the adaptive forgetting factor.

Therefore, by continuously iterating and refining the model parameters, the model-based SOC estimation techniques may be well matched to complicated working conditions such as battery aging and temperature variations. The effect of temperature on the battery SOC estimation must be taken into account, though, because temperature variations will cause changes in internal power battery properties including resistance and capacitance. To achieve dynamic identification of battery parameters, this paper takes into consideration the level of complexity, speed, and adaptability of battery model parameter identification and SOC estimation. According to the second-order RC equivalent model, it first analyzes its battery characteristics at various temperatures and establishes the connection between the battery Open-Circuit Voltage (OCV) as well as the SOC at various temperatures. Next, it adds an adjusted exponential function to improve the recursive least squares with a forgetting factor to form the variable forgetting factor least squares (VFFRLS). Finally, it incorporates the multi-new information theory based on EKF to automatically adjust the correlation between the processing noise and the measuring noise through the sliding window to constitute the Adaptive Extended Kalman Filtering (AEKF). Finally, it combines the two VFFRLS and AEKF to enhance the reliability for the estimation of the lithium battery’s SOC.

2. Battery Modeling and Parameter Identification

2.1. Second-Order RC Equivalent Circuit Model

At the moment, the most widely used models for lithium batteries are electrochemical [36], neural network models, equivalent circuit models, and other coupled models, like computational fluid dynamics (CFD) models and electro-thermal coupled models [37]. Of these, the equivalent circuit model can more accurately depict the internal properties of lithium batteries due to its straightforward construction and easily adjustable parameters. As shown in Figure 1, to more accurately describe the dynamic performance of the lithium battery, this paper chooses the second-order RC circuit as the battery equivalent model. The model’s moderate complexity makes it easy to identify parameters and is usually applied in tandem with Kalman filtering algorithms to finish estimating the SOC of lithium batteries. It is equivalent to the battery’s electrochemical polarization and concentration polarization separately, with higher accuracy [38].

In Figure 1, R₁ and R₂ are the polarization resistances, C₁ and C₂ are the polarization capacitances, R₀ is the battery’s ohmic internal resistance, U_OC stands for the open circuit voltage, U_L for the terminal voltage, and I_L for the current passing through the battery. The parallel network made up of R₁ and C₁ illustrates the polarization effect of electrochemistry, while the parallel network made up of R₂ and C₂ shows the concentration polarization effect. The equivalent circuit model’s equation can be expressed as Equation (1) under Kirchhoff’s law.

$$\left\{\begin{array}{l}{i}_{\mathrm{L}}={\displaystyle \frac{U_1}{R_1}}+C_1{\displaystyle \frac{\mathrm{d}{U}_1}{\mathrm{d}t}}\\ i_{\mathrm{L}}={\displaystyle \frac{U_2}{R_2}}+C_2{\displaystyle \frac{\mathrm{d}{U}_2}{\mathrm{d}t}}\\ U_{\mathrm{L}}=U_{\mathrm{OC}}-I{R}_0-U_1-U_2\end{array}\right.$$

(1)

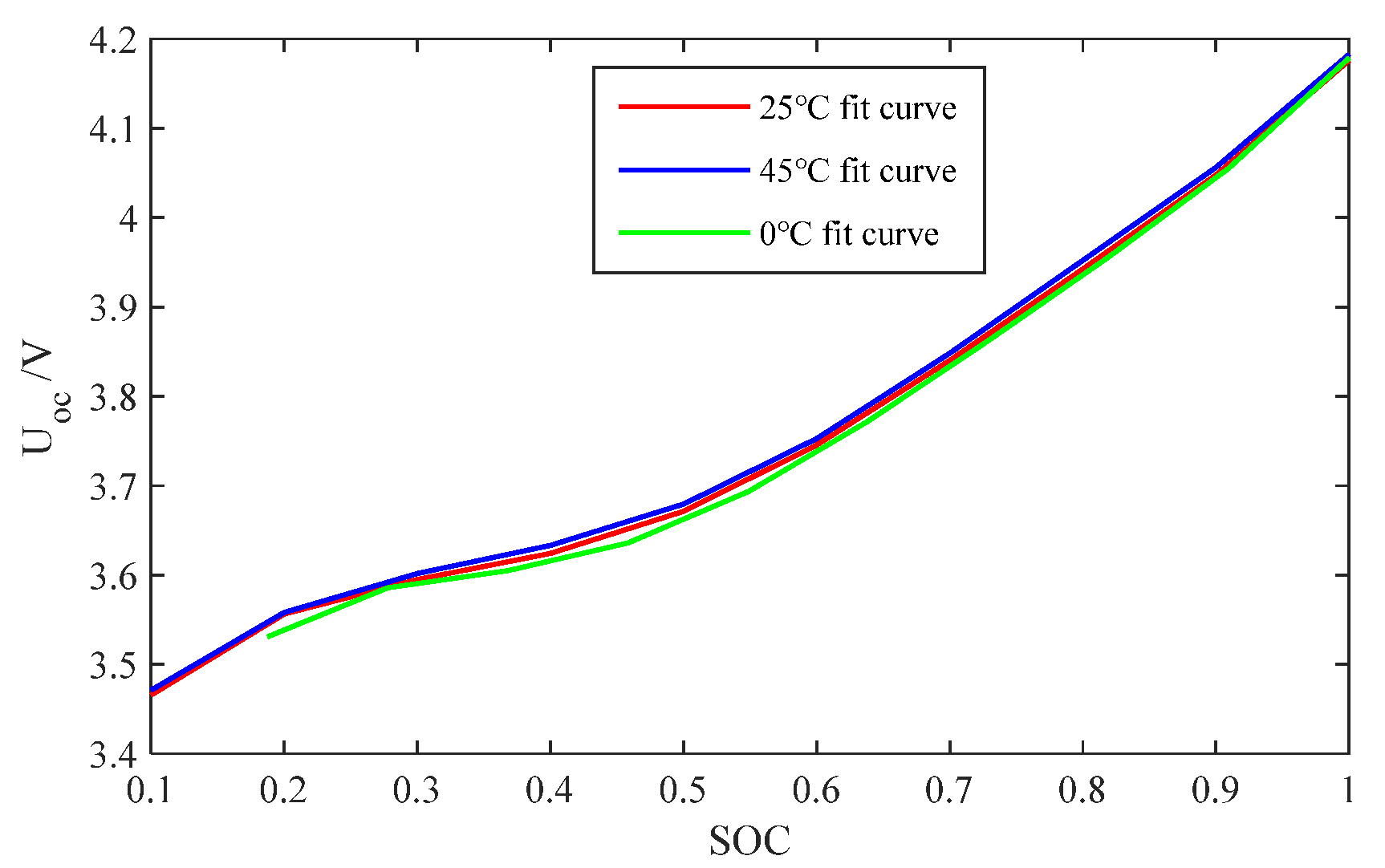
2.2. Obtaining OCV-SOC Relationships at Different Temperatures

The 18650 LiFePO4 battery used in this study is a publicly accessible battery dataset from the University of Maryland,

Table 1. Main parameters of the battery.

Parameter Type	Parameter Value
Nominal capacity/(Ah)	2
Nominal voltage/V	3.6
Charging cut-off voltage/V	4.2
Discharging cut-off voltage/V	2.5

shows the battery specifications. With fully charged lithium battery is put through a 0.5 C constant-current intermittent discharge test for 2 min at environmental temperatures of 0 °C, 25 °C, and 45 °C, respectively. After that, it is left to stand for two hours, discharged again at 0.5 C for 2 min, and then leave for 2 h. This process is repeated 10 times until the battery’s final voltage drops to the discharge threshold voltage. Among these, Figure 2 displays the lithium battery’s voltage and current as determined by the constant-current intermittent discharge test at 25 °C.

According to the aforementioned test, you can determine the end voltage value of various charging states at 0 °C, 25 °C, and 45 °C using a 0.5 C discharge multiplier pulse discharge test. During leave for 2 h, the battery’s end voltage is estimated as the open-circuit voltage (OCV), accounting for the impact of temperature on the relationship between the SOC-OCV to create the OCV-SOC-T lookup table depicted in Figure 3.

It can be seen that when the SOC value of the battery is at a lower value, a lower temperature environment will cause the battery to have a lower OCV value, while when the SOC value of the battery is at a higher value, a lower temperature environment will cause the battery to have a higher OCV value. Thus, the effect of temperature on the OCV-SOC relationship is nonlinear.

To realize the subsequent state estimation of lithium batteries and, at the same time, to ensure that the fitting effect is better and the computational volume is small, this paper adopts the sixth-order fitting of the relationship between SOC and OCV, the coefficients of the fitting polynomials at different temperatures, as well as the values of linear regression coefficients of the fitted curve. R-square (R²) values, as shown in

Table 2. Polynomial fitting coefficients at different temperatures.

Temperature	${\mathit{p}}_1$	${\mathit{p}}_2$	${\mathit{p}}_3$	${\mathit{p}}_4$	${\mathit{p}}_5$	${\mathit{p}}_6$	${\mathit{p}}_7$	${\mathit{R}}^2$
0 °C	−5.203	31.861	−67.960	68.155	−33.602	8.108	2.820	0.9997
25 °C	7.384	−17. 320	8.980	6.875	−7.650	2.636	3.271	0.9997
45 °C	12.443	−35.176	33.668	−9.983	−1.796	1.702	3.326	0.9998

, are all greater than 0.99, which indicates that the curve can be a better characterization of the relationship of the lithium battery’s OCV-SOC; and the sixth-order fitting calculation process is not complicated. The final sixth-order polynomial is obtained:

$$f_{OCV}(S)=p_1{S}^6+p_2{S}^5+p_3{S}^4+p_4{S}^3+p_5{S}^2+p_{6}S+p_7$$

(2)

In the above equation, pi is the fitting coefficient, i = 0, 1, …, 7; S is SOC.

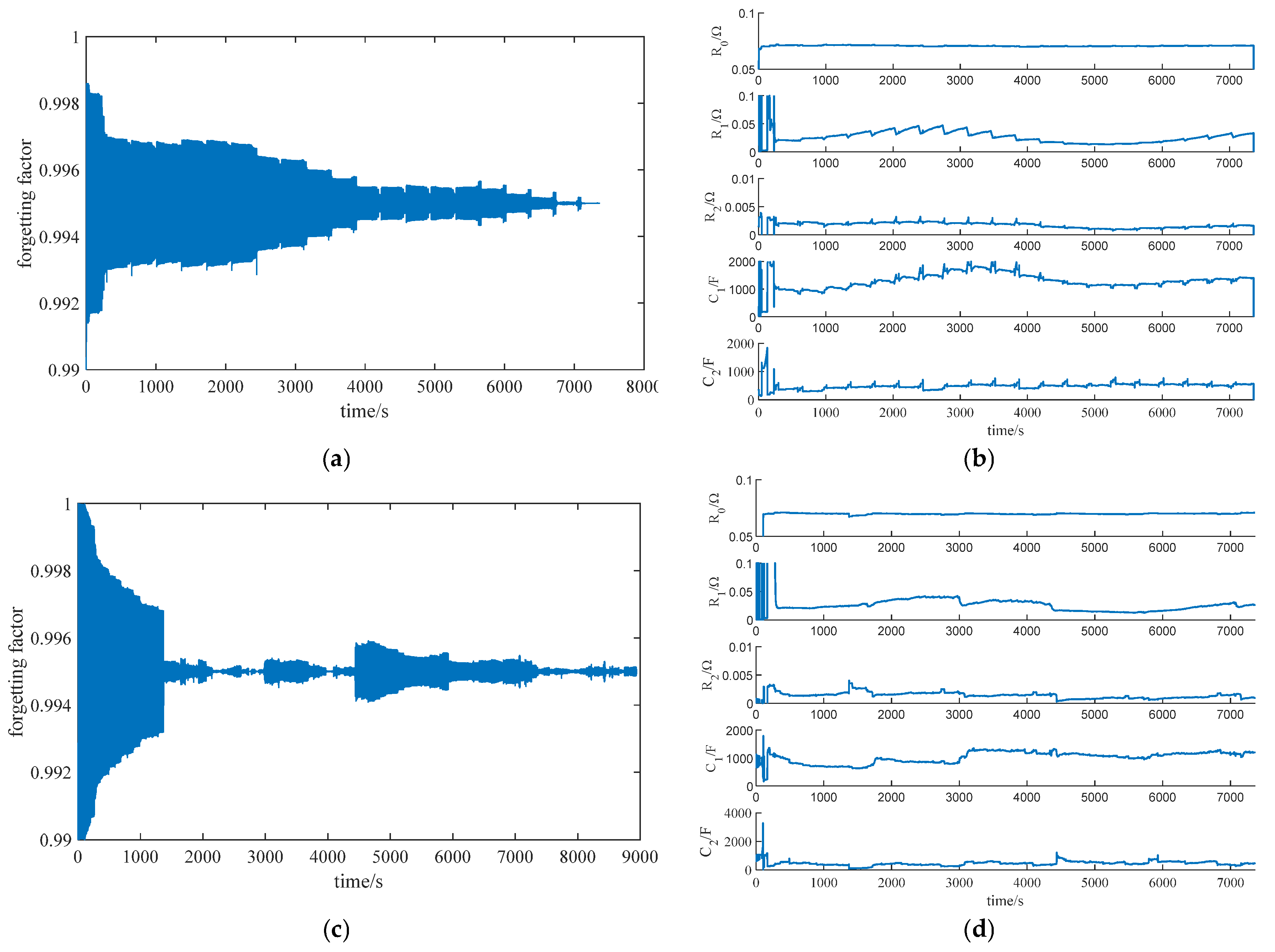
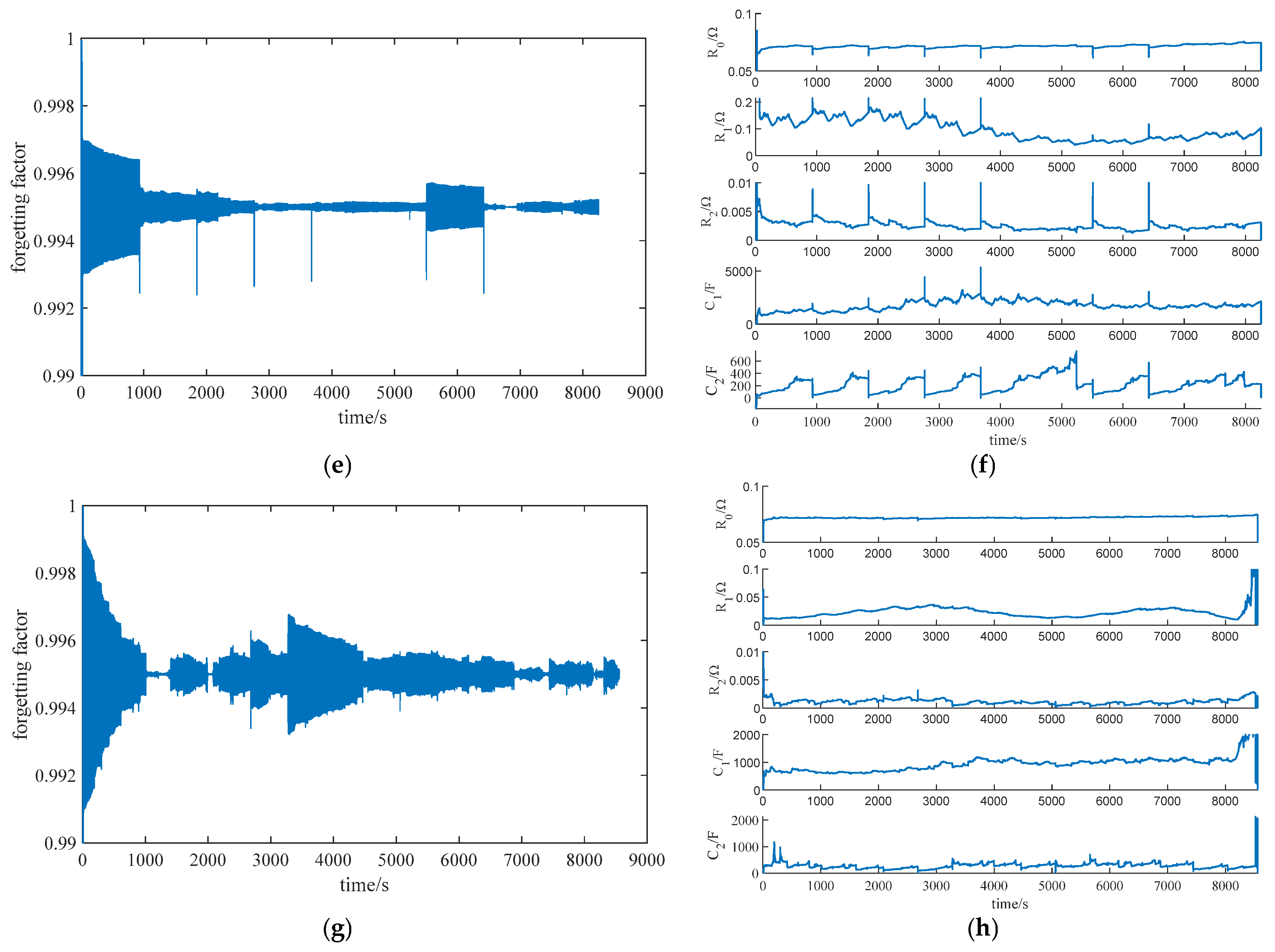
2.3. Model Parameter Identification

Because of its easy programming, quick convergence, and low computing volume, FFRLS is frequently employed in online system parameter identification [39]. However, the algorithm is less flexible, and the fixed forgetting factor is hard to adjust to the diverse dynamic situations of lithium batteries. As a result, the parameter identification results can vary significantly under different battery operating conditions.

Given this, the Variable Forgetting Factor Recursive Least Squares (VFFRLS) algorithm—an enhanced algorithm that adaptively determines the desired forgetting factor value depending on the magnitude of the estimation error in the parameter identification stage is used in this study. A variable forgetting factor technique was first developed by J.D. Park in 1991 [40]:

$${\lambda }_k={\lambda }_{\min }+({\lambda }_{\max }-{\lambda }_{\min })\cdot 2^{L_k}$$

(3)

$$L_k=-NINT(\rho e{(k)}^2)$$

(4)

Here, λ_k stands for the variable forgetting factor, λ_min for its minimum value, λ_max for its maximum value, e(k) denotes the current prediction error of the FFRLS calculation algorithm, NINT(x) for the rounding function, and ρ the sensitivity factor. The value of λ_k can adaptively change exponentially with the estimation error at the current moment. The closer the variable forgetting factor is to λ_min, the greater the estimation error; the closer it is to λ_max, the smaller the estimation error [41].

For better results in online recognition of lithium battery model parameters, either the parameter for the sensitivity coefficient ρ is adjusted, or the roundoff function NINT(x) is removed from the algorithm. If the value of the sensitivity coefficient is modified, the forgetting coefficient becomes more sensitive to the estimating error. Given that the scope of the forgetting factor increases exponentially with this variable, when the estimation error is large, If the sensitivity factor is too large, it will easily be minimized λ_k, resulting in an unstable algorithm.

The estimation error of a single data point determines the variable forgetting factor, so if the estimation error of a particular point is erroneous or disturbed, the forgetting factor will abruptly change. This will raise the subsequent estimation error, which will make the algorithm unstable. The amount of the variable forgetting factor is thus calculated in this study using the theory of data windowing by calculating the mean square value of the estimation errors of a finite number of data points over a given period.

$$L_k=-\rho {\displaystyle \frac{{\displaystyle \sum _{i=k-M+1}^k{e}_i{e}_i^T}}{M}}$$

(5)

e_i is the estimation error at moment i, and M is the window size. At this point, the mean square of the estimation errors of the previous M sampling points determines the amount of the parameter forgetting factor.

Consequently, the VFFRLS algorithm’s particular process is as follows:

(1)

Initialization ${\widehat{\theta }}_0, {\phi }_0, P_0, {\lambda }_{\min }, {\lambda }_{\max }, \rho , M$.;

(2)

Calculate the forgetting factor:

$$e_k=y_k-{{\phi }^{\mathrm{T}}}_k{\widehat{\theta }}_{k-1}$$

(6)

$$L_k=-\rho {\displaystyle \frac{{\displaystyle \sum _{i=k-M+1}^k{e}_i{e}_i^T}}{M}}$$

(7)

$${\lambda }_k={\lambda }_{\min }+({\lambda }_{\max }-{\lambda }_{\min })\cdot 2^{L_k}$$

(8)

(3)

Calculate the least squares estimate at moment k:

$$K_k={\displaystyle \frac{P_{k-1}{\phi }_k^T}{{\lambda }_k+{\phi }_k^T{P}_{k-1}{\phi }_k}}$$

(9)

$$P_k={\displaystyle \frac{P_{k-1}-K_k{\phi }_k^T{P}_{k-1}}{{\lambda }_k}}$$

(10)

$${\widehat{\theta }}_k={\widehat{\theta }}_{k-1}+K_k{e}_k$$

(11)

$\widehat{\theta }(k)$ is the estimation vector for parameter identification, φ(k) is the system observation, K(k) is the estimated gain matrix, y(k) is the system’s actual output, and P(k) is the covariance matrix.

(4)

Solve inversely for R₀,R₁,C₁,R₂,C₂, the process is as follows:

Firstly, depending on the second-order RC circuit model, the mathematical relationships between the battery voltage, current, and model parameters established in the z-domain and the discrete mathematical formulas are derived. The Lithium battery equivalent circuit model in Figure 1 is Laplace transformed, and the transfer function is derived as:

$$\left\{\begin{array}{l}{U}_{\mathrm{OCV}}(s)-U_{\mathrm{O}}(s)=I(s)\left(R_0+{\displaystyle \frac{R_1}{1+R_1{C}_{1}s}}+{\displaystyle \frac{R_2}{1+R_2{C}_{2}s}}\right)\\ G(s)={\displaystyle \frac{R_0{\tau }_1{\tau }_2{s}^2+(R_0{\tau }_1+R_0{\tau }_2+R_1{\tau }_2+R_2{\tau }_1)s+R_0+R_1+R_2}{1+({\tau }_1+{\tau }_2)s+{\tau }_1{\tau }_2{s}^2}}\end{array}\right.$$

(12)

In the above equation, ${\tau }_1=R_1{C}_1$, ${\tau }_2=R_2{C}_2$.

Secondly, the system function G(s) in the above equation is discretized using the bilinear transformation formula.

$$s={\displaystyle \frac{2}{T}}\cdot {\displaystyle \frac{1-z^{-1}}{1+z^{-1}}}$$

(13)

The discretization is then converted to a difference equation:

$$\left\{\begin{array}{l}G(z^{-1})={\displaystyle \frac{a_3+a_4{z}^{-1}+a_5{z}^{-1}}{1-a_1{z}^{-1}-a_2{z}^{-2}}}\\ y(k)=a_{1}y(k-1)+a_{2}y(k-2)+a_{3}I(k)+a_{4}I(k-1)+a_{5}I(k-2)\end{array}\right.$$

(14)

Finally, the parameters in the second-order RC model can be obtained from Equations (13) and (14):

$$\left\{\begin{array}{l}{\tau }_1+{\tau }_2=T\cdot {\displaystyle \frac{1+a_2}{1-a_1-a_2}}\\ {\tau }_1{\tau }_2={\displaystyle \frac{T^2}{4}}{\displaystyle \frac{1+a_1-a_2}{1-a_1-a_2}}\\ R_0+R_1+R_2={\displaystyle \frac{a_3+a_4+a_5}{1-a_1-a_2}}\\ R_0{\tau }_1+R_0{\tau }_2+R_1{\tau }_2+R_2{\tau }_1=T\cdot {\displaystyle \frac{a_3-a_5}{1-a_1-a_2}}\\ R_0{\tau }_1{\tau }_2={\displaystyle \frac{T^2}{4}}\cdot {\displaystyle \frac{a_3-a_4+a_5}{1-a_1-a_2}}\end{array}\right.$$

(15)

3. Joint Estimation of SOC Based on VFFRLS-AEKF

3.1. Definition of SOC

The SOC of a battery is the ratio of the available capacity to the rated capacity in the battery, usually expressed as a percentage.

$$SOC(t)=SO{C}_0-{\displaystyle \frac{1}{Q_N}}{\displaystyle {\int }_0^t\eta \cdot i(t)d\tau }$$

(16)

where SOC₀ is the initial value of SOC; Q_N is the rated capacity of the battery, the Coulomb coefficient of the battery, and i is the charge/discharge current. When estimating the SOC of lithium batteries, it is necessary to establish the discretized battery state-space equations, according to Equations (1) and (16), the state-space equations of the battery model can be obtained:

$$\begin{array}{l}\left[\begin{array}{c}{U}_1(k)\\ U_2(k)\\ SOC(k)\end{array}\right]=\left[\begin{array}{ccc}\exp (-\Delta t/(R_1{C}_1))& 0& 0\\ 0& \exp (-\Delta t/(R_2{C}_2))& 0\\ 0& 0& 1\end{array}\right]\times \left[\begin{array}{c}{U}_1(k-1)\\ U_2(k-1)\\ SOC(k-1)\end{array}\right]+\\ \left[\begin{array}{c}{R}_1(1-\exp (-\Delta t/R_1{C}_1))\\ R_2(1-\exp (-\Delta t/R_2{C}_2))\\ -\eta \Delta t/Q_N\end{array}\right]I(k-1)+{\omega }_{k-1}\end{array}$$

(17)

$${\mathrm{U}}_L(k)=U_{oc}(SOC(k))-U_1(k)-U_2(k)-i(k)R_0+v_k$$

(18)

3.2. AEKF Based on Multi-New Information

For a nonlinear discrete system, the equations of state and observation of the EKF are:

$$\left\{\begin{array}{l}{x}_k=A_{k-1}{x}_{k-1}+B_{k-1}{u}_{k-1}+{\omega }_k\\ y_k=C_k{x}_k+D_k{u}_k+v_k\end{array}\right.$$

(19)

where x_k is the state variable of the system; u_k is the input quantity; y_k is the output quantity; w_k is the process noise variable, which represents the noise and error attached to the state variable during the transfer process, with covariance Q; and v_k is the observation noise variable, which describes the noise and error generated when measuring the output quantity of the system, with covariance R.

According to Equations (17) and (18), it can be seen that $x_k={[U_1(k),U_2(k),SOC(k)]}^T$, $u_k=U_L(k)$, ${\omega }_k$ is the process noise and $v_k$ is the measurement noise, where:

$$A=\left[\begin{array}{ccc}\exp (-\Delta t/(R_1{C}_1))& 0& 0\\ 0& \exp (-\Delta t/(R_2{C}_2))& 0\\ 0& 0& 1\end{array}\right],B=\left[\begin{array}{c}{R}_1(1-\exp (-\Delta t/R_1{C}_1))\\ R_2(1-\exp (-\Delta t/R_2{C}_2))\\ -\eta \Delta t/Q_N\end{array}\right]$$

$$C=[-1,-1,{\displaystyle \frac{\partial U_{oc}(SOC)}{\partial SOC}}],D=-R_0$$

With the help of the multi-new information method proposed by Shi et al. [35], the state and observation equations can be updated in real-time by introducing multi-new information theories to form the adaptive extended Kalman filter (AEKF). This is because the EKF filtering algorithm linearizes the battery model, which by default makes the process noise and observation noise of the system invariant [33]. However, the noise of a real system is unknown and changing. The noise covariance of the state equation and observation equation can be modified in real-time by incorporating fresh information to build an adaptive extended Kalman filter (AEKF) to increase the estimation accuracy of the SOC. Where the introduced multi-new information is the difference between the measured voltage value and the predicted voltage value of the lithium battery, i.e.,

$$E_k=y_k-h({\widehat{x}}_k,u_k)$$

(20)

Using the principle of open-window estimation, different weights are assigned to the data within the window, with larger weights assigned to the near-term data and smaller weights assigned to the far-term data, resulting in a multi-new information covariance matrix H_k.

$$H_k={\displaystyle \frac{1}{M-1}}{\displaystyle \sum _{i=k-M+1}^k{E}_i{E}_i^{\mathrm{T}}}$$

(21)

When M denotes the width of the open window in the windowed estimation principle, the adaptive estimation of the process noise and observation noise covariance can be obtained based on the new multi-new information covariance matrix H_k.

$$\begin{array}{l}{Q}_k=K_k{H}_k{K}_k^{\mathrm{T}}\\ R_k=H_k-C_k{\overline{P}}_k{C}_k^{\mathrm{T}}\end{array}$$

(22)

This leads to the derivation of the specific steps for estimating the SOC for the AEKF:

(1)

Set the initial values of x₀, P₀, Q₀, R₀

$$\left\{\begin{array}{l}{\widehat{x}}_0=E[x_0]\\ P_0=E\left[(x_0-{\widehat{x}}_0){(x_0-{\widehat{x}}_0)}^T\right]\\ {\widehat{Q}}_0=Q_0\\ {\widehat{R}}_0=R_0\end{array}\right.$$

(23)

(2)

Predicted state variables and error covariance matrix:

$${\overline{x}}_k=A_{k-1}{\widehat{x}}_{k-1}+B_{k-1}{u}_{k-1}$$

(24)

$${\overline{P}}_k=A_{k-1}{\widehat{P}}_{k-1}{A}_{k-1}^{\mathrm{T}}+{\widehat{Q}}_{k-1}$$

(25)

(3)

Calculate the gain matrix:

$$K_k={\overline{P}}_k{C}_{k-1}^{\mathrm{T}}{(C_{k-1}{\overline{P}}_k{C}_{k-1}^{\mathrm{T}}+{\widehat{R}}_{k-1})}^{-1}$$

(26)

(4)

Introduce the multi-new information estimating function and compute the covariance matrix:

$$E_k=y_{k-1}-(C_{k-1}{\widehat{x}}_k+D_{k-1}{u}_{k-1})$$

(27)

$$H_k={\displaystyle \frac{1}{M-1}}{\displaystyle \sum _{i=k-M+1}^k{E}_i{E}_i^{\mathrm{T}}}$$

(28)

(5)

Update the process noise and observation noise covariance matrices:

$$Q_k=K_k{H}_k{K}_k^{\mathrm{T}}$$

(29)

$$R_k=H_k-C_k{\overline{P}}_k{C}_k^{\mathrm{T}}$$

(30)

(6)

Update the state variables and error covariance matrix:

$${\widehat{x}}_k={\overline{x}}_k+K_k{E}_k$$

(31)

$${\widehat{P}}_k=(1-K_k{C}_k){\overline{P}}_k$$

(32)

(7)

Repeat steps (2) through (6) for recursive filtering calculations.

3.3. VFFRLS-AEKF Joint Estimation of SOC

According to the above theoretical analysis, this paper fuses the two algorithms of VFFRLS-AEKF and applies them to the SOC estimation of lithium batteries. Figure 4 shows the joint estimation process.

Step 1: Different SOC-OCV relationship curves are chosen based on the battery’s operating temperature.

Step 2: Using voltage, current, temperature, and other information, the VFFRLS algorithm recognizes the lithium battery model parameters at k moments. The recognition results are then saved, along with the voltage and current values at the current moment, for parameter recognition at k + 1 moments.

Step 3: Enter the results of the VFFRLS identification into the AEKF method for combined estimation of SOC. Firstly, after initializing the state matrix and covariance matrix and combining them with the system noise model for a priori state estimation, use the length of the multi-new information that has been determined to update the gain matrix based on the covariance matrix of the multi-new information and the observation noise model. Then, use the gain matrix to combine the a priori state estimation with the observations to obtain a more accurate state estimate. Finally, use the state update to estimate the battery SOC.

Step 4: The system time should be pushed back to k + 1 to determine the parameters and estimate the SOC at the following instant.

Online model parameter identification and online SOC estimate for lithium batteries can be achieved by repeating the aforementioned four steps.

4. Experiments and Analysis of Results

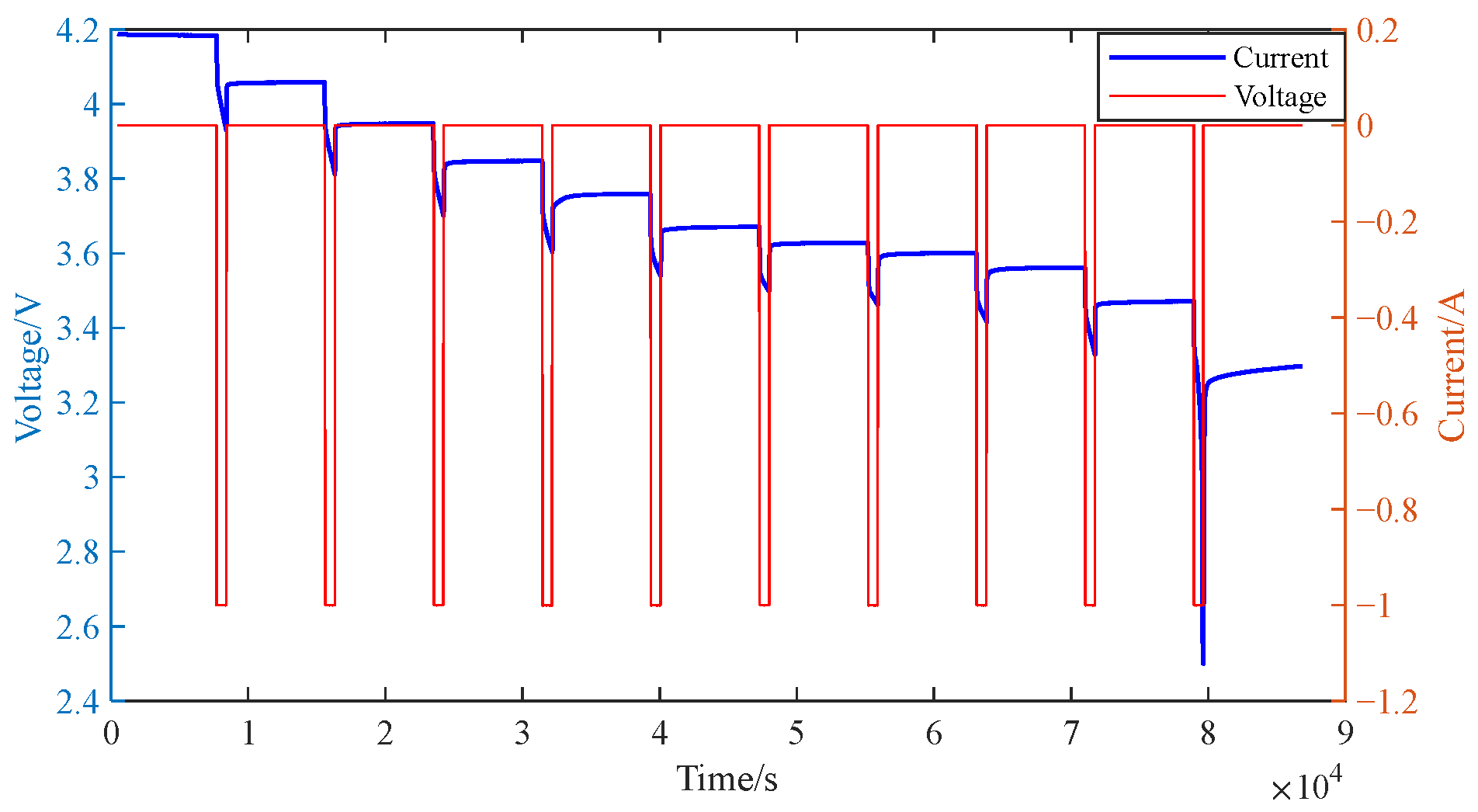
4.1. Identification of Model Parameters Under Different Operating Conditions

Based on the test data and parameter identification steps, the recursive least squares algorithm script file for the variable forgetting factor is written in MATLAB R2021a under four working conditions: DST, FUDS, BJDST, and US06 at 25 °C, where λ_max takes several 1, λ_min with a value of 0.99, and M takes the value of 80. Following identification, Figure 5 displays the forgetting factor’s change curves under various operating settings as well as the R₀, R₁, C₁, R₂, and C₂ identification results.

The parameters change more radically in the initial stage of identification, as shown in Figure 5. This is because there was a significant variance in the selection of the model parameters’ initial values. As time goes on, the forgetting factor rapidly narrows down to a smaller range, allowing the identification results to quickly converge on the true values. However, the simulation results for the BJDST condition show numerous downward spikes in the forgetting factor. This is because the voltage and current of the lithium battery have changed at these spikes, and the appearance of these spikes is advantageous for parameter identification. Additionally, lowering the forgetting factor can enhance the algorithm’s fast-tracking capability, allowing the identification results to quickly keep up with the real changes in the parameters. By comparing the four operating conditions, it is found that the VFFRLS can adaptively find the optimal value of the forgetting factor with the battery operating state.

The results of R₀, R₁, R₂, C₁, and C₂ identification are displayed in Figure 6. This paper uses VFFRLS for parameter identification based on the experimental data of DST working conditions at 0 °C, 25 °C, and 45 °C, respectively, to further discuss the variation of battery parameters at different temperatures.

The internal resistance of the ohmic Lithium-ion (Li⁺) diffusion rate decreases with increasing R₀ in low-temperature electrolyte viscosity, which lowers ionic conductivity. At the same time, the low temperature will lower the electronic conductivity of the positive and negative electrode materials, which raises R₀ significantly. High temperatures cause phase changes in the electrode materials or electrolyte breakdown, which leads to significant variations in polarization resistance. At high temperatures, polarization resistance R₁ and R₂ exhibit a declining trend. Resistance polarization C₁ is greatly reduced in the low-temperature environment, and as the temperature rises, the diffusion coefficient rises and C₂ increases. This is because, at low temperatures, the electrolyte viscosity of lithium batteries increases, ion mobility decreases, and charging speed slows down, which results in a decrease in C₁. Each parameter is within a somewhat stable range at room temperature, the polarization resistance and the polarization capacitance fluctuate at a modest rate.

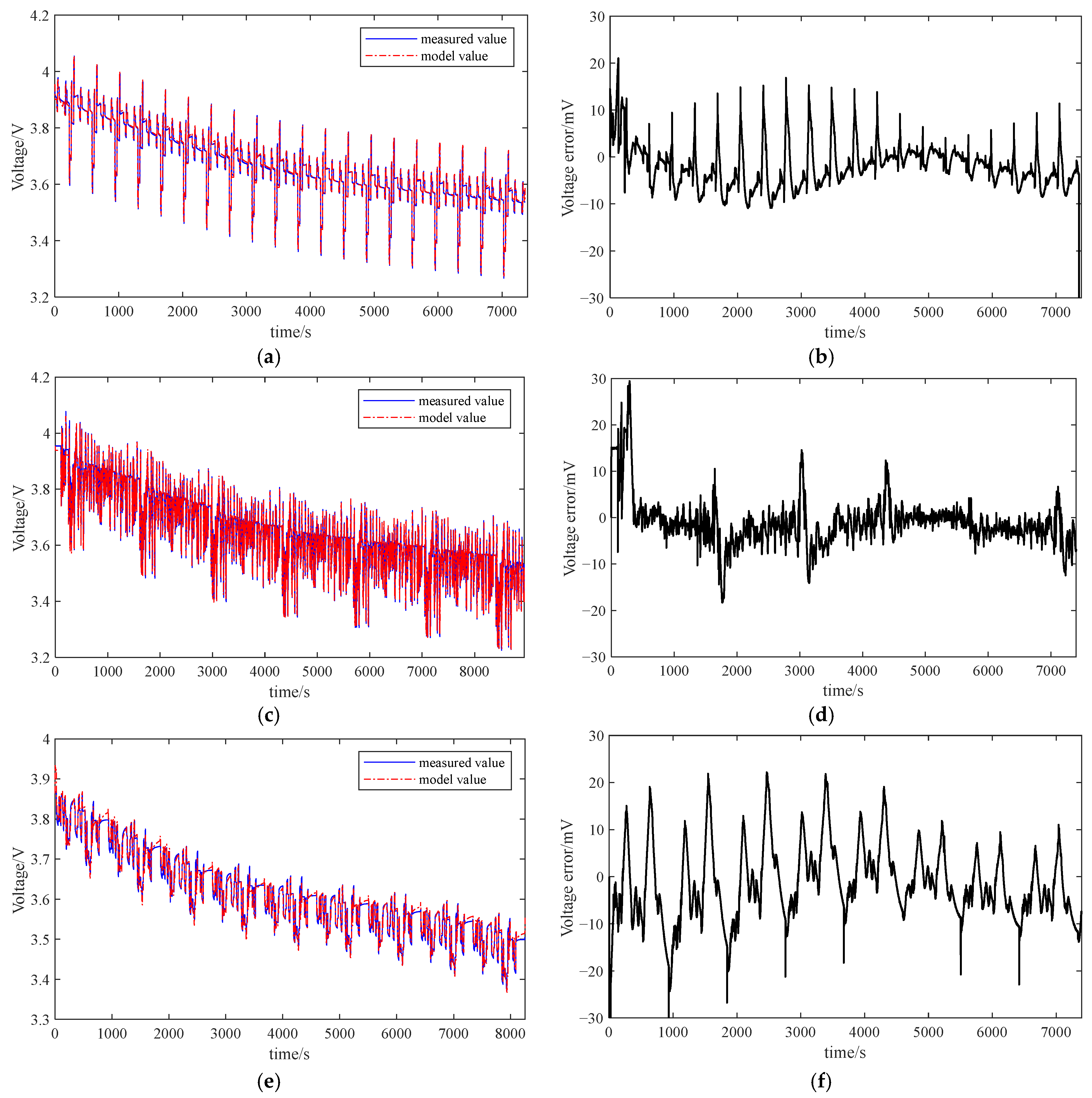
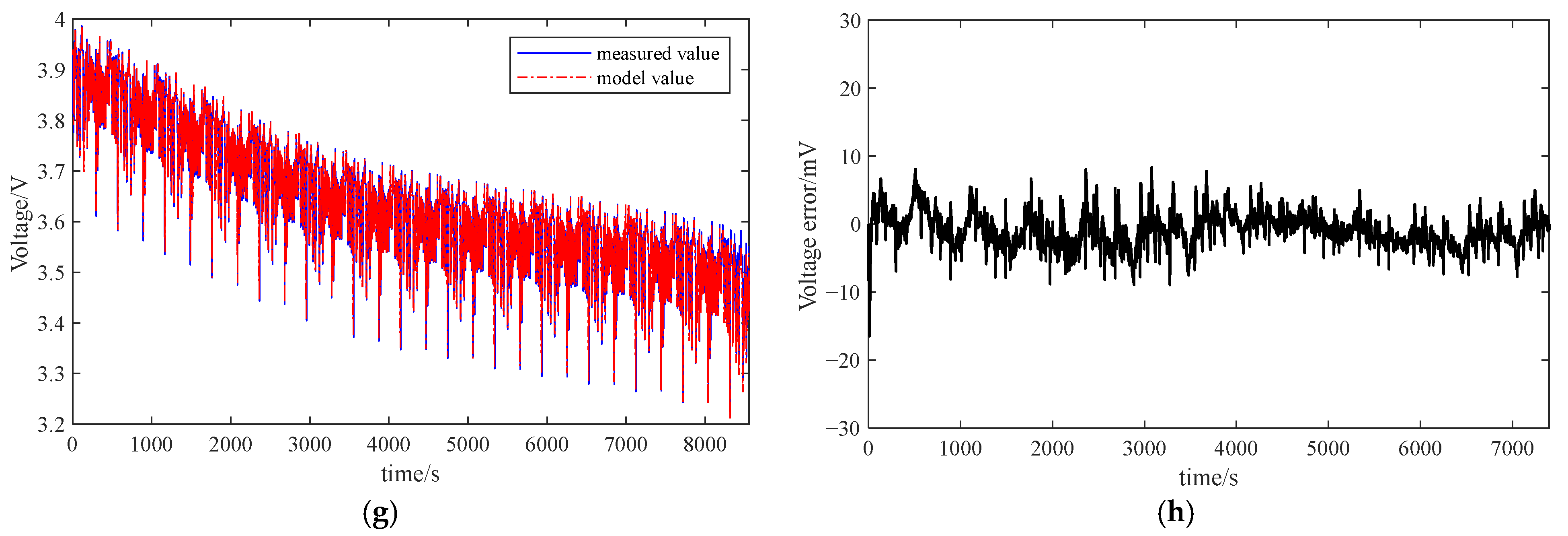
4.2. Model Accuracy Verification

By substituting the identified model parameters into the terminal voltage solution Equation (1) at different temperatures and working conditions, the model terminal voltage can be obtained and compared with the measured voltage values during the discharge test. This allows one to confirm the accuracy of the second-order RC equivalent circuit model parameter identification.

Table 3. Voltage MAE values for different working conditions at different temperatures (mV).

Temperature	DST	FUDS	BJDST	US06
0 °C	6.91	6.72	5.25	7.70
25 °C	3.96	3.34	6.61	2.92
45 °C	3.75	5.64	2.96	3.12

displays the mean absolute errors (MAE) of the voltages under various operating conditions at various temperatures. When T = 25 °C, the comparison curves of the model terminal voltage with the measured voltage under four operating conditions and the errors are displayed in Figure 7.

The greatest average absolute error between the model terminal voltage and the actual voltage detected by VFFRLS is kept within 7.7 mV, as shown in Figure 6 and Table 3, which, taken as a whole, satisfies the model accuracy requirements. It demonstrates the great accuracy of the second-order RC equivalent circuit model and the improved ability of VFFRLS to identify each parameter of the online lithium battery model. In addition, this parameter identification approach is very adaptive and is not impacted by temperature.

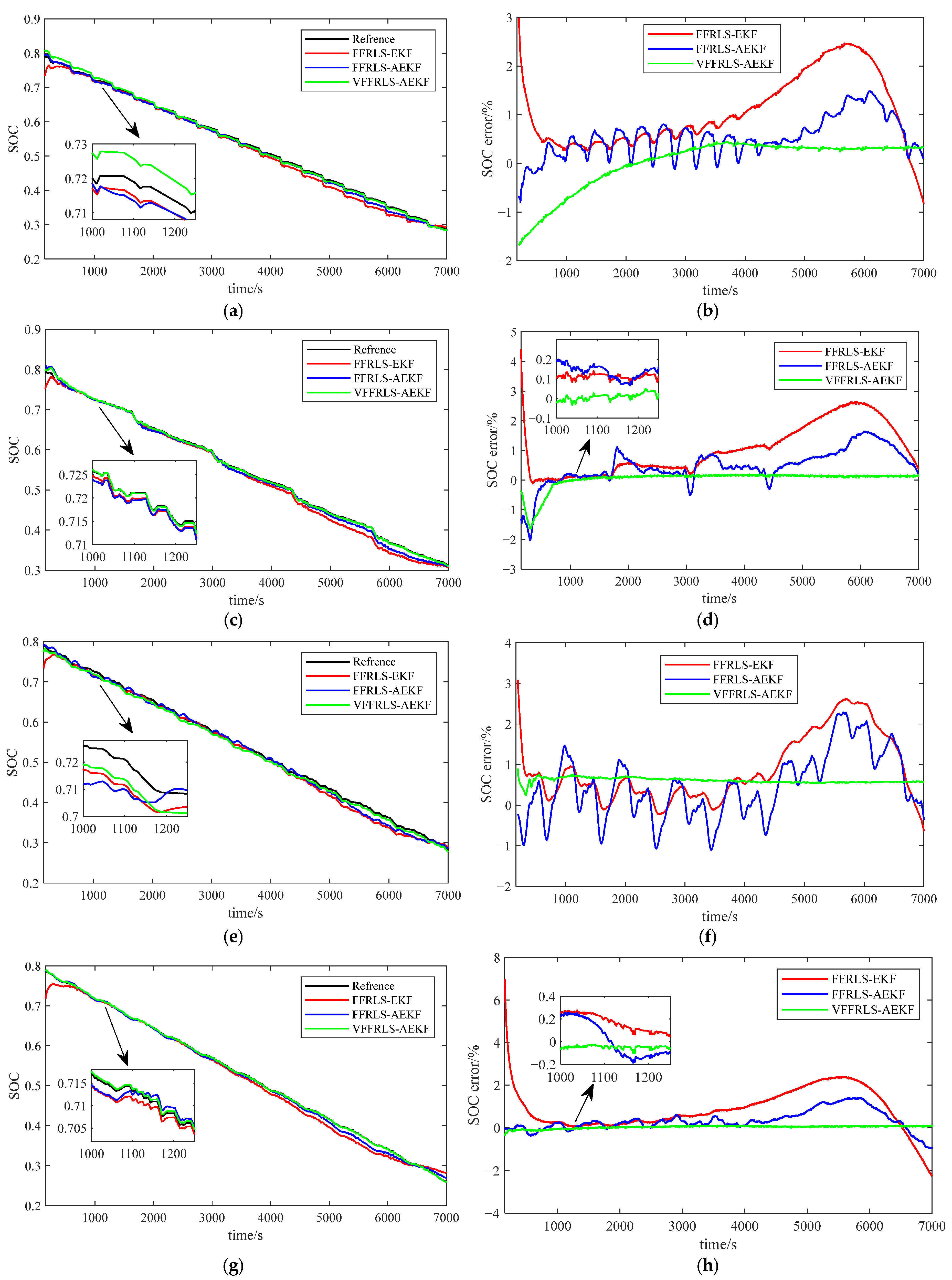
4.3. Validation of SOC Estimation Under Various Working Conditions at the Same Temperature

The joint algorithm was tested at T = 25 °C under four working conditions: BJDST, DST, US06, and FUDS. The estimation capability and reliability of the VFFRLS-AEKF joint algorithm were confirmed by using the FFRLS-EKF algorithm, the FFRLS-AEKF algorithm, and the VFFRLS-AEKF algorithm, respectively, to carry out the SOC estimation. The theoretical reference value of SOC is determined by sampling the current and using the ampere-hour integral method because the value of SOC cannot be measured directly. The estimation results and their errors are displayed in Figure 8 and are compared and analyzed with the theoretical reference value. The initial process noise covariance matrix Q is set to [1 × 10⁻¹⁰ 0 0;0 1 × 10⁻¹⁰ 0;0 0 1 × 10⁻¹⁰] The initial measurement noise covariance matrix R is set to 0.01.

To further verify the convergence and robustness of the joint algorithm proposed in this paper, firstly, under the condition of the same temperature and the same working condition (DST), the initial values of SOC are set to 0.3, 0.5 and 0.7, respectively, and the actual initial value of SOC is 0.8, and then the SOC estimation is carried out by using the joint algorithm of VFFRLS-AEKF, which leads to the convergence of the SOC quickly when it takes different initial values, and the estimation results are compared with the reference theoretical value, the error curve can be obtained, as shown in Figure 9. Meanwhile, the initial value of SOC is set to 0.38, and three different joint estimation methods are used to realize SOC estimation. The estimation results and errors are shown in Figure 10.

4.4. Validation of SOC Estimation at Different Temperatures for the Same Operating Condition

In real-world applications, lithium batteries are exposed to intricate and fluctuating environmental conditions, and their internal characteristics exhibit instability throughout a broad temperature range. The SOC estimation of the suggested joint method is performed using the measured data of Li-ion batteries at various temperatures (0 °C, 25 °C, and 45 °C) under the DST cycling condition to confirm the flexibility of the joint algorithm proposed in this paper for estimating SOC. The estimation results are shown in Figure 11 and the estimation errors are shown in Figure 12. The approach is also contrasted with the conventional algorithm, and Figure 13 displays the root mean square error (RMSE) of each algorithm for predicting SOC under various operating conditions and temperatures.

It is known from the validation results:

(1)

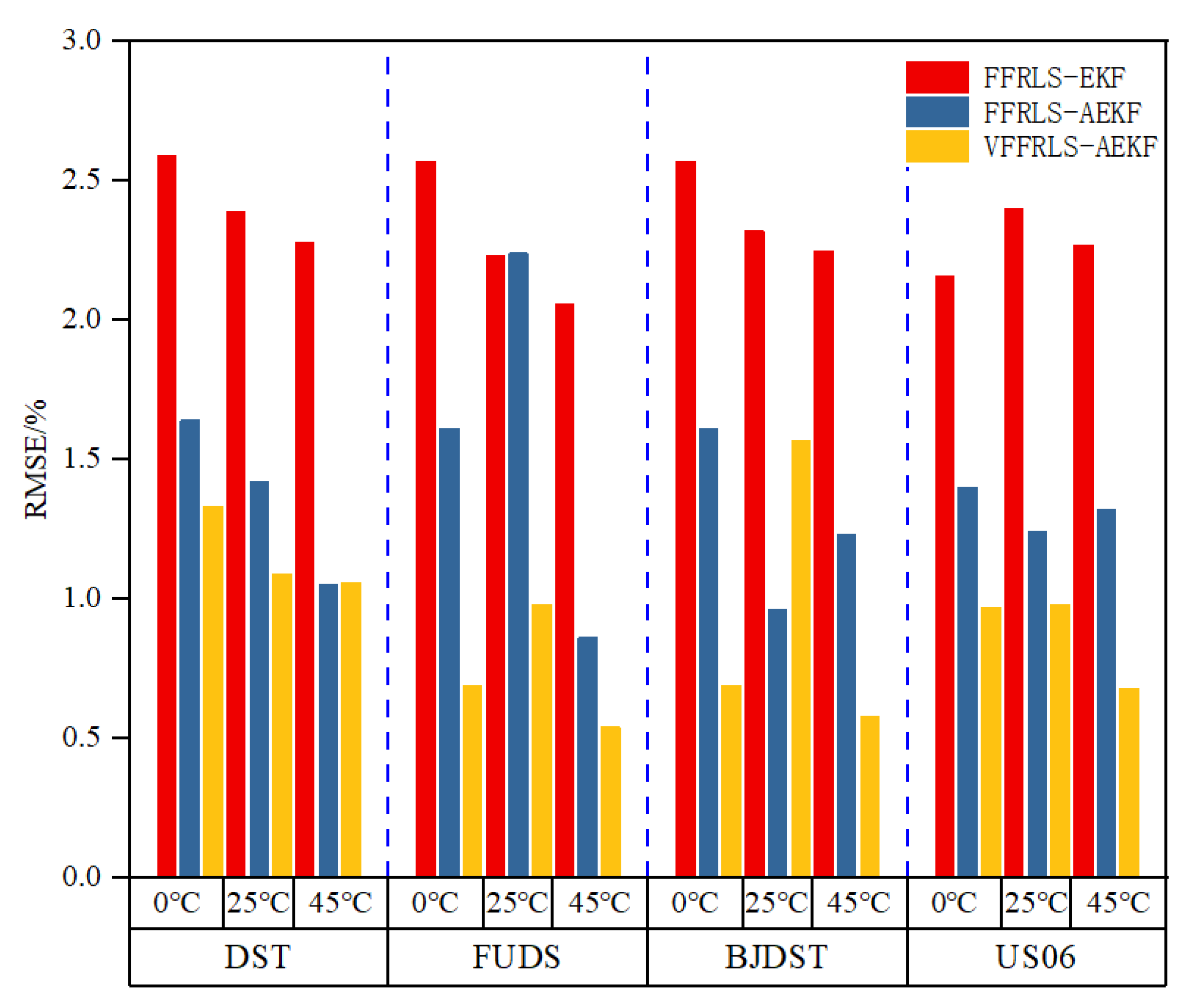
For four distinct operating situations at the same temperature, the maximum RMSE of FFRLS-EKF is 2.4%, the maximum RMSE of FFRLS-AEKF is 2.24%, and the maximum RMSE of VFFRLS-AEKF is 1.57%, as shown in Figure 8 and Figure 13. Consequently, the method proposed in this work offers extremely precise SOC estimation.

(2)

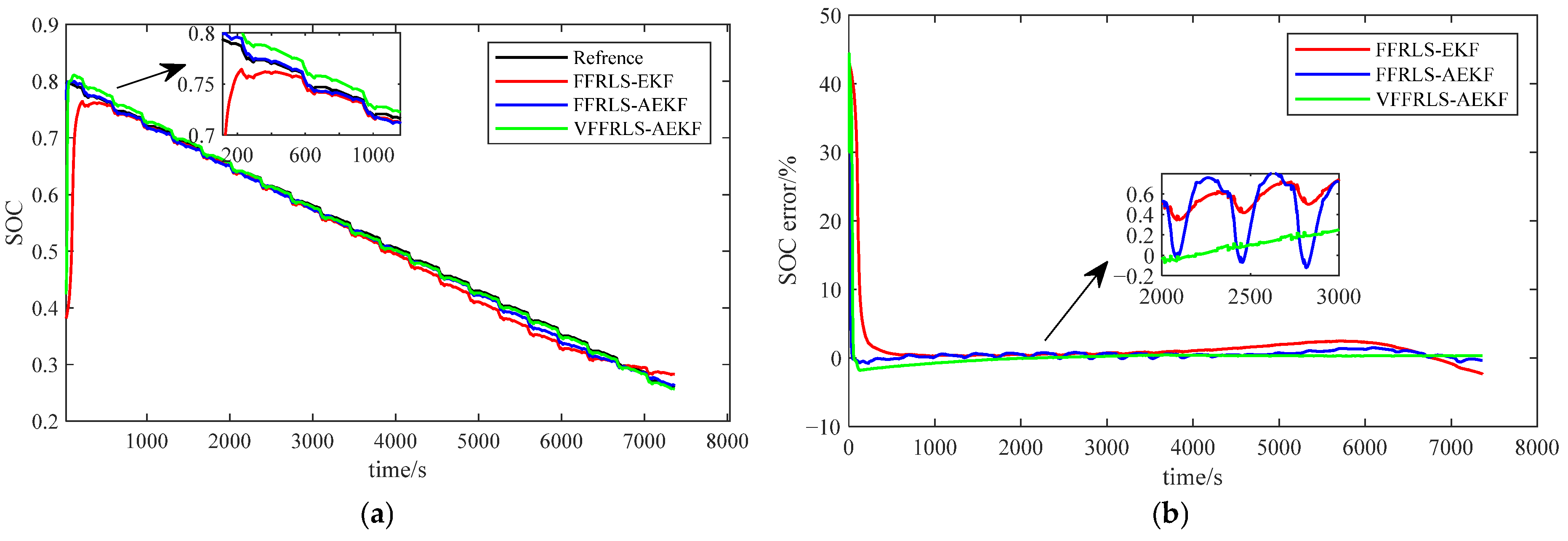
The joint algorithm effectively improves the estimation of the SOC of lithium battery under the temperature-varying environment, as shown by the maximum RMSE of FFRLS-EKF being 2.59%, the maximum RMSE of FFRLS-AEKF being 1.64%, and the maximum RMSE of VFFRLS-AEKF, being 1.33% for the same conditions with three different temperatures (Figure 11 and Figure 13).

(3)

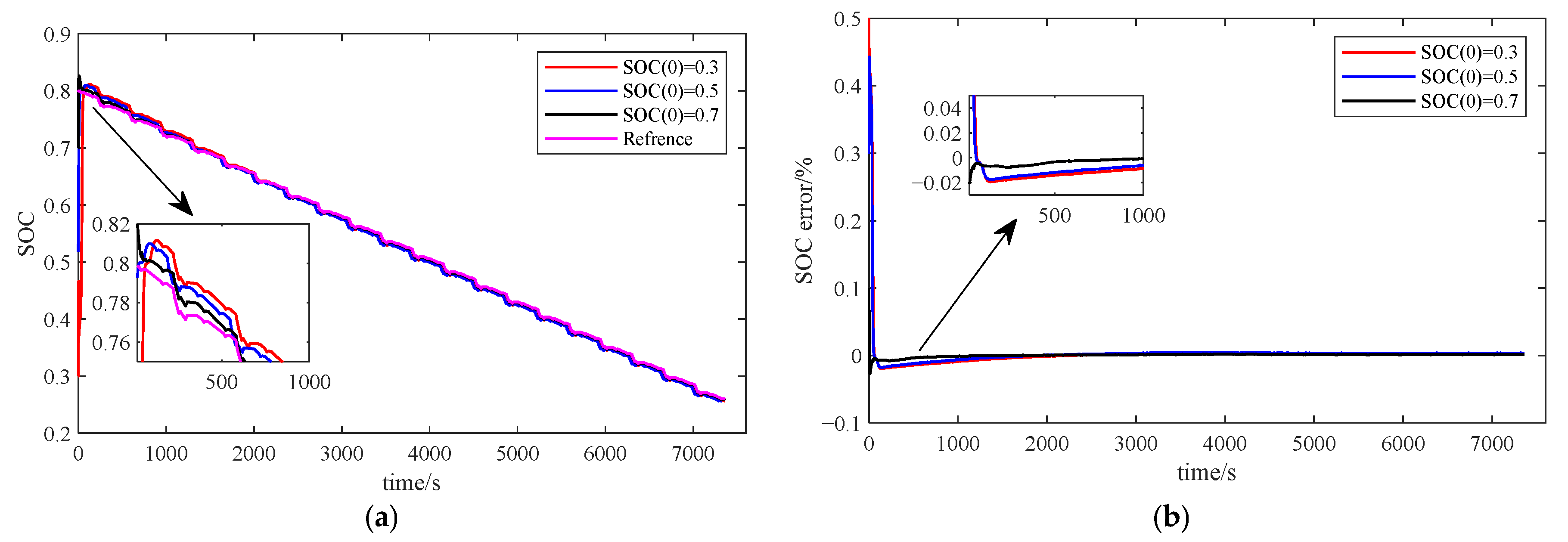
As illustrated in Figure 9, assuming that the SOC initial value is set to 0.3, 0.5, and 0.7, respectively, and that the SOC is estimated using the joint VFFRLS-AEKF algorithm, in the case of the actual SOC initial value of 0.8, the results demonstrate that, if the SOC initial value deviates from the actual initial value, the SOC estimation results can quickly converge to the actual SOC value within the error range of 2% of the time required for the time required to converge to the actual SOC value within the error range of 2% of the actual SOC value is 123 and 38 s, respectively. The VFFRLS-AEKF algorithm takes 255, 105, 183, and 62 s to converge to within 2% error of the true value under the four working conditions, while the FFRLS-EKF algorithm takes 350, 265, 359, and 571 s, and the FFRLS-AEKF algorithm takes 286, 397, 119, and 125 s, as shown in Figure 10 with the initial value of SOC set to 35%. Thus, the convergence speed of the VFFRLS-AEKF algorithm is superior to that of other algorithms with strong robustness and faster algorithm convergence.

(4)

Figure 11 and Figure 12 show that the estimation error of SOC is higher at low temperatures. This is because the internal resistance of lithium batteries rises sharply with decreasing temperature, causing the battery voltage to become unstable and resulting in a larger error in the estimation of SOC. However, as the temperature drops, Li-ion batteries’ chemical reaction rate slows down and the diffusion of lithium ions in the battery becomes more challenging, which alters the battery’s charging and discharging properties. Accurate SOC estimation becomes more challenging at low temperatures because of the battery’s decreased capacity usage, which shows up as a fall in effective capacity.

In summary, at various temperatures and situations, the joint VFFRLS-AEKF algorithm can quickly and reliably identify the battery parameters and estimate the SOC. It can also maintain high estimation accuracy at the late stage of the discharging period, which is a good self-adaptation.

5. Conclusions

This work aims to improve the accuracy and reliability of battery SOC estimates under multi-temperature circumstances by improving the identification of battery model parameters and the SOC estimation method. The variable forgetting factor is introduced based on recursive least squares to complete the model parameter identification, and the multi-new information theory is introduced based on conventional extended Kalman filtering to form the adaptive extended Kalman filtering algorithm to complete the SOC estimation of lithium battery. This is done to take advantage of the strong nonlinearity of the lithium battery itself. By using the University of Maryland’s publicly available dataset for experimental validation at various operating temperatures, the maximum root mean square error of SOC estimation is kept within the range of 1.57%. When compared to the FFRLS-EKF and FFRLS-AEKF algorithms, the joint VFFRLS-AEKF algorithm suggested in this paper improves the estimation accuracy and robustness of the algorithm while addressing the drawbacks of the EKF and traditional least squares algorithms, which use little historical data.

This study also has certain shortcomings that should be investigated in future research:

(1)

In the actual energy storage system, a single lithium-ion battery cannot provide enough energy, hence many single batteries are needed for combination. And in the production and storage process of the battery, there will be a certain inconsistency and progressive rise in the process of battery use. Therefore, to guarantee the stability and health of the battery system, SOC assessment, and battery monomer equalization are required. The algorithm will be optimized around active and passive equalization control in the following step, which will concentrate on equalization control.

(2)

Existing SOC estimating approaches are not compatible in terms of real-time, accuracy, and resilience. Among them, the model-based methods generally have the problem of dependence on model accuracy, and the SOC estimation methods with higher accuracy can be obtained by trying to estimate jointly with the methods based on data-driven, machine learning, etc., taking the advantages and complementing the shortcomings.

(3)

To increase the algorithm’s adaptability at severe temperatures, expand the experimental temperature range (for example, from −30 °C to 60 °C) and create a more thorough temperature–parameter relationship model. In the meantime, the SOC is jointly estimated with several states, including the battery’s state of aging (SOH) and power (SOP), to increase work efficiency and extend the battery’s service life.