An Electrical Equivalent Circuit Model of a Lithium Titanate Oxide Battery

Abstract

A precise lithium-ion battery model is required to specify their appropriateness for different applications and to study their dynamic behavior. In addition, it is important to design an efficient battery system for power applications. In this investigation, a second-order equivalent electrical circuit battery model, which is the most conventional method of characterizing the behavior of a lithium-ion battery, was developed. The current pulse procedure was employed for parameterization of the model. The construction of the model was described in detail, and a battery model for a 13 Ah lithium titanate oxide battery cell was demonstrated. Comprehensive characterization experiments were accomplished for an extensive range of operating situations. The outcomes were employed to parameterize the suggested dynamic model of the lithium titanate oxide battery cell. The simulation outcomes were compared to the laboratory measurements. In addition, the proposed lithium-ion battery model was validated. The recommended model was assessed, and the proposed model was able to anticipate precisely the current and voltage performance.

1. Introduction

Storage systems are gaining more interest as alternative energy because of rising environmental concerns and the limited accessibility of fossil fuels. The significance of storage devices and energy conversion has enhanced owing to the requirement for mobile and stationary energy. Lithium-ion batteries have been achieving acceptance as the preliminary technology for energy storage applications. They have several advantages such as high specific energy densities, high energy density, and long cycling life.

Battery models are a vital component of a dynamic electric vehicle simulator [1]. Battery modelling plays an important role in the approximation of battery performance and in design. Batteries have nonlinear behavior, and creating trustworthy, reliable, and realistic models in order to be able to control them is essential. Batteries go under certain cycles at the same time, taking into consideration there are some environmental conditions affecting the performance of the system, so it is indispensable to improve battery models which accurately simulate real battery characteristics.

Battery models are important for several reasons. Batteries are an essential part of a complicated system that provides critical information to controllers, so it is necessary for control engineers to develop algorithms for battery management systems. System engineers need to integrate batteries into bigger systems and assess their performance via simulations. Battery pack designers are tasked with improving the physical arrangement of the battery pack in order to maximize its performance.

Thévenin-based electrical models and impedance-based electrical models are two main categories of electrical models. Discharging and charging current pulses are used to parameterize the Thévenin-based electrical models [2]. Electrochemical impedance spectroscopy methods are used to parameterize the impedance-based electrical models [3].

It is possible to count on a trustworthy model to replace the battery with something that behaves like a battery, such as an equivalent circuit model. An equivalent circuit model is the most straight-forward and conventional method for characterizing the dynamic behavior of a lithium-ion battery [4]. A second-order equivalent circuit was suggested by Thanagasundram et al., and the parameters identification procedure was represented by using a hybrid power pulse characterization test [4]. The parameter identification and modelling procedure was accomplished in Matlab. In addition, an investigation was accomplished to study how battery cell chemistry affects the suggested model. The comparison among simulation and measurement demonstrated a good accordance [4].

Parameter identification for a Simulink model of a lithium-ion battery in a hybrid power system was investigated in [5]. Two experiments were completed for the battery. In addition, a procedure for determining battery cell model parameters by using the experiments was developed. Simulation outcomes were compared to the experimental data, and a high degree of agreement was seen [5].

A comprehensive, intuitive, and precise electrical battery model was suggested in Reference [6]. All of the dynamic characteristics of the battery (e.g., temperature, current, nonlinear open-circuit voltage, and cycle number) were considered in the model. A simplified model ignoring the effects of temperature, cycle number, and self-discharge was validated with experimental data. It was concluded that the model could also be simply developed to other energy sourcing and battery technologies [6].

An automated test system was designed by Schweighofer et al. [7]. A battery cell model was parameterized based on the obtained data, and the collected results were discussed [7]. A procedure for determination of the state of charge of lithium-ion batteries based on an extended Kalman filter and two distinct equivalent circuit diagrams was described in Reference [8]. In addition, parameter identification of the circuits was described by using characteristic measurements. It was seen that computation results and measurement were in good agreement [8].

An analytical parameter identification procedure was presented for lithium-ion batteries based on the Thévenin equivalent circuit model. The method was based on the pulse charge and pulse discharge experiments. The application of the procedure was presented for a second-order model and was validated in Reference [9].

An equivalent electrical circuit model of a Li-ion polymer battery was simulated in a Matlab environment [10]. Parameters were taken from AC (alternating current) impedance measurements. The model considered the non-homogeneous properties, such as pore geometry and particle size. The experimental and simulated outcomes were compared, and showed that the impedance model could precisely anticipate the dynamic and transient behavior and discharge power performance of the Li-ion polymer batteries [10].

A procedure integrating discharge and charge curves analysis and electrochemical impedance spectroscopy for Li-ion batteries was developed by Dong et al. The experimental and simulated outcomes were compared. It was concluded that the developed procedure presented precise estimation of the dynamic behavior of Li-ion batteries over a wide range of discharge and charge currents, and state of charge [11].

A new method for the electrical circuit modelling of a Li-ion battery was proposed by Saxena et al. The model was fast, simple, and not memory intensive. Furthermore, it did not contain any look-up table. The accuracy of the model was validated with experimental outcomes [12].

In this investigation the current pulse method was employed with the intention of parameterizing and developing a model of a 13 Ah lithium titanate oxide battery. In addition, an equivalent electrical circuit was employed to approximate the dynamics of the battery cell.

The procedure for battery parameterization, arrangement of the suggested battery dynamic model, and outcomes from the comprehensive battery characterization experiments are described in the following sections.

2. Structure of the Proposed Model

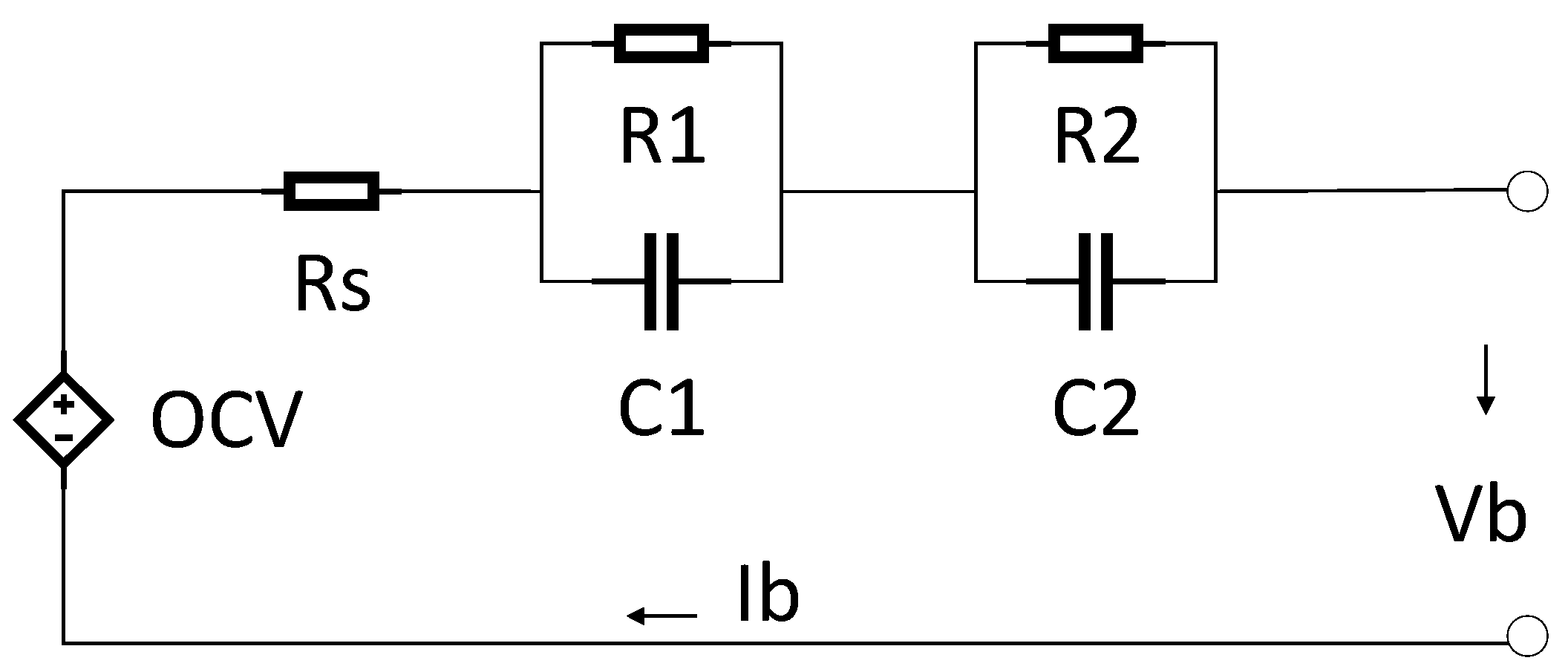
In this investigation, an equivalent electrical circuit model (shown in Figure 1) is suggested for simulation purposes and to model the transient behavior of a lithium titanate oxide battery cell. This method was used because this topology generally proposes a tradeoff between battery cell computational requirements and the approximation of voltage precision. The model was comprised of different parts, such as a series DC internal resistance or ohmic resistance, a DC voltage source, and two RC parallel circuit networks.

Series resistance shows internal DC resistance. This resistance is responsible for the immediate voltage decrease when a current is applied to the battery cell. A DC voltage source or controlled voltage source demonstrates the model open circuit voltage (OCV) of a battery cell. Note that this voltage is dependent on the state of charge (SOC).

To determine the transient response of terminal voltage, two RC parallel networks were employed. The prime RC network (R₁ and C₁) demonstrated the small-time constant of the battery cell feedback, and was employed to model double layer capacitance and the charge transfer procedures. The secondary RC network (R₂ and C₂), demonstrated the lengthy-time constant of the battery cell feedback, and was employed to model the diffusion procedures. In the investigated model, the parameters were dependent on current, SOC, and temperature. The construction of each subsystem is described in the following parts.

2.1. SOC Calculation

A subsystem was designed for determination of the SOC. Current and initial SOC were considered as inputs to the subsystem. Capacity was considered as a function of current. A lookup table was employed to determine the effect of capacity on the current of the battery cell. The following equation was used for calculation of the SOC:

$$SOC=SO{C}_0-{\displaystyle {\int }_0^t\frac{I_b}{C_c}}dt,$$

where $C_c$ is capacity, $I_b$ is current, and $SO{C}_0$ is the initial SOC.

2.2. Open Circuit Voltage Calculation

OCV is the terminal voltage of a battery cell at equilibrium condition. Open circuit voltage is one of the many parameters that need to be determined. The value of OCV was considered as a function of current rates, temperature, and SOC. A 2-D lookup table was employed to demonstrate the amount of OCV. The relationship between OCV and SOC could be determined by a polynomial equation. The OCV of the lithium titanate oxide-based battery was determined over the whole SOC interval considering a 5% SOC resolution. The measurements were reproduced for the eight investigated temperatures. The open circuit voltage test method for the battery cell is illustrated in

Table 1. Open circuit voltage test method for the battery cell. SOC: state of charge.

Step	Description
1	Tempering of the battery at 30 °C
2	Full charging of the battery to 100% SOC with 0.25C current rate
3	Rest period: 15 min.
4	Full discharging of the battery following CC–CV procedure, with 0.25C current rate
5	Rest period: 15 min.
6	Full charging of the battery with 0.25C current rate
7	Discharging the battery with 0.25C current rate to 95% SOC
8	Rest period: 180 min.
9	Discharging the battery with 0.25C current rate to 90% SOC
10	Rest period: 180 min.
11	Discharging the battery with 0.25C current rate to 85% SOC
12	Rest period: 180 min.
13	Discharging the battery with 0.25C current rate to 80% SOC
14	Rest period: 180 min.
15	Discharging the battery with 0.25C current rate to 75% SOC
16	Rest period: 180 min.
17	Discharging the battery with 0.25C current rate to 70% SOC
18	Rest period: 180 min.
19	Discharging the battery with 0.25C current rate to 65% SOC
20	Rest period: 180 min.
21	Discharging the battery with 0.25C current rate to 60% SOC
22	Rest period: 180 min.
23	Discharging the battery with 0.25C current rate to 55% SOC
24	Rest period: 180 min.
25	Discharging the battery with 0.25C current rate to 50% SOC
26	Rest period: 180 min.
27	Discharging the battery with 0.25C current rate to 45% SOC
28	Rest period: 180 min.
29	Discharging the battery with 0.25C current rate to 40% SOC
30	Rest period: 180 min.
31	Discharging the battery with 0.25C current rate to 35% SOC
32	Rest period: 180 min.
33	Discharging the battery with 0.25C current rate to 30% SOC
34	Rest period: 180 min.
35	Discharging the battery with 0.25C current rate to 25% SOC
36	Rest period: 180 min.
37	Discharging the battery with 0.25C current rate to 20% SOC
38	Rest period: 180 min.
39	Discharging the battery with 0.25C current rate to 15% SOC
40	Rest period: 180 min.
41	Discharging the battery with 0.25C current rate to 10% SOC
42	Rest period: 180 min.
43	Discharging the battery with 0.25C current rate to 5% SOC
44	Rest period: 180 min.

. A 2-D lookup table for determination of OCV is shown in

Table 2. 2-D lookup table for determination of OCV.

SOC Levels	0.25C	0.5C	1C	2C	4C
5% SOC	2.105	2.11	2.113	2.116	2.12
10% SOC	2.125	2.129	2.131	2.134	2.136
15% SOC	2.141	2.144	2.145	2.147	2.149
20% SOC	2.154	2.156	2.157	2.159	2.161
25% SOC	2.166	2.168	2.169	2.17	2.172
30% SOC	2.177	2.179	2.18	2.181	2.182
35% SOC	2.187	2.189	2.19	2.191	2.193
40% SOC	2.198	2.2	2.201	2.202	2.203
45% SOC	2.21	2.212	2.213	2.214	2.215
50% SOC	2.224	2.225	2.226	2.227	2.228
55% SOC	2.24	2.241	2.242	2.243	2.244
60% SOC	2.259	2.26	2.261	2.262	2.264
65% SOC	2.282	2.283	2.284	2.285	2.286
70% SOC	2.309	2.31	2.311	2.313	2.314
75% SOC	2.34	2.342	2.343	2.344	2.345
80% SOC	2.376	2.377	2.378	2.379	2.38
85% SOC	2.415	2.416	2.417	2.418	2.419
90% SOC	2.458	2.459	2.46	2.461	2.462
95% SOC	2.513	2.513	2.513	2.514	2.515

. The OCV and SOC characteristic, which was determined at 30 °C, is demonstrated in Figure 2. Analogous outcomes were determined for the other investigated temperatures. It should be noted that 1C corresponds to 13 A.

2.3. Calculation of Ohmic Resistance

The ohmic resistance ($Rs$) could be determined from the immediate voltage decline after the current pulse was applied. The voltage response of a lithium titanate oxide battery cell to a discharging current pulse (I) and voltage one second after current pulse is illustrated in Figure 3. A 2-D lookup table (shown in

Table 3. 2-D lookup table for determination of ohmic resistance ($Rs$).

SOC Levels	0.25C	0.5C	1C	2C	4C
5% SOC	0.002154	0.002346	0.0023	0.00235	0.002419
10% SOC	0.001846	0.001846	0.001923	0.001962	0.001962
15% SOC	0.001846	0.001846	0.001923	0.001885	0.001904
20% SOC	0.001538	0.001846	0.001846	0.001846	0.001865
25% SOC	0.001538	0.001846	0.001846	0.001808	0.001808
30% SOC	0.001646	0.001846	0.001769	0.001769	0.001769
35% SOC	0.001538	0.001692	0.001692	0.001731	0.001731
40% SOC	0.001538	0.001692	0.001692	0.001692	0.001673
45% SOC	0.001538	0.001692	0.001615	0.001654	0.001673
50% SOC	0.001646	0.001538	0.001615	0.001615	0.001615
55% SOC	0.001646	0.001538	0.001538	0.001577	0.001596
60% SOC	0.001538	0.001538	0.001538	0.001577	0.001596
65% SOC	0.001538	0.001538	0.001538	0.001538	0.001558
70% SOC	0.001538	0.001538	0.001538	0.001538	0.001558
75% SOC	0.001538	0.001538	0.001538	0.001538	0.001519
80% SOC	0.001538	0.001538	0.001462	0.001462	0.0015
85% SOC	0.001538	0.001538	0.001462	0.001462	0.001481
90% SOC	0.001538	0.001385	0.001462	0.001423	0.001462
95% SOC	0.001538	0.001385	0.001385	0.001423	0.001481

) was used to determine the ohmic resistance. The value of the resistance $Rs$ was calculated from the following equation:

$$R_s=\frac{V_0-V_1}{I}.$$

2.4. RC Values Determination

The amount of RC parallel networks (R₁, C₁, R₂, and C₂) were considered as a function of current, SOC, and temperature. In this subsystem, 2-D lookup tables were used to characterize the parameters of RC parallel networks.

2.5. R₁ Calculation

The voltage response of a lithium titanate oxide battery cell to a discharging current pulse and voltage ten seconds after current pulse is illustrated in Figure 4. The 2-D lookup table shown in

Table 4. 2-D lookup table for the determination of R₁.

SOC Levels	0.25C	0.5C	1C	2C	4C
5% SOC	0.004615	0.004769	0.005308	0.006692	0.008808
10% SOC	0.003077	0.003077	0.003385	0.003923	0.004865
15% SOC	0.002154	0.002462	0.002385	0.002654	0.003038
20% SOC	0.001846	0.001846	0.001846	0.002	0.002154
25% SOC	0.001846	0.001538	0.001538	0.001654	0.001692
30% SOC	0.001231	0.001385	0.001462	0.001423	0.001404
35% SOC	0.001231	0.001231	0.001308	0.001308	0.001269
40% SOC	0.001231	0.001231	0.001231	0.001192	0.001154
45% SOC	0.001231	0.001231	0.001231	0.001154	0.001038
50% SOC	0.000923	0.001231	0.001077	0.001077	0.001
55% SOC	0.000923	0.001077	0.001154	0.001077	0.000962
60% SOC	0.001231	0.001077	0.001077	0.001038	0.000923
65% SOC	0.001231	0.001077	0.001077	0.001	0.000904
70% SOC	0.000923	0.000923	0.001	0.001	0.000885
75% SOC	0.000923	0.001077	0.001	0.000962	0.000885
80% SOC	0.001231	0.001077	0.001077	0.001	0.000885
85% SOC	0.000923	0.001077	0.001	0.001	0.000865
90% SOC	0.000923	0.001077	0.001	0.001	0.000865
95% SOC	0.001231	0.001077	0.001154	0.001077	0.000923

was used to determine the R₁. The following equation was used to calculate the value of the resistance R₁:

$$R_1=\frac{V_1-V_2}{I}.$$

2.6. R₂ Calculation

The voltage response of a lithium titanate oxide battery cell to a discharging current pulse and voltage eighteen seconds after a current pulse is illustrated in Figure 5. A 2-D lookup table (shown in

Table 5. 2-D lookup table for determination of R₂.

SOC Levels	0.25C	0.5C	1C	2C	4C
5% SOC	0.001431	0.001577	0.001692	0.003	0.003
10% SOC	0.000615	0.000769	0.000923	0.001385	0.001385
15% SOC	0.000615	0.000615	0.000692	0.000808	0.000808
20% SOC	0.000615	0.000462	0.000615	0.000615	0.000615
25% SOC	0.000615	0.000462	0.000615	0.0005	0.0005
30% SOC	0.000615	0.000462	0.000462	0.000462	0.000462
35% SOC	0.000615	0.000462	0.000538	0.000385	0.000385
40% SOC	0.000615	0.000462	0.000462	0.000423	0.000423
45% SOC	0.000408	0.000462	0.000462	0.000385	0.000385
50% SOC	0.000615	0.000462	0.000462	0.000385	0.000385
55% SOC	0.000615	0.000462	0.000462	0.000346	0.000346
60% SOC	0.000408	0.000462	0.000462	0.000346	0.000346
65% SOC	0.000408	0.000462	0.000385	0.000346	0.000346
70% SOC	0.000615	0.000462	0.000462	0.000346	0.000346
75% SOC	0.000615	0.000462	0.000462	0.000346	0.000346
80% SOC	0.000408	0.000462	0.000462	0.000346	0.000346
85% SOC	0.000615	0.000462	0.000462	0.000346	0.000346
90% SOC	0.000615	0.000462	0.000462	0.000346	0.000346
95% SOC	0.000615	0.000615	0.000462	0.000423	0.000423

) was used to determine the R₂. The values of the resistance R₂ were calculated from the following equation:

$$R_2=\frac{V_2-V_3}{I}.$$

2.7. C₁ and C₂ Calculations

The 2-D lookup tables shown in

Table 6. 2-D lookup table for the determination of C₁.

SOC Levels	0.25C	0.5C	1C	2C	4C
5% SOC	371.8022	402.9107	411.0385	374.0317	315.6548
10% SOC	524.6926	582.9802	600.2254	590.7516	539.4481
15% SOC	711.5154	704.0472	805.8215	822.077	812.9882
20% SOC	812.015	898.6088	999.6919	1043.116	1091.251
25% SOC	812.015	1049.385	1165.96	1223.882	1338.928
30% SOC	1151.095	1147.996	1217.596	1388.746	1567.859
35% SOC	1151.095	1269.443	1337.666	1491.118	1706.911
40% SOC	1151.095	1269.443	1408.094	1611.643	1849.563
45% SOC	1151.095	1269.443	1408.094	1656.744	2021.041
50% SOC	1276.328	1269.443	1576.78	1755.835	2086.233
55% SOC	1276.328	1423.031	1487.209	1755.835	2156.2
60% SOC	1151.095	1423.031	1576.78	1810.451	2231.509
65% SOC	1151.095	1423.031	1576.78	1868.942	2271.368
70% SOC	1276.328	1624.03	1679.105	1868.942	2312.818
75% SOC	1276.328	1423.031	1679.105	1931.748	2312.818
80% SOC	1151.095	1423.031	1576.78	1868.942	2312.818
85% SOC	1276.328	1423.031	1679.105	1868.942	2355.959
90% SOC	1276.328	1423.031	1679.105	1868.942	2355.959
95% SOC	1151.095	1323.031	1487.209	1755.835	2231.509

and

Table 7. 2-D lookup table for the determination of C₂.

SOC Levels	0.25C	0.5C	1C	2C	4C
5% SOC	1023.195	1264.916	956.2855	658.9397	1292.234
10% SOC	1866.865	1688.397	1597.527	1263.218	1312.234
15% SOC	1866.865	2046.391	2040.882	1989.158	1362.234
20% SOC	1866.865	2624.584	2256.787	2503.279	2018.994
25% SOC	1866.865	2624.584	2256.787	2985.076	2587.017
30% SOC	1866.865	2624.584	2887.164	3195.054	3030.596
35% SOC	1866.865	2634.584	2529.833	3731.147	3434.219
40% SOC	1866.865	2624.584	2887.164	3440.381	3684.351
45% SOC	2426.197	2624.584	2887.164	3731.147	3825.142
50% SOC	1866.865	2624.584	2887.164	3731.147	4145.637
55% SOC	1866.865	2624.584	2887.164	4081.764	4329.232
60% SOC	2426.197	2624.584	2887.164	4081.764	4531.68
65% SOC	2426.197	2624.584	3376.794	4081.764	4756.146
70% SOC	1866.865	2624.584	2887.164	4081.764	5006.558
75% SOC	1866.865	2624.584	2887.164	4081.764	5006.558
80% SOC	2426.197	2624.584	2887.164	4081.764	5006.558
85% SOC	1866.865	2624.584	2887.164	4081.764	4756.146
90% SOC	1866.865	2624.584	2787.164	3981.764	4756.146
95% SOC	1866.865	2046.391	2687.164	3440.381	4531.68

were used to determine C₁ and C₂.

The values of the capacitances C₁ and C₂ were determined by using the following equations [13]:

$$C_1=\frac{9I}{\left(V_2-V_1\right)ln\left(\frac{V_2}{V_1}\right)},C_2=\frac{8I}{\left(V_3-V_2\right)ln\left(\frac{V_3}{V_2}\right)}.$$

2.8. Voltages of RC Parallel Networks

The voltages of RC parallel networks (V₁ and V₂) representing transient feedback of the battery cell voltage and were determined by using the following equations:

$$V_1=\left(\frac{1}{s}\right)\left[\left(\frac{1}{C_1}\right)\left[I-\frac{V_1}{R_1}\right]\right],V_2=\left(\frac{1}{s}\right)\left[\left(\frac{1}{C_2}\right)\left[I-\frac{V_2}{R_2}\right]\right].$$

2.9. $V_{R_S}$ Calculation

$V_{R_S}$ refers to the voltage reduction from $Rs$. The amount of $V_{R_S}$ was considered as a function of SOC, current, and temperature. Accordingly, a 2-D lookup table was used to demonstrate the amount of $Rs$. The amount of $V_{R_S}$ could be easily determined by employing the following equation:

$$V_{R_S}=I\times R_S.$$

The voltage of the battery cell was calculated by employing the following equation:

$$V_b=OCV-V_1-V_2-V_{R_S}$$

3. Experimental Set-Up

The experimental facilities and systems were comprised of a 13 Ah lithium titanate oxide battery which had capacity and nominal voltage of 13.4 Ah and 2.26 V, respectively. Battery experiments were accomplished by employing a Maccor automated test system and a computer to record the outcomes of the battery cell experiments. During all the experiments, the lithium titanate oxide battery cell was located inside a climatic chamber and its voltage, current, and temperatures were regularly controlled and measured by means of a Maccor battery test station.

3.1. Battery Experiments

Pulse charge and discharge experiments were carried out for parameter identification of the battery cell. A thirty-minute rest period was allowed for the battery cell in each cycle to determine voltage transient response and OCV of the battery cell.

Pulse charge and discharge experiments were conducted for 0.25C, 0.5C, 1C, 2C, and 4C. During the battery experiments, the voltage of the battery cell was kept to lower and upper limits equal to 1.5 and 2.8 V respectively, in order to prevent durable damage to the battery cell. These limitations were suggested by the battery cell manufacturer.

In this investigation, a DC pulse procedure was used for parameterization of the equivalent electrical circuit of the lithium titanate oxide-based battery. The equivalent electrical circuit parameters are variable with temperature, load current, and SOC. In order to consider all of these dependences, a specific current pulse profile was applied to the battery cell. This load profile was used to extract the equivalent electrical circuit model parameters. At each SOC level, five charge and discharge current pulses (i.e., 0.25C, 0.5C, 1C, 2C, and 4C) were applied to the battery. This load profile is illustrated in Figure 6. The SOC was changed from 5%–95% with 5% resolution. This procedure was repeated for all eight investigated temperatures. Lithium titanate oxide battery cell voltage responses owing to charging and discharging current pulse for different temperatures are illustrated in Figure 7, Figure 8 and Figure 9.

3.2. Model Validation

The equivalent electrical circuit model was able to model the transient response of the battery cell based on different types of current excitation. Different equivalent electrical circuit model procedures were employed to model the dynamic response of lithium-ion batteries.

With the intention of validating the suggested model, the simulation results were compared with the corresponding laboratory-measured results. A comparison of the model-estimated and laboratory-measured results for the experiment is shown in Figure 10. The comparison illustrates that the curves are approximately superimposed. This acknowledges that the model was precise in different charging and discharging situations.

4. Conclusions

In this investigation, a battery model for a 13 Ah lithium titanate oxide battery cell was developed. Several experiments were carried out on the battery cell with the intention of determining the parameters of the model. In addition, the parameters could be determined by using other methods, which will be investigated in future research. Notwithstanding, it is not included in the scope of this investigation. To accomplish model parameterization of the lithium titanate oxide-based battery, the performance parameters of the battery need to be determined. This model was capable of approximating the battery voltage for an extensive range of operating situations. The internal resistance, open circuit voltage, and capacity of the battery cell were measured at several SOCs, temperatures, and load currents. The battery cell model should be able to accurately predict the voltage behavior of the battery for both very large and very small currents. Experimental results were compared to those from the simulation. The precision of the parameterized and suggested model for the investigated lithium titanate oxide battery cell was evaluated by accomplishing several verification experiments.