Figure 1.
The 6 × 6 supercell used for the simulations of the doped graphene and of its interaction with Li2S6. Brown = carbon atoms; red = the heteroatom.
Figure 1.
The 6 × 6 supercell used for the simulations of the doped graphene and of its interaction with Li2S6. Brown = carbon atoms; red = the heteroatom.
Figure 2.
Optimized geometry of the Li2S6 molecule. Li and S atoms are represented, respectively, in green and yellow.
Figure 2.
Optimized geometry of the Li2S6 molecule. Li and S atoms are represented, respectively, in green and yellow.
Figure 3.
Density of states (DOS) of the three doped systems. In each graph, the blue curve represents the DOS corresponding to the doped substrate and the grey area indicates the DOS of PG. The inset contains in red the projected DOS of the heteroatom. The diagrams were shifted in order to place the Fermi level at zero in all cases.
Figure 3.
Density of states (DOS) of the three doped systems. In each graph, the blue curve represents the DOS corresponding to the doped substrate and the grey area indicates the DOS of PG. The inset contains in red the projected DOS of the heteroatom. The diagrams were shifted in order to place the Fermi level at zero in all cases.
Figure 4.
Structures of Li2S6 adsorbed on graphene substrates. Carbon atoms in brown, heteroatoms (B, Ga, Al) in the graphene layer in red, lithium atoms in green, sulfur atoms in yellow. Li2S6 suffers an important distortion of its structure interacting with doped graphene.
Figure 4.
Structures of Li2S6 adsorbed on graphene substrates. Carbon atoms in brown, heteroatoms (B, Ga, Al) in the graphene layer in red, lithium atoms in green, sulfur atoms in yellow. Li2S6 suffers an important distortion of its structure interacting with doped graphene.
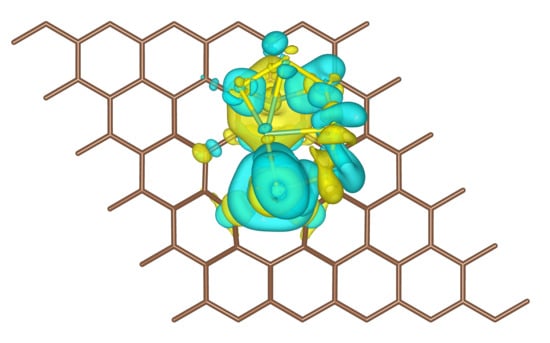
Figure 5.
(a) Iso-surface (yellow color: negative, charge accumulation; cyan color: positive, charge depletion) of differential charge density for the most stable configuration of the PG + Li2S6 system. The plotted iso-level is 1.5 × 10−2 e/Bohr3. (b) Partial density of states projected on selected atoms. The densities were shifted to align the Fermi level to zero.
Figure 5.
(a) Iso-surface (yellow color: negative, charge accumulation; cyan color: positive, charge depletion) of differential charge density for the most stable configuration of the PG + Li2S6 system. The plotted iso-level is 1.5 × 10−2 e/Bohr3. (b) Partial density of states projected on selected atoms. The densities were shifted to align the Fermi level to zero.
Figure 6.
(a) Iso-surface (yellow color: negative, charge accumulation; cyan color: positive, charge depletion) of differential charge density for the most stable configuration of the BG + Li2S6 system. The plotted iso-level is 1.5 × 10−2 e/Bohr3. (b) Partial density of states projected on selected atoms. The densities were shifted to align the Fermi level to zero.
Figure 6.
(a) Iso-surface (yellow color: negative, charge accumulation; cyan color: positive, charge depletion) of differential charge density for the most stable configuration of the BG + Li2S6 system. The plotted iso-level is 1.5 × 10−2 e/Bohr3. (b) Partial density of states projected on selected atoms. The densities were shifted to align the Fermi level to zero.
Figure 7.
(a) Iso-surface (yellow color: negative, charge accumulation; cyan color: positive, charge depletion) of differential charge density for the most stable configuration of the AG + Li2S6 system. The plotted iso-level is 1.5 × 10−3 e/Bohr3. (b,c) Partial density of states projected on selected atoms. The densities were shifted to align the Fermi level to zero.
Figure 7.
(a) Iso-surface (yellow color: negative, charge accumulation; cyan color: positive, charge depletion) of differential charge density for the most stable configuration of the AG + Li2S6 system. The plotted iso-level is 1.5 × 10−3 e/Bohr3. (b,c) Partial density of states projected on selected atoms. The densities were shifted to align the Fermi level to zero.
Figure 8.
(a) Iso-surface (yellow color: negative, charge accumulation; cyan color: positive, charge depletion) of differential charge density for the most stable configuration of the GG + Li2S6 system. The plotted iso-level is 1.5 × 10−3 e/Bohr3. (b,c) Partial density of states projected on selected atoms. The densities were shifted to align the Fermi level to zero.
Figure 8.
(a) Iso-surface (yellow color: negative, charge accumulation; cyan color: positive, charge depletion) of differential charge density for the most stable configuration of the GG + Li2S6 system. The plotted iso-level is 1.5 × 10−3 e/Bohr3. (b,c) Partial density of states projected on selected atoms. The densities were shifted to align the Fermi level to zero.
Figure 9.
Electrode potential vs. Li/Li+ as a function of the polarization of the electrode expressed as excess electrons per sulfur atom.
Figure 9.
Electrode potential vs. Li/Li+ as a function of the polarization of the electrode expressed as excess electrons per sulfur atom.
Figure 10.
Binding energy of the polysulfide on the AG substrate as a function of the charge per sulfur atom.
Figure 10.
Binding energy of the polysulfide on the AG substrate as a function of the charge per sulfur atom.
Figure 11.
(a) Iso-surface (yellow color: negative, charge accumulation; cyan color: positive, charge depletion) of differential charge density for the most stable configuration of the charged AG + Li2S6 system in solvent. The plotted iso-level is 1.5 × 10−3 e/Bohr3. (b,c) Partial density of states projected on selected atoms. The densities were shifted to align the Fermi level to zero.
Figure 11.
(a) Iso-surface (yellow color: negative, charge accumulation; cyan color: positive, charge depletion) of differential charge density for the most stable configuration of the charged AG + Li2S6 system in solvent. The plotted iso-level is 1.5 × 10−3 e/Bohr3. (b,c) Partial density of states projected on selected atoms. The densities were shifted to align the Fermi level to zero.
Table 1.
Excess charges with respect to isolated atoms calculated according to Löwdin’s approach.
Table 1.
Excess charges with respect to isolated atoms calculated according to Löwdin’s approach.
| Atom | qLöwdin (a.u.) |
|---|
| Li2 | 0.165 |
| Li2 | 0.165 |
| S1 | −0.205 |
| S2 | 0.185 |
| S3 | 0.116 |
| S4 | 0.116 |
| S5 | 0.185 |
| S6 | −0.205 |
Table 2.
Structural properties of doped graphene monolayers. PG = pristine graphene, BG, AG, GG respectively boron, aluminum and gallium doped graphene. ∆z(X) vertical displacement of heteroatom X from graphene layer, ∆z(C) vertical displacement from the graphene layer of the 3 carbon atoms nearest to X, dX-C bond length between the heteroatom and the nearest carbon atoms.
Table 2.
Structural properties of doped graphene monolayers. PG = pristine graphene, BG, AG, GG respectively boron, aluminum and gallium doped graphene. ∆z(X) vertical displacement of heteroatom X from graphene layer, ∆z(C) vertical displacement from the graphene layer of the 3 carbon atoms nearest to X, dX-C bond length between the heteroatom and the nearest carbon atoms.
| Substrate | ∆z(X) | ∆z(C) | dX-C |
|---|
| PG | 0 | 0 | 1.42 |
| BG | 0 | 0 | 1.49 |
| AG | 1.65 | 0.87 | 1.85 |
| GG | 1.59 | 0.88 | 1.83 |
Table 3.
Excess charges on heteroatom X and on its first neighbor carbon atoms calculated according to Löwdin’s approach.
Table 3.
Excess charges on heteroatom X and on its first neighbor carbon atoms calculated according to Löwdin’s approach.
| Charge (a.u.) | PG | BG | AG | GG |
|---|
| qX | -- | 0.104 | 0.805 | 0.465 |
| qC1 | 0.000 | −0.124 | −0.287 | −0.188 |
| qC2 | 0.000 | −0.123 | −0.300 | −0.196 |
| qC3 | 0.000 | −0.123 | −0.300 | −0.196 |
Table 4.
Adsorption energy of Li2S6 on doped graphene substrates.
Table 4.
Adsorption energy of Li2S6 on doped graphene substrates.
| Substrate | Adsorption Energy (eV) |
|---|
| PG | −0.75 |
| BG | −0.97 |
| AG | −2.32 |
| GG | −1.97 |
Table 5.
Charge population analysis for the PG + Li2S6 system. Excess charges are reported for the Li atom, for the carbon atom interacting with lithium (C0) and for its three nearest neighbor carbons (C1, C2 and C3) in the graphene monolayer.
Table 5.
Charge population analysis for the PG + Li2S6 system. Excess charges are reported for the Li atom, for the carbon atom interacting with lithium (C0) and for its three nearest neighbor carbons (C1, C2 and C3) in the graphene monolayer.
| Atomic Site | Charge (a.u.) |
|---|
| Li | −0.17 |
| C0 | −0.03 |
| C1 | 0.00 |
| C2 | 0.00 |
| C3 | −0.01 |
Table 6.
Charge population analysis for the BG + Li2S6 system. Excess charges are reported for the Li atom, for the boron atom and for the five carbons interacting with lithium.
Table 6.
Charge population analysis for the BG + Li2S6 system. Excess charges are reported for the Li atom, for the boron atom and for the five carbons interacting with lithium.
| Atomic Site | Charge (a.u.) |
|---|
| Li | −0.14 |
| B | −0.06 |
| C1 | 0.00 |
| C2 | −0.01 |
| C3 | −0.02 |
| C4 | −0.02 |
| C5 | −0.02 |
Table 7.
Charge population analysis for the AG + Li2S6 system. Excess charges are reported for the lithium atom near the substrate, for the sulfur atom bonded to aluminum, for the aluminum atom and for the three carbons (C1, C2, and C3) bonded to aluminum. C1 is also the atom interacting with lithium.
Table 7.
Charge population analysis for the AG + Li2S6 system. Excess charges are reported for the lithium atom near the substrate, for the sulfur atom bonded to aluminum, for the aluminum atom and for the three carbons (C1, C2, and C3) bonded to aluminum. C1 is also the atom interacting with lithium.
| Atomic Site | Charge (a.u.) |
|---|
| Li | −0.06 |
| S | 0.10 |
| Al | −0.11 |
| C1 | −0.02 |
| C2 | 0.05 |
| C3 | 0.05 |
Table 8.
Charge population analysis for the GG + Li2S6 system. Excess charges are reported for the lithium atom near the surface, for the sulfur bonded to gallium, for the gallium atom and for the three carbons (C1, C2, and C3) bonded to gallium. C1 is also the atom interacting with lithium.
Table 8.
Charge population analysis for the GG + Li2S6 system. Excess charges are reported for the lithium atom near the surface, for the sulfur bonded to gallium, for the gallium atom and for the three carbons (C1, C2, and C3) bonded to gallium. C1 is also the atom interacting with lithium.
| Atomic Site | Charge (a.u.) |
|---|
| Li | −0.06 |
| S | 0.17 |
| Ga | −0.16 |
| C1 | −0.03 |
| C2 | 0.04 |
| C3 | 0.05 |
Table 9.
Charge population analysis for the charged AG + Li2S6 system in contact with the solvent. Excess charges are reported for the lithium atom near the substrate, for the sulfur atom bonded to aluminum, for the aluminum atom and for the three carbons (C1, C2, and C3) bonded to aluminum. C1 is also the atom interacting with lithium.
Table 9.
Charge population analysis for the charged AG + Li2S6 system in contact with the solvent. Excess charges are reported for the lithium atom near the substrate, for the sulfur atom bonded to aluminum, for the aluminum atom and for the three carbons (C1, C2, and C3) bonded to aluminum. C1 is also the atom interacting with lithium.
| Atomic Site | Charge (a.u.) |
|---|
| Li | 0.05 |
| S | 0.09 |
| Al | −0.16 |
| C1 | 0.09 |
| C2 | −0.05 |
| C3 | 0.05 |