A Comprehensive Study of Degradation Characteristics and Mechanisms of Commercial Li(NiMnCo)O2 EV Batteries under Vehicle-To-Grid (V2G) Services
Abstract
:1. Introduction
- 27 sets of cyclical and 6 sets of calendar aging experiments are carried out on the commercial Li(NiMnCo)O2 batteries with nominal capacities of 24 Ah, studying different combinations of SOC, DOD, and C-rate.
- Cycling conditions are adjusted according to the decaying of the whole battery every 30 equivalent full cycles to maintain the same SOC range.
- Quantification of the aging mechanisms is investigated through a reduced freedom voltage reconstruction method, converging faster while maintaining accuracy.
- The driving, parking, charging, and discharging patterns designed based on real-world data are used to generate V2G operating profiles.
- Battery degradation maps are applied to calculate the degradation of the V2G operation and the EVs without V2G.
2. Experiment and Methodology
2.1. Experimental Setup and Test Conditions
2.2. Methodology
2.2.1. Experiment Data Processing
- (1)
- Correction of the temperature fluctuation
- (2)
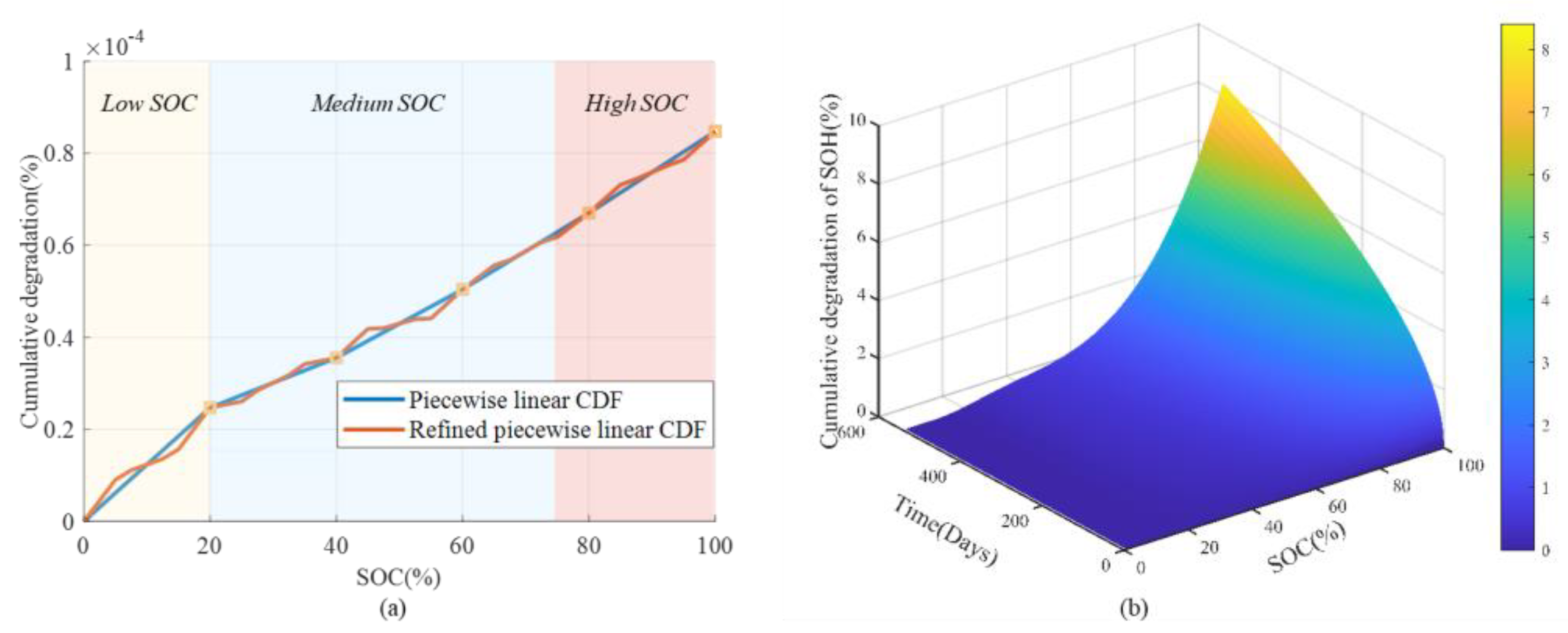
- Equivalent cycle numbers and cumulative degradation function (CDF)
2.2.2. Battery Mechanism Investigation
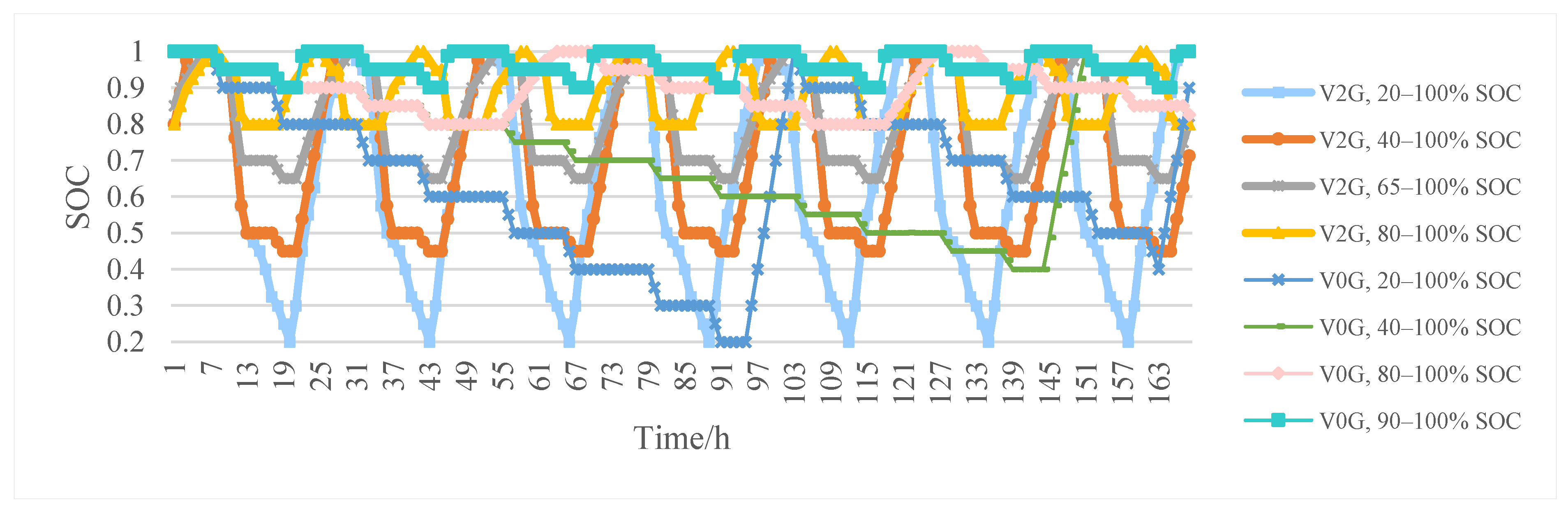
2.2.3. V2G Operation with Cumulative Battery Aging
- (1)
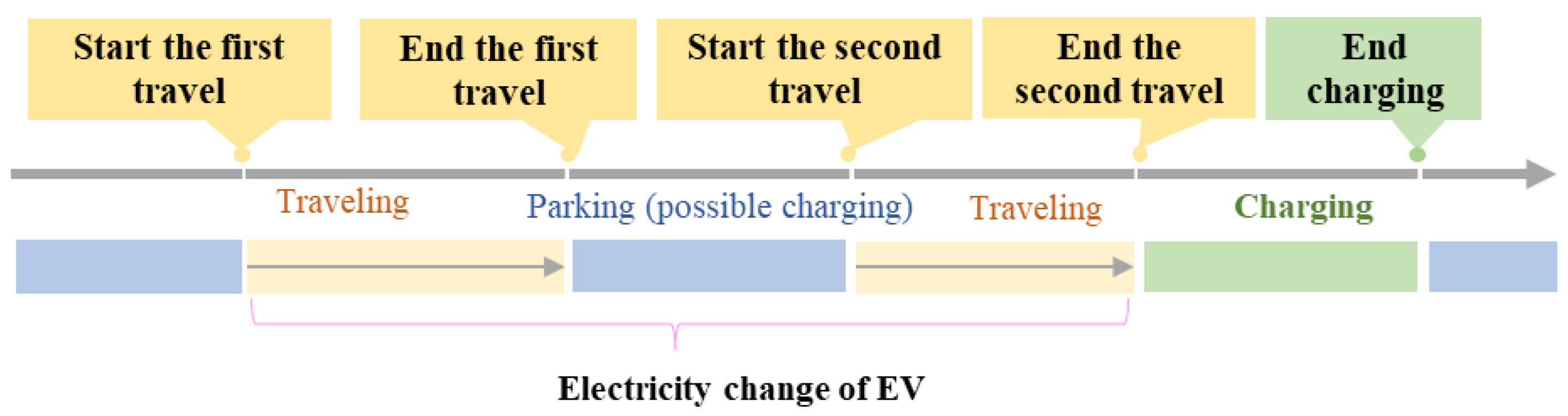
- Generation of V2G operating profiles
- (2)
- where represents the SOC at the beginning of travel, represents the SOC at the end of travel, C represents the battery capacity of the electric vehicle, represents the charging power of the electric vehicle, represents charging efficiency, is the travel mileage, and is the power consumption on one-hundred-kilometer.Battery calendar and cyclical aging
- Calendar aging
- Cumulative degradation function (CDF)
3. Battery Aging Results
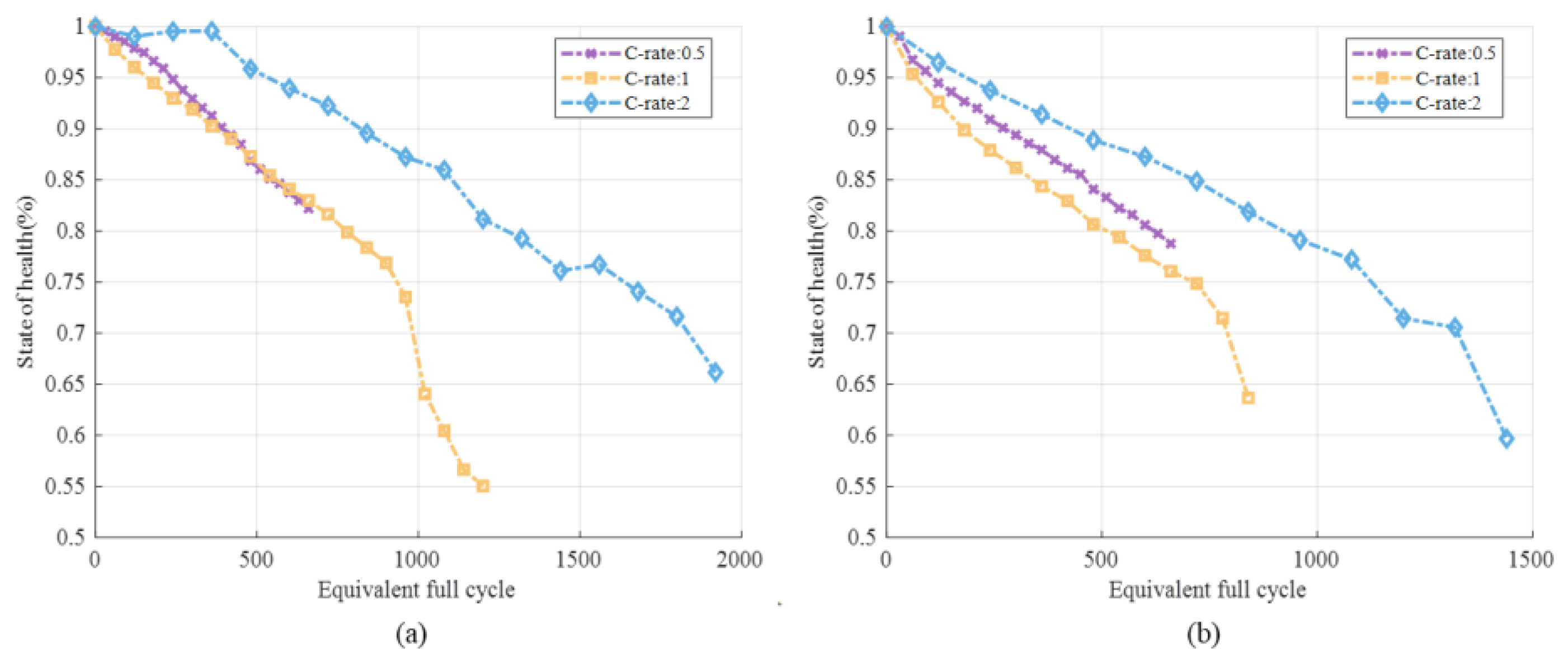
3.1. Full-Cell Degradation under Equivalent Full Cycles
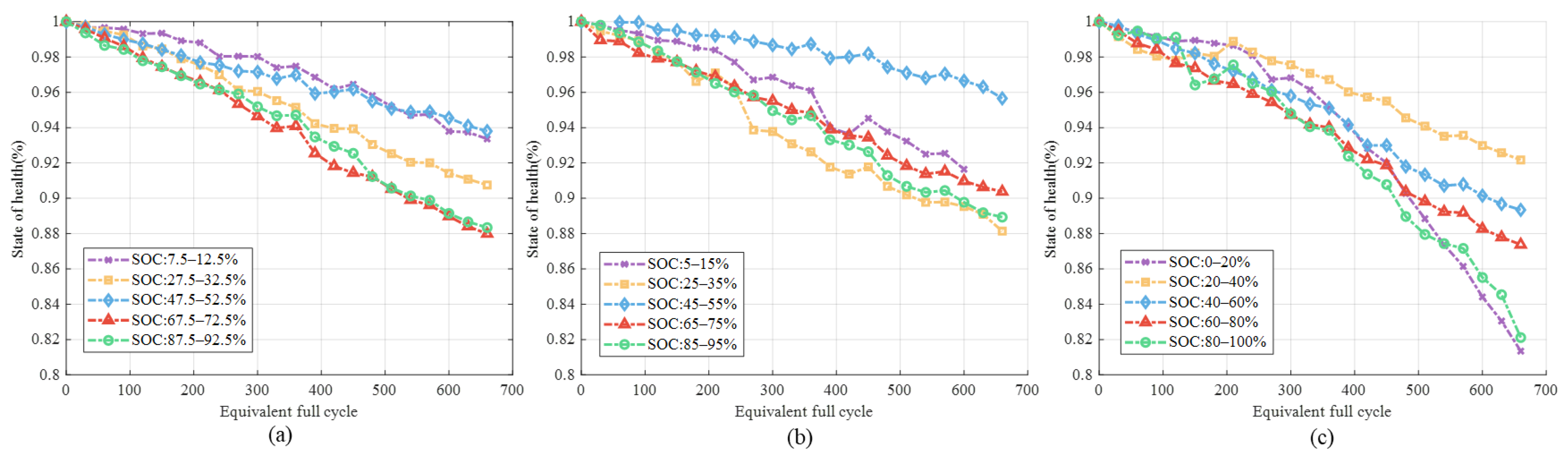
3.1.1. Different SOC Ranges
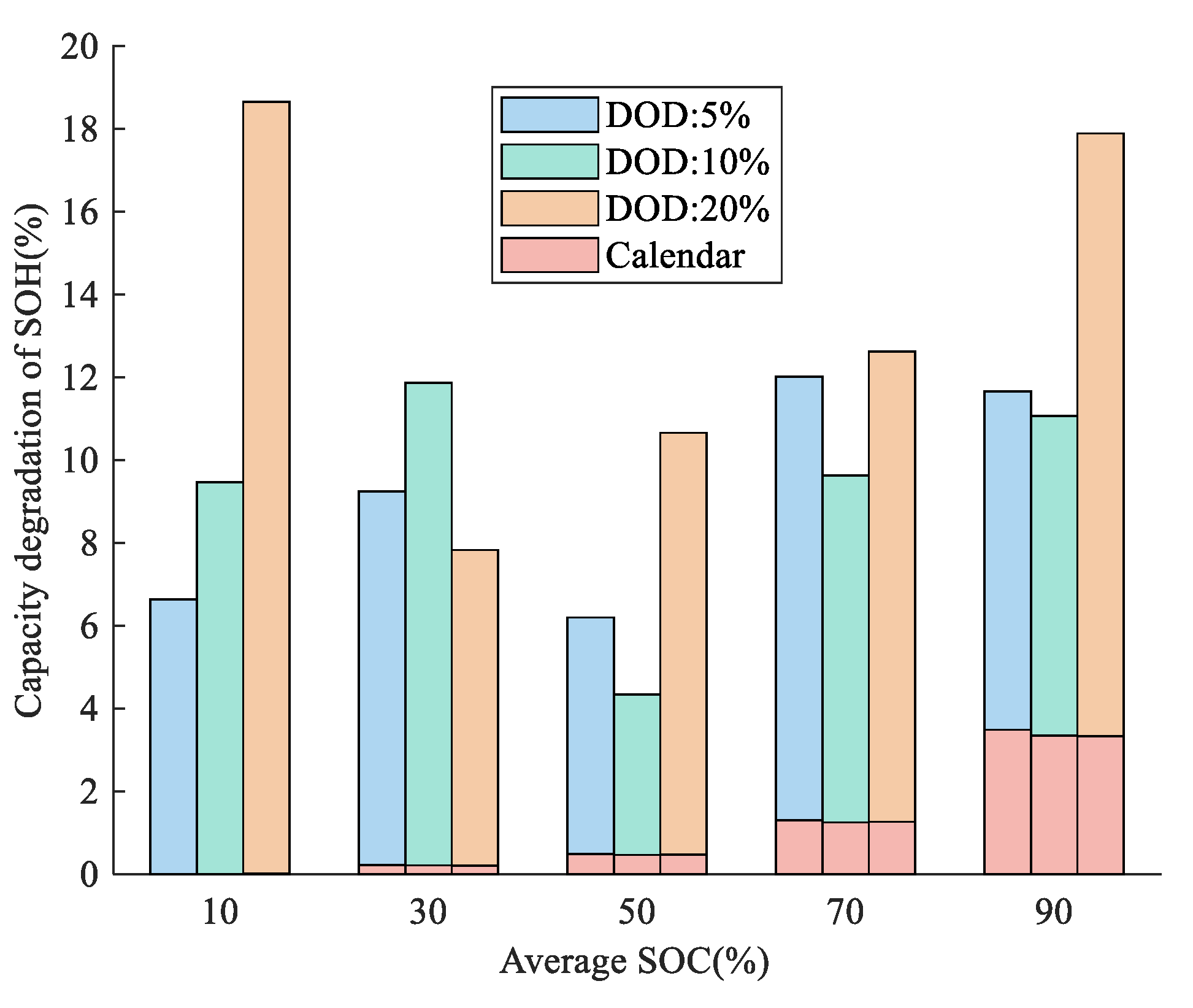
3.1.2. Different DOD and C-Rate
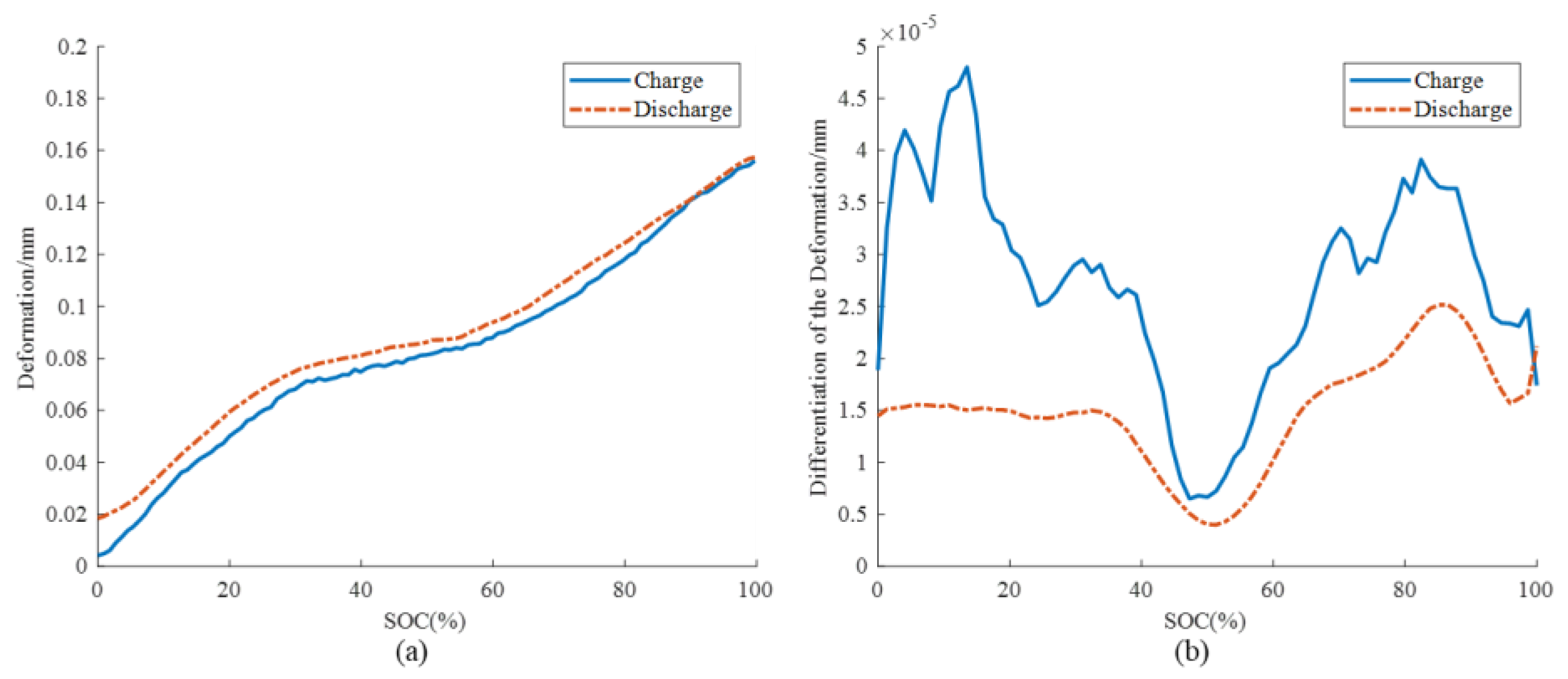
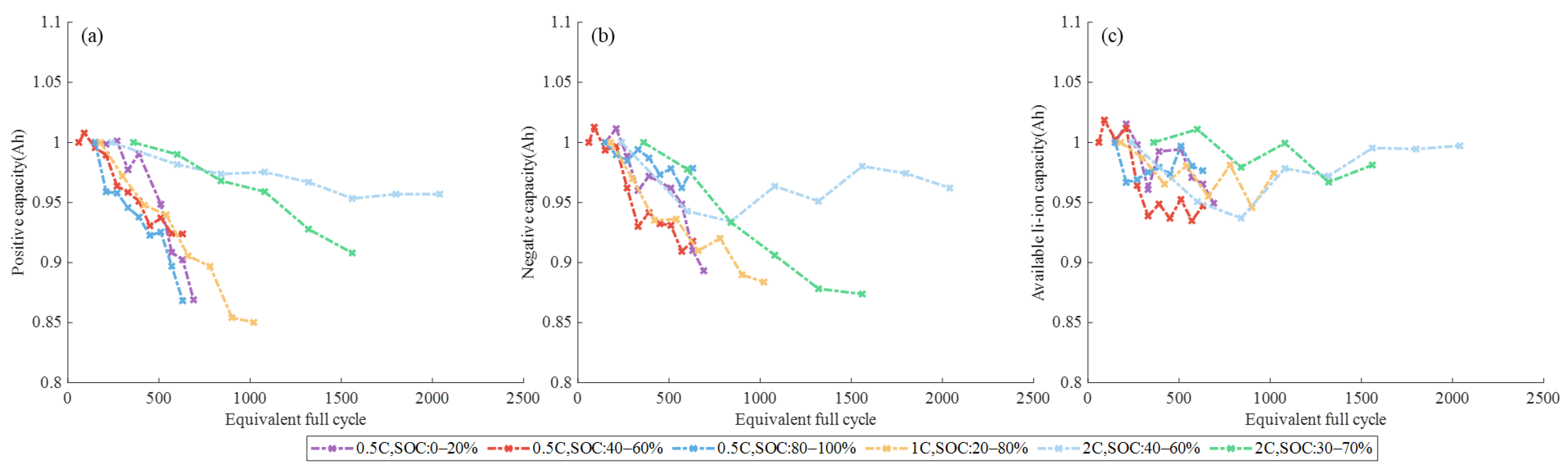
3.2. Aging Mechanism Identification
4. Map Figure and V2G Conditions
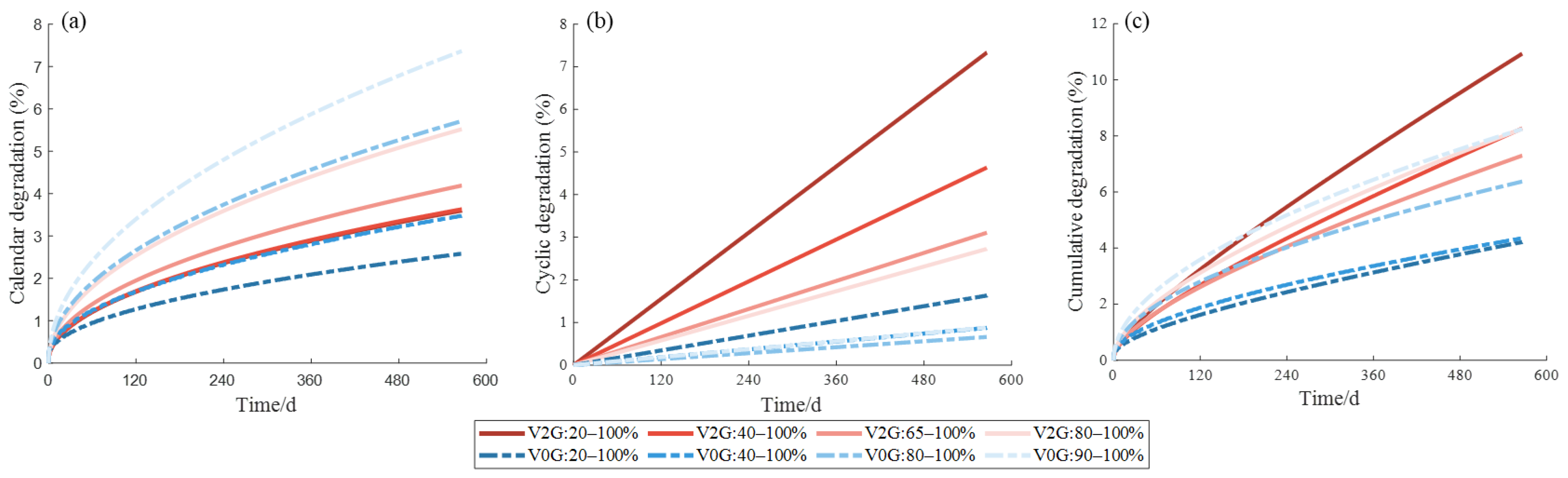
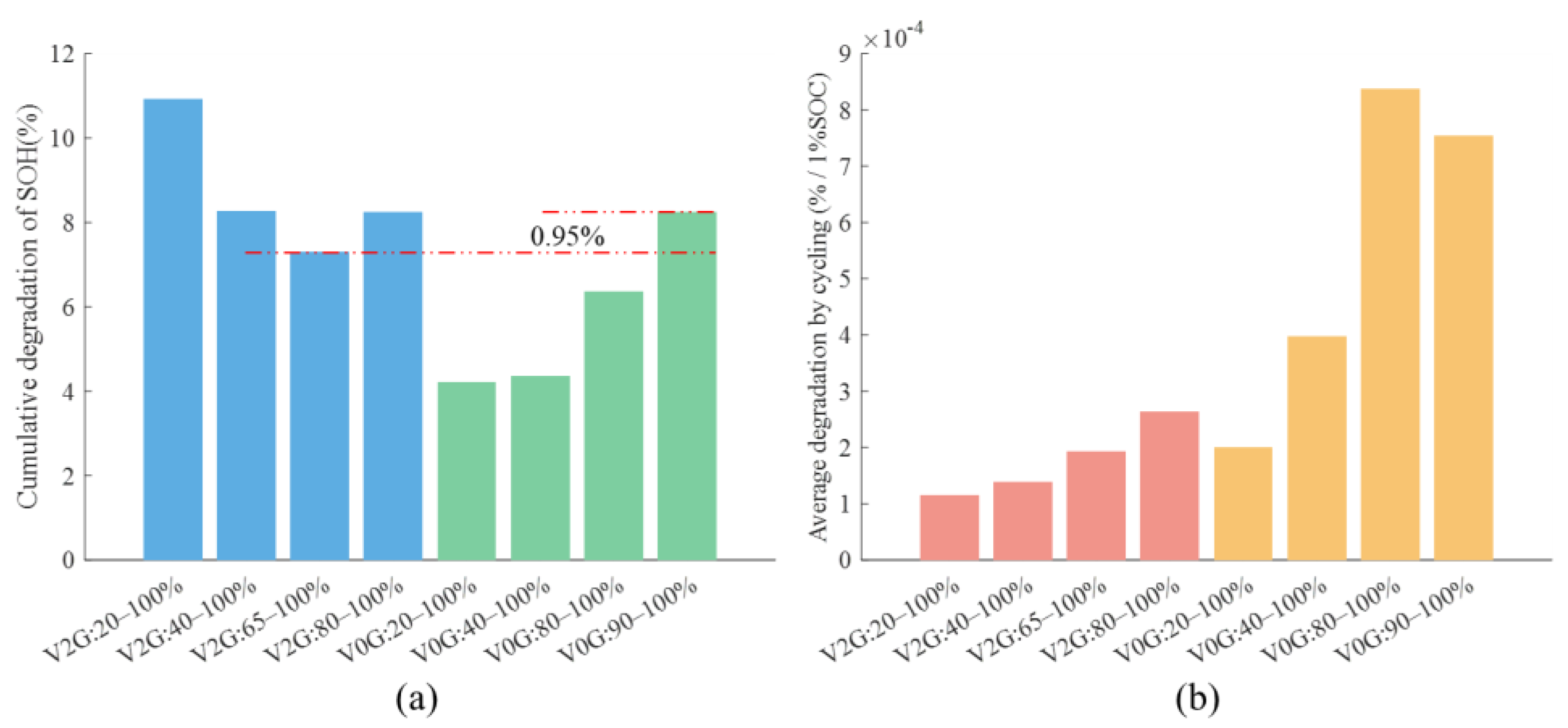
4.1. Nature of Aging and Quantification of Degradation
4.2. V2G Conditions and Battery Aging Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BESS | battery energy storage system |
| BEV | battery electric vehicle |
| C-rate | charging rate |
| CDF | cumulative degradation function |
| DOD | depth of discharge |
| EFC | equivalent full cycle |
| EC | ethylene carbonate |
| EMC | ethyl methyl carbonate |
| EV | electric vehicle |
| HPPC | hybrid pulse power characteristic |
| IC | incremental capacity |
| LAM | loss of active material |
| LLI | loss of lithium-ion inventory |
| LFP | graphite-LiFePO4 battery |
| OCV | open circuit voltage |
| PC | personal computer |
| NCM | graphite-Li(NiMnCo)O2 battery |
| RE | renewable energy |
| RMSE | root-mean-square error |
| RF-VPR | reduced freedom voltage parameter reconstruction |
| SEI | solid electrolyte interface |
| SEM | scanning electron microscope |
| SOC | state of charge |
| SOH | state of health |
| SPM | single particle model |
| VPR | voltage parameter reconstruction |
| V0G | unmanaged charging |
| V2G | vehicle-to-grid |
Variables
| capacities of the cathode, Ah | |
| capacities of the anode, Ah | |
| relative capacity of the positive and negative electrode, Ah | |
| battery capacity of electric vehicle, Ah | |
| SOC at the ending of travel, % | |
| piecewise linear degradation density function | |
| piecewise linear degradation density accumulation function | |
| power consumption per hundred kilometers | |
| current of the battery, A | |
| rate coefficient | |
| charging power of electric vehicle, kW | |
| EV charging power, kW | |
| EV discharge power, kW | |
| unit calendar aging, % | |
| total calendar aging, % | |
| total cyclic aging, % | |
| total capacity loss, % | |
| the sum of the amount of lithium in the positive electrode and that in the negative electrode, Ah | |
| internal resistance, Ω | |
| temperature corrected SOH, % | |
| SOC at the beginning of travel, % | |
| time, year | |
| average temperature, °C | |
| temperature, °C | |
| travel mileage, km | |
| positive equilibrium potential, V | |
| negative equilibrium potential, V | |
| battery terminal voltage, V | |
| nominal voltage of the battery, V | |
| lithium-ion fraction of the battery at the beginning of charging of the anode | |
| lithium-ion fraction of the battery at the beginning of charging of the cathode | |
| relative position of the positive and negative curves, Ah | |
| charging efficiency, % | |
| 20% DOD capacity loss, % | |
| 10% DOD capacity loss, % | |
| 5% DOD capacity loss, % |
References
- Wei, Y.; Han, X.; Lu, L.; Wang, H.; Ouyang, M. The potential and technical prospects of energy storage by vehicle to grid and hydrogen utilization under carbon neutrality target. Automot. Eng. 2022, 44, 449–464. [Google Scholar] [CrossRef]
- Wei, Y.; Huang, H.; Han, X.; Lu, L.; Ouyang, M.; Pang, K.; Qin, Y. Whole-system Potential and Benefit of Energy Storage by Vehicle-to-grid (V2G) under Carbon Neutrality Target in China. In Proceedings of the 2022 IEEE 5th International Electrical Energy Conference, Nangjing, China, 27–29 May 2022; pp. 4006–4012. [Google Scholar] [CrossRef]
- Qin, Y.; Chen, X.; Tomaszewska, A.; Chen, H.; Wei, Y.; Zhu, H.; Li, Y.; Cui, Z.; Huang, J.; Du, J.; et al. Lithium-ion batteries under pulsed current operation to stabilize future grids. Cell Rep. Phys. Sci. 2022, 3, 100708. [Google Scholar] [CrossRef]
- Fachrizal, R.; Shepero, M.; van der Meer, D.; Munkhammar, J.; Widén, J. Smart charging of electric vehicles considering photovoltaic power production and electricity consumption: A review. eTransportation 2020, 4, 100056. [Google Scholar] [CrossRef]
- Morsalin, S.; Haque, A.; Mahmud, A. Machine to machine performance evaluation of grid-integrated electric vehicles by using various scheduling algorithms. eTransportation 2020, 3, 100044. [Google Scholar] [CrossRef]
- Li, D.; Zouma, A.; Liao, J.T.; Yang, H.T. An energy management strategy with renewable energy and energy storage system for a large electric vehicle charging station. eTransportation 2020, 6, 100076. [Google Scholar] [CrossRef]
- Yang, Q.; Li, D.; An, D.; Yu, W.; Fu, X.; Yang, X.; Zhao, W. Towards Incentive for Electrical Vehicles Demand Response with Location Privacy Guaranteeing in Microgrids. IEEE Trans. Dependable Secur. Comput. 2022, 19, 131–148. [Google Scholar] [CrossRef]
- Darcovich, K.; Laurent, T.; Ribberink, H. Improved prospects for V2X with longer range 2nd generation electric vehicles. eTransportation 2020, 6, 100085. [Google Scholar] [CrossRef]
- Schwenk, K.; Meisenbacher, S.; Briegel, B.; Harr, T.; Hagenmeyer, V.; Mikut, R. Integrating Battery Aging in the Optimization for Bidirectional Charging of Electric Vehicles. IEEE Trans. Smart Grid. 2021, 12, 5135–5145. [Google Scholar] [CrossRef]
- Gonzalez Venegas, F.; Petit, M.; Perez, Y. Plug-in behavior of electric vehicles users: Insights from a large-scale trial and impacts for grid integration studies. eTransportation 2021, 10, 100131. [Google Scholar] [CrossRef]
- Darcovich, K.; Recoskie, S.; Ribberink, H.; Michelet, C. The impact of V2X service under local climatic conditions within Canada on EV durability. eTransportation 2021, 9, 100124. [Google Scholar] [CrossRef]
- Ahmadian, A.; Sedghi, M.; Mohammadi-Ivatloo, B.; Elkamel, A.; Aliakbar Golkar, M.; Fowler, M. Cost-Benefit Analysis of V2G Implementation in Distribution Networks Considering PEVs Battery Degradation. IEEE Trans. Sustain. Energy 2018, 9, 961–970. [Google Scholar] [CrossRef]
- Gao, S.; Li, H.; Jurasz, J.; Dai, R. Optimal Charging of Electric Vehicle Aggregations Participating in Energy and Ancillary Service Markets. IEEE J. Emerg. Sel. Top Ind. Electron. 2021, 3, 270–278. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, J.; Wu, C. Vehicle-to-Grid Coordination via Mean Field Game. IEEE Control Syst. Lett. 2022, 6, 2084–2089. [Google Scholar] [CrossRef]
- Moghaddam, V.; Ahmad, I.; Habibi, D.; Masoum, M.A.S. Dispatch management of portable charging stations in electric vehicle networks. eTransportation 2021, 8, 100112. [Google Scholar] [CrossRef]
- Unterluggauer, T.; Rich, J.; Andersen, P.B.; Hashemi, S. Electric vehicle charging infrastructure planning for integrated transportation and power distribution networks: A review. eTransportation 2022, 12, 100163. [Google Scholar] [CrossRef]
- Hussain, A.; Bui, V.H.; Kim, H.M. Optimal Sizing of Battery Energy Storage System in a Fast EV Charging Station Considering Power Outages. IEEE Trans. Transp. Electrif. 2020, 6, 453–463. [Google Scholar] [CrossRef]
- Maheshwari, A.; Paterakis, N.G.; Santarelli, M.; Gibescu, M. Optimizing the operation of energy storage using a non-linear lithium-ion battery degradation model. Appl. Energy 2020, 261, 114360. [Google Scholar] [CrossRef]
- Cao, Y.; Li, D.; Zhang, Y.; Chen, X. Joint Optimization of Delay-Tolerant Autonomous Electric Vehicles Charge Scheduling and Station Battery Degradation. IEEE Internet Things J. 2020, 7, 8590–8599. [Google Scholar] [CrossRef]
- Ebrahimi, M.; Rastegar, M.; Mohammadi, M.; Palomino, A.; Parvania, M. Stochastic Charging Optimization of V2G-Capable PEVs: A Comprehensive Model for Battery Aging and Customer Service Quality. IEEE Trans. Transp. Electrif. 2020, 6, 1026–1034. [Google Scholar] [CrossRef]
- Wei, Y.; Wang, S.; Han, X.; Lu, L.; Li, W.; Zhang, F.; Ouyang, M. Toward more realistic microgrid optimization: Experiment and high-efficient model of Li-ion battery degradation under dynamic conditions. eTransportation 2022, 14, 100200. [Google Scholar] [CrossRef]
- Wei, Y.; Han, T.; Wang, S.; Qin, Y.; Lu, L.; Han, X.; Ouyang, M. An efficient data-driven optimal sizing framework for photovoltaics-battery-based electric vehicle charging microgrid. J Energy Storage 2022, 55, 105670. [Google Scholar] [CrossRef]
- Han, X.; Lu, L.; Zheng, Y.; Feng, X.; Li, Z.; Li, J.; Ouyang, M. A review on the key issues of the lithium ion battery degradation among the whole life cycle. eTransportation 2019, 1, 100005. [Google Scholar] [CrossRef]
- Kebede, A.A.; Hosen, M.S.; Messagie, M.; Behabtu, H.A.; Jemal, T.; Van Mierlo, J.; Coosemans, T.; Berecibar, M. Development of a lifetime model for large format nickel-manganese-cobalt oxide-based lithium-ion cell validated using a real-life profile. J. Energy Storage 2022, 50, 104289. [Google Scholar] [CrossRef]
- Gao, Y.; Jiang, J.; Zhang, C.; Zhang, W.; Jiang, Y. Aging mechanisms under different state-of-charge ranges and the multi-indicators system of state-of-health for lithium-ion battery with Li(NiMnCo)O2 cathode. J. Power Sources 2018, 400, 641–651. [Google Scholar] [CrossRef]
- Jiang, J.; Gao, Y.; Zhang, C.; Zhang, W.; Jiang, Y. Lifetime Rapid Evaluation Method for Lithium-Ion Battery with Li(NiMnCo)O2 Cathode. J. Electrochem. Soc. 2019, 166, A1070–A1081. [Google Scholar] [CrossRef]
- Gauthier, R.; Luscombe, A.; Bond, T.; Bauer, M.; Johnson, M.; Harlow, J.; Louli, A.J.; Dahn, J.R. How do Depth of Discharge, C-rate and Calendar Age Affect Capacity Retention, Impedance Growth, the Electrodes, and the Electrolyte in Li-Ion Cells? J. Electrochem. Soc. 2022, 169, 020518. [Google Scholar] [CrossRef]
- Ecker, M.; Nieto, N.; Käbitz, S.; Schmalstieg, J.; Blanke, H.; Warnecke, A.; Sauer, D.U. Calendar and cycle life study of Li(NiMnCo)O2-based 18650 lithium-ion batteries. J. Power Sources 2014, 248, 839–851. [Google Scholar] [CrossRef]
- Zhu, J.; Knapp, M.; Sørensen, D.R.; Heere, M.; Darma, M.S.D.; Müller, M.; Mereacre, L.; Dai, H.; Senyshyn, A.; Wei, X.; et al. Investigation of capacity fade for 18650-type lithium-ion batteries cycled in different state of charge (SoC) ranges. J. Power Sources 2021, 489, 229422. [Google Scholar] [CrossRef]
- Liu, S.; Wang, J.; Liu, H.; Liu, Q.; Tang, J.; Li, Z. Battery degradation model and multiple-indicators based lifetime estimator for energy storage system design and operation: Experimental analyses of cycling-induced aging. Electrochim. Acta 2021, 384, 138294. [Google Scholar] [CrossRef]
- Lucu, M.; Azkue, M.; Camblong, H.; Martinez-Laserna, E. Data-Driven Nonparametric Li-Ion Battery Ageing Model Aiming at Learning from Real Operation Data: Holistic Validation with Ev Driving Profiles. In Proceedings of the ECCE 2020—IEEE Energy Conversion Congress Exposition, Detroit, MI, USA, 11–15 October 2020; Volume 30, pp. 5600–5607. [Google Scholar] [CrossRef]
- Preger, Y.; Barkholtz, H.M.; Fresquez, A.; Campbell, D.L.; Juba, B.W.; Romàn-Kustas, J.; Ferreira, S.R.; Chalamala, B. Degradation of Commercial Lithium-Ion Cells as a Function of Chemistry and Cycling Conditions. J. Electrochem. Soc. 2020, 167, 120532. [Google Scholar] [CrossRef]
- Jia, X.; Zhang, C.; Wang, L.Y.; Zhang, L.; Zhang, W. The Degradation Characteristics and Mechanism of Li[Ni0.5Co0.2Mn0.3]O2 Batteries at Different Temperatures and Discharge Current Rates. J. Electrochem. Soc. 2020, 167, 020503. [Google Scholar] [CrossRef]
- Barcellona, S.; Piegari, L. Effect of current on cycle aging of lithium ion batteries. J. Energy Storage 2020, 29, 101310. [Google Scholar] [CrossRef]
- Dubarry, M.; Devie, A.; McKenzie, K. Durability and reliability of electric vehicle batteries under electric utility grid operations: Bidirectional charging impact analysis. J. Power Sources 2017, 358, 39–49. [Google Scholar] [CrossRef]
- Uddin, K.; Jackson, T.; Widanage, W.D.; Chouchelamane, G.; Jennings, P.A.; Marco, J. On the possibility of extending the lifetime of lithium-ion batteries through optimal V2G facilitated by an integrated vehicle and smart-grid system. Energy 2017, 133, 710–722. [Google Scholar] [CrossRef]
- Petit, M.; Prada, E.; Sauvant-Moynot, V. Development of an empirical aging model for Li-ion batteries and application to assess the impact of Vehicle-to-Grid strategies on battery lifetime. Appl. Energy 2016, 172, 398–407. [Google Scholar] [CrossRef]
- Jafari, M.; Gauchia, A.; Zhao, S.; Zhang, K.; Gauchia, L. Electric Vehicle Battery Cycle Aging Evaluation in Real-World Daily Driving and Vehicle-to-Grid Services. IEEE Trans. Transp. Electrif. 2017, 4, 122–134. [Google Scholar] [CrossRef]
- Carmeli, M.S.; Toscani, N.; Mauri, M. Electrothermal Aging Model of Li-Ion Batteries for Vehicle-to-Grid Services Evaluation. Electronics 2022, 11, 1042. [Google Scholar] [CrossRef]
- Farzin, H.; Fotuhi-Firuzabad, M.; Moeini-Aghtaie, M. A Practical Scheme to Involve Degradation Cost of Lithium-Ion Batteries in Vehicle-to-Grid Applications. IEEE Trans. Sustain. Energy 2016, 7, 1730–1738. [Google Scholar] [CrossRef]
- Bhoir, S.; Caliandro, P.; Brivio, C. Impact of V2G service provision on battery life. J. Energy Storage 2021, 44, 103178. [Google Scholar] [CrossRef]
- Bakeer, A.; Chub, A.; Shen, Y.; Sangwongwanich, A. Reliability analysis of battery energy storage system for various stationary applications. J. Energy Storage 2022, 50, 104217. [Google Scholar] [CrossRef]
- Gao, Y.; Yang, S.; Jiang, J.; Zhang, C.; Zhang, W.; Zhou, X. The Mechanism and Characterization of Accelerated Capacity Deterioration for Lithium-Ion Battery with Li(NiMnCo)O2 Cathode. J. Electrochem. Soc. 2019, 166, A1623–A1635. [Google Scholar] [CrossRef]
- Jin, L.; Sun, Z.; Liu, Z.; Li, J.; Yang, M. Simulation Study on State of Charge Estimation of Lithium-ion Battery at Different Temperatures. Qiche Gongcheng Automot. Eng. 2019, 41, 590–598. [Google Scholar] [CrossRef]
- Li, K.; Zhou, P.; Lu, Y.; Han, X.; Li, X.; Zheng, Y. Battery life estimation based on cloud data for electric vehicles. J. Power Sources 2020, 468, 228192. [Google Scholar] [CrossRef]
- Han, X.; Ouyang, M.; Lu, L.; Li, J.; Zheng, Y.; Li, Z. A comparative study of commercial lithium ion battery cycle life in electrical vehicle: Aging mechanism identification. J. Power Sources 2014, 251, 38–54. [Google Scholar] [CrossRef]
- Hao, X.; Wang, H.; Lin, Z.; Ouyang, M. Seasonal effects on electric vehicle energy consumption and driving range: A case study on personal, taxi, and ridesharing vehicles. J. Clean. Prod. 2020, 249, 119403. [Google Scholar] [CrossRef]
- Redondo-Iglesias, E.; Venet, P.; Pelissier, S. Calendar and cycling ageing combination of batteries in electric vehicles. Microelectron. Reliab. 2018, 88–90, 1212–1215. [Google Scholar] [CrossRef] [Green Version]
- Harlow, J.E.; Ma, X.; Li, J.; Logan, E.; Liu, Y.; Zhang, N.; Ma, L.; Glazier, S.L.; Cormier, M.M.E.; Genovese, M.; et al. A Wide Range of Testing Results on an Excellent Lithium-Ion Cell Chemistry to be used as Benchmarks for New Battery Technologies. J. Electrochem. Soc. 2019, 166, A3031–A3044. [Google Scholar] [CrossRef]
- Bloom, I.; Jones, S.A.; Polzin, E.G.; Battaglia, V.S.; Henriksen, G.L.; Motloch, C.G.; Wright, R.B.; Jungst, R.G.; Case, H.L.; Doughty, D.H. Mechanisms of impedance rise in high-power, lithium-ion cells. J. Power Sources 2002, 111, 152–159, Erratum in J. Power Sources 2003, 114, 180. [Google Scholar] [CrossRef]
- Ploehn, H.J.; Ramadass, P.; White, R.E. Solvent Diffusion Model for Aging of Lithium-Ion Battery Cells. J. Electrochem. Soc. 2004, 151, A456. [Google Scholar] [CrossRef] [Green Version]
- Xie, Y.; Wang, S.; Li, R.; Ren, D.; Yi, M.; Xu, C.; Han, X.; Lu, L.; Friess, G.; Offer, G.; et al. Inhomogeneous degradation induced by lithium plating in a large-format lithium-ion battery. J. Power Sources 2022, 542, 231753. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, R.; He, H.; Qu, X.; Pecht, M. Aging characteristics-based health diagnosis and remaining useful life prognostics for lithium-ion batteries. eTransportation 2019, 1, 100004. [Google Scholar] [CrossRef]
- Feng, X.; Merla, Y.; Weng, C.; Ouyang, M.; He, X.; Liaw, B.Y.; Santhanagopalan, S.; Li, X.; Liu, P.; Lu, L.; et al. A reliable approach of differentiating discrete sampled-data for battery diagnosis. eTransportation 2020, 3, 100051. [Google Scholar] [CrossRef]
- Dubarry, M.; Truchot, C.; Liaw, B.Y. Synthesize battery degradation modes via a diagnostic and prognostic model. J. Power Sources 2012, 219, 204–216. [Google Scholar] [CrossRef]
- Han, S.; Aki, H.; Han, S. A practical battery wear model for electric vehicle charging applications. IEEE Power Energy Soc. Gen. Meet. 2013, 113, 1100–1108. [Google Scholar] [CrossRef]
- Rücker, F.; Schoeneberger, I.; Wilmschen, T.; Chahbaz, A.; Dechent, P.; Hildenbrand, F.; Barbers, E.; Kuipers, M.; Figgener, J.; Sauer, D.U. A Comprehensive Electric Vehicle Model for Vehicle-to-Grid Strategy Development. Energies 2022, 15, 4186. [Google Scholar] [CrossRef]
- Ben-Marzouk, M.; Pelissier, S.; Clerc, G.; Sari, A.; Venet, P. Generation of a Real-Life Battery Usage Pattern for Electrical Vehicle Application and Aging Comparison with the WLTC Profile. IEEE Trans. Veh. Technol. 2021, 70, 5618–5627. [Google Scholar] [CrossRef]
- Wei, Y.; Wang, S.; Qin, Y.; Han, T.; Tao, L.; Wang, J.; Lu, L.; Ouyang, M.; Han, X. A Novel Data Augmentation and Swift Optimal Sizing Framework for PV-based EV Charging Microgrid. In Proceedings of the 2021 IEEE 4th International Electrical Energy Conference, Wuhan, China, 28–30 May 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Qin, Y.; Han, X.; Wei, Y.; Lu, L.; Li, J.; Du, J.; Ouyang, M.; Sheng, Y. A Vehicle-to-Grid Frequency Regulation Framework for Fast Charging Infrastructures Considering Power Performances of Lithium-ion Batteries and Chargers. In Proceedings of the 2021 IEEE 4th International Electrical Energy Conference, Wuhan, China, 28–30 May 2021; pp. 1–6. [Google Scholar] [CrossRef]

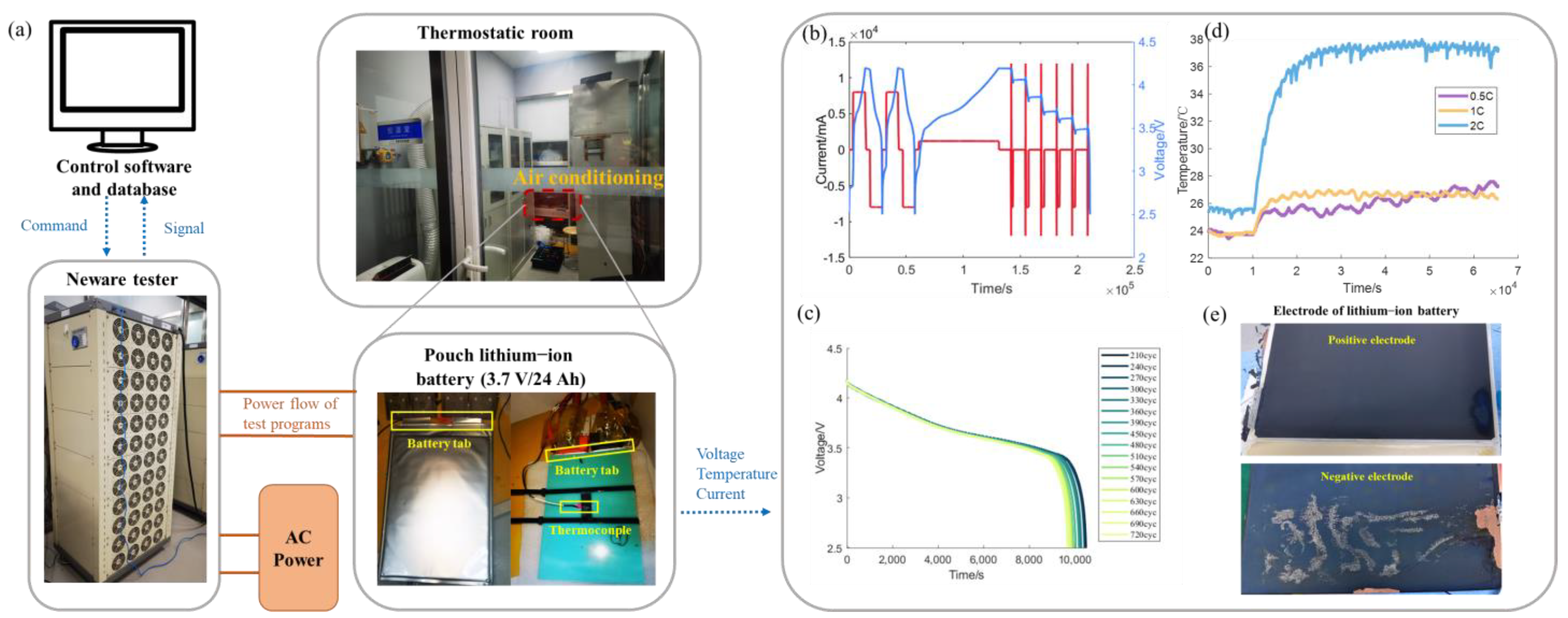



| Item Specification | |
|---|---|
| Cathode material | Li(NiMnCo)O2 |
| Anode material | Graphite |
| Electrolyte | 1 M LiPF6/EC:EMC (3:7) |
| Nominal capacity | 24 Ah |
| Nominal voltage | 3.7 V |
| Max. continuous charge current | 1 C |
| Charge cut-off voltage | 4.2 V |
| Max. continuous discharge current | 3 C |
| Discharge cut-off voltage | 2.5 V |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Y.; Yao, Y.; Pang, K.; Xu, C.; Han, X.; Lu, L.; Li, Y.; Qin, Y.; Zheng, Y.; Wang, H.; et al. A Comprehensive Study of Degradation Characteristics and Mechanisms of Commercial Li(NiMnCo)O2 EV Batteries under Vehicle-To-Grid (V2G) Services. Batteries 2022, 8, 188. https://doi.org/10.3390/batteries8100188
Wei Y, Yao Y, Pang K, Xu C, Han X, Lu L, Li Y, Qin Y, Zheng Y, Wang H, et al. A Comprehensive Study of Degradation Characteristics and Mechanisms of Commercial Li(NiMnCo)O2 EV Batteries under Vehicle-To-Grid (V2G) Services. Batteries. 2022; 8(10):188. https://doi.org/10.3390/batteries8100188
Chicago/Turabian StyleWei, Yifan, Yuan Yao, Kang Pang, Chaojie Xu, Xuebing Han, Languang Lu, Yalun Li, Yudi Qin, Yuejiu Zheng, Hewu Wang, and et al. 2022. "A Comprehensive Study of Degradation Characteristics and Mechanisms of Commercial Li(NiMnCo)O2 EV Batteries under Vehicle-To-Grid (V2G) Services" Batteries 8, no. 10: 188. https://doi.org/10.3390/batteries8100188
APA StyleWei, Y., Yao, Y., Pang, K., Xu, C., Han, X., Lu, L., Li, Y., Qin, Y., Zheng, Y., Wang, H., & Ouyang, M. (2022). A Comprehensive Study of Degradation Characteristics and Mechanisms of Commercial Li(NiMnCo)O2 EV Batteries under Vehicle-To-Grid (V2G) Services. Batteries, 8(10), 188. https://doi.org/10.3390/batteries8100188







