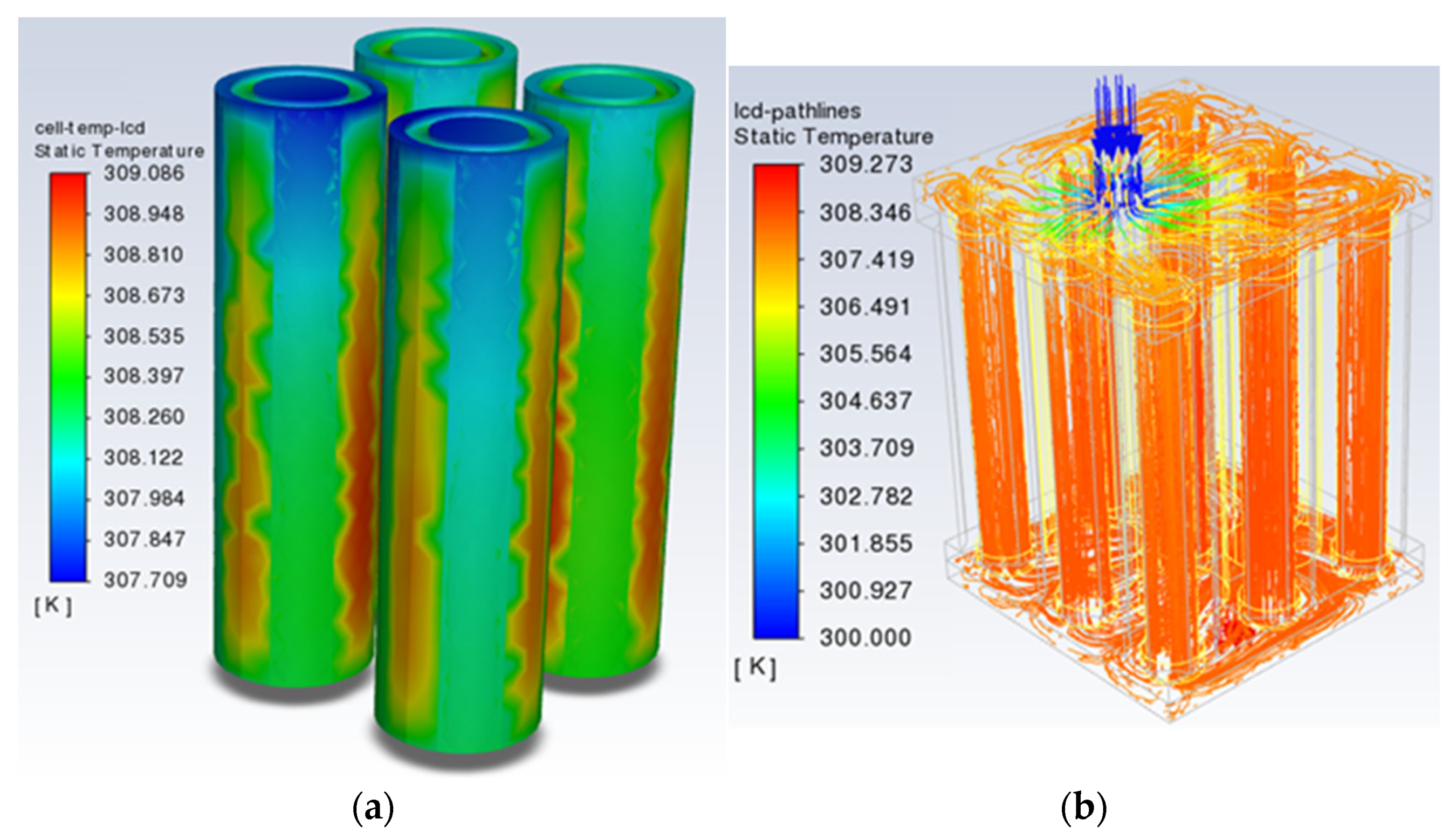
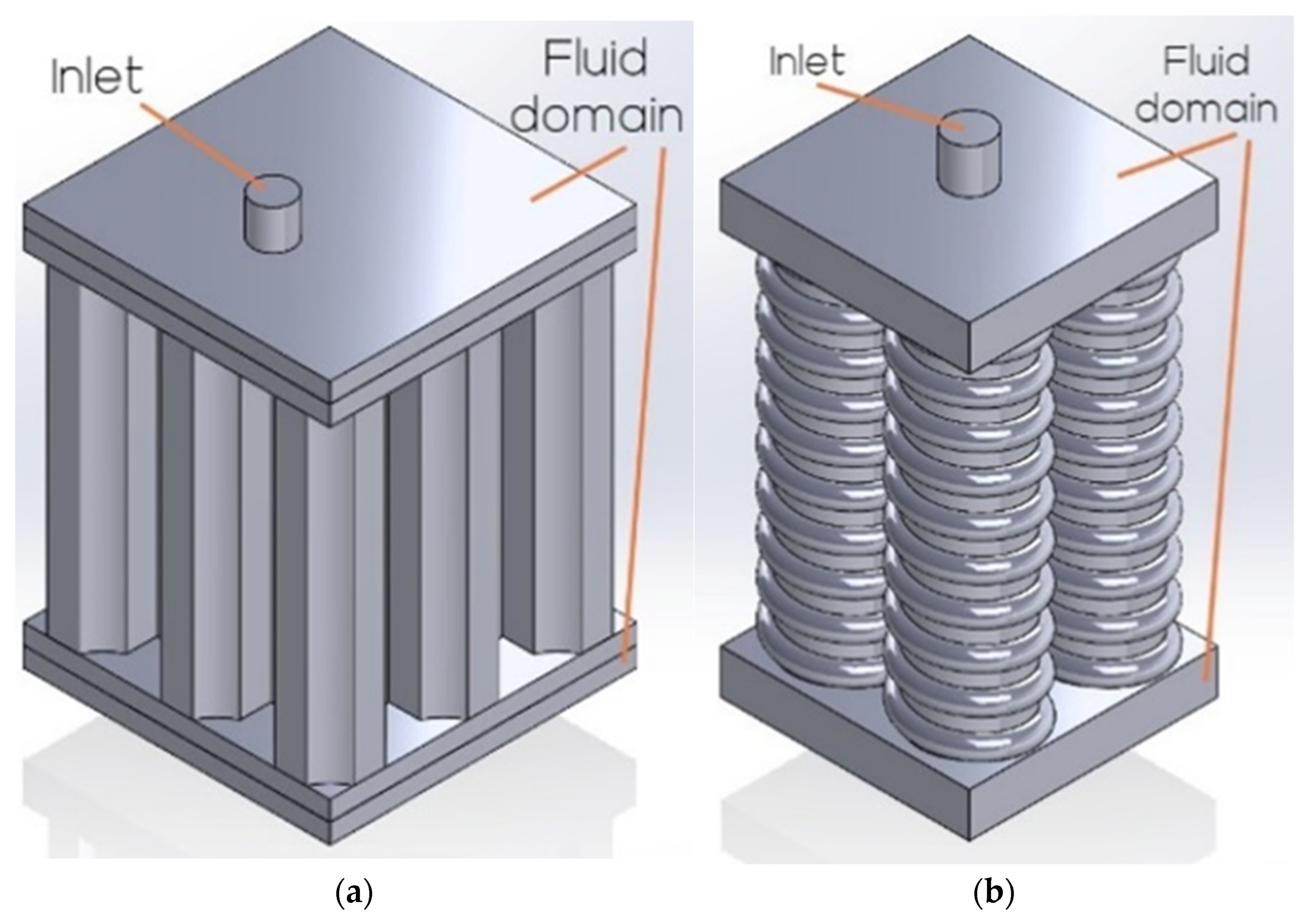
Over the past decade, extensive research has been conducted on EV lithium-ion battery packs’ thermal management systems. The demand for new innovative ways to improve battery performance from various electric car manufacturers, has always been prevalent due to cooling being a major factor in the vehicle’s overall performance and efficiency. This literature review will be categorised in order to cover the three key areas of EV battery pack cooling research, comprising PCM cooling, air cooling and liquid cooling.
1.2.1. PCM Cooling
One of the fundamental areas for research within the thermal management of EV battery packs involves the use of a PCM enclosure for the Li-ion cells. PCM cooling relies on the absorption and release of thermal energy when the coolant material changes phase. PCMs have been explored in recent research such as that of Li et al. [
7] where porous cellulose nanofibril (CNF)/silver nanowire (AgNW) hybrid supporting materials were used to increase the phonon propagation of the cellulosic material lattice and improve the thermal transmission ability of the hybrid carriers.
Multiple structural arrangements of PCM enclosures have been proposed in the literature, such as Choudhari et al. [
8] comparing the use of rectangular, triangular, trapezoidal, I-shape and T-shape fins within the PCM enclosure in order to counteract the heat accumulation in PCMs due its low heat conduction [
8]. It was concluded that the I-shape and rectangular fins had the strongest performance in terms of maximum temperature reduction and thermal uniformity. Although it should be said that each of these fin types had very similar results, leading to the conclusion that fin shape is not a major determining factor in the performance of a battery thermal management system. Additionally, this test was conducted on a single Li-ion battery and not a pack, which may limit the usefulness of this data for car manufacturers, so a battery pack should be tested for future research. Landini et al. [
9] studied the use of direct-metal-laser-sintered aluminium heat exchangers containing PCMs, finding that the system showed promising results in comparison to natural convection and maintained an even thermal uniformity.
An interesting development in the research of PCM cooling involves the combination with liquid cooling, as researched by Cao et al. [
10], who proposed a structure containing EG/RT44HC acting as a PCM alongside a cold plate situated in amongst the battery pack. It was found that in order to best control the battery pack’s thermal performance, the coolant water temperature should be limited to less than 313K and as close to the ambient temperature as possible [
10]. It was found that these low inlet temperatures reduce the general temperature of the battery pack but increase the temperature in the axial and radial directions, worsening the thermal uniformity of the Li-ion cells. Hekmat et al. [
11] investigated a hybrid PCM and liquid-cooled structure for prismatic cells, finding that the PCM was especially beneficial in creating a strong thermal uniformity. The addition of coolant pipes reduced the maximum temperature significantly compared to singularly using PCM, indicating that liquid cooling systems will majorly influence the thermal performance of an EV battery pack. Perhaps the liquid cooling structures should be researched heavily to optimise cooling performance instead of purely relying on passive cooling.
1.2.2. Air Cooling
The use of natural convection (air cooling) is commonly used for effectively managing the thermal performance of an EV battery pack. Fans are generally used in practice [
12] as opposed to purely relying on the exterior winds around the moving vehicle which would be unreliable and not keep temperatures steady enough over an extended period of time. Air cooling systems for EV battery packs are generally cheaper and simpler in design when compared to liquid cooling loops [
12]. However, some issues can arise in terms of the thermal uniformity of Li-ion cells since predicting the exact flow path of the air and making sure it evenly cools each Li-ion cell can be troublesome to model, which is why much literature has focused on this, along with minimising maximum temperatures.
Forced air cooling systems have been developed by scholars such as Wang et al. [
13], where two cooling channels were used and tested at multiple discharge rates. Results showed that the cooling efficiency reached 73%, and the maximum temperature decreased from 343 K to 328 K at a discharge rate of 1C. The main appeal of this design is the alternating airflow system, which has a noticeably beneficial impact on the thermal uniformity of the battery pack. However, it had a negligible effect in reducing maximum temperatures. The idea of alternating inlet airflow arrangements was also researched by Sharma et al. [
14], with the conclusion that dual-direction airflow provided great benefits to thermal uniformity and required a lower power consumption compared to unidirectional airflow. The airflow velocity was also optimised to be 2 ms
−1 for 1, 2 and 3C discharge rates and 4 ms
−1 for 4C.
The battery pack structure and layout of the cells are important considerations and determining factors when it comes to the thermal performance of an EV battery pack. Xi et al. [
15] proposed a novel Z-type structure, which produced promising results for thermal performance when an optimisation process was conducted. Furthermore, the addition of deflectors and rounding-off chamfers reduced the maximum temperature by 2.52 K and enhanced the thermal uniformity due to the more balanced airflow within the battery pack. A J-type airflow structure was studied by Liu et al. [
16] with a comparison to U-type and Z-type structures. It was found that after the J-type system was optimised using surrogate-based optimisation, it showed a 4.12 K reduction in maximum temperature in relation to the U-type system and a 15.42 K reduction compared to the Z-type structure since the optimised system benefits from a highly balanced and uniform airflow distribution.
1.2.3. Liquid Cooling
Liquid cooling is the method of EV battery thermal management employed by car manufacturers such as Tesla, BMW and Ford [
17] and is the most widely researched in the literature, with many different types of designs. It should be noted that liquid cooling can be split into direct and indirect cooling, where the former involves the submersion of the Li-ion cells directly into the coolant fluid. While direct cooling comes with the advantages of maximal thermal contact area for the cells and greatly improved thermal uniformity [
12], this method is uncommon in the real-world manufacturing of battery thermal management systems. This is due to the troublesome requirement of the water-resistant performance of the battery pack, where electrical short circuits and electrochemical reactions may occur [
12]. This is why indirect liquid cooling (designs involving exterior channels for coolant flow) is a well-researched area in the literature and is held at a higher degree of importance by both scholars and EV manufacturers.
Car manufacturers such as Tesla make use of a serpentine wavy channel cooling structure, which a fair level of academic research has been conducted on, such as Zhao et al. [
18], that used a simulation of a serpentine channel cooling arrangement battery pack. The pack comprises 71 18,650 Li-ion cells, where the heat generation is based on experimental data of a single cell. Zhao et al. [
18] found that increasing the discharge/charge rate of the cells increases the battery pack temperature and worsens its thermal uniformity and increasing the coolant flow rate significantly lowers the temperature and improves thermal uniformity. However, this was only tested with two inlet velocity rates, 0.1 ms
−1 and 0.5 ms
−1, providing very little sample space, so there is room to research and find an optimal flow rate. Zhao et al. [
18] also found that modelling a contact area between each cell had a negligible effect on the thermal performance and that increasing the contact area between each cell and the coolant loop resulted in lower battery pack temperatures (due to the increase in contact surface area resulting in a higher rate of thermal dissipation). Although, again this was tested arbitrarily with contact angles of 10°, 20°, 30° and 40°, so an optimal or maximum can still be researched.
The following year, this research was built upon again by Zhao et al. [
19], with the main focus being to optimise thermal uniformity with the battery pack. The removal of the coolant loop’s U-turn resulting in multiple single wavy channels was tested, with the findings that this improved the thermal uniformity and reduced the maximum temperature of the battery pack. This time, the contact area of the cell and coolant loop was tested much more in-depth. It was found that increasing the contact area improved thermal uniformity. The serpentine wavy cooling channel structure was also researched by Xu et al. [
20], comparing it with a U-shaped coolant loop with grooves. It was found that the serpentine wavy structure had better performance in terms of maximum temperature reduction, that being 0.37 K lower than the U-shaped structure, and demonstrated a better thermal uniformity. It would be potentially useful to combine the research of Zhao et al. [
18] and Xu [
19] to test a single-channel system with grooves.
In terms of alternative liquid cooling structures, many novel designs have been proposed in the literature that are not similar to those currently adopted by car manufacturers, such as the use of a helical duct structure encasing each Li-ion cell. Multiple parameters within this design were tested by Zhao et al. [
21], and it was found that the battery pack’s maximum temperature was lowered, and the temperature uniformity was improved as the inlet mass flow rate increased, concurring with the findings of Zhao et al. [
18] even for a vastly different coolant structure. It was also discovered that when the pitch and number of helical ducts were varied on the optimal flow rate model of 3 × 10
−4 kgs
−1, this had a negligible effect on the thermal performance of the battery pack. Various cases of alternating fluid flow were tested in an attempt to regulate temperature (since outlet temperature will inevitably be lower than inlet temperature). The findings highlight that having three inlets and two outlets at the positive electrode of the battery gave a T
max of 306.95 K and ΔT of 7.4 K at 40% DOD compared to a T
max of 307.85 K and ΔT of 8.7 K for a one inlet, four outlet case. This technique improved cooling effectiveness and thermal uniformity when the fluid flow is alternated. Finally, the helical duct diameters were tested with the conclusion that smaller diameter ducts result in slightly lower maximum temperatures but a worsened thermal uniformity.
The use of helical liquid ducts was also researched by Dong et al. [
22], who analysed a novel double helix structure. It was also found that an increase in coolant mass flow rate resulted in lower maximum temperatures. Although in this paper, a wider sample was used in order to derive a converging relationship, where the cooling benefits of higher mass flow rates began to diminish as the flow rate increased beyond 5 × 10
−4 kgs
−1. The pitch and diameter parameters were also tested, with the conclusion concurring with the findings of Zhao et al. [
21] that the smaller diameters result in lower maximum temperatures but a worsened thermal uniformity.
The use of linear mini-channel cooling structures has been a key area of EV battery liquid cooling research over recent years, with many design variations being proposed and evaluated in the literature. Some designs have linear channels flowing perpendicular to the length of the cells, such as the structure proposed by Rao et al. [
23], comprising aluminium blocks between the Li-ion cells with mini channels for coolant flow. The particular design shown in this paper provides adequate cooling performance for the battery pack since the temperatures are kept well within operating conditions. However, it is obvious from the schematics of this design that since the straight mini-channels flow perpendicular to the lengths of the Li-ion cells, the thermal uniformity of the cells is weakened. This is mainly due to the distance between a given coolant channel and the cells is constantly changing along the length of the channel. This is evident in the results of Rao et al. [
23], where the temperature contours demonstrate large variation within the cell volumes. This can be a major issue as denoted by Zeng et al. [
6], where the volumetric heat generation rate increases with the energy density and charge rate. There is more battery heat to be dissipated, requiring more cooling power. Zeng et al. [
6] mentions the application of the Arrhenius law, where areas of high cell temperature increase the current and accelerate electrochemical reactions, causing a local peak SOC. Uneven SOCs within electrodes shorten the operating lifespan of the cell by accelerating the ageing of the electrodes at high SOCs. From this, the thermal uniformity of the Li-ion cells shall be an important consideration for the proposed designs in this paper.
Most of the proposed linear cooling channel designs within the literature comprise channels parallel to the lengths of the cells. Lai et al. [
24] researched designs in this area and identified a gap in the literature research, being the lack of focus on the weight and compactness of the battery pack, which is an important factor for the performance of electric vehicles. A lightweight battery pack was constructed comprising multiple aluminium thermal conductive structures containing coolant channels, allowing the cooling water to flow from an upper reservoir and down the lengths of each cell to the lower reservoir. It was also stated that liquid cooling, in general, provided far superior heat transfer coefficient and power consumption levels in relation to PCM and air cooling. A similar concept was presented by Sheng et al. [
25], utilising a cellular liquid cooling jacket. Sheng et al. [
24] discovered that interlaced flow directions provide a lower temperature standard deviation and improved thermal uniformity, concurring with the findings associated with the helical channel designs of Zhao et al. [
21]. A glycol aqueous solution was also tested, with the conclusion that this is a more effective coolant than regular liquid water. Although, there is still room to potentially test more coolants to fully optimise this design.
Another such design would be the mini channel cylinder cooler proposed by Zhao et al. [
26]. Similar to the design proposed by Lai et al. [
24], the battery pack comprises an upper and lower reservoir connected via vertical ducts for the coolant to flow along the length of the cells. However, this design makes use of smaller channels (0.8 mm diameter) compared to that of the design proposed by Lai et al. [
24] (2 mm diameter), and utilises up to sixteen channels surrounding each cell as opposed to three per cell from Lai et al. [
24]. Zhao et al. [
26] and Lai et al. [
24] made use of different form factors of Li-ion batteries, 42,110 and 18,650, respectively. Comparing cooling performance among these designs provide little analytical benefit, so perhaps a comparison of these designs under the same boundary conditions and using the same battery form factor should be studied in future studies.
With liquid cooling showing very promising results within this field of research, the aim of this study shall be to further develop the specific types of cooling loops used within the literature. A comprehensive evaluation shall be conducted to determine the applicability of each design, to encourage further research for the superior model.