Comparison of an Experimental Electrolyte Wetting of a Lithium-Ion Battery Anode and Separator by a Lattice Boltzmann Simulation
Abstract
:1. Introduction
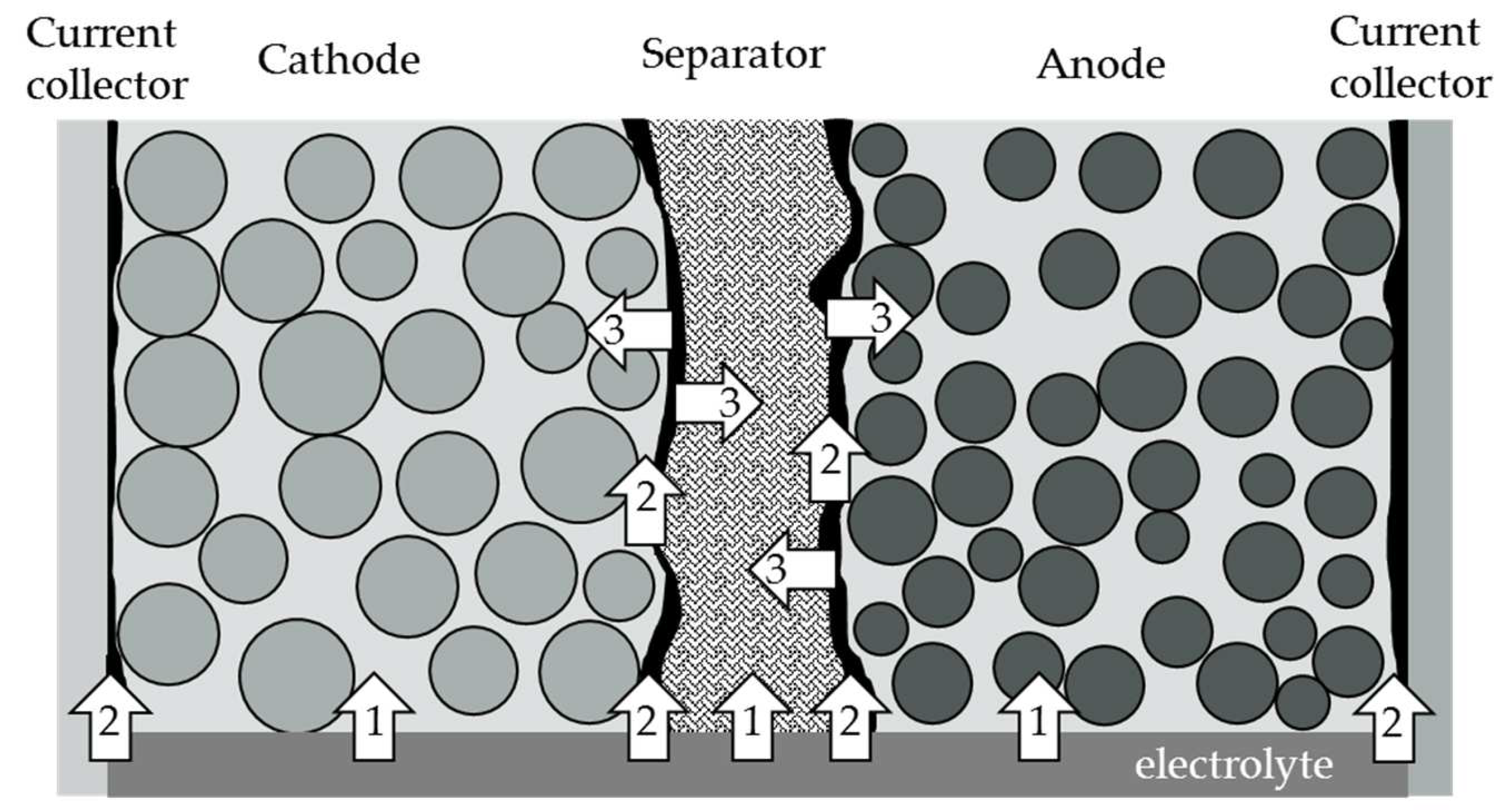
2. Theory of Capillary Wetting
- Path 1: Penetration of the electrolyte through the material’s cross-section. This wetting process depends on the contact angle of the materials to the electrolyte and the pore size distribution of the porous material.
- Path 2: The electrolyte rises at the interface between the electrodes and the separator, or the arrester. This interface depends on the morphology, or surface roughness, between the electrode and the separator or arrester and the compressive force acting on the materials.
- Path 3: After penetration with path 3, the electrolyte can penetrate laterally into the material.
3. Method
- Graphite anode;
- Separator;
- A combined approach of graphite anode and separator.
3.1. Materials
3.2. Experimental Setup
3.3. Simulation Setup
3.3.1. Artificial Generation of the Geometry
3.3.2. Lattice Boltzmann Simulation Setup
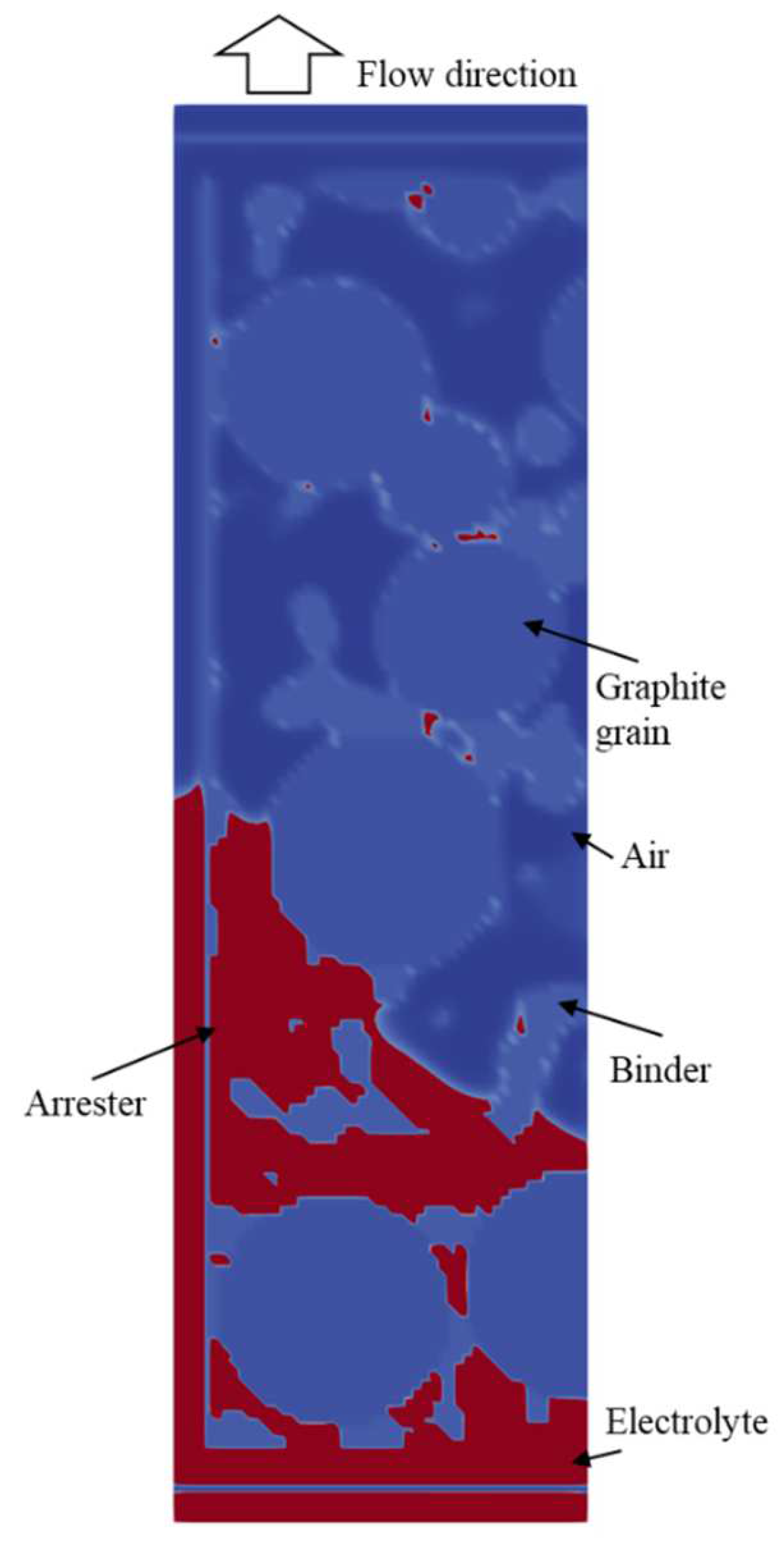
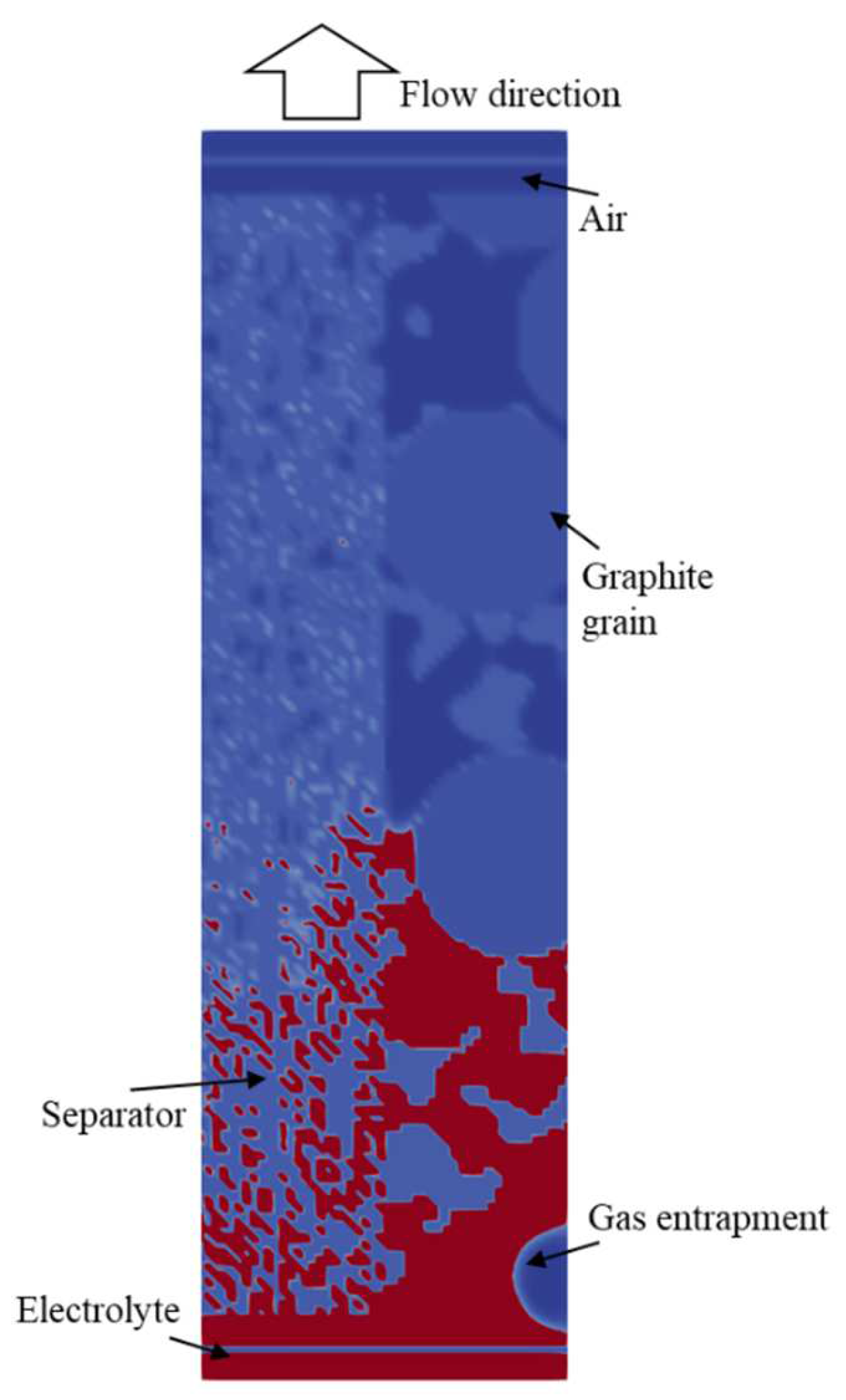
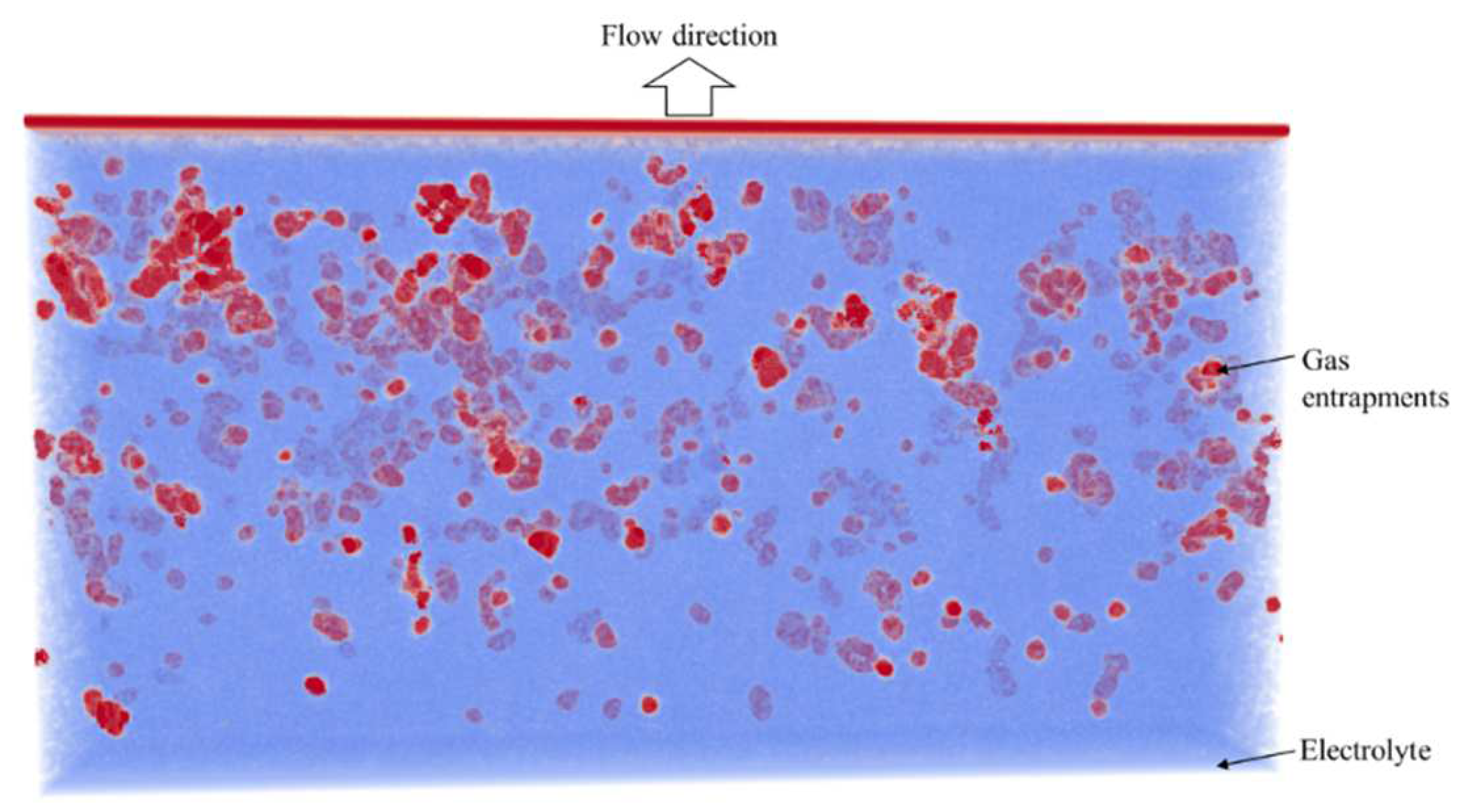
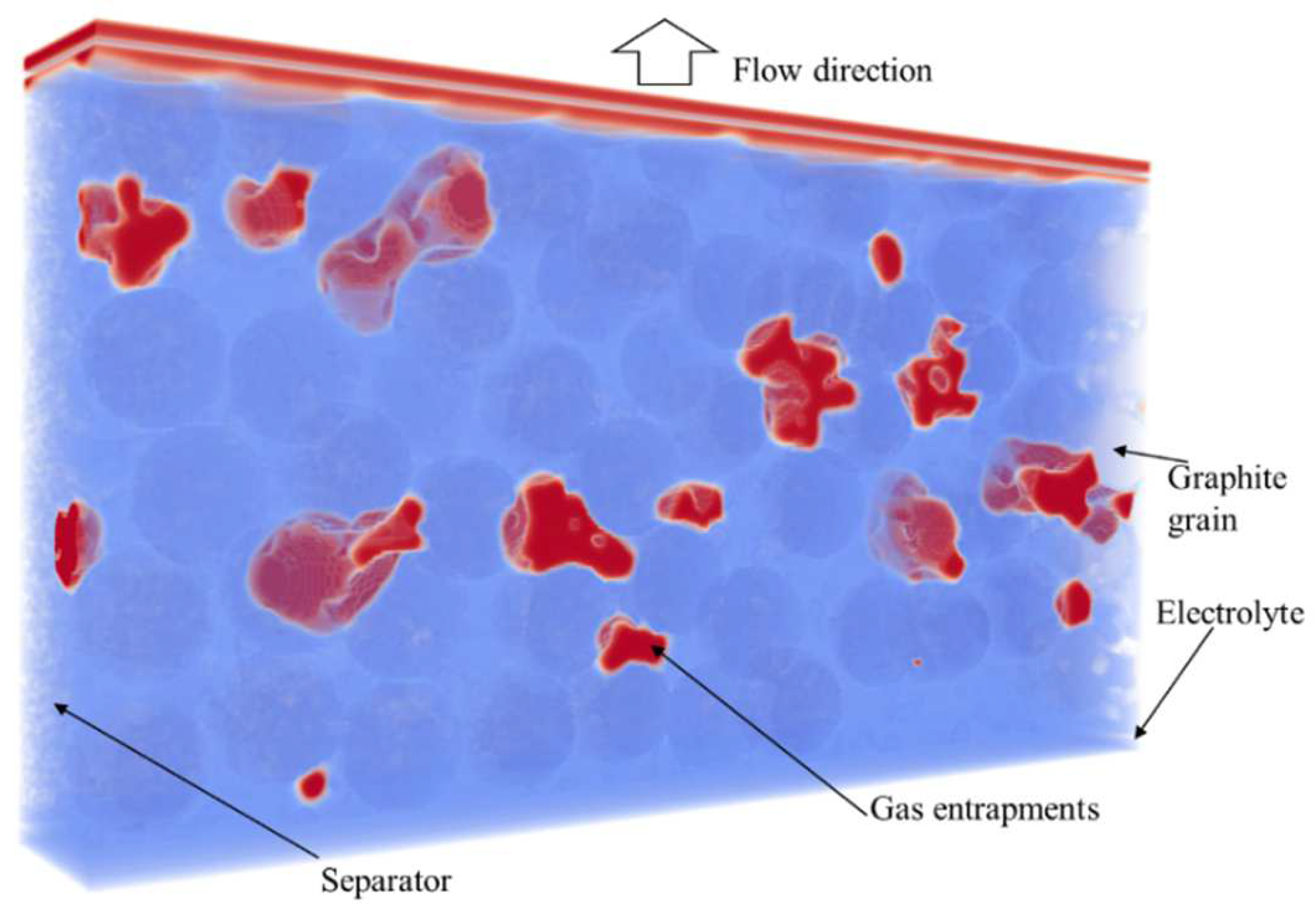
4. Results
4.1. Experimental Results
4.2. Simulation Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Model Parametrization
| Unit | Conversion Factor | Unit | Conversion Factor |
|---|---|---|---|
| Length | Time | ||
| Mass | Pressure | ||
| Kinematic viscosity | Force density | ||
| Dynamic viscosity | Velocity | ||
| Surface tension |
| SI Units | Lattice Units | |
|---|---|---|
| Length | ||
| Density | ||
| [28] | ||
| Kinematic viscosity | ||
| [28] | ||
| Surface tension | ||
| Contact angle | ||
| Relaxation coefficient |
Appendix B


References
- Birke, K.P.; Weeber, M.; Oberle, M. Handbook on Smart Battery Cell Manufacturing: The Power of Digitalization; World Scientific Publishing Co., Pte Ltd.: New Jersey, NJ, USA; London, UK; Singapore; Beijing, China; Shanghai, China; Hong Kong, China; Taipei, Taiwan; Chennai, India; Tokyo, Japan, 2022; ISBN 978-981-12-4561-9. [Google Scholar]
- Wanner, J.; Weeber, M.; Birke, K.P.; Sauer, A. Quality Modelling in Battery Cell Manufacturing Using Soft Sensoring and Sensor Fusion—A Review. In Proceedings of the 2019 9th International Electric Drives Production Conference (E|DPC), Esslingen, Germany, 3–4 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–9, ISBN 978-1-7281-4319-4. [Google Scholar]
- Weeber, M.; Wanner, J.; Schlegel, P.; Birke, K.P.; Sauer, A. Methodology for the Simulation based Energy Efficiency Assessment of Battery Cell Manufacturing Systems. Procedia Manuf. 2020, 43, 32–39. [Google Scholar] [CrossRef]
- Wanner, J.; Weeber, M.; Birke, K.P.; Sauer, A. Production planning and process optimization of a cell finishing process in battery cell manufacturing. Procedia CIRP 2022, 112, 507–512. [Google Scholar] [CrossRef]
- Günter, F.J.; Burgstaller, C.; Konwitschny, F.; Reinhart, G. Influence of the Electrolyte Quantity on Lithium-Ion Cells. J. Electrochem. Soc. 2019, 166, A1709–A1714. [Google Scholar] [CrossRef]
- Günter, F.J.; Keilhofer, J.; Rauch, C.; Rössler, S.; Schulz, M.; Braunwarth, W.; Gilles, R.; Daub, R.; Reinhart, G. Influence of pressure and temperature on the electrolyte filling of lithium-ion cells: Experiment, model and method. J. Power Sources 2022, 517, 230668. [Google Scholar] [CrossRef]
- Günter, F.J.; Habedank, J.B.; Schreiner, D.; Neuwirth, T.; Gilles, R.; Reinhart, G. Introduction to Electrochemical Impedance Spectroscopy as a Measurement Method for the Wetting Degree of Lithium-Ion Cells. J. Electrochem. Soc. 2018, 165, A3249–A3256. [Google Scholar] [CrossRef] [Green Version]
- Weydanz, W.J.; Reisenweber, H.; Gottschalk, A.; Schulz, M.; Knoche, T.; Reinhart, G.; Masuch, M.; Franke, J.; Gilles, R. Visualization of electrolyte filling process and influence of vacuum during filling for hard case prismatic lithium ion cells by neutron imaging to optimize the production process. J. Power Sources 2018, 380, 126–134. [Google Scholar] [CrossRef]
- Beyer, S.; Kobsch, O.; Pospiech, D.; Simon, F.; Peter, C.; Nikolowski, K.; Wolter, M.; Voit, B. Influence of surface characteristics on the penetration rate of electrolytes into model cells for lithium ion batteries. J. Adhes. Sci. Technol. 2020, 34, 849–866. [Google Scholar] [CrossRef]
- Knoche, T.; Zinth, V.; Schulz, M.; Schnell, J.; Gilles, R.; Reinhart, G. In situ visualization of the electrolyte solvent filling process by neutron radiography. J. Power Sources 2016, 331, 267–276. [Google Scholar] [CrossRef]
- Schilling, A.; Wiemers-Meyer, S.; Winkler, V.; Nowak, S.; Hoppe, B.; Heimes, H.H.; Dröder, K.; Winter, M. Influence of Separator Material on Infiltration Rate and Wetting Behavior of Lithium-Ion Batteries. Energy Technol. 2020, 8, 1900078. [Google Scholar] [CrossRef] [Green Version]
- Pfleging, W.; Pröll, J. A new approach for rapid electrolyte wetting in tape cast electrodes for lithium-ion batteries. J. Mater. Chem. A 2014, 2, 14918–14926. [Google Scholar] [CrossRef]
- Davoodabadi, A.; Li, J.; Liang, Y.; Wood, D.L.; Singler, T.J.; Jin, C. Analysis of electrolyte imbibition through lithium-ion battery electrodes. J. Power Sources 2019, 424, 193–203. [Google Scholar] [CrossRef] [Green Version]
- Kaden, N.; Schlüter, N.; Leithoff, R.; Savas, S.; Grundmeier, S.; Dröder, K. Influence of the Lamination Process on the Wetting Behavior and the Wetting Rate of Lithium-Ion Batteries. Processes 2021, 9, 1851. [Google Scholar] [CrossRef]
- Chen, L.; Kang, Q.; Mu, Y.; He, Y.-L.; Tao, W.-Q. A critical review of the pseudopotential multiphase lattice Boltzmann model: Methods and applications. Int. J. Heat Mass Transf. 2014, 76, 210–236. [Google Scholar] [CrossRef]
- Latt, J.; Courbebaisse, G.; Chopard, B.; Falcone, J.L. Lattice Boltzmann Modeling of Injection Moulding Process. In International Conference on Cellular Automata; Springer: Berlin/Heidelberg, Germany, 2004; pp. 345–354. [Google Scholar]
- Latt, J.; Malaspinas, O.; Kontaxakis, D.; Parmigiani, A.; Lagrava, D.; Brogi, F.; Belgacem, M.B.; Thorimbert, Y.; Leclaire, S.; Li, S.; et al. Palabos: Parallel Lattice Boltzmann Solver. Comput. Math. Appl. 2021, 81, 334–350. [Google Scholar] [CrossRef]
- Sukop, M.C. Lattice Boltzmann Modeling: An Introduction for Geoscientists and Engineers; Springer: Berlin/Heidelberg, Germany, 2010; ISBN 9783642066252. [Google Scholar]
- Shan, X.; Chen, H. Lattice Boltzmann model for simulating flows with multiple phases and components. Phys. Rev. E 1993, 47, 1815–1819. [Google Scholar] [CrossRef] [Green Version]
- Tian, Y.; Ju, B.; Chen, X.; Chen, Z.; Dong, Y.; Wu, D. Pore-Scale Investigation of Waterflooding Based on Experiments and Numerical Simulations Considering the Change in Geometry and Wettability. Energy Fuels 2021, 35, 17617–17628. [Google Scholar] [CrossRef]
- Sarkezi-Selsky, P.; Schmies, H.; Kube, A.; Latz, A.; Jahnke, T. Lattice Boltzmann simulation of liquid water transport in gas diffusion layers of proton exchange membrane fuel cells: Parametric studies on capillary hysteresis. J. Power Sources 2022, 535, 231381. [Google Scholar] [CrossRef]
- García-Salaberri, P.A.; Hwang, G.; Vera, M.; Weber, A.Z.; Gostick, J.T. Effective diffusivity in partially-saturated carbon-fiber gas diffusion layers: Effect of through-plane saturation distribution. Int. J. Heat Mass Transf. 2015, 86, 319–333. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.G.; Jeon, D.H.; Kim, B.M.; Kang, J.H.; Kim, C.-J. Lattice Boltzmann Simulation for Electrolyte Transport in Porous Electrode of Lithium Ion Batteries. J. Electrochem. Soc. 2013, 160, H258–H265. [Google Scholar] [CrossRef]
- Lee, S.G.; Jeon, D.H. Effect of electrode compression on the wettability of lithium-ion batteries. J. Power Sources 2014, 265, 363–369. [Google Scholar] [CrossRef]
- Mohammadian, S.K.; Zhang, Y. Improving wettability and preventing Li-ion batteries from thermal runaway using microchannels. Int. J. Heat Mass Transf. 2018, 118, 911–918. [Google Scholar] [CrossRef]
- Jeon, D.H. Wettability in electrodes and its impact on the performance of lithium-ion batteries. Energy Storage Mater. 2019, 18, 139–147. [Google Scholar] [CrossRef]
- Sauter, C.; Zahn, R.; Wood, V. Understanding Electrolyte Infilling of Lithium Ion Batteries. J. Electrochem. Soc. 2020, 167, 100546. [Google Scholar] [CrossRef]
- Lautenschlaeger, M.P.; Prifling, B.; Kellers, B.; Weinmiller, J.; Danner, T.; Schmidt, V.; Latz, A. Understanding Electrolyte Filling of Lithium-Ion Battery Electrodes on the Pore Scale Using the Lattice Boltzmann Method. Batter. Supercaps 2022, 5, e202200090. [Google Scholar] [CrossRef]
- Lautenschlaeger, M.P.; Weinmiller, J.; Kellers, B.; Danner, T.; Latz, A. Homogenized lattice Boltzmann model for simulating multi-phase flows in heterogeneous porous media. Adv. Water Resour. 2022, 170, 104320. [Google Scholar] [CrossRef]
- Shin, S.; Kim, H.; Maiyalagan, T.; Chul Yi, S. Sophisticated 3D microstructural reconstruction for numerical analysis of electrolyte imbibition in Li-ion battery separator and anode. Mater. Sci. Eng. B 2022, 284, 115878. [Google Scholar] [CrossRef]
- Shodiev, A.; Primo, E.; Arcelus, O.; Chouchane, M.; Osenberg, M.; Hilger, A.; Manke, I.; Li, J.; Franco, A.A. Insight on electrolyte infiltration of lithium ion battery electrodes by means of a new three-dimensional-resolved lattice Boltzmann model. Energy Storage Mater. 2021, 38, 80–92. [Google Scholar] [CrossRef]
- Hagemeister, J.; Günter, F.J.; Rinner, T.; Zhu, F.; Papst, A.; Daub, R. Numerical Models of the Electrolyte Filling Process of Lithium-Ion Batteries to Accelerate and Improve the Process and Cell Design. Batteries 2022, 8, 159. [Google Scholar] [CrossRef]
- Shodiev, A.; Zanotto, F.M.; Yu, J.; Chouchane, M.; Li, J.; Franco, A.A. Designing electrode architectures to facilitate electrolyte infiltration for lithium-ion batteries. Energy Storage Mater. 2022, 49, 268–277. [Google Scholar] [CrossRef]
- Singh, S.; Weeber, M.; Birke, K.P. Implementation of Battery Digital Twin: Approach, Functionalities and Benefits. Batteries 2021, 7, 78. [Google Scholar] [CrossRef]
- Knoche, T.; Surek, F.; Reinhart, G. A Process Model for the Electrolyte Filling of Lithium-ion Batteries. Procedia CIRP 2016, 41, 405–410. [Google Scholar] [CrossRef] [Green Version]
- Washburn, E.W. The Dynamics of Capillary Flow. Phys. Rev. 1921, 17, 273–283. [Google Scholar] [CrossRef] [Green Version]
- Fries, N.; Dreyer, M. An analytic solution of capillary rise restrained by gravity. J. Colloid Interface Sci. 2008, 320, 259–263. [Google Scholar] [CrossRef]
- Peter, C.; Nikolowski, K.; Reuber, S.; Wolter, M.; Michaelis, A. Chronoamperometry as an electrochemical in situ approach to investigate the electrolyte wetting process of lithium-ion cells. J. Appl. Electrochem. 2020, 50, 295–309. [Google Scholar] [CrossRef]
- Rokhforouz, M.R.; Akhlaghi Amiri, H.A. Effects of grain size and shape distribution on pore-scale numerical simulation of two-phase flow in a heterogeneous porous medium. Adv. Water Resour. 2019, 124, 84–95. [Google Scholar] [CrossRef]
- Dahbi, M.; Violleau, D.; Ghamouss, F.; Jacquemin, J.; Tran-Van, F.; Lemordant, D.; Anouti, M. Interfacial Properties of LiTFSI and LiPF 6 -Based Electrolytes in Binary and Ternary Mixtures of Alkylcarbonates on Graphite Electrodes and Celgard Separator. Ind. Eng. Chem. Res. 2012, 51, 5240–5245. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, M.H.T.; Oh, E.-S. Improvement of the characteristics of poly(acrylonitrile–butylacrylate) water-dispersed binder for lithium-ion batteries by the addition of acrylic acid and polystyrene seed. J. Electroanal. Chem. 2015, 739, 111–114. [Google Scholar] [CrossRef]
- Lemmon, E.W. Thermodynamic Properties of Dimethyl Carbonate. J. Phys. Chem. Ref. Data 2011, 40, 43106. [Google Scholar] [CrossRef]
- Rodríguez, A.; Canosa, J.; Domínguez, A.; Tojo, J. Viscosities of Dimethyl Carbonate or Diethyl Carbonate with Alkanes at Four Temperatures. New UNIFAC−VISCO Parameters. J. Chem. Eng. Data 2003, 48, 146–151. [Google Scholar] [CrossRef]
- Merck KGaA. 803525 Sigma-Aldrich Dimethylcarbonat: Dimethyl Carbonate for Synthesis. CAS 616-38-6, Chemical Formula (CH3O)2CO. Available online: https://www.merckmillipore.com/DE/de/product/Dimethyl-carbonate (accessed on 1 August 2022).
- Gostick, J.; Khan, Z.; Tranter, T.; Kok, M.; Agnaou, M.; Sadeghi, M.; Jervis, R. PoreSpy: A Python Toolkit for Quantitative Analysis of Porous Media Images. J. Open Source Softw. 2019, 4, 1296. [Google Scholar] [CrossRef]
- Lu, G.; Wang, X.-D.; Duan, Y.-Y. Study on initial stage of capillary rise dynamics. Colloids Surf. A Physicochem. Eng. Asp. 2013, 433, 95–103. [Google Scholar] [CrossRef]
- Krüger, T. The Lattice Boltzmann Method: Principles and Practice; Springer: Cham, Switzerland, 2017; ISBN 9783319446493. [Google Scholar]
- Hansen, C.D.; Johnson, C.R. The Visualization Handbook, 1st ed.; Elsevier-Butterworth Heinemann: Amsterdam, The Netherlands; Boston, MA, USA, 2005; ISBN 012387582X. [Google Scholar]
- Xu, H.; Bae, C. Stochastic 3D microstructure reconstruction and mechanical modeling of anisotropic battery separators. J. Power Sources 2019, 430, 67–73. [Google Scholar] [CrossRef]
- Stange, M.; Dreyer, M.E.; Rath, H.J. Capillary driven flow in circular cylindrical tubes. Phys. Fluids 2003, 15, 2587–2601. [Google Scholar] [CrossRef]
- Sheng, Y.; Fell, C.R.; Son, Y.K.; Metz, B.M.; Jiang, J.; Church, B.C. Effect of Calendering on Electrode Wettability in Lithium-Ion Batteries. Front. Energy Res. 2014, 2, 56. [Google Scholar] [CrossRef] [Green Version]
- Franken, A.; Nolten, J.; Mulder, M.; Bargeman, D.; Smolders, C.A. Wetting criteria for the applicability of membrane distillation. J. Membr. Sci. 1987, 33, 315–328. [Google Scholar] [CrossRef] [Green Version]
- Landry, C.J.; Karpyn, Z.T.; Ayala, O. Relative permeability of homogenous-wet and mixed-wet porous media as determined by pore-scale lattice Boltzmann modeling. Water Resour. Res. 2014, 50, 3672–3689. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.; Thorne, D.T.; Schaap, M.G.; Sukop, M.C. Proposed approximation for contact angles in Shan-and-Chen-type multicomponent multiphase lattice Boltzmann models. Phys. Rev. E 2007, 76, 66701. [Google Scholar] [CrossRef]


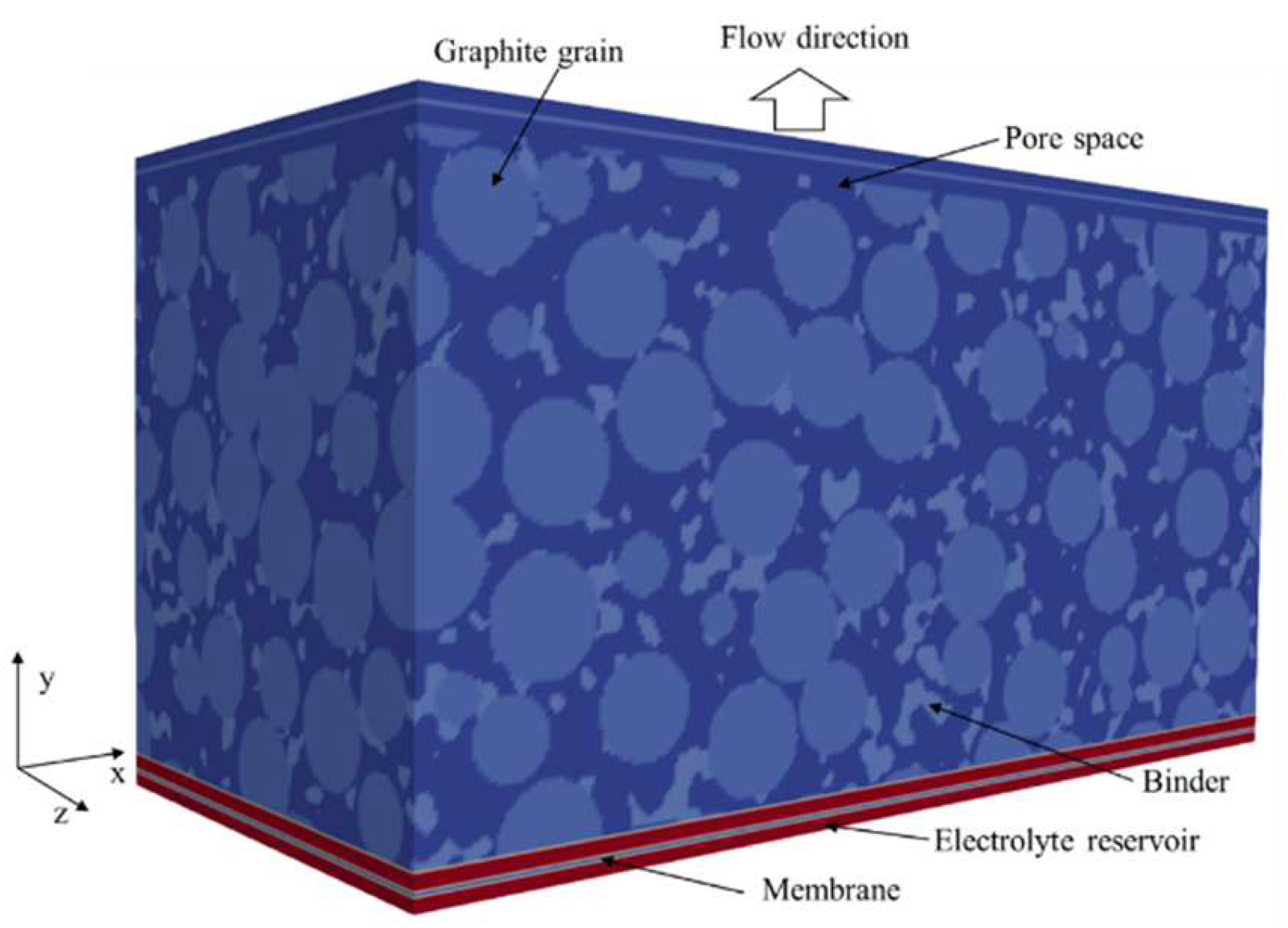
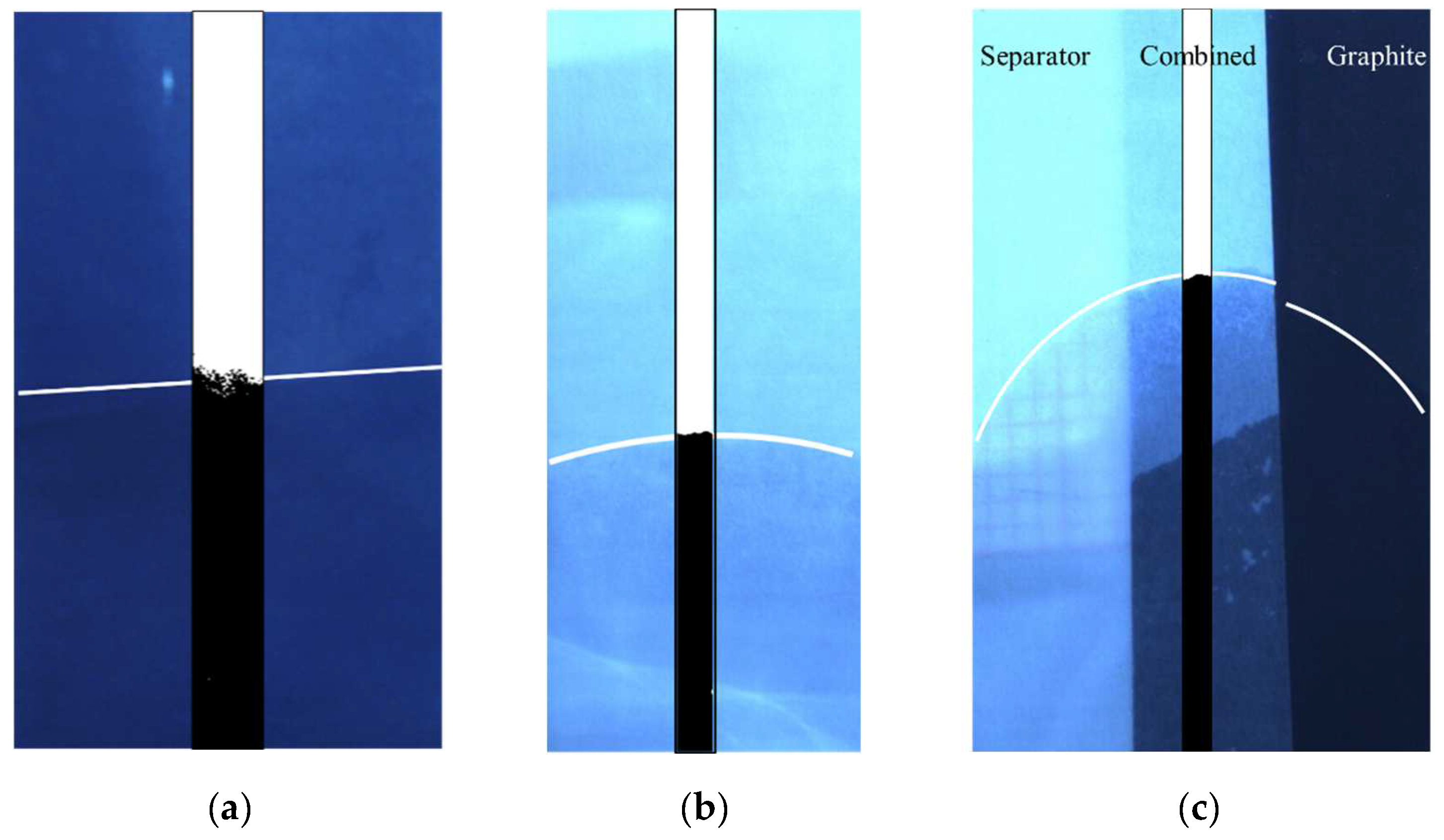


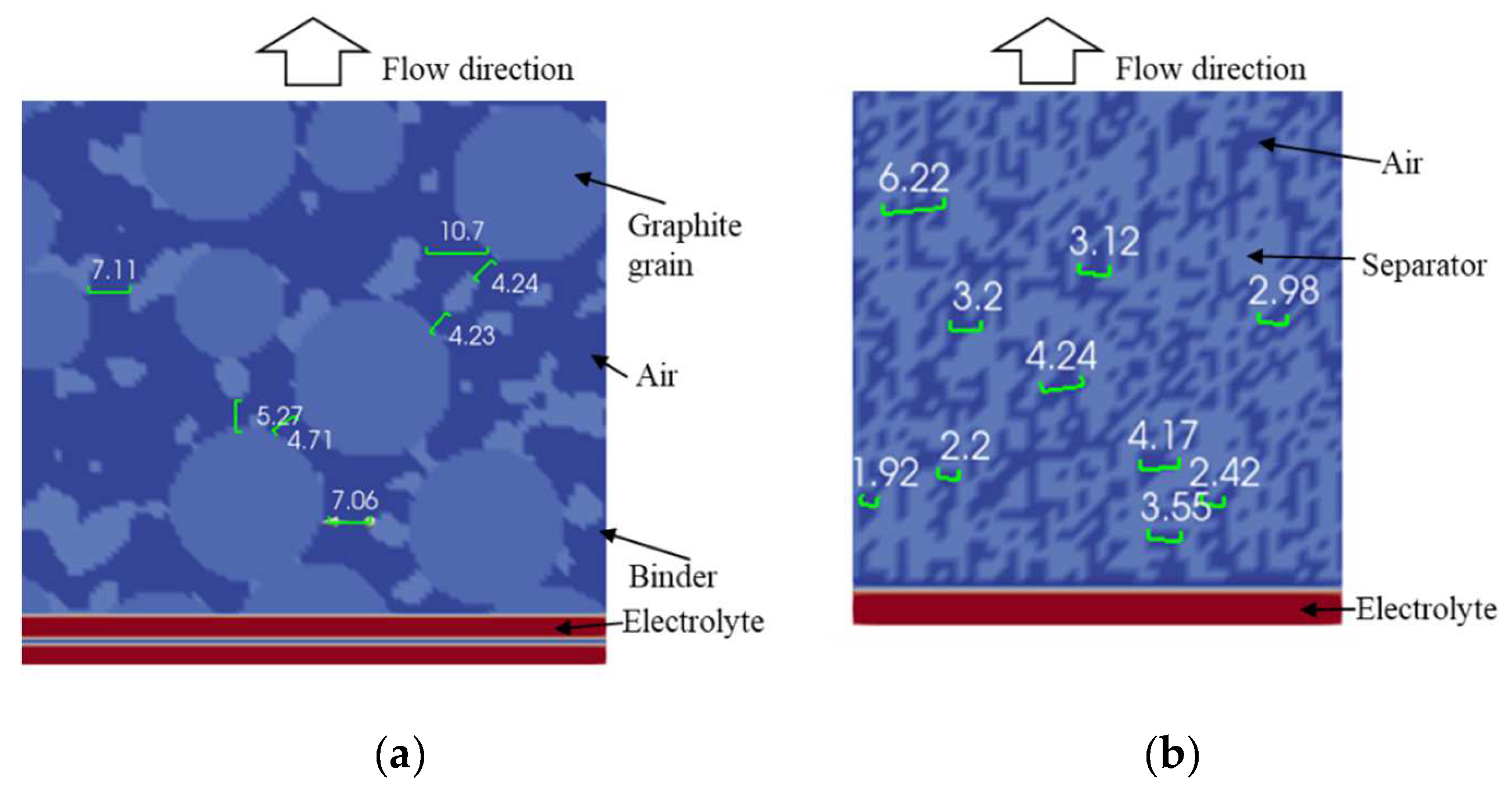
| Anode | Separator | ||
|---|---|---|---|
| Thickness | 12 × 10−5 m 50% | 25 × 10−6 m | |
| Porosity | 40% | ||
| Material | Graphite on Aluminum | Binder | Cellulose paper |
| Average grain diameter | 13.5 × 10−6 m | 1.45 × 10−6 m | 9.7 × 10−7 m |
| Contact angle | 25° [40] | 50° [41] | 30° [27,30] |
| Simulation Run | ΔP @80% Sat. | Wetting Time @80% Sat. | Wetting Rate k | Wetting Flow Rate |
|---|---|---|---|---|
| Graphite electrode | 20.2 kPa | 3.92 ms | 1.16 mm/s0.5 | 18.5 mm/s |
| Graphite with arrester | 19.3 kPa | 3.87 ms | 1.17 mm/s0.5 | 18.7 mm/s |
| Separator | 49.2 kPa | 20.9 ms | 0.501 mm/s0.5 | 3.46 mm/s |
| Combined geometry | 19.3 kPa | 3.83 ms | 1.17 mm/s0.5 | 18.9 mm/s |
| Graphite Electrode | Separator | Combined Approach | ||
|---|---|---|---|---|
| Experimental | Wetting rate k | 1.363 mm/s0.5 | 0.496 mm/s0.5 | 1.953 mm/s0.5 |
| reff (Equation (1)) | 0.187 µm | 0.026 µm | 0.385 µm | |
| reff (Equation (3)) | 0.233 µm | 0.085 µm | 0.371 µm | |
| Simulated | Wetting rate k | 1.16 mm/s0.5 | 0.501 mm/s0.5 | 1.17 mm/s0.5 |
| reff (Equation (2)) @80% Sat | 2.88 µm | 1.13 µm | 3 µm | |
| Wetting flow rate | 18.5 mm/s | 3.46 mm/s | 18.9 mm/s | |
| reff (Equation (3)) | 141.6 µm | 5.07 µm | 151.5 µm | |
| Geometry | Measured reff | 1.02 to 2.59 µm | 0.46 to 1.5 µm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wanner, J.; Birke, K.P. Comparison of an Experimental Electrolyte Wetting of a Lithium-Ion Battery Anode and Separator by a Lattice Boltzmann Simulation. Batteries 2022, 8, 277. https://doi.org/10.3390/batteries8120277
Wanner J, Birke KP. Comparison of an Experimental Electrolyte Wetting of a Lithium-Ion Battery Anode and Separator by a Lattice Boltzmann Simulation. Batteries. 2022; 8(12):277. https://doi.org/10.3390/batteries8120277
Chicago/Turabian StyleWanner, Johannes, and Kai Peter Birke. 2022. "Comparison of an Experimental Electrolyte Wetting of a Lithium-Ion Battery Anode and Separator by a Lattice Boltzmann Simulation" Batteries 8, no. 12: 277. https://doi.org/10.3390/batteries8120277
APA StyleWanner, J., & Birke, K. P. (2022). Comparison of an Experimental Electrolyte Wetting of a Lithium-Ion Battery Anode and Separator by a Lattice Boltzmann Simulation. Batteries, 8(12), 277. https://doi.org/10.3390/batteries8120277







