Review of Active Front-End Rectifiers in EV DC Charging Applications
Abstract
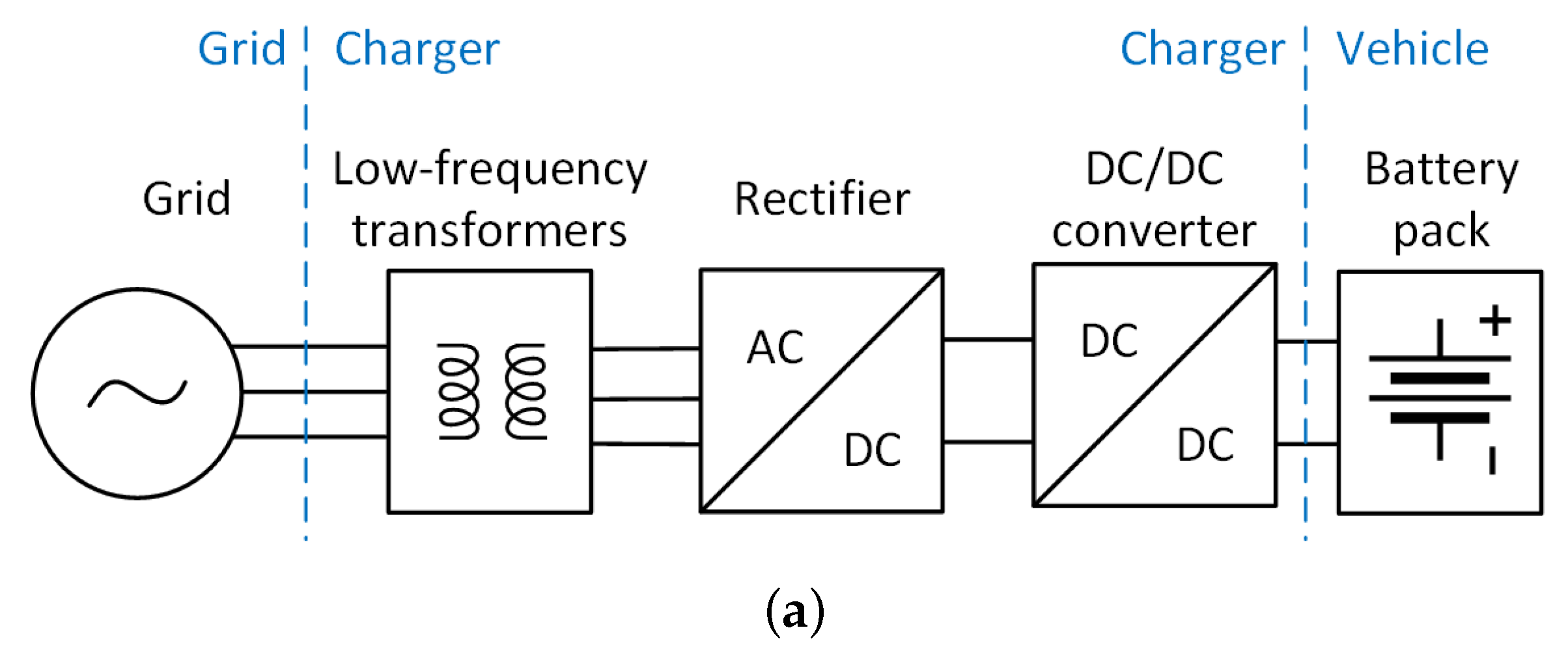
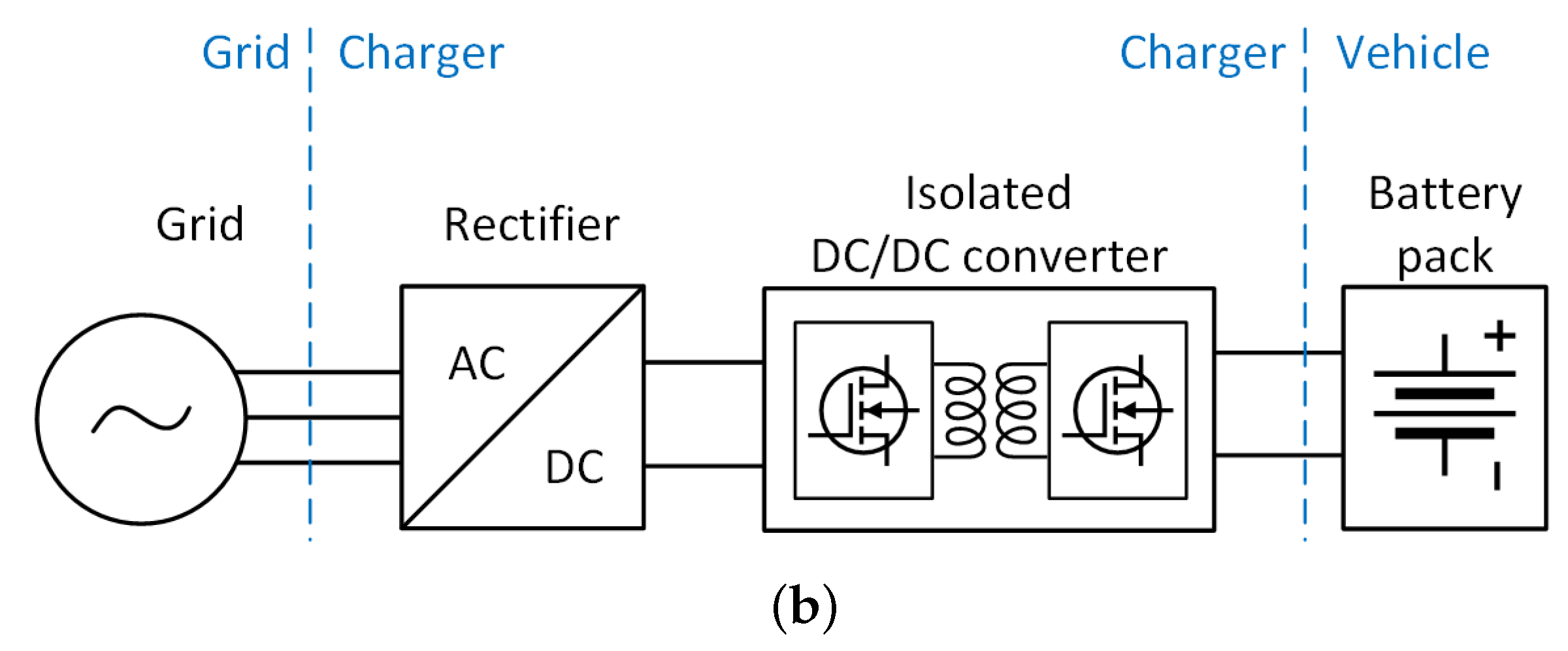
:1. Introduction
- Component availability—at high-power levels, the choice of components will become more limited and possibly more costly;
- Grid impact—increasing power and number of fast chargers introduces more harmonic distortion to the grid, damaging sensitive equipment;
- Thermal management—cooling systems will become more complex if they need to dissipate power in the range of tens of kilowatts;
- Reliability—in fast chargers, components are subjected to more stress due to higher power. Moreover, commercial off-board chargers will be cycled more compared to personal on-board chargers, which may lead to a shorter lifetime.
2. Comparison of AFE Topologies
- Three-phase boost-type rectifier topology suitable for Level 3 DC fast charging or ultra-fast charging;
- Injects minimal THD to the grid;
- Bidirectionality is advantageous since it enables a V2G operation;
- Smaller number of components is advantageous for system reliability and cost.
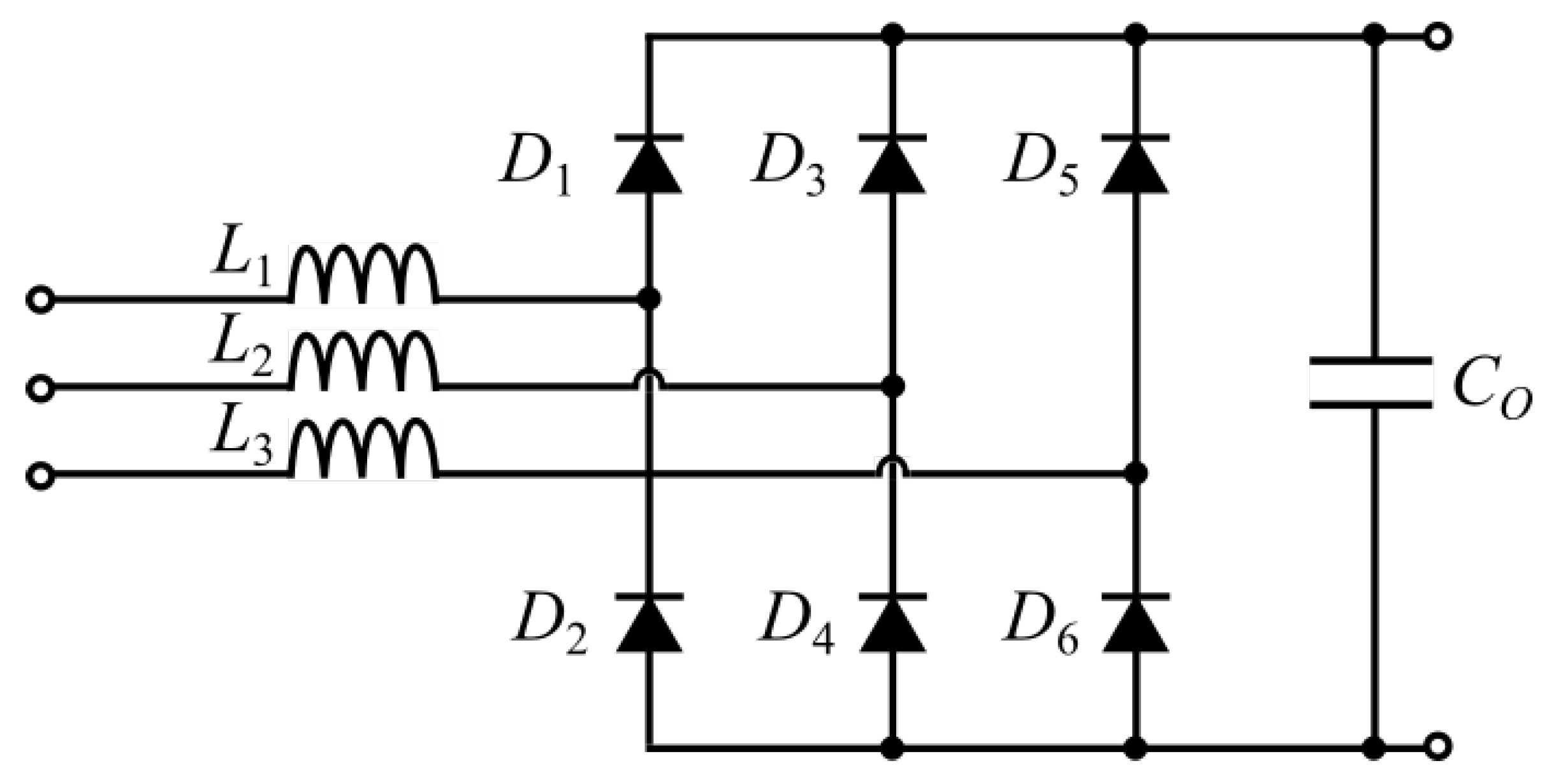
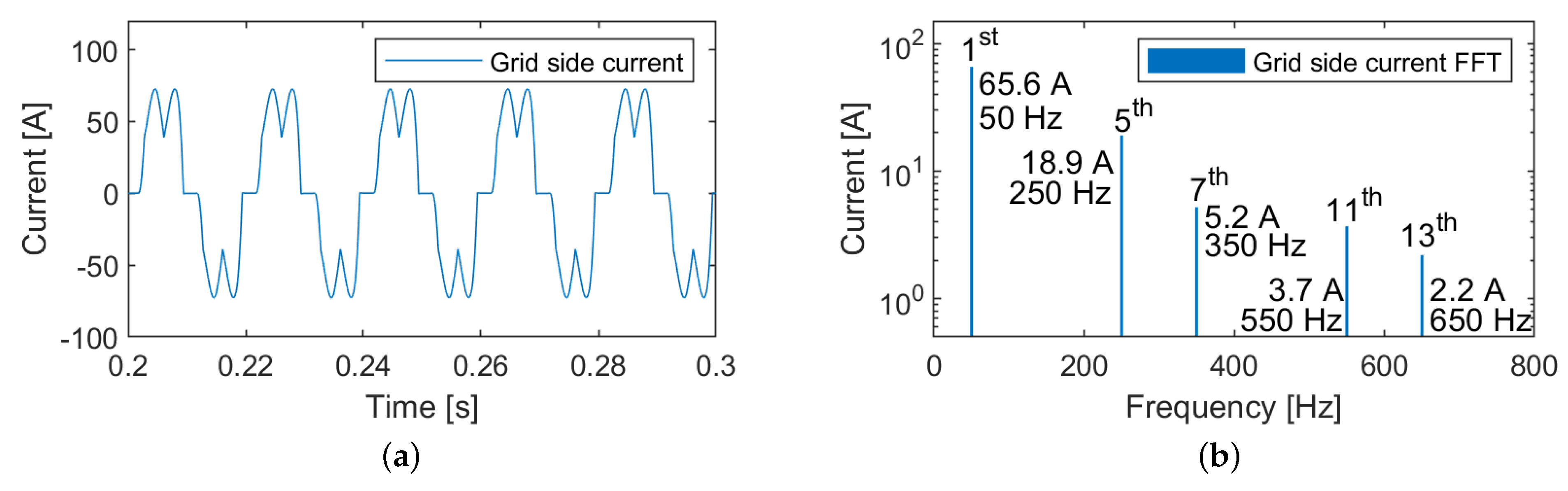
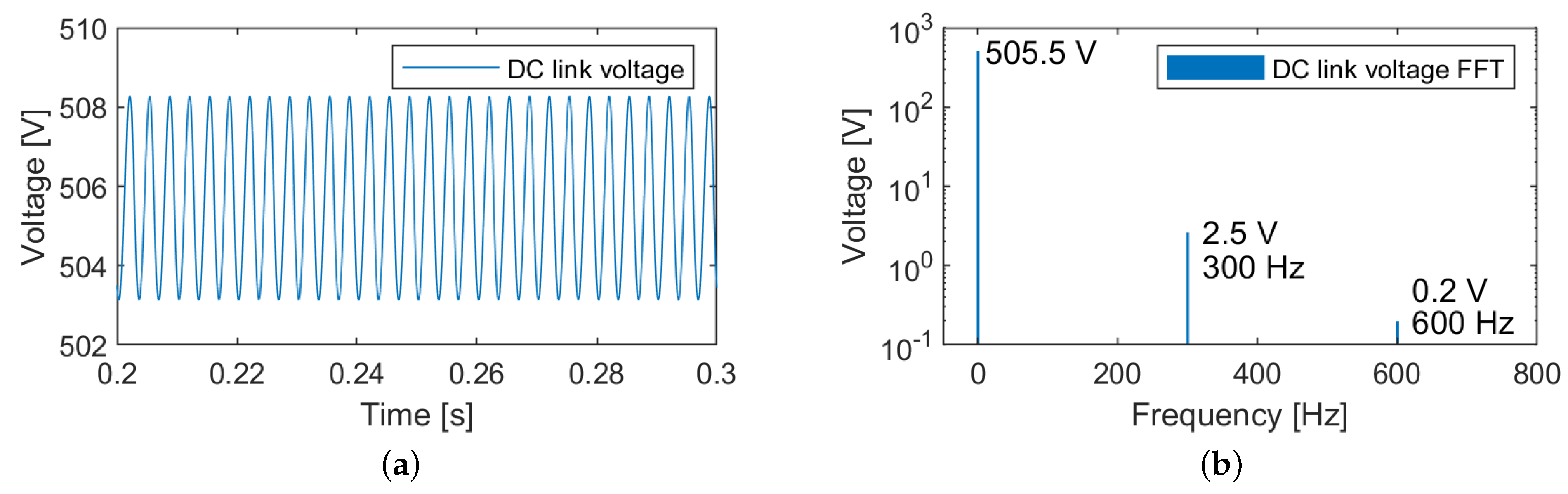
2.1. Three-Phase Passive Rectifier
- Three-phase two-level six-switch boost-type rectifier;
- Three-phase three-level neutral point clamped converter;
- Three-phase three-level T-type converter.
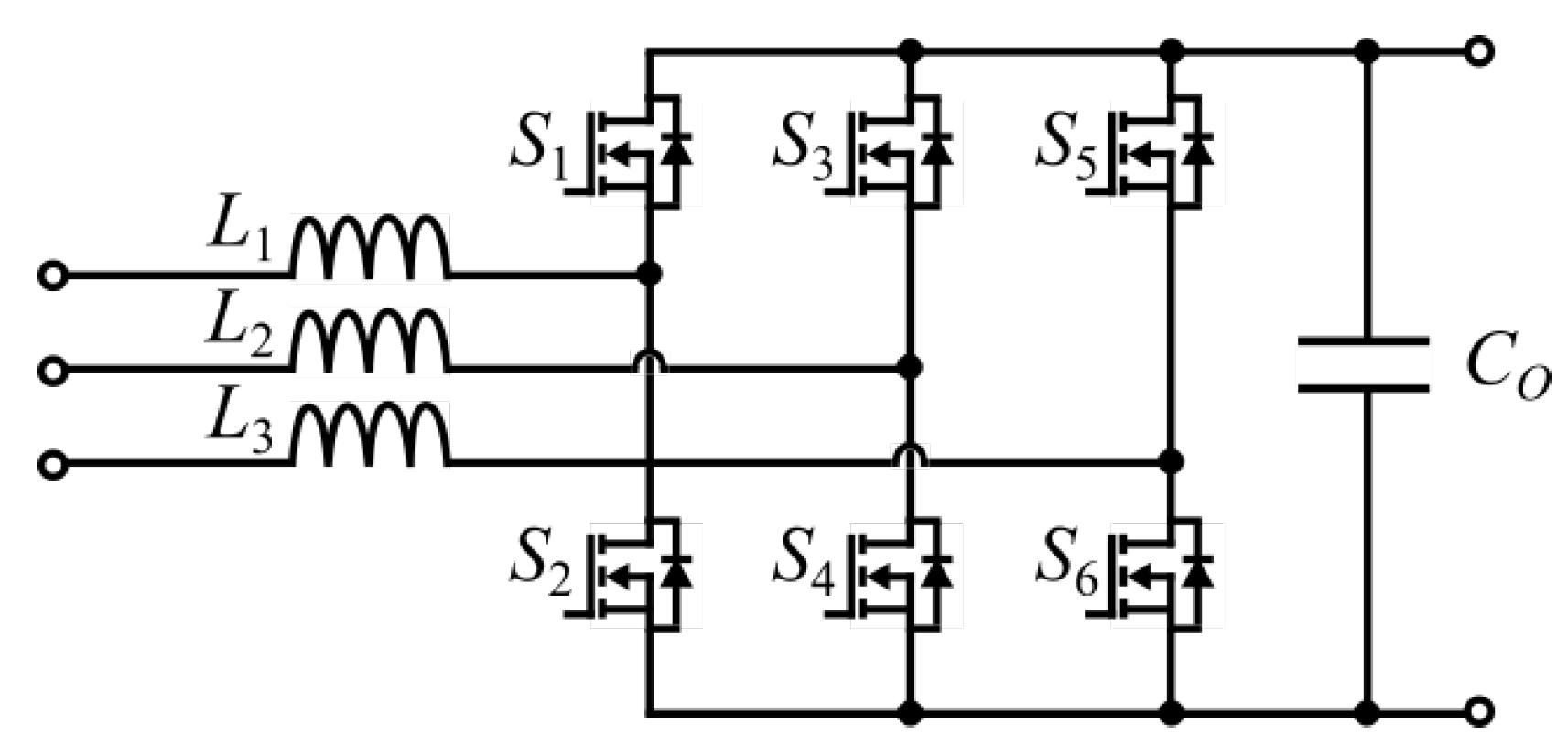
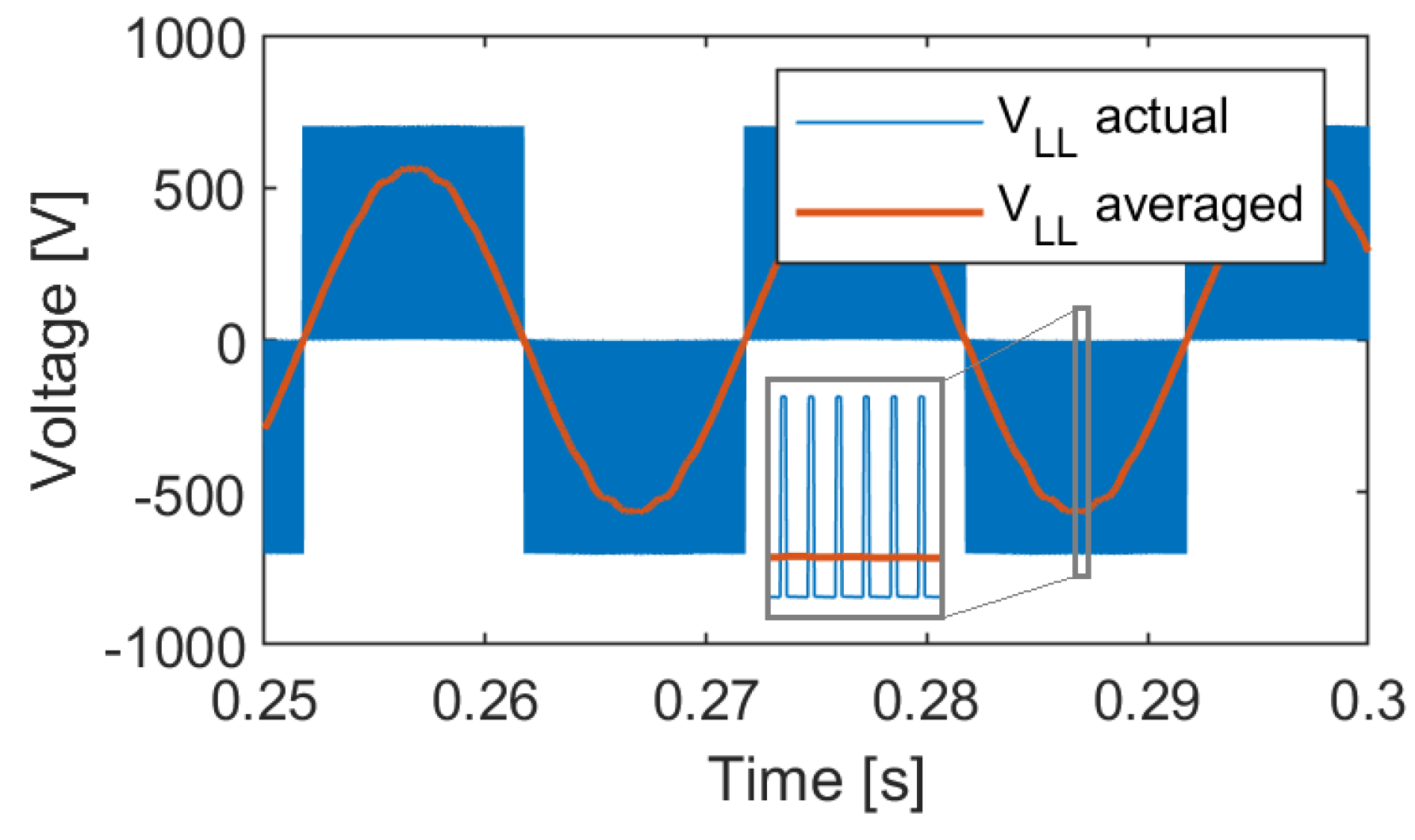
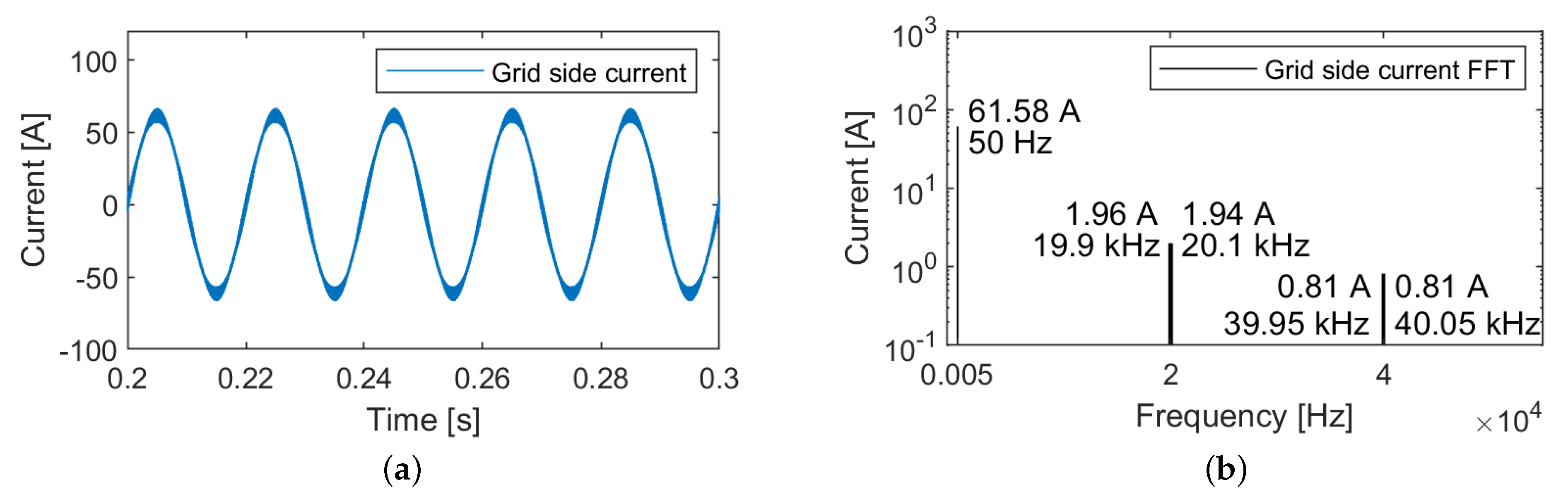
2.2. Three-Phase Two-Level Six-Switch Boost-Type Rectifier
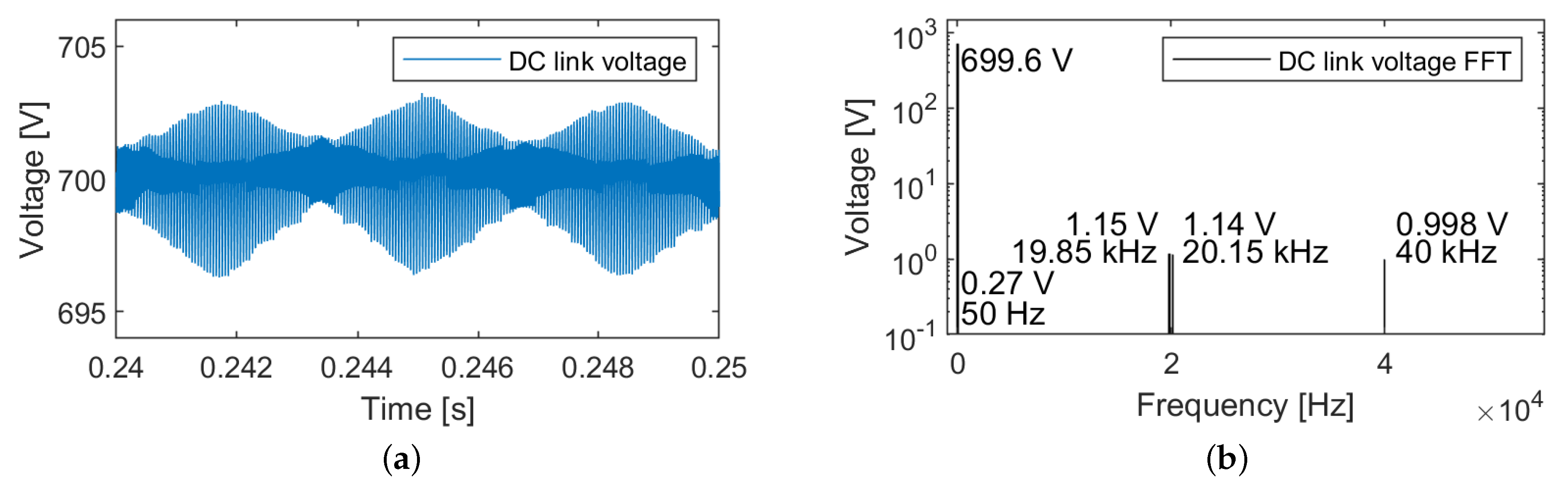
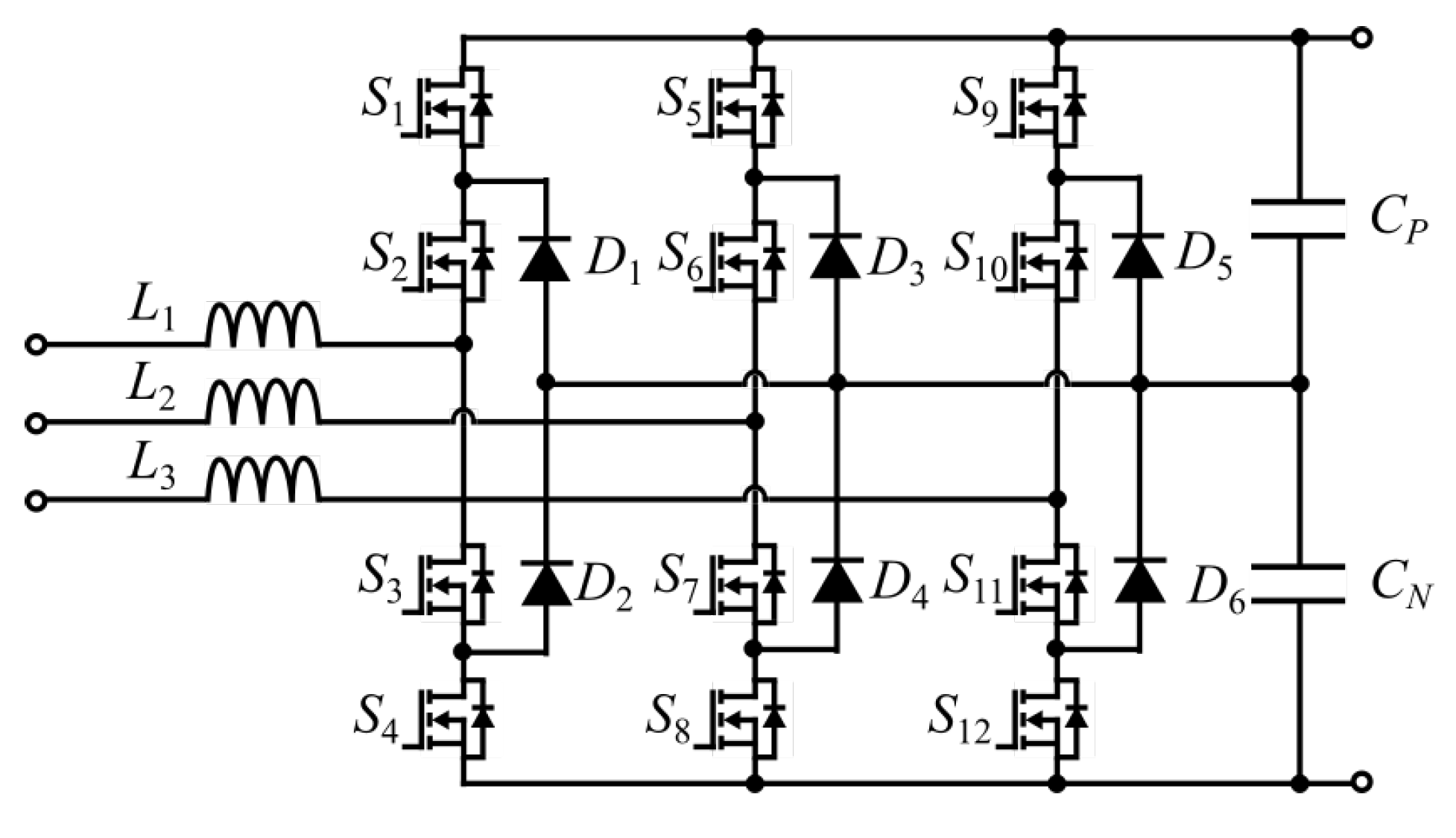
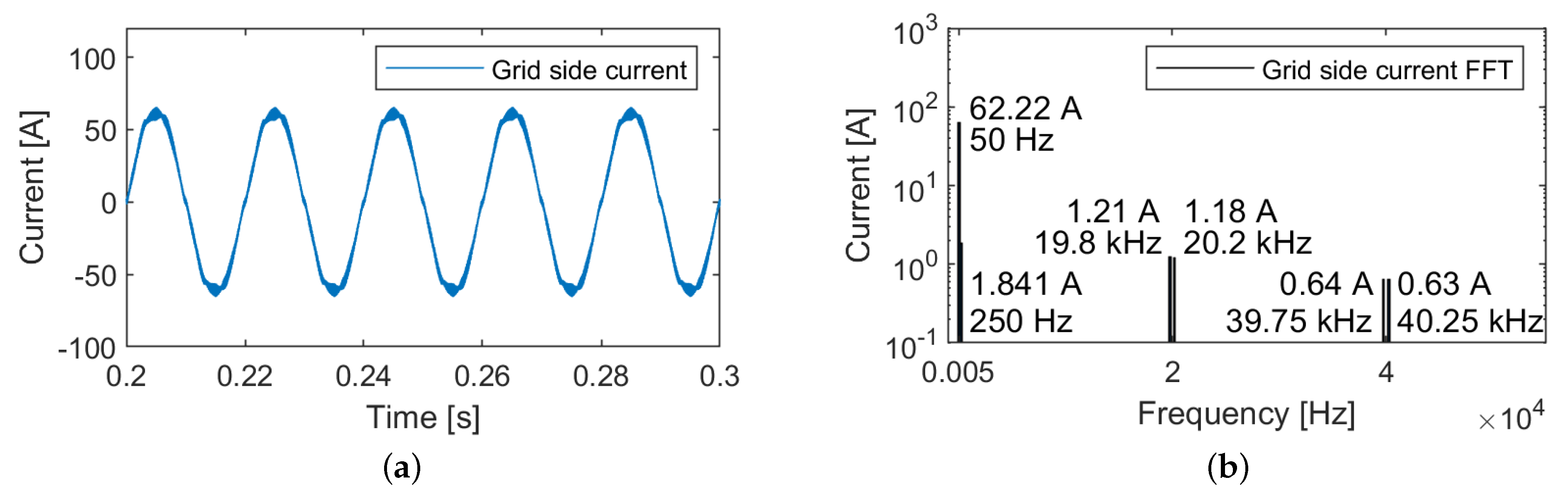
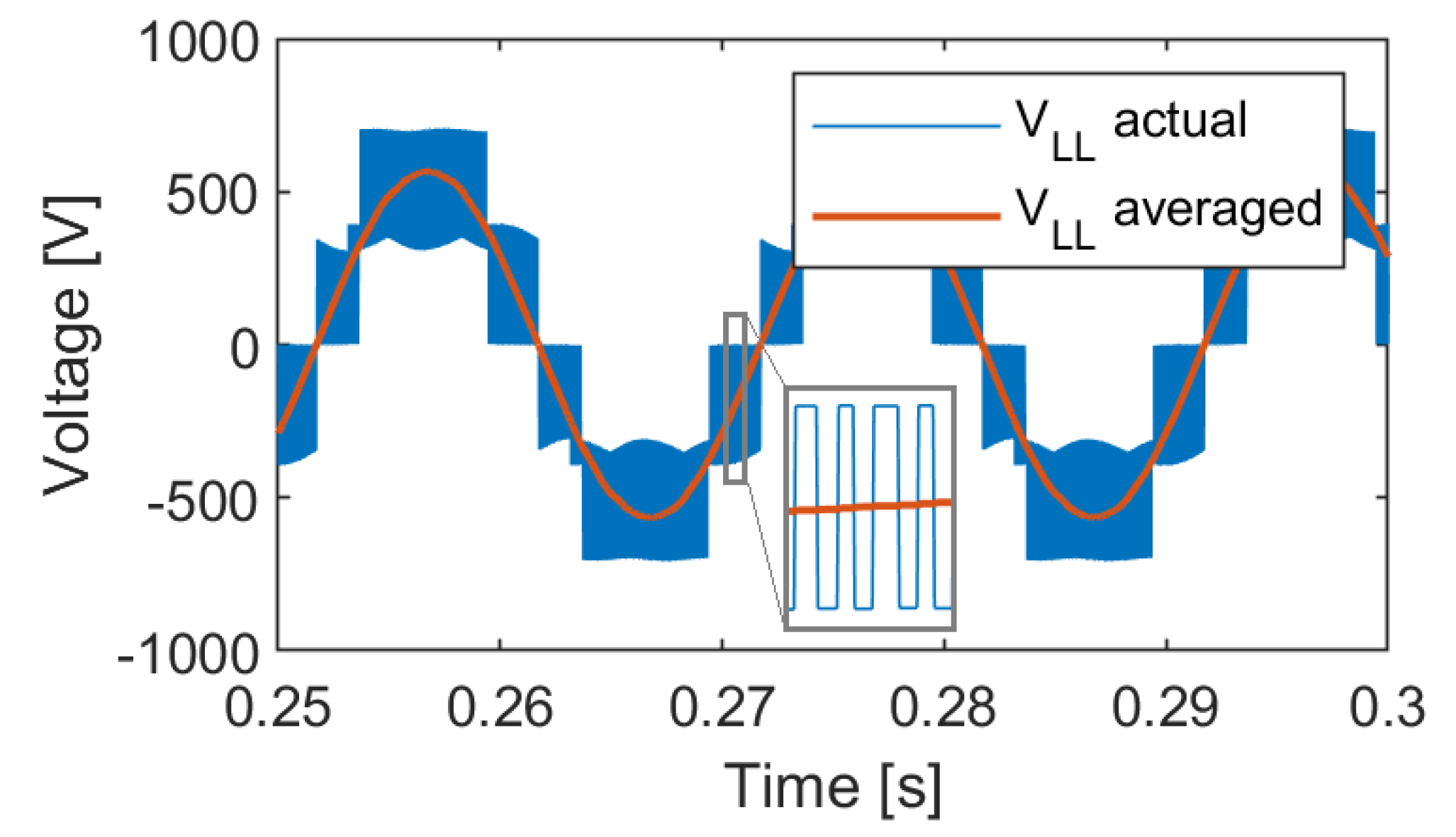
2.3. Three-Phase Three-Level Neutral Point Clamped Converter
2.4. Three-Phase Three-Level T-Type Converter
2.5. Comparison of Rectifier Topologies
3. Components of AFE Rectifiers
3.1. Power Semiconductor Selection
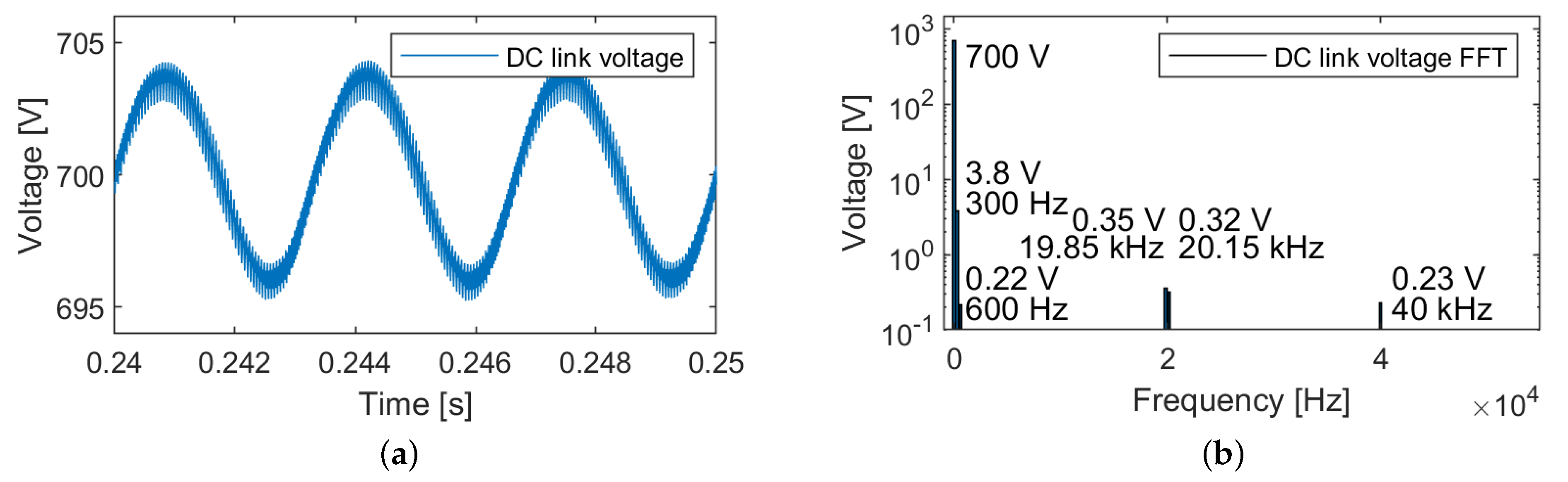
3.2. DC Link Capacitor Selection
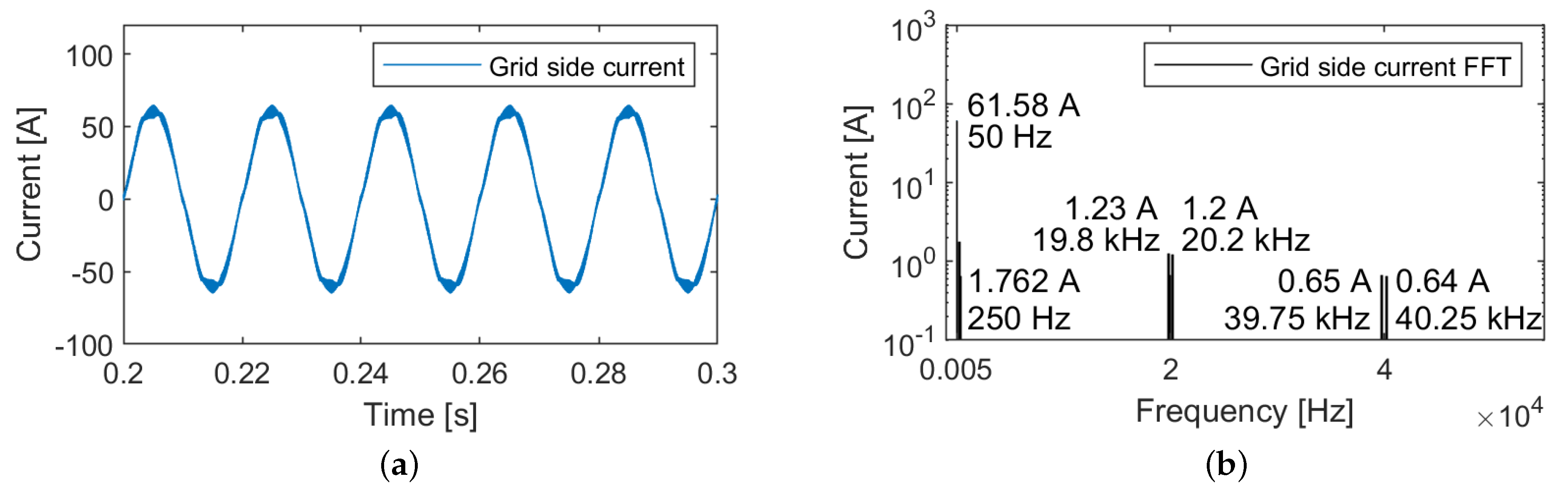
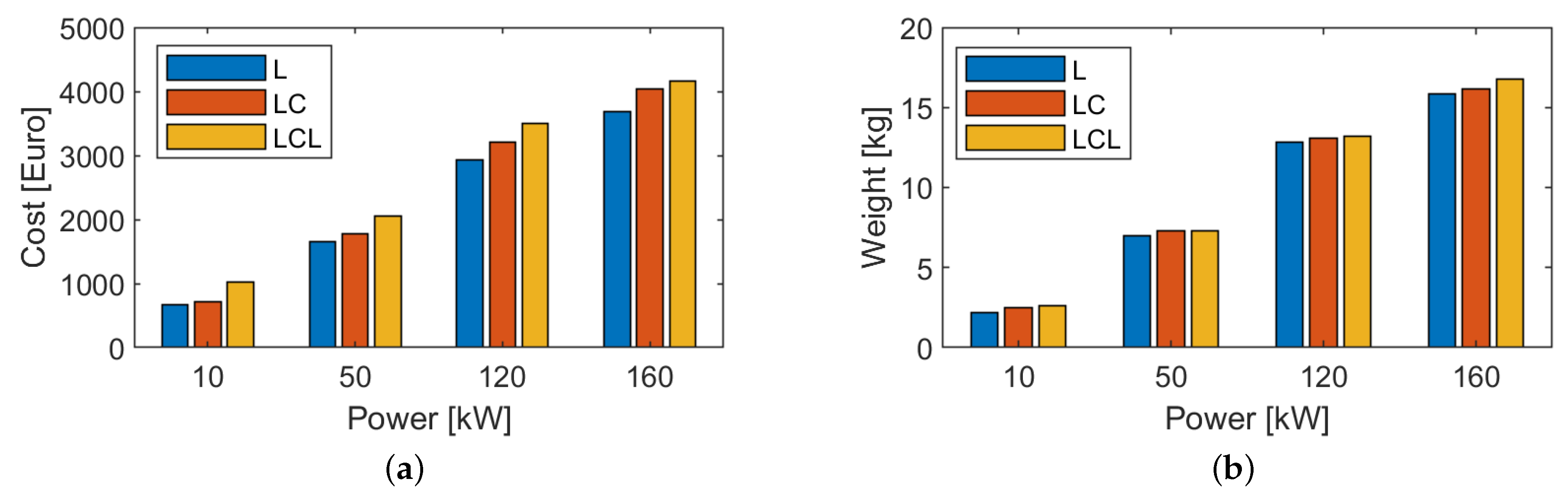
3.3. Grid Side Filters Selection
3.3.1. L Filter
3.3.2. LC Filter
3.3.3. LCL Filter
3.3.4. Comparison of Filter Topologies
3.3.5. Filter Inductor Component Selection
4. Control of a Single AFE
- Voltage Oriented Control (VOC) is a type of Linear Control with PI controllers.
- Direct Power Control (DPC) is classified under Non-linear Hysteresis Control since active and reactive power is controlled using a hysteresis controller with a lookup table.
- Optimal switching vector Model Predictive Control (MPC) is classified under Predictive Control.
- Hysteresis Current Control (HCC) is a type of Non-linear Hysteresis Control applied directly to phase currents.
4.1. Grid Synchronization
4.2. Voltage Oriented Control
4.3. Direct Power Control
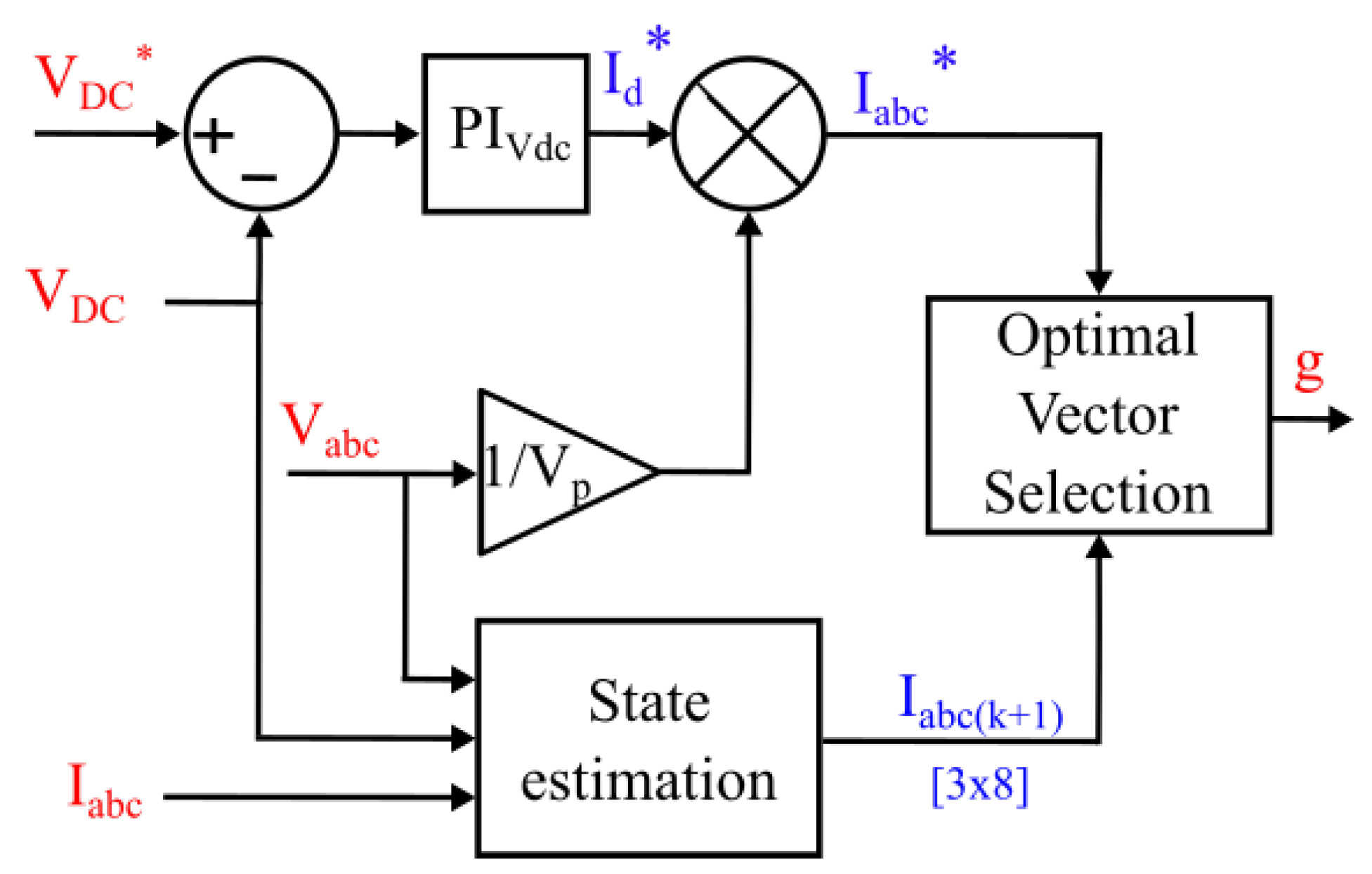
4.4. Model Predictive Control
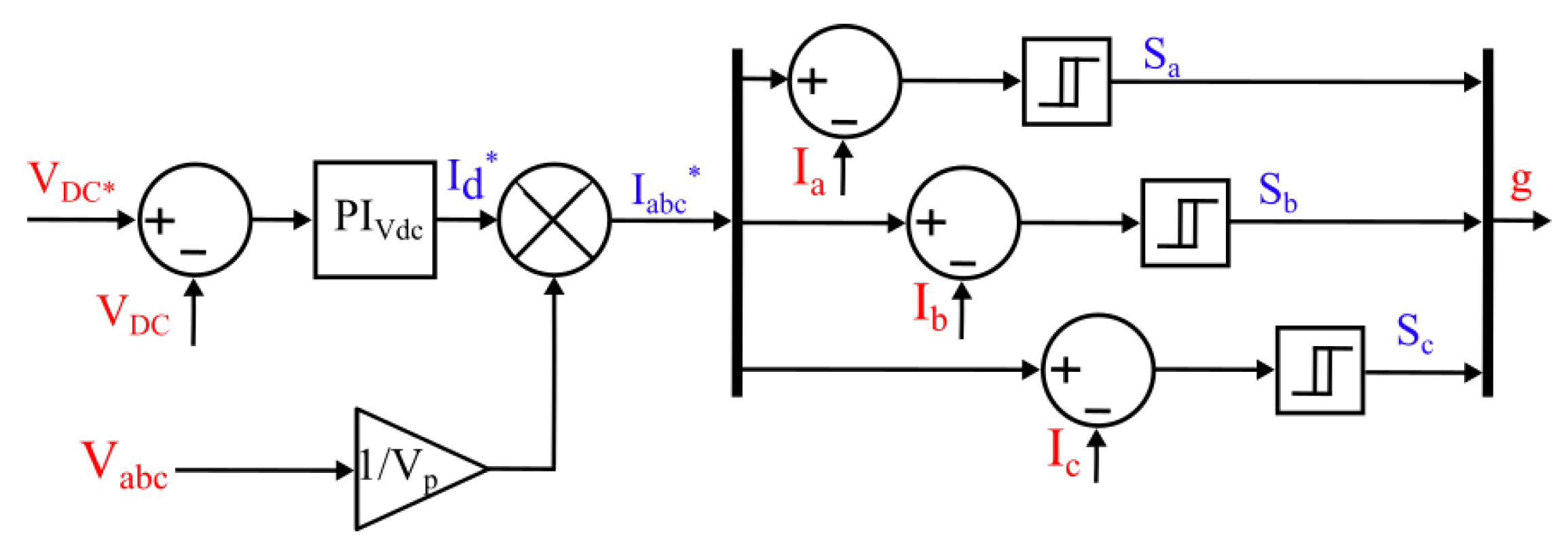
4.5. The Hysteresis Current Control
4.6. Modulation
4.6.1. Carrier-Based PWM
4.6.2. Space Vector PWM (SVM)
4.7. Comparison of Control Strategies
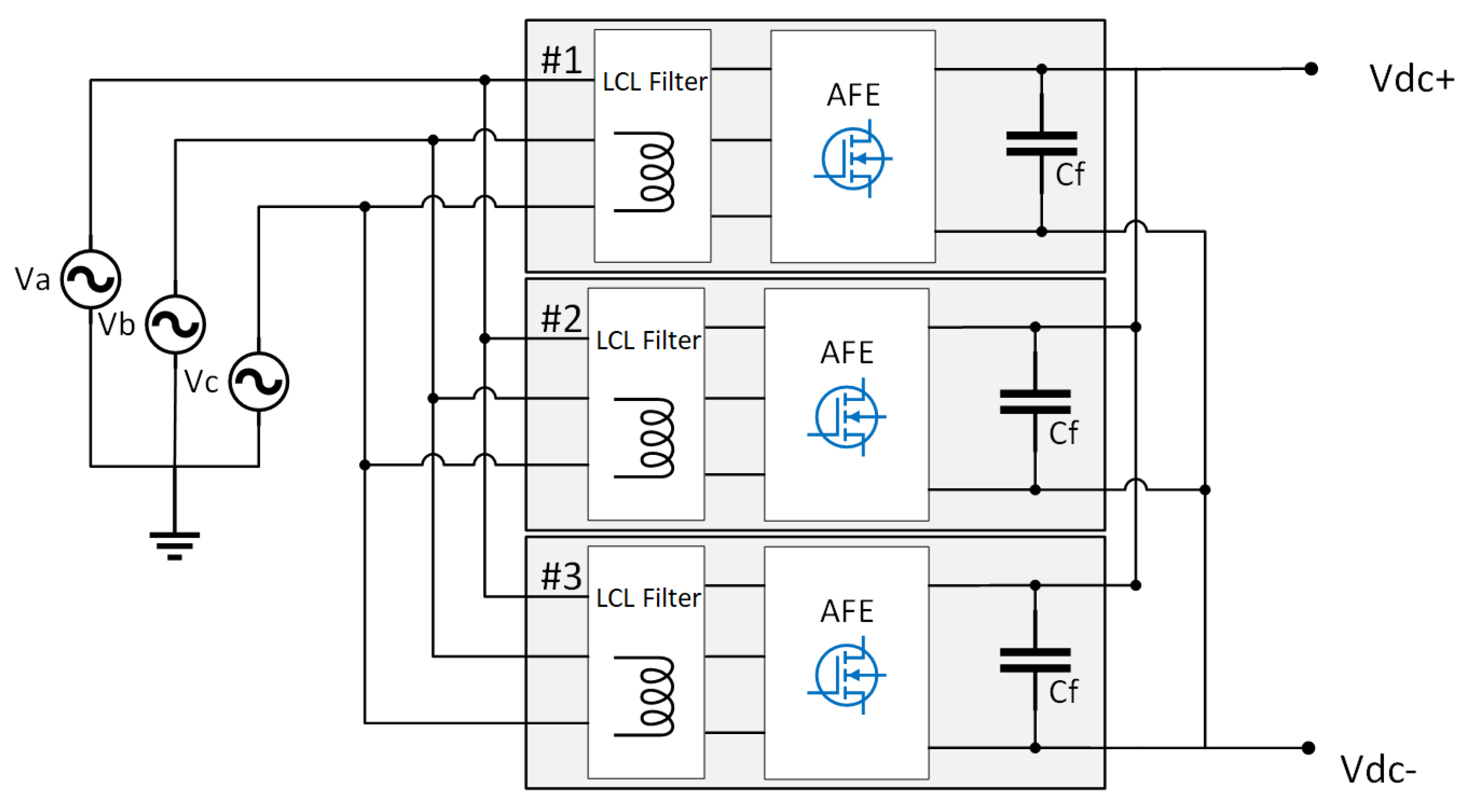
5. Modular AFE
5.1. Control of Parallel Converters
5.1.1. Circulating Currents
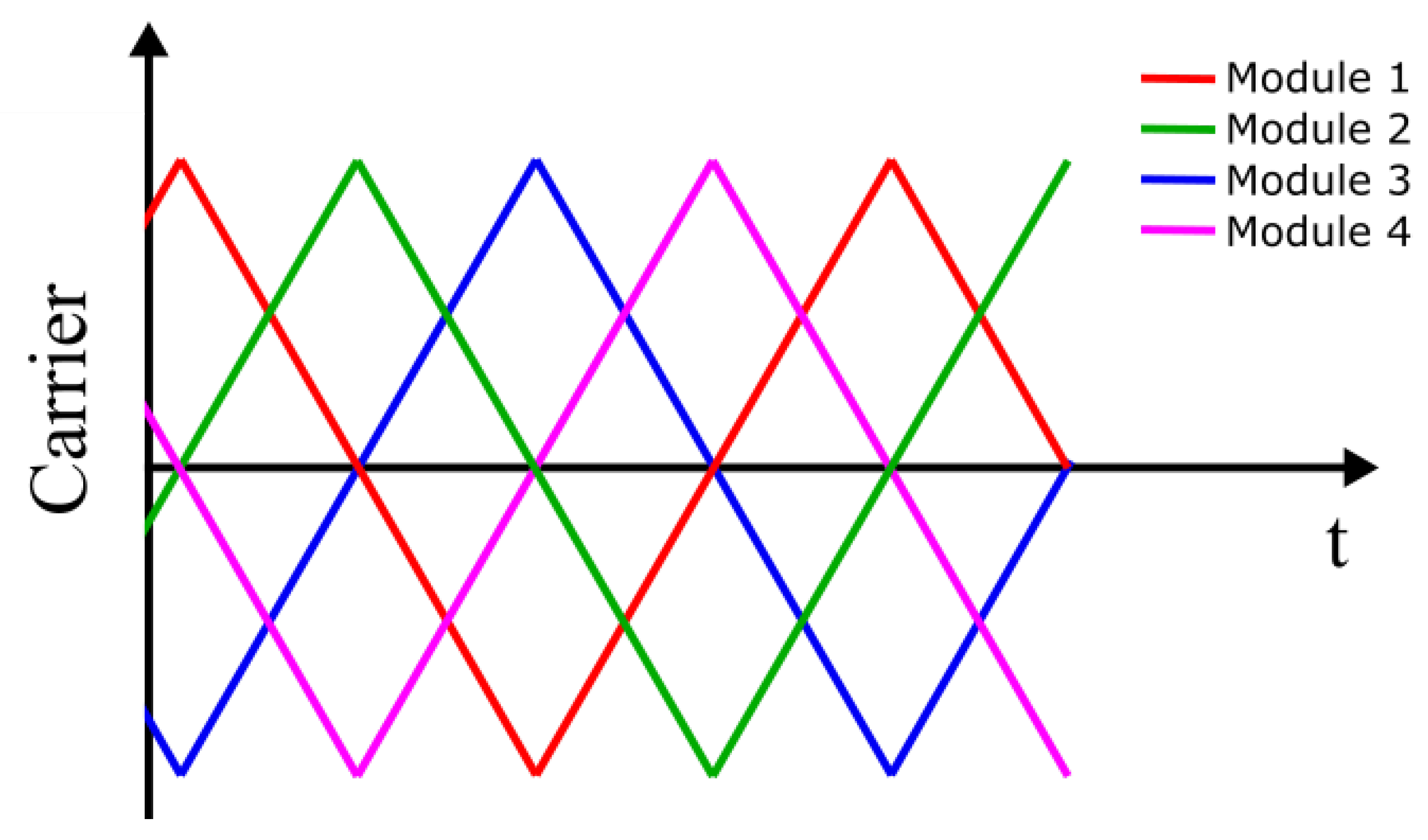
5.1.2. Interleaving
5.1.3. System Power Adapting
5.1.4. Failure Management
5.2. Centralized Control of Parallel Converters
5.3. Distributed Master-Slave
5.4. Distributed Masterless
6. Cooling System
6.1. Air Cooling
6.2. Liquid Cooling
7. Reliability
7.1. Component Level Reliability
7.1.1. Power Semiconductors Lifetime Model
7.1.2. Capacitor Lifetime Model
7.1.3. Reliability Analysis
7.2. System Level Reliability
8. Trends and Future Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- IEA. Global Electric Vehicle Stock by Region, 2010–2020; Technical Report; IEA: Paris, France, 2010.
- Electric Vehicle Charging Infrastructure Market Size, Share & Trends Analysis Report by Charger Type, by Connector, b Application, by Region, and Segment Forecasts, 2022–2030. Technical Report, Grand View Research. 2022. Available online: https://www.marketresearch.com/Grand-View-Research-v4060/Electric-Vehicle-Charging-Infrastructure-Size-31517658/ (accessed on 10 September 2022).
- Yilmaz, M.; Krein, P.T. Review of Battery Charger Topologies, Charging Power Levels, and Infrastructure for Plug-In Electric and Hybrid Vehicles. IEEE Trans. Power Electron. 2013, 28, 2151–2169. [Google Scholar] [CrossRef]
- Zamani, M.; Nagrial, M.; Rizk, J.; Hellany, A. Electric Vehicles Charging: Review of Current Status. In Proceedings of the 2018 Australasian Universities Power Engineering Conference (AUPEC), IEEE, Auckland, New Zealand, 27–30 November 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Jaman, S.; Chakraborty, S.; Tran, D.D.; Geury, T.; El Baghdadi, M.; Hegazy, O. Review on Integrated On-Board Charger-Traction Systems: V2G Topologies, Control Approaches, Standards and Power Density State-of-the-Art for Electric Vehicle. Energies 2022, 15, 5376. [Google Scholar] [CrossRef]
- Rasool, H.; Verbrugge, B.; Zhaksylyk, A.; Tran, T.M.; Baghdadi, M.E.; Geury, T.; Hegazy, O. Design Optimization and Electro-Thermal Modeling of an Off-Board Charging System for Electric Bus Applications. IEEE Access 2021, 9, 84501–84519. [Google Scholar] [CrossRef]
- Amanor-Boadu, J.M.; Guiseppi-Elie, A. Improved Performance of Li-ion Polymer Batteries Through Improved Pulse Charging Algorithm. Appl. Sci. 2020, 10, 895. [Google Scholar] [CrossRef] [Green Version]
- Safayatullah, M.; Elrais, M.T.; Ghosh, S.; Rezaii, R.; Batarseh, I. A Comprehensive Review of Power Converter Topologies and Control Methods for Electric Vehicle Fast Charging Applications. IEEE Access 2022, 10, 40753–40793. [Google Scholar] [CrossRef]
- Kolar, J.W.; Friedli, T. The Essence of Three-Phase PFC Rectifier Systems—Part I. IEEE Trans. Power Electron. 2013, 28, 176–198. [Google Scholar] [CrossRef]
- Friedli, T.; Hartmann, M.; Kolar, J.W. The Essence of Three-Phase PFC Rectifier Systems—Part II. IEEE Trans. Power Electron. 2014, 29, 543–560. [Google Scholar] [CrossRef]
- Athari, H.; Niroomand, M.; Ataei, M. Review and Classification of Control Systems in Grid-tied Inverters. Renew. Sustain. Energy Rev. 2017, 72, 1167–1176. [Google Scholar] [CrossRef]
- Tahir, S.; Wang, J.; Baloch, M.; Kaloi, G. Digital Control Techniques Based on Voltage Source Inverters in Renewable Energy Applications: A Review. Electronics 2018, 7, 18. [Google Scholar] [CrossRef] [Green Version]
- Malinowski, M.; Kazmierkowski, M.; Trzynadlowski, A. A comparative study of control techniques for PWM rectifiers in AC adjustable speed drives. IEEE Trans. Power Electron. 2003, 18, 1390–1396. [Google Scholar] [CrossRef]
- Zabetian-Hosseini, A.; Joos, G.; Boulet, B. Distributed Control Design for V2G in DC Fast Charging Stations. In Proceedings of the 2021 IEEE Energy Conversion Congress and Exposition (ECCE), IEEE, Vancouver, BC, Canada, 10–14 October 2021; pp. 655–661. [Google Scholar] [CrossRef]
- Chandler, S.; Gartner, J.; Jones, D. Integrating Electric Vehicles with Energy Storage and Grids: New Technology and Specific Capabilities Spur Numerous Applications. IEEE Electrif. Mag. 2018, 6, 38–43. [Google Scholar] [CrossRef]
- Krasselt, P.; Boßle, J.; Suriyah, M.; Leibfried, T. DC-Electric Vehicle Supply Equipment Operation Strategies for Enhanced Utility Grid Voltage Stability. World Electr. Veh. J. 2015, 7, 530–539. [Google Scholar] [CrossRef] [Green Version]
- Halbig, J. 15 kW Bidirectional Vienna PFC. In Proceedings of the APEC2020, New Orleans, LA, USA, 15–19 March 2020. [Google Scholar]
- Schweizer, M.; Kolar, J.W. Design and Implementation of a Highly Efficient Three-Level T-Type Converter for Low-Voltage Applications. IEEE Trans. Power Electron. 2013, 28, 899–907. [Google Scholar] [CrossRef]
- Qian, H.; Xu, J.; Hu, Y.; Xie, S. Design and Comparison of High-Order Output Filters for Grid-Connected Converters with Low Switching Frequency. In Proceedings of the 2021 IEEE 16th Conference on Industrial Electronics and Applications (ICIEA), IEEE, Chengdu, China, 1–4 August 2021; pp. 894–899. [Google Scholar] [CrossRef]
- Yagnik, U.P.; Solanki, M.D. Comparison of L, LC & LCL filter for grid connected converter. In Proceedings of the 2017 International Conference on Trends in Electronics and Informatics (ICEI), IEEE, Tirunelveli, India, 11–12 May 2017; pp. 455–458. [Google Scholar] [CrossRef]
- Su, G.J. Comparison of Si, SiC, and GaN based Isolation Converters for Onboard Charger Applications. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), IEEE, Portland, OR, USA, 23–27 September 2018; pp. 1233–1239. [Google Scholar] [CrossRef]
- Gu, X.; Shui, Q.; Myles, C.; Gundersen, M. Comparison of Si, GaAs, SiC and GaN FET-type switches for pulsed power applications. In Proceedings of the Digest of Technical Papers, PPC-2003, 14th IEEE International Pulsed Power Conference (IEEE Cat. No.03CH37472), IEEE, Dallas, TX, USA, 15–18 June 2003; pp. 362–365. [Google Scholar] [CrossRef] [Green Version]
- Liu, G.; Bai, K.H.; McAmmond, M.; Brown, A.; Johnson, P.M.; Taylor, A.; Lu, J. Comparison of SiC MOSFETs and GaN HEMTs based high-efficiency high-power-density 7.2 kWEV battery chargers. In Proceedings of the 2017 IEEE 5th Workshop on Wide Bandgap Power Devices and Applications (WiPDA), IEEE, Albuquerque, NM, USA, 30 October–1 November 2017; pp. 391–397. [Google Scholar] [CrossRef]
- Abramushkina, E.; Zhaksylyk, A.; Geury, T.; El Baghdadi, M.; Hegazy, O. A Thorough Review of Cooling Concepts and Thermal Management Techniques for Automotive WBG Inverters: Topology, Technology and Integration Level. Energies 2021, 14, 4981. [Google Scholar] [CrossRef]
- Zhang, D.; Guacci, M.; Haider, M.; Bortis, D.; Kolar, J.W.; Everts, J. Three-Phase Bidirectional Buck-Boost Current DC-Link EV Battery Charger Featuring a Wide Output Voltage Range of 200 to 1000 V. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), IEEE, Detroit, MI, USA, 11–15 October 2020; pp. 4555–4562. [Google Scholar] [CrossRef]
- Liu, Z.; Li, B.; Lee, F.C.; Li, Q. High-Efficiency High-Density Critical Mode Rectifier/Inverter for WBG-Device-Based On-Board Charger. IEEE Trans. Ind. Electron. 2017, 64, 9114–9123. [Google Scholar] [CrossRef]
- Flack, T.J.; Pushpakaran, B.N.; Bayne, S.B. GaN Technology for Power Electronic Applications: A Review. J. Electron. Mater. 2016, 45, 2673–2682. [Google Scholar] [CrossRef]
- Wide Bandgap Semiconductors (SiC/GaN). Available online: https://www.infineon.com/cms/en/product/technology/wide-bandgap-semiconductors-sic-gan/ (accessed on 23 October 2022).
- She, X.; Huang, A.Q.; Lucia, O.; Ozpineci, B. Review of Silicon Carbide Power Devices and Their Applications. IEEE Trans. Ind. Electron. 2017, 64, 8193–8205. [Google Scholar] [CrossRef]
- Sen, S.; Zhang, L.; Chen, T.; Zhang, J.; Huang, A.Q. Three-phase Medium Voltage DC Fast Charger based on Single-stage Soft-switching Topology. In Proceedings of the 2018 IEEE Transportation Electrification Conference and Expo (ITEC), IEEE, Long Beach, CA, USA, 13–15 June 2018; pp. 1123–1128. [Google Scholar] [CrossRef]
- Srdic, S.; Zhang, C.; Liang, X.; Yu, W.; Lukic, S. A SiC-based power converter module for medium-voltage fast charger for plug-in electric vehicles. In Proceedings of the 2016 IEEE Applied Power Electronics Conference and Exposition (APEC), IEEE, Long Beach, CA, USA, 20–24 March 2016; pp. 2714–2719. [Google Scholar] [CrossRef]
- Wang, H.; Blaabjerg, F. Reliability of Capacitors for DC-Link Applications in Power Electronic Converters—An Overview. IEEE Trans. Ind. Appl. 2014, 50, 3569–3578. [Google Scholar] [CrossRef] [Green Version]
- Das, J. Harmonic Distortion Limits According to Standards. In Power System Harmonics and Passive Filter Designs; John Wiley & Sons, Inc: Hoboken, NJ, USA, 2015; pp. 427–451. [Google Scholar] [CrossRef]
- Das, J.C. Harmonic Reduction at the Source. In Power System Harmonics and Passive Filter Designs; Wiley and Sons: Hoboken, NJ, USA, 2015; pp. 229–279. [Google Scholar] [CrossRef]
- Sanjuan, S. Voltage Oriented Control of Three-Phase Boost PWM Converters. Ph.D. Thesis, Chalmers University of Technology, Göteborg, Sweeden, 2010. [Google Scholar]
- Kazmierkowski, M.; Krishnan, R.; Blaabjerg, F. Control in Power Electronics; Elsevier: Amsterdam, The Netherland, 2002. [Google Scholar] [CrossRef]
- Hojabri, M.; Hojabri, M. Design, Application and Comparison of Passive Filters for Three-Phase Grid-Connected Renewable Energy Systems. ARPN J. Eng. Appl. Sci. 2015, 10, 10691–10697. [Google Scholar]
- Araujo, S.V.; Engler, A.; Sahan, B.; Antunes, F.L.M. LCL filter design for grid-connected NPC inverters in offshore wind turbines. In Proceedings of the 2007 7th Internatonal Conference on Power Electronics, IEEE, Daegu, Republic of Korea, 22–26 October 2007; pp. 1133–1138. [Google Scholar] [CrossRef]
- IEEE. 519-2014—IEEE Recommended Practice and Requirements for Harmonic Control in Electric Power Systems; IEEE Std 519-2014 (Revision of IEEE Std 519-1992); IEEE: Piscataway, NJ, USA, 2014; pp. 1–29. [Google Scholar] [CrossRef]
- Całus, D. Analysis of the Thermal Processes in an Electromagnetic Mill. Energies 2022, 15, 7899. [Google Scholar] [CrossRef]
- Liu, Y.; See, K.Y.; Yin, S.; Simanjorang, R.; Tong, C.F.; Nawawi, A.; Lai, J.S.J. LCL Filter Design of a 50-kW 60-kHz SiC Inverter with Size and Thermal Considerations for Aerospace Applications. IEEE Trans. Ind. Electron. 2017, 64, 8321–8333. [Google Scholar] [CrossRef]
- Kazmierkowski, M.; Malesani, L. Current control techniques for three-phase voltage-source PWM converters: A survey. IEEE Trans. Ind. Electron. 1998, 45, 691–703. [Google Scholar] [CrossRef]
- Krause, P.; Wasynczuk, O.; Sudhoff, S.; Pekarek, S. Reference-Frame Theory. In Analysis of Electric Machinery and Drive Systems; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2013; Chapter 3; pp. 86–120. [Google Scholar] [CrossRef]
- Sridharan, K.; Babu, B.C. A Novel Adaptive Bandpass Filter Based PLL for Grid Synchronization Under Distorted Grid Conditions. IEEE Trans. Instrum. Meas. 2022, 71, 9003111. [Google Scholar] [CrossRef]
- Golestan, S.; Guerrero, J.M.; Vasquez, J.C. Three-Phase PLLs: A Review of Recent Advances. IEEE Trans. Power Electron. 2017, 32, 1894–1907. [Google Scholar] [CrossRef] [Green Version]
- Zhu, D.; Zhou, S.; Zou, X.; Kang, Y. Improved Design of PLL Controller for <i>LCL</i> -Type Grid-Connected Converter in Weak Grid. IEEE Trans. Power Electron. 2020, 35, 4715–4727. [Google Scholar] [CrossRef]
- Bouafia, A.; Gaubert, J.P.; Krim, F.; Chaoui, A. Unity Power Factor Operation of Three-Phase PWM Rectifier Based on Direct Power Control. In Proceedings of the EUROCON 2007—The International Conference on “Computer as a Tool”, IEEE, Warsaw, Poland, 9–12 September 2007; pp. 1518–1523. [Google Scholar] [CrossRef]
- Gopalan, S. A comparative study of control techniques for three phase PWM rectifier. In Proceedings of the 2016 10th International Conference on Intelligent Systems and Control (ISCO), IEEE, Coimbatore, India, 7–8 January 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Cano, J.M.; Jatskevich, J.; Norniella, J.G.; Davoudi, A.; Wang, X.; Martinez, J.A.; Mehrizi-Sani, A.; Saeedifard, M.; Aliprantis, D.C. Dynamic Average-Value Modeling of Direct Power-Controlled Active Front-End Rectifiers. IEEE Trans. Power Deliv. 2014, 29, 2458–2466. [Google Scholar] [CrossRef]
- Vazquez, S.; Leon, J.I.; Franquelo, L.G.; Rodriguez, J.; Young, H.A.; Marquez, A.; Zanchetta, P. Model Predictive Control: A Review of Its Applications in Power Electronics. IEEE Ind. Electron. Mag. 2014, 8, 16–31. [Google Scholar] [CrossRef]
- Vazquez, S.; Sanchez, J.; Carrasco, J.; Leon, J.; Galvan, E. A Model-Based Direct Power Control for Three-Phase Power Converters. IEEE Trans. Ind. Electron. 2008, 55, 1647–1657. [Google Scholar] [CrossRef]
- Akter, M.P.; Mekhilef, S.; Tan, N.M.L.; Akagi, H. Model Predictive Control of Bidirectional AC-DC Converter for Energy Storage System. J. Electr. Eng. Technol. 2015, 10, 165–175. [Google Scholar] [CrossRef] [Green Version]
- Bartsch, A.G.; Negri, G.H.; Cavalca, M.S.; De Oliveira, J.; Nied, A. Cost function tuning methodology for FCS-MPC applied to PMSM drives. In Proceedings of the 14th Brazilian Power Electronics Conference, COBEP 2017, Juiz de Fora, Brazil, 19–22 November 2017; Volume 2018. [Google Scholar] [CrossRef]
- Preindl, M.; Schaltz, E.; Thogersen, P. Switching Frequency Reduction Using Model Predictive Direct Current Control for High-Power Voltage Source Inverters. IEEE Trans. Ind. Electron. 2011, 58, 2826–2835. [Google Scholar] [CrossRef]
- Ali, S.U.; Waqar, A.; Elavarasan, R.M.; Pugazhendhi, R.; Rahman, M.M.; Islam, M.R.; Aamir, M. Model Predictive Control for three phase rectifier with grid connected and standalone mode of operation. In Proceedings of the 2021 31st Australasian Universities Power Engineering Conference (AUPEC), IEEE, Perth, Australia, 26–30 September 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Jun, E.S.; Kim, J.C.; Kwak, S. Model Predictive Virtual Flux Control Method for Three-phase AFE Rectifiers Robust Against Supply Harmonics and Unbalance. In Proceedings of the 2019 10th International Conference on Power Electronics and ECCE Asia (ICPE 2019—ECCE Asia), IEEE, Busan, Republic of Korea, 27–31 May 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Vazquez, S.; Rodriguez, J.; Rivera, M.; Franquelo, L.G.; Norambuena, M. Model Predictive Control for Power Converters and Drives: Advances and Trends. IEEE Trans. Ind. Electron. 2017, 64, 935–947. [Google Scholar] [CrossRef] [Green Version]
- Leon, J.I.; Kouro, S.; Franquelo, L.G.; Rodriguez, J.; Wu, B. The Essential Role and the Continuous Evolution of Modulation Techniques for Voltage-Source Inverters in the Past, Present, and Future Power Electronics. IEEE Trans. Ind. Electron. 2016, 63, 2688–2701. [Google Scholar] [CrossRef]
- Suhara, E.M.; Nandakumar, M. Analysis of hysteresis current control techniques for three phase PWM rectifiers. In Proceedings of the 2015 IEEE International Conference on Signal Processing, Informatics, Communication and Energy Systems (SPICES), IEEE, Kozhikode, India, 19–21 February 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Malinowski, M.; Jasinski, M.; Kazmierkowski, M. Simple Direct Power Control of Three-Phase PWM Rectifier Using Space-Vector Modulation (DPC-SVM). IEEE Trans. Ind. Electron. 2004, 51, 447–454. [Google Scholar] [CrossRef]
- CortÉs, P.; RodrÍguez, J.; Antoniewicz, P.; Kazmierkowski, M. Direct Power Control of an AFE Using Predictive Control. IEEE Trans. Power Electron. 2008, 23, 2516–2523. [Google Scholar] [CrossRef]
- Eskandari-Torbati, H.; Arab Khaburi, D.; Eskandari-Torbati, V. Virtual flux based Direct Power Control (DPC) of three phase PWM rectifier using Model Predictive Control (MPC) and Space Vector Modulation (SVM). In Proceedings of the The 5th Annual International Power Electronics, Drive Systems and Technologies Conference (PEDSTC 2014), IEEE, Tehran, Iran, 5–6 February 2014; pp. 242–248. [Google Scholar] [CrossRef]
- Jiang, Y.s.; Zhao, H.m.; Guo, D. Direct Power Control of Three Phase PWM Rectifier Using Model Predictive Control. In Proceedings of the 2015 3rd International Conference on Computer and Computing Science (COMCOMS), IEEE, Hanoi, Vietnam, 22–24 October 2015; pp. 45–48. [Google Scholar] [CrossRef]
- Zhaksylyk, A.; Hasan, M.M.; Chakraborty, S.; Geury, T.; Hegazy, O. Effects of modularity on the performance and reliability of SiC MOSFET-based active front-end rectifiers in EV charging application. In Proceedings of the IECON 2022—48th Annual Conference of the IEEE Industrial Electronics Society, IEEE, Brussels, Belgium, 17–20 October 2022; pp. 1–7. [Google Scholar] [CrossRef]
- Chakraborty, S.; Hasan, M.M.; Paul, M.; Tran, D.D.; Geury, T.; Davari, P.; Blaabjerg, F.; El Baghdadi, M.; Hegazy, O. Real-Life Mission Profile Oriented Lifetime Estimation of a SiC Interleaved Bidirectional HV DC/DC Converter for Electric Vehicle Drivetrains. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 10, 5142–5167. [Google Scholar] [CrossRef]
- Gray, M.; Gao, Z.; Button, R. Distributed, Master-less Control of Modular DC-DC Converters. In Proceedings of the 2nd International Energy Conversion Engineering Conference, Rhodes, Greece, 16–19 August 2004; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2004. [Google Scholar] [CrossRef]
- Zhaksylyk, A.; Rasool, H.; Geury, T.; El Baghdadi, M.; Hegazy, O. Masterless Control of Parallel Modular Active front-end (AFE) Systems for Vehicles and Stationary Applications. In Proceedings of the 2020 Fifteenth International Conference on Ecological Vehicles and Renewable Energies (EVER), IEEE, Monte-Carlo, Monaco, 10–12 September 2020. [Google Scholar] [CrossRef]
- Salgado-Herrera, N.; Anaya-Lara, O.; Campos-Gaona, D.; Medina-Rios, A.; Tapia-Sanchez, R.; Rodriguez-Rodriguez, J. Active Front-End converter applied for the THD reduction in power systems. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), IEEE, Portland, OR, USA, 5–10 August 2018. [Google Scholar] [CrossRef] [Green Version]
- Xing, K.; Lee, F.; Borojevic, D.; Ye, Z.; Mazumder, S. Interleaved PWM with discontinuous space-vector modulation. IEEE Trans. Power Electron. 1999, 14. [Google Scholar] [CrossRef] [Green Version]
- Lyu, J.; Zhang, J.; Cai, X.; Wang, H.; Dai, J. Circulating current control strategy for parallel full-scale wind power converters. IET Power Electron. 2016, 9, 639–647. [Google Scholar] [CrossRef]
- Wang, J.; Hu, F.; Jiang, W.; Wang, W.; Gao, Y. Investigation of Zero Sequence Circulating Current Suppression for Parallel Three-Phase Grid-Connected Converters Without Communication. IEEE Trans. Ind. Electron. 2018, 65, 7620–7629. [Google Scholar] [CrossRef]
- Pan, C.T.; Liao, Y.H. Modeling and Coordinate Control of Circulating Currents in Parallel Three-Phase Boost Rectifiers. IEEE Trans. Ind. Electron. 2007, 54, 825–838. [Google Scholar] [CrossRef]
- Liccardo, F.; Marino, P.; Triggianese, M. An efficient connection between grid and wind farm by a Synchronous active front-end. In Proceedings of the International Symposium on Power Electronics, Electrical Drives, Automation and Motion, 2006, SPEEDAM 2006, IEEE, Taormina, Italy, 23–26 May 2006; pp. 1211–1216. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Z.; Xie, S.; Yang, C. A control strategy for paralleled bi-directional DC-DC converters used in energy storage systems. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), IEEE, Milwaukee, WI, USA, 18–22 September 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Pei, Y.; Jiang, G.; Yang, X.; Wang, Z. Auto-master-slave control technique of parallel inverters in distributed AC power systems and UPS. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference (IEEE Cat. No.04CH37551), IEEE, Aachen, Germany, 20–25 June 2004. [Google Scholar] [CrossRef]
- Meng, P.; Jian, Z.; Wenshan, L.; Youlong, W. The study and application of CAN communication of rectifier parallel operation control system. In Proceedings of the 2016 19th International Conference on Electrical Machines and Systems (ICEMS), Chiba, Japan, 13–16 November 2016; pp. 1–4. [Google Scholar]
- Zhang, Y.; Zane, R.; Maksimovic, D. Current Sharing in Digitally Controlled Masterless Multi-phase DC-DC Converters. In Proceedings of the IEEE 36th Conference on Power Electronics Specialists, IEEE, Dresden, Germany, 16 June 2005; pp. 2722–2728. [Google Scholar] [CrossRef]
- Zeng, Z.; Zhang, X.; Blaabjerg, F.; Chen, H.; Sun, T. Stepwise Design Methodology and Heterogeneous Integration Routine of Air-Cooled SiC Inverter for Electric Vehicle. IEEE Trans. Power Electron. 2020, 35, 3973–3988. [Google Scholar] [CrossRef]
- Zhou, R.; Jiao, Q.; Mao, Y. Natural convection cooled SiC-based LLC Resonant Converters in wide voltage range battery charger application. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), IEEE, Baltimore, MD, USA, 29 September–3 October 2019; pp. 1223–1230. [Google Scholar] [CrossRef]
- Manapadam Baskar, B.; Alok Pattnayak, R. Thermal Management of Air cooled portable Off board charger for a 3 wheeler cargo vehicle. In Proceedings of the 2020 IEEE 8th Electronics System-Integration Technology Conference (ESTC), IEEE, Tonsberg, Norway, 15–18 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Fang, X.; Li, J.; Zhang, X.; Chen, W.; Wang, W. Study on Temperature Control Design and High Protection of Charger. In Proceedings of the 2018 10th International Conference on Intelligent Human-Machine Systems and Cybernetics (IHMSC), IEEE, Hangzhou, China, 25–26 August 2018; pp. 216–219. [Google Scholar] [CrossRef]
- Wang, W.; Bian, H.; Zhang, X.; Fang, X.; Zhou, X. Protective Design of DC Charger Based on Forced Air Cooling. In Proceedings of the 2019 11th International Conference on Intelligent Human-Machine Systems and Cybernetics (IHMSC), IEEE, Hangzhou, China, 24–25 August 2019; pp. 308–311. [Google Scholar] [CrossRef]
- EVBox Troniq Modular Installation Manual. Technical Report, EVBox. Available online: https://www.manualslib.com/manual/2055544/Evbox-Troniq.html?page=4 (accessed on 10 January 2023).
- Blink. 180kW High Power DCFC Specifications Sheet. Technical Report. Available online: https://blinkcharging.com/wp-content/uploads/2022/07/UL_DCFAST_180kW_SpecSheet_March_2022.pdf (accessed on 10 January 2023).
- Bolte, S.; Henkenius, C.; Bocker, J.; Zibart, A.; Kenig, E.; Figge, H. Water-cooled on-board charger with optimized cooling channel. In Proceedings of the 2017 19th European Conference on Power Electronics and Applications (EPE’17 ECCE Europe), IEEE, Warsaw, Poland, 11–14 September 2017; pp. P.1–P.9. [Google Scholar] [CrossRef]
- New Slim Liquid Cooled Active Front End Drive Technology Increases Power Density by 100%; Technical Report; Emotron: Helsingborg, Sweden, 2022.
- Uddin, M.J.; Bahman, A.S.; Hagbign, S.; Carlson, O. Loss and Thermal Analysis of a 100 kW Converter Module Mounted on a Cold-Plate for Fast Charging Applications. In Proceedings of the 2019 21st European Conference on Power Electronics and Applications (EPE ’19 ECCE Europe), IEEE, Genova, Italy, 3–5 September 2019; pp. P.1–P.9. [Google Scholar] [CrossRef]
- European Standard 360 kw Liquid Cooled 500 A output Ultra Fast DC Charger for Electric Vehicle Charging. Technical Report, DekonPower. Available online: https://www.dekon-china.com/sale-20007478-european-standard-360kw-liquid-cooled-500a-output-ultra-fast-dc-charger-for-electric-vehicle-chargin.html (accessed on 11 January 2023).
- Blaabjerg, F.; Wang, H.; Vernica, I.; Liu, B.; Davari, P. Reliability of Power Electronic Systems for EV/HEV Applications. Proc. IEEE 2021, 109, 1060–1076. [Google Scholar] [CrossRef]
- Yang, S.; Bryant, A.; Mawby, P.; Xiang, D.; Ran, L.; Tavner, P. An industry-based survey of reliability in power electronic converters. In Proceedings of the 2009 IEEE Energy Conversion Congress and Exposition, IEEE, San Jose, CA, USA, 20–24 September 2009; pp. 3151–3157. [Google Scholar] [CrossRef]
- Peyghami, S.; Davari, P.; Wang, H.; Blaabjerg, F. The Impact of Topology and Mission Profile on the Reliability of Boost-type Converters in PV Applications. In Proceedings of the 2018 IEEE 19th Workshop on Control and Modeling for Power Electronics (COMPEL), IEEE, Padua, Italy, 25–28 June 2018; pp. 1–8. [Google Scholar] [CrossRef] [Green Version]
- Durand, C.; Klingler, M.; Coutellier, D.; Naceur, H. Power Cycling Reliability of Power Module: A Survey. IEEE Trans. Device Mater. Reliab. 2016, 16, 80–97. [Google Scholar] [CrossRef]
- Scheuermann, U.; Schmidt, R.; Newman, P. Power cycling testing with different load pulse durations. In Proceedings of the 7th IET International Conference on Power Electronics, Machines and Drives (PEMD 2014), Manchester, UK, 8–10 April 2014; Institution of Engineering and Technology: Hertfordshire, SG, USA, 2014; pp. 1–3. [Google Scholar] [CrossRef]
- Albertsen, A. Electrolytic Capacitor Lifetime Estimation; Technical Report; Jianghai Europe Electronic Components Gmb: Krefeld, Germany, 2018. [Google Scholar]
- Li, S.; Lu, S.; Mi, C.C. Revolution of Electric Vehicle Charging Technologies Accelerated by Wide Bandgap Devices. Proc. IEEE 2021, 109, 985–1003. [Google Scholar] [CrossRef]
- Husain, I.; Ozpineci, B.; Islam, M.S.; Gurpinar, E.; Su, G.J.; Yu, W.; Chowdhury, S.; Xue, L.; Rahman, D.; Sahu, R. Electric Drive Technology Trends, Challenges, and Opportunities for Future Electric Vehicles. Proc. IEEE 2021, 109, 1039–1059. [Google Scholar] [CrossRef]
- Kim, J.M.; Lee, J.; Eom, T.H.; Ryu, K.; Shin, M.H.; Won, C.Y. Modular EV Rapid Charger Design and Control Method. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), IEEE, Harbin, China, 11–14 August 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Mishima, T.; Mitsui, S. A Single-Stage High Frequency-link Modular Three-Phase Soft-Switching AC-DC Converter for EV Battery Charger. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), IEEE, Baltimore, MD, USA, 29 September–3 October 2019; pp. 2141–2147. [Google Scholar] [CrossRef]
- Schmenger, J.; Endres, S.; Zeltner, S.; Marz, M. A 22 kW on-board charger for automotive applications based on a modular design. In Proceedings of the 2014 IEEE Conference on Energy Conversion (CENCON), IEEE, Johor Bahru, Malaysia, 13–14 October 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Schmenger, J.; Zeltner, S.; Kramer, R.; Endres, S.; Marz, M. A 3.7 kW on-board charger based on modular circuit design. In Proceedings of the IECON 2015—41st Annual Conference of the IEEE Industrial Electronics Society, IEEE, Yokohama, Japan, 9–12 November 2015; pp. 001382–001387. [Google Scholar] [CrossRef]
- Drobnic, K.; Grandi, G.; Hammami, M.; Mandrioli, R.; Viatkin, A.; Vujacic, M. A Ripple-Free DC Output Current Fast Charger for Electric Vehicles Based on Grid-Tied Modular Three-Phase Interleaved Converters. In Proceedings of the 2018 International Symposium on Industrial Electronics (INDEL), IEEE, Banja Luka, Bosnia and Herzegovina, 1–3 November 2018; pp. 1–7. [Google Scholar] [CrossRef]





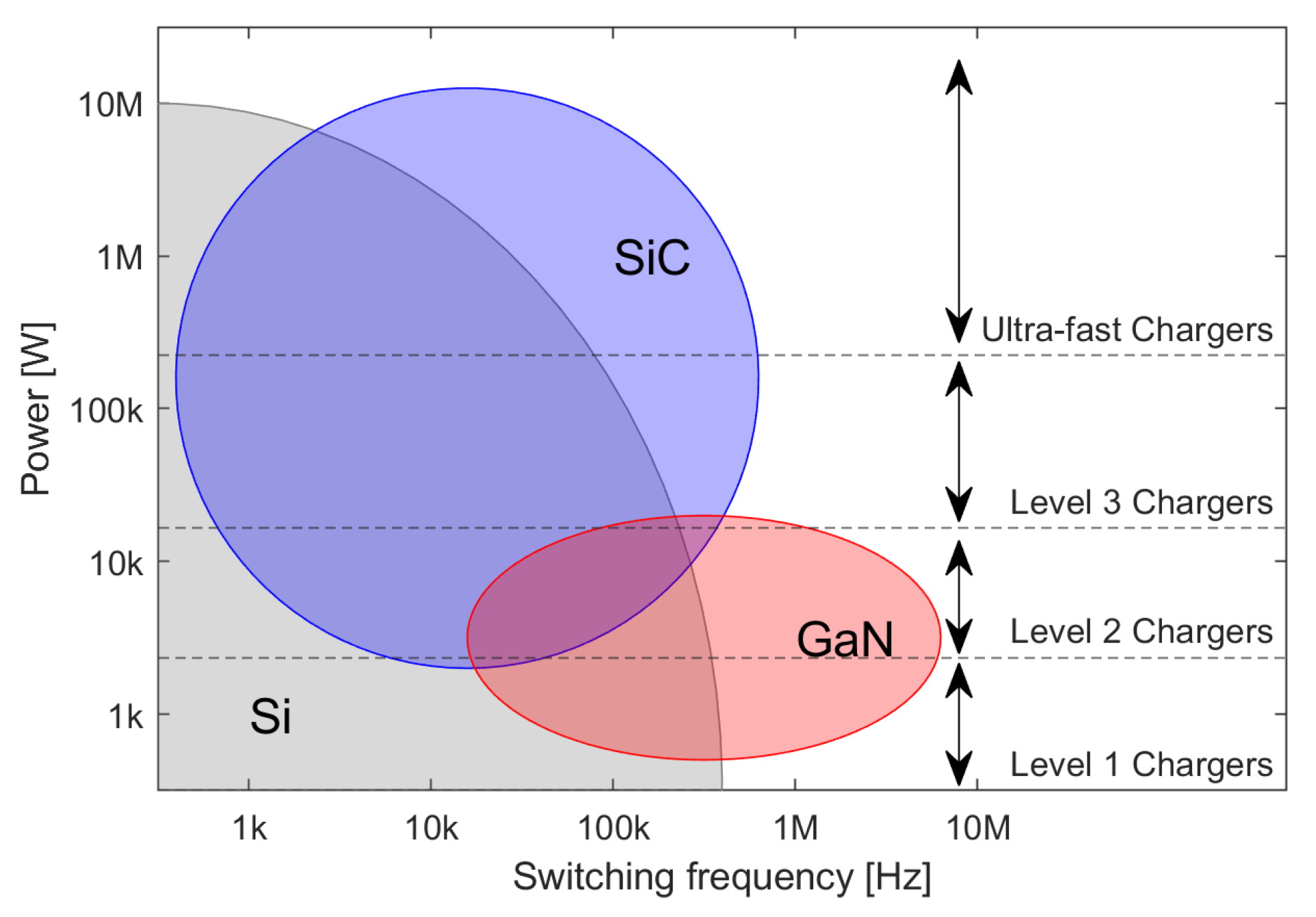









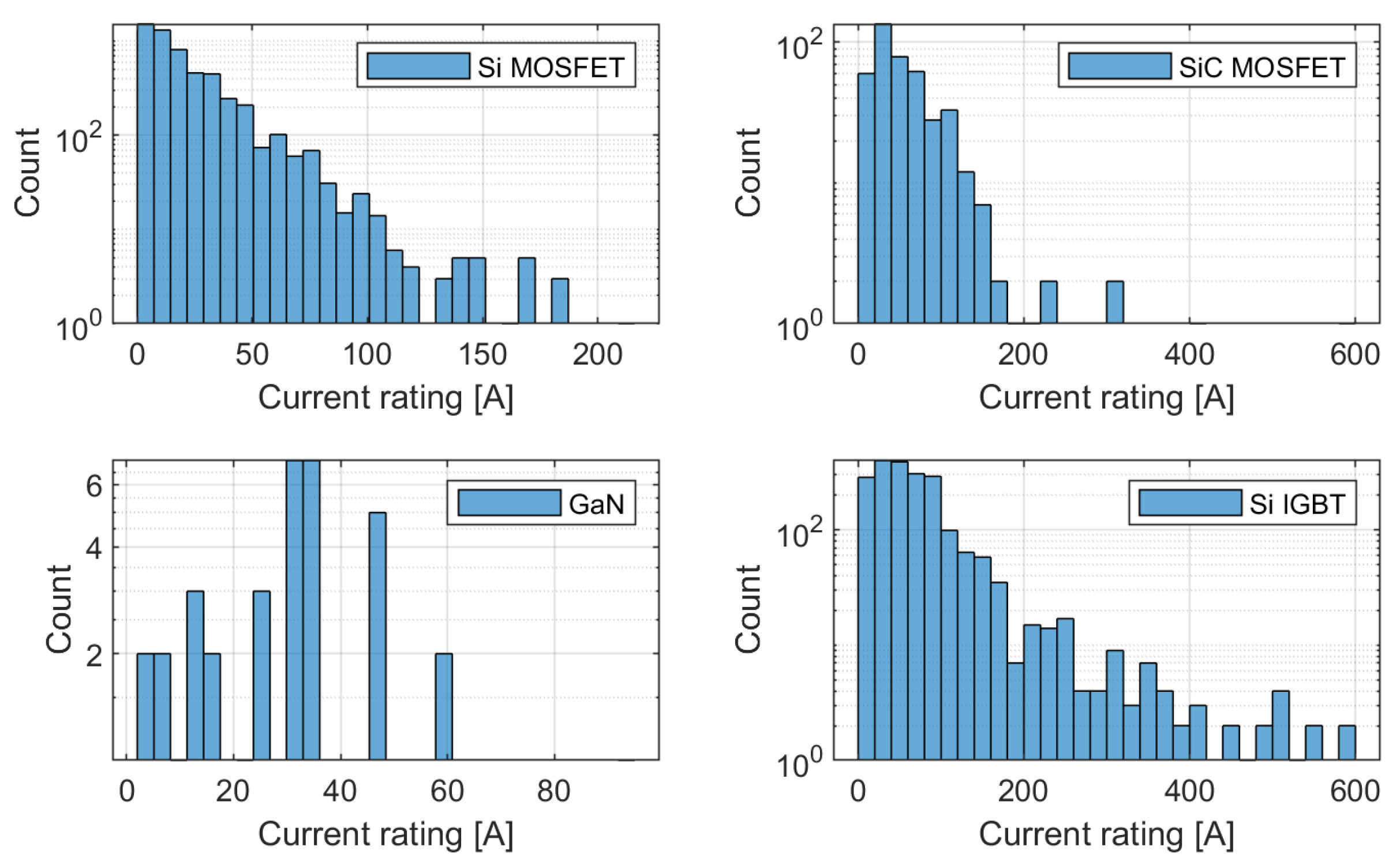


| EVC Level | Voltage Level (US/EU) | Grid Supply | Location | Power | Charging Time |
|---|---|---|---|---|---|
| Level 1 | 120/230 VAC | 1-phase | On-board | <3.7 kW | 8–16 h |
| Level 2 | 240/400 VAC | 1- or 3-phase | On- or Off-board | 3.7–22 kW | 2–6 h |
| Level 3 | 208–600 VDC | 3-phase | Off-board | 22–350 kW | 10–30 min |
| Ultra-fast charger | >800 VDC | 3-phase | Off-board | >400 kW | 5–15 min |
| Passive Rectifier | Six-Switch Rectifier | NPC Rectifier | T-Type Rectifier | |
|---|---|---|---|---|
| Bidirectional | No | Yes | Yes | Yes |
| Output DC voltage | 505.5 V | 700 V | 700 V | 700 V |
| Output DC current | 59.3 A | 42.8 A | 42.8 A | 42.8 A |
| Efficiency | 91% | 98.5% | 98.2% | 98.95% |
| Grid current THD | 30.9% | 5% | 5% | 5% |
| Power Factor | 0.87 | 0.997 | 0.997 | 0.997 |
| Number of active switches | 0 | 6 | 12 | 12 |
| Number of passive switches | 6 | 0 | 6 | 0 |
| Switch blocking voltage stress | 0.5 | (6), 0.5 (6) | ||
| DC link capacitance for 1% ripple | 3000 μF | 87 μF | 2 × 350 μF | 2 × 350 μF |
| DC link capacitor voltage rating | 0.5 | 0.5 | ||
| AC side inductance for 5% THD | 0.96 mH | 0.44 mH | 0.238 mH | 0.238 mH |
| Cost | Low | Average | High | High |
| Reliability | High | Higher stress on individual components, Lower component count | Lower stress on individual components, higher component count | Lower stress on individual components, higher component count |
| VOC | DPC | OSV-MPC | HCC | |
|---|---|---|---|---|
| AC Voltage sensors | 3(2) | 3(2) | 3(2) | 3(2) |
| DC Voltage sensors | 1 | 1 | 1 | 1 |
| AC Current sensors | 3 | 3 | 3 | 3 |
| PLL required | Yes | Optional | Optional | No |
| Modulator required | Yes | No | No | No |
| Switching frequency | Fixed | Variable | Variable | Variable |
| Parameter | Symbol | Value |
|---|---|---|
| Apparent Power | S | 22 kW |
| RMS Line-to-line voltage | 400 V | |
| DC link voltage setpoint | 700 V | |
| AC-side filter inductor | L | 0.6 mH |
| DC-side filter capacitor | C | 100 F |
| VOC | DPC | OSV-MPC | HCC | |
|---|---|---|---|---|
| Average switching frequency | 20 kHz | 17.5 kHz | 18.7 kHz | 20 kHz |
| Grid side current THD | 4.73% | 7.3% | 6.7% | 4.65% |
| Efficiency | 98.85% | 98.97% | 98.95% | 98.92% |
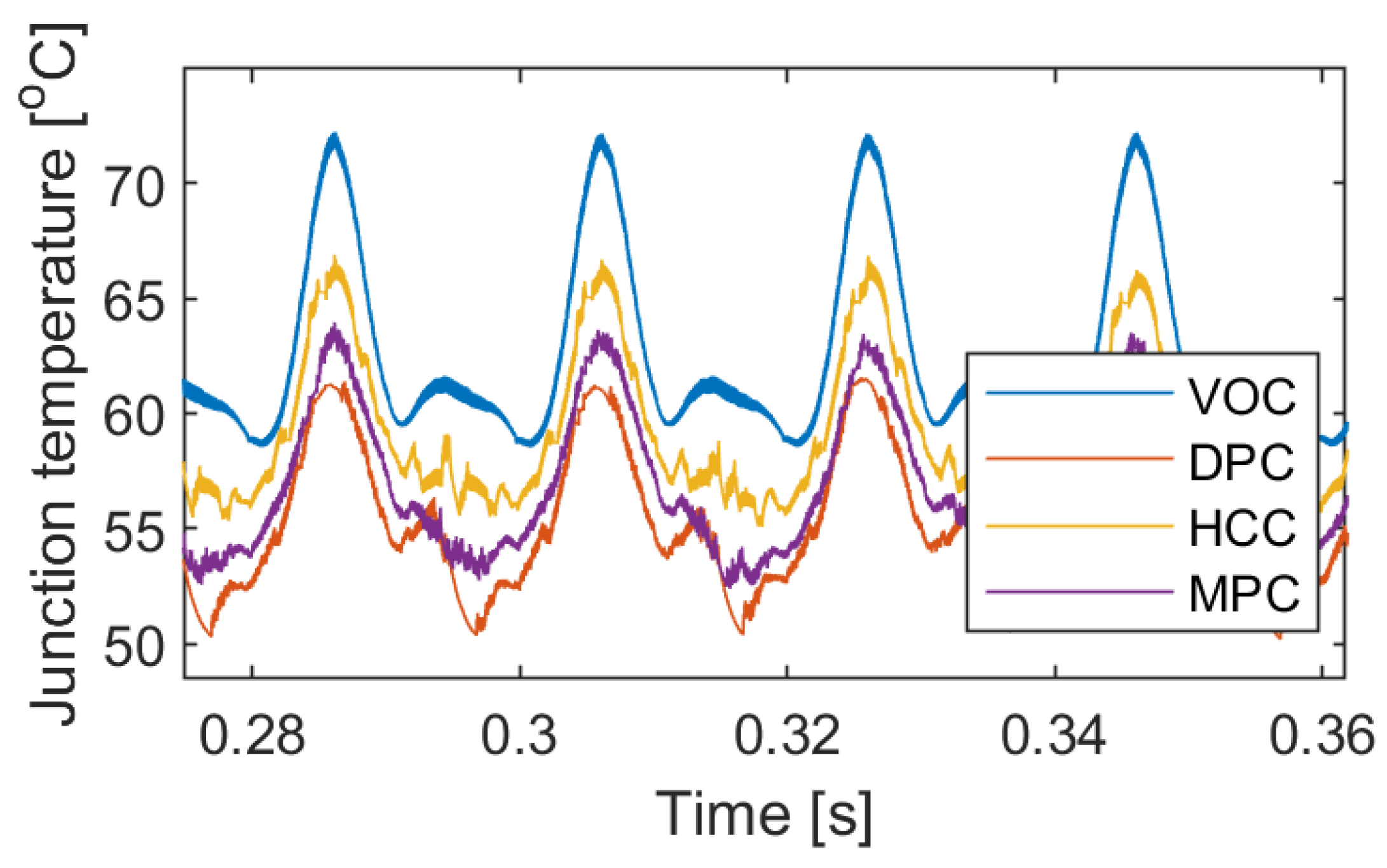
| Medium junction temperature | 65.2 C | 55.75 C | 58.1 C | 61.1 C |
| Junction temperature swing | 13.6 C | 11.1 C | 11.2 C | 11.8 C |
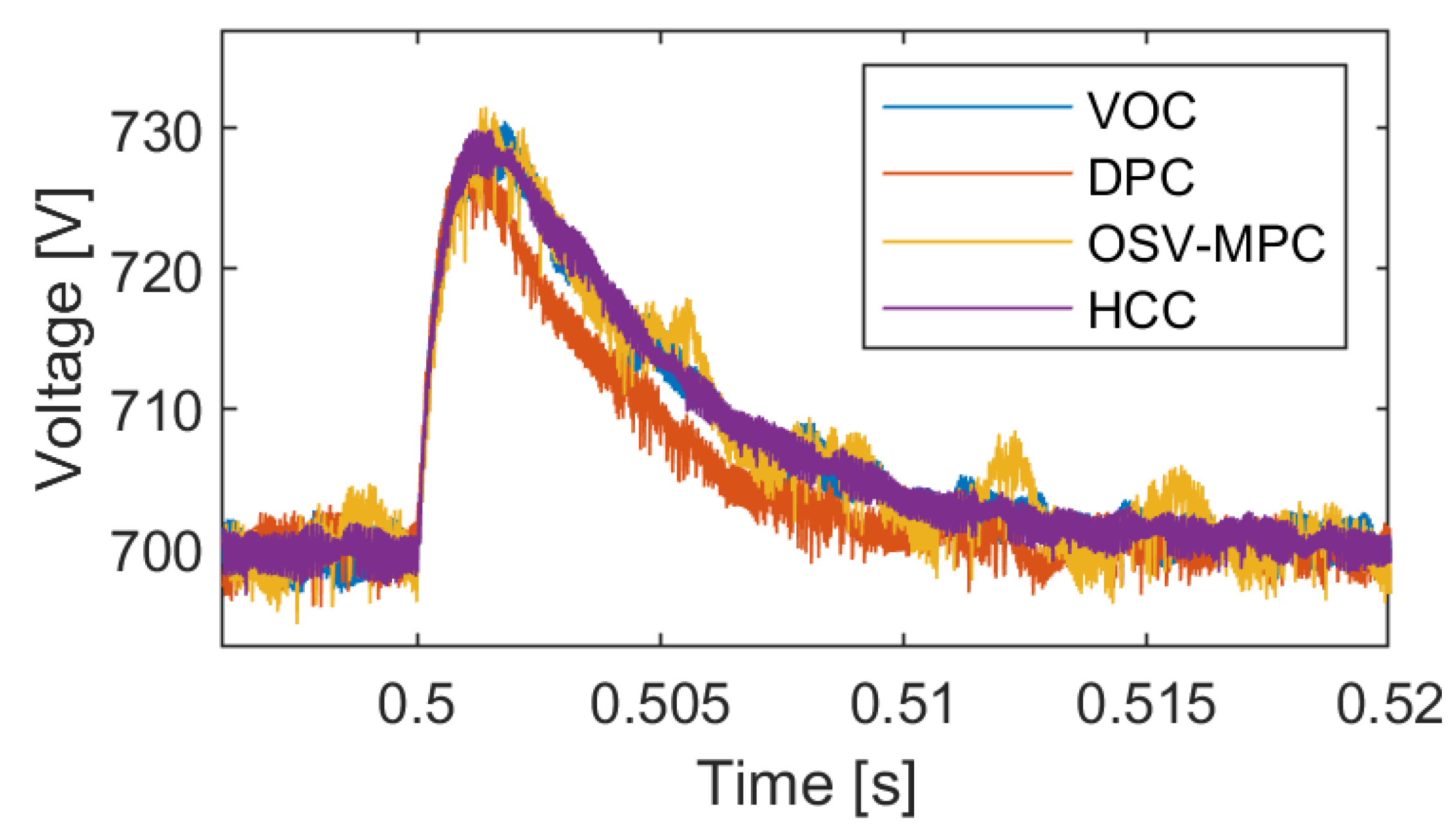
| DC Link voltage ripple | 5.9 V | 7 V | 11 V | 5.2 V |
| Simulation time | 123 s | 72 s | 82 s | 61 s |
| Settling time | 0.015 s | 0.01 s | 0.015 s | 0.015 s |
| Overshoot | 31 V | 29 V | 31.5 V | 30 V % |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhaksylyk, A.; Rasool, H.; Abramushkina, E.; Chakraborty, S.; Geury, T.; El Baghdadi, M.; Hegazy, O. Review of Active Front-End Rectifiers in EV DC Charging Applications. Batteries 2023, 9, 150. https://doi.org/10.3390/batteries9030150
Zhaksylyk A, Rasool H, Abramushkina E, Chakraborty S, Geury T, El Baghdadi M, Hegazy O. Review of Active Front-End Rectifiers in EV DC Charging Applications. Batteries. 2023; 9(3):150. https://doi.org/10.3390/batteries9030150
Chicago/Turabian StyleZhaksylyk, Assel, Haaris Rasool, Ekaterina Abramushkina, Sajib Chakraborty, Thomas Geury, Mohamed El Baghdadi, and Omar Hegazy. 2023. "Review of Active Front-End Rectifiers in EV DC Charging Applications" Batteries 9, no. 3: 150. https://doi.org/10.3390/batteries9030150
APA StyleZhaksylyk, A., Rasool, H., Abramushkina, E., Chakraborty, S., Geury, T., El Baghdadi, M., & Hegazy, O. (2023). Review of Active Front-End Rectifiers in EV DC Charging Applications. Batteries, 9(3), 150. https://doi.org/10.3390/batteries9030150











