1. Introduction
Modern transportation and logistics systems call for efficient vehicle routing solutions that can adapt to dynamic and uncertain conditions. This is particularly relevant for electric vehicles (EVs), which are gaining popularity due to their potential for reducing transportation costs and minimizing environmental impact. The increasing adoption of EVs has sparked a revolution in the automotive industry, offering a sustainable alternative to conventional internal combustion engine vehicles [
1]. However, these vehicles face several challenges when it comes to real-time route planning under dynamic scenarios, such as the need to consider weather conditions, traffic or on-site congestion, and travel time. In addition, as EVs rely heavily on batteries for their power supply, effective battery management is crucial to ensure optimal performance, an extended battery life, and enhanced driving range. Moreover, the need for an efficient battery management system (BMS) calls for a cutting-edge technology combined with a more refined software. Any BMS has to consider the uncertainty associated with the availability of charging stations along the route. Finding reliable charging infrastructure can be a daunting task, as charging stations are still relatively scarce in many areas. This lack of widespread charging infrastructure poses a significant obstacle for EV owners, as it restricts the number of feasible options.
For long-distance routes, there comes a time when the vehicle needs to face the problem of choosing the next charging station point. This can be challenging given the environmental dynamic conditions mentioned above. The distinction becomes crucial, especially for aged batteries, when considering charging up having a
charge level versus charging up having a
level. Therefore, an ‘optimal’ route towards the charging station point should be taken into account, so that given the distance from the current location to the station, the congestion and weather conditions, and the available chargers, the goal is to maximize the lifespan of the batteries while ensuring a charging time that is acceptable, as discussed in Abdollahi et al. [
2].
Initially proposed by Golden et al. [
3], the orienteering problem (OP) is named after the sport of orienteering, where a runner selects specific points to navigate between within a given time limit. The OP involves a vehicle that begins at a depot, traverses a set of nodes, and finally reaches a destination depot, with the objective of maximizing the total reward earned from visiting the nodes. The problem becomes more challenging as the vehicle has a limited distance or time to cover the path from the origin node to the destination node. The OP and its extension to multiple vehicles, the team orienteering problem, have found relevance in modern applications such as unmanned aerial vehicles and road EVs with limited battery capacity [
4,
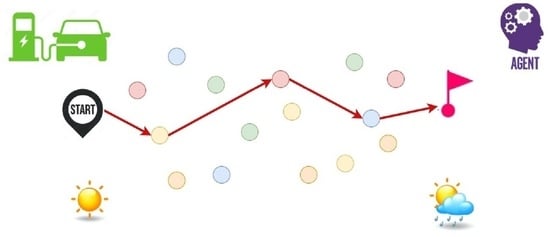
5]. This paper explores a dynamic OP where a single vehicle must travel from an origin to a destination while visiting specific charging nodes along the way to ensure it can reach its final destination (
Figure 1). The vehicle needs to pass through multiple regions and, since a region represents a set of clustered charging stations, it makes sense to assume that it will only visit one charging station per region. Once charged at a station, it can then resume its travel to the next region until it finally reaches the destination node. Each region contains different types of charging nodes, e.g., alternating current (AC) level 2, direct current (DC) fast, superchargers, etc. The reward associated with visiting each charging node is represented by a binary random variable, indicating whether or not the vehicle arrived at the charging node within the ‘optimal’ charging window to prolong the battery’s lifespan and to complete the charging process in a reasonable time period. In order to consider realistic context conditions, it is assumed that the probability of receiving a positive reward at each charging node depends on dynamic factors such as: (i) weather conditions along the route to the charger; (ii) congestion on the road or at the charging station; (iii) travel time from the vehicle’s current position to the charger’s location; and (iv) the age of the battery.
To address the aforementioned dynamic orienteering problem, this paper proposes the combination of simulation with reinforcement learning (RL) [
6] to emulate how the system would perform in a real-life scenario. Our approach involves training a machine learning model, which can be a slow process in a real-life scenario. Hence, to illustrate how this learning process works, a simulation experiment is proposed. The simulation allows us to emulate how the learning process would occur in a real-life scenario and test the quality of the learning models employed in our approach. Thus, the main contribution of this paper is the combination of reinforcement learning with simulation to illustrate how to make informed decisions in a dynamic OP with electric vehicles and binary random rewards that can be influenced by several factors, including their battery status.
The remainder of the paper is structured as follows:
Section 2 gives a more extensive context on the types of EVs and their integration into the ongoing transportation network, current research in the field, battery capacity, materials and charging time, and several factors that might influence the state of the battery.
Section 3 provides a brief review of OPs.
Section 4 describes the problem in a more formal way.
Section 5 introduces the numerical case study that is considered.
Section 6 discusses the details of the simulation experiment as well as the reinforcement learning algorithm employed.
Section 7 analyzes the results obtained in our computational test. Finally,
Section 8 highlights the main conclusions of our work and suggests open research lines.
2. Some Technical Details on EVs
The transportation sector accounted for
of energy-related emissions in 2019 [
7]. The largest source of transport emissions are road vehicles, predominantly powered by internal combustion engines. Since EVs are a promising mitigation technology to reduce the impact on climate change, air pollutants, and noise [
8], researchers have shown significant interest in studying EV energy consumption due to its importance for understanding the efficiency, performance, and environmental impact [
9,
10]. Several models can be used to calculate energy consumption in EVs, and Qi et al. [
11] classified them into three main categories: analytical, statistical, and computational models. While accurate estimation and prediction of EVs’ range is crucial for driver confidence and planning, the design and optimization of charging infrastructure networks also play an important role in ensuring efficient charging processes and minimizing energy consumption. There are several types of EVs available on the market [
12]. These range from conventional vehicles with no electric components to fully EVs, including hybrid electric vehicles (HEVs) as well as battery electric vehicles (BEVs). Each type has its own advantages and considerations, and the choice depends on factors such as driving habits, range requirements, the availability of charging infrastructure, and personal preferences.
As discussed in [
13], BEVs produce zero tailpipe emissions but require charging infrastructure to recharge their batteries. The battery is the core component of an EV, especially for BEVs, and can be categorized by qualities such as its specific energy, specific power, capacity, voltage, and chemistry [
14]. Battery modeling is quite complex and many models have been developed: empirical, equivalent circuit, physics-based, and high level stochastic [
15]. The initial technology used was a lead–acid battery that was soon replaced because of its drawbacks such as having low energy density and being heavy. Nickel-based batteries were introduced soon after as a mature technology, but they have longer recharging times and poor performance in cold weather. Currently, lithium-based batteries are the most common and widely adopted in the EV industry [
16]. Even though some methods have been proposed to predict the remaining useful life of lithium batteries [
17], there are still several open issues with their use: in particular, their safety as well as environmental impact concerns.
One of the main challenges raised by BEVs is to obtain acceptable driving ranges. The state of charge (SOC) measurement is particularly important as it indicates the maximum driving range. The capacity of EV batteries can range from around 20 kWh in smaller electric cars to over 100 kWh in larger, high-end electric vehicles. However, accurately estimating driving distance is difficult, and factors such as the vehicle’s efficiency, driving style, and weather conditions also influence the actual driving range achieved [
18,
19]. The optimal SOC range in batteries can vary depending on the specific type of lithium-based battery chemistry and the desired operating parameters [
20]. According to Koltermann et al. [
21], the capabilities are limited at the border areas of the SOC. The results show that batteries can only safely deliver full power without a detrimental impact on their health and longevity at between 20–80% of the SOC. At both ends, the battery exhibits much higher polarization impedance [
22]. The maximum SOC is usually set to ensure safe operation and prevent overcharging, stress on the material, or elevated operating temperatures [
23]. Likewise, the minimum SOC tries to avoid an unexpected system shutdown or loss of power that can occur due to low voltage levels and the risk of cell imbalance. In addition, maintaining a low SOC can potentially contribute to driver anxiety. Advancements in charging infrastructure are also reducing concerns about range anxiety by providing faster and more accessible charging options for EV owners [
24]. However, the number of charging stations is still relatively limited, so predicting the best place to charge the vehicle in dynamic conditions is important. There are several charging technologies available for EVs depending on the different power levels an EV can be charged to [
25]. Level 1 charging (120 V AC) uses a household electrical outlet and provides around
to
kW. It provides the slowest charging rate for EVs. Level 2 charging (240 V AC) requires a compatible charging station or wall-mounted charger. It delivers power ranging from
kW to 22 kW. Level 3 or DC fast charging stations can provide charging powers ranging from 50 kW to over 350 kW. The vehicle’s onboard charger and charging port specifications will determine the maximum charging rate it can accept. Among other factors, a vehicle’s charge time depends on the level of the charger and the type of EV. According to the U.S. Department of Transportation [
26], to reach an
battery level from empty can take between 40 and 50 h for a BEV, and between 5 and 6 h for a plug-in HEV (with a Level 1 charger). Likewise, it can take between 4 and 10 h for a BEV and between 1 and 2 h for a plug-in HEV (with a Level 2 charger). Finally, it can take between 20 min and 1 h for a BEV (with a Level 3 charger).
EV penetration causes significant issues on the power distribution grid, such as an increase in power demand, system losses, voltage drops, equipment overloading, and stability impact [
27]. At the same time, some exciting opportunities appear with EV deployment on the smart grid, such as grid flexibility through vehicle-to-grid (V2G) technology, demand response, and the integration of renewable energy sources [
25]. V2G mode allows EVs to discharge power back to the grid. This can support grid balancing, frequency regulation, and voltage stabilization. The weather conditions directly affect the battery temperature [
28], the climate control [
29], and the charging efficiency [
30]. Extreme weather conditions can affect the temperature of the EV’s battery. High temperatures can increase the risk of the battery overheating, which may reduce its performance and lifespan. Likewise, very cold temperatures can decrease the battery’s efficiency and capacity temporarily. EVs often rely on climate control systems to maintain a comfortable cabin temperature. This includes features such as air conditioning in hot weather and heating in cold weather. The use of these systems can impact the overall energy consumption and range of the vehicle. Extreme temperatures can also affect the efficiency of charging systems. Congestion can generate an increase in the stop-and-go driving style. This can lead to more energy-intensive acceleration and braking, and thus result in increased energy consumption and a higher load on the battery, potentially reducing its overall range [
31]. In addition, when stuck in congestion, EVs may be required to idle for extended periods, especially in situations where traffic is at a standstill. Idling consumes energy from the battery to power auxiliary systems such as climate control and entertainment systems. Prolonged idling can drain the battery charge faster and reduce the available range [
32].
3. Related Work on Vehicle Orienteering Problems
The orienteering problem was first introduced by Golden et al. [
3], who proved it to be NP hard. Early research examined the deterministic version of the problem within the framework of vehicle routing, where one vehicle chooses the nodes to visit and the order of visits within a defined time frame. In contrast, research on the stochastic OP is relatively recent. The first study to include stochasticity in the OP was conducted by Ilhan et al. [
33], which assumed that only node rewards were stochastic. Other researchers, including Campbell et al. [
34], Papapanagiotou et al. [
35], Verbeeck et al. [
36], or Evers et al. [
37], focused on cases where service and travel times were stochastic, with service times typically incorporated into travel times. Several approaches have been employed to solve the stochastic orienteering problem, including a combination of branch and bound algorithms with local search [
34] and local search simulations [
38]. Further refinements were made to these methods, with Varakantham and Kumar [
39] utilizing a sample average approximation technique to improve on the results of Lau et al. [
38]. Additionally, Zhang et al. [
40] expanded the method of Campbell et al. [
34] to include time windows for arriving at nodes. Gama and Fernandes [
41] introduced a solution to the orienteering problem with time windows, employing Pointer Network models trained through reinforcement learning. A comprehensive review of the orienteering problem and its variants can be found in Gunawan et al. [
42]. Still, to the best of our knowledge, our work is the first one that proposes the combined use of RL and simulation to deal with a version of the problem with stochastic rewards that depend upon dynamic conditions. In our view, this dynamic OP with stochastic rewards has relevant applications to scenarios involving EVs that require an efficient management of their batteries.
4. Modeling the Dynamic OP with Binary Random Rewards
Let
be a directed graph with node set
V and edge set
E. Node
is the origin node, while node
is the destination node. Each node
has a reward
associated with it, which is a binary random variable that takes the value 1 with probability
and 0 with probability
. Let us denote this by region
, with
, a subset of
. The problem is to find a path
P that starts at
O and ends at
D, maximizes the expected total reward collected along the path, and visits at most one node in each region
. In our case, the reward is based on extending the battery’s lifespan [
21], as well as on completing the charging process within a certain time interval. Thus, the probability of obtaining a reward for a recharging node
i depends on the type of node as well as on the current status at the region
. This status is determined by dynamic context conditions, i.e.,
for an unknown (black-box) function
f.
Let
be a binary decision variable that takes the value 1 if node
i is visited along the path
P, and 0 otherwise. Let
be a binary decision variable that takes the value 1 if there is an arc from node
i to node
along the path
P, and 0 otherwise. Then, the problem can be formulated as follows:
subject to:
The objective function Equation (
1) maximizes the expected total reward collected along the path
P. Constraint Equations (
2) and (
4) ensure that the path starts at the origin node
O and ends at the destination node
D, respectively. Constraint Equation (
3) ensures that the flow of the path
P is conserved at each node
, i.e., the number of incoming arcs is equal to the number of outgoing arcs. Constraint Equation (
5) ensures that at most one node in each region
is visited. Constraint Equations (
6) and (
7) enforce the binary variables.
5. A Numerical Case Study
Consider a dynamic OP, with binary random demands
, similar to the one represented in
Figure 1. Let us assume that a vehicle must now cross six consecutive regions, with each region containing five different types of charging nodes, each type with a different probability of obtaining a reward. In accordance with
Section 2, let us assume that such probability will depend on a vector of factors that describe the context conditions at each region–node pair, which are: battery age, congestion, weather, battery status, and time of charge. The logistic sigmoid function
maps real-valued numbers to a range between 0 and 1. In particular, for each type of node
, let us assume that the real-life probability of obtaining a reward
is modeled as a logistic function
f, which is defined for each region,
to
(
Table 1), and each of the following factors: (i) battery age (cycles)
; (ii) current battery status (in %)
; (iii) congestion
(where
represents high congestion and
represents low congestion); (iv) weather conditions
(where
represents good weather and
represents bad weather); and (v) time of charge (in hours)
. Hence, the real-life probability
of obtaining a reward when visiting a node of type
i in region
under context conditions
is given by:
For each of the five considered nodes,
Figure 2 shows the real probability of obtaining a reward of 1 when the node is visited under different combinations of congestion, weather conditions, battery age, and battery status. Notice also that charging time has a great influence on this probability for all nodes since the objective is to extend the lifetime of the battery without compromising the time at which the vehicle reaches its destination. Moreover, the node offering a higher probability of reward might vary according to the current weather, congestion, and other conditions in the region.
Despite the fact that the function
f that represents the real probability of obtaining a reward has been properly defined, this will not usually be possible in a real-life application. In effect, the real-life parameters shown in
Table 1 will be unknown in many practical applications. Then, given a vector
x of five factors associated with a region–node combination, the goal will be to predict
y, i.e.,
, so the next charging node
i to be visited can be selected using this estimated probability. Hence, from this point on, it is assumed that the true values of the parameters
to
are unknown, and a reinforcement learning algorithm is proposed in order to predict the real probability of obtaining a reward. In a real-life application, the algorithm achieves this predictive capacity by making decisions, observing the associated outcomes, and then learning from these interactions with reality. In online RL, the learning agent interacts directly with the environment in real-time. The agent makes decisions, receives feedback (rewards), and updates its policy based on the observed outcomes. The agent explores (tries out different options) and exploits (selects the best-known option) the environment simultaneously, making decisions and adapting its behavior as it interacts with the environment. In order to illustrate this learning process, simulation is employed to emulate this interaction between the algorithm and reality. A total of
trips were simulated.
At each region , the algorithm must select a node type i to visit. This selection is based on the current estimate of the expected reward for each node type i, and the parameter controls the balance between exploration and exploitation. Specifically, with probability , the algorithm selects the node type with the highest expected reward (exploitation), and with probability , it selects a node type at random (exploration). After selecting a node type, the algorithm receives feedback from reality (the simulation in our case) in the form of a binary reward, and updates its estimate of the expected reward for each node type accordingly.
In the computational experiments a hybrid gradient boosting with decision trees model is utilized to estimate the expected reward for each region–node combination based on the feedback provided by the simulation environment. During the simulation, random values are generated to emulate the context conditions of each region. Then, using the black-box function f, the response that would be obtained in a real-life environment is estimated. The algorithm uses this response to iteratively enhance the model that predicts, for each node and contextual values, the probability of obtaining a reward. Thus, for example, suppose that after several simulation runs, the algorithm learns that nodes of type 1 are the most rewarding under good weather and low congestion conditions, nodes of type 2 are the most rewarding under bad weather and high congestion, nodes of type 3 are the most rewarding under good weather and high congestion, nodes of type 4 are the most rewarding under bad weather and low congestion, and nodes of type 5 are the most rewarding under any other context condition, it then adjusts its policy accordingly and continues to improve over time.
A conceptual schema summarizing the described methodology is provided in
Figure 3. The simulation component provides new testing conditions for the RL component to make decisions (step 1). The RL component makes decisions by selecting the next charging node in the routing plan (step 2). Then, the black-box function emulating real life is employed to check the real impact of the decision suggested by the RL agent (step 3) and provide feedback to it (step 4). Finally, the simulation of a new scenario is activated and the process is repeated until a complete solution (a selection of charging nodes connecting the origin depot with the destination depot) is built. At this stage, the entire loop is iterated for a number of runs. As more and more runs are executed, the more trained the RL model becomes and, hence, the better its decisions are in terms of which charging node has to be visited next according to the vector of factors.
6. Simulation and Algorithm Details
Using the Python programming language as a base, this section provides insights on the reinforcement learning algorithm employed to predict the probability of reward for each node and contextual conditions. It also describes the simulation process utilized to illustrate how the learning process works in a practical application. Notice that only the key parts of the code are provided here.
Listing 1 defines a multivariate logistic function, real_reward_p, which provides the real probability of obtaining a binary reward of 1 for a given node, based on the inputs weather conditions, congestion, battery age, expected battery, and charging time. This function acts as a black-box model (unknown for the learning algorithm) that emulates reality. This logistic function takes in a node, weather (0 or 1 where 1 is good weather and 0 is bad), congestion (0 or 1 where 1 is high congestion and 0 is low congestion), battery age (an integer between 10 and 1000), expected battery (an integer between 0 and 100), and charging time (an integer between 1 and 40) as parameters. Inside the function, a linear combination of the parameters and some weights stored in the params dictionary for that node are computed. The result of the linear combination is passed through the sigmoid function to obtain a probability of obtaining a reward of 1 for that node given the input parameters. For instance, if the parameters associated with a giving node i are , , , , , and , then real_reward_p(i, 1, 0, 20, 10, 20) would return the probability of obtaining a reward of 1 for node i when the weather is good, congestion is low, the charging time is 40, the age of the battery is 10 cycles, and the battery status is 20.
In a similar fashion, Listing 2 defines a CatBoost model (gradient boosting with decision trees) [
43] to predict the probabilities of obtaining a reward of 1 for a given node–region pair and context inputs. In order to train the model, the data are divided into two sets: training and testing. The training set is utilized to construct the model, while the test data serve the purpose of preventing overfitting by employing an early stopping strategy [
44]. The model’s performance improves significantly when more data are available. To ensure calibrated probabilities, Platt scaling is applied to fine-tune the model’s probability outputs [
45]. This model acts as a white-box one that aims at predicting how reality will behave, i.e., it tries to predict the real-life probability provided by the black-box function described in Listing 1. Given that the CatBoost Python library is employed, it is possible to use the inbuilt function
to generate predictions. Notice, however, that a different predictive model—e.g., a neural network—could have been used as a white box.
| Listing 1. Python code illustrating the black box used to compute the real probability of reward. |
![Batteries 09 00416 i001]() |
| Listing 2. Python code illustrating the trained model used to predict the probability of reward. |
![Batteries 09 00416 i002]() |
The code in Listing 3 defines a Python function called
select_node_eps that selects a node from a dictionary
predicted_reward_p based on a slightly modified epsilon-greedy strategy. The function takes in two optional parameters:
eps, the value of epsilon used in the epsilon-greedy algorithm, and
uniform, a Boolean flag that specifies whether to choose the node uniformly at random among all nodes with the same probability. The function first sorts the nodes in descending order based on their corresponding probability of reward. It then checks whether a random number between 0 and 1 is greater than
eps. If it is, the function returns the node with the highest probability of reward (i.e., the first element in the sorted list). If the random number is less than or equal to
eps, the function randomly selects a node from the sorted list, either uniformly or non-uniformly depending on the value of the uniform flag. If
uniform is
True, the function selects a node uniformly at random. If uniform is
False, the function selects the node with the second highest probability of reward (i.e., the best ‘alternative’). This function is typically used in reinforcement learning algorithms to balance the exploration and exploitation of different nodes based on their predicted rewards. Still, other strategies, such as the Thompson sampling [
46], could also be used instead.
The code in Listing 4 simulates the generation of new regions in our route and selects the node to visit. The code uses a for loop to iterate over the number of observations specified by the variable . At each iteration, it simulates weather conditions, congestion, battery age, expected battery, and charging time. The code then selects nodes using a round-robin (balanced) selection method for the first n_update iterations. From that point on, it uses a trained model and the epsilon-greedy strategy to select the next node. The code then simulates the real probability of reward when this node is selected and updates the accumulated regrets. Since rewards are binary, the expected reward for each node is computed as the estimated probability of success. The code records the new data, increasing the size of observations for X (predictors), y (response), and z (regrets), and updates the models every iterations.
| Listing 3. Python code illustrating a modified epsilon-greedy strategy. |
![Batteries 09 00416 i003]() |
| Listing 4. Python code illustrating the core part of the simulation. |
![Batteries 09 00416 i004]() |
7. Computational Experiments
Table 2 shows a comparison between the predicted and the actual (real-life) probability of obtaining a reward of 1 for a randomly selected set of nodes and factor configurations. This table confirms that the trained model is capable of estimating the real-life probability with a relatively low average error.
After training the predictive model, it is possible to apply it to the proposed case study on dynamic OP with binary random rewards. Whenever the EV reaches a new region and receives updated contextual information such as weather, congestion, battery age, expected battery, and time of charge, it will use the predictive model to select one of the nodes with a higher probability of obtaining a reward. Since selecting a node in one region might affect our options in subsequent regions, following a greedy approach in each region—i.e., always selecting the node with the highest expected reward at each step—would not necessarily lead us to an optimal solution for the entire trip. In a situation such as this, it is often convenient to employ diversification strategies based on biased randomization and agile optimization techniques [
47].
A total of 10,000 trips for the case study were simulated, which considered six regions and five types of nodes per region.
Figure 4 shows boxplots with the expected accumulated reward for solutions generated by our approach (in which the trip is guided by the predictive model) and a non-guided approach (in which a node is randomly chosen in each region). Hence, while solutions proposed by our methodology show an average value of
and a standard deviation of
for the expected accumulated reward, solutions provided by a non-guided approach show an average value of
and a standard deviation of
for the expected accumulated reward. As expected, a
t-test provides a
t-statistic =
, with an associated
p-value =
, which clearly indicates that the solutions generated by our reinforcement learning approach are significantly better than the ones constructed without taking into account the dynamic contextual conditions.
Figure 5 illustrates a comparative analysis between a non-guided solution and the route provided by our approach. The blue nodes (N1, N2, N3, N4, N5) in the figure represent the chargers in each region, and the weight of the edges in the graph represents the real probabilities of reward based on the original solution. Notably, the selections made by our approach consistently demonstrate higher probabilities of obtaining rewards.
8. Conclusions
This paper proposes a hybrid methodology combining simulation and reinforcement learning to explore a vehicle orienteering problem with binary random rewards and dynamic conditions. This problem is discussed in the context of electric vehicles that, while covering a long trip, have to cross different regions and choose, in each of these region, a charging station with a high probability of reward. The challenge lies in the fact that the reward for visiting each charging node is a binary random variable and depends on dynamic context conditions, such as: weather conditions, road or on-site congestion, current battery status, etc. In order to emulate the learning process in real-life conditions under uncertainty, a simulation is employed. Thus, a black-box model is used to estimate the real-life probability of obtaining a reward for each node based on the dynamic context conditions at a given time. A reinforcement learning mechanism is then employed to make informed decisions at each stage of the problem, and a logistic regression model is used to predict the aforementioned probabilities. Through the simulation results, it is shown that the proposed reinforcement learning approach can effectively learn to make informed decisions based on the dynamic context conditions. The computational experiments show that a statistically significant improvement is obtained when the proposed approach is utilized. All in all, the proposed approach can be useful in a range of real-life scenarios such as transportation logistics, delivery services, and resource allocation.
One potential direction is to explore more complex models for the probability of obtaining a reward, such as neural networks or models that account for additional context conditions. To mitigate some of the downsides of the strategy chosen in this paper (
greedy), various enhancements could be carried out, such as using decaying exploration rates or dynamically adjusting the exploration rate based on the agent’s learning progress. Another potential area for future work is to investigate the impact of different reinforcement learning algorithms and strategies on the performance of the model. For example, analyzing different exploration strategies (beyond the epsilon-greedy strategy used in this study) may lead to more efficient learning and better decision making. Furthermore, it may be valuable to consider the use of more advanced optimization techniques, such as metaheuristics and simheuristics [
48], that can be combined with the reinforcement learning approach introduced in this paper. Finally, this study focused on a single vehicle traveling through a fixed set of regions. Future work could explore more complex scenarios, such as the involvement of multiple vehicles, i.e., a dynamic team orienteering problem with stochastic rewards.