Predicting Ionic Conductivity in Thin Films of Garnet Electrolytes Using Machine Learning
Abstract
:1. Introduction
2. Materials and Methods
2.1. Methodology
2.2. Computational Procedures
3. Results and Discussion
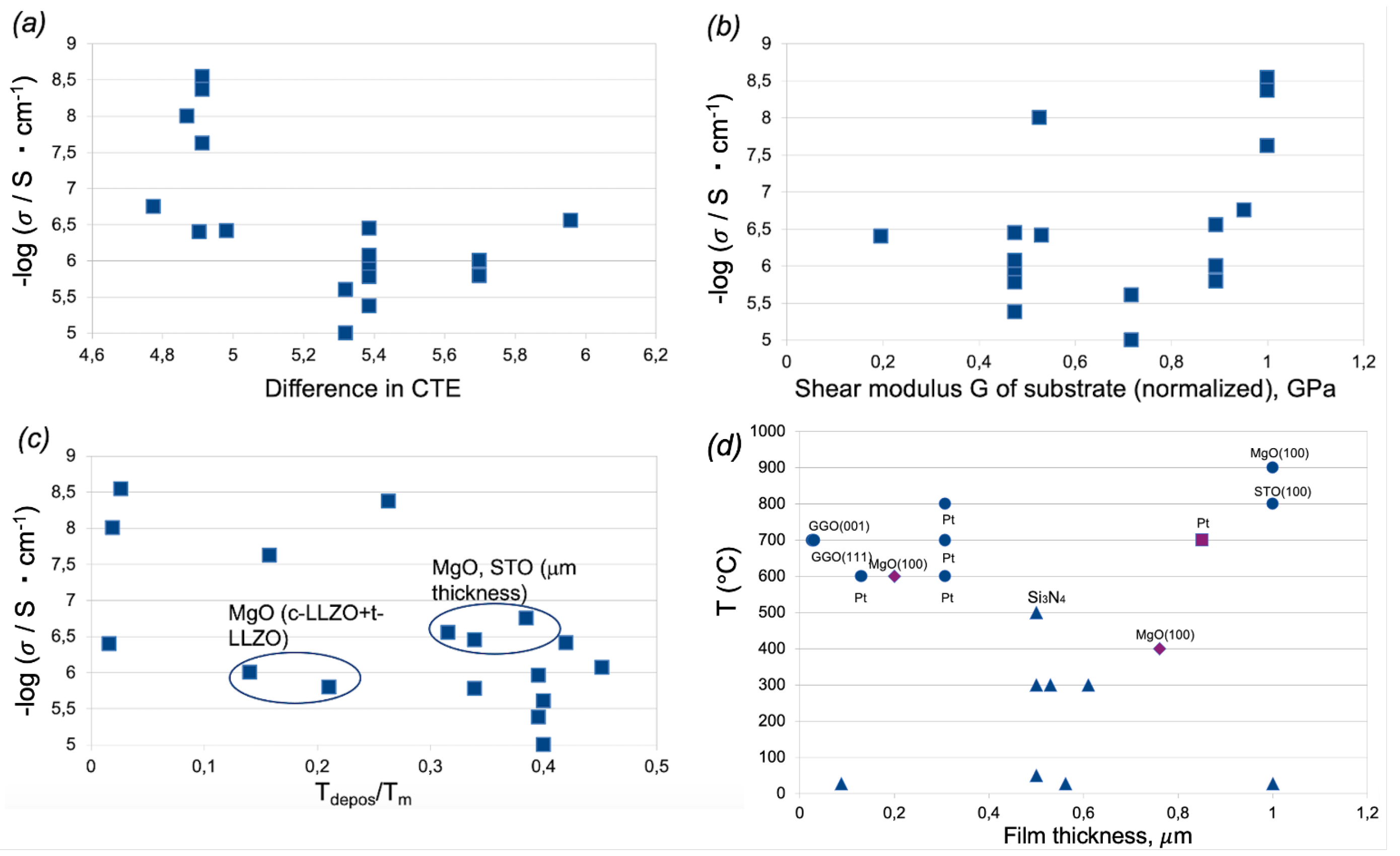
3.1. Analysis of Experimental Data on Ionic Conductivity Values in Garnet Thin Films
3.2. Models of Strain
3.3. Descriptors Refinement
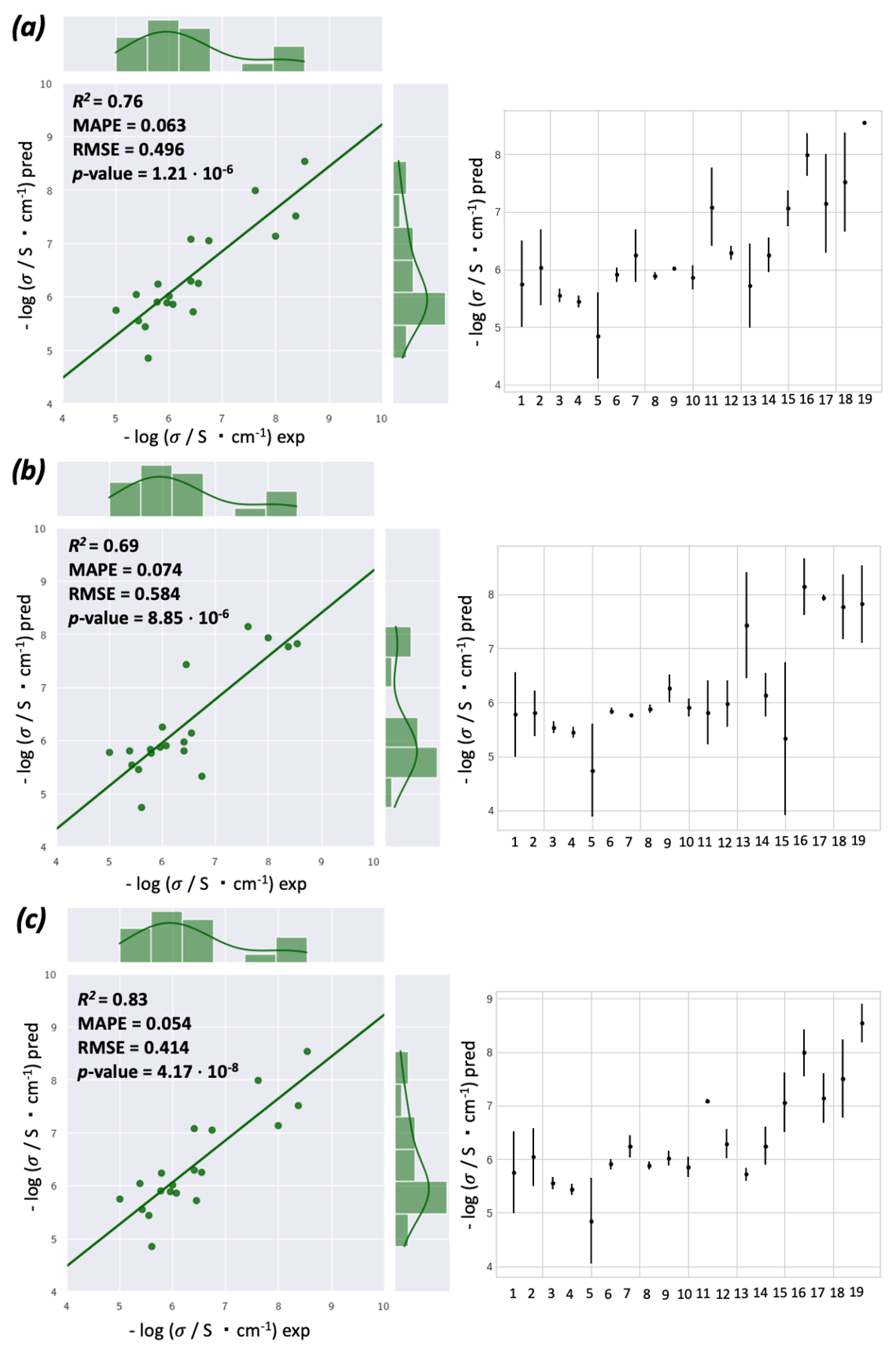
3.4. Machine Learning Modeling and Data Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Goodenough, J.B.; Singh, P. Review—Solid Electrolytes in Rechargeable Electrochemical Cells. J. Electrochem. Soc. 2015, 162, A2387. [Google Scholar] [CrossRef]
- Lotsch, B.V.; Maier, J. Relevance of solid electrolytes for lithium-based batteries: A realistic view. J. Electroceramics 2017, 38, 128–141. [Google Scholar] [CrossRef]
- Bachman, J.C.; Muy, S.; Grimaud, A.; Chang, H.H.; Pour, N.; Lux, S.F.; Paschos, O.; Maglia, F.; Lupart, S.; Lamp, P.; et al. Inorganic Solid-State Electrolytes for Lithium Batteries: Mechanisms and Properties Governing Ion Conduction. Chem. Rev. 2016, 116, 140–162. [Google Scholar] [CrossRef]
- Oudenhoven, J.F.M.; Baggetto, L.; Notten, P.H.L. All-Solid-State Lithium-Ion Microbatteries: A Review of Various Three-Dimensional Concepts. Adv. Energy Mater. 2011, 1, 10–33. [Google Scholar] [CrossRef]
- Garbayo, I.; Struzik, M.; Bowman, W.J.; Pfenninger, R.; Stilp, E.; Rupp, J.L.M. Glass-Type Polyamorphism in Li-Garnet Thin Film Solid State Battery Conductors. Adv. Energy Mater. 2018, 8, 1702265. [Google Scholar] [CrossRef]
- Huang, K.J.; Ceder, G.; Olivetti, E.A. Manufacturing scalability implications of materials choice in inorganic solid-state batteries. Joule 2021, 5, 564–580. [Google Scholar] [CrossRef]
- Thangadurai, V.; Kaack, H.; Weppner, W.J.F. Novel Fast Lithium Ion Conduction in Garnet-Type Li5La3M2O12 (M = Nb, Ta). J. Am. Ceram. Soc. 2003, 86, 437–440. [Google Scholar] [CrossRef]
- Thangadurai, V.; Weppner, W. Effect of sintering on the ionic conductivity of garnet-related structure Li5La3Nb2O12 and In- and K-doped Li5La3Nb2O12. J. Solid State Chem. 2006, 179, 974–984. [Google Scholar] [CrossRef]
- Murugan, R.; Thangadurai, V.; Weppner, W. Effect of lithium ion content on the lithium ion conductivity of the garnet-like structure Li5 + xBaLa2Ta2O11.5 + 0.5x (x = 0–2). Appl. Phys. A 2008, 91, 615–620. [Google Scholar] [CrossRef]
- Murugan, R.; Thangadurai, V.; Weppner, W. Fast Lithium Ion Conduction in Garnet-Type Li7La3Zr2O12. Angew. Chem. Int. Ed. 2007, 46, 7778–7781. [Google Scholar] [CrossRef]
- Chen, Y.; Rangasamy, E.; Liang, C.; An, K. Origin of High Li+ Conduction in Doped Li7La3Zr2O12 Garnets. Chem. Mater. 2015, 27, 5491–5494. [Google Scholar] [CrossRef]
- Li, J.; Liu, Z.; Ma, W.; Dong, H.; Zhang, K.; Wang, R. Low-temperature synthesis of cubic phase Li7La3Zr2O12 via sol-gel and ball milling induced phase transition. J. Power Sources 2019, 412, 189–196. [Google Scholar] [CrossRef]
- Orera, A.; Larraz, G.; Rodriguez-Velamazan, J.A.; Campo, J.; Sanjuan, M.L. Influence of Li and H Distribution on the Crystal Structure of Li7–xHxLa3Zr2O12 (0 =< x =<5) Garnets. Inorg. Chem. 2016, 55, 1324–1332. [Google Scholar] [CrossRef]
- Bernstein, N.; Johannes, M.D.; Hoang, K. Origin of the Structural Phase Transition in Li7La3Zr2O12. Phys. Rev. Lett. 2012, 109, 205702. [Google Scholar] [CrossRef]
- Wagner, R.; Redhammer, G.J.; Rettenwander, D.; Senyshyn, A.; Schmidt, W.; Wilkening, M.; Amthauer, G. Crystal Structure of Garnet-Related Li-Ion Conductor Li7–3xGaxLa3Zr2O12: Fast Li-Ion Conduction Caused by a Different Cubic Modification? Chem. Mater. 2016, 28, 1861–1871. [Google Scholar] [CrossRef]
- Rondinelli, J.M.; Spaldin, N.A. Structure and Properties of Functional Oxide Thin Films: Insights From Electronic-Structure Calculations. Adv. Mater. 2011, 23, 3363–3381. [Google Scholar] [CrossRef]
- Schlom, D.G.; Chen, L.Q.; Fennie, C.J.; Gopalan, V.; Muller, D.A.; Pan, X.; Ramesh, R.; Uecker, R. Elastic strain engineering of ferroic oxides. MRS Bull. 2014, 39, 118–130. [Google Scholar] [CrossRef]
- Keppner, J.; Schubert, J.; Ziegner, M.; Mogwitz, B.; Janek, J.; Korte, C. Influence of texture and grain misorientation on the ionic conduction in multilayered solid electrolytes—Interface strain effects in competition with blocking grain boundaries. Phys. Chem. Chem. Phys. 2018, 20, 9269–9280. [Google Scholar] [CrossRef]
- Hwang, H.Y.; Iwasa, Y.; Kawasaki, M.; Keimer, B.; Nagaosa, N.; Tokura, Y. Emergent phenomena at oxide interfaces. Nat. Mater. 2012, 11, 103–113. [Google Scholar] [CrossRef]
- Aslan, O.B.; Datye, I.M.; Mleczko, M.J.; Sze Cheung, K.; Krylyuk, S.; Bruma, A.; Kalish, I.; Davydov, A.V.; Pop, E.; Heinz, T.F. Probing the Optical Properties and Strain-Tuning of Ultrathin Mo1-xWxTe2. Nano Lett. 2018, 18, 2485–2491. [Google Scholar] [CrossRef]
- Choi, S.Y.; Kim, S.D.; Choi, M.; Lee, H.S.; Ryu, J.; Shibata, N.; Mizoguchi, T.; Tochigi, E.; Yamamoto, T.; Kang, S.J.L.; et al. Assessment of Strain-Generated Oxygen Vacancies Using SrTiO3 Bicrystals. Nano Lett. 2015, 15, 4129–4134. [Google Scholar] [CrossRef] [PubMed]
- Sohier, T.; Gibertini, M.; Campi, D.; Pizzi, G.; Marzari, N. Valley-Engineering Mobilities in Two-Dimensional Materials. Nano Lett. 2019, 19, 3723–3729. [Google Scholar] [CrossRef] [PubMed]
- Martin, L.W.; Rappe, A.M. Thin-film ferroelectric materials and their applications. Nat. Rev. Mater. 2016, 2, 16087. [Google Scholar] [CrossRef]
- Schlom, D.G.; Chen, L.Q.; Eom, C.B.; Rabe, K.M.; Streiffer, S.K.; Triscone, J.M. Strain Tuning of Ferroelectric Thin Films. Annu. Rev. Mater. Res. 2007, 37, 589–626. [Google Scholar] [CrossRef]
- Xu, Y.; Park, J.H.; Yao, Z.; Wolverton, C.; Razeghi, M.; Wu, J.; Dravid, V.P. Strain-Induced Metastable Phase Stabilization in Ga2O3 Thin Films. ACS Appl. Mater. Interfaces 2019, 11, 5536–5543. [Google Scholar] [CrossRef] [PubMed]
- Sagotra, A.K.; Cazorla, C. Stress-Mediated Enhancement of Ionic Conductivity in Fast-Ion Conductors. ACS Appl. Mater. Interfaces 2017, 9, 38773–38783. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Li, J.; Zhu, F.; Liu, T.; Xu, B.; Kim, T.H.; Kramer, M.J.; Ma, C.; Zhou, L.; Nan, C.W. Atomically Intimate Contact between Solid Electrolytes and Electrodes for Li Batteries. Matter 2019, 1, 1001–1016. [Google Scholar] [CrossRef]
- Aidhy, D.S.; Rawat, K. Coupling between interfacial strain and oxygen vacancies at complex-oxides interfaces. J. Appl. Phys. 2021, 129, 171102. [Google Scholar] [CrossRef]
- Gupta, S.; Sachan, R.; Narayan, J. Nanometer-Thick Hexagonal Boron Nitride Films for 2D Field-Effect Transistors. ACS Appl. Nano Mater. 2020, 3, 7930–7941. [Google Scholar] [CrossRef]
- Chen, B.; Ju, J.; Ma, J.; Du, H.; Xiao, R.; Cui, G.; Chen, L. Strain tunable ionic transport properties and electrochemical window of Li10GeP2S12 superionic conductor. Comput. Mater. Sci. 2018, 153, 170–175. [Google Scholar] [CrossRef]
- Jia, M.; Wang, H.; Sun, Z.; Chen, Y.; Guo, C.; Gan, L. Exploring ion migration in Li2MnSiO4 for Li-ion batteries through strain effects. RSC Adv. 2017, 7, 26089–26096. [Google Scholar] [CrossRef]
- O’Rourke, C.; Morgan, B.J. Interfacial strain effects on lithium diffusion pathways in the spinel solid electrolyte Li-doped MgAl2O4. Phys. Rev. Mater. 2018, 2, 045403. [Google Scholar] [CrossRef]
- Wei, J.; Ogawa, D.; Fukumura, T.; Hirose, Y.; Hasegawa, T. Epitaxial Strain-Controlled Ionic Conductivity in Li-Ion Solid Electrolyte Li0.33La0.56TiO3 Thin Films. Cryst. Growth Des. 2015, 15, 2187–2191. [Google Scholar] [CrossRef]
- Korte, C.; Keppner, J.; Peters, A.; Schichtel, N.; Aydin, H.; Janek, J. Coherency strain and its effect on ionic conductivity and diffusion in solid electrolytes—An improved model for nanocrystalline thin films and a review of experimental data. Phys. Chem. Chem. Phys. 2014, 16, 24575–24591. [Google Scholar] [CrossRef] [PubMed]
- Harrington, G.F.; Cavallaro, A.; McComb, D.W.; Skinner, S.J.; Kilner, J.A. The effects of lattice strain, dislocations, and microstructure on the transport properties of YSZ films. Phys. Chem. Chem. Phys. 2017, 19, 14319–14336. [Google Scholar] [CrossRef] [PubMed]
- Wen, K.; Lv, W.; He, W. Interfacial lattice-strain effects on improving the overall performance of micro-solid oxide fuel cells. J. Mater. Chem. A 2015, 3, 20031–20050. [Google Scholar] [CrossRef]
- Rupp, J.L.M.; Fabbri, E.; Marrocchelli, D.; Han, J.W.; Chen, D.; Traversa, E.; Tuller, H.L.; Yildiz, B. Scalable Oxygen-Ion Transport Kinetics in Metal-Oxide Films: Impact of Thermally Induced Lattice Compaction in Acceptor Doped Ceria Films. Adv. Funct. Mater. 2014, 24, 1562–1574. [Google Scholar] [CrossRef]
- Jamnik, J.; Maier, J.; Pejovnik, S. Interfaces in solid ionic conductors: Equilibrium and small signal picture. Solid State Ionics 1995, 75, 51–58. [Google Scholar] [CrossRef]
- Maier, J. Space Charge Regions in Solid Two Phase Systems and Their Conduction Contribution—II Contact Equilibrium at the Interface of Two Ionic Conductors and the Related Conductivity Effect. Berichte Bunsenges. Phys. Chem. 1985, 89, 355–362. [Google Scholar] [CrossRef]
- Maier, J. Ionic conduction in space charge regions. Prog. Solid State Chem. 1995, 23, 171–263. [Google Scholar] [CrossRef]
- Li, C.; Maier, J. Ionic space charge effects in lithium fluoride thin films. Solid State Ionics 2012, 225, 408–411. [Google Scholar] [CrossRef]
- Frenkel, J. Kinetic Theory of Liquids; Oxford University Press: New York, NY, USA, 1946. [Google Scholar]
- Wang, S.H.; Yue, J.; Dong, W.; Zuo, T.T.; Li, J.Y.; Liu, X.; Zhang, X.D.; Liu, L.; Shi, J.L.; Yin, Y.X.; et al. Tuning wettability of molten lithium via a chemical strategy for lithium metal anodes. Nat. Commun. 2019, 10, 4930. [Google Scholar] [CrossRef] [PubMed]
- Cha, E.; Yun, J.H.; Ponraj, R.; Kim, D.K. A mechanistic review of lithiophilic materials: Resolving lithium dendrites and advancing lithium metal-based batteries. Mater. Chem. Front. 2021, 5, 6294–6314. [Google Scholar] [CrossRef]
- Chen, Y.T.; Jena, A.; Pang, W.K.; Peterson, V.K.; Sheu, H.S.; Chang, H.; Liu, R.S. Voltammetric Enhancement of Li-Ion Conduction in Al-Doped Li7–xLa3Zr2O12 Solid Electrolyte. J. Phys. Chem. C 2017, 121, 15565–15573. [Google Scholar] [CrossRef]
- Reichert, S.; Flemming, J.; An, Q.; Vaynzof, Y.; Pietschmann, J.F.; Deibel, C. Improved evaluation of deep-level transient spectroscopy on perovskite solar cells reveals ionic defect distribution. arXiv 2019, arXiv:1910.04583. [Google Scholar]
- Zhu, Y.; Wu, S.; Pan, Y.; Zhang, X.; Yan, Z.; Xiang, Y. Reduced Energy Barrier for Li+ Transport Across Grain Boundaries with Amorphous Domains in LLZO Thin Films. Nanoscale Res. Lett. 2020, 15, 153. [Google Scholar] [CrossRef] [PubMed]
- Koresh, I.; Tang, Z.; Troczynski, T. A novel approach to prepare Li-La-Zr-O solid state electrolyte films by suspension plasma spray. Solid State Ionics 2021, 368, 115679. [Google Scholar] [CrossRef]
- Koresh, I.; Klein, B.A.; Tang, Z.; Michaelis, V.K.; Troczynski, T. Li ion transport properties of amorphous/crystalline Li-La-Zr-Nb-O solid electrolyte thick films prepared by suspension plasma spraying. Solid State Ionics 2022, 380, 115938. [Google Scholar] [CrossRef]
- Pervov, V.S.; Zotova, A.E. On Some Problems of Inorganic Supramolecular Chemistry. ChemPhysChem 2013, 14, 3865–3867. [Google Scholar] [CrossRef]
- Anosov, V.; Pogodin, S. Fundamental Principles of Physical-Chemical Analysis; AS: Moskow, Russia, 1947; pp. 269–309. [Google Scholar]
- Hassabis, D.; Kumaran, D.; Summerfield, C.; Botvinick, M. Neuroscience-Inspired Artificial Intelligence. Neuron 2017, 95, 245–258. [Google Scholar] [CrossRef]
- Hochreiter, S. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Graves, A. Supervised Sequence Labelling with Recurrent Neural Networks Supervised Sequence Labelling with Recurrent Neural Networks. Ph.D. Thesis, Technical University of Munich, Munich, Germany, 2008. [Google Scholar]
- Shahriari, B.; Swersky, K.; Wang, Z.; Adams, R.P.; de Freitas, N. Taking the Human Out of the Loop: A Review of Bayesian Optimization. Proc. IEEE 2016, 104, 148–175. [Google Scholar] [CrossRef]
- Kushner, H.J.; Yin, G. Stochastic Approximation Algorithms and Applications; Springer: New York, NY, USA, 1997. [Google Scholar]
- Mockus, J.; Tiesis, V.Z.A. Toward Global Optimization: Chapter The Application of Bayesian Methods for Seeking the Extremum; Elsevier: Amsterdam, The Netherlands, 1978; Volume 2. [Google Scholar]
- Hernandez-Lobato, J.; Adams, R. Probabilistic Backpropagation for Scalable Learning of Bayesian Neural Networks. In Proceedings of the Machine Learning Research, Lille, France, 7–9 July 2015; Volume 37. [Google Scholar]
- Frye, C.; Mijolla, D.; Begley, T.; Cowton, L.; Stanley, M.; Feige, I. Shapley Explainability on the Data Manifold. arXiv 2021, arXiv:2006.01272. [Google Scholar]
- Shapley, L. A value for n-person games. Contribution to the Theory of Games; Princeton University Press: Princeton, NJ, USA, 1953. [Google Scholar]
- Hernandez-Lobato, J.M.; Hoffman, M.W.; Ghahramani, Z. Predictive entropy search for efficient global optimization of black-box functions. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2014; pp. 918–926. [Google Scholar]
- Chen, R.J.; Huang, M.; Huang, W.Z.; Shen, Y.; Lin, Y.H.; Nan, C.W. Sol–gel derived Li–La–Zr–O thin films as solid electrolytes for lithium-ion batteries. J. Mater. Chem. A 2014, 2, 13277–13282. [Google Scholar] [CrossRef]
- Kalita, D.; Lee, S.; Lee, K.; Ko, D.; Yoon, Y. Ionic conductivity properties of amorphous Li–La–Zr–O solid electrolyte for thin film batteries. Solid State Ionics 2012, 229, 14–19. [Google Scholar] [CrossRef]
- Katsui, H.; Goto, T. Impedance of Cubic Li7La3Zr2O12 Film Deposited on Strontium Ruthenate Substrate by Chemical Vapor Deposition. Mater. Today Proc. 2017, 4, 11445–11448. [Google Scholar] [CrossRef]
- Kazyak, E.; Chen, K.H.; Wood, K.N.; Davis, A.L.; Thompson, T.; Bielinski, A.R.; Sanchez, A.J.; Wang, X.; Wang, C.; Sakamoto, J.; et al. Atomic Layer Deposition of the Solid Electrolyte Garnet Li7La3Zr2O12. Chem. Mater. 2017, 29, 3785–3792. [Google Scholar] [CrossRef]
- Kim, S.; Hirayama, M.; Taminato, S.; Kanno, R. Epitaxial growth and lithium ion conductivity of lithium-oxide garnet for an all solid-state battery electrolyte. Dalton Trans. 2013, 42, 13112–13117. [Google Scholar] [CrossRef]
- Loho, C.; Djenadic, R.; Bruns, M.; Clemens, O.; Hahn, H. Garnet-Type Li7La3Zr2O12Solid Electrolyte Thin Films Grown by CO2-Laser Assisted CVD for All-Solid-State Batteries. J. Electrochem. Soc. 2016, 164, A6131–A6139. [Google Scholar] [CrossRef]
- Loho, C.; Djenadic, R.; Mundt, P.; Clemens, O.; Hahn, H. On processing-structure-property relations and high ionic conductivity in garnet-type Li5La3Ta2O12 solid electrolyte thin films grown by CO2-laser assisted CVD. Solid State Ionics 2017, 313, 32–44. [Google Scholar] [CrossRef]
- Nong, J.; Xu, H.; Yu, Z.; Zhu, G.; Yu, A. Properties and preparation of Li–La–Ti–Zr–O thin film electrolyte. Mater. Lett. 2015, 154, 167–169. [Google Scholar] [CrossRef]
- Song, S.; Xu, Y.; Ruan, Y.; Wang, H.; Zhang, D.; Thokchom, J.; Mei, D. Isomeric Li-La-Zr-O Amorphous-Crystalline Composite Thin-Film Electrolytes for All-Solid-State Lithium Batteries. ACS Appl. Energy Mater. 2021, 4, 8517–8528. [Google Scholar] [CrossRef]
- Park, J.S.; Cheng, L.; Zorba, V.; Mehta, A.; Cabana, J.; Chen, G.; Doeff, M.M.; Richardson, T.J.; Park, J.H.; Son, J.W.; et al. Effects of crystallinity and impurities on the electrical conductivity of Li–La–Zr–O thin films. Thin Solid Film. 2015, 576, 55–60. [Google Scholar] [CrossRef]
- Rawlence, M.; Filippin, A.N.; Wäckerlin, A.; Lin, T.Y.; Cuervo-Reyes, E.; Remhof, A.; Battaglia, C.; Rupp, J.L.M.; Buecheler, S. Effect of Gallium Substitution on Lithium-Ion Conductivity and Phase Evolution in Sputtered Li7–3xGaxLa3Zr2O12 Thin Films. ACS Appl. Mater. Interfaces 2018, 10, 13720–13728. [Google Scholar] [CrossRef] [PubMed]
- Reinacher, J.; Berendts, S.; Janek, J. Preparation and electrical properties of garnet-type Li6BaLa2Ta2O12 lithium solid electrolyte thin films prepared by pulsed laser deposition. Solid State Ionics 2014, 258, 1–7. [Google Scholar] [CrossRef]
- Tadanaga, K.; Egawa, H.; Hayashi, A.; Tatsumisago, M.; Mosa, J.; Aparicio, M.; Duran, A. Preparation of lithium ion conductive Al-doped Li7La3Zr2O12 thin films by a sol–gel process. J. Power Sources 2015, 273, 844–847. [Google Scholar] [CrossRef]
- Tan, J.; Tiwari, A. Fabrication and Characterization of Li7La3Zr2O12 Thin Films for Lithium Ion Battery. ECS Solid State Lett. 2012, 1, Q57–Q60. [Google Scholar] [CrossRef]
- Zarabian, M.; Bartolini, M.; Pereira-Almao, P.; Thangadurai, V. X-ray Photoelectron Spectroscopy and AC Impedance Spectroscopy Studies of Li-La-Zr-O Solid Electrolyte Thin Film/LiCoO2 Cathode Interface for All-Solid-State Li Batteries. J. Electrochem. Soc. 2017, 164, A1133–A1139. [Google Scholar] [CrossRef]
- Jiang, J.; Zhang, L.; Hu, Y.; Guo, Y.; Chen, Z.; Jia, R.; Pendse, S.; Xiang, Y.; Wang, G.C.; Shi, Y.; et al. Metal–Insulator Transition of Single-Crystal V2O3 through van der Waals Interface Engineering. ACS Nano 2023, 17, 11783–11793. [Google Scholar] [CrossRef]
- Fluri, A.; Pergolesi, D.; Wokaun, A.; Lippert, T. Stress generation and evolution in oxide heteroepitaxy. Phys. Rev. B 2018, 97, 125412. [Google Scholar] [CrossRef]
- Matthews, J.; Blakeslee, A. Defects in epitaxial multilayers. J. Cryst. Growth 1974, 27, 118–125. [Google Scholar] [CrossRef]
- Matthews, J.W.; Mader, S.; Light, T.B. Accommodation of Misfit Across the Interface between Crystals of Semiconducting Elements or Compounds. J. Appl. Phys. 1970, 41, 3800–3804. [Google Scholar] [CrossRef]
- Van Der Merwe, J.H. Crystal Interfaces. Part I. Semi-Infinite Crystals. J. Appl. Phys. 1963, 34, 117–122. [Google Scholar] [CrossRef]
- Cammarata, R.C.; Sieradzki, K. Effects of surface stress on the elastic moduli of thin films and superlattices. Phys. Rev. Lett. 1989, 62, 2005–2008. [Google Scholar] [CrossRef] [PubMed]
- Cammarata, R.C.; Sieradzki, K.; Spaepen, F. Simple model for interface stresses with application to misfit dislocation generation in epitaxial thin films. J. Appl. Phys. 2000, 87, 1227–1234. [Google Scholar] [CrossRef]
- Prandtl, L. Ein Gedankenmodell zur kinetischen Theorie der festen Körper. Z. Angew. Math. Mech. 1928, 8, 85–106. [Google Scholar] [CrossRef]
- Frenkel, Y.I.; Kontorova, T.A. To the Theory of Plastic Deformation and Twinning. Zh. Eksp. Teor. Fiz. 1938, 8, 89. [Google Scholar]
- Frenkel, Y.; Kontorova, T. On the Theory of Plastic Deformation and Twinning. Zh. Eksp. Teor. Fiz. 1938, 8, 1340. [Google Scholar]
- Braun, O.; Yuri, S.K. The Frenkel-Kontorova Model: Concepts, Methods, and Applications; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Pervov, V.S.; Makhonina, E.V. Incommensurate suprastructures: New problems of inorganic solid-state chemistry. Russ. Chem. Rev. 2000, 69, 481. [Google Scholar] [CrossRef]
- Pervov, V.S.; Mikheikin, I.D.; Makhonina, E.V.; Butskii, V.D. Supramolecular ensembles in eutectic alloys. Russ. Chem. Rev. 2003, 72, 759–768. [Google Scholar] [CrossRef]
- Mikheikin, I.D.; Kuznetsov, M.Y.; Makhonina, E.V.; Pervov, V.S. Defects in Inorganic Suprastructures with Incommensurate Structural Elements: The Static Frenkel–Kontorova Model for Finite Systems. Dokl. Phys. Chem. 2001, 376, 52–55. [Google Scholar] [CrossRef]
- Bruinsma, R.; Zangwill, A. Structural transitions in epitaxial overlayers. J. Physique 1986, 47, 2055–2073. [Google Scholar] [CrossRef]
- Sills, R.B.; Bertin, N.; Aghaei, A.; Cai, W. Dislocation Networks and the Microstructural Origin of Strain Hardening. Phys. Rev. Lett. 2018, 121, 085501. [Google Scholar] [CrossRef] [PubMed]
- Connell, J.G.; Zhu, Y.; Zapol, P.; Tepavcevic, S.; Sharafi, A.; Sakamoto, J.; Curtiss, L.A.; Fong, D.D.; Freeland, J.W.; Markovic, N.M. Crystal Orientation-Dependent Reactivity of Oxide Surfaces in Contact with Lithium Metal. ACS Appl. Mater. Interfaces 2018, 10, 17471–17479. [Google Scholar] [CrossRef]
- Assat, G.; Tarascon, J.M. Fundamental understanding and practical challenges of anionic redox activity in Li-ion batteries. Nat. Energy 2018, 3, 373–386. [Google Scholar] [CrossRef]
- Saubanère, M.; McCalla, E.; Tarascon, J.M.; Doublet, M.L. The intriguing question of anionic redox in high-energy density cathodes for Li-ion batteries. Energy Environ. Sci. 2016, 9, 984–991. [Google Scholar] [CrossRef]
- Thouless, M.D. Modeling the Development and Relaxation of Stresses in Films. Annu. Rev. Mater. Sci. 1995, 25, 69–96. [Google Scholar] [CrossRef]
- Chen, Y.; He, M.; Zhao, N.; Fu, J.; Huo, H.; Zhang, T.; Li, Y.; Xu, F.; Guo, X. Nanocomposite intermediate layers formed by conversion reaction of SnO2 for Li/garnet/Li cycle stability. J. Power Sources 2019, 420, 15–21. [Google Scholar] [CrossRef]
- Maier, J. Defect chemistry at interfaces. Solid State Ionics 1994, 70/71, 43. [Google Scholar] [CrossRef]
- Lee, D.; You, D.; Lee, D.; Li, X.; Kim, S. Machine-Learning-Guided Prediction Models of Critical Temperature of Cuprates. J. Phys. Chem. Lett. 2021, 12, 6211–6217. [Google Scholar] [CrossRef]
- Yang, G.; Wu, K. Two-dimensional nonlinear optical materials predicted by network visualization. Mol. Syst. Des. Eng. 2019, 4, 586–596. [Google Scholar] [CrossRef]
- Patel, A.G.; Johnson, L.; Arroyave, R.; Lutkenhaus, J.L. Design of multifunctional supercapacitor electrodes using an informatics approach. Mol. Syst. Des. Eng. 2019, 4, 654–663. [Google Scholar] [CrossRef]
- Kireeva, N.V.; Tsivadze, A.Y.; Pervov, V.S. Modeling ionic conductivity and activation energy in garnet-structured solid electrolytes: The role of composition, grain boundaries and processing. Solid State Ionics 2023, 399, 116293. [Google Scholar] [CrossRef]
- Kireeva, N.; Solov’ev, V.P. Machine learning analysis of microwave dielectric properties for seven structure types: The role of the processing and composition. J. Phys. Chem. Solids 2021, 156, 110178. [Google Scholar] [CrossRef]
- Graser, J.; Kauwe, S.K.; Sparks, T.D. Machine Learning and Energy Minimization Approaches for Crystal Structure Predictions: A Review and New Horizons. Chem. Mater. 2018, 30, 3601–3612. [Google Scholar] [CrossRef]
- Young, S.R.; Maksov, A.; Ziatdinov, M.; Cao, Y.; Burch, M.; Balachandran, J.; Li, L.; Somnath, S.; Patton, R.M.; Kalinin, S.V.; et al. Data mining for better material synthesis: The case of pulsed laser deposition of complex oxides. J. Appl. Phys. 2018, 123, 115303. [Google Scholar] [CrossRef]
- Borvick, E.; Anderson, A.Y.; Barad, H.N.; Priel, M.; Keller, D.A.; Ginsburg, A.; Rietwyk, K.J.; Meir, S.; Zaban, A. Process-Function Data Mining for the Discovery of Solid-State Iron-Oxide PV. ACS Comb. Sci. 2017, 19, 755–762. [Google Scholar] [CrossRef] [PubMed]
- Takeda, H.; Fukuda, H.; Nakano, K.; Hashimura, S.; Tanibata, N.; Nakayama, M.; Ono, Y.; Natori, T. Process optimisation for NASICON-type solid electrolyte synthesis using a combination of experiments and bayesian optimisation. Mater. Adv. 2022, 3, 8141–8148. [Google Scholar] [CrossRef]
- Olivetti, E.A.; Cole, J.M.; Kim, E.; Kononova, O.; Ceder, G.; Han, T.Y.J.; Hiszpanski, A.M. Data-driven materials research enabled by natural language processing and information extraction. Appl. Phys. Rev. 2020, 7, 041317. [Google Scholar] [CrossRef]
- He, T.; Huo, H.; Bartel, C.J.; Wang, Z.; Cruse, K.; Ceder, G. Precursor recommendation for inorganic synthesis by machine learning materials similarity from scientific literature. Sci. Adv. 2023, 9, eadg8180. [Google Scholar] [CrossRef]
- Torrisi, S.B.; Carbone, M.R.; Rohr, B.A.; Montoya, J.H.; Ha, Y.; Yano, J.; Suram, S.K.; Hung, L. Random forest machine learning models for interpretable X-ray absorption near-edge structure spectrum-property relationships. NPJ Comput. Mater. 2020, 6, 109. [Google Scholar] [CrossRef]
- Tiong, L.C.O.; Kim, J.; Han, S.S.; Kim, D. Identification of crystal symmetry from noisy diffraction patterns by a shape analysis and deep learning. NPJ Comput. Mater. 2020, 6, 196. [Google Scholar] [CrossRef]
- Xu, L.; Hoffman, N.; Wang, Z.; Xu, H. Harnessing structural stochasticity in the computational discovery and design of microstructures. Mater. Des. 2022, 223, 111223. [Google Scholar] [CrossRef]
- Wodo, O.; Broderick, S.; Rajan, K. Microstructural informatics for accelerating the discovery of processing-microstructure-property relationships. MRS Bull. 2016, 41, 603–609. [Google Scholar] [CrossRef]
- Aquistapace, F.; Amigo, N.; Troncoso, J.F.; Deluigi, O.; Bringa, E.M. MultiSOM: Multi-layer Self Organizing Maps for local structure identification in crystalline structures. Comput. Mater. Sci. 2023, 227, 112263. [Google Scholar] [CrossRef]
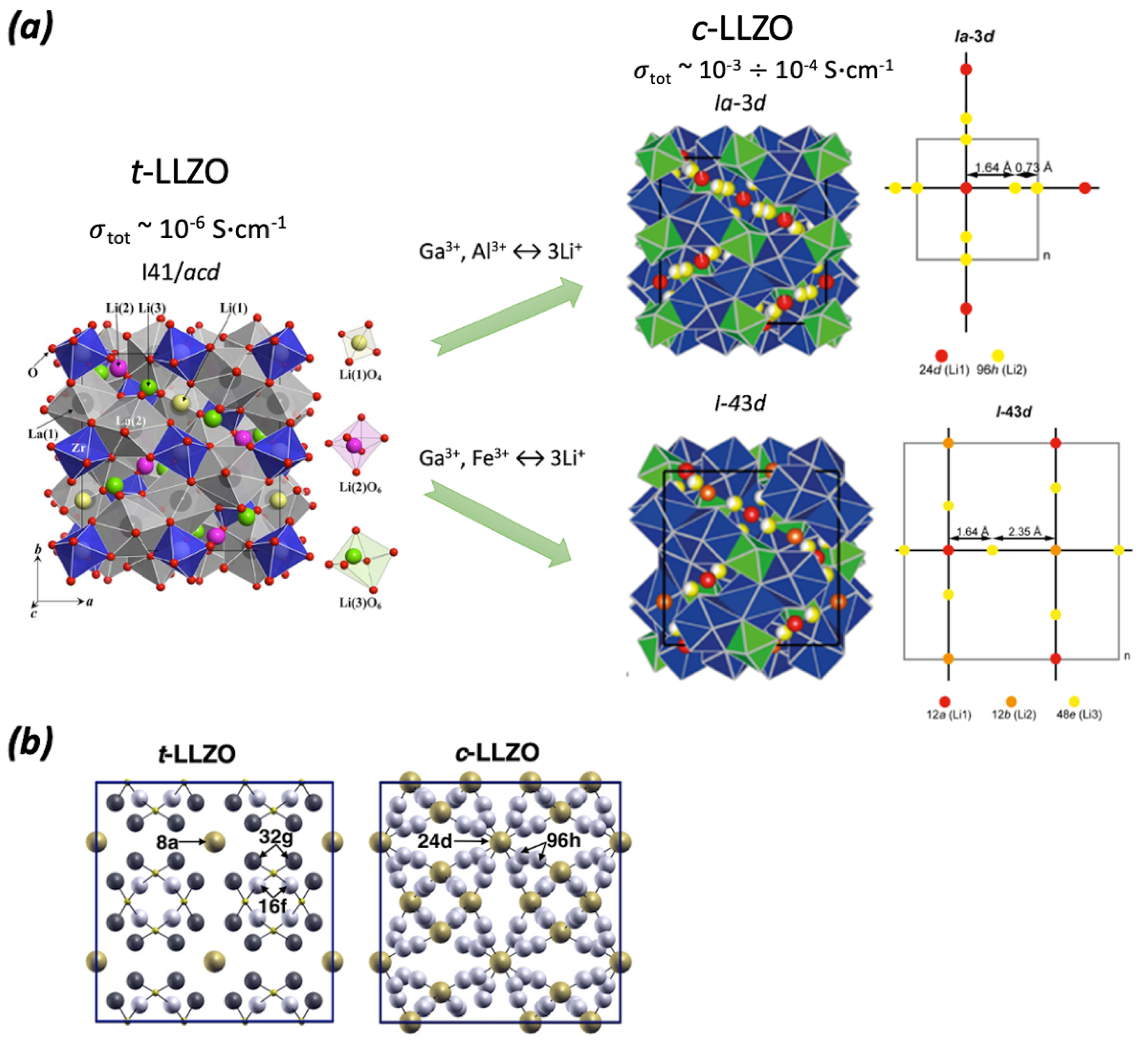
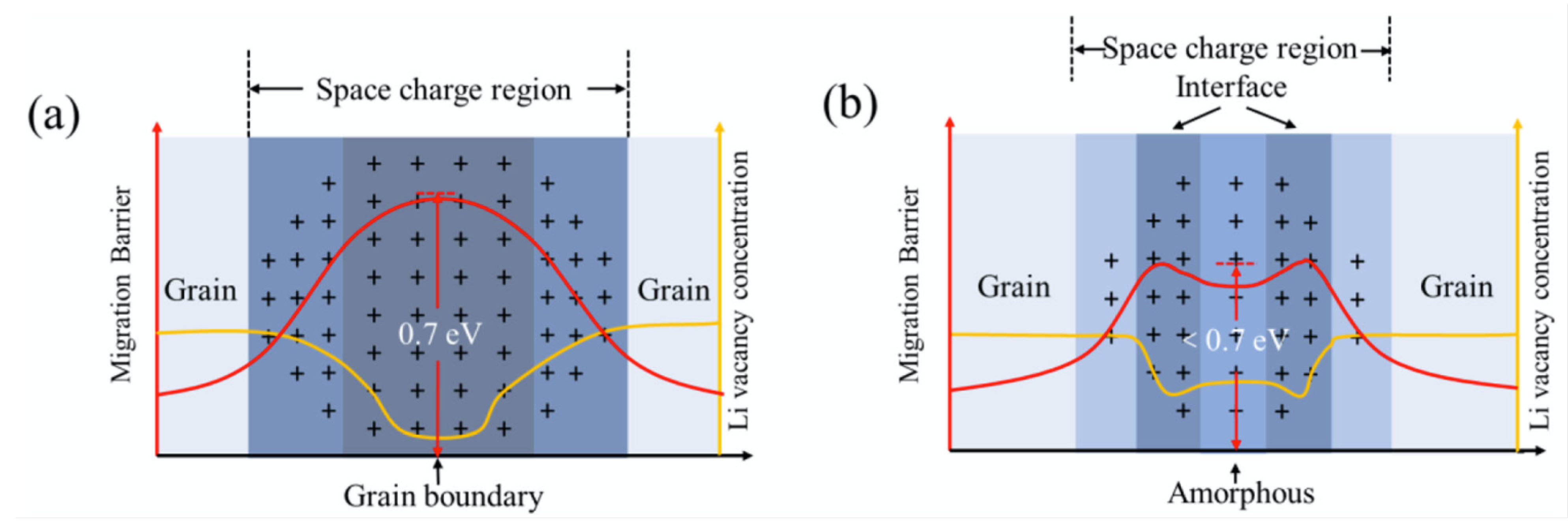
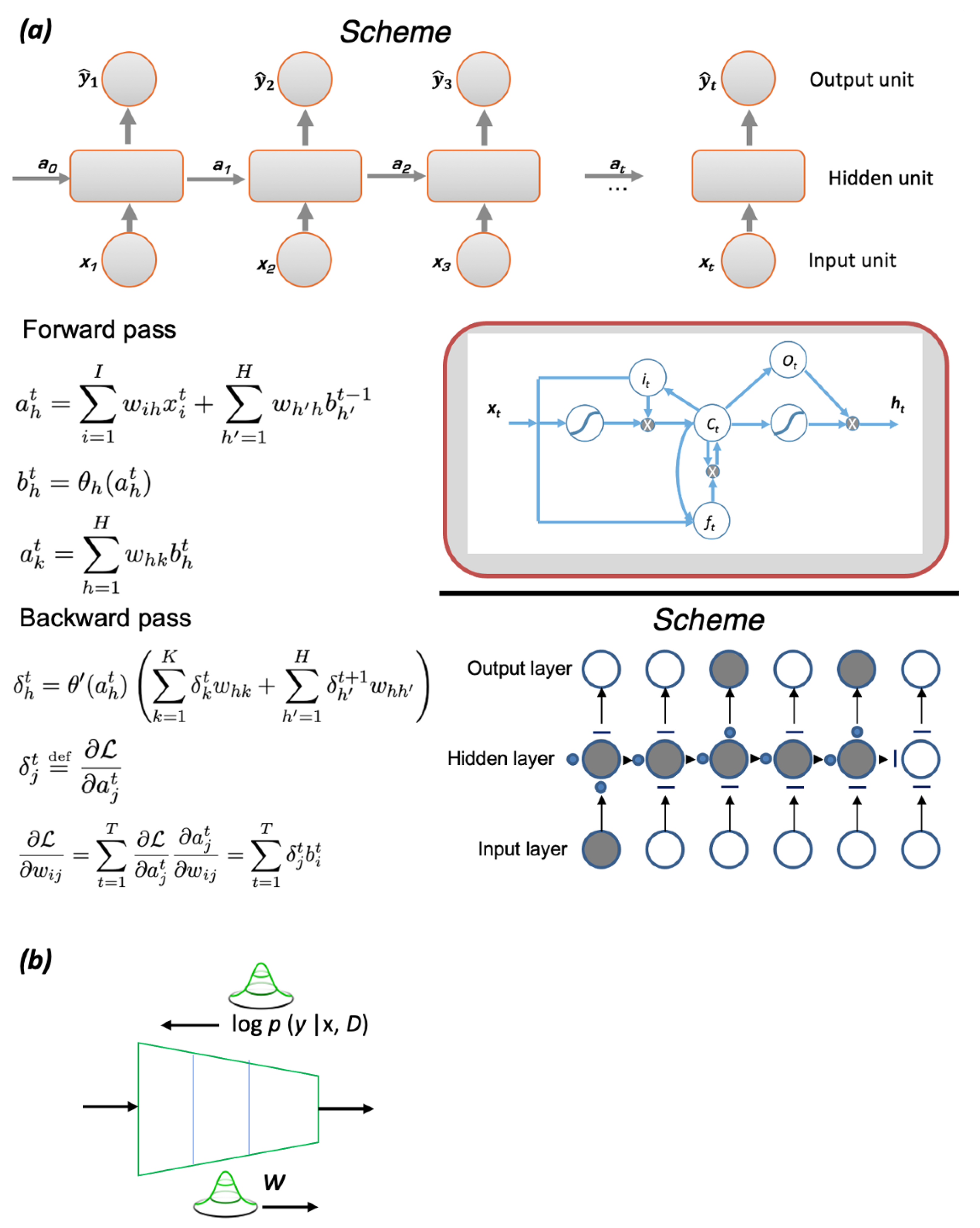
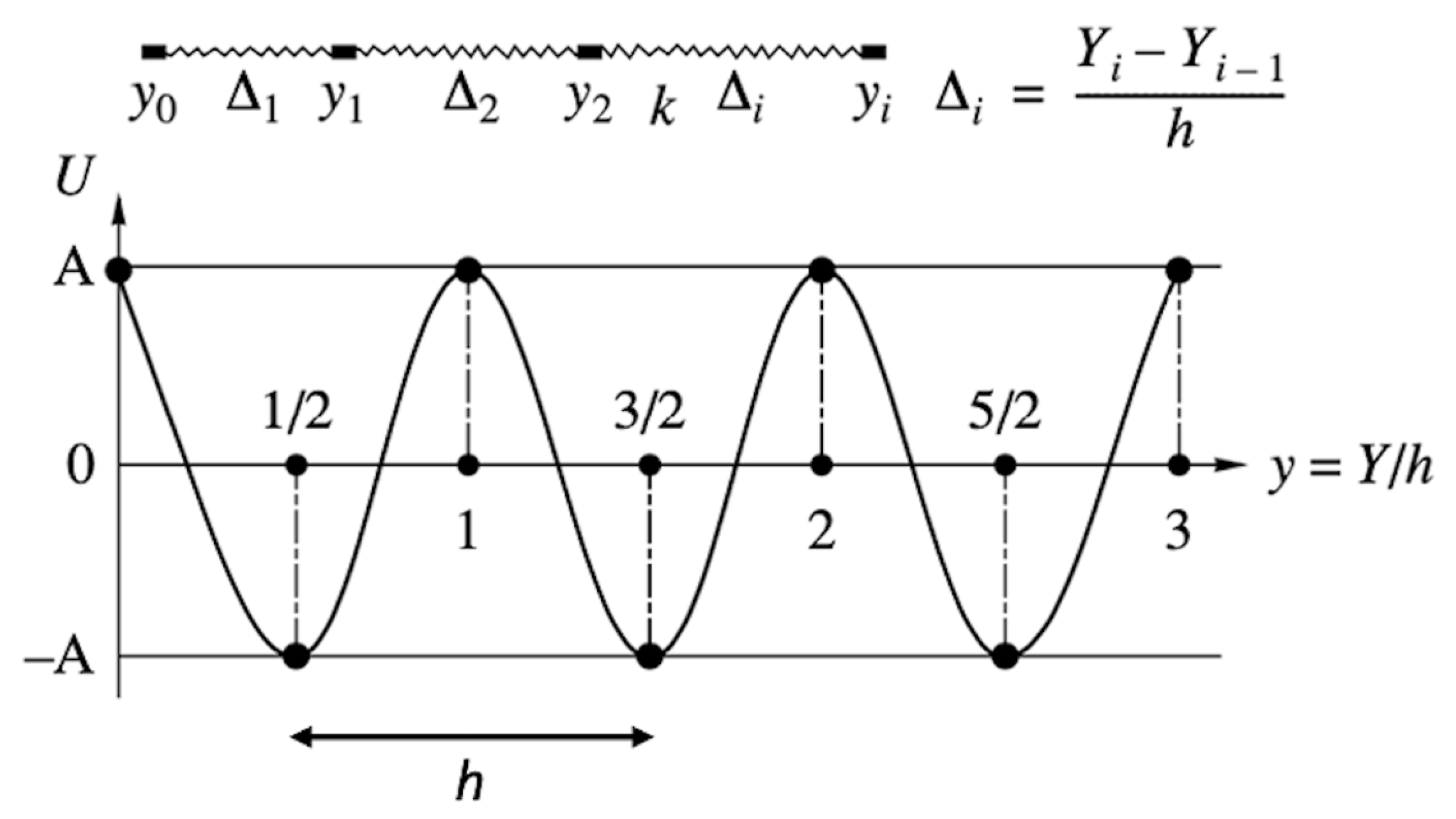

| Ref. | Target Compound/Precursors | Method of Deposition | Deposition Temperature | Substrate | Structure | Film Thickness, nm | Conductivity, S cm−1 |
|---|---|---|---|---|---|---|---|
| [62] | Li-La-Zr sol | Sol-gel: spin-coating | 600 | Si-Pt | amorphous | 307 nm | 1.67 × 10 |
| [62] | Li-La-Zr sol | Sol-gel: spin-coating | 700 | Si-Pt | amorphous | 307 nm | 1.10 × 10 |
| [62] | Li-La-Zr sol | Sol-gel: spin coating | 800 | Si-Pt | amorphous | 307 nm | 8.53 × 10 |
| [62] | Li-La-Zr sol | Sol-gel: spin coating | 600 | Si-Pt | amorphous | 130 nm | 3.56 × 10 |
| [5] | LiAlLaZrTaO | PE-CVD | 50 | SiN | amorphous | 500 nm | 2.86 × 10 |
| [5] | LiAlLaZrTaO | PE-CVD | 300 | SiN | amorphous | 500 nm | 2.39 × 10 |
| [5] | LiAlLaZrTaO | PE-CVD | 500 | SiN | amorphous | 500 nm | 4.27 × 10 |
| [63] | Li–La–Zr–O | RF magnetron sputtering | 27 | SiO-Si | amorphous | 561 nm | 4.00 × 10 |
| [64] | LLZO | CVD | 950 | SrRuO | c-LLZO | 4500 nm | 1.40 × 10 |
| [65] | Li tert-butoxide, La tris-diisopropylformamidinate, tetrakis(dimethylamido)zirconium, trimethylaluminium | ALD | 27 | Si (100) | amorphous | 86.5 nm | 1.00 × 10 |
| [66] | LLZO | PLD | 700 | GGG (001) | c-LLZO | 26.2 nm | 2.50 × 10 |
| [66] | LLZO | PLD | 700 | GGG (111) | c-LLZO | 30.3 nm | 1.00 × 10 |
| [67] | 2,2,6,6-tetramethyl-3,5-heptanedionato lithium, lanthanum (III) acetylacetonate hydrate, zirconium (IV) acetylacetonate | LA-CVD | 700 | Pt | t-LLZO | 850 nm | 4.20 × 10 |
| [68] | 2,2,6,6-tetramethyl-3,5-heptanedionato lithium, lanthanum (III) acetylacetonate hydrate, tantalum (V) tetraethoxyacetylacetonate | LA-CVD | 600 | Pt | amorphous | 500 nm | 2.10 × 10 |
| [69] | LLTO | Magnetron sputtering | 300 | ITO | amorphous | 530.4 nm | 3.68 × 10 |
| [69] | LLZTO | Magnetron sputtering | 300 | ITO | amorphous | 611.5 nm | 2.83 × 10 |
| [70] | LLZO | Sol-gel: spin-coating | 600 | Si (100) | amorphous | 720 nm | 3.90 × 10 |
| [68] | 2,2,6,6-tetramethyl-3,5-heptanedionato lithium, lanthanum (III) acetylacetonate hydrate, tantalum (V) tetraethoxyacetylacetonate | LA-CVD | 700 | Pt | c-LLZO | 1400 nm | 2.93 × 10 |
| [69] | LiLaTiO, LiLaZrO (LLTO) | RF magnetron sputtering | 300 | ITO | amorphous | 530.4 nm | 3.68 × 10 |
| [69] | LiLaTiO, LiLaZrO (LLTO) | RF magnetron sputtering | 300 | ITO | amorphous | 611.5 nm | 2.83 × 10 |
| [69] | LiLaTiO, LiLaZrO (LLTO) | RF magnetron sputtering | 300 | ITO | amorphous | 593.6 nm | 6.18 × 10 |
| [71] | LiLaZrO | PLD | 600 | MgO (100) | c-LLZO+t-LLZO | 200 nm | 1.61 × 10 |
| [72] | LiLaZrO, LiO, GaO | RF magnetron sputtering | 27 | MgO (100) | amorphous | 600 nm | 1.61 × 10 |
| [73] | LiBaLaTaO | PLD | 550 | MgO (100) | c-LLZO | 200 nm | 1.70 × 10 |
| [74] | Li-La-Zr sol | Sol-gel: dip-coating | 900 | MgO (100) | c-LLZO | 1000 nm | 2.80 × 10 |
| [75] | LLZO | PLD | 27 | STO (100) | amorphous | 1000 nm | 3.35 × 10 |
| [75] | LLZO | PLD | 800 | STO (100) | c-LLZO | 1000 nm | 1.78 × 10 |
| [76] | Li-La-Zr sol | Sol-gel: spin-coating | 400 | MgO (100) | t-LLZO+c-LLZO+ LaZrO | 760 nm | 1.00 × 10 |
| Substrate | Crystal Structure | Lattice Constant/ Mismatch | , K−1 | Poisson’s Coefficient | Young’s Modulus E, GPa | Bulk Modulus B, GPa | Shear Modulus G, GPa | Dielectric Constant |
|---|---|---|---|---|---|---|---|---|
| Si (100) | amorphous | 2.6 × 10 | 0.22 | 162 | 97.7 | 66.39 | 11.68 | |
| SiN | amorphous | 3.3 × 10 | 0.27 | 297 | 241 | 116.9 | 10 | |
| SiO | amorphous | 5.6 × 10 | 0.17 | 73 | 36.8 | 31.2 | 3.9 | |
| SrRuO | Cubic, Pmm | 3.95/−0.09 | 1.03 × 10 | 0.31 | 161 | 192.3 | 60.1 | na |
| Pt | Cubic, Fmm | 3.92/−0.09 | 8.9 × 10 | 0.38 | 168 | 230 | 60.87 | 58 |
| ITO | amorphous | 8.5 × 10 | 0.33 | 116 | 99 | 43.6 | 3.33 | |
| MgO (100) | Cubic, Fmm | 4.212/−0.03 | 1.5 × 10 | 0.18 | 249 | 155 | 105.5 | 9.5 |
| SrTiO (100) | Cubic, Pmm | 3.94/−0.09 | 2.98 × 10 | 0.24 | 277 | 173 | 111.7 | 300 |
| GGG (001), (111) | Cubic, Iad | 12.383/−0.05 | 8.2 × 10 | 0.28 | 222 | 169 | 86.7 | 12.24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kireeva, N.; Tsivadze, A.Y.; Pervov, V.S. Predicting Ionic Conductivity in Thin Films of Garnet Electrolytes Using Machine Learning. Batteries 2023, 9, 430. https://doi.org/10.3390/batteries9090430
Kireeva N, Tsivadze AY, Pervov VS. Predicting Ionic Conductivity in Thin Films of Garnet Electrolytes Using Machine Learning. Batteries. 2023; 9(9):430. https://doi.org/10.3390/batteries9090430
Chicago/Turabian StyleKireeva, Natalia, Aslan Yu. Tsivadze, and Vladislav S. Pervov. 2023. "Predicting Ionic Conductivity in Thin Films of Garnet Electrolytes Using Machine Learning" Batteries 9, no. 9: 430. https://doi.org/10.3390/batteries9090430






