Stress Analysis and Stiffness Degradation of Open Cracks Composite Laminates Subjected to External Loads
Abstract
:1. Introduction
2. Boundary Conditions and Stress Components
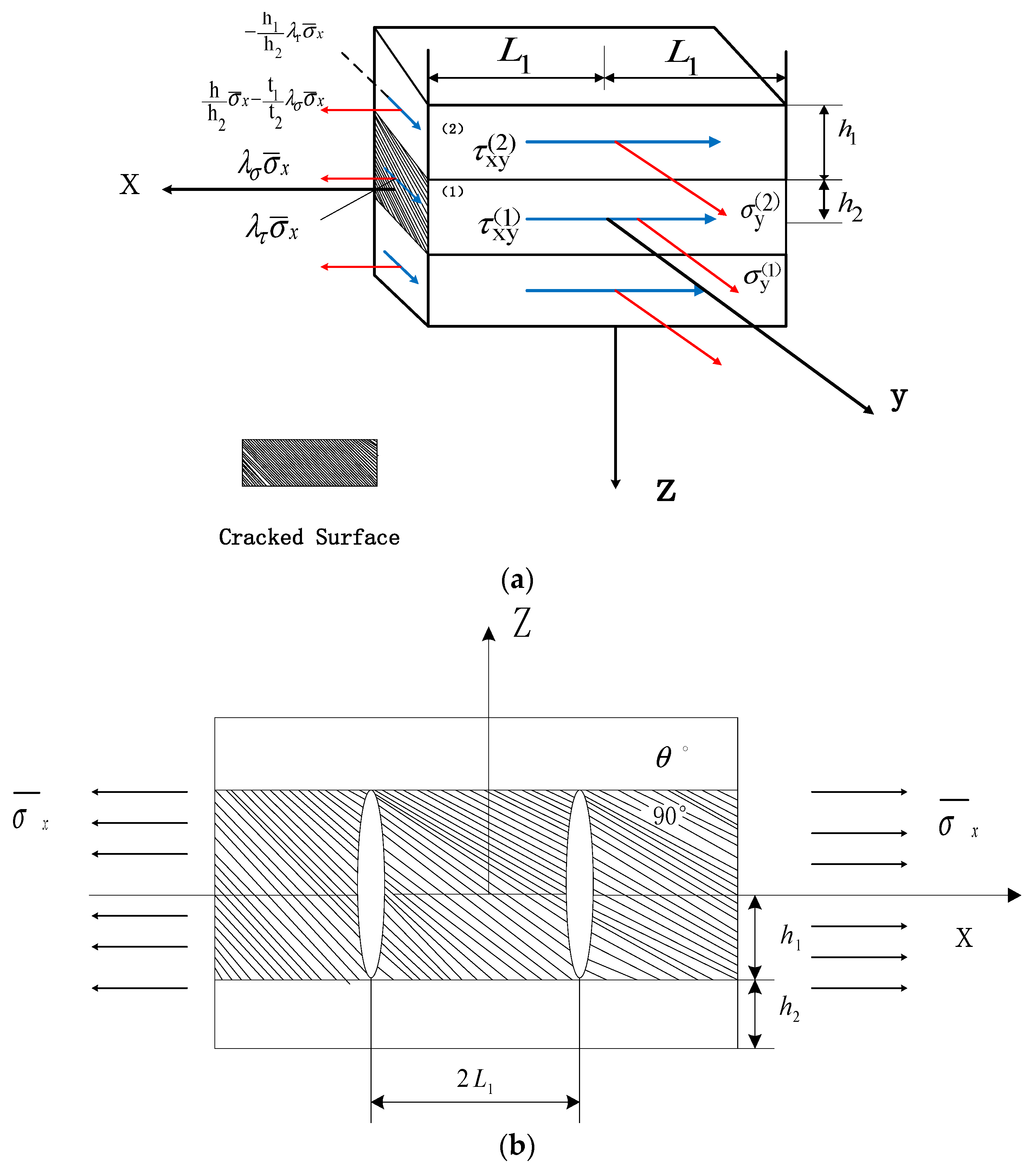
2.1. Element Volume Model
2.2. No Thickness Spring Model
2.3. Boundary Conditions
2.4. The Stress Components Within Each Layer
3. Governing Equation and Supplementary Equation
3.1. Establishing Governing Equations and Supplementary Equations
3.2. Solution to Governing and Supplementary Equations
4. Stiffness Degradation Research
4.1. Assumed Stress Distributions
4.2. Minimization of Complementary Energy
4.3. Shear Modulus Expression
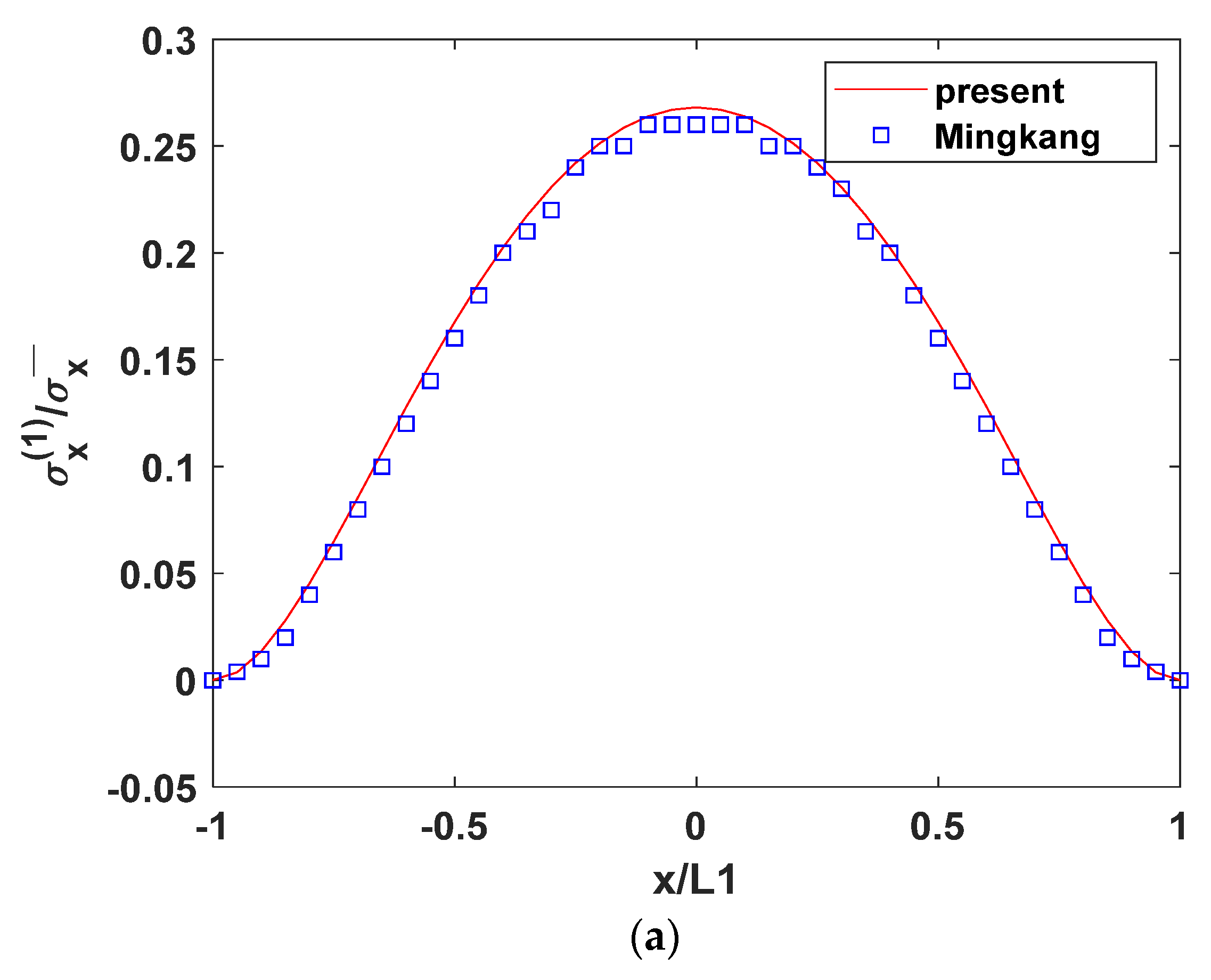
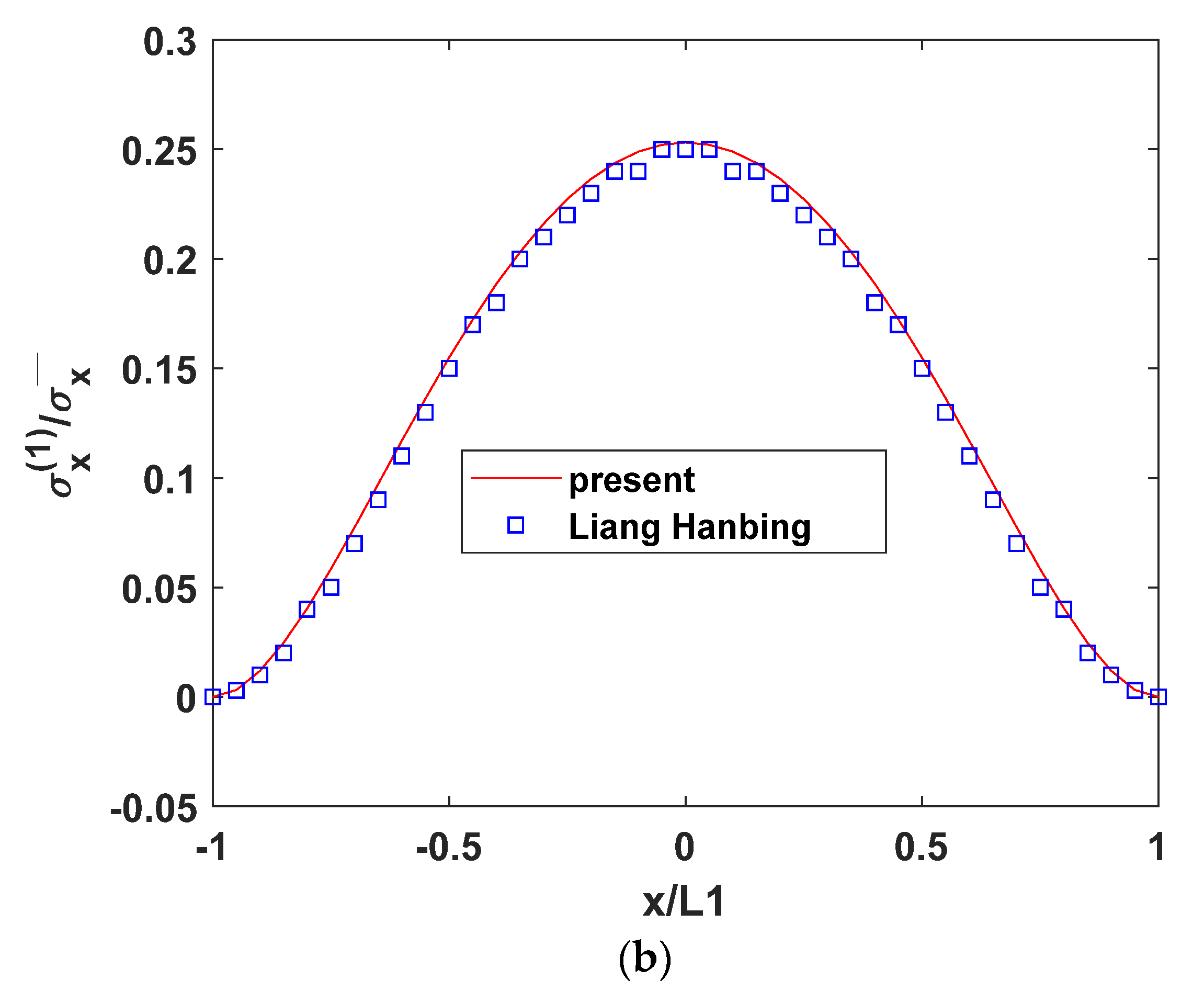
5. Validation of Model Feasibility
6. Stress Distribution Analysis
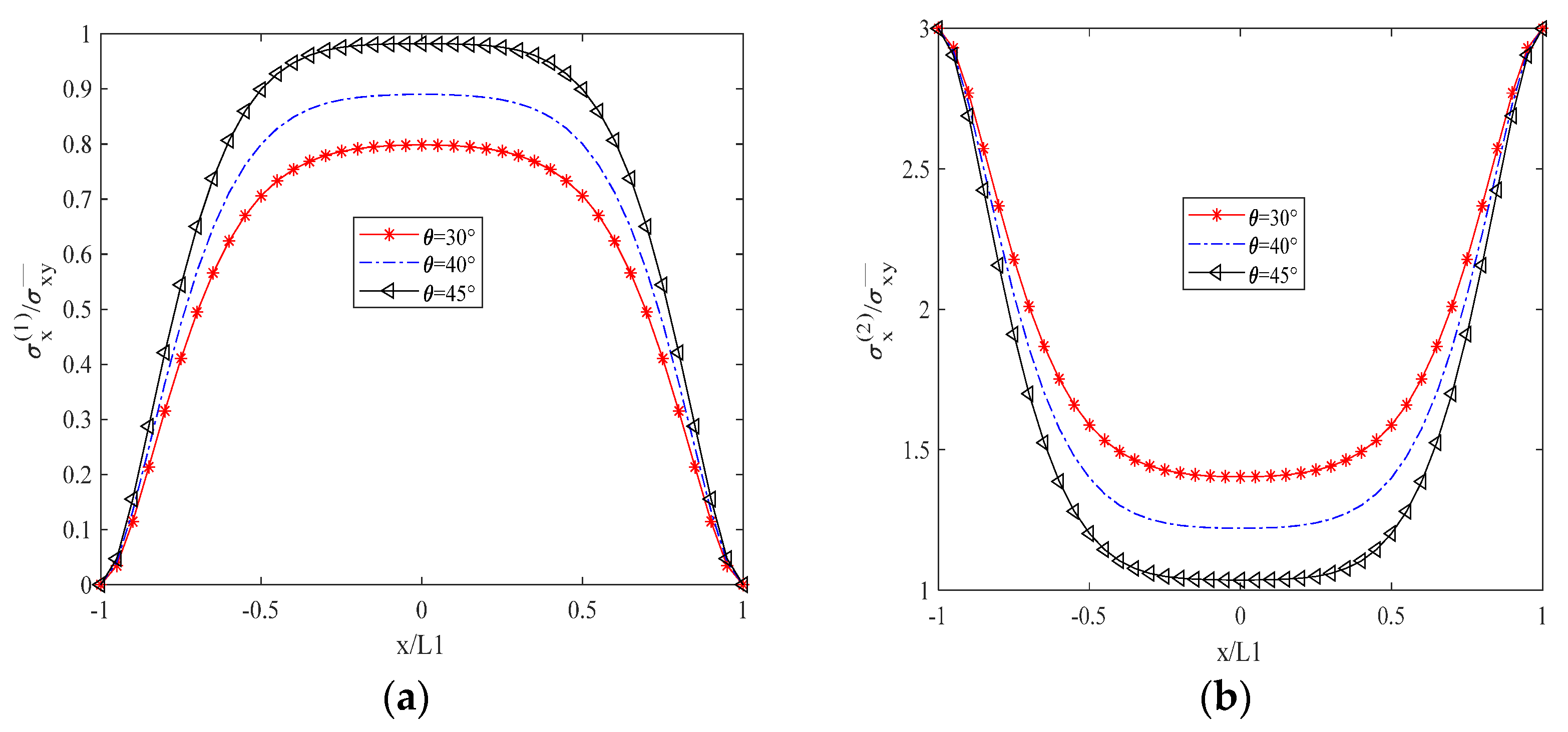
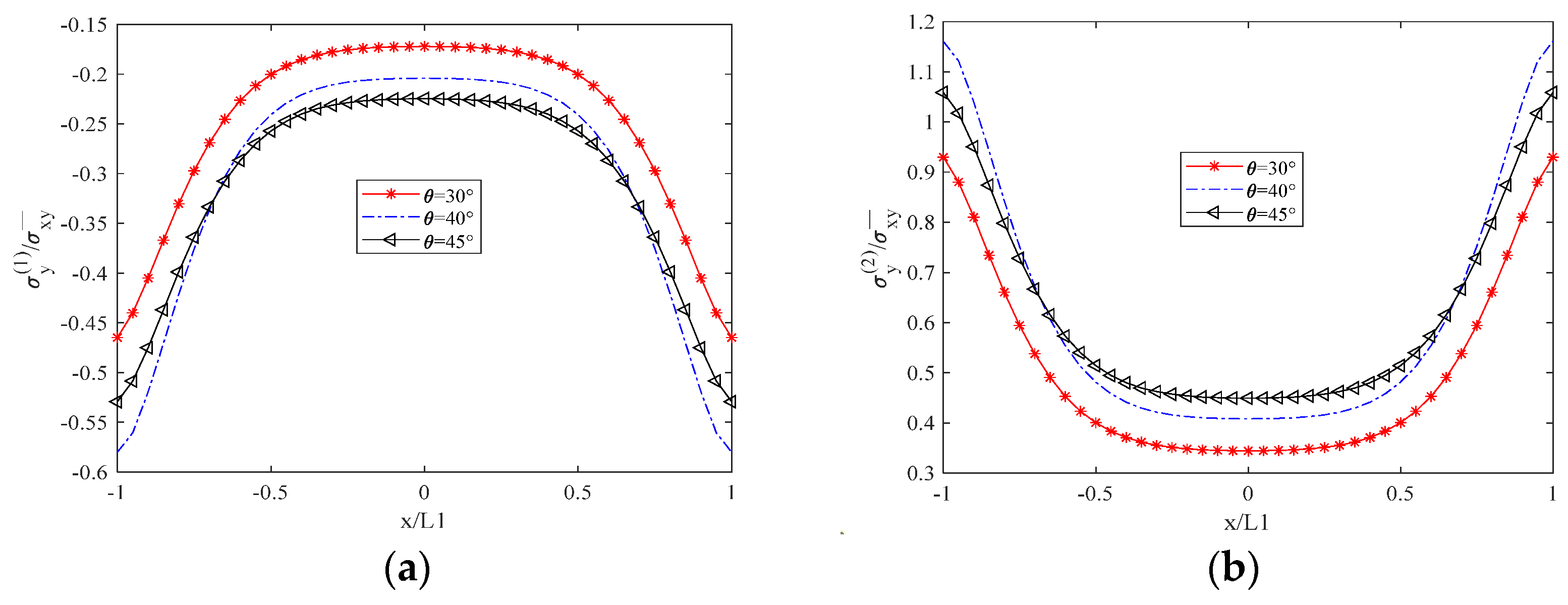
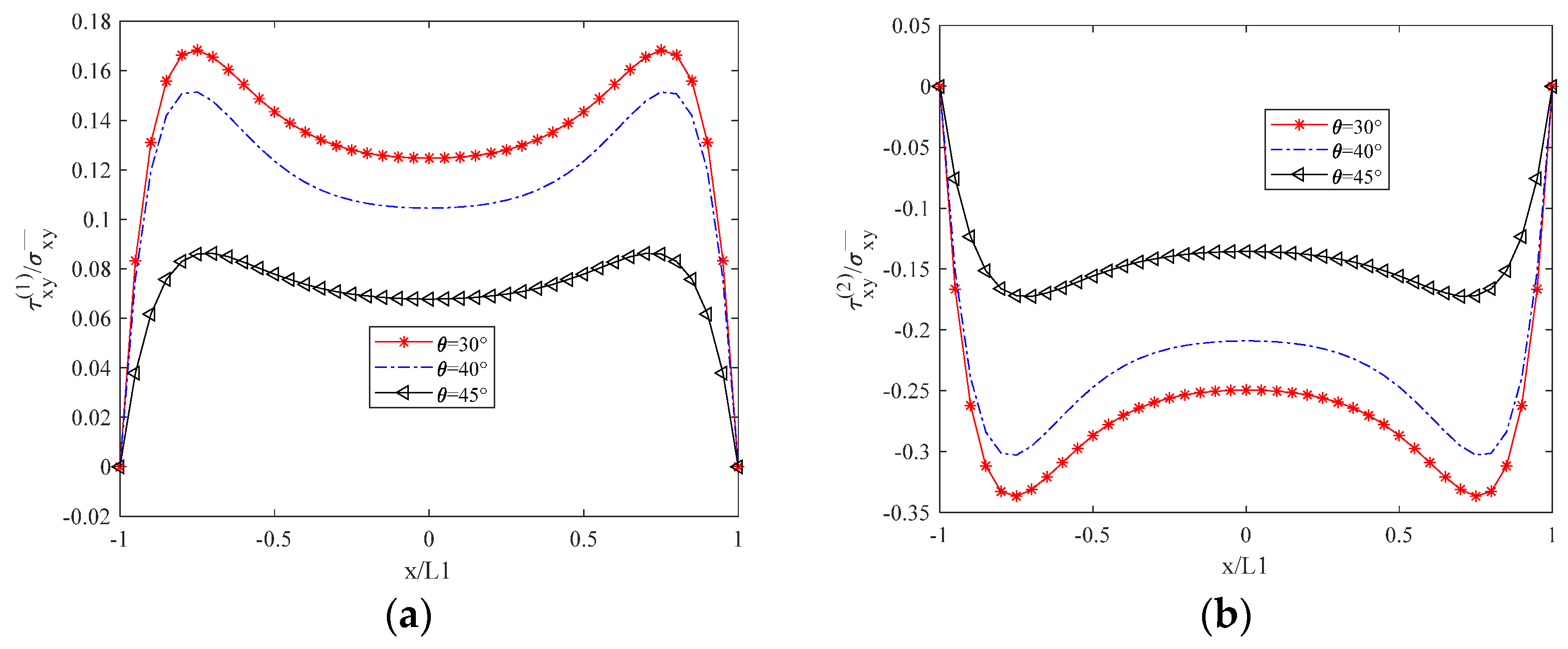
6.1. Influence of Fiber Laying Angle on Stress Distribution of Laminates with Matrix Cracks
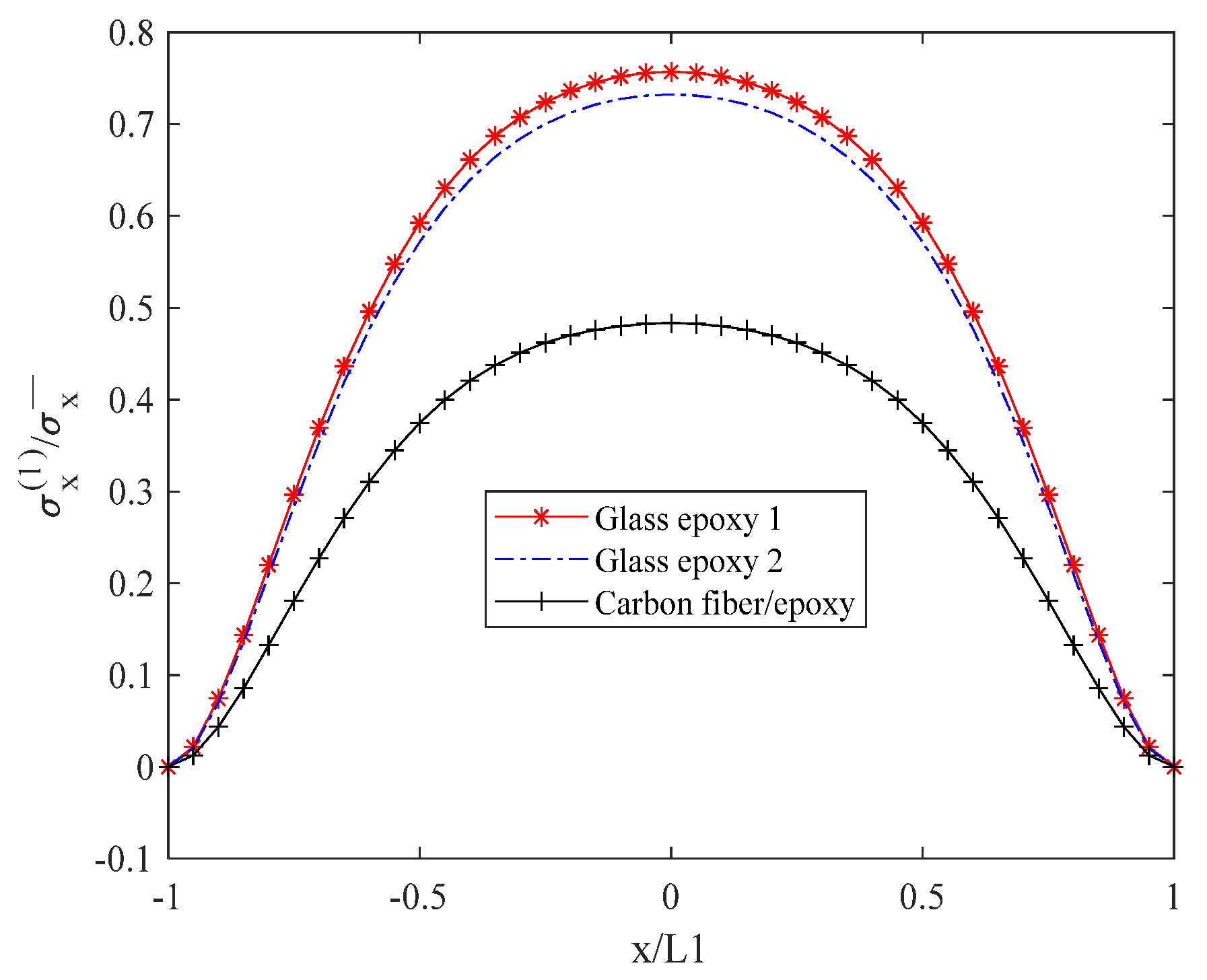
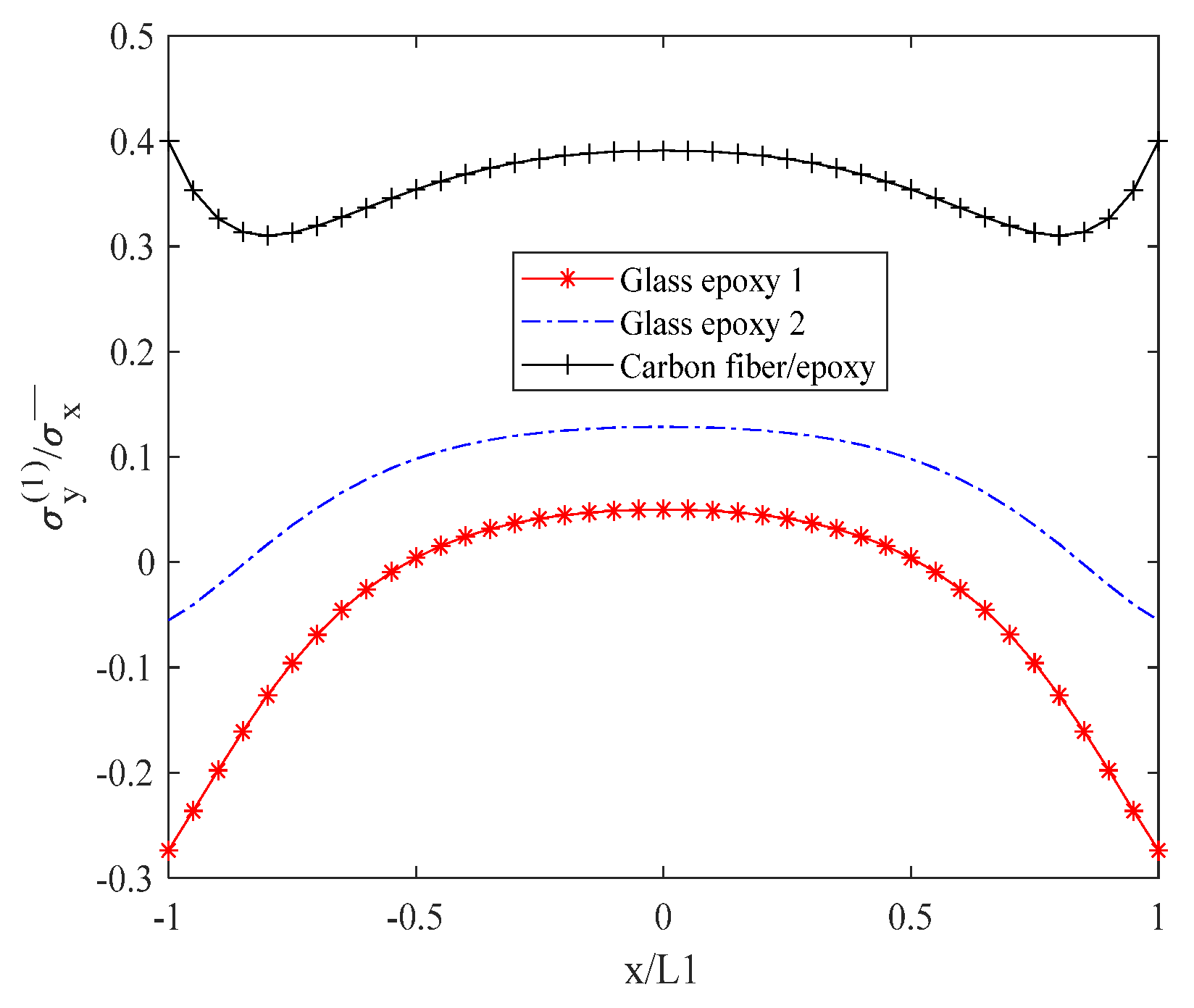
6.2. Influence of Material Properties on Stress Distribution of Laminates with Matrix Cracks
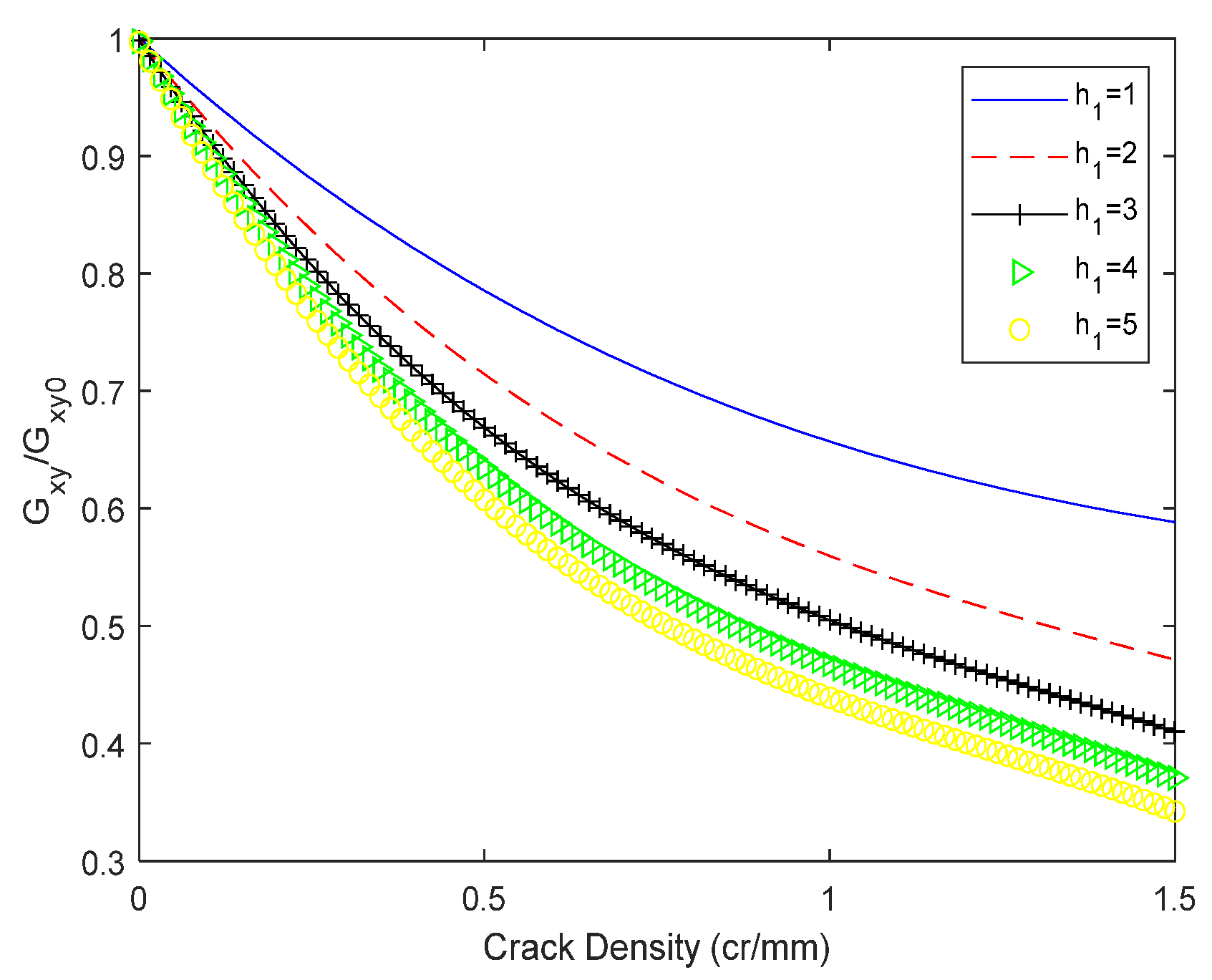
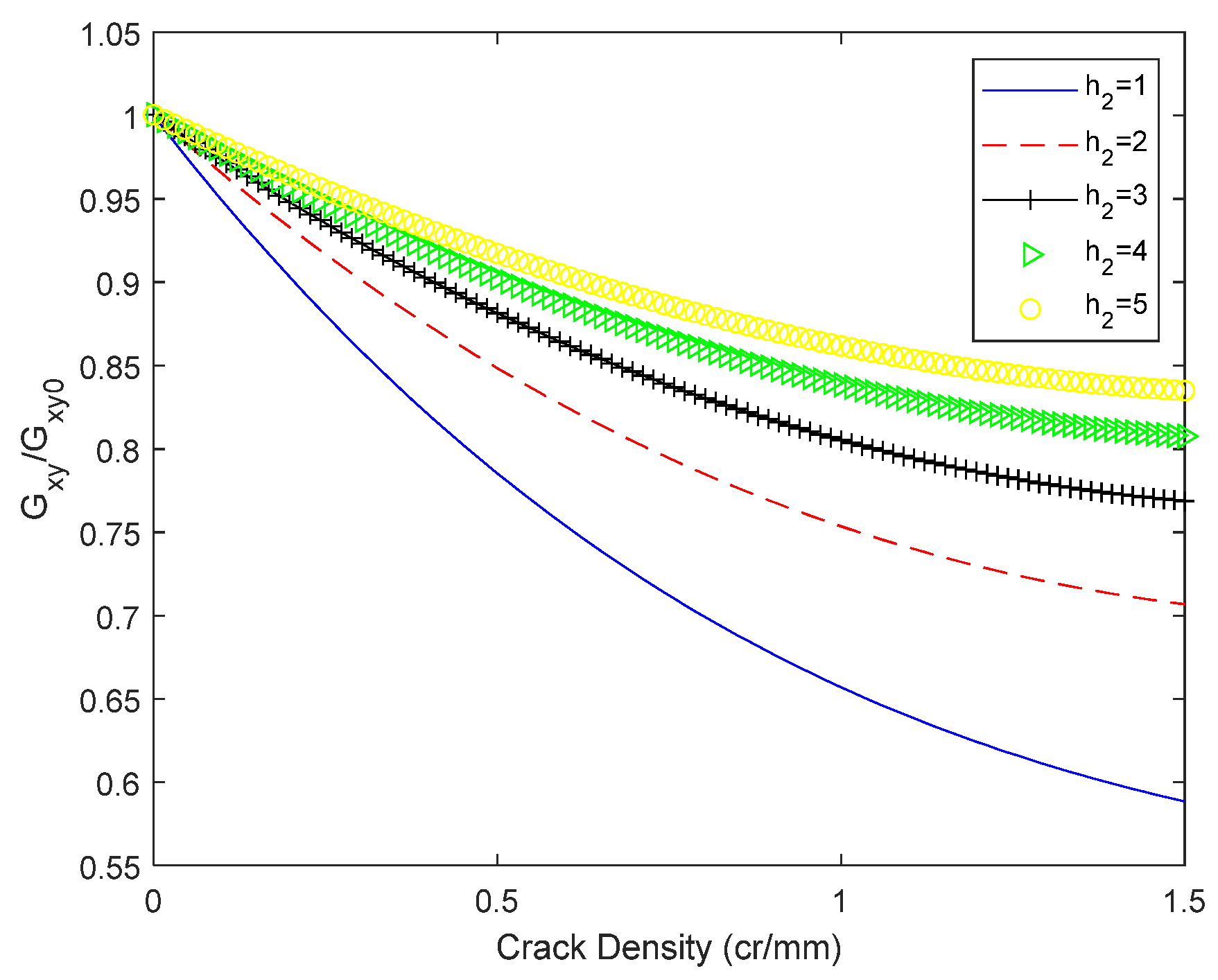
7. Shear Modulus Evolution
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Su, Y.; Zhu, J.; Long, X.; Zhao, L.; Chen, C.; Liu, C. Statistical effects of pore features on mechanical properties and fracture behaviours of heterogeneous random porous materials by phase-field modelling. Int. J. Solids Struct. 2023, 264, 112098. [Google Scholar] [CrossRef]
- Huang, M.; Wang, L.; Wang, C.; Li, Y.; Wang, J.; Yuan, J.; Hu, J.; Huang, M.; Xu, W. Optimizing crack initiation energy in austenitic steel via controlled martensitic transformation. Mater. Sci. Technol. 2024, 198, 231–242. [Google Scholar] [CrossRef]
- Wang, H.; Qian, D.; Wang, F.; Dong, Z.; Chen, J. Predictive mechanical property and fracture behaviour in high-carbon steel containing high-density carbides via artificial RVE modelling. Mater. Des. 2024, 247, 113383. [Google Scholar] [CrossRef]
- Kashtalyan, M.; Soutis, C. Analysis of local delaminations in composite laminates with angle-ply matrix cracks. Int. J. Solids Struct. 2002, 39, 1515–1537. [Google Scholar] [CrossRef]
- Kashtalyan, M.; Soutis, C. Analysis of composite laminates within- and interlaminar damage. Prog. Aerosp. Sci. 2005, 41, 152–173. [Google Scholar] [CrossRef]
- Li, S.; Hafeez, F. Variation-based cracked laminate analysis was revisited and fundamentally extended. Int. J. Solids Struct. 2009, 46, 3505–3515. [Google Scholar] [CrossRef]
- Wurkner, M.; Berger, H.; Gabbert, U. Numerical study of effective elastic properties of fibre reinforced composites with rhombic cell arrangements and imperfect interface. Int. J. Eng. Sci. 2013, 63, 1–9. [Google Scholar] [CrossRef]
- Kang, M. Research of the Material Properties of Angleply Symmetrical Laminated with Non-Ideal Transverse Matrix Crack; Wuhan Institute of Technology: Wuhan, China, 2020. [Google Scholar]
- Peng, X. Finite Element Analysis of In-plane Mechanical Properties of Defective Composite Laminates; Wuhan Institute of Technology: Wuhan, China, 2023. [Google Scholar]
- Hajikazemi, M.; Sadr, M.H.; Hosseini-Toudeshky, H.; Mohammadi, B. Thermo-elastic constants of cracked symmetric laminates: A refined variational approach. Int. J. Mech. Sci. 2014, 89, 47–57. [Google Scholar] [CrossRef]
- Huang, Z.Q.; Zhou, J.C.; He, X.Q.; Liew, K.M. Variational analysis for angle-ply laminates with matrix cracks. Int. J. Solids Struct. 2014, 51, 3669–3678. [Google Scholar] [CrossRef]
- Huang, Z.Q.; He, X.Q. Stress distributions and mechanical properties of laminates [θm/90n]s with closed and open cracks in shear loading. Int. J. Solids Struct. 2017, 118, 97–108. [Google Scholar] [CrossRef]
- Huang, Z.Q.; Yi, S.H.; Chen, H.X.; He, X.Q. Parameter analysis of damaged region for laminates with matrix defects. J. Sandw. Struct. Mater. 2021, 23, 580–620. [Google Scholar] [CrossRef]
- Cortes, D.H.; Barbero, E.J. Stiffness reduction and fracture evolution of oblique matrix cracks in composite laminates. Ann. Solid Struct. Mech. 2010, 1, 29–40. [Google Scholar] [CrossRef]
- Carraro, P.A.; Quaresimin, M. A stiffness degradation model for cracked multidirectional laminates with cracks in multiple layers. Int. J. Solids Struct. 2015, 58, 34–51. [Google Scholar] [CrossRef]
- Liang, H. Analysis Model of Fibre Laminates with Transverse Matrix Defects; Wuhan Institute of Technology: Wuhan, China, 2022. [Google Scholar]
- Huang, Z.Q.; Nie, G.H.; Chan, C.K. An exact solution for stresses in cracked composite laminates and evaluation of the characteristic damage state. Compos. Part B Eng. 2011, 42, 1008–1014. [Google Scholar] [CrossRef]
- Duan, W.; Gan, T.-H. Investigation of guided wave properties of anisotropic composite laminates using a semi-analytical finite element method. Compos. Part B Eng. 2019, 173, 106898. [Google Scholar] [CrossRef]
- Hajikazemi, M.; Sadr, M.H. Stiffness reduction of cracked general symmetric laminates using a variational approach. Int. J. Solids Struct. 2014, 51, 1483–1493. [Google Scholar] [CrossRef]
- Li, L.; Song, H.; Zhang, Q.; Yao, J.; Chen, X. Effect of compounding process on the structure and electrochemical properties of ordered mesoporous carbon/polyaniline composites as electrodes for supercapacitors. J. Power Sources 2009, 187, 268–274. [Google Scholar] [CrossRef]
- Xu, C.; Wang, Y.; Yu, X.; Chen, X.; Li, X.; Yang, X.; Li, S.; Zhang, X.; Xiang, A.P. Evaluation of human mesenchymal stem cells response to biomimetic bioglass-collagen-hyaluronic acid-phosphatidylserine composite scaffolds for bone tissue engineering. J. Biomed. Mater. Res. Part A 2010, 88, 264–273. [Google Scholar] [CrossRef]
- Zhang, Q.; Huang, J.Q.; Qian, W.Z.; Zhang, Y.Y.; Wei, F. The road for nanomaterials industry: A review of carbon nanotube production, post-treatment, and bulk applications for composites and energy storage. Small 2013, 9, 1237–1265. [Google Scholar] [CrossRef]
- Nairn, J.A. The Strain Energy Release Rate of Composite Microcracking: A Variational Approach. J. Compos. Mater. 1989, 23, 1106–1129. [Google Scholar] [CrossRef]
- Varna, J.; Berglund, L. Multiple transverse cracking and stiffness reduction in cross-ply laminates. J. Compos. Technol. Res. 1991, 13, 97–106. [Google Scholar]
- Varna, J.; Berglund, L.A. A model for prediction of the transverse cracking strain in cross-ply laminates. J. Reinf. Plast. Compos. 1992, 11, 708–728. [Google Scholar] [CrossRef]
- Varna, J.; Berglund, L.A. ThermoElastic Properties of Composite Laminates with Transverse Cracks. J. Compos. Res. 1994, 16, 77–87. [Google Scholar]
- Gunel, M.; Kayran, A. Nonlinear progressive failure analysis of open-hole composite laminates under combined loading. J. Sandw. Struct. Mater. 2013, 15, 309–339. [Google Scholar] [CrossRef]
- Vejen, N.; Pyrz, R. Transverse crack growth in glass/epoxy composites with exactly positioned long ®bres. Part II: Numerical. Compos. Part B Eng. 2002, 33, 279–290. [Google Scholar] [CrossRef]
- Joshi, R.; Pal, P.; Duggal, S.K. Ply-by-ply failure analysis of laminates using finite element method. Eur. J. Mech.-A/Solids 2020, 81, 103964. [Google Scholar] [CrossRef]
- Hashin, Z. Analysis of cracked laminates: A variational approach. Mech. Mater. 1985, 4, 121–136. [Google Scholar] [CrossRef]
- Xu, D.; Huang, Z.; Chen, S.; Xie, J. Interface parameter analysis of laminates with non-ideal defects. Compos. Mater. Sci. Eng. 2025, 1–16. [Google Scholar]
- Giannadakis, K.; Varna, J. Minimization of complementary energy to predict shear modulus of laminates with intralaminar cracks. IOP Conf. 2012, 31, 012003. [Google Scholar] [CrossRef]
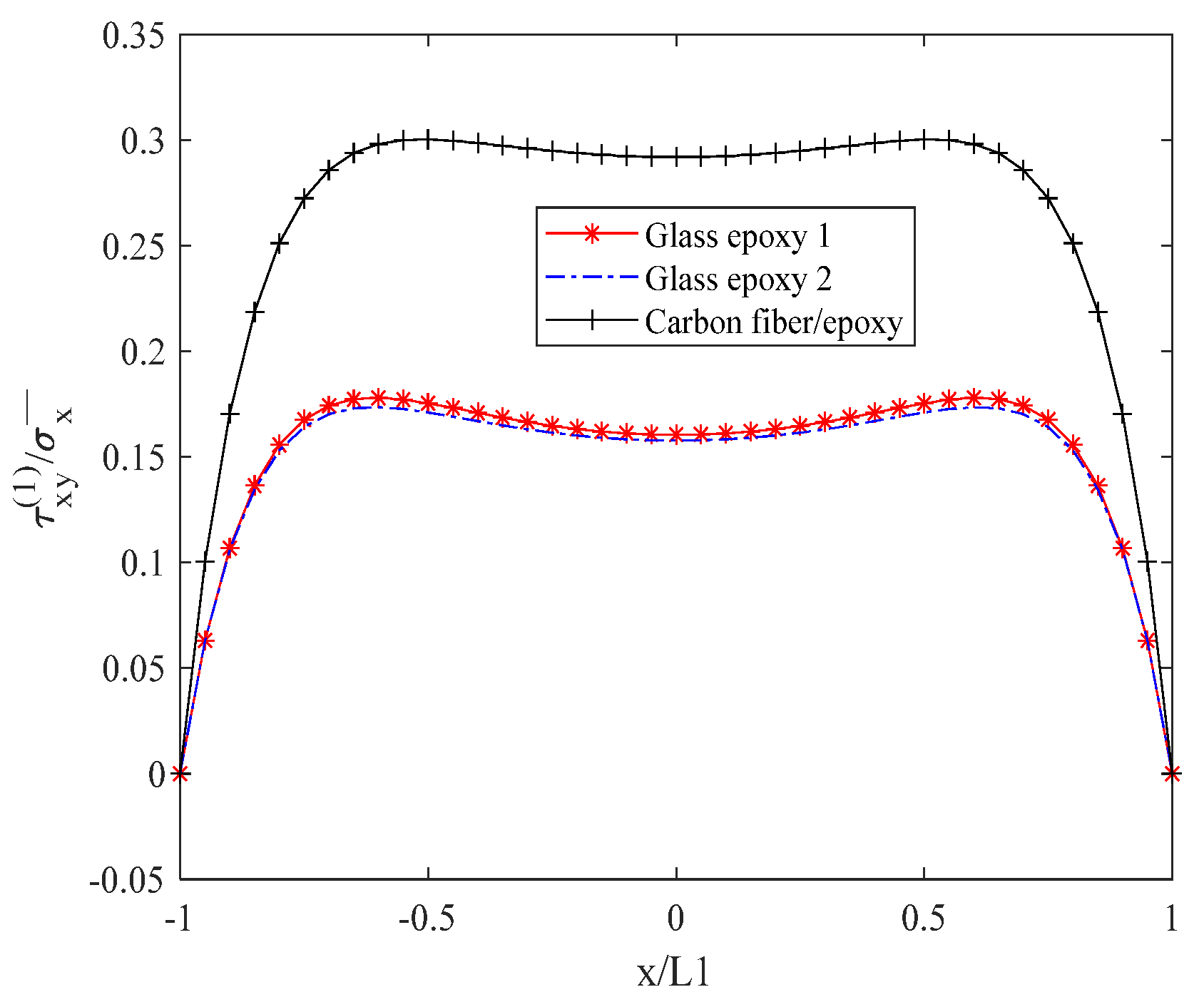
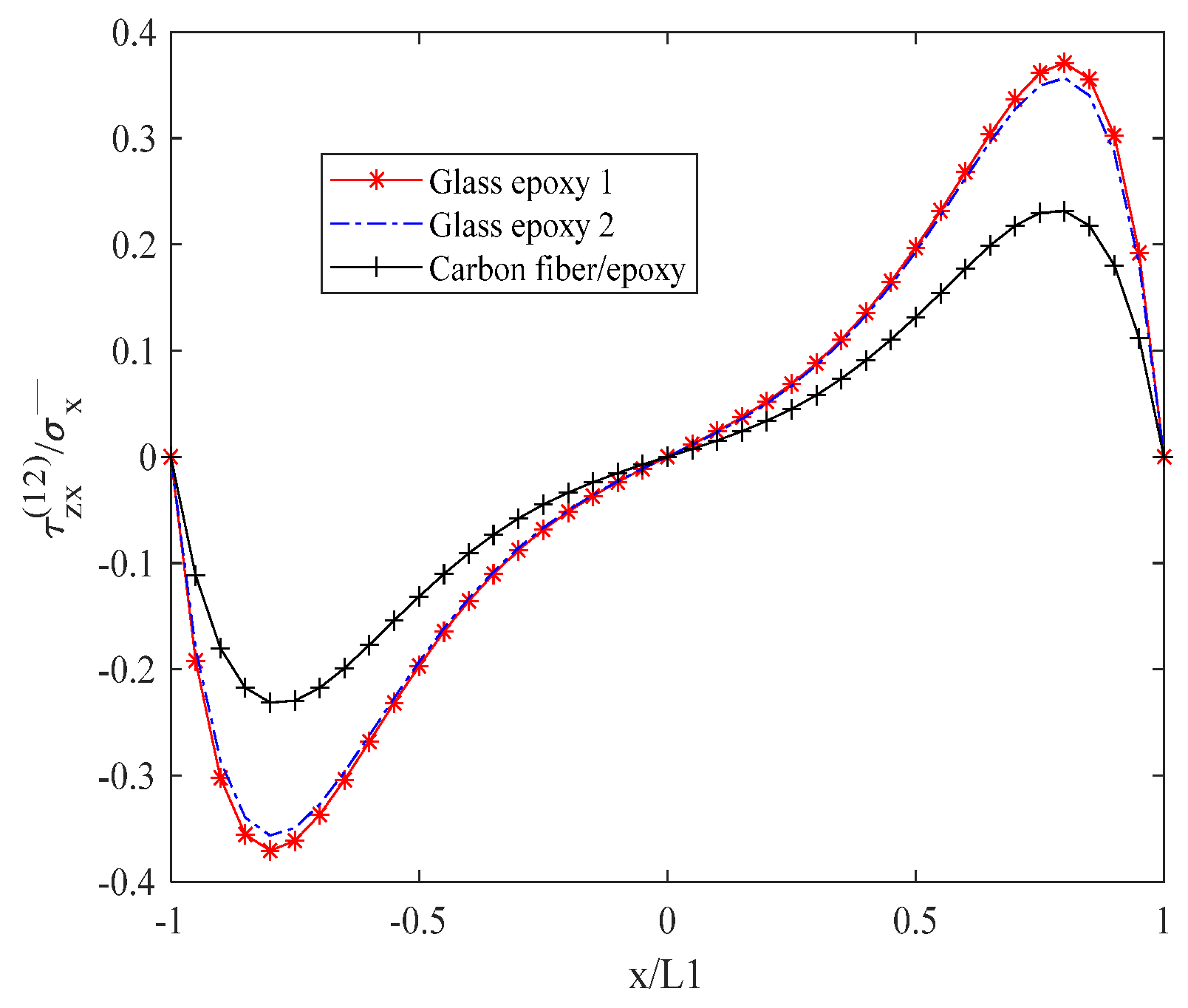



| glass/epoxy 1 | 41.7 Gpa | 13.0 GPa | 3.40 | 4.58 | 0.3 | 0.42 |
| glass/epoxy 2 | 45.0 Gpa | 15.0 Gpa | 5.00 | 5.36 | 0.30 | 0.40 |
| carbon fiber/epoxy resin | 148 | 9.57 | 4.5 | 4.2 | 0.356 | 0.49 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Su, S.; Wang, X.; Chu, F. Stress Analysis and Stiffness Degradation of Open Cracks Composite Laminates Subjected to External Loads. Biomimetics 2025, 10, 177. https://doi.org/10.3390/biomimetics10030177
Huang Z, Su S, Wang X, Chu F. Stress Analysis and Stiffness Degradation of Open Cracks Composite Laminates Subjected to External Loads. Biomimetics. 2025; 10(3):177. https://doi.org/10.3390/biomimetics10030177
Chicago/Turabian StyleHuang, Zhicheng, Shengyun Su, Xingguo Wang, and Fulei Chu. 2025. "Stress Analysis and Stiffness Degradation of Open Cracks Composite Laminates Subjected to External Loads" Biomimetics 10, no. 3: 177. https://doi.org/10.3390/biomimetics10030177
APA StyleHuang, Z., Su, S., Wang, X., & Chu, F. (2025). Stress Analysis and Stiffness Degradation of Open Cracks Composite Laminates Subjected to External Loads. Biomimetics, 10(3), 177. https://doi.org/10.3390/biomimetics10030177







