Abstract
To better address the issue of multi-threshold image segmentation, this paper proposes a hybrid adaptive crayfish optimization algorithm with differential evolution for color multi-threshold image segmentation (ACOADE). Due to the insufficient convergence ability of the crayfish optimization algorithm in later stages, it is challenging to find a more optimal solution for optimization. ACOADE optimizes the maximum foraging quantity parameter p and introduces an adaptive foraging quantity adjustment strategy to enhance the randomness of the algorithm. Furthermore, the core formula of the differential evolution (DE) algorithm is incorporated to balance ACOADE’s exploration and exploitation capabilities better. To validate the optimization performance of ACOADE, the IEEE CEC2020 test function was selected for experimentation, and eight other algorithms were chosen for comparison. To verify the effectiveness of ACOADE for threshold image segmentation, the Kapur entropy method and Otsu method were used as objective functions for image segmentation and compared with eight other algorithms. Subsequently, the peak signal-to-noise ratio (PSNR), feature similarity index measure (FSIM), structural similarity index measure (SSIM), and Wilcoxon test were employed to evaluate the quality of the segmented images. The results indicated that ACOADE exhibited significant advantages in terms of objective function value, image quality metrics, convergence, and robustness.
1. Introduction
Image segmentation is a crucial research direction in the field of computer vision, aiming to partition images into multiple regions with similar properties or meanings for further analysis and processing []. With the continuous advancement of digital technology, image segmentation has demonstrated extensive application prospects in numerous fields, including medical image analysis [], autonomous driving [], intelligent monitoring [], and remote sensing image processing []. Compared with grayscale images, color images exhibit significant advantages in visual perception, reversible information hiding, and technological applications, making them widely utilized and valued in various domains [,,].
The existing image segmentation methods are mainly divided into the following categories: threshold-based segmentation methods [], color-based methods [], edge-based segmentation methods [], clustering-based segmentation methods [], region-based segmentation methods [], etc. Among them, threshold-based methods are widely used due to their simple algorithm implementation and good segmentation results. The existing image threshold segmentation algorithms include two classic algorithms: the Kapur entropy method and the Otsu method. The Kapur entropy method is a threshold selection method based on information theory. The basic idea is to select the optimal threshold by calculating the entropy of pixels at different grayscale levels in the image. In an image, the grayscale values of pixels are considered random variables, and the distribution of pixel values can reflect the information content of the image. By calculating the entropy of pixels at different grayscale levels, the Kapur entropy method can find an optimal threshold that maximizes the information difference between segmented foreground and background pixels []. Therefore, the Kapur entropy method can serve as an objective function to optimize the effectiveness of image segmentation. This method has a wide range of applications in the field of image processing, especially in scenes that require precise image segmentation []. The Otsu method is a widely used image segmentation algorithm []. Its core idea is to determine a threshold based on the grayscale characteristics of the image, dividing it into two parts: a set of pixels that meet specific threshold conditions and a set of pixels that do not meet specific threshold conditions. In this process, the Otsu method aims to minimize the intra-class variance by finding a threshold that minimizes the difference between the two segmented pixel sets. This difference is quantified by calculating the grayscale distribution and intra-class variance of pixels. By continuously updating the threshold and recalculating the intra-class variance, the threshold that minimizes the intra-class variance is ultimately found, which is the optimal segmentation or binarization threshold. This method performs well in image segmentation, especially suitable for scenes that require precise differentiation between foreground and background []. The Kapur entropy method and Otsu method have been widely applied in image processing after years of in-depth research and practice [,,]. However, these two methods have also exhibited some shortcomings in their applications. The Kapur entropy method, due to its relatively complex calculation process, may result in longer processing time, especially when dealing with large-scale images with lower efficiency. In addition, for certain images with complex textures or noise interference, the Kapur entropy method may be difficult to use to accurately identify the boundaries of different regions, resulting in less accurate segmentation results. The Otsu method may find it difficult to accurately identify the optimal segmentation threshold when processing images with bimodal or multimodal grayscale distributions, resulting in inaccurate segmentation results [,,]. Furthermore, when there is noise or uneven lighting interference in the image, the segmentation effect of the Otsu method may also be affected [].
To overcome these shortcomings, researchers have proposed a method that combines metaheuristic optimization algorithms to enhance the segmentation performance of the algorithm []. Metaheuristic optimization algorithms are a type of universal problem solver inspired by mechanisms such as biological evolution, swarm intelligence, and natural physical and chemical processes. This algorithm type boasts advantages such as robust global search capabilities, fast convergence speed, and relatively straightforward parameter settings. It can iteratively search for the optimal solution to the problem without requiring prior strict mathematical modeling of the problem structure. Therefore, it exhibits significant advantages in solving complex optimization problems. In recent years, numerous metaheuristic optimization algorithms have been employed for image segmentation []. For instance, Qingxin Liu proposed the chimpanzee-inspired remora optimization algorithm (HCROA) in 2023. HCROA improves the optimization effect of the remora optimization algorithm and achieves promising results in color multi-threshold image segmentation []. Guoyuan Ma presented an enhanced whale optimization algorithm for multi-threshold image segmentation in 2022, addressing the shortcomings of the traditional whale optimization algorithm (WOA) and enhancing the quality and stability of segmentation results in color multi-threshold image segmentation [].
In 2023, Heming Jia et al. proposed a crayfish optimization algorithm (COA) []. This algorithm mainly simulates the foraging, summer avoidance, and competitive behavior of crayfish. The COA has fast search speed and strong search ability, which can effectively balance the ability of global search and local search. The COA is a promising new optimization algorithm. However, there are still problems, such as insufficient convergence ability in the later stage and susceptibility to falling into global optima. Yi Zhang et al. proposed an improved crawfish optimization algorithm, which effectively improved the optimization effect of the algorithm []. Nabila H. Shikoun proposed a new binary crayfish optimization algorithm (BinCOA) in 2024, which adds a crisscrossing strategy to the original COA and improves the convergence accuracy of the COA [].
To better solve the problem of image segmentation, this article proposes a hybrid adaptive crayfish optimization algorithm with differential evolution for color multi-threshold image segmentation (ACOADE). This method significantly improves the flexibility and efficiency of the algorithm in exploring the solution space by finely adjusting the key parameters in the crayfish optimization algorithm, especially the maximum foraging amount p, and introducing an adaptive foraging amount adjustment strategy. Meanwhile, in order to balance the exploration and exploitation capabilities of the algorithm, we cleverly incorporated the core formula of the differential evolution algorithm, ensuring that ACOADE can balance global and local searches when searching for the optimal threshold. To verify the optimization performance of ACOADE, we selected the IEEE CEC2020 test function as the benchmark and conducted in-depth comparisons with eight algorithms. The experimental results showed that ACOADE showed excellent superiority in optimization problems, achieving significant advantages in both solution quality and convergence speed. In addition, in order to verify the practical application effect of ACOADE in image segmentation, we used the classical Kapur entropy method and Otsu method as the objective function of RGB primary color and carried out segmentation experiments on multiple images. To verify the optimization effect of ACOADE, we comprehensively and objectively evaluated the segmentation results using evaluation metrics such as the peak signal noise ratio (PSNR), the feature similarity index (FSIM), and the structural similarity index (SSIM). The experimental results showed that ACOADE had significant advantages in objective function value, image quality measurement, convergence, and robustness. The results fully proved the effectiveness and practicability of ACOADE in the field of color multi-threshold image segmentation.
2. Related Work
This section describes the related work. Table 1 shows that different researchers use different methods to solve the problem of image segmentation. They use different test methods to solve the problem of image segmentation and improve the algorithm to enhance the effect. These works show that various improved versions of meta heuristic optimization algorithms are proposed and combined with traditional methods to obtain the optimal threshold in the search process. These traditional methods have different effects and advantages. Table 2 compares Otsu’s method, Rényi entropy, Tsallis entropy, and Kapur’s entropy in image segmentation. In principle, Otsu’s method determines the threshold by maximizing the variance between classes, and the other three use different entropy concepts to find the threshold based on information theory. In terms of computational complexity, Otsu’s method is relatively low, while the other three methods are relatively high. The application scenarios are different. Otsu’s method is suitable for simple bimodal images, Rényi entropy is suitable for images with regular distribution and high accuracy requirements, Tsallis entropy is used for complex distribution images, and Kapur’s entropy performs well in texture rich images. Otsu’s method is average in terms of image detail processing ability, and others are better or very good. They are similar in that they are threshold segmentation methods based on gray information, which are designed to complete the task of image segmentation and are widely used.

Table 1.
Overview of applications in multi-level threshold image segmentation.

Table 2.
Comparison of different methods.
In this paper, the Kapur entropy method and the Otsu method are used to realize threshold segmentation. Based on information theory, the Kapur entropy method determines the threshold by maximizing the sum of entropy of foreground and background, which is suitable for texture rich images and can effectively retain details; the Otsu method is based on the image gray characteristics and maximizes the variance between classes. It is simple to calculate and has a good segmentation effect for a bimodal histogram image. The ACOADE algorithm can enhance randomness and exploration ability, can perform well in multi-threshold image segmentation experiments, and can more effectively solve the problem of color multi-threshold image segmentation.
3. Image Segmentation Theory and Methods
Threshold-based image segmentation is the process of obtaining the optimal threshold through a certain method, comparing the pixels of the image, and distinguishing the target from the background. Threshold-based image segmentation methods can be divided into two categories: single-threshold segmentation and multi-threshold segmentation. Single-threshold segmentation divides the histogram into target and background based on the threshold, while multi-threshold segmentation divides the image into multiple categories through the threshold and maximizes the inter-class variance between each category. In complex images containing various objects, single-threshold methods are not as effective as multi-threshold images. Therefore, multi-threshold image segmentation methods have been widely studied [,]. There are many methods for multi-threshold image segmentation, and this article mainly uses the Kapur entropy method and the Otsu method to achieve multi-threshold image segmentation.
The main idea of the Kapur entropy method and the Otsu method is to divide images into multiple categories. Assume an image has L grayscale values. Let ni represent the number of pixels in the ith class of grayscale values in the image. The total number of pixels Sum_N = n0 + n1 + … + NL − 1. Assuming there are K thresholds, the grayscale of a given image can be divided into K + 1 categories. The threshold set can be represented by [th1, th2, th3,…, thK]. The details are as follows.
3.1. Kapur Entropy Method
The Kapur entropy method divides the histogram of an image into different types through multiple thresholds, calculates the sum of entropy for each type, and maximizes it []. The specific formula of the Kapur entropy method is as follows:
where
In the formula, H0, H1, ⋯, Hk represent the entropy of different classes. ω0, ω1, ω2, ⋯, ωK represents the sum of probabilities for each part. And pi represents the probability of the ith grayscale level. The formula is as follows:
To obtain the optimal threshold, it is necessary to maximize the objective function (4) by controlling the parameters {th1, th2 … thK}.
3.2. Otsu Method
The main idea of the Otsu method is to divide the histogram of an image into different types through multiple thresholds, calculate the inter-class variance of each type, and sum it up. The Otsu method states that when the sum of inter-class variances is maximized, selecting the segmentation threshold at this time results in the best image segmentation effect [,]. The specific formula for the Otsu method is as follows:
where
In the formula, μT represents the average grayscale level of the image as shown below:
To obtain the optimal threshold, it is necessary to maximize the objective function (8) by controlling the parameters {th1, th2 … thK}:
From the above formula, it can be seen that as the threshold K increases, the complexity increases, and the requirements for parameters become more precise. It is particularly important to find a better threshold. Therefore, this article proposes the ACOADE algorithm to search for more precise threshold parameters.
4. Crayfish Optimization Algorithm (COA)
4.1. Initialization Phase
In the initialization phase, each crayfish represents a 1 × dim matrix, and each column matrix represents a solution to a problem. The initialization of the COA involves randomly generating N sets of candidate solutions X between upper and lower bounds. COA initialization is as follows:
Among them, N is the population size. dim is the population dimension. Xi,j is the position of the ith crayfish in the j dimension. And Xi,j is obtained by the following formula:
where lb represents the lower bound, ub represents the upper bound, and rand is a random number of [0, 1].
4.2. Defining Temperature and Foraging Volume
The suitable foraging temperature for crayfish is 20–30 °C, with 25 °C being the optimal foraging temperature []. When the temperature is above 30 °C, crayfish will choose caves to escape the heat []. The temperature is defined as Formula (11). The foraging amount of crayfish is approximately a normal distribution, obtained using Formula (12):
Among them, temp represents the temperature of the environment, and µ refers to the temperature most suitable for crayfish, σ. The feeding amount of crayfish at different temperatures is controlled with C1.
4.3. Summer Resort Stage
When temp > 30, crayfish will be close to the cave for summer escape. The cave is defined as follows:
where XG represents the optimal position obtained from the population, and XL represents the optimal position obtained after the update of the previous generation population.
When rand < 0.5, the COA enters the summer resort stage. At this time, the crayfish will directly approach the cave, as follows:
where t is the current number of evaluations and maxFES is the maximum number of evaluations.
4.4. Competition Stage
When temp > 30 and rand ≥ 0.5, the COA enters the competitive stage. At this time, other crayfish will compete for the same cave. The formula is as follows:
4.5. Foraging Stage
When the temperature is between 20 and 30 degrees, the COA enters the foraging stage. The foraging stage is divided into two types. When the food is large, crayfish will tear up the food before eating. When the food is suitable for eating, crayfish will eat directly. The definition of food and the definition of food size are as follows:
where C3 is the food factor and the value is the constant 3. fitnessi represents the fitness value of the ith crayfish, and fitnessfood represents the fitness value of the food location.
When Q > (C3 + 1)/2, the COA shreds the food using Formula (20). Afterward, the feeding behavior of crayfish is simulated using Formula (21):
When Q ≤ (C3 + 1)/2, the crayfish move directly toward the food and eat through Formula (22):
The pseudo code of the COA is shown in Algorithm 1.
| Algorithm 1. Crayfish Optimization Algorithm Pseudo-Code |
| Define parameters: maximum number of evaluations maxFES, population N, and dimension dim |
| Initialize population X and obtain XG, XL |
| While t < maxFES |
| Defining temperature temp by Formula (11) |
| For i = 1:N |
| If temp > 30 |
| Define cave Xshade according to Formula (13) |
| If rand < 0.5 |
| Crayfish conducts the summer resort stage according to Formula (14) |
| Else |
| Crayfish compete for caves through Formula (16) |
| End |
| Else |
| The food intake p and food size Q are obtained by Formulas (12) and (19) |
| If Q > (C3 + 1)/2 |
| Crayfish shreds food by Formula (20) |
| Crayfish foraging according to Formula (21) |
| Else |
| Crayfish foraging according to Formula (22) |
| End |
| End |
| Update fitness values, XG, XL |
| t = t + 1 |
| End |
| End |
5. Improvement and Implementation of the COA
5.1. Adaptive Feed Seeking Adjustment Strategy (AFSAS)
In the COA, C1 is used to control the maximum foraging amount of the crayfish algorithm and plays an important role in optimization ability. This article enhances the randomness of the COA through the AFSAS. The AFSAS obtains Fit by the difference between its own fitness value (fitnessi) and the optimal fitness value (fitnessbest) and then divides Fit + 1 by fitnessi + 1 to obtain foraging quantity. Specifically, as shown in Formula (23), through the AFSAS strategy, each individual can adjust their foraging amount based on their position at the optimal position, as shown in Figure 1. By adjusting the foraging amount, each individual can adjust according to their own position, enhancing the algorithm’s exploration ability and enabling better convergence.
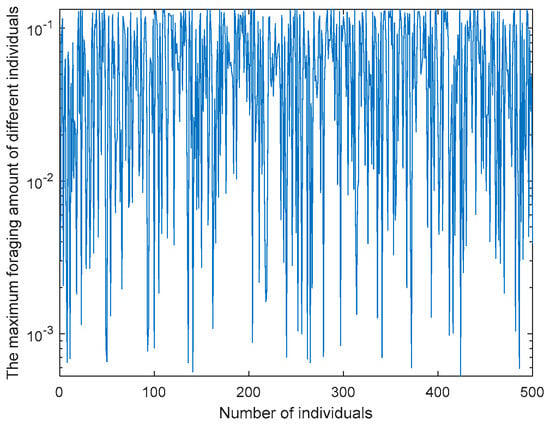
Figure 1.
Feeding capacity curve.
5.2. Differential Evolution Strategy
The differential evolution strategy improves the optimization effect of ACOADE by interacting with individuals in the population and enhancing the connections between populations through the differential evolution strategy. This can enable ACOADE to converge better and find more optimal solutions. The schematic diagram of the differential evolution strategy is shown in Figure 2. The specific formula is as follows.
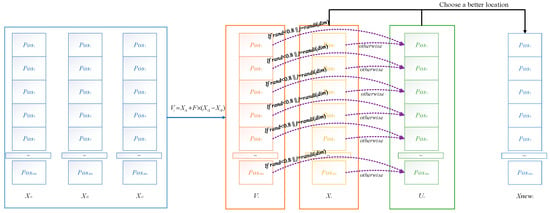
Figure 2.
Schematic diagram of differential evolution strategy.
5.2.1. Mutation Stage
In the mutation stage, three vectors in the population are selected, and mutation is achieved through a differential operation:
Among them, Xr1, Xr2, and Xr3 are three random individuals in the population. F is the variation factor with a constant value of 0.85. Vi is a new individual obtained during the mutation stage.
5.2.2. Crossover Stage
In the crossover stage, each individual undergoes crossover with the individuals generated by the mutation. This is selected based on probability, and each individual chooses whether to mutate according to a certain probability, as shown in Formula (25):
where Ui,j represents the individuals obtained during the selection stage.
5.2.3. Selection Stage
In the selection stage, greedy algorithms are used to obtain better individuals based on fitness values as the next generation, as shown in Formula (26):
where f(Ui) represents the fitness value obtained by the Ui individual, and f(Xi) represents the fitness value obtained by the Xi individual.
5.3. ACOADE Pseudocode and Flowchart
The pseudocode of ACOADE is shown in Algorithm 2. The flowchart is shown in Figure 3.
| Algorithm 2. ACOADE Pseudo-Code |
| Define parameters: maximum number of evaluations maxFES, population N, and dimension dim |
| Initialize population X and obtain XG, XL |
| While t < maxFES |
| Defining temperature temp by Formula (11) |
| For i = 1:N |
| If temp > 30 |
| Define cave Xshade according to Formula (13) |
| If rand < 0.5 |
| Crayfish conducts the summer resort stage according to Formula (14) |
| Else |
| Crayfish compete for caves through Formula (16) |
| End |
| Else |
| The food intake p and food size Q are obtained by Formulas (19) and (23) |
| If Q > (C3 + 1)/2 |
| Crayfish shreds food by Formula (20) |
| Crayfish foraging according to Formula (21) |
| Else |
| Crayfish foraging according to Formula (22) |
| End |
| End |
| Update fitness values, XG, XL |
| t = t + 1 |
| End |
| For i = 1:N |
| Perform the mutation stage through Formula (24) |
| Perform the crossover stage according to Formula (25) |
| Perform the selection stage according to Formula (26) |
| t = t + 1 |
| End |
| End |
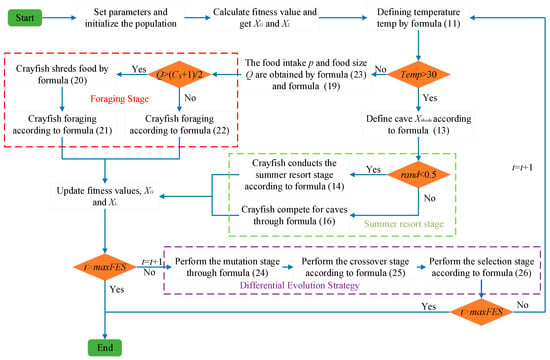
Figure 3.
ACOADE flowchart.
6. Experimental Results and Discussion
This section uses the IEEE CEC2020 test function to verify the optimization effect of the ACOADE algorithm. The crayfish optimization algorithm (COA), differential evolution (DE) [], particle swarm optimization (PSO) [], the arithmetic optimization algorithm (AOA) [], the whale optimization algorithm (WOA) [], the sand cat swarm optimization (SCSO) [], the grey wolf optimization (GWO) [], and the moss growth optimization (MGO) [] were selected as comparison algorithms. The ACOADE algorithm and eight comparison algorithms all had a population size of N = 20, dimension dim = 30/50, and a maximum evaluation frequency of maxFES = dim × 10,000. The comparative experimental results showed that the ACOADE algorithm had better optimization performance. The parameter settings for these algorithms are shown in Table 3.

Table 3.
Parameter settings for each algorithm.
All the experiments in this paper were completed on a computer with the 11th Gen Intel(R) Core(TM) i7-11700 processor with the primary frequency of 2.50 GHz, 16 GB memory, and the operating system of 64-bit windows 11 using matlab2021a.
6.1. IEEE CEC2020 Test Function Experimental Results
Table 4 shows the statistical results obtained by running ACOADE and eight comparison algorithms independently for 30 times at dim = 30. “Best” represents the best fitness value, “mean” represents the average fitness value, “std” represents the variance of fitness values, and “rank” represents the Friedman ranking result. From F1, it could be concluded that ACOADE could achieve better fitness values, except for the best, which did not achieve the best results. Compared with other comparative algorithms, ACOADE had better optimization performance. DE could achieve the best, indicating that DE had a good convergence effect, but its stability was insufficient. In F2, the performance of ACOADE was poor, and the results obtained were not as good as other comparison algorithms, resulting in poor optimization effects. In F2 and F3, MGO had good performance, ranking first and exhibiting good optimization effects. ACOADE also had good performance in F3, ranking slightly higher than PSO and MGO. In F4, most algorithms had good optimization effects and could achieve good fitness values. In F5, ACOADE achieved good results, except for “best”, which did not achieve the best results. Compared with other comparative algorithms, ACOADE had better optimization performance. In F6, ACOADE achieved the best, but MGO had better optimization results. In F7, DE had a better optimization effect and better performance. The optimization effect of ACOADE was relatively stable. In F8, ACOADE performed better than other compared algorithms and could achieve the best optimization results. PSO could also achieve better “best” results and have good optimization effects. In F9, ACOADE could achieve better results. The overall optimization effect of MGO was better than other comparative algorithms, with better results. In F10, ACOADE performed better and could achieve better optimization results. Figure 4 shows the ranking results of each algorithm. Compared with other algorithms, ACOADE ranked better and ultimately ranked better.

Table 4.
Statistical results of each algorithm in IEEE CEC2020 (dim = 30).
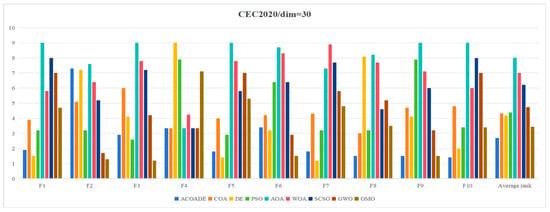
Figure 4.
Friedman ranking of each algorithm in IEEE CEC2020 (dim = 30).
Table 5 shows the statistical results obtained by running ACOADE and eight comparison algorithms independently for 30 times at dim = 50. “Best” represents the best fitness value, “mean” represents the average fitness value, “std” represents the variance of fitness values, and “rank” represents the Friedman ranking result. In F1, ACOADE had a good optimization effect and could achieve good optimization results, only slightly higher than MGO at best. In F2, F3, F8, and F9, MGO had a good optimization effect, and the overall effect was due to other algorithms. ACOADE also had good performance in these functions, with good optimization effects. In F4, most algorithms had good performance and could find a good fitness value. In F5, the optimization effect of DE was better, but its stability was not as good as ACOADE, and the Friedman ranking was the same. In F6, ACOADE and GWO had the same ranking, and both had good performance. ACOADE had better performance in best and mean, but its stability was limited. In F7, ACOADE had a better overall optimization effect than other compared algorithms and could achieve better rankings. In F10, ACOADE ranked second and also had good optimization effects. The overall optimization effect of DE was better. Figure 5 shows the ranking results of each algorithm. Compared with other algorithms, ACOADE ranked better and ultimately ranked better. MGO also had good optimization effects, with ACOADE being superior to MGO.

Table 5.
Statistical results of each algorithm in IEEE CEC2020 (dim = 50).
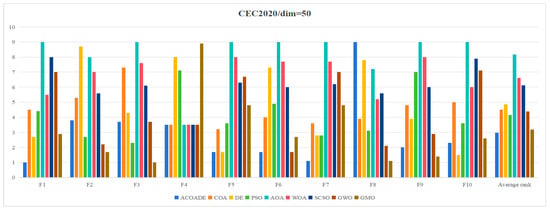
Figure 5.
Friedman ranking of each algorithm in IEEE CEC2020 (dim = 50).
6.2. Convergence Curve Analysis of IEEE CEC2020 Test Function
Figure 6 shows the convergence curves of eight algorithms in IEEE CEC2020, with dimensions dim = 30/50. In F1, the ACOADE algorithm had a good convergence curve at dim = 30 and could continuously converge close to the theoretical optimal solution. The ACOADE algorithm had a significantly better convergence curve than other algorithms at dim = 50 and could quickly converge to obtain a solution close to the theoretical optimal solution. The convergence curve obtained by the DE algorithm was also very excellent. In F2, ACOADE could quickly converge to obtain a better fitness value. GWO and MGO could continuously converge in the iteration to obtain better fitness value, but the convergence speed was slow. In F3, ACOADE converged well and could jump out of the local optimum on the way of convergence. PSO and MGO also had this good effect and could continuously converge, but the effect was not as good as MGO. Function F4 was relatively simple, and all nine algorithms had excellent convergence ability, which could quickly converge and find excellent solutions. In F5, the ACOADE algorithm obtained the best convergence curve at dim = 30, followed by the DE algorithm. The curves obtained by ACOADE and DE algorithms at dim = 50 were similar, and both could continuously converge and obtain better solutions. In F6, ACOADE could jump out of the local optimum in the process of convergence and obtain a better fitness value. The convergence of MGO and GWO was better, and better fitness values could be obtained. In F7, ACOADE, DE, and PSO algorithms all had excellent convergence performance, continuously converging at dim = 30 and dim = 50. In F8, ACOADE and the COA had a good effect at dim = 30 and could find very excellent solutions in the early stage. At dim = 50, ACOADE outperformed other comparative algorithms. In F9, the ACOADE algorithm could jump out of local optima and find better solutions. MGO could also continuously converge and obtain better fitness values. In F10, the convergence curves of the eight algorithms had a small difference and could all obtain good solutions.

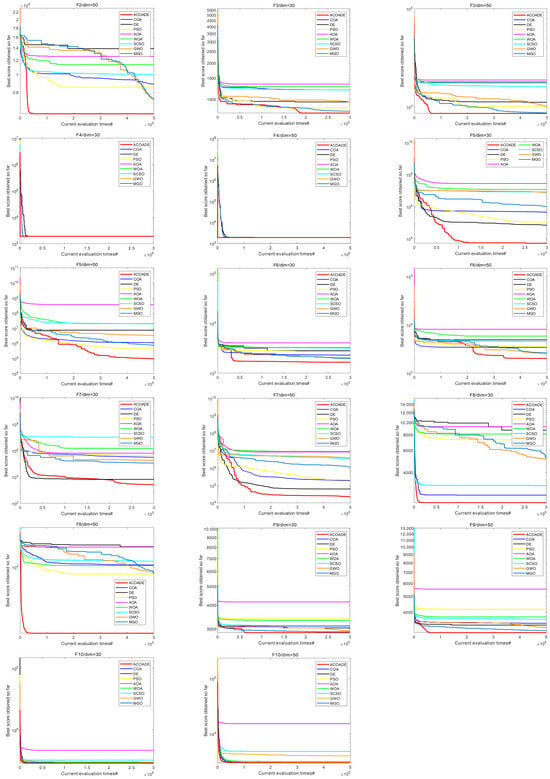
Figure 6.
Convergence curves of each algorithm in IEEE CEC2020.
6.3. Time Complexity Analysis
In order to verify the time complexity of each algorithm, this paper analyzes each algorithm with reference to the time complexity evaluation standard of IEEE CEC 2020 special meeting []. The specific steps are as follows:
(a) Calculate the system runtime T0, run the test program below:
(b) Calculate the complete computing time with 100,000 evaluations of the same dim dimensional function, which is T1.
(c) Calculate the complete computing time for the algorithm with 100,000 evaluations of the same D dimensional function, which is T2.
(d) The complexity of the algorithm is reflected by (T2 − T1)/T0.
Table 6 shows the (T2 − T1)/T0 results obtained by eight algorithms in the IEEE CEC2020 test function, with dimension dim = 30. From the table, it can be concluded that the SCSO algorithm was relatively large. The time complexity of ACOADE, the COA, and DE algorithms was similar. PSO, AOA, and GWO algorithms had lower time complexity.

Table 6.
Comparison of time complexity of each algorithm.
7. Multi-Threshold Image Segmentation Experiment
This section will use ACOADE and eight comparison algorithms for image segmentation to verify the optimization effect of ACOADE. To verify the optimization effect of ACOADE, this study selected 12 images with a size of 321 × 481 × 3 from the Berkeley segmentation dataset and the benchmark 500 (BSDS500). The Berkeley segmentation dataset and the benchmark 500 (BSDS500) can be found at the website https://www2.eecs.berkeley.edu/Research/Projects/CS/vision/bsds/ (accessed on 31 March 2025). These original images and RGB are shown in Figure 7. The red curve represents the R of the three primary colors, the green curve represents the G of the three primary colors, and the blue curve represents the B of the three primary colors. For ease of comparison, the population size of all algorithms was N = 20; the threshold K was the algorithm dimension dim, which was 15, 20, 25, and 30; and the evaluation frequency was maxFES = dim × 3000.
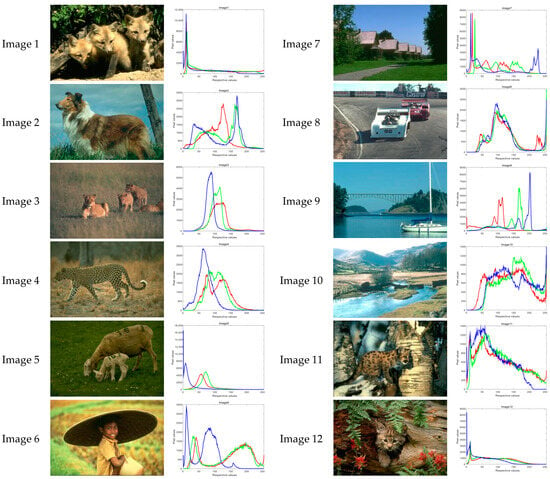
Figure 7.
Image selection and RGB curve.
7.1. Statistical Results and Analysis of Image Segmentation
Table A1 presents the average fitness values derived from using the Kapur entropy method as the fitness metric and conducting 30 independent runs, while Table A2 shows the average fitness values obtained by adopting the Otsu method as the fitness value and also running independently for 30 times. The bolded values signify that among the eight algorithms, they achieved the best results. From an overall perspective, the ACOADE algorithm generally performed quite well and could obtain better results. Specifically, ACOADE secured the best average fitness values for most images, with the exceptions being in image 10 when K equaled 20 and 25. However, other algorithms also exhibited their own advantages. For instance, among image 2, image 4, and image 6, at K = 15, ACOADE failed to attain the best average fitness value, indicating that other algorithms outperformed it in these specific scenarios. In image 3, the COA algorithm demonstrated its strength by obtaining the best average fitness values at K = 15 and K = 20, suggesting that the COA was effective in optimizing the fitness values for image 3 under these conditions. In image 5, the GWO algorithm shone by achieving the best average fitness value at K = 30, showing its superiority in dealing with the fitness evaluation of image 5 at this parameter setting. Additionally, in image 8 and image 10, the COA managed to obtain the best average fitness values at K = 15, K = 20, and K = 25, highlighting its good performance in these two images across multiple parameter values.
Through a comprehensive analysis of the data in the two tables, it is evident that while ACOADE could achieve better fitness values in most images, demonstrating its relatively better optimization effect, other algorithms like the COA and GWO also had their moments of excellence in specific images and parameter settings, contributing to a more diverse and competitive performance landscape among the algorithms.
7.2. Analysis of Image Segmentation Convergence Curve
Figure A1 shows the convergence curve of image segmentation obtained by using the Kapur entropy method between ACOADE and eight comparison algorithms. Figure A2 shows the image segmentation convergence curves obtained by ACOADE and eight comparison algorithms using the Otsu method. It could be inferred from these two figures that among the four thresholds, ACOADE could achieve a very excellent fitness value in the early stage. The COA, WOA, GWO, and PSO algorithms also had good convergence performance. But overall, it was not as good as ACOADE. The DE, AOA, and SCSO algorithms were difficult to converge, resulting in insufficient fitness values. Overall, it can be seen that ACOADE had better optimization effects.
7.3. Analysis of ACOADE Image Segmentation Results
Figure A3 shows the image segmentation results obtained by ACOADE using the Kapur entropy method. Figure A4 is an image segmentation result obtained by ACOADE using the Otsu method. It can be seen that the result of ACOADE segmentation was better than that of the image. With the increase in the threshold, ACOADE segmentation results were better.
7.4. Results and Analysis of Wilcoxon Rank Sum Test
Table 7 and Table 8 are Wilcoxon rank sum test tables obtained by using the Kapur entropy method and the Otsu method with ACOADE and eight comparison algorithms at threshold K = 30. The Wilcoxon rank sum test was used to detect differences between algorithms. The p in the table represents the Wilcoxon rank sum test results obtained, h = 1 indicates significant differences between algorithms, and h = 0 indicates no significant differences between algorithms. From the two tables, it can be concluded that there were significant differences between ACOADE and the eight comparison algorithms, with only some images showing no significant differences. Compared with the traditional COA, it had significant differences, indicating significant improvements.

Table 7.
Wilcoxon rank sum test results based on the Kapur entropy method.

Table 8.
Wilcoxon rank sum test results based on the Ostu method.
7.5. Segmentation Effect Evaluation Index
The Kapur entropy method and the Otsu method were used to obtain the average fitness value as the index. This part used three indicators: the feature similarity index measure (FSIM), the peak signal to noise ratio (PSNR), and the structural similarity index measure (SSIM) [,,]. Details are as follows.
FSIM measures the quality of the segmented image by comparing the similarity of features between the original image and the segmented image. The specific formula is as follows:
where Ω represents the whole image pixel domain, SL(x) is the similarity index, and PCm(x) is the phase consistency feature, which is defined as
Among them, PC1(x) and PC2(x) represent the phase consistency characteristics of the two regions.
Among them, SPC(x) represents the similarity measure of phase consistency; SG(x) represents the gradient size between two regions G1(x) and G2(x); and α, β, T1, and T2 are constants.
PSNR is an indicator used to measure the similarity between segmented images and original images, which is defined as
Among them, MSE represents mean square error, I(i,j) represents the grayscale level of the ith row and jth column of the original image, K(i,j) represents the grayscale level of the ith row and jth column of the segmented image, and M and N are the number of rows and columns in the image matrix.
SSIM compares the similarity between two images through brightness, contrast, and similarity. The specific formula is as follows:
where x and y represents two images, and μx and μy represent the average values of x and y. σx2 and σy2 represent the variance of x and y. σxy is the covariance of x and y, and c1 and c2 are constants.
7.6. Statistical Results and Analysis of Each Algorithm
Table A3 and Table A6 are FSIM data. Table A4 and Table A7 are PSNR data. Table A5 and Table A8 are SSIM data. These tables are based on the average values of FSIM, PSNR and SSIM obtained from the above formula by using Kapur entropy method and Otsu method to segment the image. Bold is the optimal value obtained by comparing the eight algorithms and the proportion of the optimal value in the last row. From the six tables, it can be clearly concluded that ACOADE outperformed other algorithms significantly, having the most optimal values and demonstrating the best optimization effect. Specifically, for Table A3, Table A4 and Table A5, which are based on the Kapur entropy method, ACOADE is the best. Following ACOADE, PSO took second place, showing very excellent performance. PSO had a relatively high proportion of optimal values in these tables, indicating that it could achieve good results in image segmentation using the Kapur entropy method, especially in terms of FSIM, PSNR, and SSIM values. Although not as good as ACOADE, PSO could still be a viable option when ACOADE was not applicable. For Table A6, Table A7 and Table A8, which are based on the Otsu method, ACOADE was also the best. SCSO ranked second and had a higher proportion of the optimal value compared with other algorithms except ACOADE. SCSO showed good performance in image segmentation using the Otsu method, particularly excelling in obtaining relatively high FSIM, PSNR, and SSIM values. In general, ACOADE achieved the best FSIM, PSNR, and SSIM in image segmentation based on the Kapur entropy method and the Otsu method. The FSIM, PSNR, and SSIM obtained by PSO based on the Kapur entropy method were better, but the FSIM, PSNR, and SSIM obtained by the Otsu method were poor. This indicated that PSO was more suitable for image segmentation tasks using the Kapur entropy method. The FSIM, PSNR, and SSIM obtained by SCSO based on the Otsu method were also good, but the FSIM, PSNR, and SSIM obtained by the Kapur entropy method were poor, suggesting that SCSO performed better with the Otsu method for image segmentation. Figure A5, Figure A6, Figure A7, Figure A8, Figure A9 and Figure A10 are line graphs of eight algorithms corresponding to FSIM, PSNR, and SSIM. From these figures, we can see that ACOADE had always been at the highest value, indicating that the result of ACOADE was excellent and the segmentation effect was good.
8. Conclusions
The complexity of multi-level threshold image segmentation increases with the increase in the threshold, and it is difficult to select a better threshold. An improved crayfish optimization algorithm was proposed. First, the parameter p of the COA was modified to increase the flexibility of the ACOADE algorithm. After that, the core formula of the DE algorithm was added to improve the convergence ability of the ACOADE algorithm. To prove the optimization effect of ACOADE, in the experimental part, the IEEE CEC2020 test function was selected for the experiment, and eight comparative algorithms were used for the comparative experiment. The results showed that ACOADE had a better optimization effect. In the experimental part of image segmentation, the Kapur entropy method and the Otsu method were selected to evaluate the performance of the improved algorithm. The multi-threshold performance of the algorithm was tested by 12 BSD500 images. Then, the segmentation results were analyzed according to the average values of the fitness function, FSIM, PSNR, and SSIM as indicators. The experimental results showed that ACOADE had good application prospects and could better solve the problem of multi-threshold image segmentation. In future work, we will look for better methods to improve the optimization effect of the COA and solve engineering problems.
Author Contributions
Conceptualization, H.R.; methodology, H.R.; software, H.J. and H.R.; validation, H.J. and X.Z.; formal analysis, H.R. and X.Z.; investigation, H.R. and H.J.; resources, H.R. and H.J.; data curation, H.R. and H.J.; writing—original draft preparation, H.R. and X.Z.; writing—review and editing, H.J. and L.A.; visualization, H.J.; supervision, H.J., and L.A.; funding acquisition, H.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Guiding Science and Technology Projects in Sanming City (2023-G-5).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The authors would like to acknowledge the support of the Fujian Key Lab of Agriculture IOT Application, IOT Application Engineering Research Center of Fujian Province Colleges and Universities.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
Statistical results based on the Kapur entropy method.
Table A1.
Statistical results based on the Kapur entropy method.
| Different Images | Metric | ACOADE | COA | DE | PSO | AOA | WOA | SCSO | GWO | MGO |
| Image 1 | K = 15 | 42.4189 | 42.3872 | 40.9124 | 42.0223 | 38.3013 | 42.3564 | 41.3787 | 42.3278 | 40.0292 |
| K = 20 | 49.9905 | 49.8488 | 47.4201 | 49.4014 | 43.9298 | 49.8716 | 48.5662 | 49.8933 | 46.2150 | |
| K = 25 | 56.4083 | 55.9410 | 52.7168 | 55.4794 | 48.6062 | 56.2292 | 54.6524 | 56.0221 | 51.3665 | |
| K = 30 | 61.6432 | 60.9763 | 57.0001 | 60.9890 | 52.5880 | 61.4314 | 59.5284 | 61.0223 | 55.5319 | |
| Image 2 | K = 15 | 41.8515 | 41.7944 | 40.3581 | 41.4623 | 37.6679 | 41.7211 | 40.6184 | 41.7229 | 39.2923 |
| K = 20 | 49.4134 | 49.2583 | 46.9375 | 48.8274 | 43.2134 | 49.2394 | 47.8200 | 49.2029 | 45.5202 | |
| K = 25 | 55.6733 | 55.2837 | 51.9964 | 54.6056 | 47.6570 | 55.4200 | 53.7583 | 55.3189 | 50.5009 | |
| K = 30 | 60.8527 | 60.2036 | 56.0620 | 60.1401 | 51.6224 | 60.4397 | 58.4480 | 60.3143 | 54.6486 | |
| Image 3 | K = 15 | 39.9393 | 39.8987 | 38.0131 | 39.3086 | 35.4251 | 39.5718 | 38.4455 | 39.8143 | 36.6794 |
| K = 20 | 46.9729 | 46.8272 | 43.7862 | 46.1444 | 40.0022 | 46.3806 | 44.8137 | 46.7628 | 41.9860 | |
| K = 25 | 52.5136 | 52.3958 | 48.3274 | 51.6439 | 44.0845 | 51.9424 | 49.5934 | 51.9108 | 46.5254 | |
| K = 30 | 56.8369 | 56.6694 | 51.9759 | 56.0725 | 47.4531 | 56.2430 | 53.9496 | 56.3230 | 50.2339 | |
| Image 4 | K = 15 | 41.0635 | 41.0121 | 39.4237 | 40.5931 | 36.7200 | 40.9068 | 39.8841 | 40.9464 | 38.3009 |
| K = 20 | 48.3645 | 48.2956 | 45.5550 | 47.5888 | 41.8119 | 48.2807 | 46.4961 | 48.2323 | 44.2028 | |
| K = 25 | 54.3129 | 54.1722 | 50.4362 | 53.3772 | 46.4523 | 54.0318 | 52.2003 | 54.1124 | 48.9436 | |
| K = 30 | 59.2495 | 58.8385 | 54.2841 | 58.3111 | 49.6528 | 58.8301 | 56.4138 | 58.8272 | 52.9043 | |
| Image 5 | K = 15 | 40.6244 | 40.5649 | 38.7703 | 39.9243 | 36.0563 | 40.3940 | 39.6137 | 40.5806 | 37.5724 |
| K = 20 | 47.7630 | 47.4959 | 44.6175 | 46.5928 | 40.9916 | 47.2919 | 46.1515 | 47.5533 | 43.1110 | |
| K = 25 | 53.5100 | 53.0527 | 49.2695 | 52.2626 | 44.9853 | 52.9151 | 51.3247 | 53.1891 | 47.5231 | |
| K = 30 | 58.3273 | 57.4114 | 53.0085 | 56.9793 | 48.5013 | 57.3637 | 55.6195 | 57.6468 | 51.2566 | |
| Image 6 | K = 15 | 41.3152 | 41.2257 | 39.4705 | 40.8486 | 36.9771 | 41.2391 | 40.0394 | 41.2387 | 38.3992 |
| K = 20 | 48.6627 | 48.5265 | 45.7118 | 48.1438 | 42.0967 | 48.4027 | 46.6503 | 48.5037 | 44.3872 | |
| K = 25 | 54.6796 | 54.3355 | 50.6650 | 53.7134 | 46.4626 | 54.4381 | 52.3517 | 54.4732 | 49.0705 | |
| K = 30 | 59.5930 | 58.8796 | 54.5860 | 59.0092 | 50.0120 | 59.1833 | 56.9444 | 59.1560 | 52.9086 | |
| Image 7 | K = 15 | 41.5258 | 41.4462 | 39.9755 | 41.1839 | 37.3975 | 41.3574 | 40.4920 | 41.4812 | 38.8389 |
| K = 20 | 49.0401 | 48.8234 | 46.3508 | 48.3327 | 42.9216 | 48.6741 | 47.4053 | 48.7584 | 45.0599 | |
| K = 25 | 55.3568 | 54.8602 | 51.5606 | 54.5709 | 47.6923 | 54.7847 | 53.5042 | 54.9380 | 50.2130 | |
| K = 30 | 60.7753 | 59.8646 | 55.7715 | 59.8907 | 51.3258 | 59.7983 | 58.0460 | 59.9558 | 54.2435 | |
| Image 8 | K = 15 | 41.2688 | 41.2551 | 39.7933 | 40.8768 | 37.1133 | 41.1455 | 40.1393 | 41.1957 | 38.6367 |
| K = 20 | 48.8240 | 48.7634 | 46.3435 | 48.2195 | 42.5521 | 48.6698 | 46.9323 | 48.4380 | 44.9944 | |
| K = 25 | 54.9292 | 54.9071 | 51.5904 | 54.4518 | 47.2995 | 54.8401 | 52.5676 | 54.6813 | 49.7805 | |
| K = 30 | 60.1956 | 59.8743 | 55.6199 | 59.6966 | 51.2077 | 59.8220 | 57.4685 | 59.4348 | 54.0735 | |
| Image 9 | K = 15 | 42.8060 | 42.6672 | 41.3992 | 42.6731 | 38.8370 | 42.6231 | 41.8059 | 42.6990 | 40.5781 |
| K = 20 | 50.7075 | 50.5005 | 48.4156 | 50.3913 | 45.0766 | 50.4623 | 49.2559 | 50.4959 | 47.2360 | |
| K = 25 | 57.3871 | 56.9316 | 54.1265 | 56.9199 | 50.2804 | 56.9739 | 55.5348 | 57.0800 | 52.8415 | |
| K = 30 | 62.8881 | 62.2860 | 58.7238 | 62.7154 | 54.3812 | 62.4282 | 60.7157 | 62.6237 | 57.2605 | |
| Image 10 | K = 15 | 40.5527 | 40.5203 | 39.1183 | 40.0383 | 36.6387 | 40.3660 | 39.0954 | 40.3995 | 38.0019 |
| K = 20 | 47.8911 | 47.9984 | 45.3713 | 47.4045 | 41.7556 | 48.0064 | 45.7671 | 47.8569 | 44.0868 | |
| K = 25 | 53.8739 | 54.0951 | 50.4478 | 53.3803 | 46.3038 | 54.1408 | 51.2830 | 53.9038 | 48.9514 | |
| K = 30 | 58.9730 | 58.9001 | 54.5390 | 58.6186 | 49.9265 | 58.6990 | 56.0074 | 58.5067 | 53.0520 | |
| Image 11 | K = 15 | 42.8002 | 42.7519 | 41.3868 | 42.3661 | 39.0574 | 42.7678 | 41.8661 | 42.7193 | 40.7081 |
| K = 20 | 50.4782 | 50.2647 | 48.0249 | 49.7333 | 44.4983 | 50.3810 | 49.2114 | 50.3013 | 46.8861 | |
| K = 25 | 56.9108 | 56.4964 | 53.3186 | 56.2184 | 49.3844 | 56.6542 | 55.0692 | 56.5306 | 52.0905 | |
| K = 30 | 62.3696 | 61.6228 | 57.8068 | 61.6776 | 53.4586 | 61.8461 | 60.0776 | 61.8519 | 56.2031 | |
| Image 12 | K = 15 | 42.2099 | 42.1479 | 40.7124 | 41.8602 | 38.2493 | 42.1147 | 41.3291 | 42.0875 | 39.6906 |
| K = 20 | 49.8190 | 49.5961 | 47.2773 | 49.1314 | 43.7807 | 49.6737 | 48.5218 | 49.6320 | 45.9661 | |
| K = 25 | 56.1680 | 55.7125 | 52.4447 | 55.4466 | 48.5820 | 55.7844 | 54.3875 | 55.9603 | 51.1059 | |
| K = 30 | 61.3955 | 60.6098 | 56.6211 | 60.5207 | 52.2275 | 60.8735 | 59.0753 | 60.9206 | 55.1672 |

Table A2.
Statistical results based on the Otsu method.
Table A2.
Statistical results based on the Otsu method.
| Different Images | Metric | ACOADE | COA | DE | PSO | AOA | WOA | SCSO | GWO | MGO |
| Image 1 | K = 15 | 5322.36 | 5321.97 | 5315.51 | 5320.53 | 5305.57 | 5321.98 | 5319.06 | 5321.93 | 5310.00 |
| K = 20 | 5328.06 | 5327.73 | 5322.91 | 5326.85 | 5315.31 | 5327.79 | 5326.05 | 5327.79 | 5319.59 | |
| K = 25 | 5330.82 | 5330.56 | 5326.90 | 5330.32 | 5320.88 | 5330.67 | 5329.35 | 5330.71 | 5324.32 | |
| K = 30 | 5332.12 | 5330.49 | 5329.33 | 5331.52 | 5324.61 | 5331.05 | 5330.97 | 5331.76 | 5327.56 | |
| Image 2 | K = 15 | 2481.66 | 2481.76 | 2475.41 | 2480.13 | 2467.28 | 2481.16 | 2478.52 | 2481.33 | 2470.21 |
| K = 20 | 2486.29 | 2486.17 | 2481.53 | 2485.41 | 2475.05 | 2485.80 | 2484.23 | 2485.99 | 2478.01 | |
| K = 25 | 2488.54 | 2488.31 | 2484.74 | 2487.95 | 2479.66 | 2488.01 | 2486.86 | 2488.35 | 2482.29 | |
| K = 30 | 2489.44 | 2488.36 | 2486.81 | 2488.83 | 2482.40 | 2488.38 | 2488.37 | 2488.57 | 2484.96 | |
| Image 3 | K = 15 | 771.60 | 771.62 | 767.93 | 770.55 | 762.37 | 770.83 | 768.89 | 771.28 | 763.82 |
| K = 20 | 773.75 | 773.75 | 770.98 | 773.46 | 766.32 | 773.27 | 771.86 | 773.50 | 768.12 | |
| K = 25 | 774.93 | 774.85 | 772.55 | 774.63 | 769.19 | 774.41 | 773.50 | 774.58 | 770.63 | |
| K = 30 | 775.28 | 774.84 | 773.76 | 775.13 | 770.19 | 774.28 | 774.37 | 774.81 | 772.03 | |
| Image 4 | K = 15 | 1435.40 | 1435.50 | 1430.02 | 1433.67 | 1423.95 | 1434.72 | 1432.25 | 1435.20 | 1425.08 |
| K = 20 | 1438.74 | 1438.73 | 1434.77 | 1437.70 | 1429.61 | 1438.21 | 1436.56 | 1438.44 | 1431.47 | |
| K = 25 | 1440.40 | 1440.32 | 1437.25 | 1439.89 | 1432.70 | 1440.14 | 1438.81 | 1439.96 | 1434.52 | |
| K = 30 | 1440.94 | 1440.27 | 1438.89 | 1440.70 | 1434.50 | 1440.16 | 1439.70 | 1440.35 | 1437.04 | |
| Image 5 | K = 15 | 1358.07 | 1357.88 | 1353.74 | 1356.55 | 1348.32 | 1357.48 | 1355.59 | 1357.86 | 1350.06 |
| K = 20 | 1360.28 | 1360.11 | 1357.01 | 1359.42 | 1352.25 | 1359.82 | 1358.53 | 1360.17 | 1354.20 | |
| K = 25 | 1361.36 | 1361.13 | 1358.76 | 1360.73 | 1354.79 | 1360.97 | 1359.92 | 1361.13 | 1356.85 | |
| K = 30 | 1361.42 | 1361.15 | 1359.94 | 1361.28 | 1356.65 | 1361.03 | 1360.83 | 1361.59 | 1358.38 | |
| Image 6 | K = 15 | 5711.20 | 5711.24 | 5705.13 | 5709.50 | 5695.96 | 5711.09 | 5707.42 | 5711.17 | 5699.94 |
| K = 20 | 5716.32 | 5716.14 | 5711.59 | 5715.65 | 5704.46 | 5716.16 | 5713.75 | 5716.17 | 5708.04 | |
| K = 25 | 5718.85 | 5718.63 | 5715.14 | 5718.50 | 5709.84 | 5718.81 | 5717.17 | 5718.66 | 5712.85 | |
| K = 30 | 5720.02 | 5718.62 | 5717.44 | 5719.61 | 5712.58 | 5719.13 | 5718.62 | 5719.09 | 5715.69 | |
| Image 7 | K = 15 | 4319.50 | 4319.26 | 4313.66 | 4317.80 | 4305.37 | 4318.93 | 4316.64 | 4319.19 | 4308.97 |
| K = 20 | 4323.90 | 4323.50 | 4319.36 | 4322.87 | 4312.75 | 4323.24 | 4322.08 | 4323.31 | 4316.47 | |
| K = 25 | 4325.97 | 4325.58 | 4322.43 | 4325.35 | 4317.14 | 4325.33 | 4324.56 | 4325.68 | 4319.91 | |
| K = 30 | 4326.86 | 4325.61 | 4324.20 | 4326.03 | 4320.13 | 4325.56 | 4325.76 | 4326.16 | 4322.58 | |
| Image 8 | K = 15 | 2886.66 | 2887.16 | 2881.17 | 2885.41 | 2872.96 | 2886.40 | 2882.55 | 2886.21 | 2876.05 |
| K = 20 | 2891.25 | 2891.70 | 2887.24 | 2890.79 | 2880.48 | 2891.29 | 2889.15 | 2891.07 | 2884.26 | |
| K = 25 | 2893.71 | 2893.86 | 2890.47 | 2893.46 | 2885.10 | 2893.64 | 2892.25 | 2893.36 | 2888.12 | |
| K = 30 | 2894.79 | 2893.90 | 2892.49 | 2894.49 | 2887.98 | 2893.66 | 2893.59 | 2893.90 | 2890.83 | |
| Image 9 | K = 15 | 4626.40 | 4626.45 | 4621.53 | 4624.94 | 4614.08 | 4625.91 | 4624.47 | 4626.19 | 4617.62 |
| K = 20 | 4631.01 | 4630.89 | 4627.26 | 4630.17 | 4621.58 | 4630.31 | 4629.18 | 4630.69 | 4624.51 | |
| K = 25 | 4633.25 | 4633.10 | 4630.19 | 4632.88 | 4625.75 | 4632.59 | 4632.06 | 4632.87 | 4628.36 | |
| K = 30 | 4634.35 | 4633.09 | 4632.21 | 4633.64 | 4628.15 | 4632.85 | 4633.30 | 4633.54 | 4630.76 | |
| Image 10 | K = 15 | 3981.61 | 3982.44 | 3975.21 | 3980.50 | 3966.69 | 3981.77 | 3976.74 | 3981.14 | 3969.97 |
| K = 20 | 3987.37 | 3987.93 | 3982.76 | 3987.02 | 3975.57 | 3987.73 | 3984.93 | 3987.12 | 3978.43 | |
| K = 25 | 3990.45 | 3990.69 | 3986.71 | 3990.32 | 3981.01 | 3990.61 | 3988.50 | 3990.28 | 3984.18 | |
| K = 30 | 3991.82 | 3990.79 | 3989.19 | 3991.68 | 3983.91 | 3991.06 | 3990.49 | 3990.88 | 3987.45 | |
| Image 11 | K = 15 | 3828.42 | 3828.32 | 3821.16 | 3826.54 | 3810.40 | 3828.36 | 3825.15 | 3828.04 | 3814.68 |
| K = 20 | 3835.61 | 3835.28 | 3829.65 | 3834.70 | 3821.41 | 3835.52 | 3833.28 | 3835.15 | 3825.75 | |
| K = 25 | 3839.06 | 3838.73 | 3834.58 | 3838.59 | 3827.92 | 3838.89 | 3837.29 | 3838.71 | 3831.48 | |
| K = 30 | 3840.72 | 3838.74 | 3837.43 | 3839.95 | 3831.76 | 3839.56 | 3839.41 | 3840.11 | 3835.34 | |
| Image 12 | K = 15 | 2793.98 | 2793.62 | 2787.03 | 2791.88 | 2778.89 | 2793.43 | 2791.19 | 2793.58 | 2781.17 |
| K = 20 | 2798.83 | 2798.51 | 2793.47 | 2797.29 | 2786.70 | 2798.31 | 2796.67 | 2798.60 | 2790.04 | |
| K = 25 | 2801.21 | 2800.82 | 2797.17 | 2800.32 | 2791.37 | 2800.93 | 2799.70 | 2801.03 | 2794.51 | |
| K = 30 | 2802.09 | 2800.86 | 2799.28 | 2801.68 | 2794.30 | 2801.29 | 2801.16 | 2801.86 | 2797.28 |
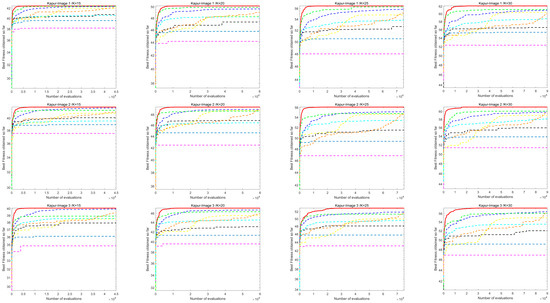
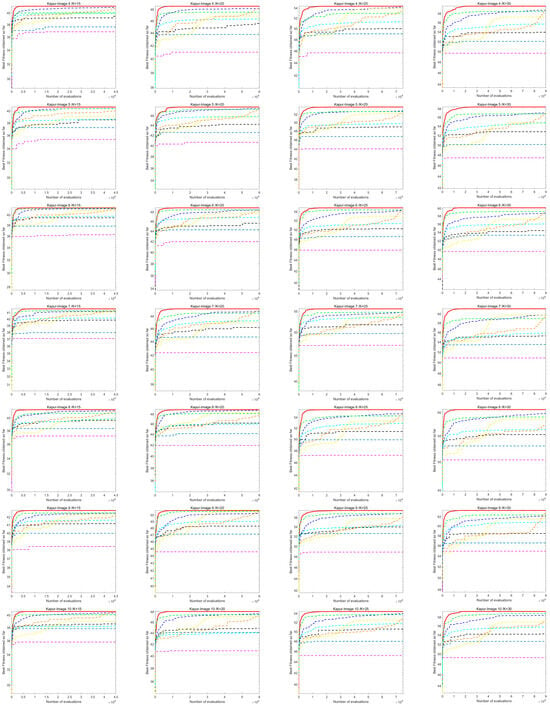
Figure A1.
Convergence curves of each algorithm based on the Kapur entropy method.
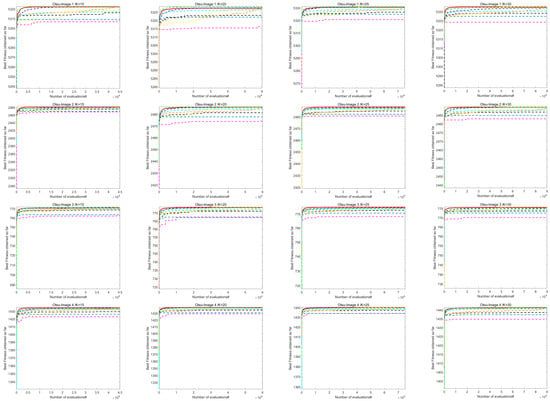
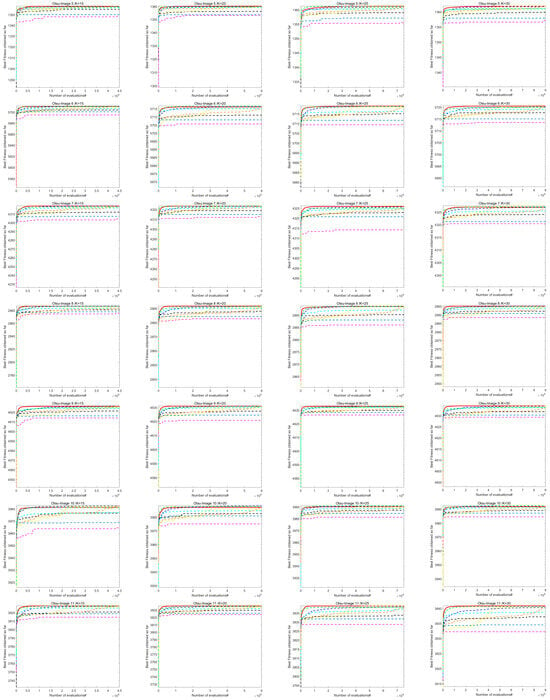
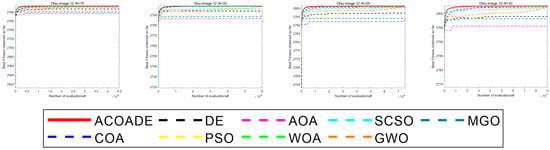
Figure A2.
Convergence curves of each algorithm based on the Otsu method.


Figure A3.
ACOADE segmentation results based on the Kapur entropy method.


Figure A4.
ACOADE segmentation results based on the Otsu method.

Table A3.
FSIM statistical results based on the Kapur entropy method.
Table A3.
FSIM statistical results based on the Kapur entropy method.
| Different Images | Metric | ACOADE | COA | DE | PSO | AOA | WOA | SCSO | GWO | MGO |
| Image 1 | K = 15 | 0.9608 | 0.9542 | 0.8643 | 0.9582 | 0.9135 | 0.9570 | 0.9622 | 0.9572 | 0.9293 |
| K = 20 | 0.9758 | 0.9647 | 0.8953 | 0.9718 | 0.9339 | 0.9706 | 0.9750 | 0.9732 | 0.9465 | |
| K = 25 | 0.9838 | 0.9738 | 0.9221 | 0.9807 | 0.9478 | 0.9781 | 0.9808 | 0.9816 | 0.9622 | |
| K = 30 | 0.9884 | 0.9793 | 0.9355 | 0.9864 | 0.9563 | 0.9819 | 0.9856 | 0.9868 | 0.9695 | |
| Image 2 | K = 15 | 0.9486 | 0.9391 | 0.8357 | 0.9416 | 0.8895 | 0.9397 | 0.9484 | 0.9422 | 0.9090 |
| K = 20 | 0.9698 | 0.9577 | 0.8751 | 0.9608 | 0.9154 | 0.9605 | 0.9683 | 0.9622 | 0.9306 | |
| K = 25 | 0.9793 | 0.9687 | 0.9081 | 0.9768 | 0.9334 | 0.9720 | 0.9764 | 0.9756 | 0.9506 | |
| K = 30 | 0.9846 | 0.9750 | 0.9236 | 0.9838 | 0.9456 | 0.9779 | 0.9814 | 0.9820 | 0.9590 | |
| Image 3 | K = 15 | 0.9200 | 0.9196 | 0.7942 | 0.9172 | 0.8551 | 0.9105 | 0.9108 | 0.9181 | 0.8681 |
| K = 20 | 0.9497 | 0.9470 | 0.8274 | 0.9496 | 0.8794 | 0.9443 | 0.9414 | 0.9486 | 0.8987 | |
| K = 25 | 0.9651 | 0.9613 | 0.8556 | 0.9671 | 0.8991 | 0.9590 | 0.9591 | 0.9653 | 0.9124 | |
| K = 30 | 0.9749 | 0.9698 | 0.8798 | 0.9773 | 0.9137 | 0.9689 | 0.9690 | 0.9739 | 0.9322 | |
| Image 4 | K = 15 | 0.9545 | 0.9510 | 0.8293 | 0.9514 | 0.8903 | 0.9500 | 0.9514 | 0.9516 | 0.9088 |
| K = 20 | 0.9714 | 0.9665 | 0.8728 | 0.9708 | 0.9148 | 0.9667 | 0.9680 | 0.9720 | 0.9326 | |
| K = 25 | 0.9807 | 0.9766 | 0.8993 | 0.9806 | 0.9294 | 0.9751 | 0.9769 | 0.9802 | 0.9494 | |
| K = 30 | 0.9854 | 0.9797 | 0.9205 | 0.9865 | 0.9477 | 0.9800 | 0.9823 | 0.9861 | 0.9600 | |
| Image 5 | K = 15 | 0.9660 | 0.9563 | 0.8393 | 0.9596 | 0.8942 | 0.9532 | 0.9654 | 0.9624 | 0.9004 |
| K = 20 | 0.9802 | 0.9692 | 0.8698 | 0.9777 | 0.9183 | 0.9690 | 0.9769 | 0.9782 | 0.9345 | |
| K = 25 | 0.9871 | 0.9747 | 0.8923 | 0.9855 | 0.9362 | 0.9775 | 0.9843 | 0.9858 | 0.9529 | |
| K = 30 | 0.9900 | 0.9785 | 0.9173 | 0.9897 | 0.9443 | 0.9811 | 0.9884 | 0.9878 | 0.9594 | |
| Image 6 | K = 15 | 0.9066 | 0.9082 | 0.7968 | 0.9076 | 0.8432 | 0.9076 | 0.8951 | 0.9068 | 0.8622 |
| K = 20 | 0.9454 | 0.9414 | 0.8295 | 0.9466 | 0.8756 | 0.9436 | 0.9332 | 0.9439 | 0.8950 | |
| K = 25 | 0.9645 | 0.9588 | 0.8619 | 0.9659 | 0.8962 | 0.9617 | 0.9561 | 0.9619 | 0.9129 | |
| K = 30 | 0.9756 | 0.9684 | 0.8781 | 0.9772 | 0.9110 | 0.9698 | 0.9686 | 0.9704 | 0.9275 | |
| Image 7 | K = 15 | 0.9530 | 0.9375 | 0.8598 | 0.9421 | 0.9035 | 0.9368 | 0.9539 | 0.9453 | 0.9187 |
| K = 20 | 0.9729 | 0.9567 | 0.9023 | 0.9649 | 0.9281 | 0.9586 | 0.9705 | 0.9683 | 0.9403 | |
| K = 25 | 0.9812 | 0.9666 | 0.9164 | 0.9768 | 0.9412 | 0.9707 | 0.9792 | 0.9790 | 0.9539 | |
| K = 30 | 0.9861 | 0.9737 | 0.9348 | 0.9854 | 0.9514 | 0.9762 | 0.9834 | 0.9845 | 0.9648 | |
| Image 8 | K = 15 | 0.9594 | 0.9506 | 0.8699 | 0.9526 | 0.9062 | 0.9521 | 0.9588 | 0.9523 | 0.9282 |
| K = 20 | 0.9743 | 0.9686 | 0.8944 | 0.9735 | 0.9306 | 0.9698 | 0.9712 | 0.9722 | 0.9472 | |
| K = 25 | 0.9816 | 0.9772 | 0.9167 | 0.9825 | 0.9436 | 0.9778 | 0.9779 | 0.9803 | 0.9561 | |
| K = 30 | 0.9856 | 0.9812 | 0.9348 | 0.9870 | 0.9545 | 0.9828 | 0.9826 | 0.9843 | 0.9660 | |
| Image 9 | K = 15 | 0.9407 | 0.9354 | 0.8516 | 0.9399 | 0.8858 | 0.9321 | 0.9363 | 0.9388 | 0.9076 |
| K = 20 | 0.9593 | 0.9553 | 0.8834 | 0.9606 | 0.9144 | 0.9549 | 0.9544 | 0.9583 | 0.9246 | |
| K = 25 | 0.9700 | 0.9665 | 0.8950 | 0.9724 | 0.9233 | 0.9650 | 0.9659 | 0.9690 | 0.9428 | |
| K = 30 | 0.9770 | 0.9733 | 0.9176 | 0.9795 | 0.9401 | 0.9732 | 0.9733 | 0.9761 | 0.9555 | |
| Image 10 | K = 15 | 0.9736 | 0.9708 | 0.8813 | 0.9748 | 0.9236 | 0.9738 | 0.9668 | 0.9685 | 0.9417 |
| K = 20 | 0.9838 | 0.9812 | 0.9096 | 0.9851 | 0.9455 | 0.9835 | 0.9796 | 0.9824 | 0.9581 | |
| K = 25 | 0.9885 | 0.9864 | 0.9322 | 0.9900 | 0.9612 | 0.9871 | 0.9848 | 0.9886 | 0.9693 | |
| K = 30 | 0.9911 | 0.9882 | 0.9493 | 0.9926 | 0.9677 | 0.9896 | 0.9879 | 0.9905 | 0.9763 | |
| Image 11 | K = 15 | 0.9642 | 0.9599 | 0.8571 | 0.9625 | 0.9112 | 0.9614 | 0.9608 | 0.9618 | 0.9308 |
| K = 20 | 0.9782 | 0.9727 | 0.8937 | 0.9772 | 0.9313 | 0.9751 | 0.9754 | 0.9760 | 0.9472 | |
| K = 25 | 0.9851 | 0.9795 | 0.9142 | 0.9858 | 0.9477 | 0.9819 | 0.9823 | 0.9837 | 0.9611 | |
| K = 30 | 0.9893 | 0.9840 | 0.9335 | 0.9902 | 0.9571 | 0.9859 | 0.9864 | 0.9882 | 0.9673 | |
| Image 12 | K = 15 | 0.9770 | 0.9688 | 0.8682 | 0.9734 | 0.9235 | 0.9702 | 0.9772 | 0.9729 | 0.9416 |
| K = 20 | 0.9868 | 0.9783 | 0.9058 | 0.9845 | 0.9466 | 0.9812 | 0.9860 | 0.9846 | 0.9597 | |
| K = 25 | 0.9911 | 0.9841 | 0.9356 | 0.9903 | 0.9568 | 0.9853 | 0.9902 | 0.9900 | 0.9702 | |
| K = 30 | 0.9933 | 0.9866 | 0.9473 | 0.9932 | 0.9670 | 0.9883 | 0.9924 | 0.9925 | 0.9771 |

Table A4.
PSNR statistical results based on the Kapur entropy method.
Table A4.
PSNR statistical results based on the Kapur entropy method.
| Different Images | Metric | ACOADE | COA | DE | PSO | AOA | WOA | SCSO | GWO | MGO |
| Image 1 | K = 15 | 29.1657 | 28.1592 | 23.6648 | 28.6929 | 25.8114 | 28.4047 | 29.6044 | 28.4899 | 27.1300 |
| K = 20 | 31.6597 | 29.6623 | 25.5052 | 30.8372 | 27.5440 | 30.3769 | 31.7745 | 30.9279 | 28.8791 | |
| K = 25 | 33.7493 | 31.4284 | 27.1371 | 32.8323 | 28.8166 | 32.0260 | 33.2505 | 32.9219 | 30.7393 | |
| K = 30 | 35.4486 | 32.6358 | 28.4820 | 34.7572 | 30.0438 | 33.2404 | 34.8117 | 34.4900 | 31.8603 | |
| Image 2 | K = 15 | 29.2612 | 28.1730 | 22.5261 | 28.5928 | 25.0613 | 28.1674 | 29.0220 | 28.3999 | 26.4718 |
| K = 20 | 32.1559 | 30.4375 | 24.9601 | 31.0281 | 26.9743 | 30.5979 | 31.6714 | 31.0495 | 28.4849 | |
| K = 25 | 33.8900 | 32.2094 | 25.9121 | 33.5968 | 28.5689 | 32.3434 | 33.3331 | 32.9244 | 30.5401 | |
| K = 30 | 35.4485 | 33.5391 | 28.2936 | 35.3106 | 29.7637 | 33.7873 | 34.7019 | 34.3881 | 31.4786 | |
| Image 3 | K = 15 | 30.6888 | 30.2471 | 23.7093 | 30.5132 | 26.6128 | 29.6693 | 30.0567 | 30.1628 | 27.7295 |
| K = 20 | 32.9939 | 32.3314 | 25.6552 | 32.9945 | 28.1511 | 32.0876 | 32.3432 | 32.3570 | 29.7752 | |
| K = 25 | 34.6291 | 33.8767 | 27.3297 | 34.7918 | 29.4894 | 33.5862 | 34.0193 | 34.1054 | 30.8423 | |
| K = 30 | 36.0473 | 34.9641 | 28.8810 | 36.3238 | 31.1815 | 34.8580 | 35.4175 | 35.3548 | 32.3825 | |
| Image 4 | K = 15 | 30.3536 | 29.5145 | 23.3122 | 30.0325 | 25.6003 | 29.4992 | 30.0496 | 29.6243 | 27.2002 |
| K = 20 | 32.5468 | 31.5023 | 25.1981 | 32.3508 | 27.2808 | 31.4693 | 32.1082 | 32.0660 | 29.1812 | |
| K = 25 | 34.3314 | 33.2356 | 26.8437 | 34.1588 | 28.6473 | 32.9795 | 33.7450 | 33.6632 | 30.8576 | |
| K = 30 | 35.6454 | 34.2474 | 28.6487 | 35.7078 | 30.5087 | 34.2208 | 34.9888 | 35.1752 | 32.2161 | |
| Image 5 | K = 15 | 31.6270 | 30.3235 | 25.0446 | 30.6472 | 27.3377 | 30.0678 | 31.8635 | 30.7362 | 28.1077 |
| K = 20 | 33.9186 | 32.1265 | 26.8106 | 33.1397 | 28.9420 | 31.9586 | 33.8328 | 33.0928 | 30.2610 | |
| K = 25 | 35.8836 | 33.2302 | 28.2986 | 34.9748 | 30.2484 | 33.6460 | 35.6092 | 35.0232 | 31.9006 | |
| K = 30 | 37.1370 | 34.4156 | 29.9266 | 36.4818 | 30.9499 | 34.6656 | 37.0305 | 36.3623 | 32.7737 | |
| Image 6 | K = 15 | 29.6864 | 28.7816 | 23.2823 | 29.1966 | 25.6676 | 28.6592 | 29.2321 | 28.8888 | 27.0741 |
| K = 20 | 32.2559 | 30.8323 | 25.0769 | 31.8945 | 27.4326 | 31.1763 | 31.4846 | 31.5115 | 28.9447 | |
| K = 25 | 34.0679 | 32.3584 | 26.9583 | 33.8326 | 28.7713 | 32.7888 | 33.3525 | 33.3500 | 30.3929 | |
| K = 30 | 35.5620 | 33.6847 | 28.4914 | 35.5375 | 29.9820 | 34.0035 | 34.6999 | 34.6233 | 31.6406 | |
| Image 7 | K = 15 | 28.6020 | 27.0950 | 23.0687 | 27.7088 | 25.2156 | 27.2031 | 28.7986 | 27.8865 | 26.4319 |
| K = 20 | 31.7707 | 29.7308 | 25.2747 | 30.7411 | 27.1702 | 30.0914 | 31.1937 | 31.0014 | 28.3722 | |
| K = 25 | 33.7947 | 31.2355 | 26.7131 | 32.9646 | 28.4100 | 31.7957 | 33.3578 | 33.1830 | 30.1213 | |
| K = 30 | 35.3154 | 32.7106 | 28.5118 | 35.2399 | 29.6107 | 33.1379 | 34.3389 | 34.6129 | 31.6929 | |
| Image 8 | K = 15 | 29.4145 | 28.4340 | 22.4722 | 28.9681 | 25.0292 | 28.5963 | 29.1621 | 28.5826 | 26.7175 |
| K = 20 | 31.6820 | 30.9731 | 24.8026 | 31.7729 | 27.0972 | 31.0564 | 30.9381 | 31.2504 | 28.7564 | |
| K = 25 | 33.2322 | 32.6363 | 26.3560 | 33.8797 | 28.3286 | 32.6071 | 32.5270 | 32.9568 | 30.0954 | |
| K = 30 | 34.6124 | 33.9674 | 28.0561 | 35.3373 | 29.7977 | 33.8503 | 33.8110 | 34.4028 | 31.6198 | |
| Image 9 | K = 15 | 28.4674 | 28.4962 | 22.6454 | 28.5862 | 25.5520 | 28.3612 | 27.8213 | 28.2714 | 26.2948 |
| K = 20 | 31.1093 | 30.9484 | 24.9925 | 31.6613 | 27.0507 | 30.7561 | 29.8136 | 31.0487 | 28.5127 | |
| K = 25 | 33.0519 | 32.2940 | 26.9066 | 33.5074 | 28.1056 | 32.2209 | 31.8696 | 32.6258 | 30.1525 | |
| K = 30 | 34.5357 | 33.6549 | 27.9173 | 35.1445 | 29.6110 | 33.6638 | 33.4201 | 34.0374 | 31.5905 | |
| Image 10 | K = 15 | 28.7275 | 28.6959 | 22.7249 | 29.5013 | 24.7254 | 29.1380 | 27.2447 | 28.5770 | 26.4355 |
| K = 20 | 31.1027 | 31.2018 | 24.6105 | 32.1236 | 26.8902 | 31.5893 | 29.6632 | 31.2649 | 28.4690 | |
| K = 25 | 32.7213 | 32.9767 | 26.4947 | 34.1149 | 28.7642 | 33.2493 | 31.3480 | 33.1777 | 30.1812 | |
| K = 30 | 34.0151 | 34.0220 | 28.1065 | 35.7144 | 29.9070 | 34.4192 | 32.5861 | 34.3848 | 31.5645 | |
| Image 11 | K = 15 | 29.7143 | 28.8759 | 23.0195 | 29.4689 | 25.4055 | 28.9975 | 29.3695 | 29.0990 | 27.1012 |
| K = 20 | 32.0108 | 30.8731 | 24.9212 | 31.7492 | 27.0655 | 31.0652 | 31.5309 | 31.2708 | 28.6958 | |
| K = 25 | 33.8034 | 32.3012 | 26.4151 | 33.7916 | 28.6285 | 32.5398 | 33.1180 | 33.0277 | 30.3870 | |
| K = 30 | 35.2473 | 33.5574 | 28.0640 | 35.3888 | 29.8731 | 33.8353 | 34.6289 | 34.5231 | 31.5028 | |
| Image 12 | K = 15 | 30.1687 | 29.0167 | 23.4634 | 29.6149 | 25.7644 | 29.0337 | 30.1469 | 29.3329 | 27.1404 |
| K = 20 | 32.5459 | 30.9828 | 25.6287 | 32.1075 | 27.6814 | 31.2708 | 32.4482 | 31.7826 | 29.1918 | |
| K = 25 | 34.4509 | 32.5238 | 27.6058 | 34.1266 | 28.8127 | 32.7110 | 34.1385 | 33.7499 | 30.6317 | |
| K = 30 | 35.8611 | 33.5763 | 28.6656 | 35.7533 | 30.1738 | 34.0049 | 35.5522 | 35.1572 | 32.0211 |

Table A5.
SSIM statistical results based on the Kapur entropy method.
Table A5.
SSIM statistical results based on the Kapur entropy method.
| Different Images | Metric | ACOADE | COA | DE | PSO | AOA | WOA | SCSO | GWO | MGO |
| Image 1 | K = 15 | 0.7978 | 0.7520 | 0.7140 | 0.7702 | 0.7311 | 0.7795 | 0.8692 | 0.7769 | 0.7729 |
| K = 20 | 0.8870 | 0.7933 | 0.7697 | 0.8399 | 0.7949 | 0.8307 | 0.9180 | 0.8692 | 0.8298 | |
| K = 25 | 0.9405 | 0.8558 | 0.8014 | 0.8922 | 0.8291 | 0.8786 | 0.9352 | 0.9198 | 0.8882 | |
| K = 30 | 0.9647 | 0.8808 | 0.8443 | 0.9308 | 0.8617 | 0.9164 | 0.9627 | 0.9452 | 0.9049 | |
| Image 2 | K = 15 | 0.9178 | 0.9016 | 0.7882 | 0.9058 | 0.8459 | 0.9027 | 0.9168 | 0.9071 | 0.8721 |
| K = 20 | 0.9452 | 0.9297 | 0.8414 | 0.9336 | 0.8808 | 0.9328 | 0.9424 | 0.9379 | 0.9019 | |
| K = 25 | 0.9583 | 0.9490 | 0.8767 | 0.9554 | 0.9040 | 0.9487 | 0.9546 | 0.9541 | 0.9259 | |
| K = 30 | 0.9680 | 0.9574 | 0.8966 | 0.9662 | 0.9198 | 0.9595 | 0.9632 | 0.9648 | 0.9366 | |
| Image 3 | K = 15 | 0.8969 | 0.8969 | 0.7703 | 0.8941 | 0.8366 | 0.8868 | 0.8883 | 0.8951 | 0.8495 |
| K = 20 | 0.9278 | 0.9263 | 0.8074 | 0.9279 | 0.8608 | 0.9225 | 0.9183 | 0.9273 | 0.8816 | |
| K = 25 | 0.9456 | 0.9439 | 0.8398 | 0.9472 | 0.8816 | 0.9403 | 0.9389 | 0.9468 | 0.8965 | |
| K = 30 | 0.9577 | 0.9546 | 0.8584 | 0.9600 | 0.9082 | 0.9526 | 0.9511 | 0.9576 | 0.9171 | |
| Image 4 | K = 15 | 0.9253 | 0.9220 | 0.8005 | 0.9221 | 0.8584 | 0.9202 | 0.9222 | 0.9218 | 0.8826 |
| K = 20 | 0.9470 | 0.9427 | 0.8428 | 0.9459 | 0.8870 | 0.9417 | 0.9443 | 0.9481 | 0.9091 | |
| K = 25 | 0.9610 | 0.9578 | 0.8641 | 0.9597 | 0.9052 | 0.9552 | 0.9563 | 0.9612 | 0.9286 | |
| K = 30 | 0.9688 | 0.9636 | 0.8961 | 0.9694 | 0.9280 | 0.9625 | 0.9646 | 0.9705 | 0.9415 | |
| Image 5 | K = 15 | 0.8876 | 0.8302 | 0.6618 | 0.8453 | 0.7522 | 0.8307 | 0.9122 | 0.8603 | 0.7632 |
| K = 20 | 0.9376 | 0.8675 | 0.7377 | 0.9099 | 0.7855 | 0.8794 | 0.9402 | 0.9179 | 0.8535 | |
| K = 25 | 0.9606 | 0.8992 | 0.7922 | 0.9397 | 0.8382 | 0.9137 | 0.9589 | 0.9465 | 0.8819 | |
| K = 30 | 0.9695 | 0.9128 | 0.8219 | 0.9577 | 0.8525 | 0.9261 | 0.9689 | 0.9607 | 0.8956 | |
| Image 6 | K = 15 | 0.8664 | 0.8309 | 0.7132 | 0.8348 | 0.7695 | 0.8360 | 0.8687 | 0.8454 | 0.8097 |
| K = 20 | 0.9189 | 0.8855 | 0.7748 | 0.9030 | 0.8135 | 0.8891 | 0.9132 | 0.9076 | 0.8525 | |
| K = 25 | 0.9425 | 0.9077 | 0.8135 | 0.9323 | 0.8478 | 0.9188 | 0.9371 | 0.9364 | 0.8825 | |
| K = 30 | 0.9572 | 0.9326 | 0.8438 | 0.9509 | 0.8737 | 0.9364 | 0.9515 | 0.9502 | 0.9009 | |
| Image 7 | K = 15 | 0.8918 | 0.8351 | 0.7498 | 0.8647 | 0.8031 | 0.8533 | 0.8945 | 0.8749 | 0.8390 |
| K = 20 | 0.9424 | 0.8984 | 0.8364 | 0.9181 | 0.8557 | 0.9087 | 0.9360 | 0.9295 | 0.8824 | |
| K = 25 | 0.9595 | 0.9219 | 0.8528 | 0.9448 | 0.8794 | 0.9359 | 0.9570 | 0.9550 | 0.9134 | |
| K = 30 | 0.9691 | 0.9378 | 0.8882 | 0.9665 | 0.9035 | 0.9449 | 0.9657 | 0.9650 | 0.9355 | |
| Image 8 | K = 15 | 0.9249 | 0.9179 | 0.7848 | 0.9158 | 0.8470 | 0.9160 | 0.9216 | 0.9155 | 0.8783 |
| K = 20 | 0.9508 | 0.9455 | 0.8346 | 0.9487 | 0.8841 | 0.9447 | 0.9451 | 0.9480 | 0.9094 | |
| K = 25 | 0.9650 | 0.9598 | 0.8676 | 0.9654 | 0.9052 | 0.9586 | 0.9598 | 0.9628 | 0.9248 | |
| K = 30 | 0.9737 | 0.9684 | 0.8965 | 0.9739 | 0.9218 | 0.9666 | 0.9687 | 0.9711 | 0.9414 | |
| Image 9 | K = 15 | 0.9301 | 0.9185 | 0.8361 | 0.9281 | 0.8766 | 0.9161 | 0.9285 | 0.9238 | 0.8989 |
| K = 20 | 0.9460 | 0.9376 | 0.8768 | 0.9442 | 0.9035 | 0.9376 | 0.9431 | 0.9424 | 0.9109 | |
| K = 25 | 0.9557 | 0.9494 | 0.8844 | 0.9557 | 0.9097 | 0.9463 | 0.9540 | 0.9524 | 0.9299 | |
| K = 30 | 0.9638 | 0.9568 | 0.9014 | 0.9644 | 0.9272 | 0.9563 | 0.9609 | 0.9598 | 0.9431 | |
| Image 10 | K = 15 | 0.9538 | 0.9522 | 0.8426 | 0.9554 | 0.8933 | 0.9543 | 0.9442 | 0.9497 | 0.9150 |
| K = 20 | 0.9698 | 0.9686 | 0.8733 | 0.9718 | 0.9223 | 0.9706 | 0.9633 | 0.9690 | 0.9385 | |
| K = 25 | 0.9780 | 0.9767 | 0.9059 | 0.9805 | 0.9402 | 0.9777 | 0.9727 | 0.9787 | 0.9531 | |
| K = 30 | 0.9829 | 0.9805 | 0.9192 | 0.9856 | 0.9513 | 0.9820 | 0.9783 | 0.9826 | 0.9628 | |
| Image 11 | K = 15 | 0.9380 | 0.9192 | 0.8025 | 0.9267 | 0.8638 | 0.9250 | 0.9421 | 0.9293 | 0.8942 |
| K = 20 | 0.9642 | 0.9465 | 0.8501 | 0.9551 | 0.8956 | 0.9520 | 0.9631 | 0.9580 | 0.9208 | |
| K = 25 | 0.9750 | 0.9590 | 0.8820 | 0.9720 | 0.9204 | 0.9638 | 0.9727 | 0.9708 | 0.9425 | |
| K = 30 | 0.9814 | 0.9670 | 0.9095 | 0.9805 | 0.9351 | 0.9716 | 0.9791 | 0.9790 | 0.9519 | |
| Image 12 | K = 15 | 0.9285 | 0.8883 | 0.7611 | 0.9042 | 0.8328 | 0.9010 | 0.9404 | 0.9121 | 0.8658 |
| K = 20 | 0.9636 | 0.9292 | 0.8364 | 0.9464 | 0.8818 | 0.9364 | 0.9649 | 0.9519 | 0.9105 | |
| K = 25 | 0.9759 | 0.9509 | 0.8790 | 0.9688 | 0.9013 | 0.9501 | 0.9767 | 0.9709 | 0.9309 | |
| K = 30 | 0.9830 | 0.9556 | 0.9026 | 0.9794 | 0.9208 | 0.9640 | 0.9826 | 0.9793 | 0.9471 |

Table A6.
FSIM statistical results based on the Otsu method.
Table A6.
FSIM statistical results based on the Otsu method.
| Different Images | Metric | ACOADE | COA | DE | PSO | AOA | WOA | SCSO | GWO | MGO |
| Image 1 | K = 15 | 0.9688 | 0.9662 | 0.8687 | 0.9652 | 0.9312 | 0.9674 | 0.9655 | 0.9677 | 0.9396 |
| K = 20 | 0.9792 | 0.9764 | 0.8958 | 0.9769 | 0.9489 | 0.9781 | 0.9776 | 0.9790 | 0.9432 | |
| K = 25 | 0.9851 | 0.9822 | 0.9157 | 0.9832 | 0.9596 | 0.9836 | 0.9840 | 0.9843 | 0.9565 | |
| K = 30 | 0.9885 | 0.9806 | 0.9413 | 0.9849 | 0.9660 | 0.9826 | 0.9868 | 0.9855 | 0.9663 | |
| Image 2 | K = 15 | 0.9493 | 0.9378 | 0.8456 | 0.9357 | 0.9056 | 0.9428 | 0.9552 | 0.9417 | 0.9204 |
| K = 20 | 0.9697 | 0.9543 | 0.8849 | 0.9552 | 0.9246 | 0.9640 | 0.9709 | 0.9619 | 0.9432 | |
| K = 25 | 0.9801 | 0.9675 | 0.9046 | 0.9665 | 0.9396 | 0.9732 | 0.9802 | 0.9740 | 0.9565 | |
| K = 30 | 0.9864 | 0.9705 | 0.9232 | 0.9724 | 0.9531 | 0.9752 | 0.9832 | 0.9784 | 0.9663 | |
| Image 3 | K = 15 | 0.9571 | 0.9477 | 0.8001 | 0.9422 | 0.8920 | 0.9527 | 0.9555 | 0.9484 | 0.9116 |
| K = 20 | 0.9765 | 0.9661 | 0.8443 | 0.9626 | 0.9156 | 0.9707 | 0.9730 | 0.9674 | 0.9363 | |
| K = 25 | 0.9858 | 0.9753 | 0.8729 | 0.9719 | 0.9360 | 0.9783 | 0.9813 | 0.9776 | 0.9519 | |
| K = 30 | 0.9884 | 0.9769 | 0.8868 | 0.9772 | 0.9461 | 0.9785 | 0.9844 | 0.9818 | 0.9623 | |
| Image 4 | K = 15 | 0.9641 | 0.9531 | 0.8428 | 0.9478 | 0.9221 | 0.9555 | 0.9641 | 0.9526 | 0.9310 |
| K = 20 | 0.9803 | 0.9693 | 0.8820 | 0.9656 | 0.9346 | 0.9734 | 0.9787 | 0.9713 | 0.9509 | |
| K = 25 | 0.9886 | 0.9785 | 0.9057 | 0.9762 | 0.9498 | 0.9836 | 0.9865 | 0.9809 | 0.9624 | |
| K = 30 | 0.9912 | 0.9792 | 0.9197 | 0.9821 | 0.9594 | 0.9833 | 0.9885 | 0.9840 | 0.9724 | |
| Image 5 | K = 15 | 0.9820 | 0.9768 | 0.8249 | 0.9737 | 0.9399 | 0.9785 | 0.9759 | 0.9784 | 0.9485 |
| K = 20 | 0.9894 | 0.9854 | 0.8719 | 0.9846 | 0.9553 | 0.9861 | 0.9846 | 0.9872 | 0.9622 | |
| K = 25 | 0.9927 | 0.9892 | 0.9026 | 0.9892 | 0.9624 | 0.9900 | 0.9889 | 0.9904 | 0.9720 | |
| K = 30 | 0.9930 | 0.9881 | 0.9241 | 0.9907 | 0.9699 | 0.9895 | 0.9912 | 0.9919 | 0.9788 | |
| Image 6 | K = 15 | 0.9311 | 0.9290 | 0.7947 | 0.9227 | 0.8636 | 0.9296 | 0.9170 | 0.9302 | 0.8802 |
| K = 20 | 0.9584 | 0.9536 | 0.8271 | 0.9538 | 0.8948 | 0.9556 | 0.9487 | 0.9556 | 0.9094 | |
| K = 25 | 0.9727 | 0.9671 | 0.8617 | 0.9684 | 0.9173 | 0.9682 | 0.9664 | 0.9699 | 0.9325 | |
| K = 30 | 0.9792 | 0.9632 | 0.8899 | 0.9728 | 0.9274 | 0.9683 | 0.9734 | 0.9703 | 0.9459 | |
| Image 7 | K = 15 | 0.9596 | 0.9539 | 0.8675 | 0.9541 | 0.9247 | 0.9568 | 0.9605 | 0.9569 | 0.9349 |
| K = 20 | 0.9728 | 0.9662 | 0.9070 | 0.9676 | 0.9398 | 0.9697 | 0.9749 | 0.9711 | 0.9529 | |
| K = 25 | 0.9800 | 0.9724 | 0.9272 | 0.9739 | 0.9522 | 0.9771 | 0.9819 | 0.9794 | 0.9634 | |
| K = 30 | 0.9863 | 0.9727 | 0.9383 | 0.9790 | 0.9607 | 0.9774 | 0.9855 | 0.9820 | 0.9712 | |
| Image 8 | K = 15 | 0.9468 | 0.9380 | 0.8763 | 0.9350 | 0.9140 | 0.9414 | 0.9535 | 0.9383 | 0.9293 |
| K = 20 | 0.9673 | 0.9549 | 0.8974 | 0.9506 | 0.9324 | 0.9594 | 0.9712 | 0.9545 | 0.9460 | |
| K = 25 | 0.9793 | 0.9649 | 0.9279 | 0.9621 | 0.9415 | 0.9700 | 0.9807 | 0.9691 | 0.9603 | |
| K = 30 | 0.9844 | 0.9708 | 0.9369 | 0.9684 | 0.9563 | 0.9742 | 0.9832 | 0.9768 | 0.9680 | |
| Image 9 | K = 15 | 0.9514 | 0.9482 | 0.8592 | 0.9456 | 0.9081 | 0.9472 | 0.9468 | 0.9491 | 0.9190 |
| K = 20 | 0.9684 | 0.9657 | 0.8799 | 0.9649 | 0.9296 | 0.9639 | 0.9627 | 0.9659 | 0.9409 | |
| K = 25 | 0.9780 | 0.9753 | 0.9014 | 0.9765 | 0.9440 | 0.9732 | 0.9740 | 0.9750 | 0.9545 | |
| K = 30 | 0.9831 | 0.9734 | 0.9217 | 0.9784 | 0.9524 | 0.9724 | 0.9789 | 0.9772 | 0.9638 | |
| Image 10 | K = 15 | 0.9509 | 0.9408 | 0.8758 | 0.9314 | 0.9157 | 0.9410 | 0.9641 | 0.9364 | 0.9367 |
| K = 20 | 0.9745 | 0.9606 | 0.9093 | 0.9515 | 0.9358 | 0.9654 | 0.9788 | 0.9633 | 0.9574 | |
| K = 25 | 0.9826 | 0.9735 | 0.9384 | 0.9656 | 0.9545 | 0.9753 | 0.9861 | 0.9743 | 0.9672 | |
| K = 30 | 0.9898 | 0.9768 | 0.9499 | 0.9752 | 0.9665 | 0.9795 | 0.9888 | 0.9827 | 0.9764 | |
| Image 11 | K = 15 | 0.9640 | 0.9614 | 0.8617 | 0.9597 | 0.9279 | 0.9624 | 0.9595 | 0.9622 | 0.9355 |
| K = 20 | 0.9779 | 0.9750 | 0.8958 | 0.9753 | 0.9454 | 0.9762 | 0.9741 | 0.9763 | 0.9538 | |
| K = 25 | 0.9850 | 0.9817 | 0.9214 | 0.9834 | 0.9563 | 0.9825 | 0.9817 | 0.9836 | 0.9645 | |
| K = 30 | 0.9885 | 0.9797 | 0.9383 | 0.9851 | 0.9630 | 0.9827 | 0.9858 | 0.9855 | 0.9723 | |
| Image 12 | K = 15 | 0.9817 | 0.9796 | 0.8782 | 0.9784 | 0.9551 | 0.9802 | 0.9794 | 0.9804 | 0.9589 |
| K = 20 | 0.9891 | 0.9858 | 0.9137 | 0.9854 | 0.9659 | 0.9864 | 0.9866 | 0.9874 | 0.9714 | |
| K = 25 | 0.9928 | 0.9890 | 0.9337 | 0.9895 | 0.9725 | 0.9896 | 0.9908 | 0.9909 | 0.9783 | |
| K = 30 | 0.9939 | 0.9872 | 0.9552 | 0.9913 | 0.9761 | 0.9896 | 0.9924 | 0.9915 | 0.9831 |

Table A7.
PSNR statistical results based on the Otsu method.
Table A7.
PSNR statistical results based on the Otsu method.
| Different Images | Metric | ACOADE | COA | DE | PSO | AOA | WOA | SCSO | GWO | MGO |
| Image 1 | K = 15 | 30.3843 | 29.7086 | 24.0619 | 29.8521 | 26.8780 | 29.8179 | 30.0062 | 29.8462 | 27.8288 |
| K = 20 | 32.5978 | 31.4833 | 25.6337 | 31.7787 | 28.4145 | 31.7376 | 32.1434 | 31.8947 | 29.7611 | |
| K = 25 | 34.4344 | 32.9228 | 26.8485 | 33.4187 | 29.7050 | 33.1750 | 33.8926 | 33.4439 | 31.4052 | |
| K = 30 | 35.6375 | 33.0110 | 28.9007 | 34.2543 | 30.8221 | 33.4991 | 34.9931 | 34.1603 | 32.7880 | |
| Image 2 | K = 15 | 30.2407 | 28.6731 | 22.9566 | 28.7753 | 26.1166 | 29.0945 | 30.5491 | 29.0326 | 27.6639 |
| K = 20 | 33.0871 | 30.7115 | 25.4453 | 31.1685 | 27.7124 | 31.7313 | 32.8648 | 31.5736 | 29.7611 | |
| K = 25 | 35.1410 | 32.6767 | 26.8950 | 32.9655 | 29.1141 | 33.3544 | 34.6635 | 33.5563 | 31.4052 | |
| K = 30 | 36.6151 | 33.3562 | 28.5398 | 34.1793 | 30.6971 | 33.9473 | 35.7687 | 34.5372 | 32.7880 | |
| Image 3 | K = 15 | 33.0543 | 30.8385 | 24.1847 | 30.4576 | 27.6497 | 32.0337 | 33.5111 | 31.1122 | 30.0403 |
| K = 20 | 36.3577 | 33.5678 | 26.6366 | 33.1504 | 29.1996 | 34.6983 | 35.7565 | 34.0669 | 32.0911 | |
| K = 25 | 38.6775 | 35.5689 | 28.4729 | 34.8934 | 31.3220 | 36.1953 | 37.3478 | 36.1906 | 33.7769 | |
| K = 30 | 39.7077 | 36.4789 | 29.4393 | 36.5519 | 32.7978 | 36.6888 | 38.3881 | 37.5548 | 35.1625 | |
| Image 4 | K = 15 | 31.4357 | 29.5405 | 23.5290 | 29.2774 | 27.3310 | 29.9538 | 31.6050 | 29.5657 | 28.6121 |
| K = 20 | 34.3224 | 31.9986 | 25.8109 | 31.6624 | 28.2868 | 32.6636 | 33.9455 | 32.3877 | 30.6588 | |
| K = 25 | 36.6455 | 33.8554 | 27.5072 | 33.5946 | 29.9602 | 34.9203 | 35.7961 | 34.5144 | 32.2607 | |
| K = 30 | 37.8258 | 34.4993 | 28.5798 | 35.3556 | 31.3562 | 35.2731 | 36.6967 | 35.6660 | 33.8470 | |
| Image 5 | K = 15 | 35.7630 | 34.4808 | 25.0911 | 34.3668 | 30.4411 | 34.4590 | 34.3899 | 34.7504 | 31.4454 |
| K = 20 | 38.1548 | 36.5743 | 27.1712 | 36.7948 | 31.7860 | 36.5125 | 36.4616 | 36.9841 | 33.0033 | |
| K = 25 | 39.9101 | 38.0964 | 28.8614 | 38.6694 | 32.6431 | 38.0284 | 37.9095 | 38.4070 | 34.5297 | |
| K = 30 | 40.0113 | 38.1762 | 30.1117 | 39.7253 | 33.7851 | 38.1618 | 39.2187 | 39.3819 | 35.7700 | |
| Image 6 | K = 15 | 30.4420 | 29.1591 | 22.9341 | 29.3321 | 26.1433 | 29.3512 | 30.0365 | 29.5221 | 27.7245 |
| K = 20 | 32.9970 | 31.1960 | 24.9157 | 31.7789 | 28.0445 | 31.4064 | 32.2203 | 31.8014 | 29.4753 | |
| K = 25 | 34.9483 | 32.8563 | 27.2461 | 33.4905 | 29.4710 | 33.0455 | 34.1408 | 33.7467 | 31.3234 | |
| K = 30 | 36.1001 | 33.1293 | 28.9542 | 34.3934 | 30.7583 | 33.6256 | 35.2897 | 34.3611 | 32.6953 | |
| Image 7 | K = 15 | 29.6142 | 28.4640 | 23.4300 | 28.7723 | 26.2253 | 28.9408 | 29.9732 | 28.8797 | 27.4192 |
| K = 20 | 32.3434 | 30.6768 | 25.8466 | 31.1704 | 27.6575 | 31.1024 | 32.5056 | 31.4424 | 29.6323 | |
| K = 25 | 34.2258 | 32.1087 | 27.5013 | 32.8385 | 29.0580 | 33.0899 | 34.2830 | 33.4730 | 31.0068 | |
| K = 30 | 36.1156 | 32.3951 | 28.7417 | 34.1960 | 30.5679 | 33.4035 | 35.6086 | 34.3928 | 32.7196 | |
| Image 8 | K = 15 | 28.1438 | 26.6318 | 23.1445 | 26.4163 | 24.8828 | 27.1728 | 28.6265 | 26.7460 | 26.6777 |
| K = 20 | 31.2486 | 29.2105 | 24.8717 | 28.7921 | 26.8169 | 30.0106 | 31.5369 | 29.3275 | 28.8478 | |
| K = 25 | 33.6197 | 31.1875 | 27.3388 | 30.8294 | 27.9412 | 32.1004 | 33.5482 | 32.0150 | 30.9675 | |
| K = 30 | 35.1006 | 32.6591 | 28.3926 | 32.4600 | 30.2144 | 33.0947 | 34.6657 | 33.6962 | 32.3549 | |
| Image 9 | K = 15 | 30.8923 | 30.3825 | 23.2234 | 30.3812 | 27.1708 | 30.2664 | 30.2714 | 30.4295 | 28.2966 |
| K = 20 | 33.3555 | 32.6149 | 25.3693 | 32.8664 | 29.0365 | 32.4050 | 32.4757 | 32.6875 | 30.4337 | |
| K = 25 | 35.2488 | 34.3217 | 26.8529 | 34.9797 | 30.4735 | 33.9299 | 34.3818 | 34.3463 | 32.0389 | |
| K = 30 | 36.6034 | 34.4493 | 28.7622 | 35.7572 | 31.5009 | 34.2019 | 35.5997 | 35.0119 | 33.4650 | |
| Image 10 | K = 15 | 27.3755 | 26.2174 | 22.4100 | 25.4297 | 24.0947 | 26.2631 | 28.1500 | 25.7708 | 26.0880 |
| K = 20 | 30.5295 | 29.0571 | 24.5447 | 28.0057 | 26.0475 | 29.5859 | 30.6990 | 29.2962 | 28.6587 | |
| K = 25 | 32.4714 | 31.3983 | 26.9529 | 30.2880 | 28.2842 | 31.6533 | 32.4317 | 31.4963 | 30.2561 | |
| K = 30 | 34.2346 | 32.2495 | 28.2272 | 32.3874 | 29.7942 | 32.6502 | 33.6571 | 33.0871 | 31.9466 | |
| Image 11 | K = 15 | 30.0077 | 29.3690 | 23.0794 | 29.4610 | 26.5286 | 29.4211 | 29.4208 | 29.4090 | 27.4072 |
| K = 20 | 32.3332 | 31.4561 | 25.0597 | 31.8676 | 28.1049 | 31.6163 | 31.6034 | 31.6053 | 29.3589 | |
| K = 25 | 34.1569 | 33.0296 | 26.8210 | 33.7549 | 29.4034 | 33.2150 | 33.3150 | 33.3279 | 30.8363 | |
| K = 30 | 35.4001 | 33.0424 | 28.4714 | 34.6506 | 30.4969 | 33.6638 | 34.5367 | 34.1918 | 32.2282 | |
| Image 12 | K = 15 | 31.8454 | 31.0820 | 23.9401 | 31.1469 | 27.9237 | 31.1346 | 31.2492 | 31.1876 | 28.6510 |
| K = 20 | 34.2560 | 33.0602 | 26.0467 | 33.1708 | 29.3367 | 33.1093 | 33.2517 | 33.3192 | 30.5129 | |
| K = 25 | 36.0264 | 34.5312 | 27.4976 | 35.0079 | 30.4804 | 34.7231 | 34.9624 | 35.0318 | 31.9794 | |
| K = 30 | 36.7953 | 34.4141 | 29.4646 | 36.3070 | 31.3522 | 35.0224 | 36.0481 | 35.8398 | 33.1593 |

Table A8.
SSIM statistical results based on the Otsu method.
Table A8.
SSIM statistical results based on the Otsu method.
| Different Images | Metric | ACOADE | COA | DE | PSO | AOA | WOA | SCSO | GWO | MGO |
| Image 1 | K = 15 | 0.8693 | 0.8452 | 0.7396 | 0.8550 | 0.7714 | 0.8535 | 0.8981 | 0.8603 | 0.8053 |
| K = 20 | 0.9140 | 0.8750 | 0.7842 | 0.8879 | 0.8238 | 0.8915 | 0.9322 | 0.9028 | 0.9160 | |
| K = 25 | 0.9445 | 0.8991 | 0.8233 | 0.9067 | 0.8608 | 0.9118 | 0.9570 | 0.9229 | 0.9345 | |
| K = 30 | 0.9645 | 0.9076 | 0.8589 | 0.9179 | 0.8918 | 0.9171 | 0.9630 | 0.9321 | 0.9476 | |
| Image 2 | K = 15 | 0.9248 | 0.9063 | 0.8047 | 0.9047 | 0.8590 | 0.9127 | 0.9317 | 0.9120 | 0.8853 |
| K = 20 | 0.9539 | 0.9322 | 0.8554 | 0.9344 | 0.8886 | 0.9447 | 0.9535 | 0.9424 | 0.9160 | |
| K = 25 | 0.9679 | 0.9519 | 0.8760 | 0.9516 | 0.9101 | 0.9589 | 0.9661 | 0.9602 | 0.9345 | |
| K = 30 | 0.9754 | 0.9564 | 0.9003 | 0.9607 | 0.9287 | 0.9618 | 0.9715 | 0.9663 | 0.9476 | |
| Image 3 | K = 15 | 0.9524 | 0.9432 | 0.7793 | 0.9380 | 0.8805 | 0.9453 | 0.9458 | 0.9440 | 0.9011 |
| K = 20 | 0.9709 | 0.9634 | 0.8294 | 0.9618 | 0.9066 | 0.9645 | 0.9634 | 0.9645 | 0.9266 | |
| K = 25 | 0.9803 | 0.9734 | 0.8586 | 0.9721 | 0.9277 | 0.9735 | 0.9729 | 0.9749 | 0.9432 | |
| K = 30 | 0.9831 | 0.9737 | 0.8741 | 0.9773 | 0.9374 | 0.9725 | 0.9777 | 0.9778 | 0.9545 | |
| Image 4 | K = 15 | 0.9507 | 0.9402 | 0.8071 | 0.9335 | 0.9004 | 0.9407 | 0.9467 | 0.9394 | 0.9092 |
| K = 20 | 0.9694 | 0.9603 | 0.8535 | 0.9566 | 0.9155 | 0.9628 | 0.9646 | 0.9623 | 0.9337 | |
| K = 25 | 0.9788 | 0.9715 | 0.8828 | 0.9700 | 0.9334 | 0.9752 | 0.9743 | 0.9732 | 0.9466 | |
| K = 30 | 0.9824 | 0.9717 | 0.8992 | 0.9766 | 0.9440 | 0.9747 | 0.9781 | 0.9768 | 0.9591 | |
| Image 5 | K = 15 | 0.9694 | 0.9584 | 0.6959 | 0.9569 | 0.9017 | 0.9593 | 0.9617 | 0.9617 | 0.9075 |
| K = 20 | 0.9815 | 0.9731 | 0.7513 | 0.9742 | 0.9236 | 0.9735 | 0.9758 | 0.9767 | 0.9346 | |
| K = 25 | 0.9869 | 0.9802 | 0.8090 | 0.9829 | 0.9334 | 0.9810 | 0.9820 | 0.9833 | 0.9499 | |
| K = 30 | 0.9868 | 0.9798 | 0.8449 | 0.9861 | 0.9440 | 0.9805 | 0.9857 | 0.9861 | 0.9613 | |
| Image 6 | K = 15 | 0.8789 | 0.8445 | 0.7142 | 0.8455 | 0.7634 | 0.8532 | 0.8861 | 0.8596 | 0.8135 |
| K = 20 | 0.9257 | 0.8912 | 0.7836 | 0.8992 | 0.8164 | 0.8966 | 0.9209 | 0.9073 | 0.8569 | |
| K = 25 | 0.9493 | 0.9196 | 0.8223 | 0.9249 | 0.8559 | 0.9234 | 0.9458 | 0.9383 | 0.8951 | |
| K = 30 | 0.9604 | 0.9231 | 0.8478 | 0.9358 | 0.8833 | 0.9313 | 0.9563 | 0.9436 | 0.9165 | |
| Image 7 | K = 15 | 0.8926 | 0.8523 | 0.7796 | 0.8691 | 0.8091 | 0.8760 | 0.9168 | 0.8727 | 0.8515 |
| K = 20 | 0.9391 | 0.9058 | 0.8320 | 0.9151 | 0.8519 | 0.9150 | 0.9499 | 0.9281 | 0.8991 | |
| K = 25 | 0.9552 | 0.9260 | 0.8735 | 0.9373 | 0.8843 | 0.9474 | 0.9627 | 0.9524 | 0.9186 | |
| K = 30 | 0.9699 | 0.9289 | 0.8940 | 0.9538 | 0.9140 | 0.9472 | 0.9700 | 0.9605 | 0.9456 | |
| Image 8 | K = 15 | 0.9304 | 0.9142 | 0.8098 | 0.9092 | 0.8669 | 0.9193 | 0.9349 | 0.9150 | 0.8938 |
| K = 20 | 0.9582 | 0.9438 | 0.8409 | 0.9390 | 0.8986 | 0.9495 | 0.9596 | 0.9437 | 0.9221 | |
| K = 25 | 0.9730 | 0.9583 | 0.8850 | 0.9564 | 0.9167 | 0.9642 | 0.9722 | 0.9634 | 0.9438 | |
| K = 30 | 0.9793 | 0.9647 | 0.8987 | 0.9650 | 0.9379 | 0.9676 | 0.9762 | 0.9717 | 0.9550 | |
| Image 9 | K = 15 | 0.9379 | 0.9294 | 0.8586 | 0.9294 | 0.8935 | 0.9284 | 0.9338 | 0.9316 | 0.9062 |
| K = 20 | 0.9574 | 0.9522 | 0.8740 | 0.9521 | 0.9152 | 0.9495 | 0.9503 | 0.9534 | 0.9278 | |
| K = 25 | 0.9694 | 0.9641 | 0.8944 | 0.9670 | 0.9317 | 0.9616 | 0.9636 | 0.9651 | 0.9421 | |
| K = 30 | 0.9755 | 0.9640 | 0.9116 | 0.9705 | 0.9408 | 0.9628 | 0.9699 | 0.9686 | 0.9523 | |
| Image 10 | K = 15 | 0.9372 | 0.9254 | 0.8371 | 0.9153 | 0.8836 | 0.9256 | 0.9444 | 0.9197 | 0.9123 |
| K = 20 | 0.9641 | 0.9514 | 0.8778 | 0.9430 | 0.9125 | 0.9559 | 0.9654 | 0.9534 | 0.9389 | |
| K = 25 | 0.9753 | 0.9668 | 0.9132 | 0.9606 | 0.9370 | 0.9688 | 0.9758 | 0.9675 | 0.9543 | |
| K = 30 | 0.9835 | 0.9700 | 0.9294 | 0.9709 | 0.9514 | 0.9729 | 0.9809 | 0.9757 | 0.9653 | |
| Image 11 | K = 15 | 0.9409 | 0.9255 | 0.8064 | 0.9274 | 0.8841 | 0.9293 | 0.9419 | 0.9319 | 0.8993 |
| K = 20 | 0.9637 | 0.9491 | 0.8566 | 0.9532 | 0.9131 | 0.9542 | 0.9623 | 0.9570 | 0.9291 | |
| K = 25 | 0.9761 | 0.9625 | 0.8907 | 0.9679 | 0.9297 | 0.9655 | 0.9736 | 0.9703 | 0.9449 | |
| K = 30 | 0.9816 | 0.9608 | 0.9123 | 0.9729 | 0.9440 | 0.9694 | 0.9781 | 0.9740 | 0.9580 | |
| Image 12 | K = 15 | 0.9500 | 0.9360 | 0.7921 | 0.9386 | 0.8916 | 0.9425 | 0.9559 | 0.9424 | 0.9056 |
| K = 20 | 0.9500 | 0.9360 | 0.7921 | 0.9386 | 0.8916 | 0.9425 | 0.9559 | 0.9424 | 0.9348 | |
| K = 25 | 0.9837 | 0.9668 | 0.8766 | 0.9699 | 0.9339 | 0.9701 | 0.9813 | 0.9763 | 0.9494 | |
| K = 30 | 0.9858 | 0.9611 | 0.9154 | 0.9778 | 0.9432 | 0.9725 | 0.9841 | 0.9804 | 0.9611 |
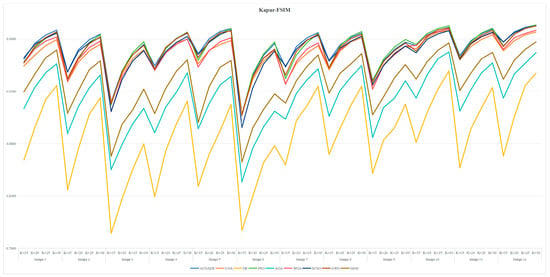
Figure A5.
FSIM line graph based on the Kapur entropy method.
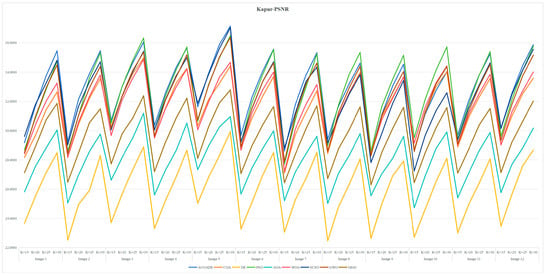
Figure A6.
PSNR line graph based on the Kapur entropy method.
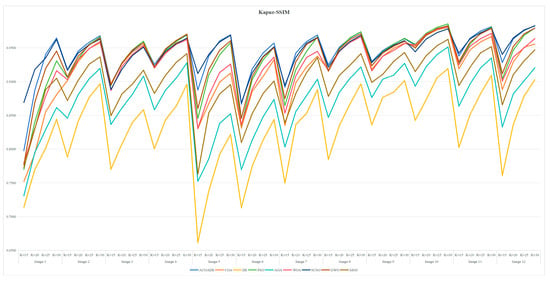
Figure A7.
SSIM line graph based on the Kapur entropy method.
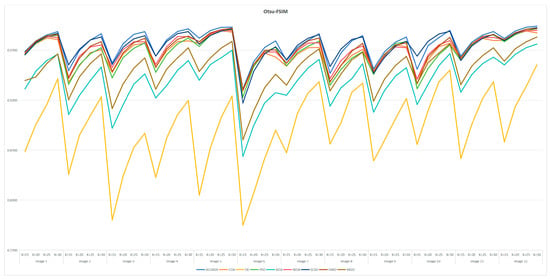
Figure A8.
FSIM line graph based on the Otsu method.
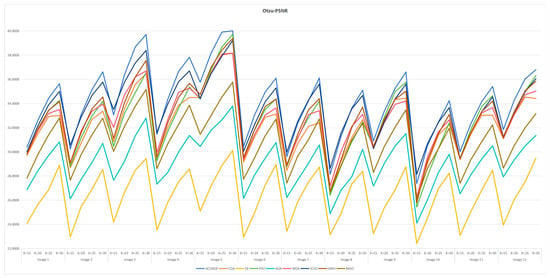
Figure A9.
PSNR line graph based on the Otsu method.
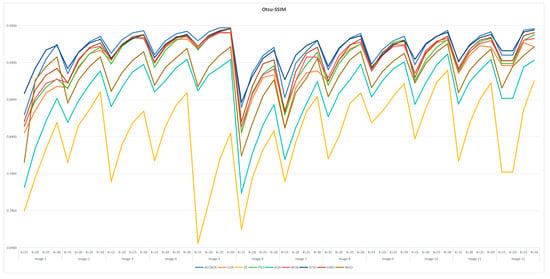
Figure A10.
SSIM line graph based on the Otsu method.
References
- Dong, Y.; Li, M.; Zhou, M. Multi-Threshold Image Segmentation Based on the Improved Dragonfly Algorithm. Mathematics 2024, 12, 854. [Google Scholar] [CrossRef]
- Liu, Y.; Yun, H.; Xiao, Y.; Luan, J.; Li, M. MSGAT: Multi-scale gated axial reverse attention transformer network for medical image segmentation. Biomed. Signal Process. Control 2024, 95, 106341. [Google Scholar]
- Gutiérrez-Zaballa, J.; Basterretxea, K.; Echanobe, J.; Martínez, M.V.; Martinez-Corral, U.; Mata-Carballeira, Ó.; del Campo, I. On-chip hyperspectral image segmentation with fully convolutional networks for scene understanding in autonomous driving. J. Syst. Archit. 2023, 139, 102878. [Google Scholar]
- Liu, H. Image Segmentation Techniques for Intelligent Monitoring of Putonghua Examinations. Adv. Math. Phys. 2022, 1, 4302666. [Google Scholar]
- Blaschke, T. Object based image analysis for remote sensing. ISPRS J. Photogramm. Remote Sens. 2010, 65, 2–16. [Google Scholar] [CrossRef]
- Tao, S.; Zhang, Z.; Zhao, R.; Tang, Z.; Todo, Y. A novel artificial visual system for motion direction detection in color images. Knowl. Based Syst. 2024, 295, 111816. [Google Scholar]
- Peng, Y.; Zhao, Y.; Mao, N.; Wang, J.; Fang, Y.; Zhang, T.; Shi, F. Color image reversible data hiding based on multi—Channel synchronized histogram. J. King Saud Univ. Comput. Inf. Sci. 2023, 35, 101804. [Google Scholar]
- Shah, T.; Safdar, M.U.; Ali, A.; ul Haq, T. Color image encryption by a non—Chain Galois ring extension. Phys. Scr. 2023, 98, 125117. [Google Scholar]
- Dirami, A.; Hammouche, K.; Diaf, M.; Siarry, P. Fast multilevel thresholding for image segmentation through a multiphase level set method. Signal Process. 2013, 93, 139–153. [Google Scholar]
- Panić, B.; Nagode, M.; Klemenc, J.; Oman, S. Combining color and spatial image features for unsupervised image segmentation with mixture modelling and spectral clustering. Mathematics 2023, 11, 4800. [Google Scholar] [CrossRef]
- Kumar, A.; Jain, S.K. ECDM: Enhanced edge based coupled deformable model for image segmentation in the presence of speckle noise and severe intensity inhomogeneity. Appl. Math. Model. 2024, 128, 659–684. [Google Scholar] [CrossRef]
- Wu, C.; Zhao, J. Joint Learning Framework of Superpixel Generation and Fuzzy Sparse Subspace Clustering for Color Image Segmentation. Signal Process. 2024, 222, 109515. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, L.; Li, S.; Xu, K.; Yin, B. Area—Keywords cross—Modal alignment for referring image segmentation. Neurocomputing 2024, 581, 127475. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Abouhawwash, M. A new fusion of whale optimizer algorithm with Kapur’s entropy for multi—Threshold image segmentation: Analysis and validations. Artif. Intell. Rev. 2022, 55, 6389–6459. [Google Scholar] [CrossRef]
- Upadhyay, P.; Chhabra, J.K. Kapur’s entropy based optimal multilevel image segmentation using crow search algorithm. Appl. Soft Comput. 2020, 97, 105522. [Google Scholar] [CrossRef]
- Bhandari, A.K.; Ghosh, A.; Kumar, I.V. A local contrast fusion based 3D Otsu algorithm for multilevel image segmentation. IEEE CAA J. Autom. Sin. 2020, 7, 200–213. [Google Scholar] [CrossRef]
- Fan, Q.; Ma, Y.; Wang, P.; Bai, F. Otsu Image Segmentation Based on a Fractional Order Moth–Flame Optimization Algorithm. Fractal Fract. 2024, 8, 87. [Google Scholar] [CrossRef]
- Bhandari, A.K.; Singh, A.; Kumar, I.V. Spatial context energy curve—Based multilevel 3-D Otsu algorithm for image segmentation. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 2760–2773. [Google Scholar] [CrossRef]
- Ma, G.; Yue, X. An improved whale optimization algorithm based on multilevel threshold image segmentation using the Otsu method. Eng. Appl. Artif. Intell. 2022, 113, 104960. [Google Scholar] [CrossRef]
- Wu, B.; Zhou, J.; Ji, X.; Yin, Y.; Shen, X. An ameliorated teaching–learning—Based optimization algorithm based study of image segmentation for multilevel thresholding using Kapur’s entropy and Otsu’s between class variance. Inf. Sci. 2020, 533, 72–107. [Google Scholar] [CrossRef]
- Sathya, P.D.; Kalyani, R.; Sakthivel, V.P. Color image segmentation using Kapur, Otsu and minimum cross entropy functions based on exchange market algorithm. Expert Syst. Appl. 2021, 172, 114636. [Google Scholar] [CrossRef]
- Bhandari, A.K.; Kumar, A.; Singh, G.K. Modified artificial bee colony based computationally efficient multilevel thresholding for satellite image segmentation using Kapur’s, Otsu and Tsallis functions. Expert Syst. Appl. 2015, 42, 1573–1601. [Google Scholar] [CrossRef]
- Houssein, E.H.; Helmy, B.E.D.; Oliva, D.; Elngar, A.A.; Shaban, H. A novel black widow optimization algorithm for multilevel thresholding image segmentation. Expert Syst. Appl. 2021, 167, 114159. [Google Scholar] [CrossRef]
- Li, K.; Yu, L.; Heng, P.A. Towards reliable cardiac image segmentation: Assessing image—Level and pixel—Level segmentation quality via self—Reflective references. Med. Image Anal. 2022, 78, 102426. [Google Scholar] [CrossRef] [PubMed]
- Akopov, A.S. MBHGA: A Matrix-Based Hybrid Genetic Algorithm for Solving an Agent-Based Model of Controlled Trade Interactions. IEEE Access 2025, 13. [Google Scholar]
- Canales, J.C.; Canales, J.C.; García-Lamont, F.; Yee-Rendon, A.; Castilla, J.S.R.; Mazahua, L.R. Optimal segmentation of image datasets by genetic algorithms using color spaces. Expert Syst. Appl. 2024, 238, 121950. [Google Scholar] [CrossRef]
- Liu, Q.; Li, N.; Jia, H.; Qi, Q.; Abualigah, L. A chimp-inspired remora optimization algorithm for multilevel thresholding image segmentation using cross entropy. Artif. Intell. Rev. 2023, 56 (Suppl. S1), 159–216. [Google Scholar] [CrossRef]
- Jia, H.; Rao, H.; Wen, C.; Mirjalili, S. Crayfish optimization algorithm. Artif. Intell. Rev. 2023, 56 (Suppl. S2), 1919–1979. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, P.; Li, Y. Implementation of an Enhanced Crayfish Optimization Algorithm. Biomimetics 2024, 9, 341. [Google Scholar] [CrossRef]
- Shikoun, N.H.; Al-Eraqi, A.S.; Fathi, I.S. BinCOA: An Efficient Binary Crayfish Optimization Algorithm for Feature Selection. IEEE Access 2024, 12, 28621–28635. [Google Scholar]
- Li, K.; Tan, Z. An improved flower pollination optimizer algorithm for multilevel image thresholding. IEEE Access 2019, 7, 165571–165582. [Google Scholar]
- Yue, X.; Zhang, H. Modified hybrid bat algorithm with genetic crossover operation and smart inertia weight for multilevel image segmentation. Appl. Soft Comput. 2020, 90, 106157. [Google Scholar] [CrossRef]
- Peng, L.; Zhang, D. An adaptive Lévy flight firefly algorithm for multilevel image thresholding based on Rényi entropy. J. Supercomput. 2022, 78, 6875–6896. [Google Scholar]
- Gharehchopogh, F.S.; Ibrikci, T. An improved African vultures optimization algorithm using different fitness functions for multi-level thresholding image segmentation. Multimed. Tools Appl. 2024, 83, 16929–16975. [Google Scholar]
- Jia, H.; Su, Y.; Rao, H.; Liang, M.; Abualigah, L.; Liu, C.; Chen, X. Improved artificial rabbits algorithm for global optimization and multi-level thresholding color image segmentation. Artif. Intell. Rev. 2024, 58, 55. [Google Scholar] [CrossRef]
- Nie, F.; Liu, M.; Zhang, P. Multilevel thresholding with divergence measure and improved particle swarm optimization algorithm for crack image segmentation. Sci. Rep. 2024, 14, 7642. [Google Scholar] [CrossRef] [PubMed]
- Mostafa, R.R.; Houssein, E.H.; Hussien, A.G.; Singh, B.; Emam, M.M. An enhanced chameleon swarm algorithm for global optimization and multi—Level thresholding medical image segmentation. Neural Comput. Appl. 2024, 36, 8775–8823. [Google Scholar]
- Yang, X.; Ye, X.; Zhao, D.; Heidari, A.A.; Xu, Z.; Chen, H.; Li, Y. Multi-threshold image segmentation for melanoma based on Kapur’s entropy using enhanced ant colony optimization. Front. Neuroinformatics 2022, 16, 1041799. [Google Scholar]
- Li, N.; Lv, X.; Xu, S.; Li, B.; Gu, Y. An improved water surface images segmentation algorithm based on the Otsu method. J. Circuits Syst. Comput. 2020, 29, 2050251. [Google Scholar]
- Huang, C.; Li, X.; Wen, Y. An OTSU image segmentation based on fruitfly optimization algorithm. Alex. Eng. J. 2021, 60, 183–188. [Google Scholar]
- García-Guerrero, M.; Hernández-Sandoval, P.; Orduña-Rojas, J.; Cortés-Jacinto, E. Effect of temperature on weight increase, survival, and thermal preference of juvenile redclaw crayfish Cherax quadricarinatus. Hidrobiológica 2013, 23, 73–81. [Google Scholar]
- Payette, A.L.; McGaw, I.J. Thermoregulatory behavior of the crayfish Procambarus clarki in a burrow environment. Comp. Biochem. Physiol. Part A Mol. Integr. Physiol. 2003, 136, 539–556. [Google Scholar] [CrossRef]
- Price, K.V.; Storn, R.M.; Lampinen, J.A. The Differential Evolution Algorithm. In Differential Evolution: A Practical Approach to Global Optimization; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2005; pp. 37–134. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference On Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The arithmetic optimization algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar]
- Seyyedabbasi, A.; Kiani, F. Sand Cat swarm optimization: A nature-inspired algorithm to solve global optimization problems. Eng. Comput. 2023, 39, 2627–2651. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Zheng, B.; Chen, Y.; Wang, C.; Heidari, A.A.; Liu, L.; Chen, H. The moss growth optimization (MGO): Concepts and performance. J. Comput. Des. Eng. 2024, 11, 184–221. [Google Scholar]
- Jia, H.; Shi, S.; Wu, D.; Rao, H.; Zhang, J.; Abualigah, L. Improve coati optimization algorithm for solving constrained engineering optimization problems. J. Comput. Des. Eng. 2023, 10, 2223–2250. [Google Scholar] [CrossRef]
- John, J.; Nair, M.S.; Kumar, P.A.; Wilscy, M. A novel approach for detection and delineation of cell nuclei using feature similarity index measure. Biocybern. Biomed. Eng. 2016, 36, 76–88. [Google Scholar]
- Vishnuvarthanan, G.; Pallikonda Rajasekaran, M. Segmentation of MR brain images for tumor extraction using fuzzy. Curr. Med. Imaging 2013, 9, 2–6. [Google Scholar]
- Mudeng, V.; Kim, M.; Choe, S.W. Prospects of structural similarity index for medical image analysis. Appl. Sci. 2022, 12, 3754. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).