Advanced Modular Honeycombs with Biomimetic Density Gradients for Superior Energy Dissipation
Abstract
:1. Introduction
2. Design and Method
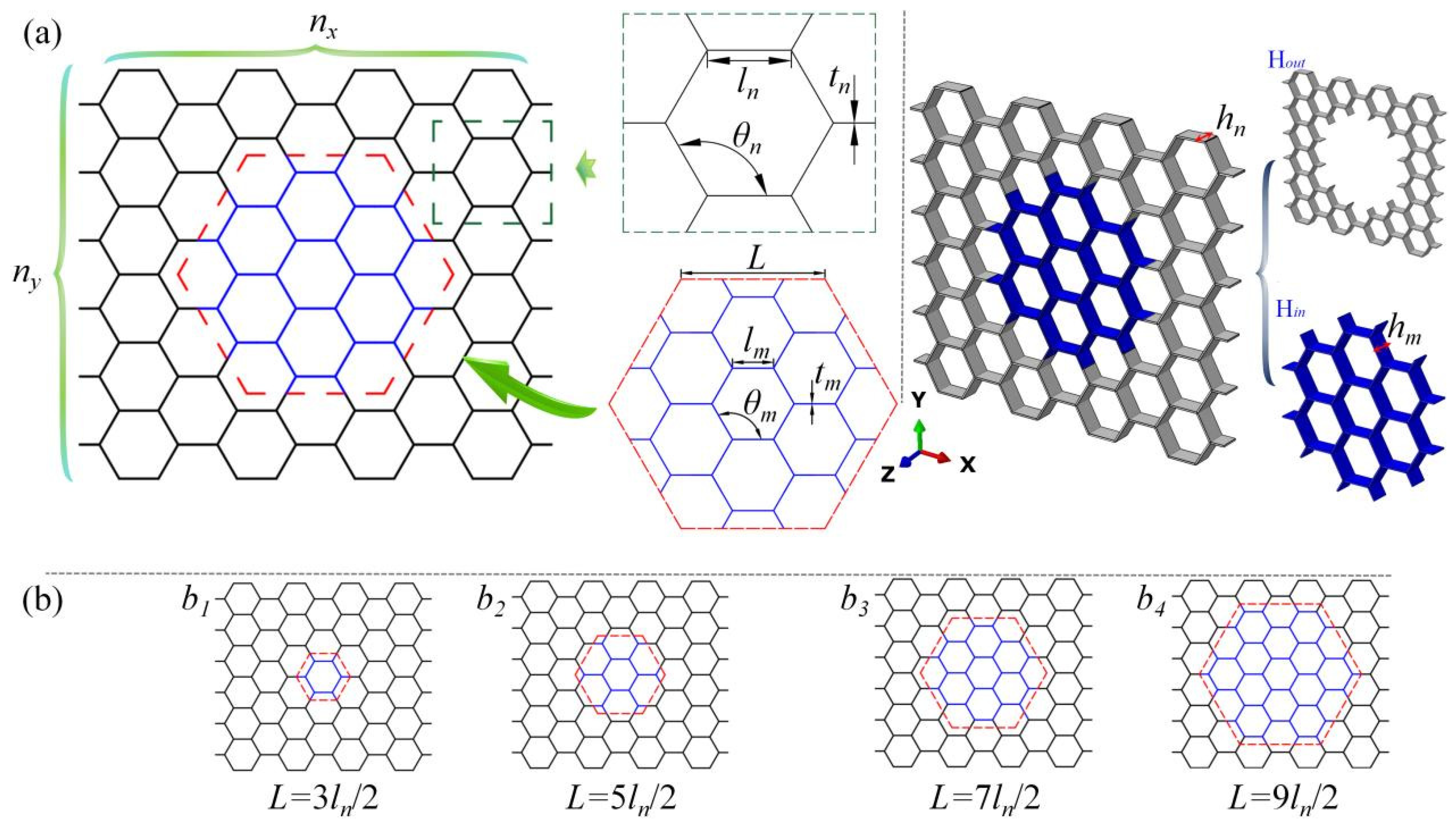
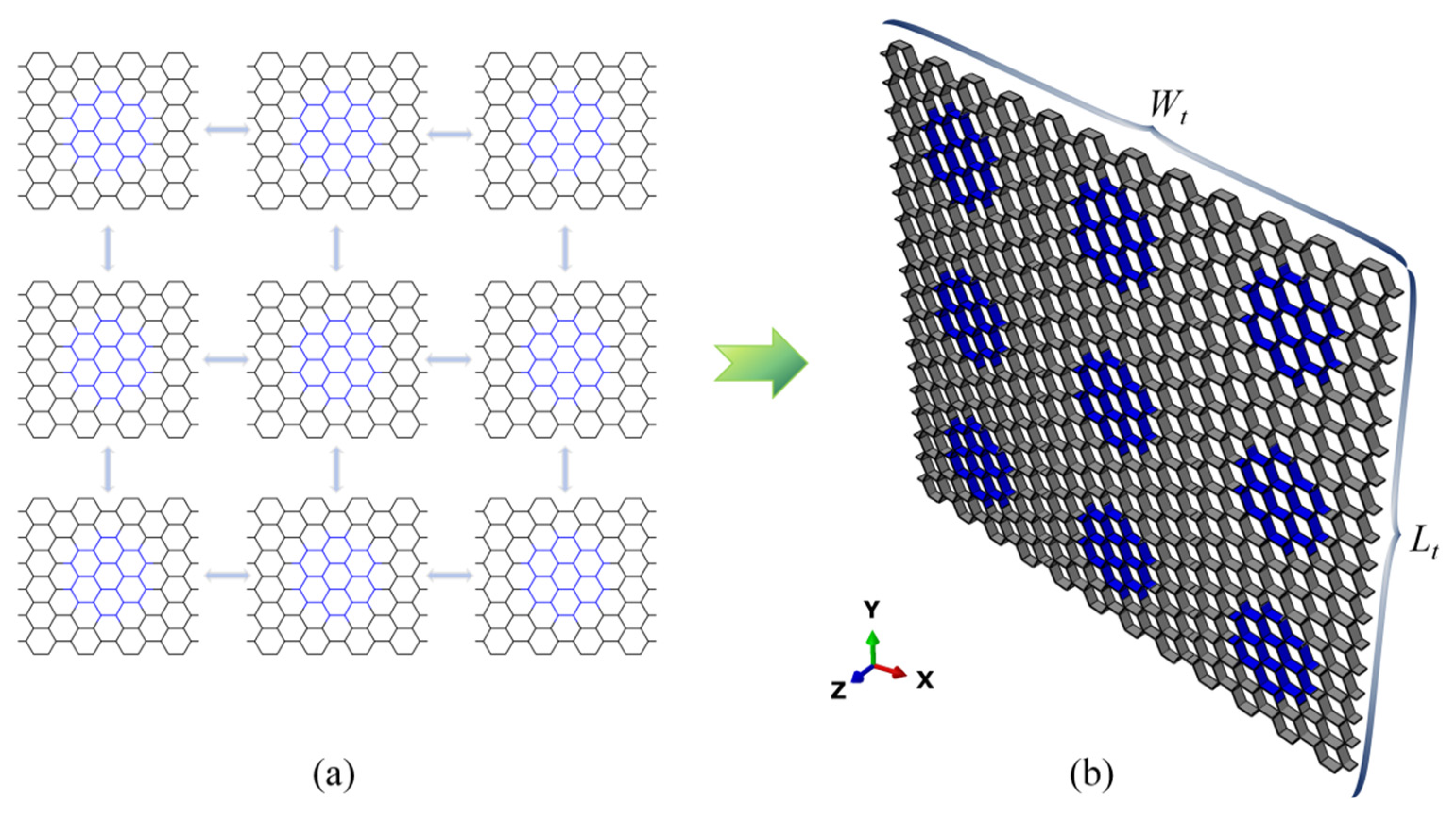
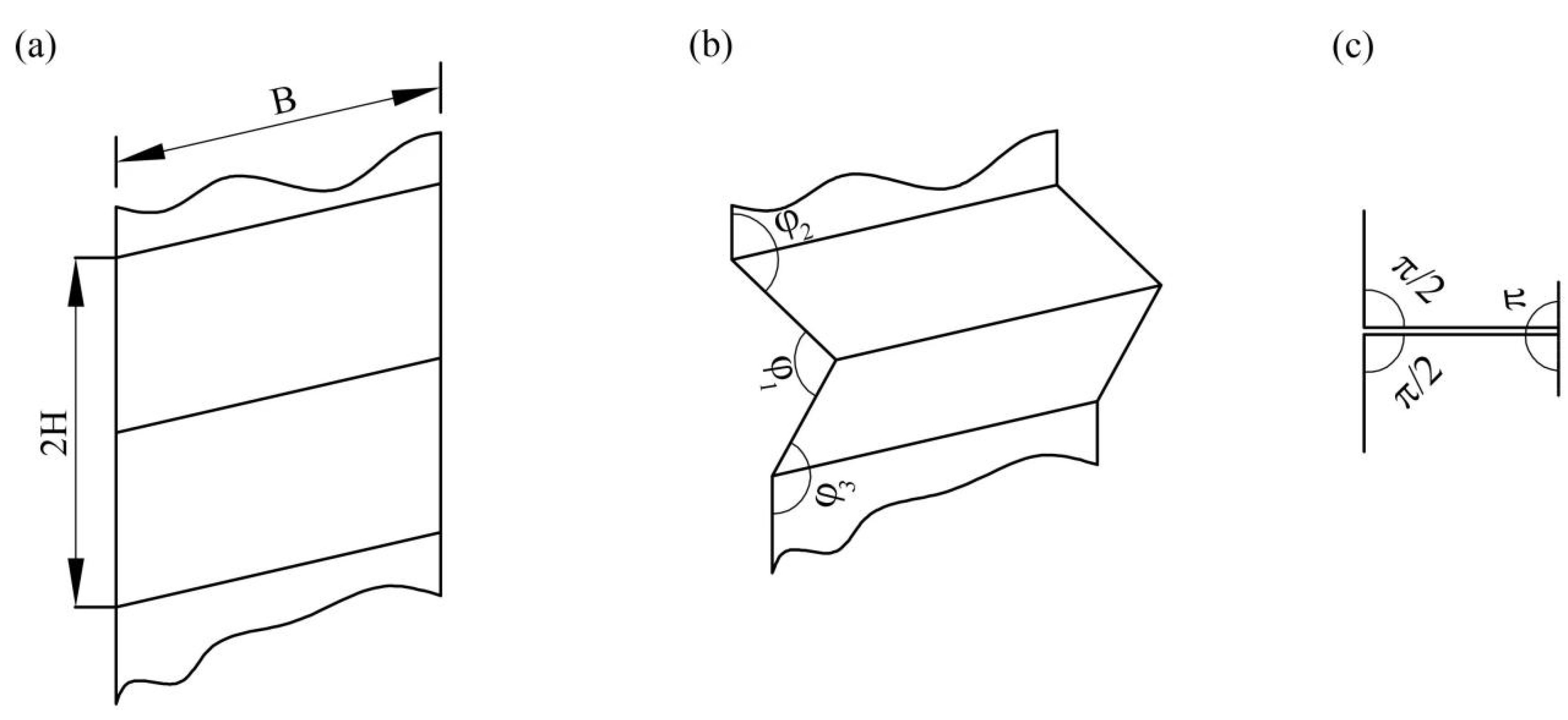
2.1. Modular Honeycomb Design
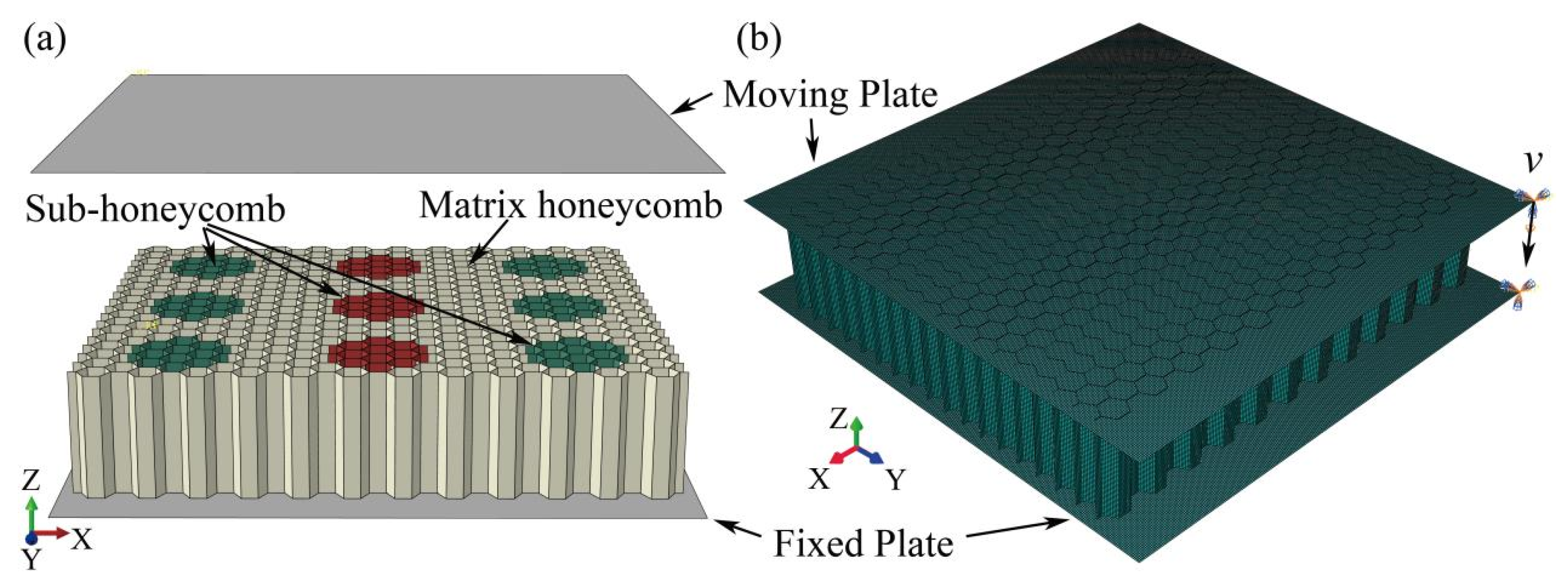
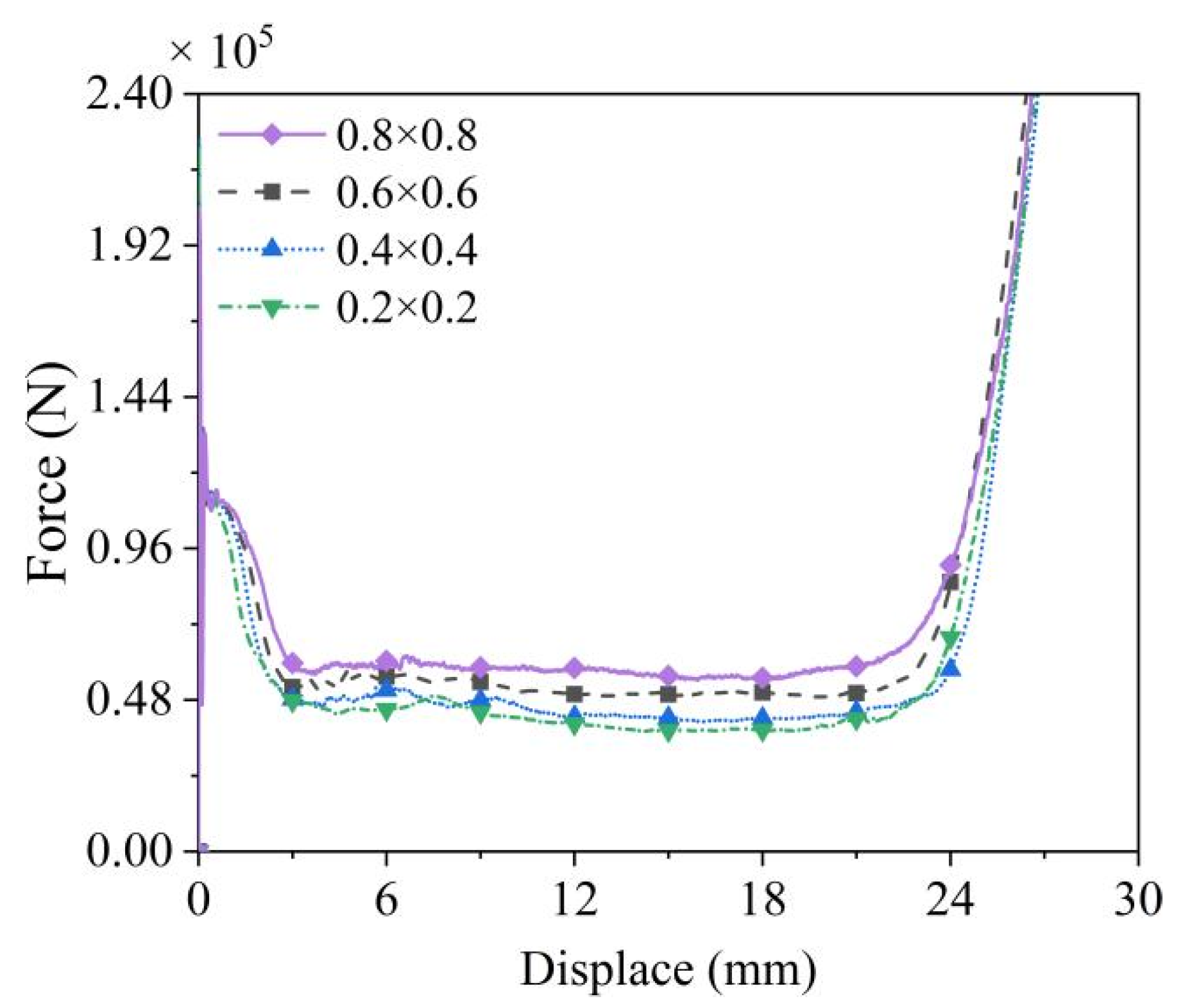
2.2. Numerical Method
3. Quasi-Static Compression
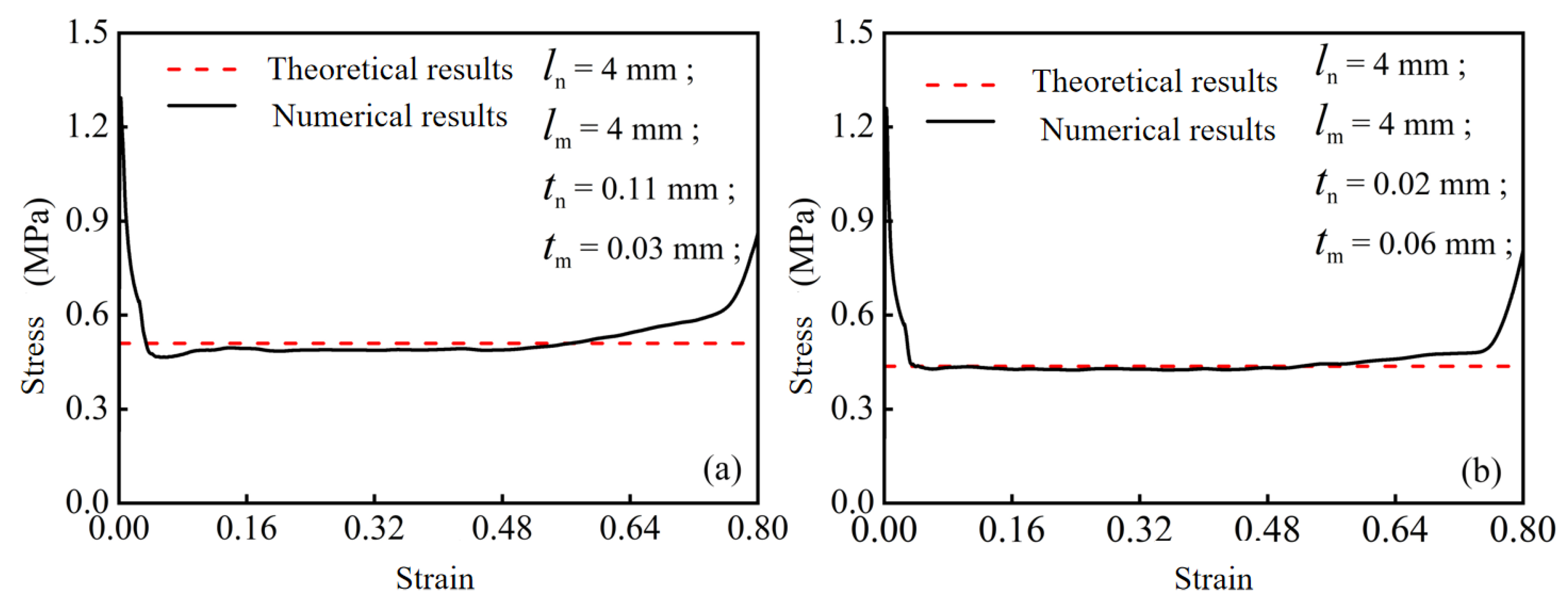
3.1. Theoretical Model for Plateau Stress
3.2. Numerical Verification
4. High-Speed Crushing
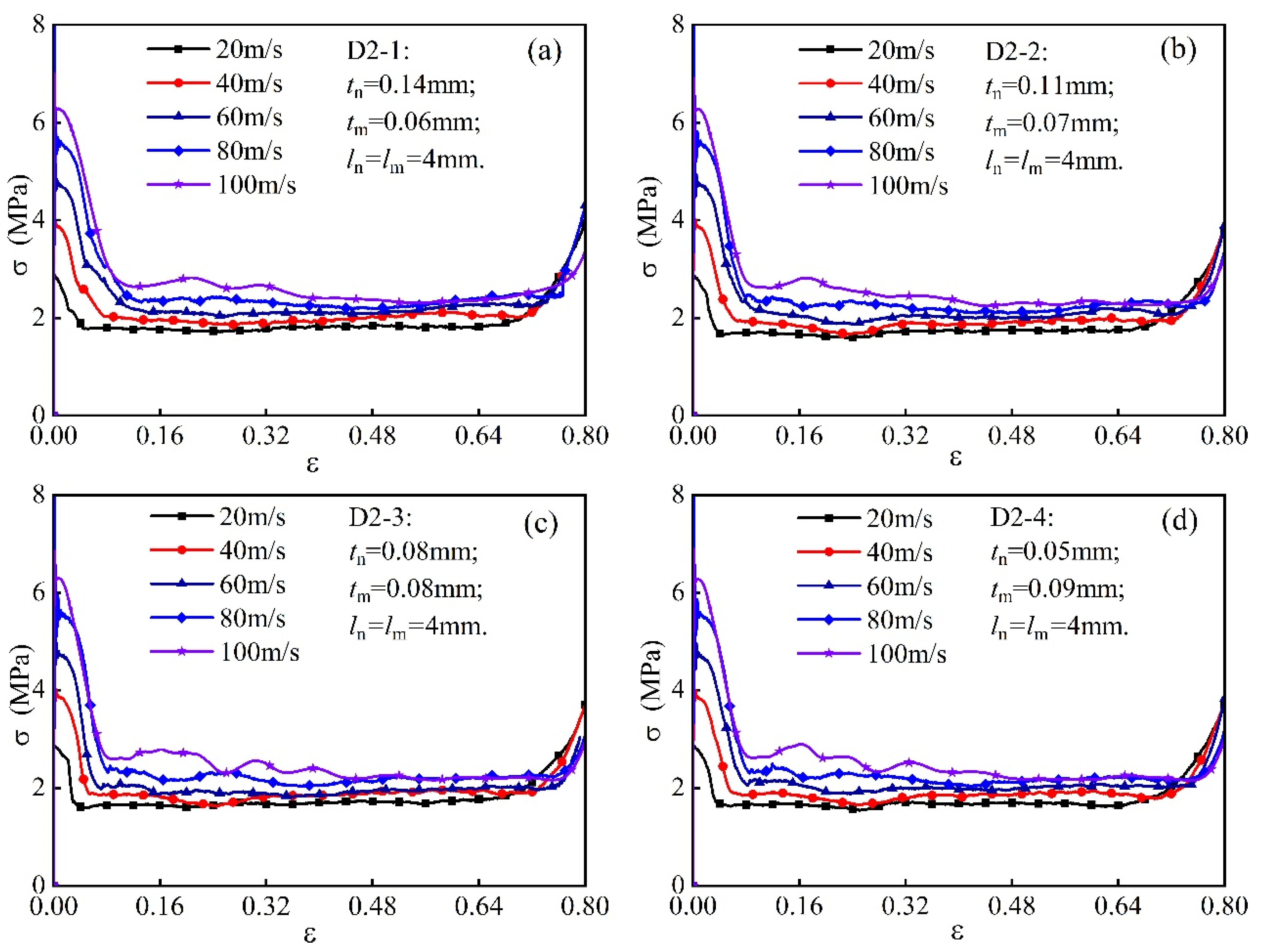
4.1. Plateau Stress
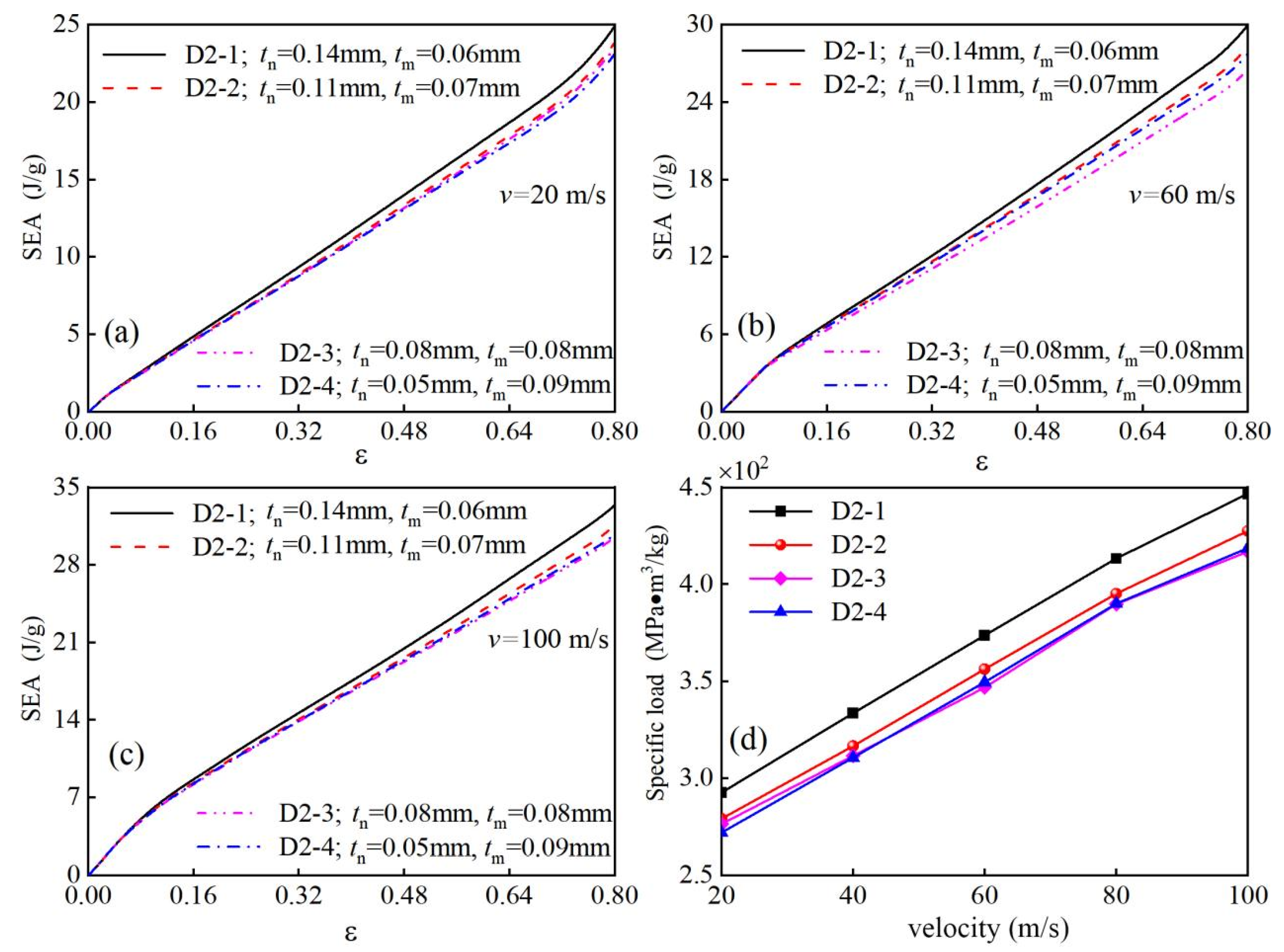
4.2. Specific Energy Absorption
5. Discussion
5.1. Matching Effect Under the Quasi-Static Compression
5.2. Boundary Effects Under the Quasi-Static Compression
6. Conclusions
- (1)
- The theoretical model for the out-of-plane plateau stress of the modular honeycomb, derived from the principle of energy conservation between the work performed by external forces and the total energy absorbed by plastic hinges, demonstrates strong concordance with the numerical model and can be utilized to predict the out-of-plane mechanical performance of the modular honeycomb. Mathematical analysis of the theoretical model reveals that the enhanced compressive strength of modular honeycombs under quasi-static compression, when compared to uniform-wall-thickness counterparts, stems from the superior load-bearing capacity conferred by thick-walled sub-honeycombs;
- (2)
- Modular honeycomb configurations surpass traditional honeycomb structures of equivalent density in out-of-plane load-bearing capacity and energy absorption. This superiority is consistently observed across impact velocities of 20 m/s, 60 m/s, and 100 m/s, with the modular honeycomb D2-1 exhibiting 5.8%, 7.78%, and 7.19% higher specific loads, along with 5.82%, 10.56%, and 8.97% greater energy absorption than conventional counterparts, thereby demonstrating the mechanical performance advantages in modular design;
- (3)
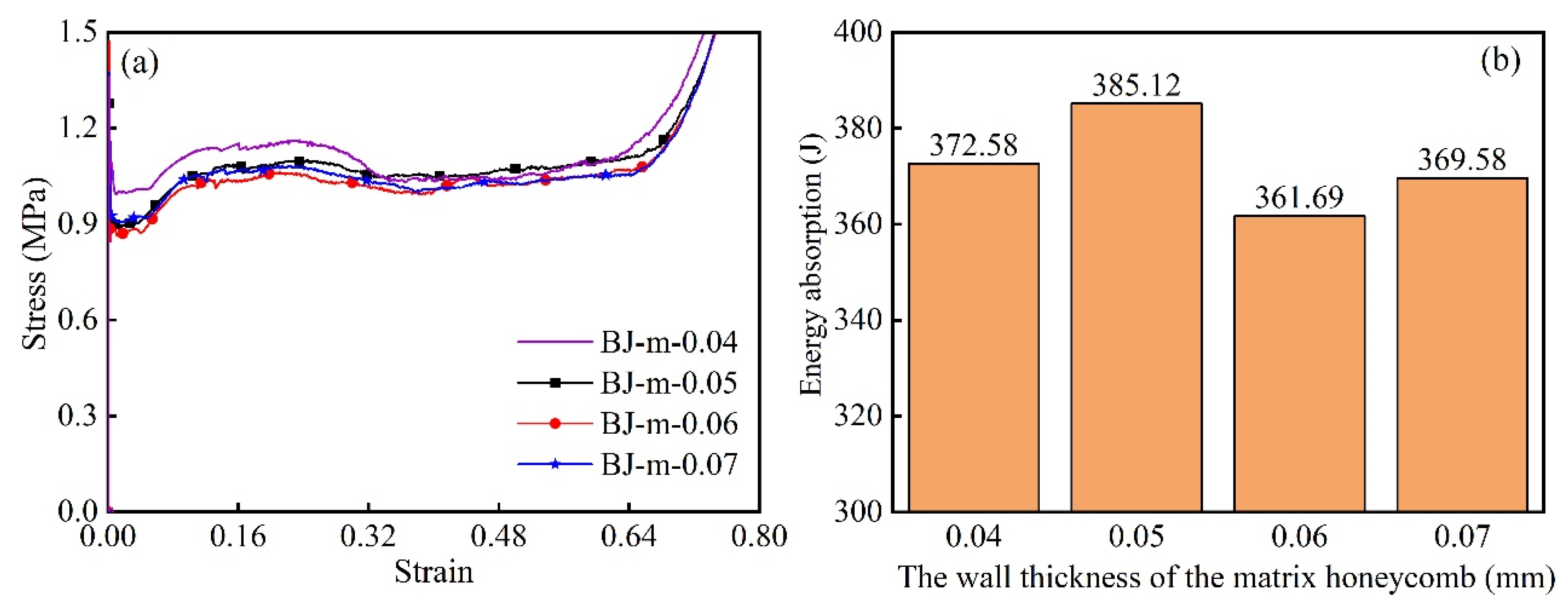
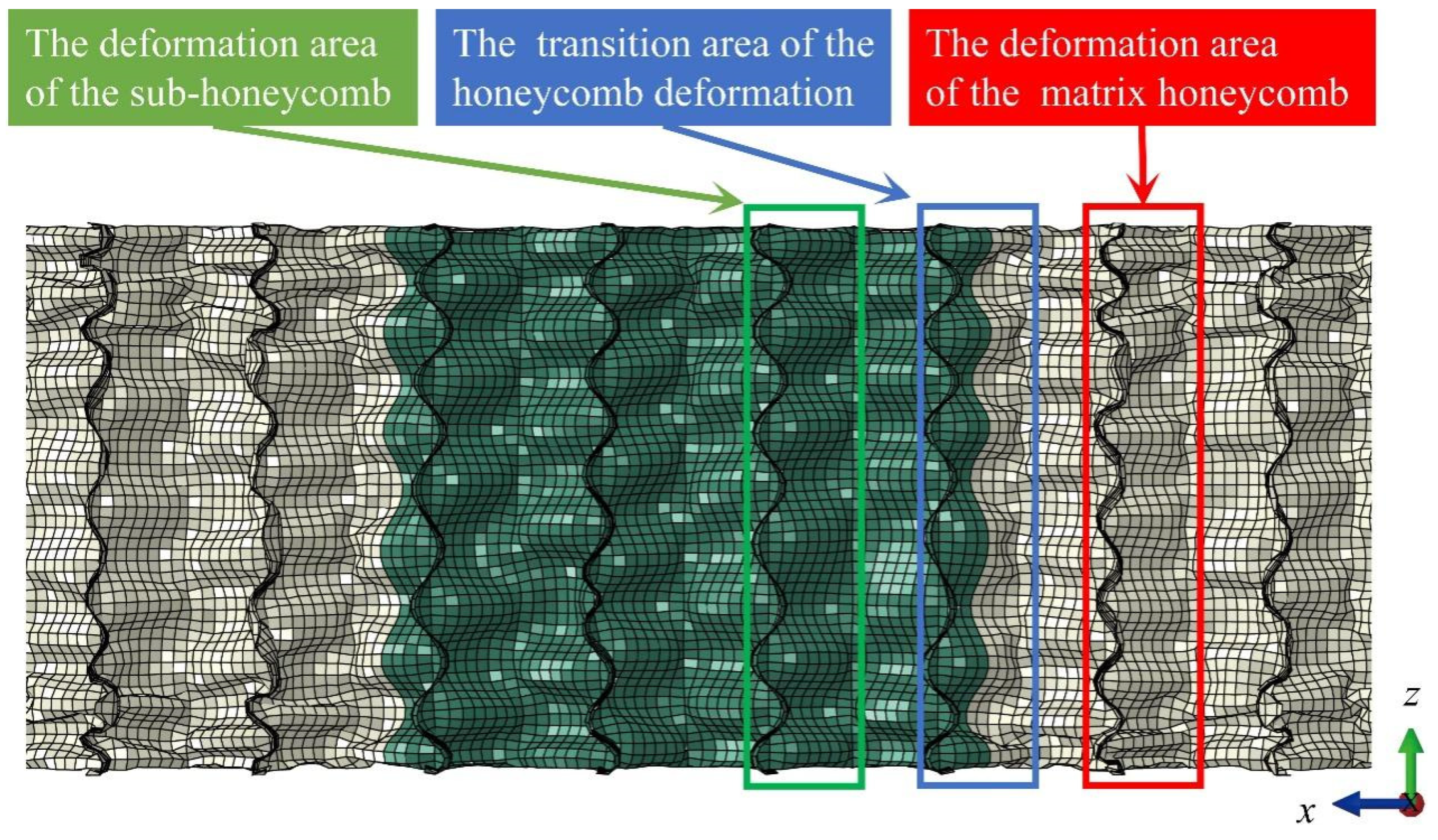
- Adjusting the wall thickness of sub- and matrix honeycombs can optimize the impact resistance of modular honeycombs. A proper wall-thickness matching relationship prevents the shifting of densification points, the reduction of energy-absorbing wrinkles in the transition zone, and instability, thereby fully leveraging the enhanced impact resistance of modular honeycombs;
- (4)
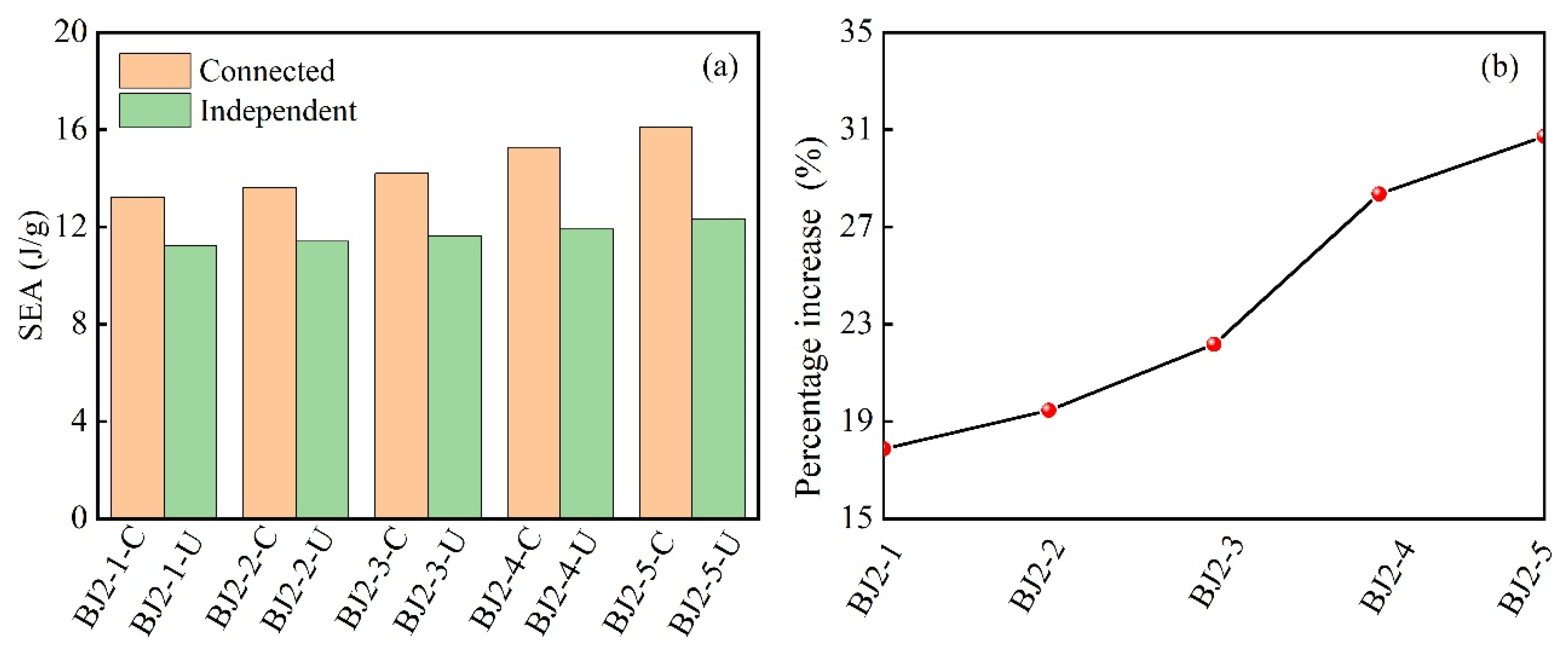
- The boundary effect can decrease the mechanical performance of modular honeycombs, and it should be limited in practical applications.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hyon, J.; Lawal, O.; Thevamaran, R.; Song, Y.E.; Thomas, E.L. Extreme energy dissipation via material evolution in carbon nanotube mats. Adv. Sci. 2021, 8, 2003142. [Google Scholar]
- Mueller, J.; Matlack, K.H.; Shea, K.; Daraio, C. Energy absorption properties of periodic and stochastic 3D lattice materials. Adv. Theory Simul. 2019, 2, 1900081. [Google Scholar]
- Shen, L.; Wang, Z.; Wang, X.; Wei, K. Negative Poisson’s ratio and effective Young’s modulus of a vertex-based hierarchical re-entrant honeycomb structure. Int. J. Mech. Sci. 2021, 206, 106611. [Google Scholar]
- Mirhakimi, A.S.; Dubey, D.; Elbestawi, M.A. Laser Powder Bed Fusion of Bio-inspired Metamaterials for Energy Absorption Applications: A review. J. Mater. Res. Technol. 2024, 31, 2126–2155. [Google Scholar]
- Ha, N.S.; Lee, T.-U.; Tran, D.T.; Zhang, J.; Lu, G.; Ren, X.; Xie, Y.M. Efficient energy absorption of bio-inspired bi-directional gradient hierarchical multi-cell structure. Int. J. Mech. Sci. 2024, 278, 109492. [Google Scholar]
- Shen, L.; Wang, X.; Li, Z.; Wei, K.; Wang, Z. Elastic properties of an additive manufactured three-dimensional vertex-based hierarchical re-entrant structure. Mater. Des. 2022, 216, 110527. [Google Scholar]
- Greco, L.; Buccino, F.; Xu, Z.; Vergani, L.; Berto, F.; Guagliano, M.; Razavi, N.; Bagherifard, S. Design and analysis of energy absorbent bioinspired lattice structures. J. Bionic Eng. 2023, 20, 1670–1686. [Google Scholar]
- Li, L.; Yang, F.; Li, P.; Wu, W.; Wang, L. A novel hybrid lattice design of nested cell topology with enhanced energy absorption capability. Aerosp. Sci. Technol. 2022, 128, 107776. [Google Scholar]
- Mohammadi, H.; Ahmad, Z.; Petrů, M.; Mazlan, S.A.; Johari, M.A.F.; Hatami, H.; Koloor, S.S.R. An insight from nature: Honeycomb pattern in advanced structural design for impact energy absorption. J. Mater. Res. Technol. 2023, 22, 2862–2887. [Google Scholar]
- Farooq, U.; Ahmad, M.; Rakha, S.; Ali, N.; Khurram, A.; Subhani, T. Interfacial mechanical performance of composite honeycomb sandwich panels for aerospace applications. Arab. J. Sci. Eng. 2017, 42, 1775–1782. [Google Scholar]
- Chantarapanich, N.; Laohaprapanon, A.; Wisutmethangoon, S.; Jiamwatthanachai, P.; Chalermkarnnon, P.; Sucharitpwatskul, S.; Puttawibul, P.; Sitthiseripratip, K. Fabrication of three-dimensional honeycomb structure for aeronautical applications using selective laser melting: A preliminary investigation. Rapid Prototyp. J. 2014, 20, 551–558. [Google Scholar]
- Gu, Z.; Hui, J.; Wang, J.; Wu, D.; Lu, L.; Wang, Z. Modelling multiple impacts on the out-of-plane cushioning properties of honeycomb paperboard. Packag. Technol. Sci. 2021, 34, 541–556. [Google Scholar]
- Gao, Z.; Dong, W.; Xiaomin, J. Research on the reduction design of fragile product cushion packaging under the green development concept. In Proceedings of the 2020 International Symposium on Energy Environment and Green Development, Chongqing, China, 20–22 November 2020; p. 012057. [Google Scholar]
- Meng, Y.; Xu, J.; He, J.; Tao, S.; Gupta, D.; Moreira, C.; Tiwari, P.; Guo, C. A cluster UAV inspired honeycomb defense system to confront military IoT: A dynamic game approach. Soft Comput. 2023, 27, 1033–1043. [Google Scholar]
- Jaikumar, M.; Koenig, P.; Vignesh, S.; Bentgens, F.; Hariram, V. Impact of vehicle collision using modified crash box in the crumple zone-A perspective assessment. Int. J. Veh. Struct. Syst. 2022, 14, 524–529. [Google Scholar]
- Wei, X.; Xiong, J.; Wang, J.; Xu, W. New advances in fiber-reinforced composite honeycomb materials. Sci. China Technol. Sci. 2020, 63, 1348–1370. [Google Scholar]
- Lu, X.; Wang, X.; Song, W.; Ma, X.; Yin, F.; Zhao, Z.; Li, D.; Zheng, Y.; Sun, B. Sustainable lignocellulose bio-based foam with good cushioning performance and thermal insulation for transportation packaging. Ind. Crops Prod. 2024, 216, 118758. [Google Scholar] [CrossRef]
- Nguyen, T.B.H.; Nguyen, H.T. Lightweight panel for building construction based on honeycomb paper composite/core-fiberglass composite/face materials. Nano Hybrids Compos. 2021, 32, 15–23. [Google Scholar]
- Çakan, B.G.; Ensarioğlu, C.; Küçükakarsu, V.M.; Tekin, İ.E.; Çakır, M.C. Experimental and Numerical Investigation of In-Plane and Out-of-Plane Impact Behaviour of Auxetic Honeycomb Boxes Produced by Material Extrusion. 2021. Available online: https://avesis.uludag.edu.tr/yayin/efc9f1b8-4813-49df-9e3c-747ec716c258/experimental-and-numerical-investigation-of-in-plane-and-out-of-plane-impact-behaviour-of-auxetic-honeycomb-boxes-produced-by-material-extrusion (accessed on 5 March 2025).
- Fu, B.; Gao, J. Study on the application of graphene polymer material in sports equipment. In Proceedings of the 2020 6th International Conference on Materials, Mechanical Engineering and Automation Technology, Zhuhai, China, 1–3 May 2020; p. 012044. [Google Scholar]
- Kaczyński, P.; Skwarski, M.; Dmitruk, A.; Makuła, P.; Ludwiczak, J. The Designs and Testing of Biodegradable Energy-Absorbing Inserts for Enhanced Crashworthiness in Sports Helmets. Materials 2024, 17, 4407. [Google Scholar] [CrossRef]
- Yang, D.; Guo, L.; Fan, C. Mechanical Behavior of 3D-Printed Thickness Gradient Honeycomb Structures. Materials 2024, 17, 2928. [Google Scholar] [CrossRef]
- Mussini, A.; Carter, L.; Villapun, V.; Cao, E.; Cox, S.; Ginestra, P. 3D printing for Growth Adaptive Medical Devices: An alternative approach for craniosynostosis. Procedia CIRP 2024, 125, 319–324. [Google Scholar]
- Liu, T.; Feng, H.; Jin, C.; Pawlak, M.; Saeb, M.R.; Kuang, T. Green segregated honeycomb biopolymer composites for electromagnetic interference shielding biomedical devices. Chem. Eng. J. 2024, 493, 152438. [Google Scholar] [CrossRef]
- Zou, Q.; Zhou, X.; Wang, R.; Ning, Y.; Chen, Z.; Kong, F.; Liu, Y. Load-carrying and energy-absorbing performance of honeycombs with different cross sections under cyclic loading. Mater. Today Commun. 2022, 33, 104582. [Google Scholar] [CrossRef]
- Ha, N.S.; Pham, T.M.; Tran, T.T.; Hao, H.; Lu, G. Mechanical properties and energy absorption of bio-inspired hierarchical circular honeycomb. Compos. Part B Eng. 2022, 236, 109818. [Google Scholar] [CrossRef]
- Shen, L.; Wei, K.; Yuan, K.; Shi, C.; Li, Z.; Wang, Z. A novel metamaterial incorporating both auxeticity and thermal shrinkage. Int. J. Mech. Sci. 2022, 233, 107650. [Google Scholar] [CrossRef]
- Wang, Z. Recent advances in novel metallic honeycomb structure. Compos. Part B Eng. 2019, 166, 731–741. [Google Scholar] [CrossRef]
- Thomas, T.; Tiwari, G. Crushing behavior of honeycomb structure: A review. Int. J. Crashworthiness 2019, 24, 555–579. [Google Scholar] [CrossRef]
- Qi, C.; Jiang, F.; Yang, S. Advanced honeycomb designs for improving mechanical properties: A review. Compos. Part B Eng. 2021, 227, 109393. [Google Scholar] [CrossRef]
- Wang, Z.; Lei, Z.; Li, Z.; Yuan, K.; Wang, X. Mechanical reinforcement mechanism of a hierarchical Kagome honeycomb. Thin-Walled Struct. 2021, 167, 108235. [Google Scholar] [CrossRef]
- Wang, Z.; Yao, S.; Liu, K.; Wei, K.; Gao, T.; Zhao, M. Origami embedded honeycomb with three-axial comparable and improved energy absorption performance. Thin-Walled Struct. 2023, 193, 111295. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, X.; Liu, K.; Zhang, J.; Lu, Z. Crashworthiness index of honeycomb sandwich structures under low-speed oblique impact. Int. J. Mech. Sci. 2021, 208, 106683. [Google Scholar] [CrossRef]
- Dalave, P.A.; Joseph, T.; Patil, D.; Patadiya, J.; Naebe, M.; Kandasubramanian, B. Meta-structures for energy absorption: Materials, designs, and applications in additive manufacturing and its future scope. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 518. [Google Scholar]
- Liu, F.; Shao, S.; Wang, W.; Xia, R.; Negahban, M.; Li, Z. A Novel Cross Tetrachiral Honeycomb Metamaterial with Designable Static and Dynamic Performances. Materials 2024, 17, 4652. [Google Scholar] [CrossRef]
- Liu, H.-T.; Liu, J.-Y.; Wu, W.-J. Energy absorption characteristics and multi-objective optimization of 3D bionic negative Poisson’s ratio honeycomb. Mater. Today Commun. 2024, 39, 109044. [Google Scholar]
- Wang, S.; Pei, W.; Jin, S.; Yu, H. Numerical and theoretical analysis of the out-of-plane crushing behavior of a sinusoidal-shaped honeycomb structure with tunable mechanical properties. Structures 2024, 61, 106147. [Google Scholar]
- Liu, Z.; Zou, K.; Zhang, Z. Energy Absorption Behavior of Carbon-Fiber-Reinforced Plastic Honeycombs under Low-Velocity Impact Considering Their Ply Characteristics. Materials 2024, 17, 4257. [Google Scholar] [CrossRef]
- Miao, S.; Zhong, Y.; Zhang, M.; Liu, R. Forced-Vibration Characteristics of Bowtie-Shaped Honeycomb Composite Sandwich Panel with Viscoelastic Damping Layer. Materials 2024, 17, 4067. [Google Scholar] [CrossRef]
- Yin, Y.; Zhang, X. Misalignment Assembly Effect on the Impact Mechanical Response of Tandem Nomex Honeycomb-Core Sandwich Structures. Materials 2024, 17, 4024. [Google Scholar] [CrossRef] [PubMed]
- Yuan, H.; Zhong, Y.; Tang, Y.; Liu, R. Dynamic Characteristics of Composite Sandwich Panel with Triangular Chiral (Tri-Chi) Honeycomb under Random Vibration. Materials 2024, 17, 3973. [Google Scholar] [CrossRef]
- Shen, L.; Wu, Y.; Ye, T.; Gao, T.; Zheng, S.; Long, Z.; Ren, X.; Zhang, H.; Huang, J.; Liu, K. Biomimetic Modular Honeycomb with Enhanced Crushing Strength and Flexible Customizability. Materials 2024, 17, 4950. [Google Scholar] [CrossRef]
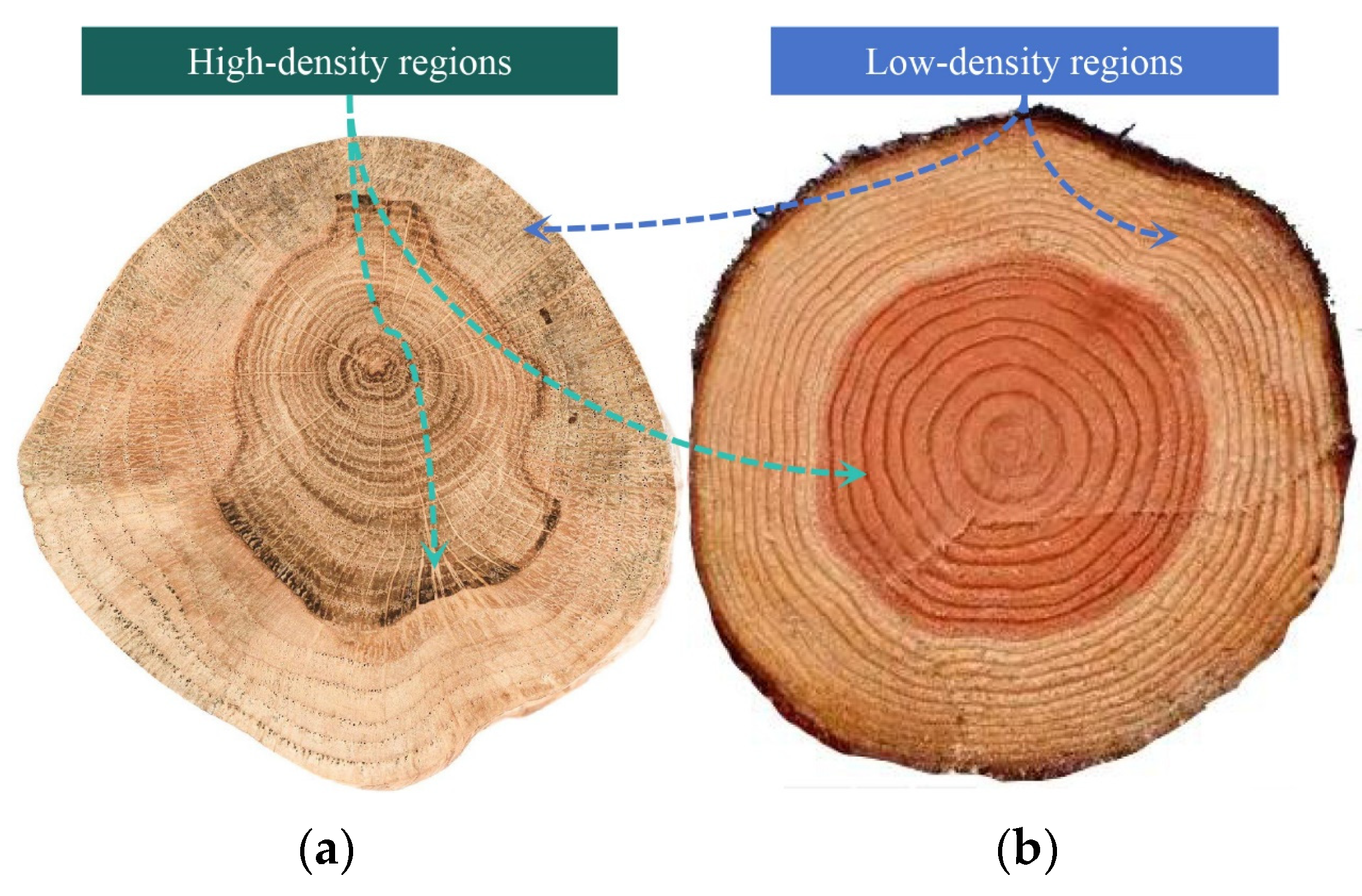
- Ziemińska, K.; Westoby, M.; Wright, I.J. Broad anatomical variation within a narrow wood density range—A study of twig wood across 69 Australian angiosperms. PLoS ONE 2015, 10, e0124892. [Google Scholar]
- Koubaa, A.; Zhang, S.T.; Makni, S. Defining the transition from earlywood to latewood in black spruce based on intra-ring wood density profiles from X-ray densitometry. Ann. For. Sci. 2002, 59, 511–518. [Google Scholar] [CrossRef]
- Kallarackal, J.; Ramírez, F. Wood Density: Functional Trait in Plants. Springer Nature: Berlin/Heidelberg, Germany, 2024. [Google Scholar]
- Panshin, A.J.; Zeeuw, C.d. Textbook of Wood Technology; McGraw-Hill Book, Co.: New York, NY, USA, 1981. [Google Scholar]
- Zhu, Y.; Pan, B.; Yu, C.; Yin, Y.; Zhang, Y. Comparative study on DBH growth and wood density of Taxodium hybrid ‘Zhongshanshan 118′and Taxodium distichum. J. Nanjing For. Univ. 2019, 43, 201. [Google Scholar]




| Group | Serial Number | Sub-Honeycomb | Matrix Honeycomb | Relative Density | ||
|---|---|---|---|---|---|---|
| /mm | /g | /mm | /g | |||
| D1 | D1-1 | 0.11 | 11.55 | 0.03 | 9.45 | 1.44% |
| D1-2 | 0.08 | 8.40 | 0.04 | 12.60 | ||
| D1-3 | 0.05 | 5.25 | 0.05 | 15.75 | ||
| D1-4 | 0.02 | 2.10 | 0.06 | 18.90 | ||
| D2 | D2-1 | 0.14 | 14.70 | 0.06 | 18.90 | 2.31% |
| D2-2 | 0.11 | 11.55 | 0.07 | 22.05 | ||
| D2-3 | 0.08 | 8.40 | 0.08 | 25.19 | ||
| D2-4 | 0.05 | 5.25 | 0.09 | 28.34 | ||
| D3 | D3-1 | 0.18 | 18.90 | 0.10 | 31.49 | 3.46% |
| D3-2 | 0.15 | 15.75 | 0.11 | 34.64 | ||
| D3-3 | 0.12 | 12.60 | 0.12 | 37.79 | ||
| D3-4 | 0.09 | 9.45 | 0.13 | 40.94 | ||
| Serial Number | Layout Form | Sub-Honeycomb | Matrix Honeycomb | Relative Density | ||
|---|---|---|---|---|---|---|
| /mm | /g | /mm | /g | |||
| BJ2-m-0.04 | BJ2 | 0.12 | 12.6 | 0.04 | 12.60 | 1.73% |
| BJ2-m-0.05 | 0.09 | 9.45 | 0.05 | 15.75 | ||
| BJ2-m-0.06 | 0.06 | 6.30 | 0.06 | 18.90 | ||
| BJ2-m-0.07 | 0.03 | 3.15 | 0.07 | 22.05 | ||
| Group | Serial Number | Connection State | Sub-Honeycomb | Matrix Honeycomb | ||
|---|---|---|---|---|---|---|
| /g | /mm | |||||
| B1 | BJ2-1-C | connected | 0.02 | 2.10 | 0.06 | 18.90 |
| BJ2-1-U | independent | 0.02 | 2.10 | 0.06 | 18.90 | |
| B2 | BJ2-2-C | connected | 0.04 | 4.20 | 0.06 | 18.90 |
| BJ2-2-U | independent | 0.04 | 4.20 | 0.06 | 18.90 | |
| B3 | BJ2-3-C | connected | 0.06 | 6.30 | 0.06 | 18.90 |
| BJ2-3-U | independent | 0.06 | 6.30 | 0.06 | 18.90 | |
| B4 | BJ2-4-C | connected | 0.08 | 8.40 | 0.06 | 18.90 |
| BJ2-4-U | independent | 0.08 | 8.40 | 0.06 | 18.90 | |
| B5 | BJ2-5-C | connected | 0.10 | 10.50 | 0.06 | 18.90 |
| BJ2-5-U | independent | 0.10 | 10.50 | 0.06 | 18.90 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Y.; He, J.; Wang, D.; Luo, D.; Zeng, Y.; Feng, H.; You, X.; Shen, L. Advanced Modular Honeycombs with Biomimetic Density Gradients for Superior Energy Dissipation. Biomimetics 2025, 10, 221. https://doi.org/10.3390/biomimetics10040221
Dong Y, He J, Wang D, Luo D, Zeng Y, Feng H, You X, Shen L. Advanced Modular Honeycombs with Biomimetic Density Gradients for Superior Energy Dissipation. Biomimetics. 2025; 10(4):221. https://doi.org/10.3390/biomimetics10040221
Chicago/Turabian StyleDong, Yong, Jie He, Dongtao Wang, Dazhi Luo, Yanghui Zeng, Haixia Feng, Xizhen You, and Lumin Shen. 2025. "Advanced Modular Honeycombs with Biomimetic Density Gradients for Superior Energy Dissipation" Biomimetics 10, no. 4: 221. https://doi.org/10.3390/biomimetics10040221
APA StyleDong, Y., He, J., Wang, D., Luo, D., Zeng, Y., Feng, H., You, X., & Shen, L. (2025). Advanced Modular Honeycombs with Biomimetic Density Gradients for Superior Energy Dissipation. Biomimetics, 10(4), 221. https://doi.org/10.3390/biomimetics10040221





