Bio-Inspired Swarm Confrontation Algorithm for Complex Hilly Terrains
Abstract
1. Introduction
- In contrast to purely 2D or 3D confrontation environments [15,16,17,18,19,20,21], this is the first time that a semi-3D confrontation environment, i.e., hilly terrain, has been considered regarding the swarm confrontation problem, which brings many challenges. First, the ability of the agent to gather information about opponents is limited. Second, virtual projectiles or actions executed by agents may be blocked by the terrain. Furthermore, the terrain constrains the agents’ postures, adding even more complexity to decision-making.
- Compared to agents that employ a particle model for movement [8,16,22,23,24], to suit the semi-3D confrontation environment, this paper adopts the unicycle model as a kinematic model of agents, which is more realistic yet complicated for confrontation scenarios. In addition, the rotating module responsible for targeting can freely spin on its supporting plane, while the elevation unit is capable of vertical adjustment. As a result, incorporating the additional degrees of freedom introduced by these rotational components leads to a more complex kinematic model compared to the standard unicycle model.
- Drawing on the behavioral characteristics exhibited by prides of lions and packs of wild dogs during their hunts, this paper proposes key algorithms suited to swarm confrontations. Compared with algorithms based on reinforcement learning or target-based assignment [15,25,26], the proposed approach focuses on specific behaviors throughout the confrontation, enhancing its interpretability and practical applicability—particularly in simulation-based environments such as electronic games. In direct comparisons against the aforementioned algorithms, the proposed method achieves a win rate exceeding 80%.
- For the evaluation of confrontation algorithms, in addition to traditional win rate assessment [24,25,27,28,29], two more performance indices are adopted, i.e., the agents’ quantity loss rate and the agents’ health loss rate. These two indices reflect the cost paid by the swarm confrontation algorithm to win from different perspectives, and the test results further highlight the superiority of the proposed bio-inspired swarm confrontation algorithm.
2. Related Work
2.1. Optimization Algorithms
2.2. Multi-Agent Reinforcement Learning
3. Problem Description
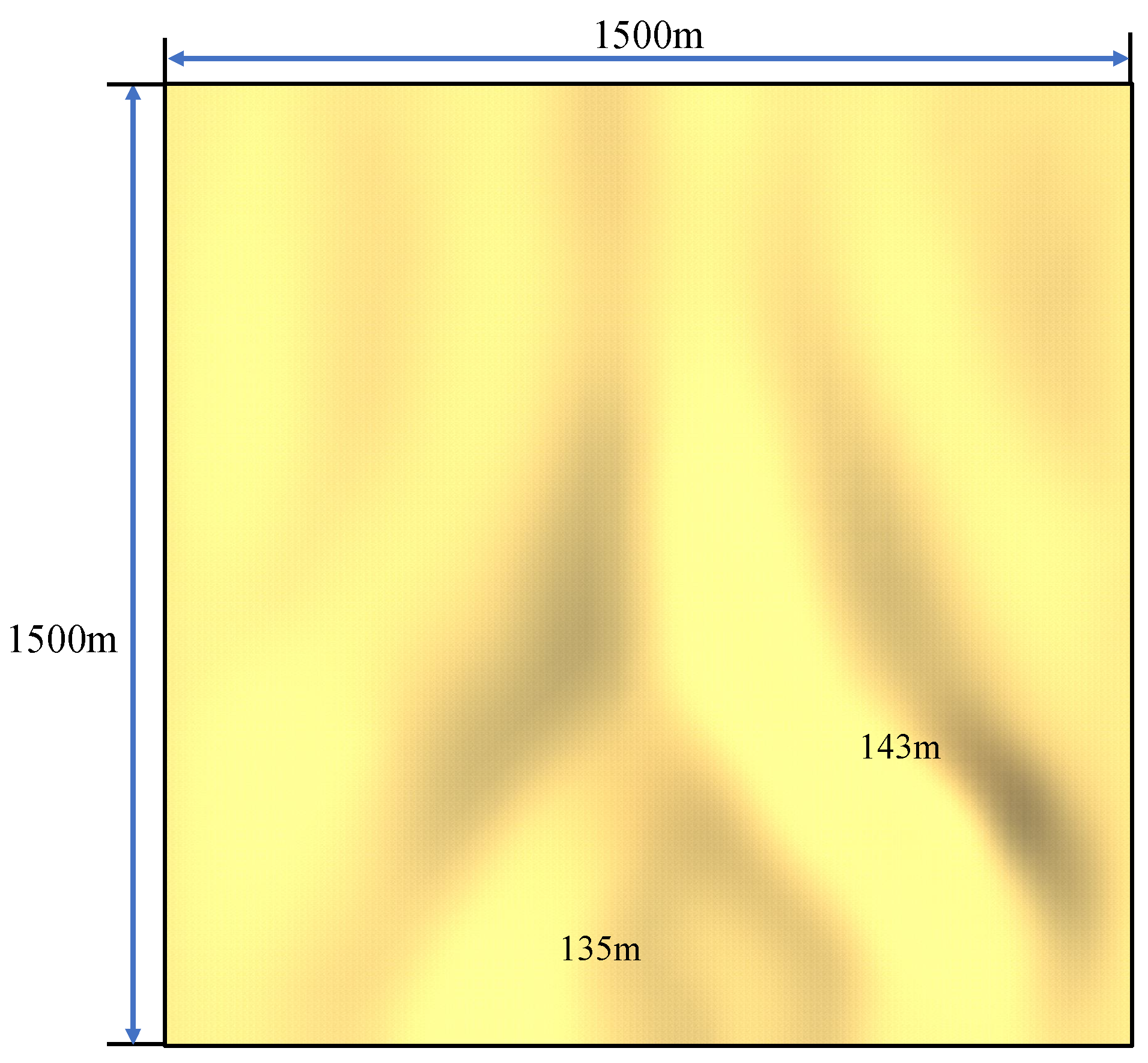
3.1. Confrontation Environment
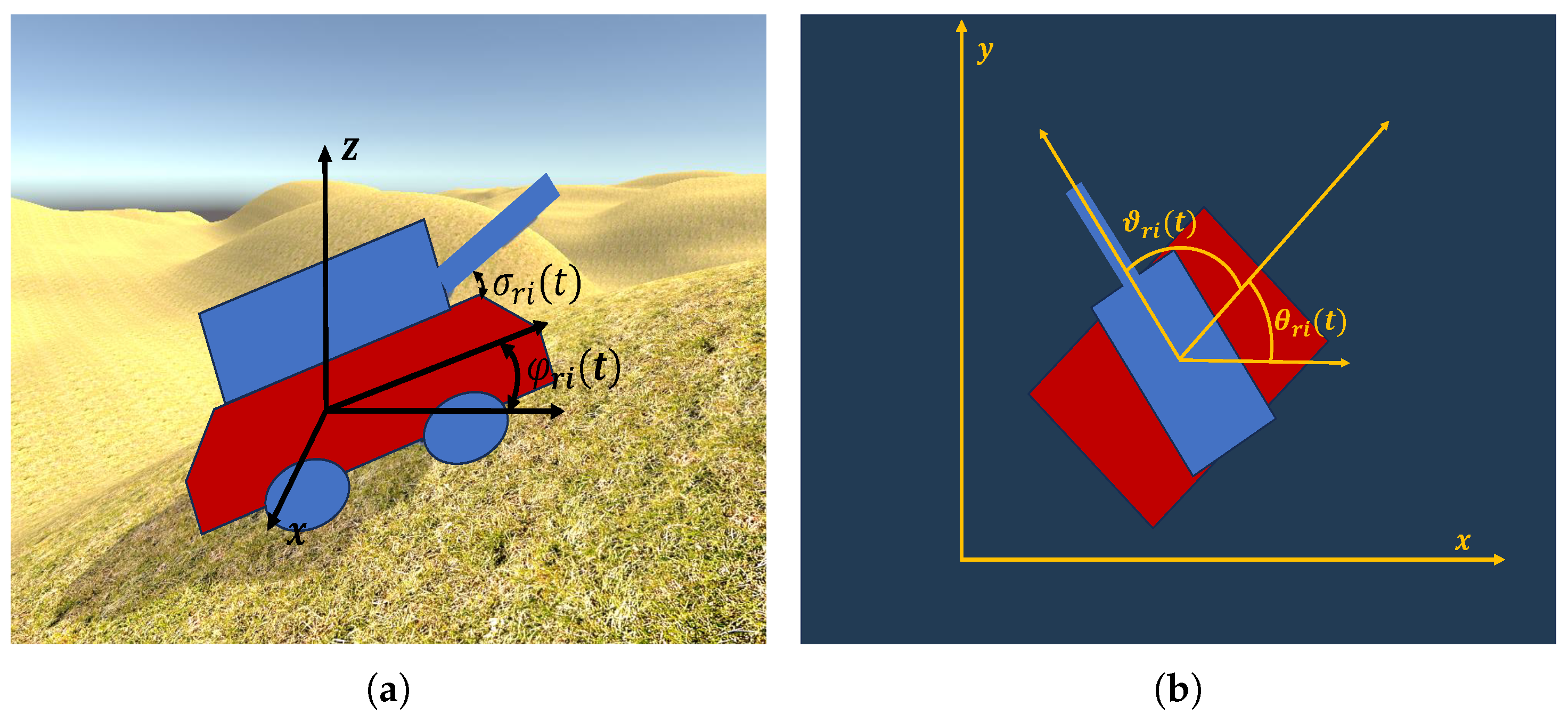
3.2. Agent Model
3.2.1. Kinematics
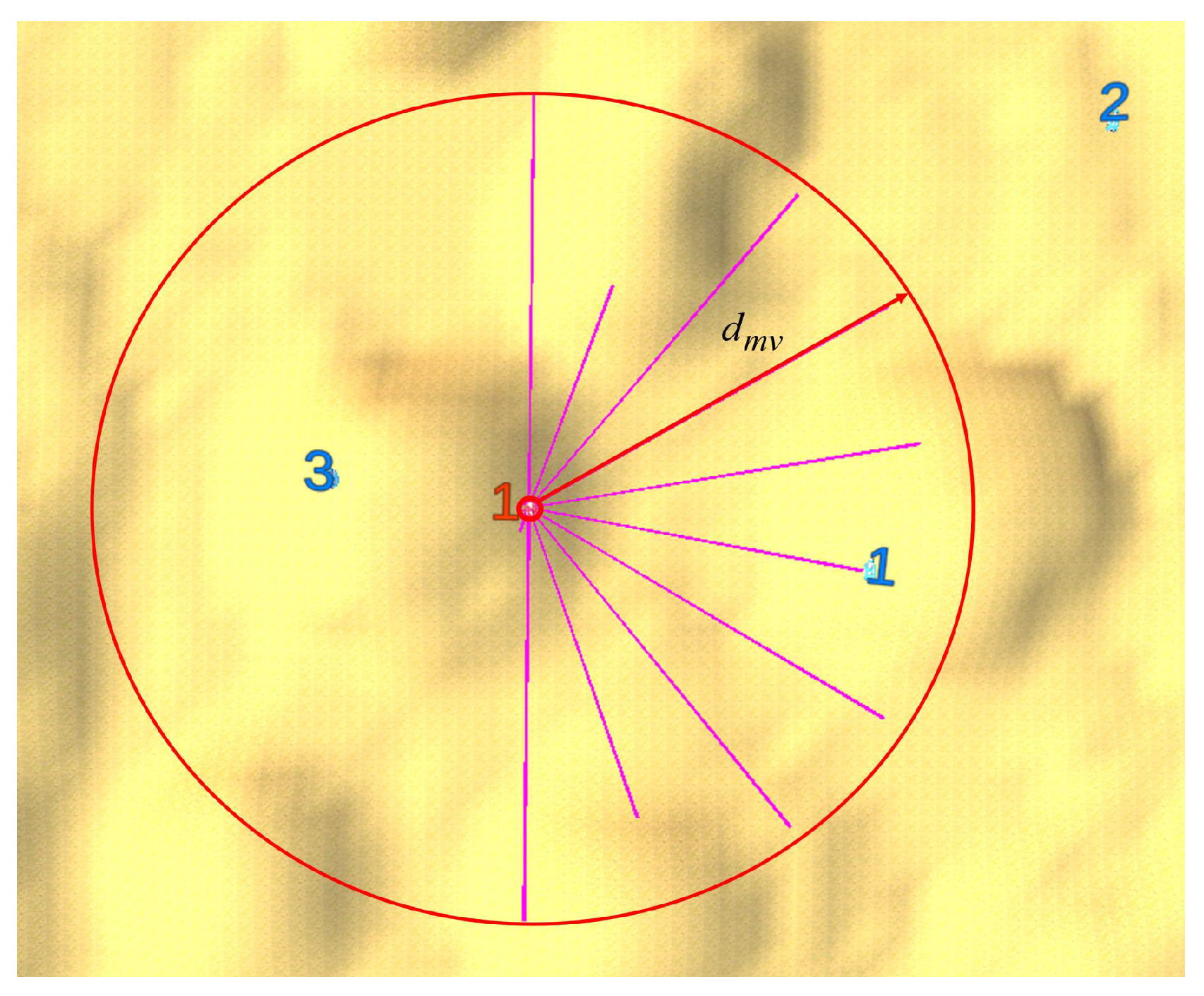
3.2.2. Information Acquisition
- The positions of all the surviving agents of the red team at time t.
- The positions of all the surviving agents of the blue team belonging to the set .
3.2.3. Attack and Damage
3.3. Winning of the Confrontation
3.4. Algorithm Performance Indices
- Winning rate :
- Average agent quantity loss rate :
- Average agent health loss rate :
4. Bio-Inspired Swarm Confrontation Algorithm Design
4.1. Bio-Inspired Rules
4.2. Design of Swarm Confrontation Algorithm
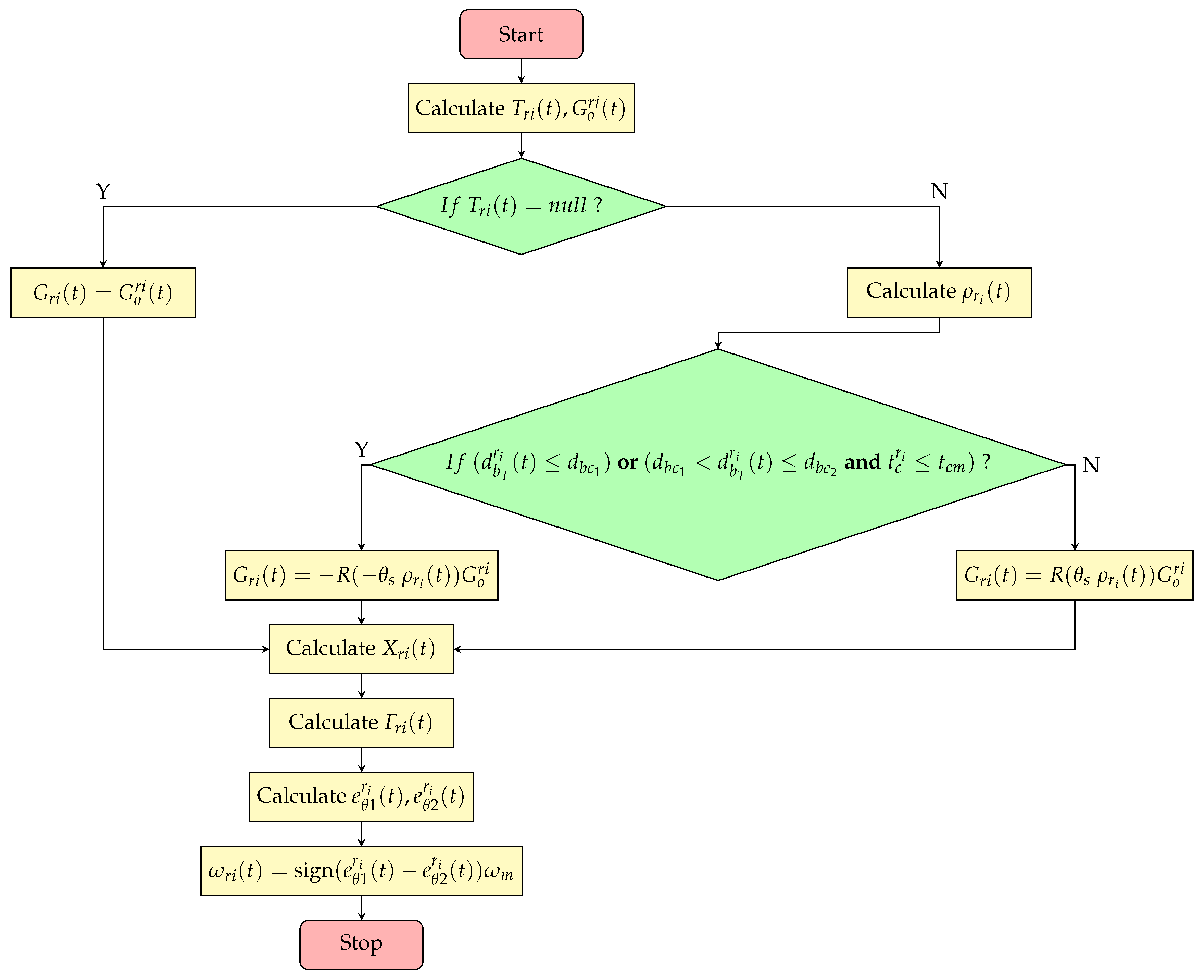
4.2.1. Target Selection
| Algorithm 1 Target Selection Algorithm |
|
4.2.2. Motion Planning
| Algorithm 2 Motion Planning Algorithm |
|
4.2.3. Automatic Aiming Algorithm
| Algorithm 3 Automatic Aiming Algorithm |
|
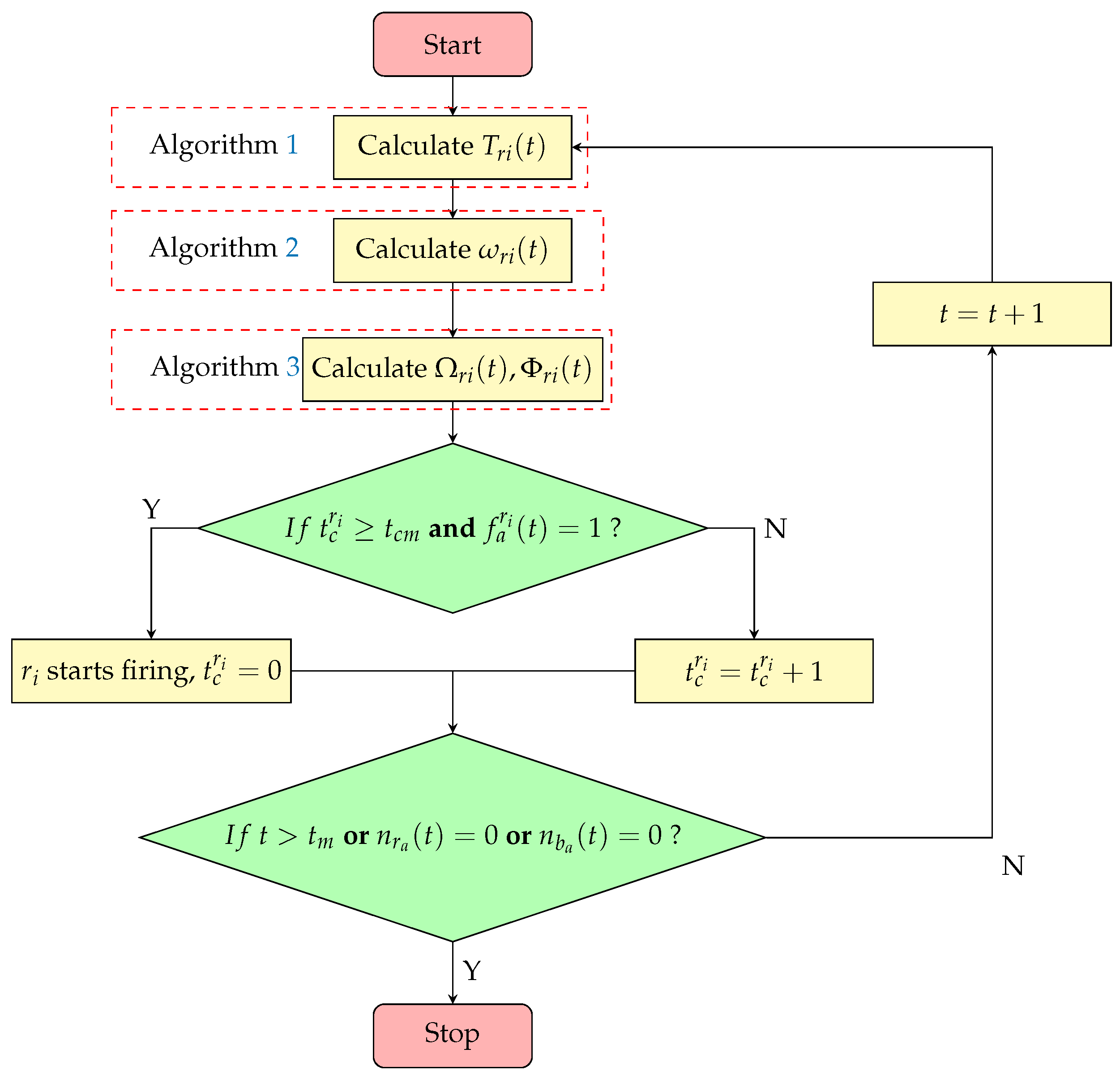
4.2.4. Bio-Inspired Swarm Confrontation Algorithm
| Algorithm 4 Bio-inspired Swarm Confrontation Algorithm |
|
4.3. Algorithm Complexity Analysis
5. Result Analysis
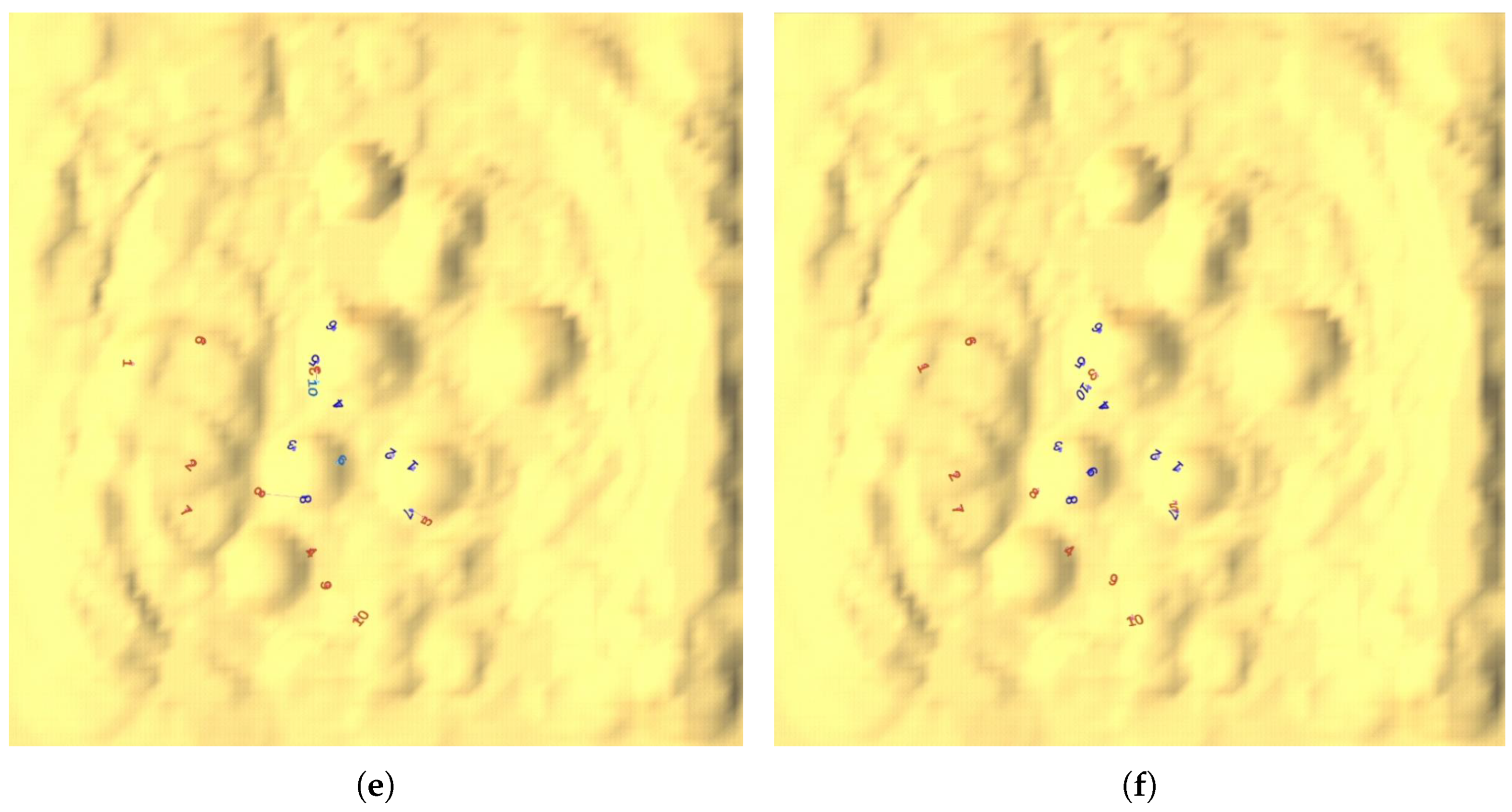
5.1. Results Analysis for a Single Match
5.2. Analysis of Results Under Different Scenarios
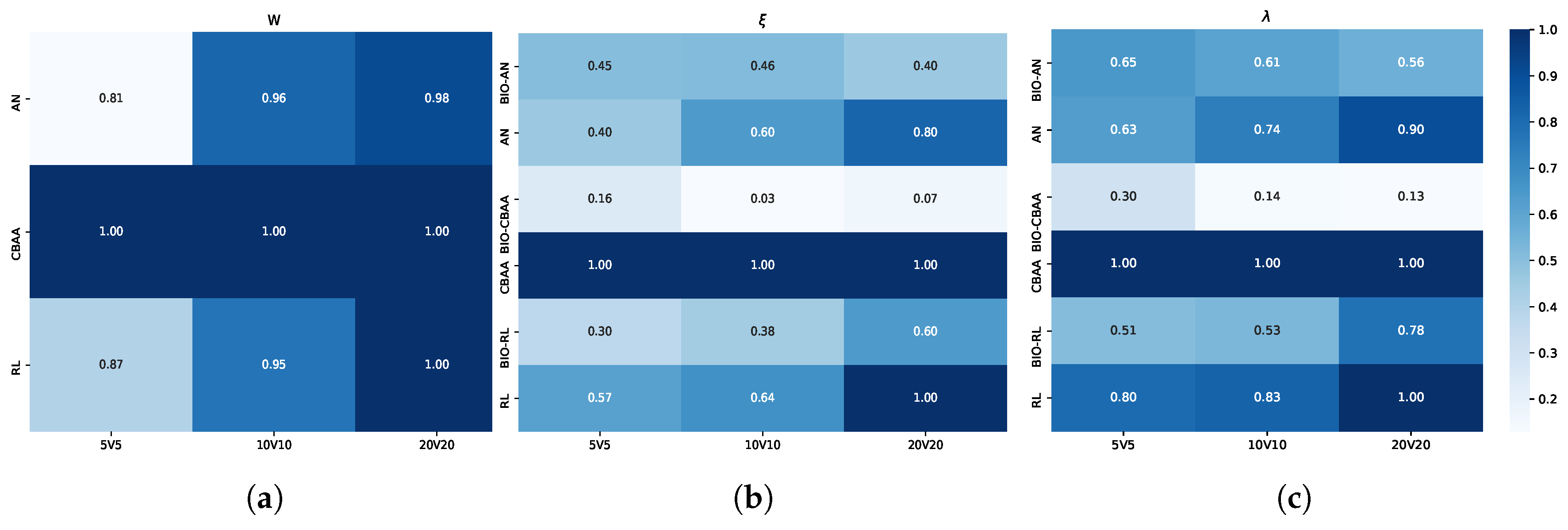
5.2.1. Analysis of Results Under Different Algorithm Parameters
5.2.2. Analysis of Results Under Different Confrontation Scales
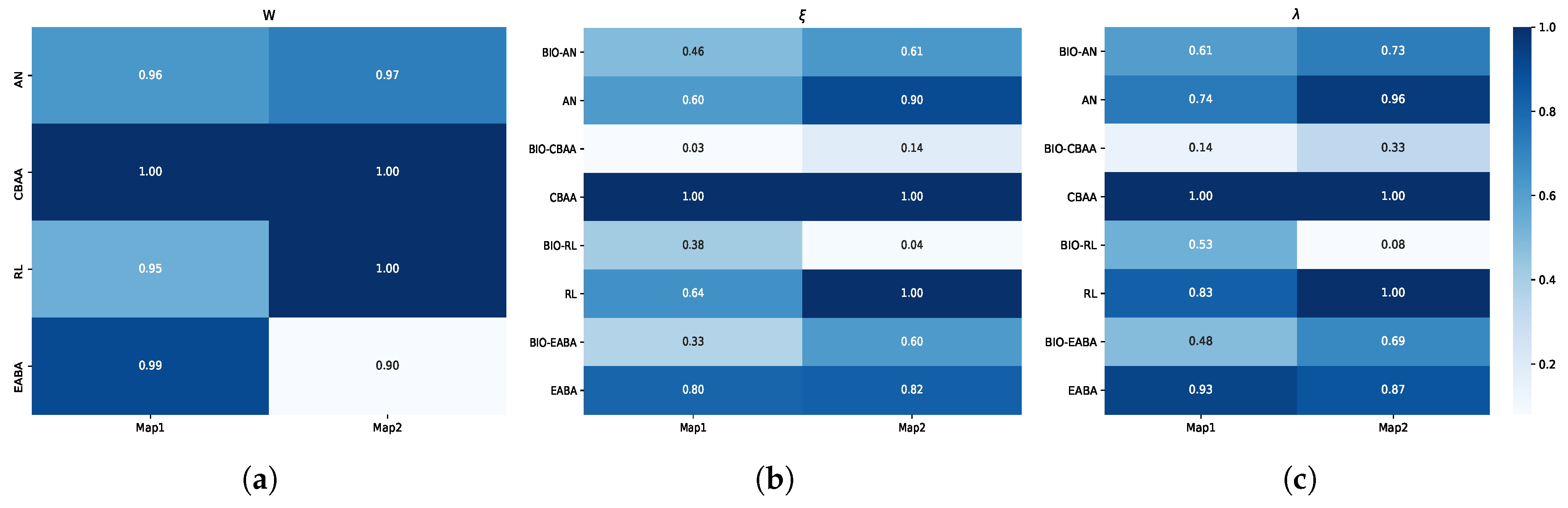
5.2.3. Result Analysis on Different Maps
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| N | The total number of agents in each team |
| The ith agent of the red team | |
| The ith agent of the blue team | |
| The position of agent | |
| v | The linear speed |
| The angular velocity of agent | |
| The heading angle of agent | |
| The pitch angle of agent | |
| The heading angle of agent ’s turret | |
| The rotation speed of agent ’s turret | |
| The heading angle of agent ’s barrel | |
| The rotation speed of agent ’s barrel | |
| The sampling time | |
| The maximum detection range of the agents | |
| The set of opponents whose information can be obtained by agent at time t | |
| The maximum speed of | |
| The maximum speed of | |
| The maximum speed of | |
| The initial speed of the shells | |
| The damage inflicted on an agent upon being hit by a single shell | |
| The health point of at time t | |
| The maximum execution time per confrontation | |
| M | The total number of matches played between the red and blue teams |
| The total number of matches won by the red team | |
| The initial health points of all members of the red team | |
| The number of agents lost by the red team in the kth winning match | |
| The total health points lost by the red team in the kth winning match | |
| The winning rate of | |
| The average agent quantity loss rate of the red team | |
| The average agent health loss rate of the red team | |
| The number of surviving opponents detectable by | |
| The number of surviving agents on the blue team | |
| The central position of these opponents | |
| The label of the xth closest surviving opponent to | |
| The final attack target selected by | |
| The position of ’s current attack target | |
| The position of the nearest hilltop to | |
| The movement direction of without obstacle avoidance | |
| The position of the opponent labeled | |
| The obstacle avoidance vector induced by teammate on | |
| The sum of obstacle avoidance vectors exerted by all teammates on | |
| The final desired movement direction of | |
| The relative position of within the friendly team that shares the same opponent | |
| The position of the agent closest to among the group of agents sharing the same attack target | |
| The unit direction vector from to | |
| The unit direction vector along the z-axis | |
| The projected offset within a team sharing the same attack target | |
| The reference value used to determine the position interval | |
| The distance between and | |
| The distance between and | |
| The time elapsed since fired its last shell | |
| The minimum firing interval between two attacks | |
| The maximum distance threshold for to execute a retreating flanking encirclement strategy | |
| The minimum distance threshold for to execute a flanking maneuver during an advance, as well as the minimum retreat distance for flanking when | |
| The distance for avoiding teammates | |
| The heading angle of | |
| The clockwise angle between the current movement direction and the final target direction | |
| The counterclockwise angle between the current movement direction and the final target direction | |
| The unit direction vector of ’s turret | |
| The unit direction vector of ’s barrel | |
| The flag indicating whether is actively aiming at an opponent | |
| The unit vector from to | |
| The projection of onto the plane | |
| The projection of onto the plane | |
| The angle formed between and | |
| The angle formed between and | |
| The deviation range between the target angle and the actual angle |
References
- Ayamga, M.; Akaba, S.; Nyaaba, A.A. Multifaceted applicability of drones: A review. Technol. Forecast. Soc. Change 2021, 167, 120677. [Google Scholar] [CrossRef]
- Day, M. Multi-Agent Task Negotiation Among UAVs to Defend Against Swarm Attacks. Ph.D. Thesis, Naval Postgraduate School, Monterey, CA, USA, 2012. [Google Scholar]
- Kong, L.; Liu, Z.; Pang, L.; Zhang, K. Research on UAV Swarm Operations. In Man-Machine-Environment System Engineering; Long, S., Dhillon, B.S., Eds.; Springer: Singapore, 2023; pp. 533–538. [Google Scholar]
- Niu, W.; Huang, J.; Miu, L. Research on the concept and key technologies of unmanned aerial vehicle swarm concerning naval attack. Command. Control. Simul. 2018, 40, 20–27. [Google Scholar]
- Xiaoning, Z. Analysis of military application of UAV swarm technology. In Proceedings of the IEEE 2020 3rd International Conference on Unmanned Systems (ICUS), Harbin, China, 27–28 November 2020; pp. 1200–1204. [Google Scholar]
- Vinyals, O.; Babuschkin, I.; Czarnecki, W.M.; Mathieu, M.; Dudzik, A.; Chung, J.; Choi, D.H.; Powell, R.; Ewalds, T.; Georgiev, P.; et al. Grandmaster level in StarCraft II using multi-agent reinforcement learning. Nature 2019, 575, 350–354. [Google Scholar] [CrossRef] [PubMed]
- Xia, W.; Zhou, Z.; Jiang, W.; Zhang, Y. Dynamic UAV Swarm Confrontation: An Imitation Based on Mobile Adaptive Networks. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 7183–7202. [Google Scholar] [CrossRef]
- Zhang, L.; Yu, X.; Zhang, S. Research on Collaborative and Confrontation of UAV Swarms Based on SAC-OD Rules. In Proceedings of the 4th International Conference on Information Management and Management Science. Association for Computing Machinery, Chengdu, China, 27–29 August 2021; pp. 273–278. [Google Scholar]
- Raslan, H.; Schwartz, H.; Givigi, S.; Yang, P. A Learning Invader for the “Guarding a Territory” Game. J. Intelligent Robot. Syst. 2016, 83, 55–70. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S.; Zhao, Y.X.; Fong, S.; He, X. Swarm intelligence: Past, present and future. Soft Comput. 2018, 22, 5923–5933. [Google Scholar] [CrossRef]
- Zervoudakis, K.; Tsafarakis, S. A mayfly optimization algorithm. Comput. Ind. Eng. 2020, 145, 106559. [Google Scholar] [CrossRef]
- Połap, D.; Woźniak, M. Red fox optimization algorithm. Expert Syst. Appl. 2021, 166, 114107. [Google Scholar] [CrossRef]
- Zervoudakis, K.; Tsafarakis, S. A global optimizer inspired from the survival strategies of flying foxes. Eng. Comput. 2023, 39, 1583–1616. [Google Scholar] [CrossRef]
- Li, J.; Yang, S.X. Intelligent Fish-Inspired Foraging of Swarm Robots with Sub-Group Behaviors Based on Neurodynamic Models. Biomimetics 2024, 9, 16. [Google Scholar] [CrossRef]
- Chi, P.; Wei, J.; Wu, K.; Di, B.; Wang, Y. A Bio-Inspired Decision-Making Method of UAV Swarm for Attack-Defense Confrontation via Multi-Agent Reinforcement Learning. Biomimetics 2023, 8, 222. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, J.; Zu, P.; Zhou, M. Evolutionary Algorithm-Based Attack Strategy With Swarm Robots in Denied Environments. IEEE Trans. Evol. Comput. 2023, 27, 1562–1574. [Google Scholar] [CrossRef]
- Wang, Y.; Bai, P.; Liang, X.; Wang, W.; Zhang, J.; Fu, Q. Reconnaissance Mission Conducted by UAV Swarms Based on Distributed PSO Path Planning Algorithms. IEEE Access 2019, 7, 105086–105099. [Google Scholar] [CrossRef]
- Yu, Y.; Liu, J.; Wei, C. Hawk and pigeon’s intelligence for UAV swarm dynamic combat game via competitive learning pigeon-inspired optimization. Sci. China Technol. Sci. 2022, 65, 1072–1086. [Google Scholar] [CrossRef]
- Zhang, T.; Chai, L.; Wang, S.; Jin, J.; Liu, X.; Song, A.; Lan, Y. Improving Autonomous Behavior Strategy Learning in an Unmanned Swarm System Through Knowledge Enhancement. IEEE Trans. Reliab. 2022, 71, 763–774. [Google Scholar] [CrossRef]
- Xiang, L.; Xie, T. Research on UAV Swarm Confrontation Task Based on MADDPG Algorithm. In Proceedings of the 2020 5th International Conference on Mechanical, Control and Computer Engineering (ICMCCE), Harbin, China, 25–27 December 2020; pp. 1513–1518. [Google Scholar] [CrossRef]
- Finand, B.; Loeuille, N.; Bocquet, C.; Fédérici, P.; Monnin, T. Solitary foundation or colony fission in ants: An intraspecific study shows that worker presence and number increase colony foundation success. Oecologia 2024, 204, 517–527. [Google Scholar] [CrossRef]
- Liu, F.; Dong, X.; Yu, J.; Hua, Y.; Li, Q.; Ren, Z. Distributed Nash Equilibrium Seeking of N-Coalition Noncooperative Games With Application to UAV Swarms. IEEE Trans. Netw. Sci. Eng. 2022, 9, 2392–2405. [Google Scholar] [CrossRef]
- Guo, Z.; Li, Y.; Wang, Y.; Wang, L. Group motion control for UAV swarm confrontation using distributed dynamic target assignment. Aerosp. Syst. 2023, 6, 689–701. [Google Scholar] [CrossRef]
- Wang, L.; Qiu, T.; Pu, Z.; Yi, J.; Zhu, J.; Zhao, Y. A Decision-making Method for Swarm Agents in Attack-defense Confrontation. IFAC-PapersOnLine 2023, 56, 7858–7864. [Google Scholar] [CrossRef]
- Xing, D.; Zhen, Z.; Gong, H. Offense-defense confrontation decision making for dynamic UAV swarm versus UAV swarm. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 5689–5702. [Google Scholar] [CrossRef]
- Gergal, E.K. Drone Swarming Tactics Using Reinforcement Learning and Policy Optimization; Trident Scholar Report 506; U.S. Naval Academy: Annapolis, MD, USA, 2021. [Google Scholar]
- Cai, H.; Luo, Y.; Gao, H.; Chi, J.; Wang, S. A Multiphase Semistatic Training Method for Swarm Confrontation Using Multiagent Deep Reinforcement Learning. Comput. Intell. Neurosci. 2023, 2023, 2955442. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Li, S.; Gao, X.; Xie, T. UAV Swarm Confrontation Using Hierarchical Multiagent Reinforcement Learning. Int. J. Aerosp. Eng. 2021, 2021, 3360116. [Google Scholar] [CrossRef]
- Shahid, S.; Zhen, Z.; Javaid, U.; Wen, L. Offense-Defense Distributed Decision Making for Swarm vs. Swarm Confrontation While Attacking the Aircraft Carriers. Drones 2022, 6, 271. [Google Scholar] [CrossRef]
- Wang, J.; Duan, S.; Ju, S.; Lu, S.; Jin, Y. Evolutionary Task Allocation and Cooperative Control of Unmanned Aerial Vehicles in Air Combat Applications. Robotics 2022, 11, 124. [Google Scholar] [CrossRef]
- Xu, C.; Xu, M.; Yin, C. Optimized multi-UAV cooperative path planning under the complex confrontation environment. Comput. Commun. 2020, 162, 196–203. [Google Scholar] [CrossRef]
- Xuan, W.; Weijia, W.; Kepu, S.; Minwen, W. UAV Air Combat Decision Based on Evolutionary Expert System Tree. Ordnance Ind. Autom. 2019, 38, 42–47. [Google Scholar]
- Sun, B.; Zeng, Y.; Zhu, D. Dynamic task allocation in multi autonomous underwater vehicle confrontational games with multi-objective evaluation model and particle swarm optimization algorithm. Appl. Soft Comput. 2024, 153, 111295. [Google Scholar] [CrossRef]
- Hu, S.; Ru, L.; Lv, M.; Wang, Z.; Lu, B.; Wang, W. Evolutionary game analysis of behaviour strategy for UAV swarm in communication-constrained environments. IET Control. Theory Appl. 2024, 18, 350–363. [Google Scholar] [CrossRef]
- Shefaei, A.; Mohammadi-Ivatloo, B. Wild Goats Algorithm: An Evolutionary Algorithm to Solve the Real-World Optimization Problems. IEEE Trans. Ind. Inform. 2018, 14, 2951–2961. [Google Scholar] [CrossRef]
- Wu, M.; Zhu, X.; Ma, L.; Wang, J.; Bao, W.; Li, W.; Fan, Z. Torch: Strategy evolution in swarm robots using heterogeneous–homogeneous coevolution method. J. Ind. Inf. Integr. 2022, 25, 100239. [Google Scholar] [CrossRef]
- Bai, Z.; Zhou, H.; Shi, J.; Xing, L.; Wang, J. A hybrid multi-objective evolutionary algorithm with high solving efficiency for UAV defense programming. Swarm Evol. Comput. 2024, 87, 101572. [Google Scholar] [CrossRef]
- Xu, D.; Chen, G. Autonomous and cooperative control of UAV cluster with multi-agent reinforcement learning. Aeronaut. J. 2022, 126, 1–20. [Google Scholar] [CrossRef]
- Xu, D.; Chen, G. The research on intelligent cooperative combat of UAV cluster with multi-agent reinforcement learning. Aerosp. Syst. 2022, 5, 107–121. [Google Scholar] [CrossRef]
- Nian, X.; Li, M.; Wang, H.; Gong, Y.; Xiong, H. Large-scale UAV swarm confrontation based on hierarchical attention actor-critic algorithm. Appl. Intell. 2024, 54, 3279–3294. [Google Scholar] [CrossRef]
- Kong, W.; Zhou, D.; Yang, Z.; Zhang, K.; Zeng, L. Maneuver Strategy Generation of UCAV for within Visual Range Air Combat Based on Multi-Agent Reinforcement Learning and Target Position Prediction. Appl. Sci. 2020, 10, 5198. [Google Scholar] [CrossRef]
- Zhou, K.; Wei, R.; Zhang, Q.; Wu, Z. Research on Decision-making Method for Territorial Defense Based on Fuzzy Reinforcement Learnin. In Proceedings of the 2019 Chinese Automation Congress (CAC), Hangzhou, China, 22–24 November 2019; pp. 3759–3763. [Google Scholar] [CrossRef]
- Jiang, F.; Xu, M.; Li, Y.; Cui, H.; Wang, R. Short-range air combat maneuver decision of UAV swarm based on multi-agent transformer introducing virtual objects. Eng. Appl. Artif. Intell. 2023, 123, 106358. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, F.; Guo, J.; Hong, C.; Chen, M.; Wang, E.; Zhao, Y. UAV Swarm Confrontation Based on Multi-agent Deep Reinforcement Learning. In Proceedings of the 2022 41st Chinese Control Conference (CCC), Hefei, China, 25–27 July 2022; pp. 4996–5001. [Google Scholar] [CrossRef]
- Fang, J.; Han, Y.; Zhou, Z.; Chen, S.; Sheng, S. The collaborative combat of heterogeneous multi-UAVs based on MARL. J. Phys. Conf. Ser. 2021, 1995, 012023. [Google Scholar] [CrossRef]
- Kouzeghar, M.; Song, Y.; Meghjani, M.; Bouffanais, R. Multi-Target Pursuit by a Decentralized Heterogeneous UAV Swarm using Deep Multi-Agent Reinforcement Learning. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; pp. 3289–3295. [Google Scholar] [CrossRef]
- Youtube. Wild Dogs vs. Wildebeests. Available online: https://www.youtube.com/watch?v=h4SlAc2U1A4 (accessed on 7 February 2025).
- Youtube. Lions vs. Buffalo—A Wild Encounter. Available online: https://www.youtube.com/watch?v=t7KMsIdlx1E (accessed on 7 February 2025).







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, H.; Ma, F.; Ni, R.; Xu, W.; Gao, H. Bio-Inspired Swarm Confrontation Algorithm for Complex Hilly Terrains. Biomimetics 2025, 10, 257. https://doi.org/10.3390/biomimetics10050257
Cai H, Ma F, Ni R, Xu W, Gao H. Bio-Inspired Swarm Confrontation Algorithm for Complex Hilly Terrains. Biomimetics. 2025; 10(5):257. https://doi.org/10.3390/biomimetics10050257
Chicago/Turabian StyleCai, He, Fu Ma, Ruifeng Ni, Weiyuan Xu, and Huanli Gao. 2025. "Bio-Inspired Swarm Confrontation Algorithm for Complex Hilly Terrains" Biomimetics 10, no. 5: 257. https://doi.org/10.3390/biomimetics10050257
APA StyleCai, H., Ma, F., Ni, R., Xu, W., & Gao, H. (2025). Bio-Inspired Swarm Confrontation Algorithm for Complex Hilly Terrains. Biomimetics, 10(5), 257. https://doi.org/10.3390/biomimetics10050257






