Numerical Investigation on the Aerodynamic Benefits of Corrugated Wing in Dragonfly-like Hovering Flapping Wing
Abstract
:1. Introduction
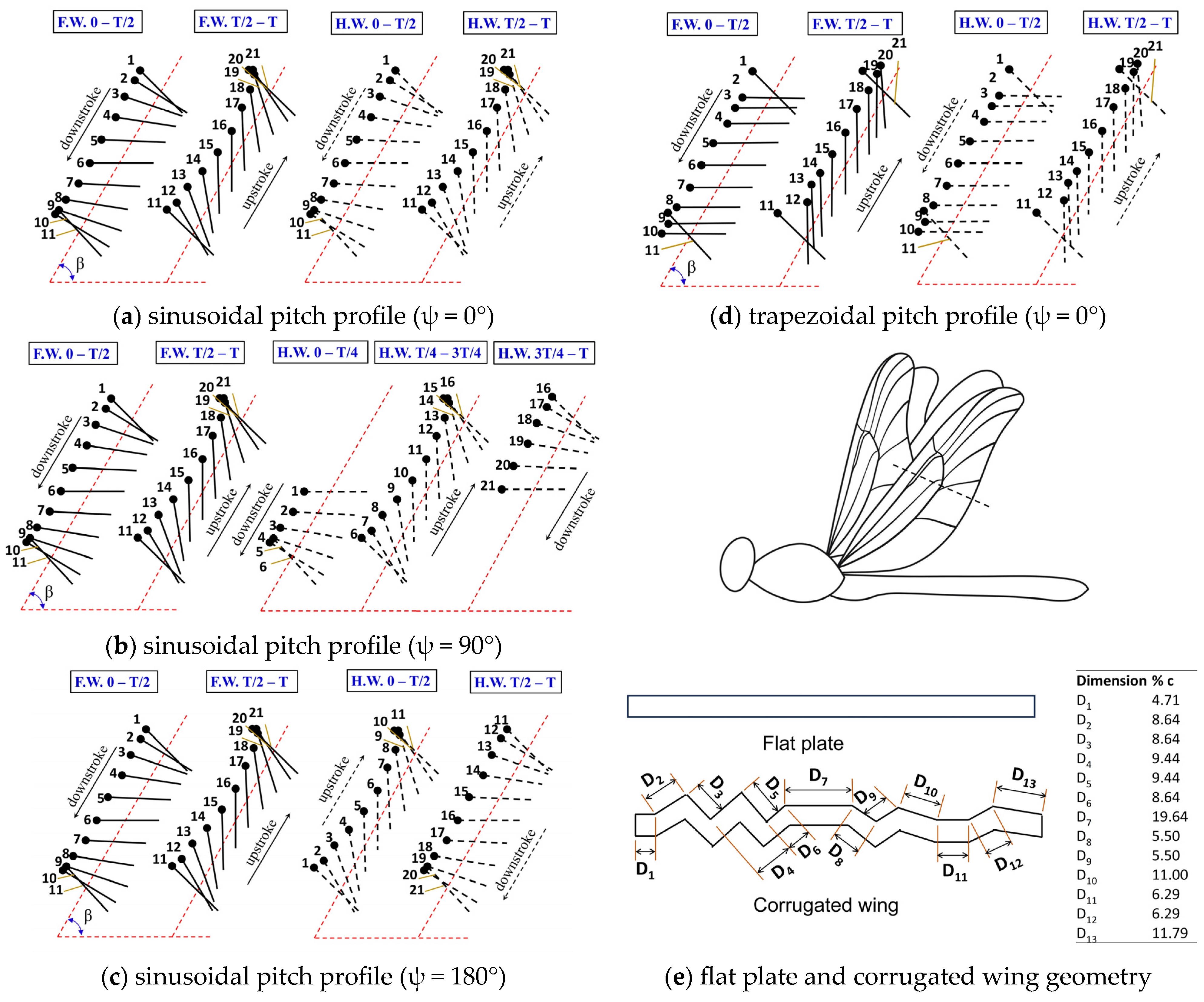
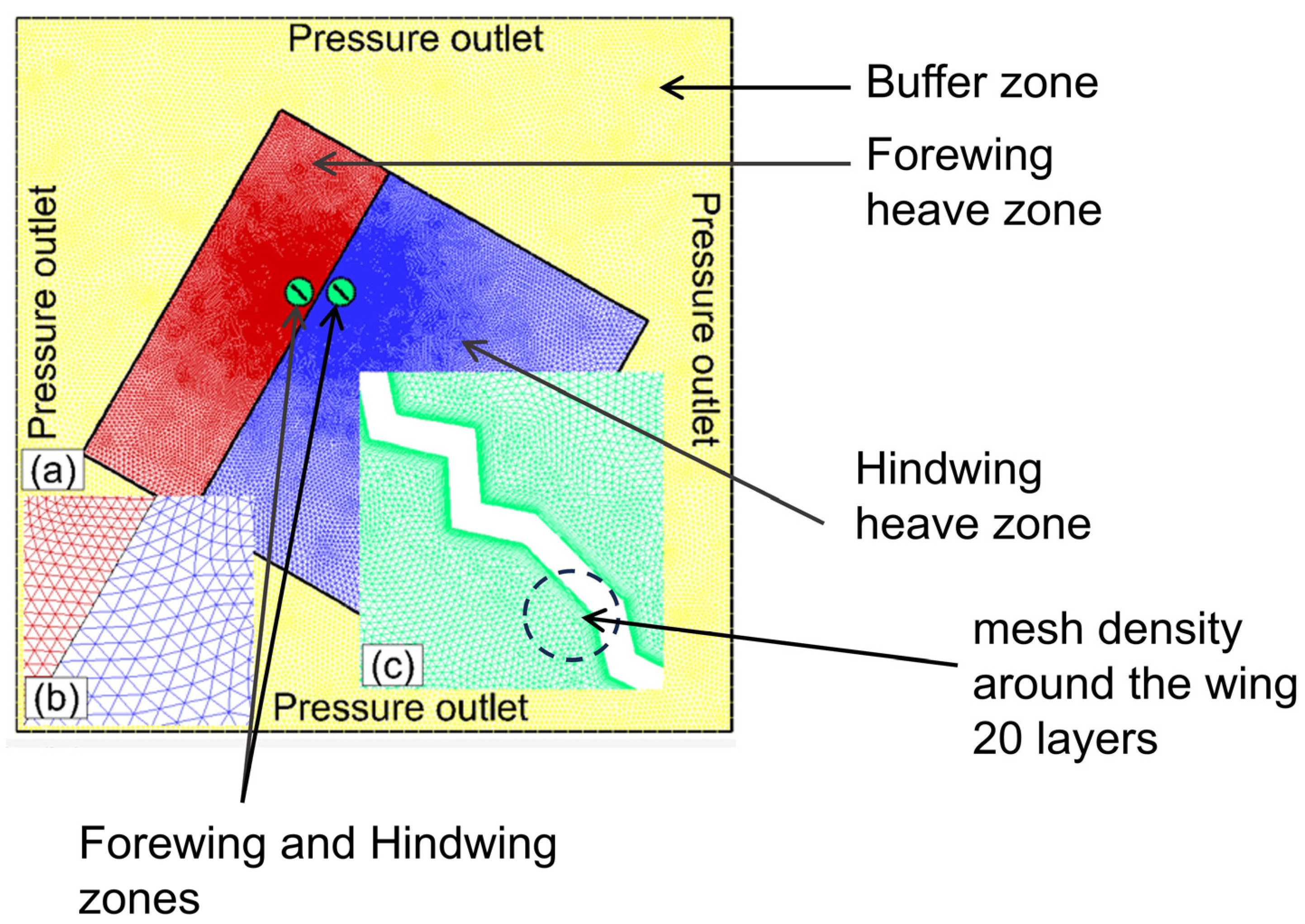
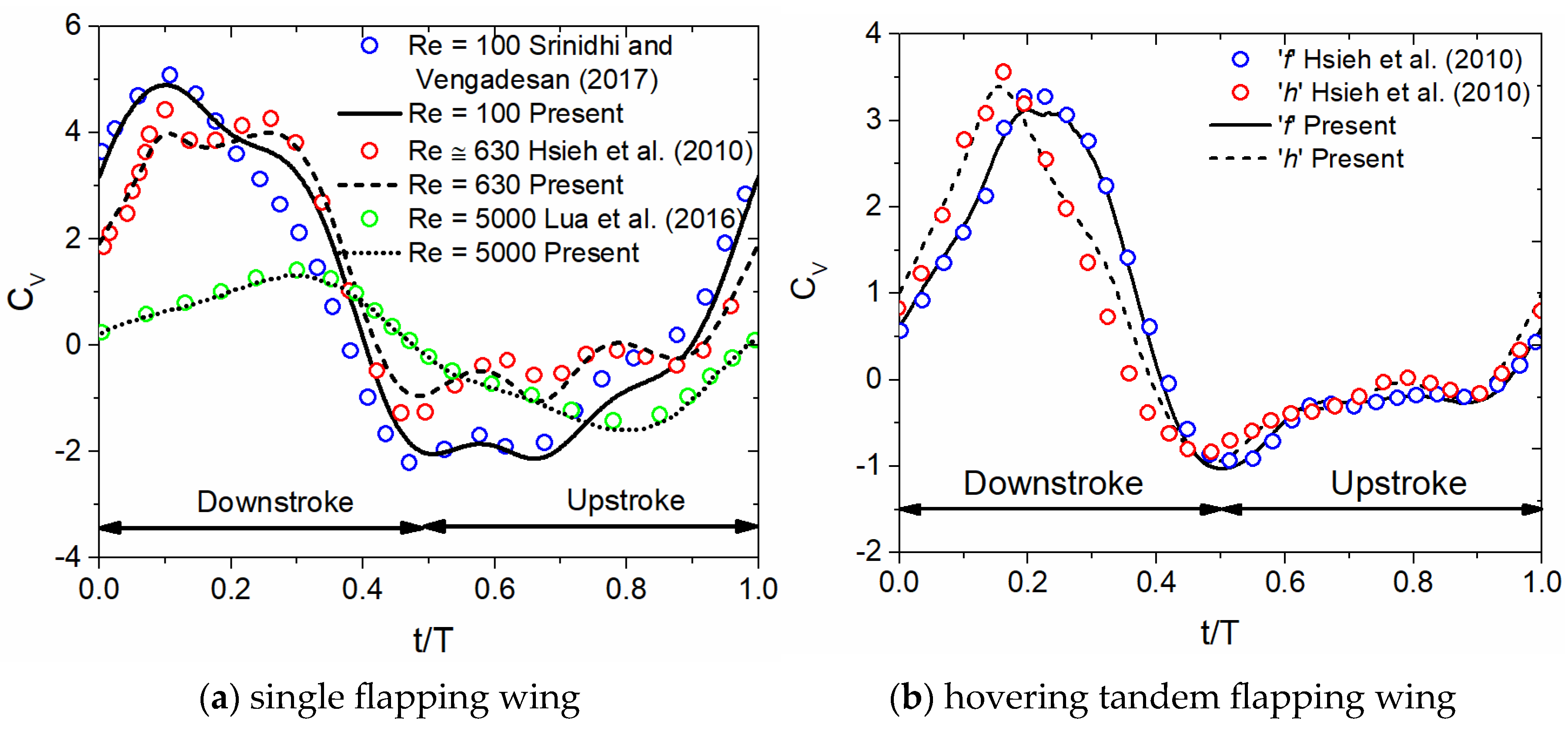
2. Numerical Methodology
- The flapping wing trajectory is assumed to be linear, whereas real dragonflies exhibit a complex figure-eight motion, with the upstroke and downstroke motions following different trajectory.
- The downstroke and upstroke durations are assumed equal, while in reality, the downstroke is significantly longer than the upstroke.
- The wings are treated as rigid, without considering flexibility or twisting.
- Three-dimensional effects are neglected.
3. Results and Discussion
3.1. Hovering Tandem Wing with Sinusoidal Pitch Profile
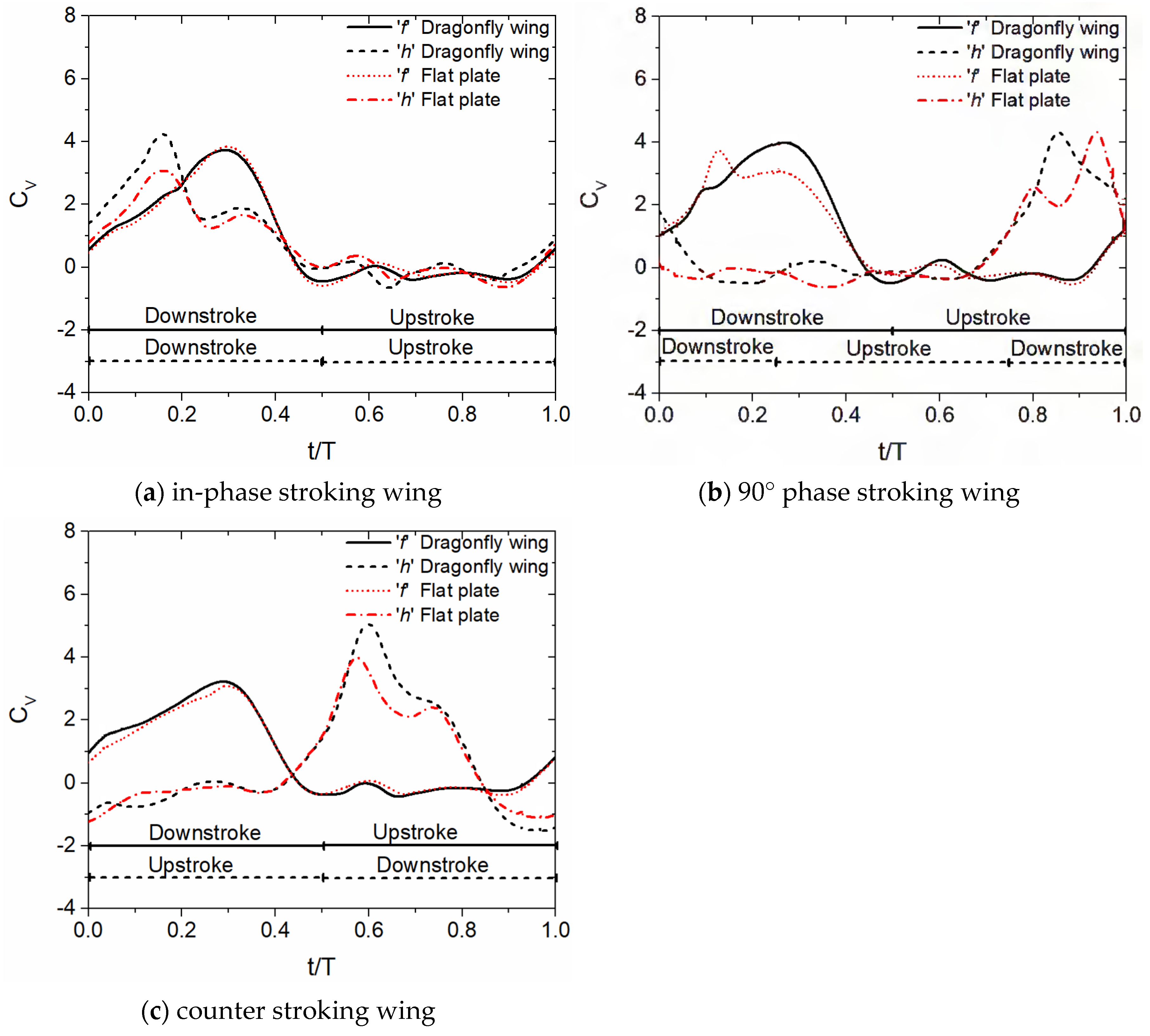
3.1.1. Comparison of Vertical Force for Various Flapping Patterns with Sinusoidal Pitch Profile
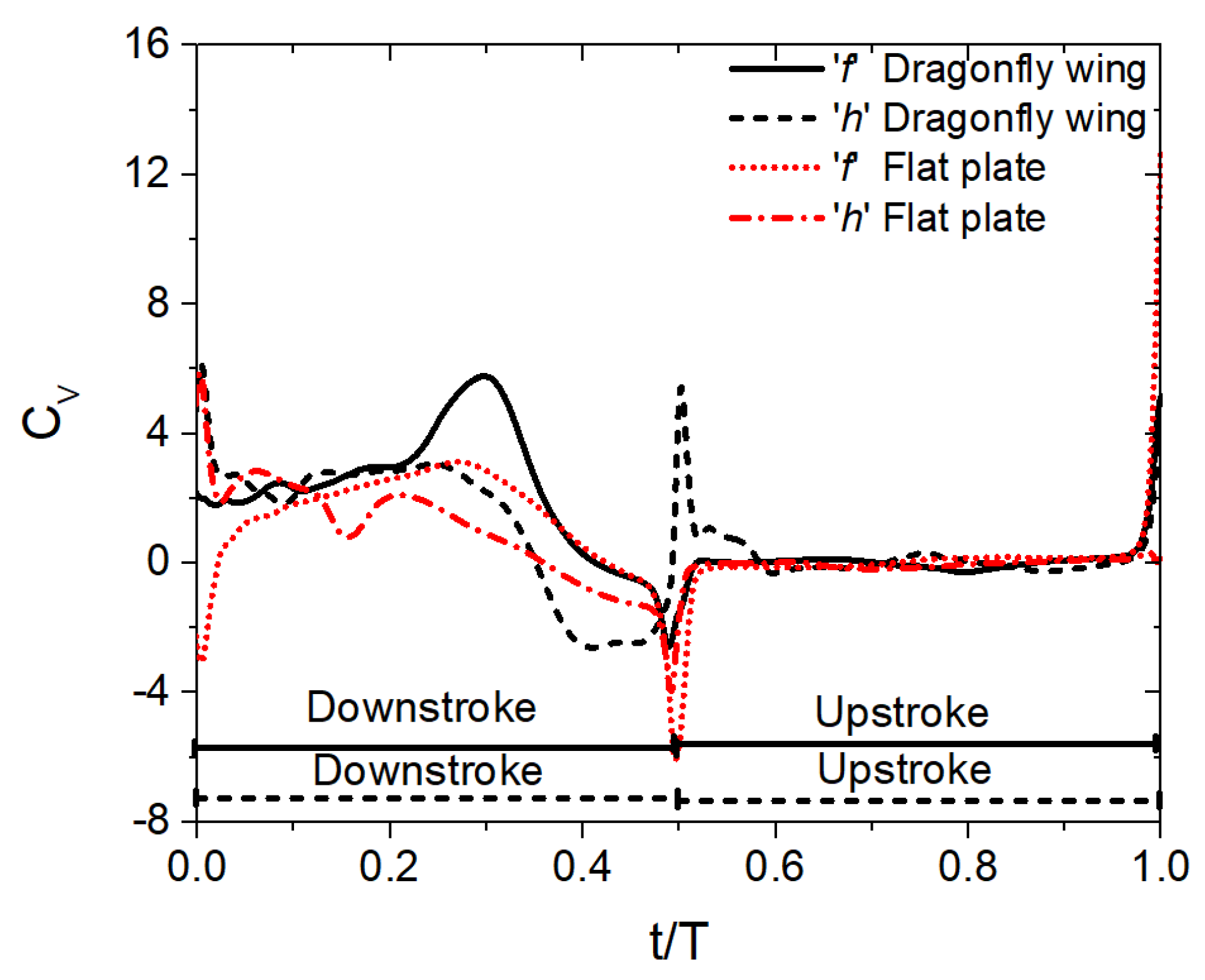
3.1.2. Time History of Vertical Force Coefficient Cv for Various Flapping Patterns with Sinusoidal Pitch Profile
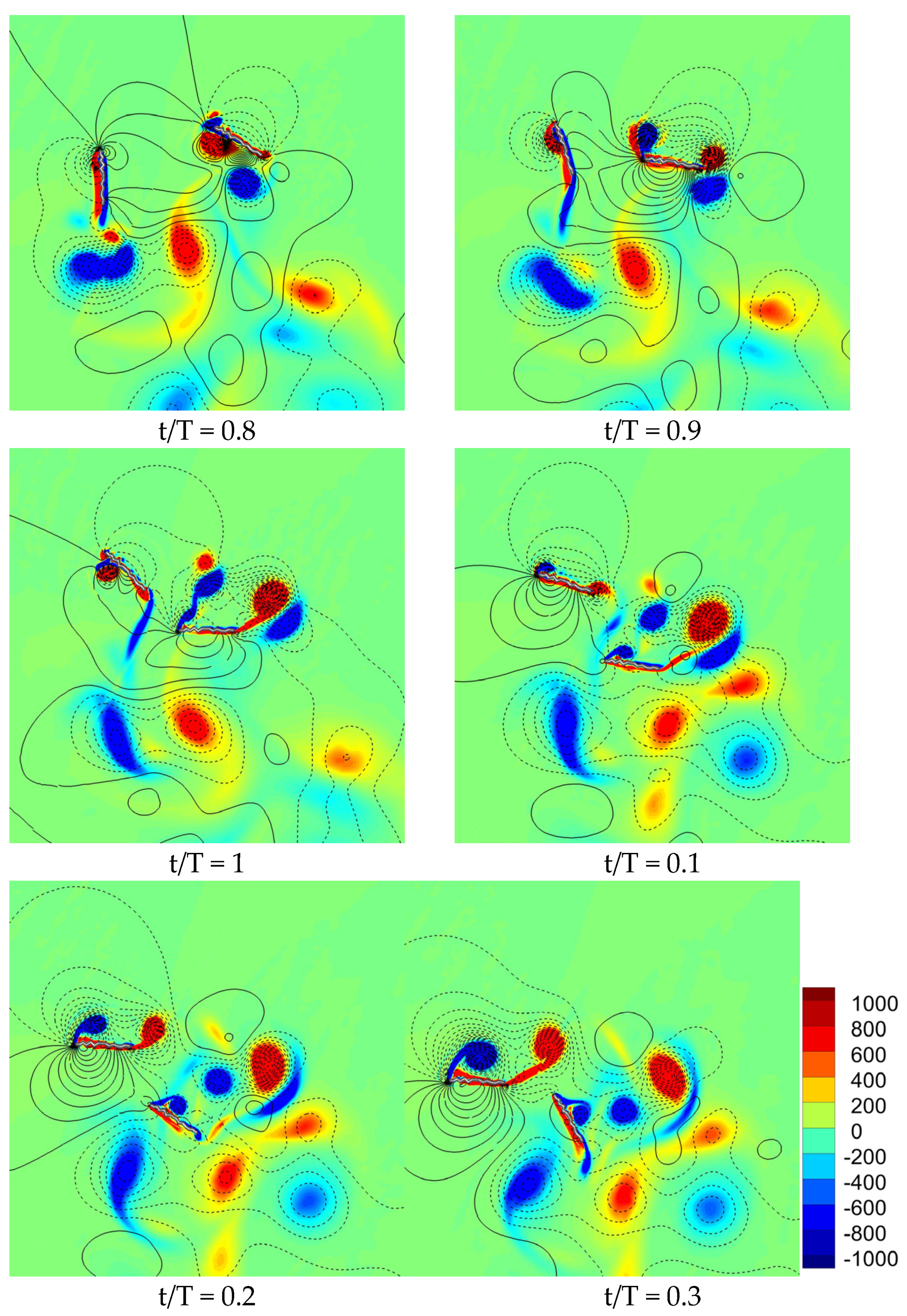
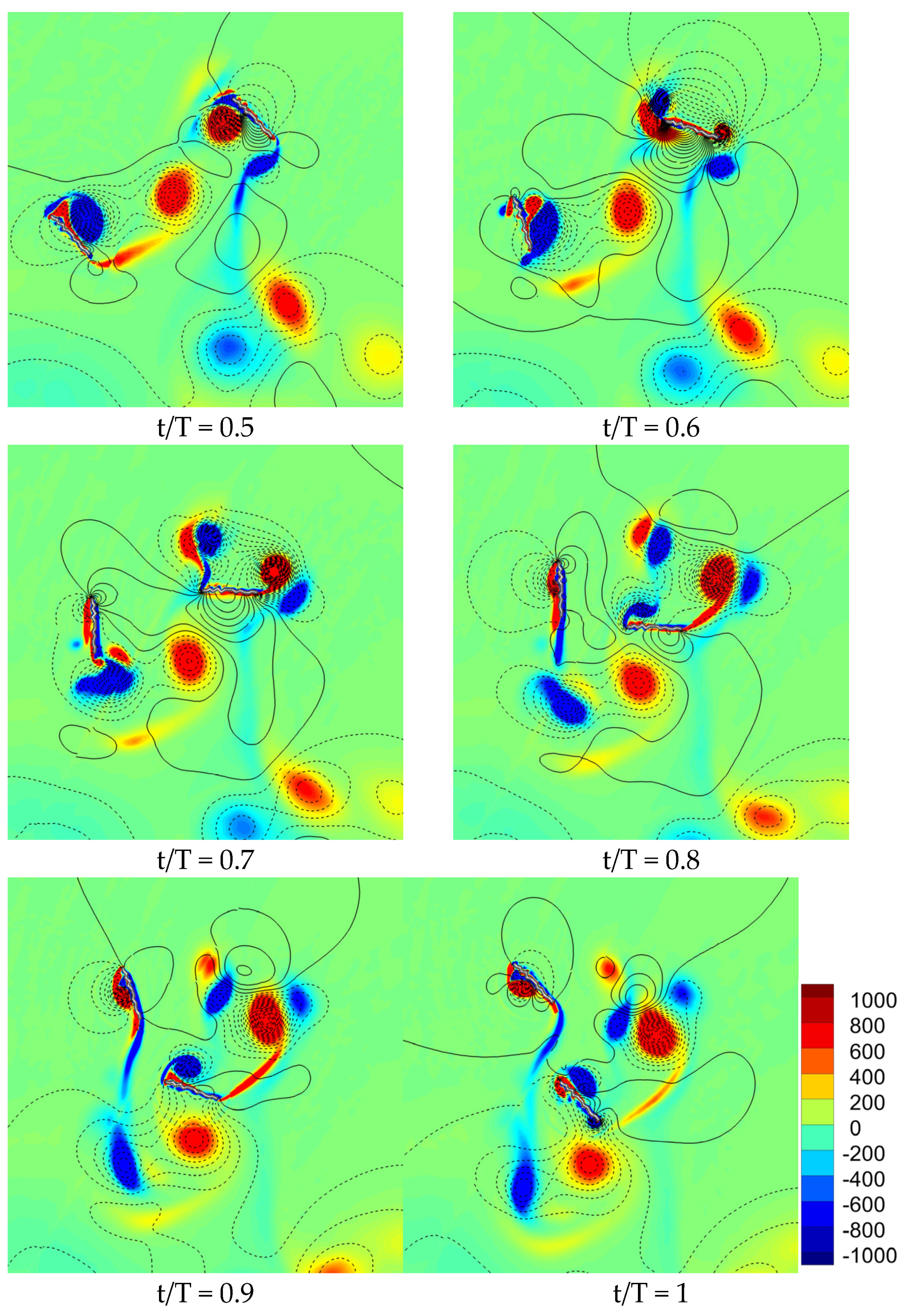
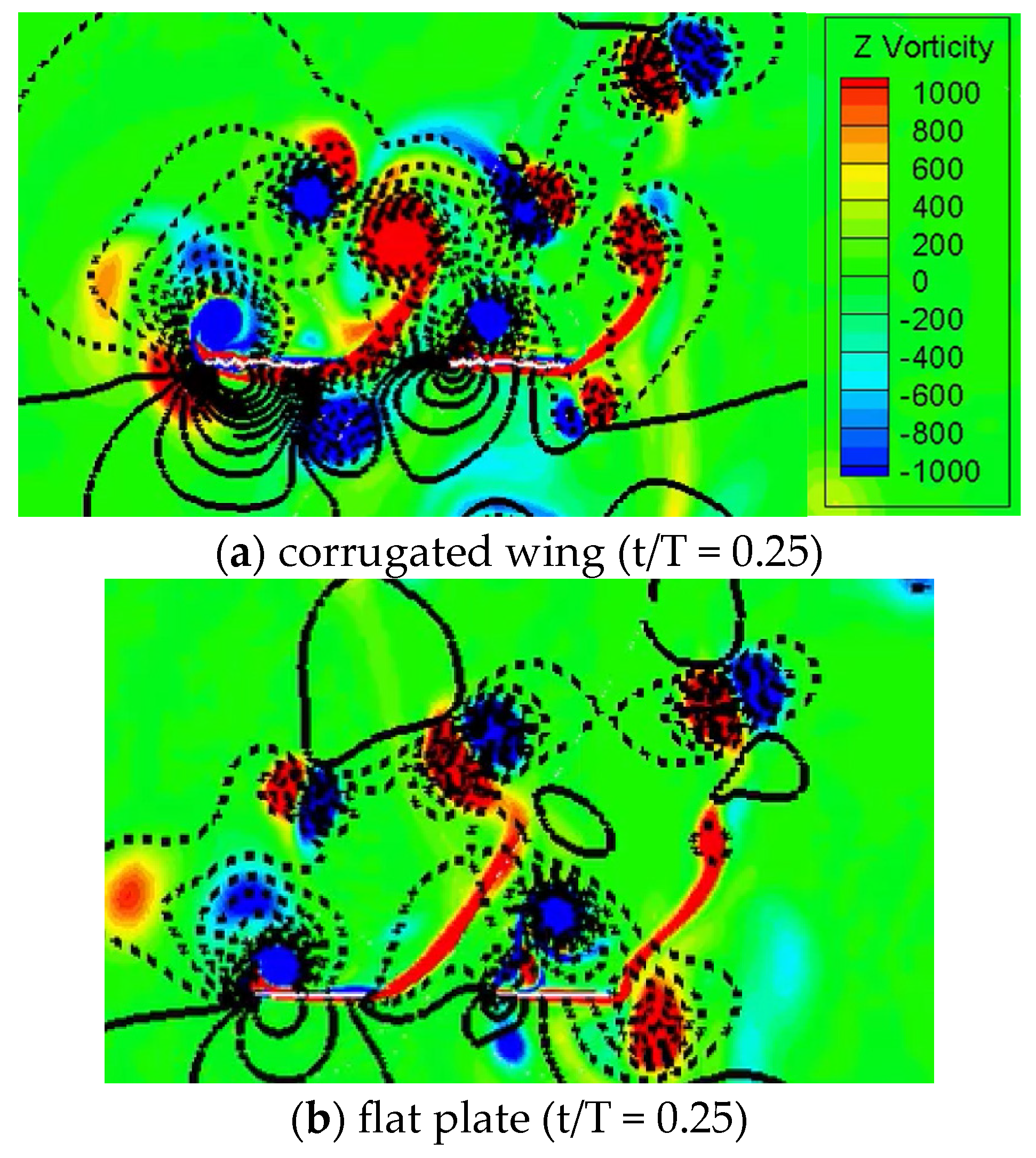
3.1.3. Comparison of Flow Field for Various Flapping Patterns with Sinusoidal Pitch Profile
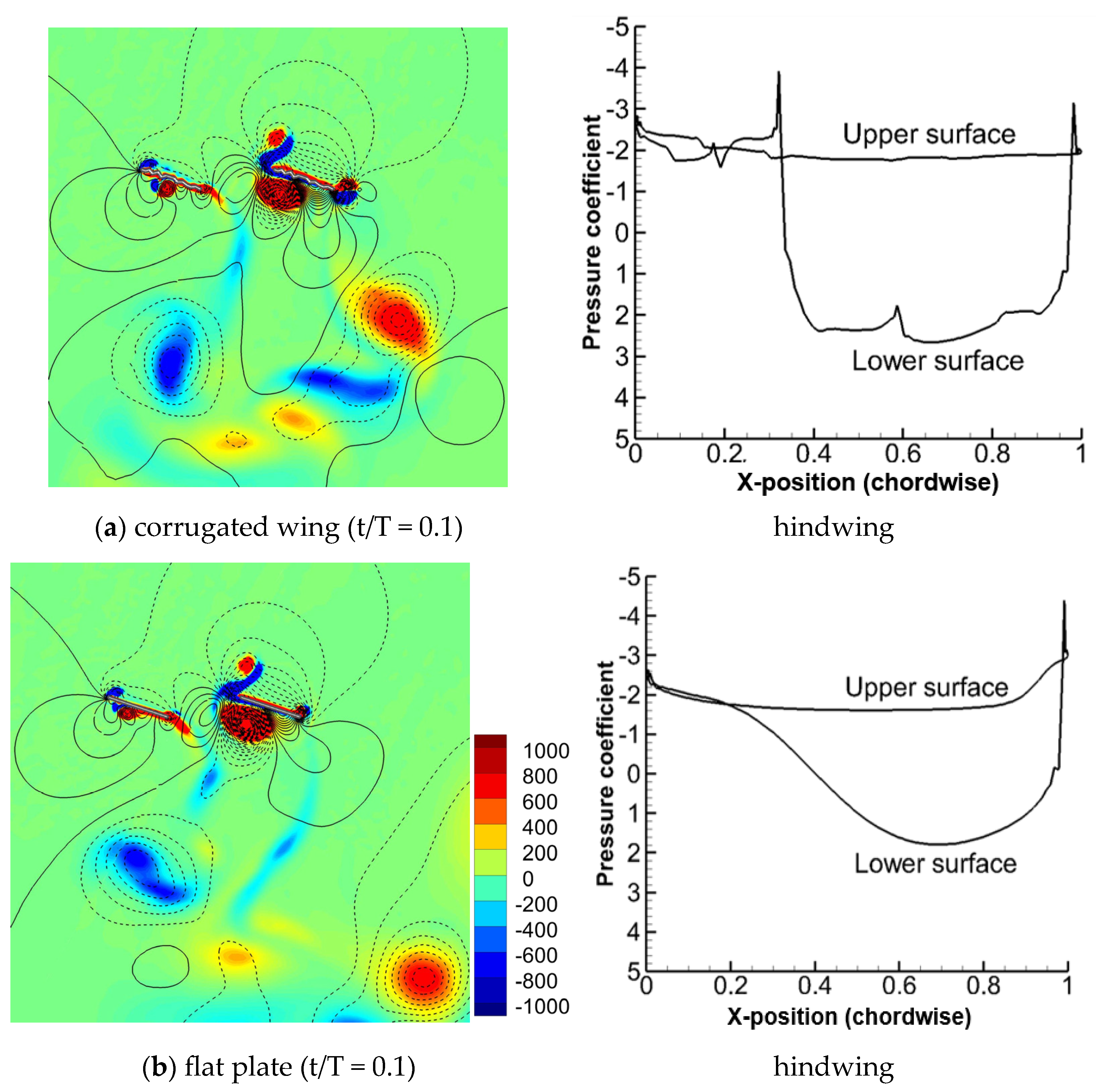
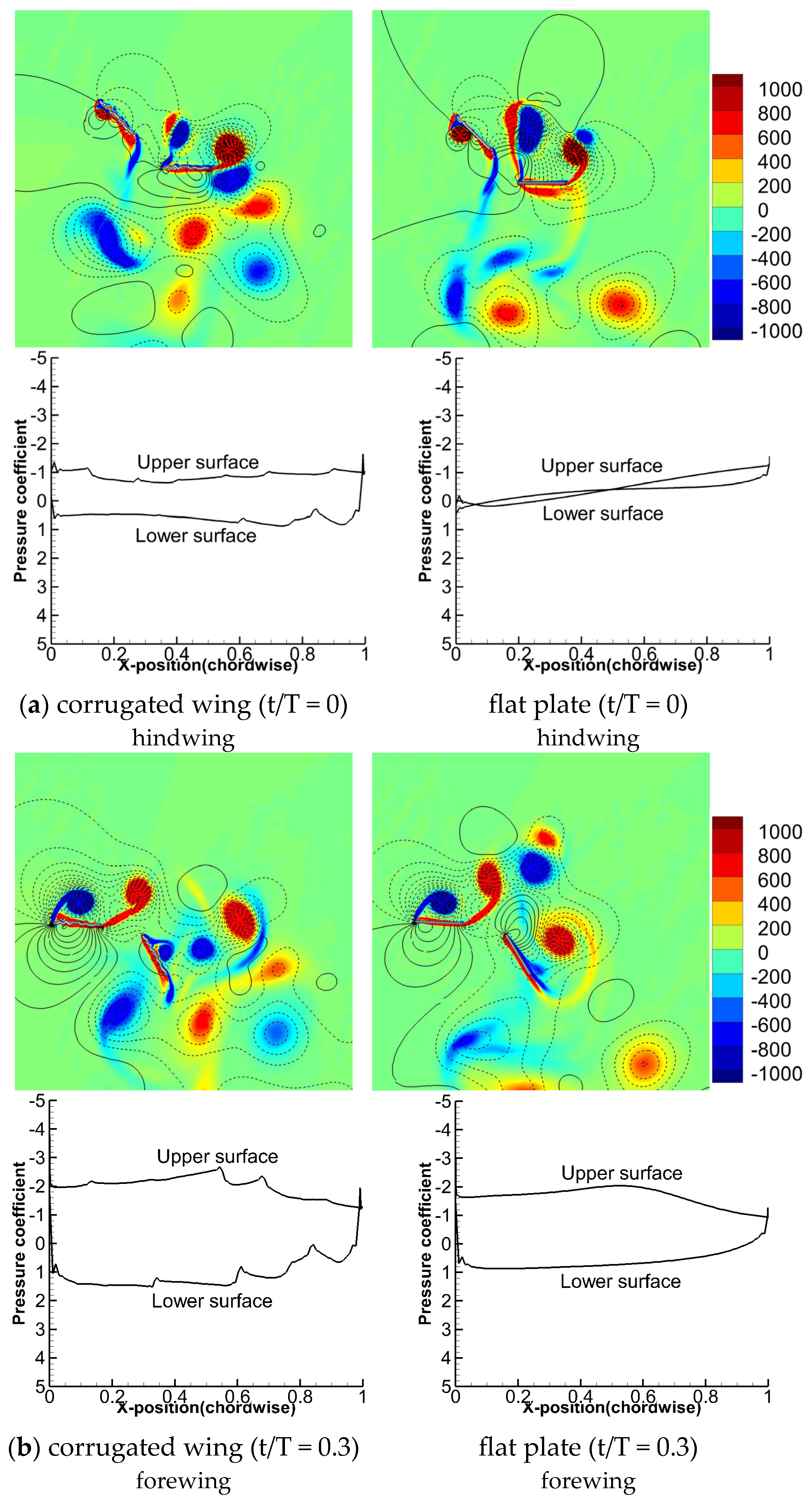
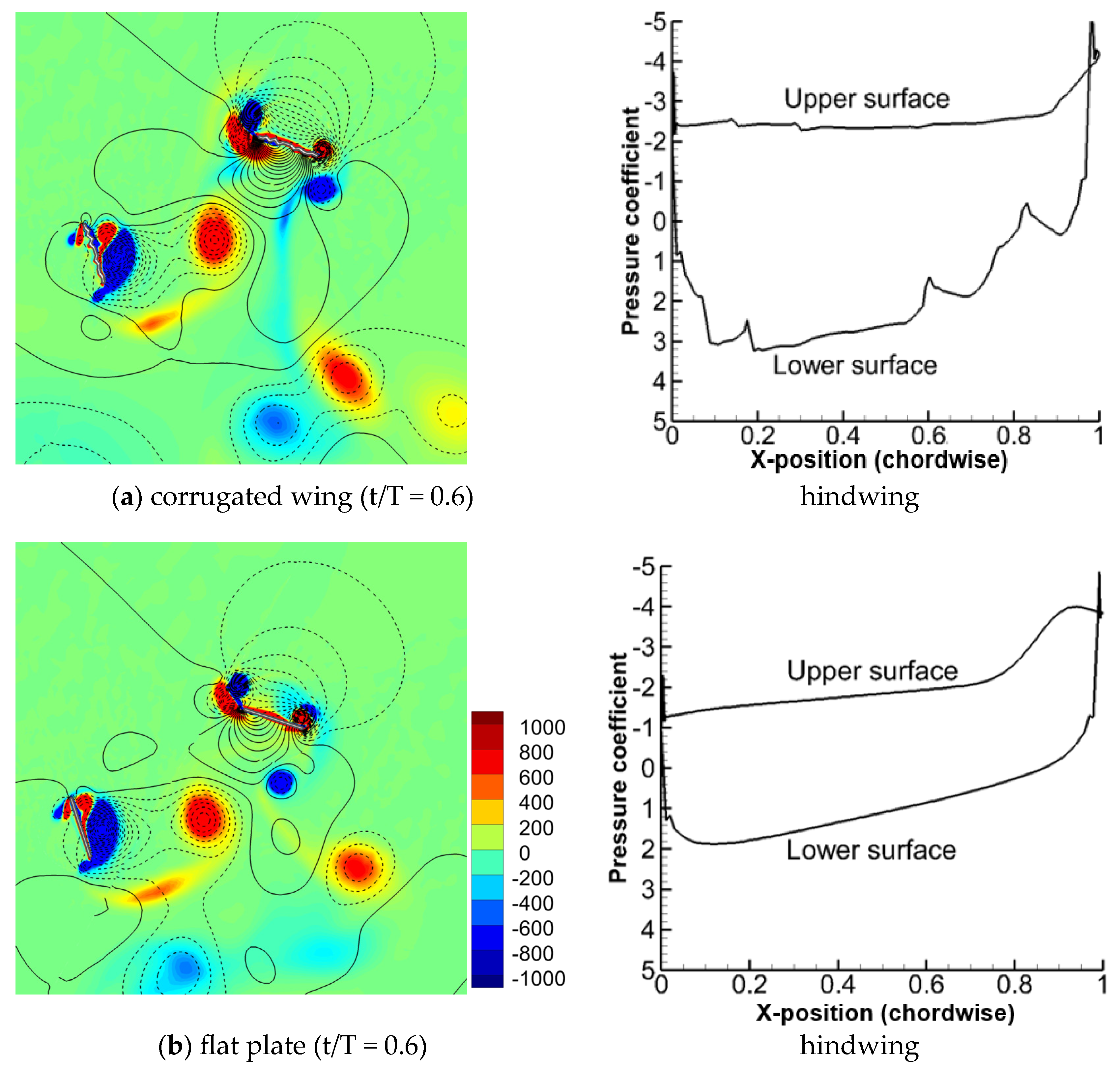
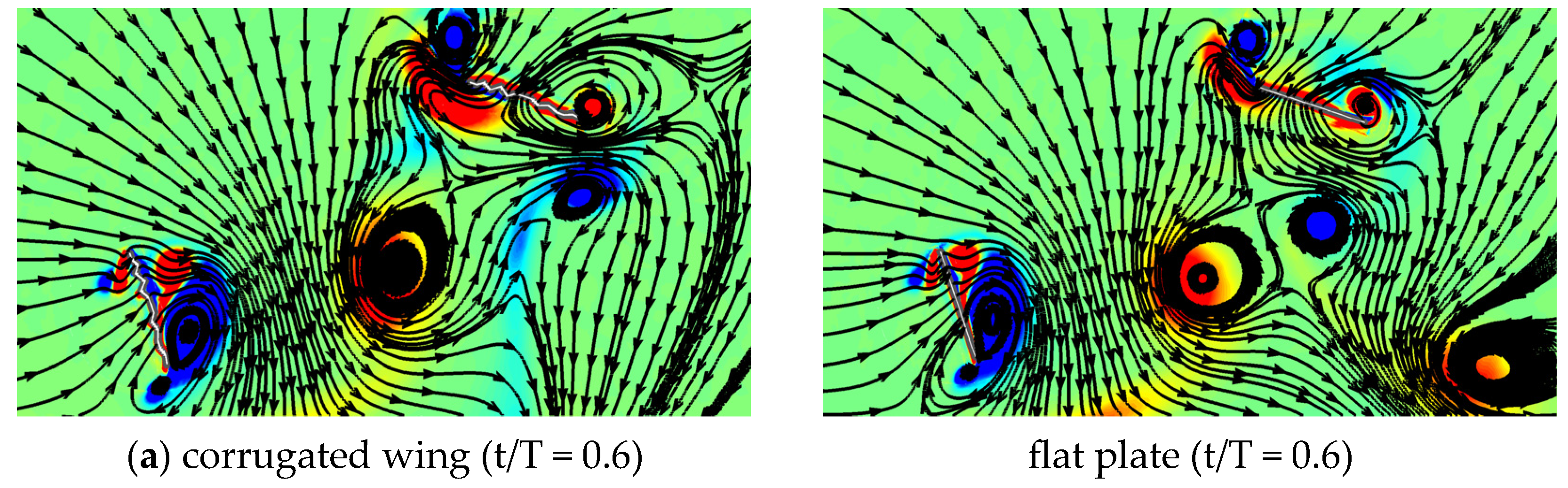
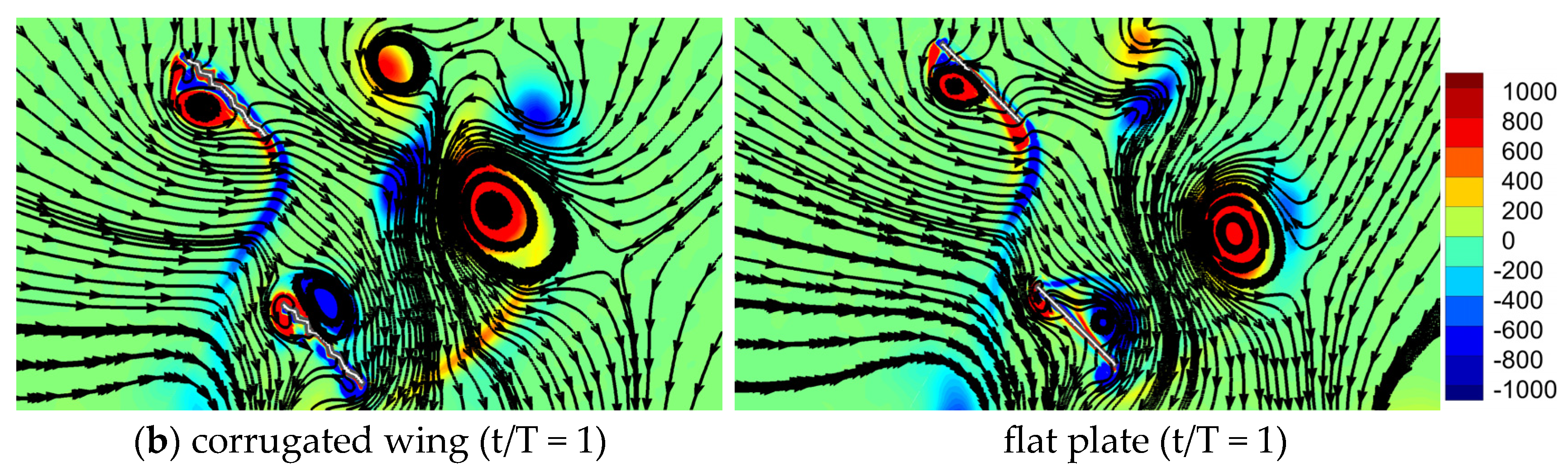
3.1.4. Comparison of Flow Field for Corrugated Wings and Flat Plates Flapping with Sinusoidal Pitch Profile
3.2. Hovering Tandem Wing with Trapezoidal Pitch Profile
3.2.1. Comparison of Vertical Force Generation for Various Flapping Patterns with Trapezoidal Pitch Profile
3.2.2. Time History of Vertical Force Coefficient Cv for Various Flapping Patterns with Trapezoidal Pitch Profile
3.2.3. Comparison of Flow Field for Corrugated Wing and Flat Plate with Trapezoidal Pitch Profile
4. Conclusions
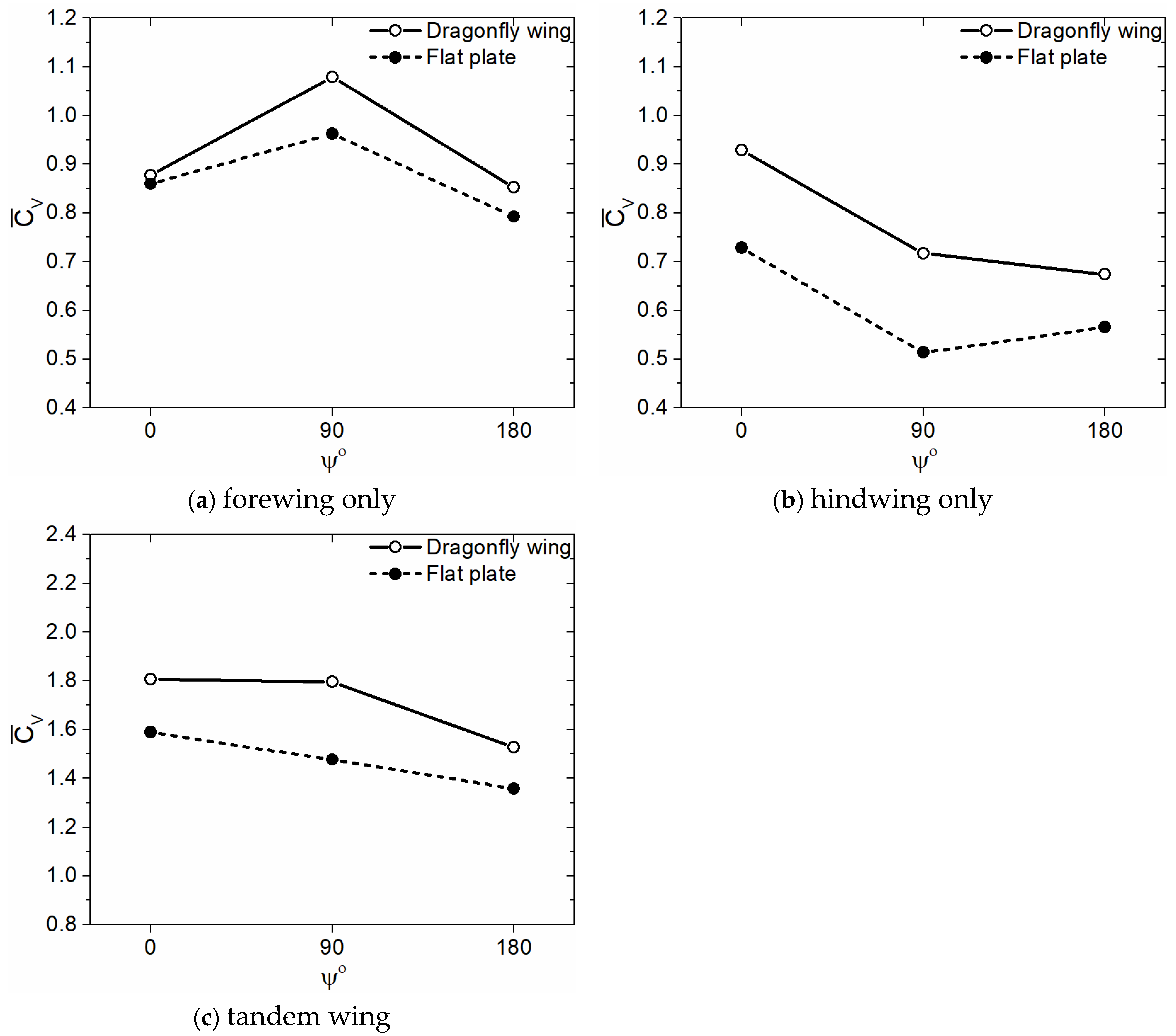
- The corrugated wing performs better than the flat plate in all three flapping patterns for both sinusoidal and trapezoidal pitch profiles. In the sinusoidal pitch profile, the vertical force generation of tandem wings is highest for in-phase stroking whereas it is lowest for counter stroking. In the trapezoidal pitch profile, the vertical force generation of tandem wings is highest for a 90° phase stroking whereas it is lowest for a counter stroking.
- In the sinusoidal pitch profile, the vertical force generation of tandem wing obtained for corrugated wing geometries is nearly 14%, 22%, and 12% higher than the flat plate geometries for ψ = 0°, 90°, and 180°, respectively.
- The corrugated wing sheds a relatively stronger detached CCWV vortex on the lower surface as compared to the flat plate, and hence, the vertical force is much higher for the corrugated wing.
- In the trapezoidal pitch profile, the vertical force generation of tandem wing obtained for corrugated wing geometries is nearly 27%, 22%, and 57% higher than the flat plate geometries for ψ = 0°, 90°, and 180°, respectively.
- By comparison, a flapping wing with sinusoidal pitch profile kinematics generates more vertical force than a flapping wing with trapezoidal pitch profile kinematics in all three flapping patterns.
- The delayed stall mechanism is further postponed in corrugated wing geometry as the corrugation shape traps the vortex structures which has a significant positive influence on the vertical force generation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MAV | Micro aerial vehicle |
| LE | Leading edge |
| PISO | Pressure Implicit with Split Operator algorithm |
| TW | Tandem wing |
| CWV | Clockwise vortex |
| CCWV | Counter clockwise vortex |
References
- Pan, Y.; Guo, S.; Whidborne, J.; Huang, X. Aerodynamic performance of a flyable flapping wing rotor with dragonfly-like flexible wings. Aerosp. Sci. Technol. 2024, 148, 109090. [Google Scholar] [CrossRef]
- Yang, X.; Luo, Y.; Lang, X.; Wang, W. Investigation of the aerodynamic performance of the dragonfly-inspired tandem wings considering the coupling between the stroke plane and phase difference. Aerosp. Sci. Technol. 2024, 155, 109717. [Google Scholar] [CrossRef]
- Sun, W.; Wang, Y.; He, G.; Wang, Q.; Yu, F.; Song, W. Effects of kinematic parameters and corrugated structure on the aerodynamic performance of flexible dragonfly wings. J. Fluids Struct. 2024, 125, 104058. [Google Scholar] [CrossRef]
- Li, H.; Weigert, S.; Nabawy, M.R. Controlling the utility of wake capture in hovering flapping flight: An experimental investigation. Aerosp. Sci. Technol. 2025, 159, 110008. [Google Scholar] [CrossRef]
- Addo-Akoto, R.; Yang, H.H.; Han, J.S.; Han, J.H. Wing flexibility effect on aerodynamic performance of different flapping wing planforms. J. Fluids Struct. 2023, 123, 104006. [Google Scholar] [CrossRef]
- Lee, H.; Jang, J.; Lee, S. An investigation of kinematic parameters and stroke function on stroke reversal for three-dimensional vortex structures around a flapping insect wing. Eur. J. Mech.-B/Fluids 2020, 79, 165–180. [Google Scholar] [CrossRef]
- Shanmugam, A.R.; Sohn, C.H. Numerical investigation on thrust production and unsteady mechanisms of three-dimensional oscillating wing. J. Mech. Sci. Technol. 2019, 33, 5889–5900. [Google Scholar] [CrossRef]
- Martínez-Muriel, C.; García-Villalba, M.; Flores, O. On the role of wake-capture and resonance in spanwise-flexible flapping wings in tandem. J. Fluids Struct. 2024, 130, 104175. [Google Scholar] [CrossRef]
- Cong, L.; Teng, B.; Chen, L.; Bai, W.; Jin, R.; Chen, B. Aerodynamic performance of low aspect-ratio flapping wing with active wing-chord adjustment. J. Fluids Struct. 2023, 122, 103964. [Google Scholar] [CrossRef]
- Lin, T.; Xia, W.; Pecora, R.; Wang, K.; Hu, S. Performance improvement of flapping propulsions from spanwise bending on a low-aspect-ratio foil. Ocean Eng. 2023, 284, 115305. [Google Scholar] [CrossRef]
- Li, G.; Wu, J.; Zhang, Y.; Chen, L. Unsteady Aerodynamic Performance of Tandem Configurations of Three Flapping and Fixed Airfoils. Aerosp. Sci. Technol. 2025, 160, 110032. [Google Scholar] [CrossRef]
- Li, K.; Zhou, D.; Sun, X. Performance characteristics of flapping foil flow energy harvester that mimics movement of swimming fish. Ocean Eng. 2023, 280, 114850. [Google Scholar] [CrossRef]
- Bao, T.; Cao, Y.; Cao, Y.; Pan, G.; Lu, Y.; Xing, C.; Huang, Q. Effects of motion parameters on the propulsion characteristics of flexible pectoral fins in bio-manta robots. Ocean Eng. 2024, 309, 118377. [Google Scholar] [CrossRef]
- Nguyen, K.; Park, H.C. Feasibility study on mimicking the tail-beating supported gliding flight of Flying Fish. Ocean Eng. 2023, 287, 115745. [Google Scholar] [CrossRef]
- Chin, D.D.; Lentink, D. Flapping wing aerodynamics: From insects to vertebrates. J. Exp. Biol. 2016, 219, 920–932. [Google Scholar] [CrossRef] [PubMed]
- Shyy, W.; Kang, C.K.; Chirarattananon, P.; Ravi, S.; Liu, H. Aerodynamics, sensing and control of insect-scale flapping-wing flight. Proc. R. Soc. A Math. Phys. Eng. Sci. 2016, 472, 20150712. [Google Scholar] [CrossRef]
- Pesavento, U.; Wang, Z.J. Flapping wing flight can save aerodynamic power compared to steady flight. Phys. Rev. Lett. 2009, 103, 118102. [Google Scholar] [CrossRef]
- Liu, C.; Shen, T.; Shen, H.; Lu, B.; Sun, L.; Chen, G.; Chi, W. Mimicking Nature’s Insects: A Review of Bio-inspired Flapping-Wing Micro Robots (FWMRs). J. Bionic Eng. 2025, 22, 458–479. [Google Scholar] [CrossRef]
- Liu, F.; Li, S.; Xiang, J.; Li, D.; Tu, Z. A Dragonfly-inspired Flapping Wing Robot Mimicking Force Vector Control Approach. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024; pp. 6029–6035. [Google Scholar] [CrossRef]
- Jones, S.K.; Laurenza, R.; Hedrick, T.L.; Griffith, B.E.; Miller, L.A. Lift vs. drag based mechanisms for vertical force production in the smallest flying insects. J. Theor. Biol. 2015, 384, 105–120. [Google Scholar] [CrossRef]
- Weis-Fogh, T. Quick estimates of flight fitness in hovering animals, including novel mechanisms for lift production. J. Exp. Biol. 1973, 59, 169–230. [Google Scholar] [CrossRef]
- Lehmann, F.O. The mechanisms of lift enhancement in insect flight. Naturwissenschaften 2004, 91, 101–122. [Google Scholar] [CrossRef]
- Ellington, C.P. The aerodynamics of hovering insect flight. IV. Aerodynamic mechanisms. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1984, 305, 79–113. [Google Scholar] [CrossRef]
- Sane, S.P. The aerodynamics of insect flight. J. Exp. Biol. 2003, 206, 4191–4208. [Google Scholar] [CrossRef] [PubMed]
- Cheng, X.; Sun, M. Very small insects use novel wing flapping and drag principle to generate the weight-supporting vertical force. J. Fluid Mech. 2018, 855, 646–670. [Google Scholar] [CrossRef]
- Norberg, R.Å. Hovering flight of the dragonfly Aeschna juncea L., kinematics and aerodynamics. In Swimming and Flying in Nature; Springer: Boston, MA, USA, 1975; Volume 2, pp. 763–781. [Google Scholar] [CrossRef]
- Wang, Z.J. Two dimensional mechanism for insect hovering. Phys. Rev. Lett. 2000, 85, 2216. [Google Scholar] [CrossRef]
- Li, D.; Mu, Y.; Lau, G.K.; Chin, Y.; Lu, Z. Numerical study on the aerodynamic performance of dragonfly (Anax parthenope julius) maneuvering flight during synchronized-stroking. Phys. Fluids. 2024, 36, 091911. [Google Scholar] [CrossRef]
- Li, C.; Dong, H. Wing kinematics measurement and aerodynamics of a dragonfly in turning flight. Bioinspir. Biomim. 2017, 12, 026001. [Google Scholar] [CrossRef]
- Bode-Oke, A.T.; Zeyghami, S.; Dong, H. Flying in reverse: Kinematics and aerodynamics of a dragonfly in backward free flight. J. R. Soc. Interface 2018, 15, 20180102. [Google Scholar] [CrossRef]
- Rüppell, G. Kinematic analysis of symmetrical flight manoeuvres of Odonata. J. Exp. Biol. 1989, 144, 13–42. [Google Scholar] [CrossRef]
- Wang, Z.J. The role of drag in insect hovering. J. Exp. Biol. 2004, 207, 4147–4155. [Google Scholar] [CrossRef]
- Hsieh, C.T.; Chang, C.C.; Chu, C.C. Revisiting the aerodynamics of hovering flight using simple models. J. Fluid Mech. 2009, 623, 121–148. [Google Scholar] [CrossRef]
- Hsieh, C.T.; Kung, C.F.; Chang, C.C.; Chu, C.C. Unsteady aerodynamics of dragonfly using a simple wing–wing model from the perspective of a force decomposition. J. Fluid Mech. 2010, 663, 233–252. [Google Scholar] [CrossRef]
- Sudhakar, Y.; Vengadesan, S. Flight force production by flapping insect wings in inclined stroke plane kinematics. Comput. Fluids 2010, 39, 683–695. [Google Scholar] [CrossRef]
- Kim, D.; Choi, H. Two-dimensional mechanism of hovering flight by single flapping wing. J. Mech. Sci. 2007, 21, 207–221. [Google Scholar] [CrossRef]
- Bomphrey, R.J.; Nakata, T.; Henningsson, P.; Lin, H.T. Flight of the dragonflies and damselflies. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2016, 371, 20150389. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, Z. Dragonfly locomotion: Ecology, form and function. Ph.D. thesis, University of Leeds, West Yorkshire, UK, 2018. [Google Scholar]
- Shumway, N.; Gabryszuk, M.; Laurence, S. The impact of dragonfly wing deformations on aerodynamic performance during forward flight. Bioinspir. Biomim. 2020, 15, 026005. [Google Scholar] [CrossRef] [PubMed]
- Azuma, A.; Watanabe, T. Flight performance of a dragonfly. J. Exp. Biol. 1988, 137, 221–252. [Google Scholar] [CrossRef]
- Maybury, W.J.; Lehmann, F.O. The fluid dynamics of flight control by kinematic phase lag variation between two robotic insect wings. J. Exp. Biol. 2004, 207, 4707–4726. [Google Scholar] [CrossRef]
- Dickinson, M.H.; Lehmann, F.O.; Sane, S.P. Wing rotation and the aerodynamic basis of insect flight. Science 1999, 284, 1954–1960. [Google Scholar] [CrossRef]
- Zheng, Y.; Wu, Y.; Tang, H. An experimental study on the forewing–hindwing interactions in hovering and forward flights. Int. J. Heat Fluid Flow 2016, 59, 62–73. [Google Scholar] [CrossRef]
- Shanmugam, A.R.; Sohn, C.H. Numerical investigation of the aerodynamic benefits of wing-wing interactions in a dragonfly-like flapping wing. J. Mech. Sci. Technol. 2019, 33, 2725–2735. [Google Scholar] [CrossRef]
- Bie, D.; Li, D. Numerical analysis of the wing–wake interaction of tandem flapping wings in forward flight. Aerosp. Sci. Technol. 2022, 121, 107389. [Google Scholar] [CrossRef]
- Nagai, H.; Fujita, K.; Murozono, M. Experimental study on forewing–hindwing phasing in hovering and forward flapping flight. AIAA. J. 2019, 57, 3779–3790. [Google Scholar] [CrossRef]
- Chen, Z.; Xie, Y.; Meng, X. Unsteady aerodynamic forces of tandem flapping wings with different forewing kinematics. Biomimetics 2024, 9, 565. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Wang, C.; Jia, P.; Zhong, Z. The effect of hindwing trajectories on wake–wing interactions in the configuration of two flapping wings in tandem. Biomimetics 2024, 9, 406. [Google Scholar] [CrossRef]
- Wang, J.K.; Sun, M. A computational study of the aerodynamics and forewing-hindwing interaction of a model dragonfly in forward flight. J. Exp. Biol. 2005, 208, 3785–3804. [Google Scholar] [CrossRef] [PubMed]
- Gravish, N.; Peters, J.M.; Combes, S.A.; Wood, R.J. Collective flow enhancement by tandem flapping wings. Phys. Rev. Lett. 2015, 115, 188101. [Google Scholar] [CrossRef]
- Meng, X.G.; Sun, M. Aerodynamic effects of wing corrugation at gliding flight at low Reynolds numbers. Phys. Fluids 2013, 25, 071905. [Google Scholar] [CrossRef]
- Hu, H.; Tamai, M. Bioinspired corrugated airfoil at low Reynolds numbers. J. Aircr. 2008, 45, 2068–2077. [Google Scholar] [CrossRef]
- Shi, X.; Huang, X.; Zheng, Y.; Zhao, S. Effects of cambers on gliding and hovering performance of corrugated dragonfly airfoils. Int. J. Numer. Methods Heat Fluid Flow 2016, 26, 1092–1120. [Google Scholar] [CrossRef]
- Meng, X.G.; Xu, L.; Sun, M. Aerodynamic effects of corrugation in flapping insect wings in hovering flight. J. Exp. Biol. 2011, 214, 432–444. [Google Scholar] [CrossRef] [PubMed]
- Lian, Y.; Broering, T.; Hord, K.; Prater, R. The characterization of tandem and corrugated wings. Prog. Aerosp. Sci. 2014, 65, 41–69. [Google Scholar] [CrossRef]
- Flint, T.J.; Jermy, M.C.; New, T.H.; Ho, W.H. Computational study of a pitching bio-inspired corrugated airfoil. Int. J. Heat Fluid Flow 2017, 65, 328–341. [Google Scholar] [CrossRef]
- Zhang, Q.; Xue, R.; Li, H. Aerodynamic exploration for tandem wings with smooth or corrugated surfaces at low Reynolds number. Aerospace 2023, 10, 427. [Google Scholar] [CrossRef]
- Dao, T.T.; Loan Au, T.K.; Park, S.H.; Park, H.C. Effect of wing corrugation on the aerodynamic efficiency of two-dimensional flapping wings. Appl. Sci. 2020, 10, 7375. [Google Scholar] [CrossRef]
- Chitsaz, N.; Siddiqui, K.; Marian, R.; Chahl, J. Numerical and experimental analysis of three-dimensional microcorrugated wing in gliding flight. J. Fluids Eng. 2022, 144, 011205. [Google Scholar] [CrossRef]
- Chitsaz, N.; Siddiqui, K.; Marian, R.; Chahl, J. An experimental study of the aerodynamics of micro corrugated wings at low Reynolds number. Exp. Therm. Fluid Sci. 2021, 121, 110286. [Google Scholar] [CrossRef]
- Hou, D.; Tan, B.; Shi, B.; Zhong, Z. Aerodynamic effects of time-varying corrugations on dragonfly wings in flapping flight. Biomimetics 2024, 9, 433. [Google Scholar] [CrossRef]
- Broering, T.M.; Lian, Y.S. The effect of phase angle and wing spacing on tandem flapping wings. Acta Mech. Sin. 2012, 28, 1557–1571. [Google Scholar] [CrossRef]
- Sudhakar, Y.; Vengadesan, S. The functional significance of delayed stall in insect flight. Numer. Heat Transf. Part A Appl. 2010, 58, 65–83. [Google Scholar] [CrossRef]
- Bhat, S.S.; Zhao, J.; Sheridan, J.; Hourigan, K.; Thompson, M.C. Effects of flapping-motion profiles on insect-wing aerodynamics. J. Fluid Mech. 2020, 884, A8. [Google Scholar] [CrossRef]
- Kesel, A.B. Aerodynamic characteristics of dragonfly wing sections compared with technical aerofoils. J. Exp. Biol. 2000, 203, 3125–3135. [Google Scholar] [CrossRef] [PubMed]
- Lentink, D.A.; Dickinson, M.H. Biofluid dynamic scaling of flapping, spinning and translating fins and wings. J. Exp. Biol. 2009, 212, 2691–2704. [Google Scholar] [CrossRef]
- Han, J.S.; Chang, J.W.; Han, J.H. The advance ratio effect on the lift augmentations of an insect-like flapping wing in forward flight. J. Fluid Mech. 2016, 808, 485–510. [Google Scholar] [CrossRef]
- Han, J.S.; Chang, J.W.; Han, J.H. An aerodynamic model for insect flapping wings in forward flight. Bioinspir. Biomim. 2017, 12, 036004. [Google Scholar] [CrossRef]
- Shanmugam, A.R.; Sohn, C.H. Numerical investigation of the aerodynamic performance of dragonfly-like flapping foil in take-off flight. Proc. Inst. Mech. Eng. Part G. J. Aerosp. Eng. 2019, 233, 5801–5815. [Google Scholar] [CrossRef]
- Srinidhi, N.G.; Vengadesan, S. Ground effect on tandem flapping wings hovering. Comput. Fluids 2017, 152, 40–56. [Google Scholar] [CrossRef]
- Lua, K.B.; Lu, H.; Zhang, X.H.; Lim, T.T.; Yeo, K.S. Aerodynamics of two-dimensional flapping wings in tandem configuration. Phys. Fluids 2016, 28, 121901. [Google Scholar] [CrossRef]
- Wu, D.; Yeo, K.S.; Lim, T.T. A numerical study on the free hovering flight of a model insect at low Reynolds number. Comput. Fluids 2014, 103, 234–261. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| thickness-to-chord ratio (t/c) | 0.04 |
| free-stream velocity U∞ | 0 m/s |
| Reynolds number Re | 2150 |
| flapping frequency f | 40 Hz |
| mean angle of attack αo | 45° |
| pitch amplitude B | 45° |
| phase difference between the heave and pitch motion φ | 0° |
| stroke plane inclination β | 60° |
| stroke amplitude Ao/c | 2.5 |
| phase difference between the forewing and the hindwing ψ | 0°, 90°, and 180° |
| wing spacing (L/c) | 2.1 |
| Case | Cells | Δt (s) | (TW) |
|---|---|---|---|
| Medium M1 | 75,000 | T/500 | 1.719 |
| Fine M2 | 150,000 | T/750 | 1.808 |
| Refined M3 | 225,000 | T/1000 | 1.847 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shanmugam, A.R.; Sohn, C.H.; Park, K.S. Numerical Investigation on the Aerodynamic Benefits of Corrugated Wing in Dragonfly-like Hovering Flapping Wing. Biomimetics 2025, 10, 256. https://doi.org/10.3390/biomimetics10050256
Shanmugam AR, Sohn CH, Park KS. Numerical Investigation on the Aerodynamic Benefits of Corrugated Wing in Dragonfly-like Hovering Flapping Wing. Biomimetics. 2025; 10(5):256. https://doi.org/10.3390/biomimetics10050256
Chicago/Turabian StyleShanmugam, Arun Raj, Chang Hyun Sohn, and Ki Sun Park. 2025. "Numerical Investigation on the Aerodynamic Benefits of Corrugated Wing in Dragonfly-like Hovering Flapping Wing" Biomimetics 10, no. 5: 256. https://doi.org/10.3390/biomimetics10050256
APA StyleShanmugam, A. R., Sohn, C. H., & Park, K. S. (2025). Numerical Investigation on the Aerodynamic Benefits of Corrugated Wing in Dragonfly-like Hovering Flapping Wing. Biomimetics, 10(5), 256. https://doi.org/10.3390/biomimetics10050256






