Topologically Optimized Anthropomorphic Prosthetic Limb: Finite Element Analysis and Mechanical Evaluation Using Plantogram-Derived Foot Pressure Data
Abstract
1. Introduction
2. Materials and Methods
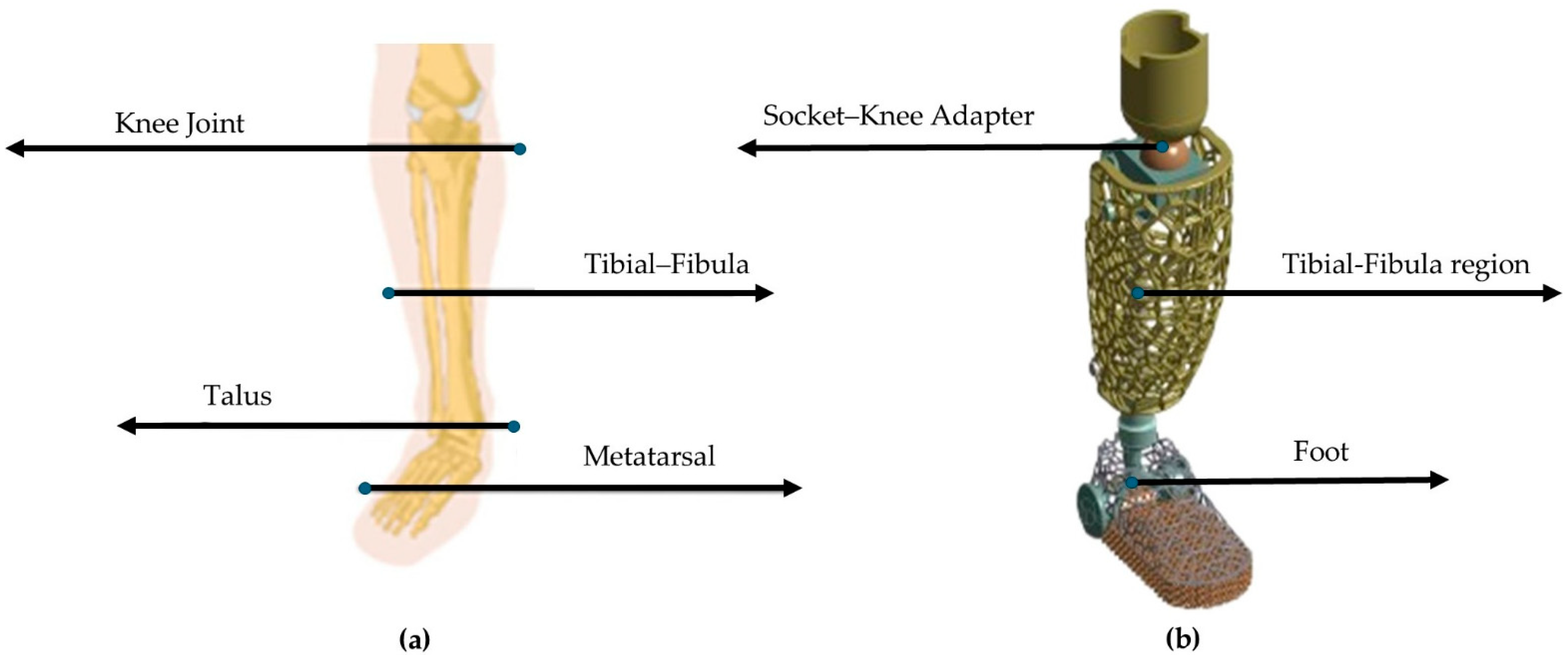
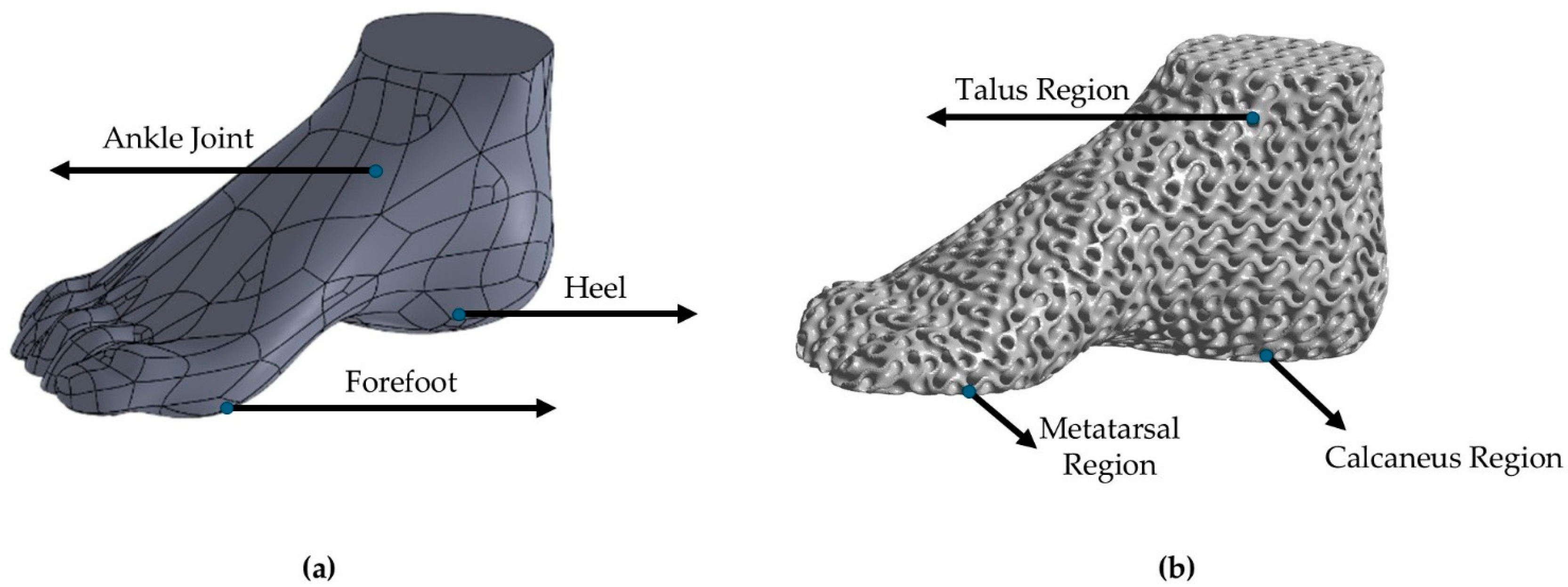
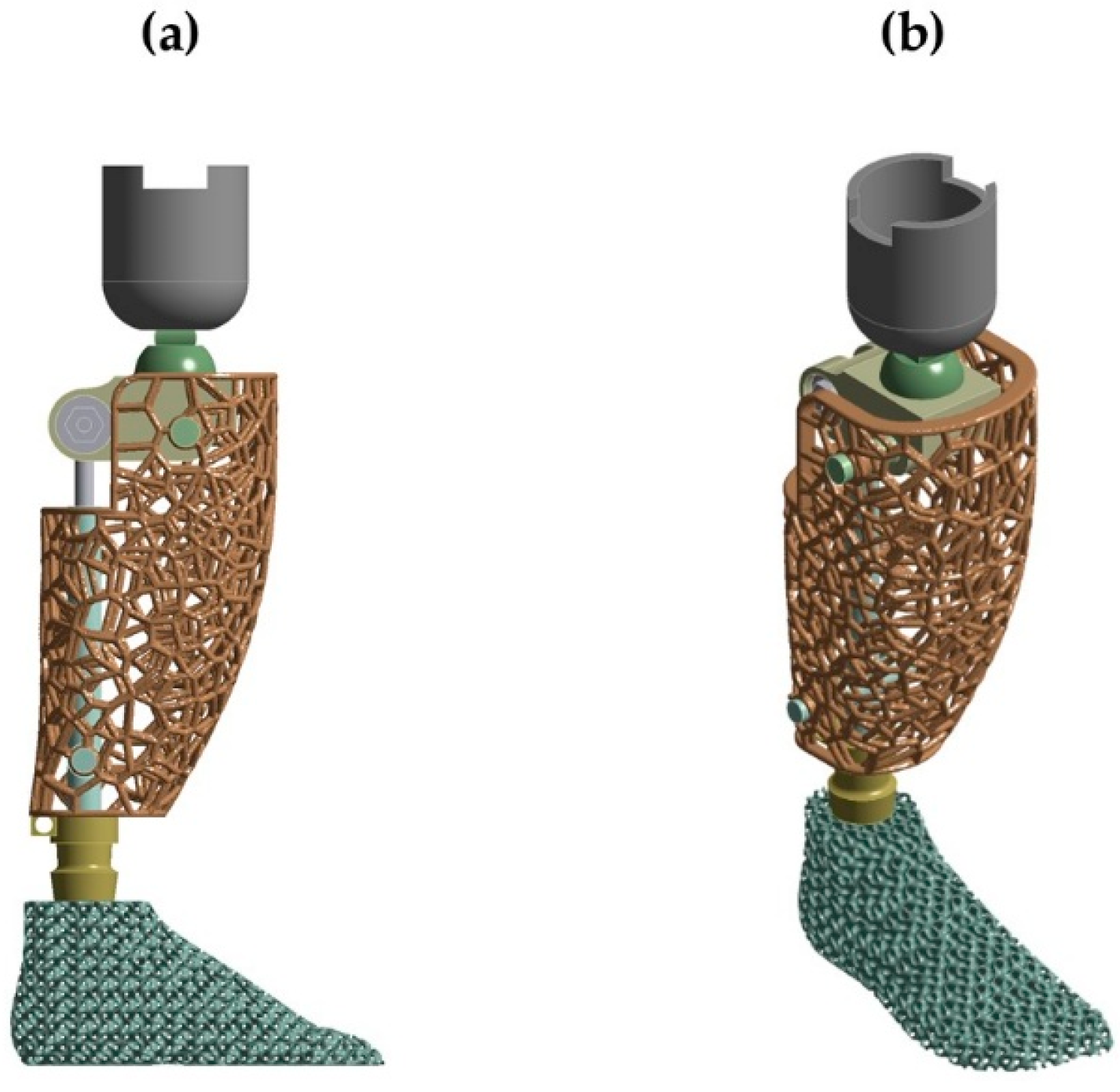
2.1. Initial Anthropomorphic Design
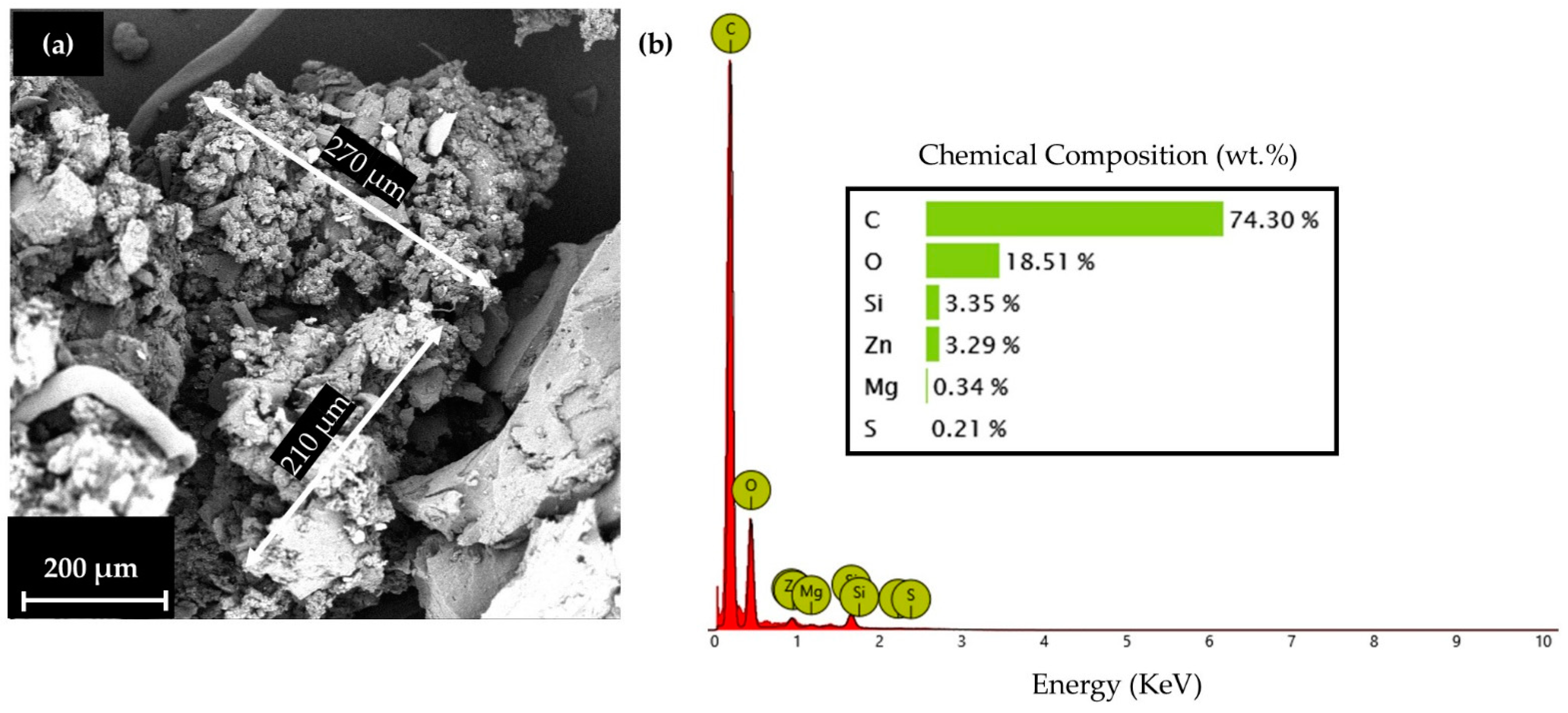
2.2. Materials
2.3. Additive Manufacturing
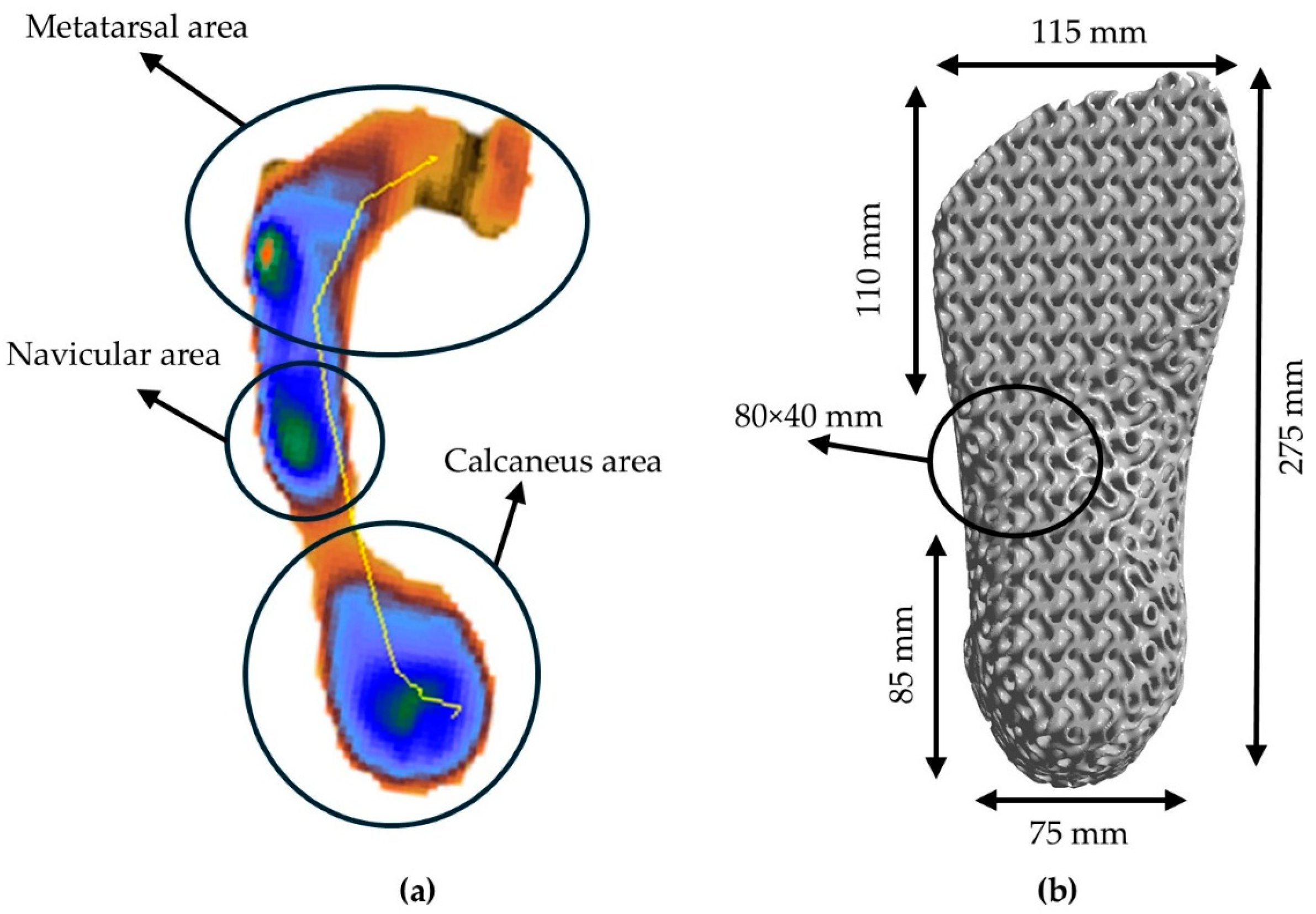
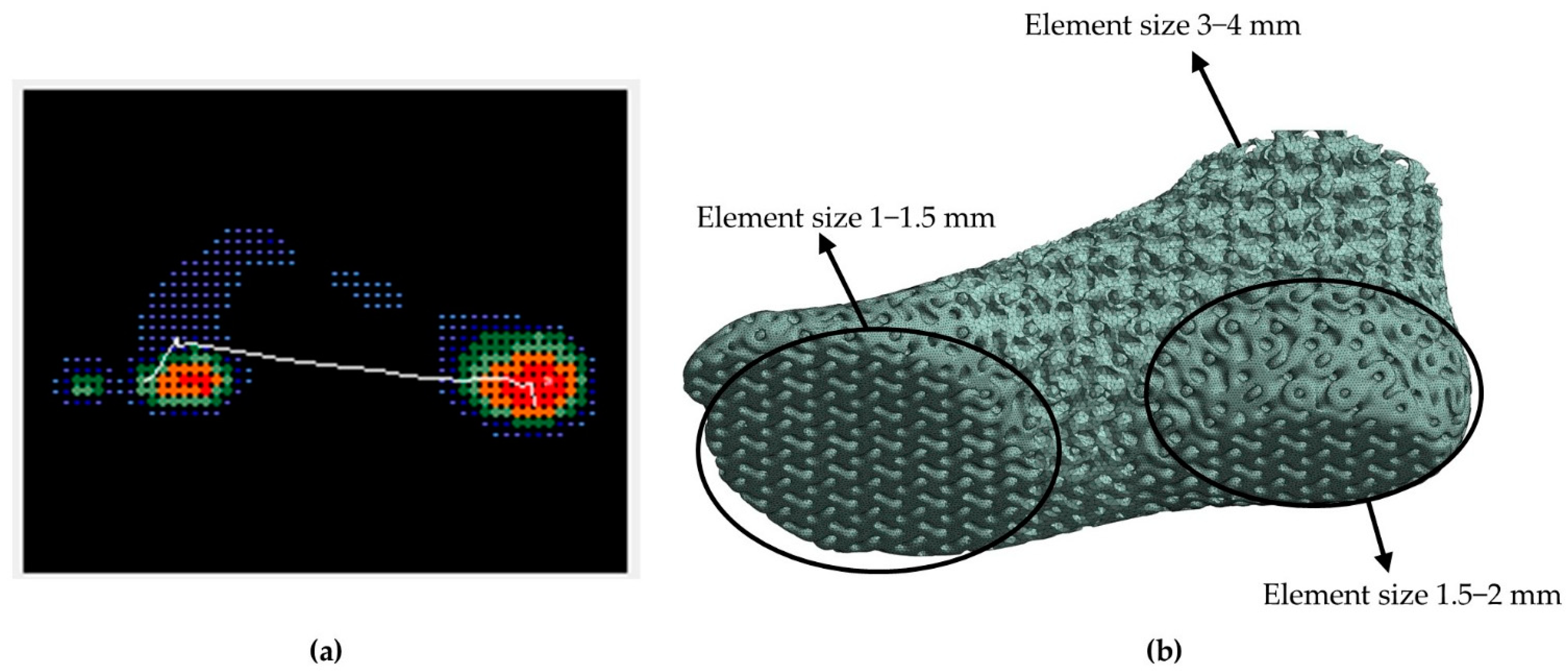
2.4. Plantogram Foot Pressure Data
2.5. Compression and Compression Cycling Mechanical Testing
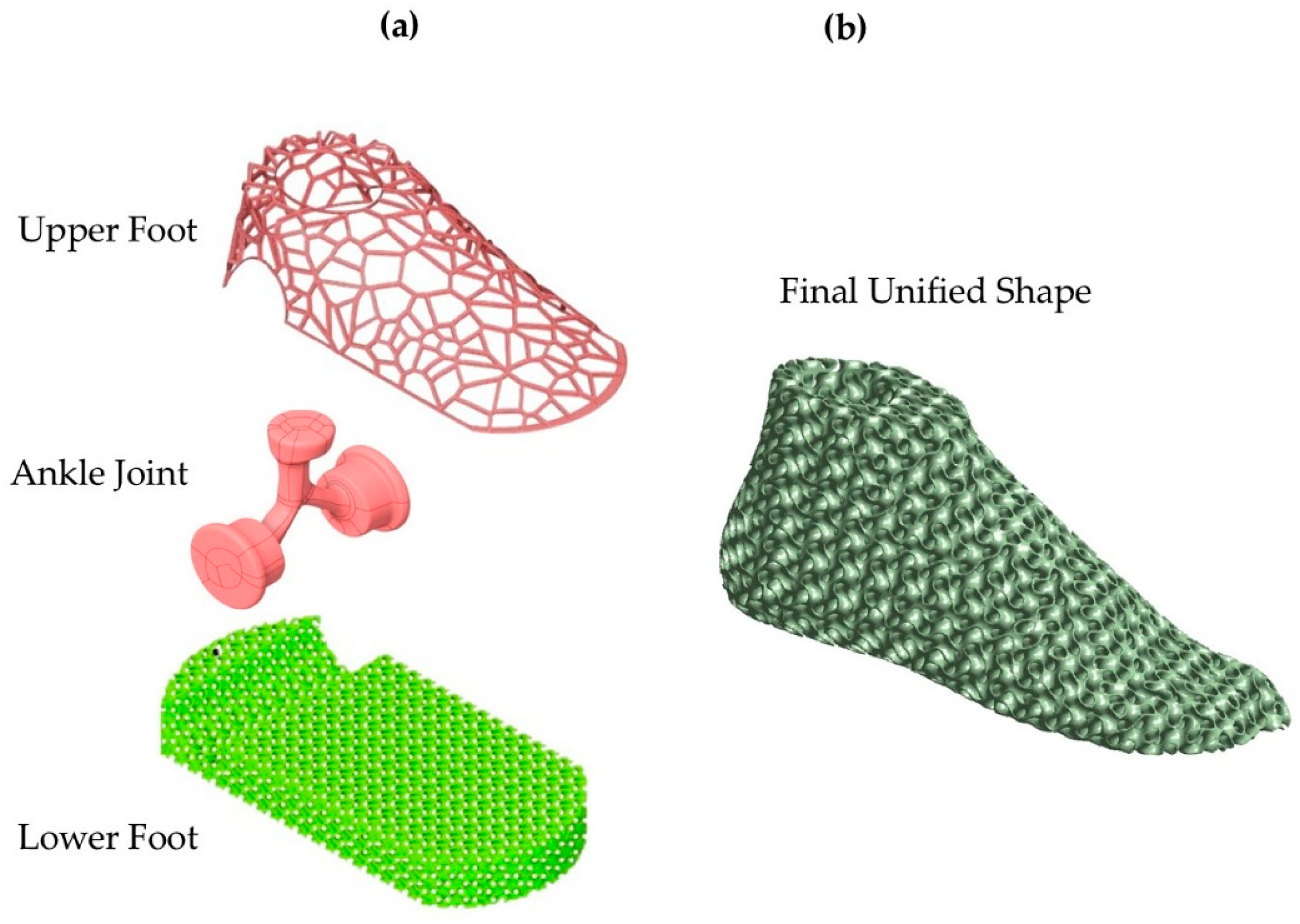
2.6. Topological Optimization
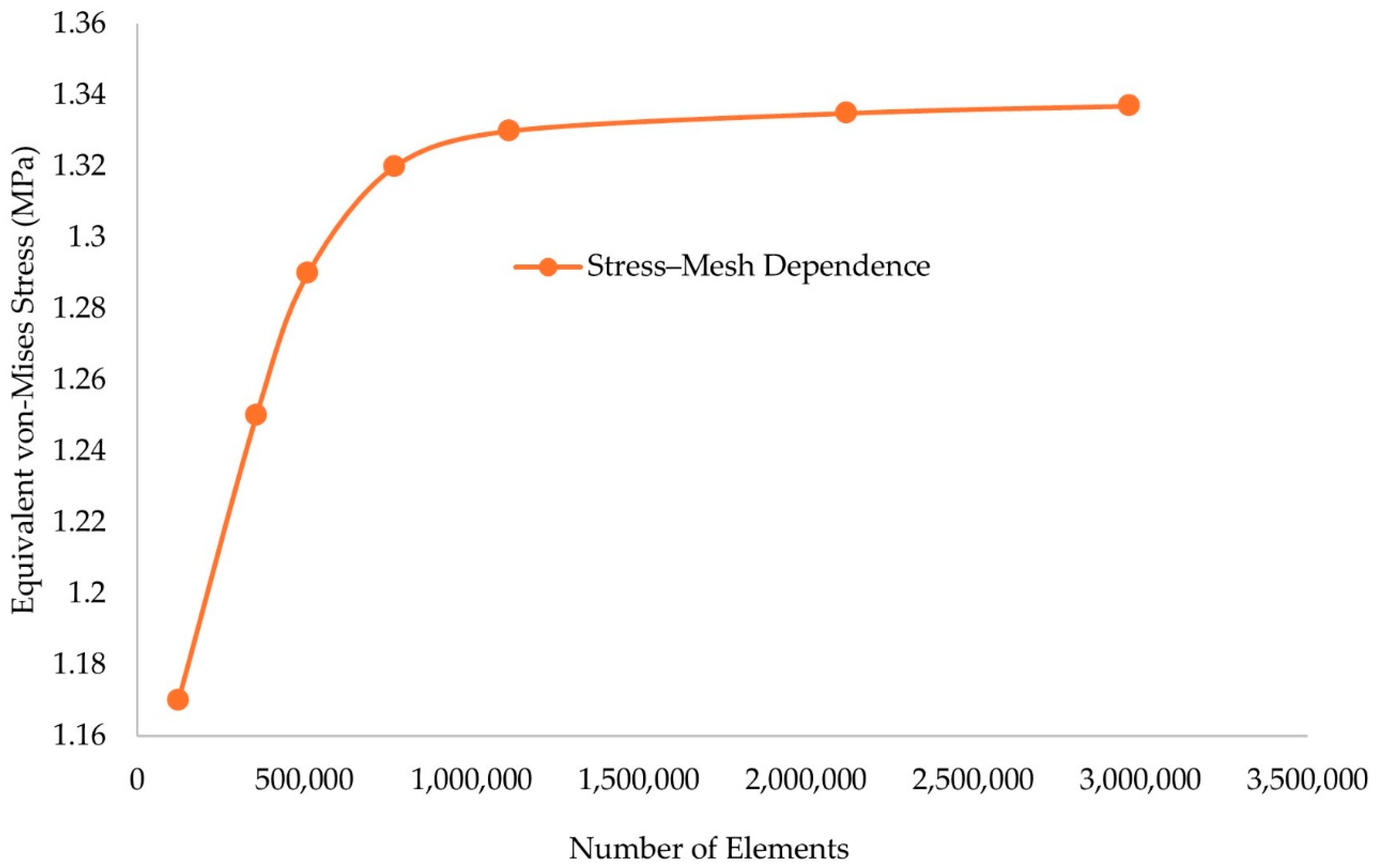
2.7. Finite Element Analysis
3. Results
3.1. Results of the Preliminary Design
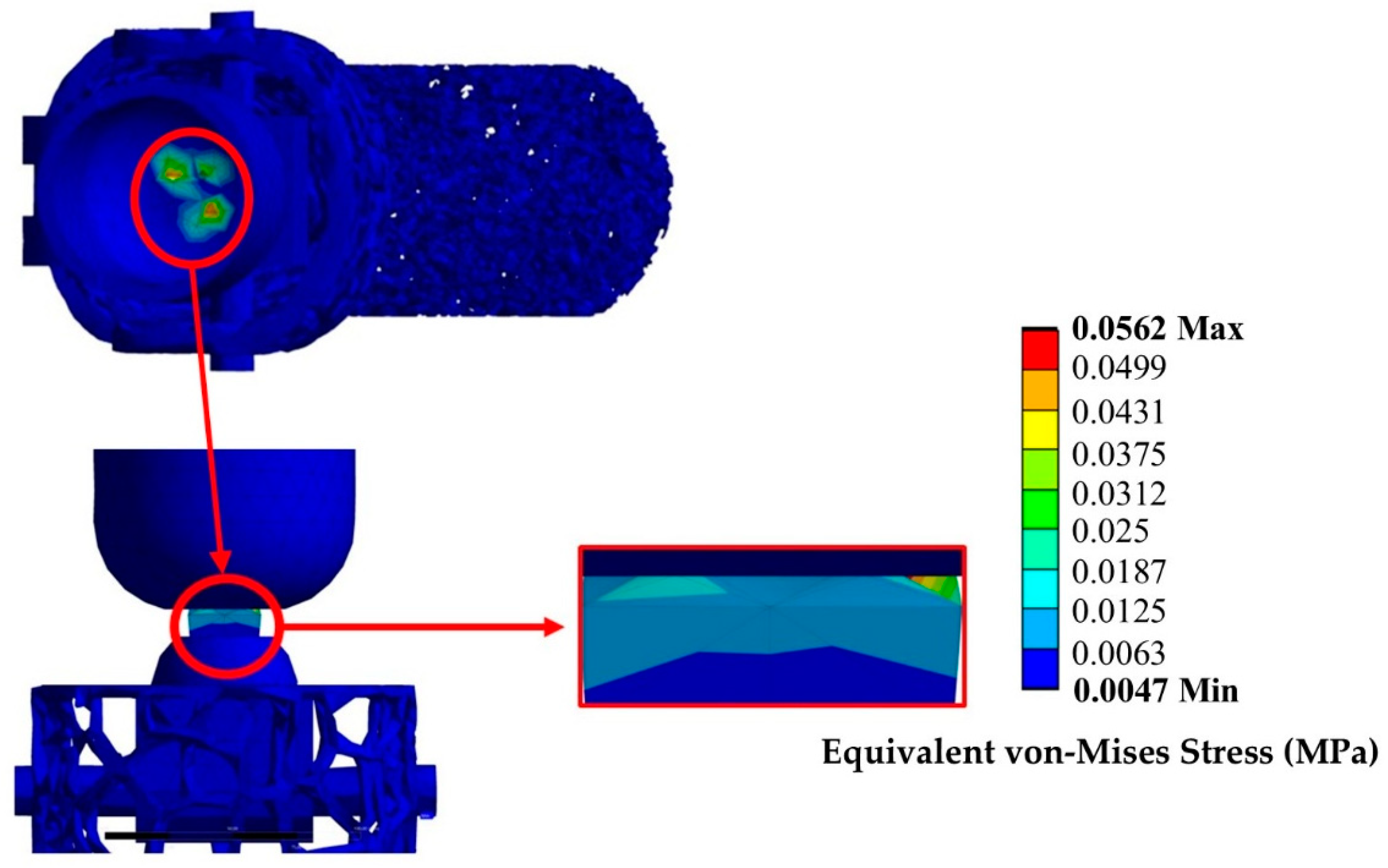
3.1.1. FEA Results
3.1.2. Plantogram-Derived Results
3.2. Optimization Process-Insertion of Bioinspired Lattice Structures
3.2.1. Compression Test Results
3.2.2. Identification of the Scaling Laws
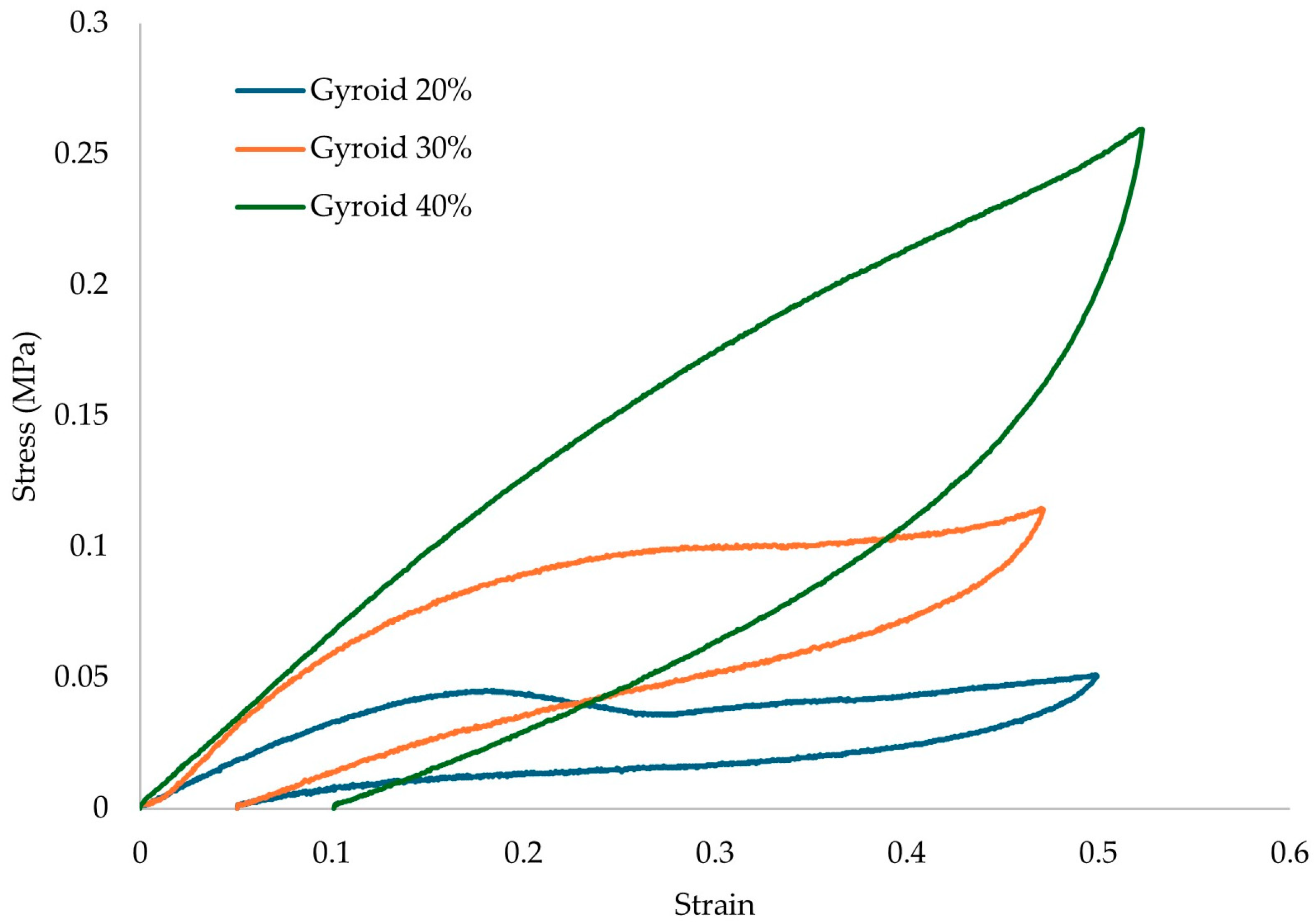
3.2.3. Loading/Unloading Results
3.3. Optimized Model Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yuan, B.; Hu, D.; Gu, S.; Xiao, S.; Song, F. The Global Burden of Traumatic Amputation in 204 Countries and Territories. Front. Public Health 2023, 11, 1258853. [Google Scholar] [CrossRef] [PubMed]
- Amputee-Coalition. Available online: https://amputee-coalition.org/5-6-million-americans-living-with-limb-loss-limb-difference/ (accessed on 22 March 2025).
- McDonald, C.L.; Westcott-McCoy, S.; Weaver, M.R.; Haagsma, J.; Kartin, D. Global Prevalence of Traumatic Non-Fatal Limb Amputation. Prosthet. Orthot. Int. 2020, 45, 105–114. [Google Scholar] [CrossRef]
- Sarvestani, A.S.; Azam, A.T. Amputation: A Ten-Year Survey. Trauma Mon. 2013, 18, 126–129. [Google Scholar] [CrossRef]
- Anastasio, A.T.; Bagheri, K.; Johnson, L.; Hubler, Z.; Hendren, S.; Adams, S.B. Outcomes Following Total Ankle Total Talus Replacement: A Systematic Review. Foot Ankle Surg. 2024, 30, 245–251. [Google Scholar] [CrossRef] [PubMed]
- Gupta, R.; Grove, K.; Wei, A.; Lee, J.; Akkouch, A. Ankle and Foot Arthroplasty and Prosthesis: A Review on the Current and Upcoming State of Designs and Manufacturing. Micromachines 2023, 14, 2081. [Google Scholar] [CrossRef]
- Kyriakidis, I.F.; Kladovasilakis, N.; Pechlivani, E.M.; Tsongas, K. Mechanical Performance of Recycled 3D Printed Sustainable Polymer-Based Composites: A Literature Review. J. Compos. Sci. 2024, 8, 215. [Google Scholar] [CrossRef]
- Varsavas, S.D.; Riemelmoser, F.; Arbeiter, F.; Faller, L.-M. A Review of Parameters Affecting Success of Lower-Limb Prosthetic Socket and Liners and Implementation of 3D Printing Technologies. Mater. Today Proc. 2022, 70, 425–430. [Google Scholar] [CrossRef]
- Quintero-Quiroz, C.; Pérez, V.Z. Materials for Lower Limb Prosthetic and Orthotic Interfaces and Sockets: Evolution and Associated Skin Problems. Rev. Fac. Med. 2019, 67, 117–125. [Google Scholar] [CrossRef]
- Nashar, M.A.; Sutradhar, A. Design of Hierarchical Architected Lattices for Enhanced Energy Absorption. Materials 2021, 14, 5384. [Google Scholar] [CrossRef]
- Beloshenko, V.; Beygelzimer, Y.; Chishko, V.; Savchenko, B.; Sova, N.; Verbylo, D.; Voznyak, A.; Vozniak, I. Mechanical Properties of Flexible TPU-Based 3D Printed Lattice Structures: Role of Lattice Cut Direction and Architecture. Polymers 2021, 13, 2986. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Crittenden, K.; Weiss, L.; Bardaweel, H. Recycle of Waste Tire Rubber in a 3D Printed Composite With Enhanced Damping Properties. J. Clean. Prod. 2022, 368, 133085. [Google Scholar] [CrossRef]
- Paterno, L.; Ibrahimi, M.; Gruppioni, E.; Menciassi, A.; Ricotti, L. Sockets for Limb Prostheses: A Review of Existing Technologies and Open Challenges. IEEE Trans. Biomed. Eng. 2018, 65, 1996–2010. [Google Scholar] [CrossRef]
- Hanspal, R.; Fisher, K.; Nieveen, R. Prosthetic Socket Fit Comfort Score. Disabil. Rehabil. 2003, 25, 1278–1280. [Google Scholar] [CrossRef]
- Rosenblatt, N.J.; Stachowiak, A.; Reddin, C. Prosthetic Disuse Leads to Lower Balance Confidence in a Long-Term User of a Transtibial Prosthesis. Adv. Wound Care 2019, 10, 529–533. [Google Scholar] [CrossRef]
- Kyriakidis, I.F.; Kladovasilakis, N.; Pechlivani, E.M.; Korlos, A.; David, C.; Tsongas, K. In Situ Investigation of Tensile Response for Inconel 718 Micro-Architected Materials Fabricated by Selective Laser Melting. Materials 2024, 17, 4433. [Google Scholar] [CrossRef] [PubMed]
- Ozmen, O.; Surmen, H.K. Design of 3D Printed Below-Knee Prosthetic—A Finite Element and Topology Optimization Study. Stroj. Vestn.-J. Mech. Eng. 2024, 70, 517–530. [Google Scholar] [CrossRef]
- Babamiri, B.B.; Barnes, B.; Soltani-Tehrani, A.; Shamsaei, N.; Hazeli, K. Designing Additively Manufactured Lattice Structures Based on Deformation Mechanisms. Addit. Manuf. 2021, 46, 102143. [Google Scholar] [CrossRef]
- Ghorbani, F.; Gharehbaghi, H.; Farrokhabadi, A.; Bolouri, A. Evaluation of the Mechanical Properties and Energy Absorption in a Novel Hybrid Cellular Structure. Aerosp. Sci. Technol. 2024, 148, 109105. [Google Scholar] [CrossRef]
- Górski, F.; Denysenko, Y.; Kuczko, W.; Żukowska, M.; Wichniarek, R.; Zawadzki, P.; Rybarczyk, J. Individualized 3D Printed Orthopaedic and Prosthetic Devices Using AutoMedPrint Technology—Methodologies and Examples. Adv. Sci. Technol.-Res. J. 2024, 18, 145–158. [Google Scholar] [CrossRef]
- Li, N.; Xue, C.; Chen, S.; Aiyiti, W.; Khan, S.B.; Liang, J.; Zhou, J.; Lu, B. 3D Printing of Flexible Mechanical Metamaterials: Synergistic Design of Process and Geometric Parameters. Polymers 2023, 15, 4523. [Google Scholar] [CrossRef]
- Kladovasilakis, N.; Kyriakidis, I.F.; Tzimtzimis, E.K.; Pechlivani, E.M.; Tsongas, K.; Tzetzis, D. Development of 4D-Printed Arterial Stents Utilizing Bioinspired Architected Auxetic Materials. Biomimetics 2025, 10, 78. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Collini, L.; Ursini, C.; Jeng, J.-Y. Energy Absorption and Stiffness of Thin and Thick-Walled Closed-Cell 3D-Printed Structures Fabricated from a Hyperelastic Soft Polymer. Materials 2022, 15, 2441. [Google Scholar] [CrossRef]
- Shen, F.; Yuan, S.; Guo, Y.; Zhao, B.; Bai, J.; Qwamizadeh, M.; Chua, C.K.; Wei, J.; Zhou, K. Energy Absorption of Thermoplastic Polyurethane Lattice Structures via 3D Printing: Modeling and Prediction. Int. J. Appl. Mech. 2016, 08, 1640006. [Google Scholar] [CrossRef]
- Yavas, D.; Liu, Q.; Zhang, Z.; Wu, D. Design and Fabrication of Architected Multi-Material Lattices with Tunable Stiffness, Strength, and Energy Absorption. Mater. Des. 2022, 217, 110613. [Google Scholar] [CrossRef]
- Thahabi, A.R.N.A.; Martulli, L.M.; Sorrentino, A.; Lavorgna, M.; Gruppioni, E.; Bernasconi, A. Stiffness-Driven Design and Optimization of a 3D-Printed Composite Prosthetic Foot: A Beam Finite Element-Based Framework. Compos. Struct. 2024, 337, 118053. [Google Scholar] [CrossRef]
- Claybrook, F.R.; Southee, D.J.; Mohammed, M. Mechanical Evaluation of Elastomeric Thermoplastic Polyurethane Additively Manufactured Triply Periodic Minimal Surface Area Lattice Structures for Adjustable Cushioning Properties. Rapid Prototyp. J. 2024, 30, 1070–1086. [Google Scholar] [CrossRef]
- Xie, F.; Wu, W.; Hu, H.; Ye, J.; Cui, L.; Wang, Z.; Zhang, W. Coating of Mussel-inspired PDA Modified SiC Whiskers for Enhancing the Mechanical Properties of SLS-formed TPU Parts. J. Appl. Polym. Sci. 2024, 142, e56320. [Google Scholar] [CrossRef]
- Kladovasilakis, N.; Charalampous, P.; Boumpakis, A.; Kontodina, T.; Tsongas, K.; Tzetzis, D.; Kostavelis, I.; Givissis, P.; Tzovaras, D. Development of Biodegradable Customized Tibial Scaffold with Advanced Architected Materials Utilizing Additive Manufacturing. J. Mech. Behav. Biomed. Mater. 2023, 141, 105796. [Google Scholar] [CrossRef] [PubMed]
- Pitkin, M. The Moment Criterion of Anthropomorphicity of Prosthetic Feet as a Potential Predictor of Their Functionality for Transtibial Amputees. Biomimetics 2023, 8, 572. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Rowshan, R. Topology-Mechanical Property Relationship of 3D Printed Strut, Skeletal, and Sheet Based Periodic Metallic Cellular Materials. Addit. Manuf. 2018, 19, 167–183. [Google Scholar] [CrossRef]
- Kladovasilakis, N.; Natsios, I.; Pechlivani, E.M.; Tzetzis, D.; Tzovaras, D. Valorizing Automotive Tire Waste via Additive Manufacturing Technologies. In Communications in Computer and Information Science; Springer: Cham, Switzerland, 2024; pp. 39–51. [Google Scholar]
- Alkadi, F.; Lee, J.; Yeo, J.-S.; Hwang, S.-H.; Choi, J.-W. 3D Printing of Ground Tire Rubber Composites. Int. J. Precis. Eng. Manuf.-Green Technol. 2019, 6, 211–222. [Google Scholar] [CrossRef]
- Jasiewicz, B.; Klimiec, E.; Guzdek, P.; Kołaszczyński, G.; Piekarski, J.; Zaraska, K.; Potaczek, T. Investigation of Impact of Walking Speed on Forces Acting on a Foot–Ground Unit. Sensors 2022, 22, 3098. [Google Scholar] [CrossRef] [PubMed]
- Hayafune, N.; Hayafune, Y.; Jacob, H.A.C. Pressure and Force Distribution Characteristics under the Normal Foot during the Push-off Phase in Gait. Foot 1999, 9, 88–92. [Google Scholar] [CrossRef]
- Nilsson, J.; Thorstensson, A. Ground Reaction Forces at Different Speeds of Human Walking and Running. Acta Physiol. Scand. 1989, 136, 217–227. [Google Scholar] [CrossRef]
- ISO 7743:2017; Prosthetics—Structural Testing of Lower-Limb Prostheses—Requirements and Test Methods. ISO: Geneva, Switzerland, 2017.
- Bai, L.; Gong, C.; Chen, X.; Sun, Y.; Xin, L.; Pu, H.; Peng, Y.; Luo, J. Mechanical Properties and Energy Absorption Capabilities of Functionally Graded Lattice Structures: Experiments and Simulations. Int. J. Mech. Sci. 2020, 182, 105735. [Google Scholar] [CrossRef]
- Fischer, S.F. Energy Absorption Efficiency of Open-Cell Pure Aluminum Foams. Mater. Lett. 2016, 184, 208–210. [Google Scholar] [CrossRef]
- ISO 10328:2016; Prosthetics—Structural Testing of Lower-Limb Prostheses—Requirements and Test Methods. ISO: Geneva, Switzerland, 2016.
- ISO 22675:2024; Prosthetics—Testing of Ankle-Foot Devices and Foot Units—Requirements and Test Methods. ISO: Geneva, Switzerland, 2024.





| Material | Compressive Strength at the Densification Point (MPa) | Damping (Loss) Factor (%) | Overall Energy Absorption (kJ/m3) |
|---|---|---|---|
| TPU | 4.04 ± 0.5 | 15.1 ± 1.5 | 246 ± 21 |
| TPU-GTR 10 wt.% | 4.85 ± 0.5 | 18.4 ± 1.7 | 321 ± 27 |
| TPU-GTR 20 wt.% | 5.69 ± 0.6 | 21.0 ± 2.2 | 414 ± 32 |
| Human Motion | Stress (MPa) | Effective Area (cm2) | Velocity (m/s) |
|---|---|---|---|
| Standing | 0.044 | 229 | 0 |
| Mild Exercise | 0.245 | 201 | 1.02 |
| Intense Exercise | 0.349 | 125 | 3.11 |
| Surface | Max Length (cm) | Max Width (cm) | Effective Area (cm2) |
|---|---|---|---|
| Metatarsal (Forefoot) | 11 | 11.5 | 126.5 |
| Navicular (Middle foot) | 8 | 3.5 | 28 |
| Calcaneus (Heel) | 8.5 | 7.5 | 63.75 |
| Overall | 27.5 | 7.5–11.5 | 220.25 |
| Structure | Densification Point Stress (MPa) | Densification Point Strain (-) |
|---|---|---|
| Solid | 4.85 ± 0.5 | 0.42 ± 0.04 |
| Gyroid 20% r.d. | 0.21 ± 0.02 | 0.71 ± 0.06 |
| Gyroid 30% r.d. | 0.38 ± 0.03 | 0.61 ± 0.05 |
| Gyroid 40% r.d. | 0.52 ± 0.04 | 0.59 ± 0.05 |
| Structure | SEAv (kJ/m3) | SEAm (kJ/kg) | η(εα) (%) |
|---|---|---|---|
| Solid | 320 ± 27 | 272 ± 23 | 41 ± 3 |
| Gyroid 20% r.d. | 11 ± 1 | 46 ± 4 | 59 ± 6 |
| Gyroid 30% r.d. | 34 ± 3 | 96 ± 8 | 58 ± 5 |
| Gyroid 40% r.d. | 44 ± 4 | 93 ± 7 | 57 ± 5 |
| Gyroid 20% r.d. | Gyroid 30% r.d. | Gyroid 40% r.d. | Solid | |
|---|---|---|---|---|
| Damping factor (%) | 17.8 ± 1.4 | 18.8 ± 1.6 | 17.6 ± 1.3 | 18.4 ± 1.7 |
| Property Direction | Young’s Modulus (E), MPa | Shear Modulus (G), MPa | Poisson’s Ratio |
|---|---|---|---|
| X-axis | 35.35 | 12.42 | 0.411 |
| Y-axis | 35.42 | 12.49 | 0.413 |
| Z-axis | 35.25 | 12.55 | 0.412 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kyriakidis, I.F.; Kladovasilakis, N.; Gavriilopoulos, M.; Tzetzis, D.; Pechlivani, E.M.; Tsongas, K. Topologically Optimized Anthropomorphic Prosthetic Limb: Finite Element Analysis and Mechanical Evaluation Using Plantogram-Derived Foot Pressure Data. Biomimetics 2025, 10, 261. https://doi.org/10.3390/biomimetics10050261
Kyriakidis IF, Kladovasilakis N, Gavriilopoulos M, Tzetzis D, Pechlivani EM, Tsongas K. Topologically Optimized Anthropomorphic Prosthetic Limb: Finite Element Analysis and Mechanical Evaluation Using Plantogram-Derived Foot Pressure Data. Biomimetics. 2025; 10(5):261. https://doi.org/10.3390/biomimetics10050261
Chicago/Turabian StyleKyriakidis, Ioannis Filippos, Nikolaos Kladovasilakis, Marios Gavriilopoulos, Dimitrios Tzetzis, Eleftheria Maria Pechlivani, and Konstantinos Tsongas. 2025. "Topologically Optimized Anthropomorphic Prosthetic Limb: Finite Element Analysis and Mechanical Evaluation Using Plantogram-Derived Foot Pressure Data" Biomimetics 10, no. 5: 261. https://doi.org/10.3390/biomimetics10050261
APA StyleKyriakidis, I. F., Kladovasilakis, N., Gavriilopoulos, M., Tzetzis, D., Pechlivani, E. M., & Tsongas, K. (2025). Topologically Optimized Anthropomorphic Prosthetic Limb: Finite Element Analysis and Mechanical Evaluation Using Plantogram-Derived Foot Pressure Data. Biomimetics, 10(5), 261. https://doi.org/10.3390/biomimetics10050261











