Fluid–Structure Interaction for Biomimetic Design of an Innovative Lightweight Turboexpander
Abstract
:1. Introduction
Biomimetic Design of Turboexpanders
2. Numerical Simulations
2.1. CFD Simulations
2.1.1. Geometry
2.1.2. Mesh for Fluid Analysis
2.1.3. CFD Model Setup
2.2. FEA Simulations
2.2.1. Mesh for Structural Analysis
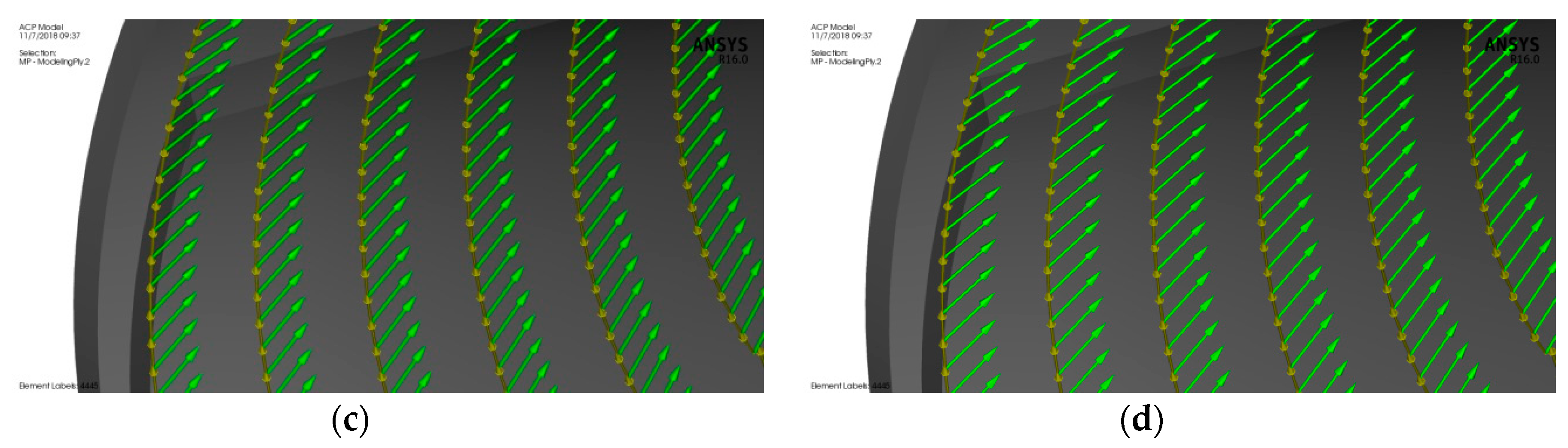
2.2.2. Turbine Composite Materials
2.2.3. Fluid–Structure Interaction Model Setup
3. Results and Discussion
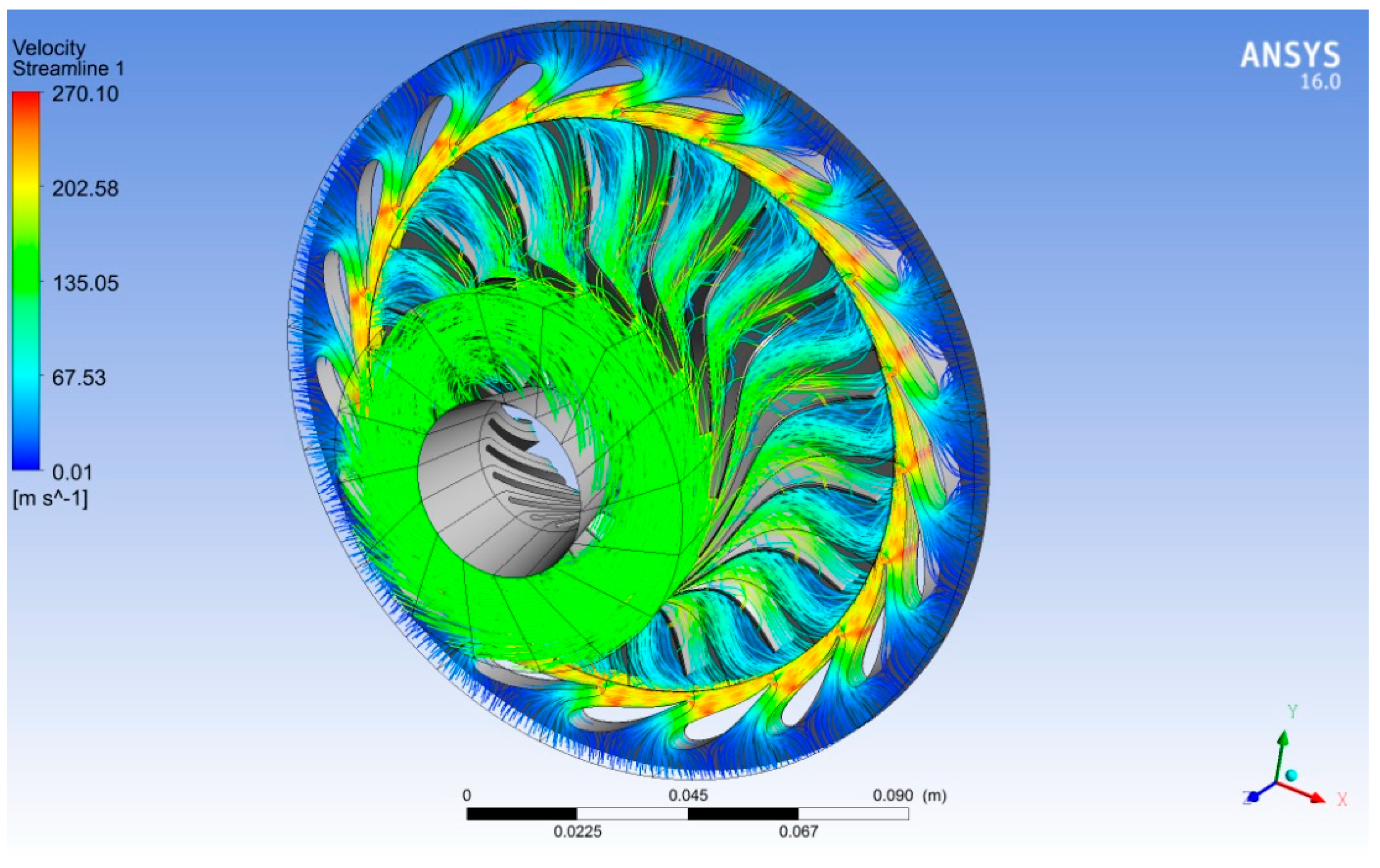
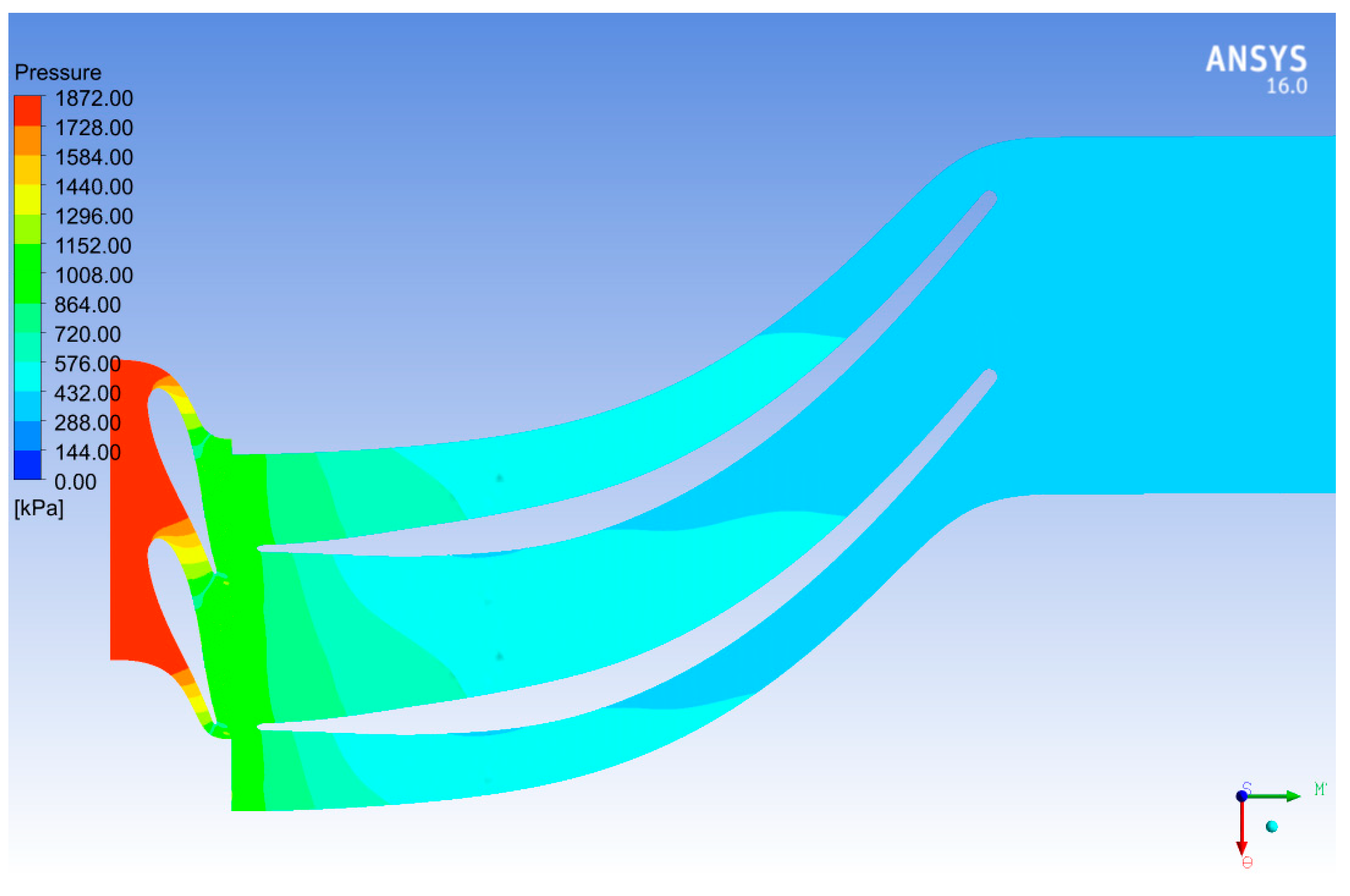
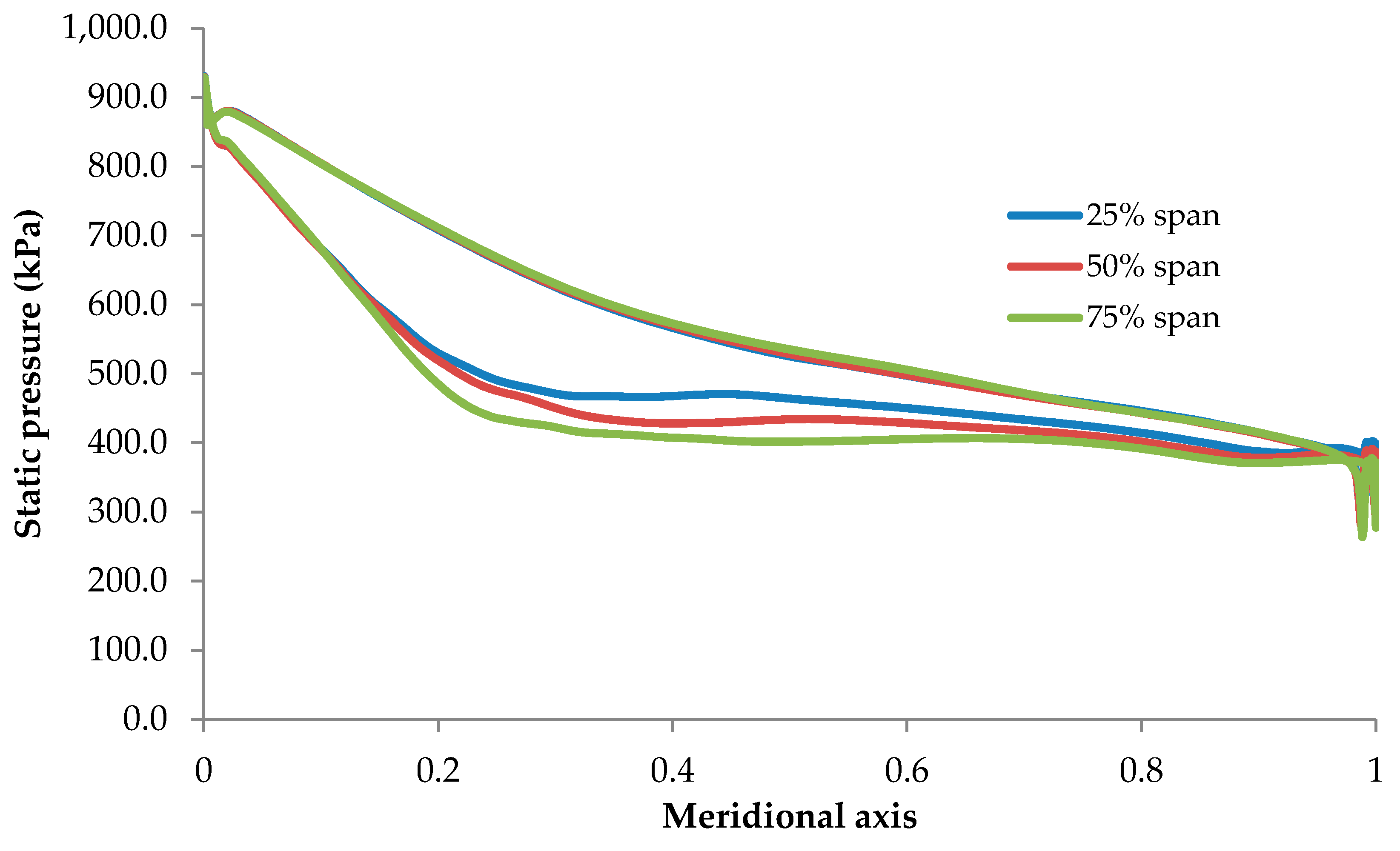
3.1. Validation of the CFD Model
3.2. Static Structural Results
3.3. Blade Weight
4. Conclusions
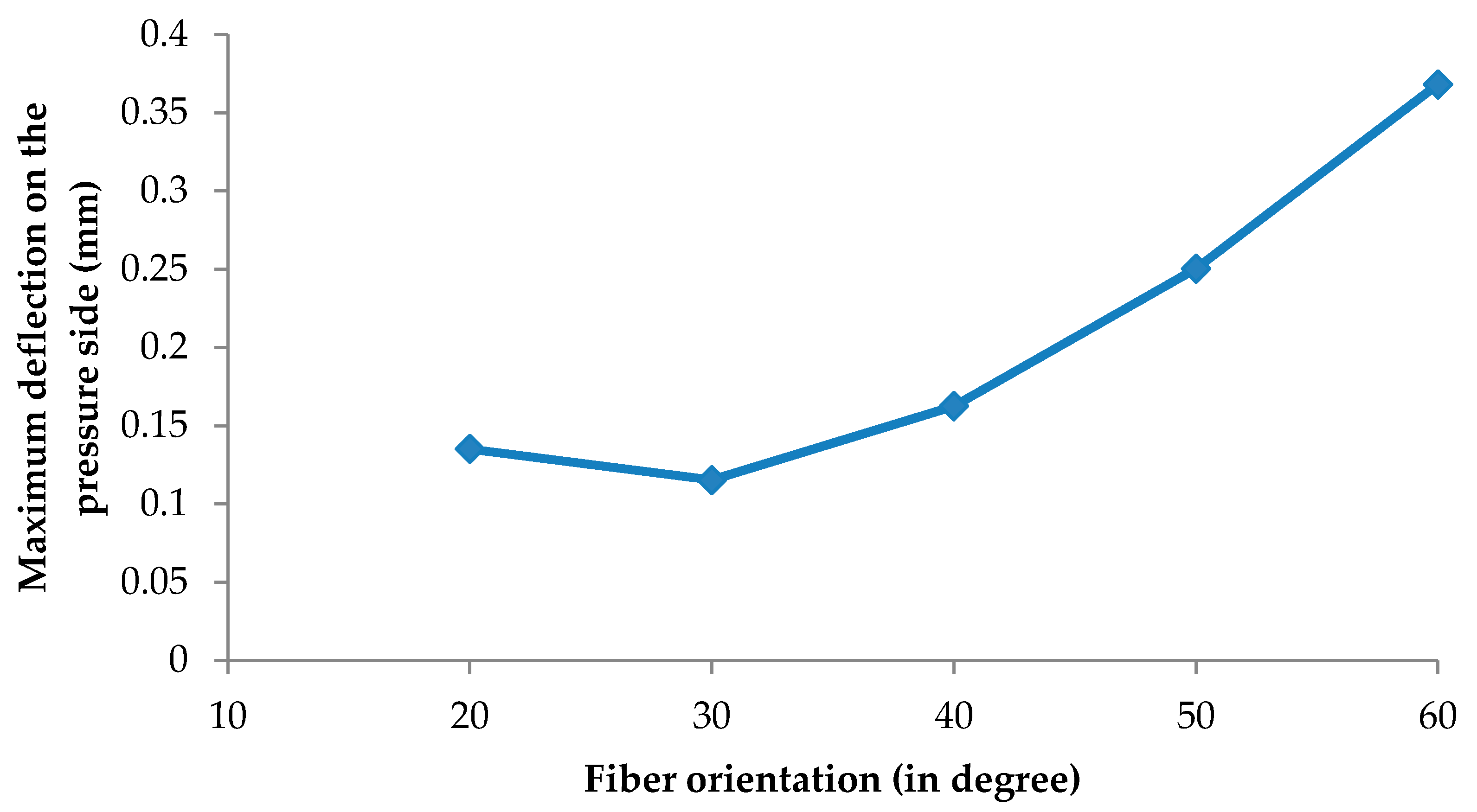
- The fiber orientation angle has a significant effect on the deformation of the rotor blades and the minimum deflection value was observed with 30° fiber orientation which is consistent with the barb angle at the tip leading of the flight feather. A little change in the fiber orientation has a greater effect on the deformation; the deformation was increased by 219.3% by using 60° fiber orientation compared with the deflection observed at 30° fiber orientation.
- The composite rotor blades weighed 0.0237 kg instead of 0.1234 kg, which means a weight reduction of 80%, and was proven to be structurally robust. This weight reduction can contribute to increasing the turbine rotational speed, which will increase the specific work without increasing the centrifugal stresses on the turbine.
Funding
Conflicts of Interest
References
- Lemmens, S. A Perspective on Costs and Cost Estimation Techniques for Organic Rankine Cycle Systems. In Proceedings of the 3rd International Seminar on ORC Power Systems (ASME ORC 2015), Brussels, Belgium, 12 October 2015; pp. 12–14. [Google Scholar]
- Schuster, A.; Karellas, S.; Kakaras, E.; Spliethoff, H. Energetic and economic investigation of organic Rankine cycle applications. Appl. Therm. Eng. 2009, 29, 1809–1817. [Google Scholar] [CrossRef]
- Jumel, S.; Feidt, M.; Kheiri, A. Working Fluid Selection and Performance Comparison of Subcritical and Supercritical Organic Rankine Cycle (ORC) for Low-Temperature Waste Heat Recovery. In Proceedings of the ECEEE Summer Study on Energy Efficiency in Industry, Arnhem, The Netherlands, 11–14 September 2012; pp. 559–569. [Google Scholar]
- Gao, H.; Liu, C.; He, C.; Xu, X.; Wu, S.; Li, Y. Performance analysis and working fluid selection of a supercritical organic Rankine cycle for low grade waste heat recovery. Energies 2012, 5, 3233–3247. [Google Scholar] [CrossRef]
- Chen, H.; Goswami, D.Y.; Stefanakos, E.K. A review of thermodynamic cycles and working fluids for the conversion of low-grade heat. Renew. Sustain. Energy Rev. 2010, 14, 3059–3067. [Google Scholar] [CrossRef]
- Bao, J.; Zhao, L. A review of working fluid and expander selections for organic Rankine cycle. Renew. Sustain. Energy Rev. 2013, 24, 325–342. [Google Scholar] [CrossRef]
- Darvish, K.; Ehyaei, M.A.; Atabi, F.; Rosen, M.A. Selection of optimum working fluid for organic Rankine cycles by exergy and exergy-economic analyses. Sustainability 2015, 11, 15362–15383. [Google Scholar] [CrossRef]
- Sauret, E.; Rowlands, A.S. Candidate radial-inflow turbines and high-density working fluids for geothermal power systems. Energy 2011, 36, 4460–4467. [Google Scholar] [CrossRef]
- Qiu, G.; Liu, H.; Riffat, S. Expanders for micro-CHP systems with organic Rankine cycle. Appl. Therm. Eng. 2011, 31, 3301–3307. [Google Scholar] [CrossRef]
- Fiaschi, D.; Manfrida, G.; Maraschiello, F. Thermo-fluid dynamics preliminary design of turbo-expanders for ORC cycles. Appl. Energy 2012, 97, 601–608. [Google Scholar] [CrossRef]
- Sauret, E.; Gu, Y. Three-dimensional off-design numerical analysis of an organic Rankine cycle radial-inflow turbine. Appl. Energy 2014, 135, 202–211. [Google Scholar] [CrossRef]
- Pennycuick, C.J. Modelling the Flying Bird, 1st ed.; Academic Press: Burlington, MA, USA, 2008. [Google Scholar]
- Feo, T.J.; Field, D.J.; Prum, R.O. Barb geometry of asymmetrical feathers reveals a transitional morphology in the evolution of avian flight. Proc. R. Soc. B 2015, 282, 20142864. [Google Scholar] [CrossRef] [PubMed]
- Ennos, A.; Hickson, J.; Roberts, A.N.N.A. Functional morphology of the vanes of the flight feathers of the pigeon Columba livia. J. Exp. Biol. 1995, 198, 1219–1228. [Google Scholar] [PubMed]
- Jones, A.C. Design and Test of a Small, High Pressure Ratio Radial Turbine. In Proceedings of the ASME International Gas Turbine and Aeroengine Congress and Exposition, The Hague, The Netherlands, 13–16 June 1994. [Google Scholar]
- Sauret, E. Open Design of High Pressure ratio radial-inflow Turbine for Academic Validation. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Houston, TX, USA, 9–15 November 2012; pp. 3183–3197. [Google Scholar]
- Peng, D.Y.; Robinson, D.B. A new two-constant equation of state. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Dowell, E.H. A Modern Course in Aeroelasticity, 5th ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2015. [Google Scholar]
- Dixon, S.L.; Hall, C. Fluid Mechanics and Thermodynamics of Turbomachinery; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]

















| Cases | Inlet Turbine Pressure (kPa) | Inlet Turbine Temperature (K) | Outlet Turbine Pressure (kPa) | Rotational Turbine Speed (RPM) |
|---|---|---|---|---|
| Air | 413.6 | 477.6 | 72.4 | 71700 |
| R600a | 1872 | 370 | 395 | 40219 |
| Material | Density (kg/m3) | Ex (MPa) | Ey = Ez (MPa) | Gyz (MPa) | Gxy = Gxz (MPa) | Xt (MPa) | Yt = Zt (MPa) | νxy = νxz | νyz |
|---|---|---|---|---|---|---|---|---|---|
| Epoxy carbon UD prepreg | 1490 | 121000 | 8600 | 3100 | 4700 | 2231 | 29 | 0.27 | 0.4 |
| Stainless steel | 7750 | 193000 | 193000 | 73664 | 73664 | 207 | 207 | 0.31 | 0.31 |
| Case | Mass Flow Tate (kg/s) | Total-to-Static Efficiency (%) | ||
|---|---|---|---|---|
| CFD | Error (%) | CFD | Error (%) | |
| Jones [15] | 0.339 | 2.7 | 87.6 | 1.4 |
| Case | Maximum von Mises Stress (Mpa) | Maximum Deflection on the Presure Side (mm) | Percentage of Deflection from 30° Fiber Orientation (%) |
|---|---|---|---|
| Stainless steel | 1277 | 0.0045 | −96.09 |
| 20° fiber orientation | 2486.3 | 0.1351 | 17.17 |
| 30° fiber orientation | 2387.9 | 0.1153 | - |
| 40° fiber orientation | 2327.8 | 0.1625 | 40.93 |
| 50° fiber orientation | 2280.6 | 0.2504 | 117.1 |
| 60° fiber orientation | 2238.2 | 0.3682 | 219.3 |
| Case | Weight (kg) | Percentage in Reduction of Blades Weight Using Composite Material (%) |
|---|---|---|
| Stainless teel rotor blades | 0.1234 | - |
| Composite rotor blades | 0.0237 | 80.0 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gad-el-Hak, I. Fluid–Structure Interaction for Biomimetic Design of an Innovative Lightweight Turboexpander. Biomimetics 2019, 4, 27. https://doi.org/10.3390/biomimetics4010027
Gad-el-Hak I. Fluid–Structure Interaction for Biomimetic Design of an Innovative Lightweight Turboexpander. Biomimetics. 2019; 4(1):27. https://doi.org/10.3390/biomimetics4010027
Chicago/Turabian StyleGad-el-Hak, Ibrahim. 2019. "Fluid–Structure Interaction for Biomimetic Design of an Innovative Lightweight Turboexpander" Biomimetics 4, no. 1: 27. https://doi.org/10.3390/biomimetics4010027
APA StyleGad-el-Hak, I. (2019). Fluid–Structure Interaction for Biomimetic Design of an Innovative Lightweight Turboexpander. Biomimetics, 4(1), 27. https://doi.org/10.3390/biomimetics4010027




