Implementation of Deep Deterministic Policy Gradients for Controlling Dynamic Bipedal Walking
Abstract
:1. Introduction
2. Methods
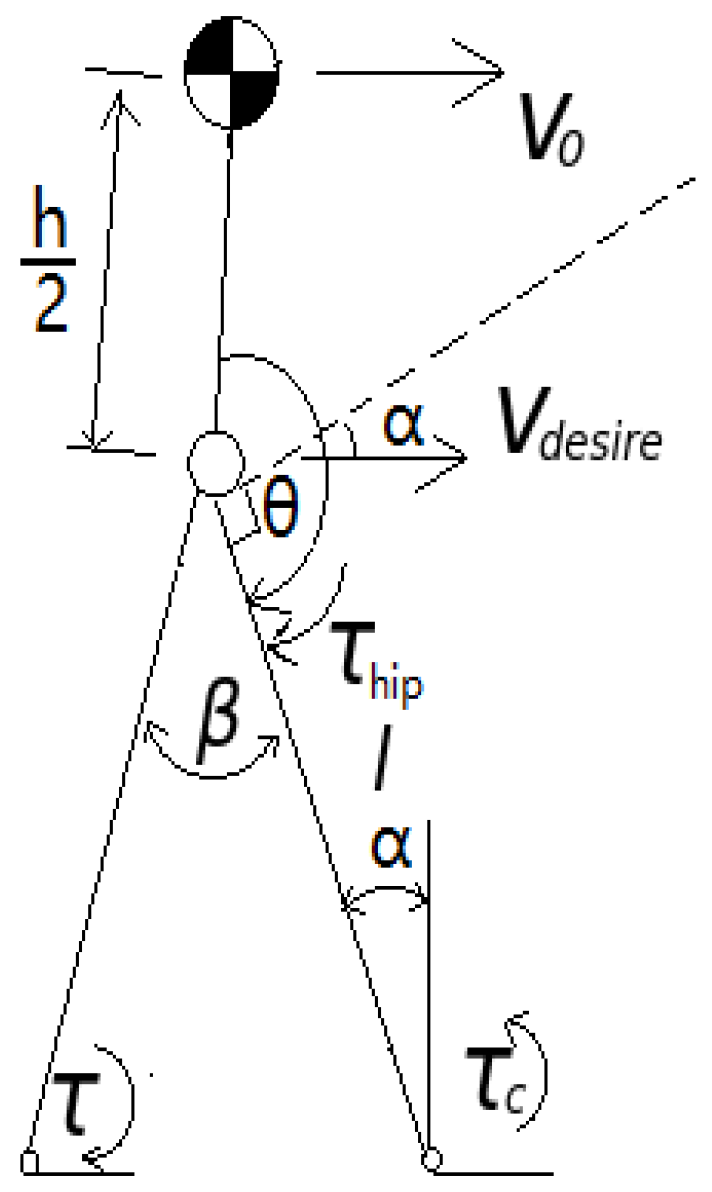
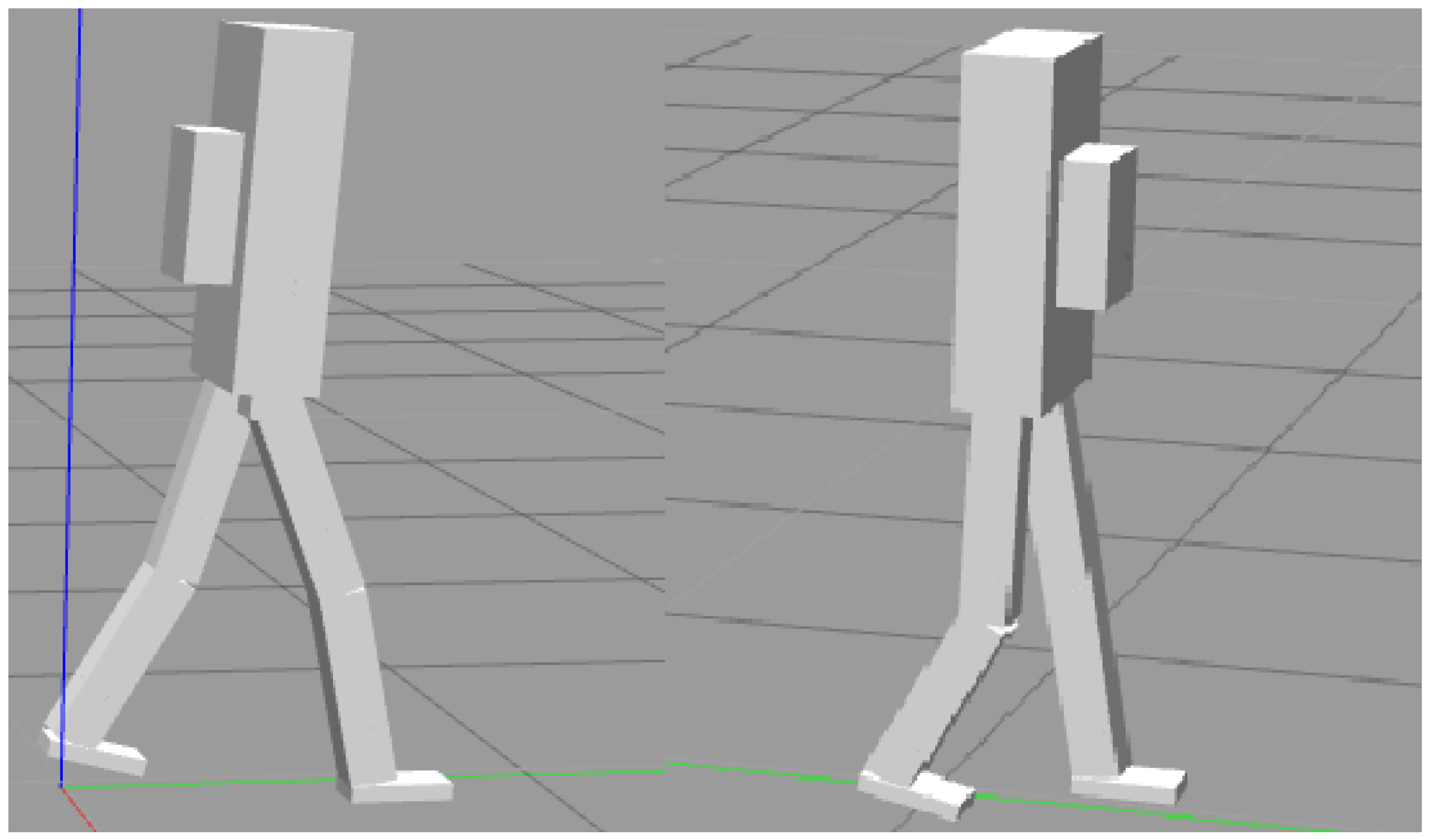
2.1. Biped Model
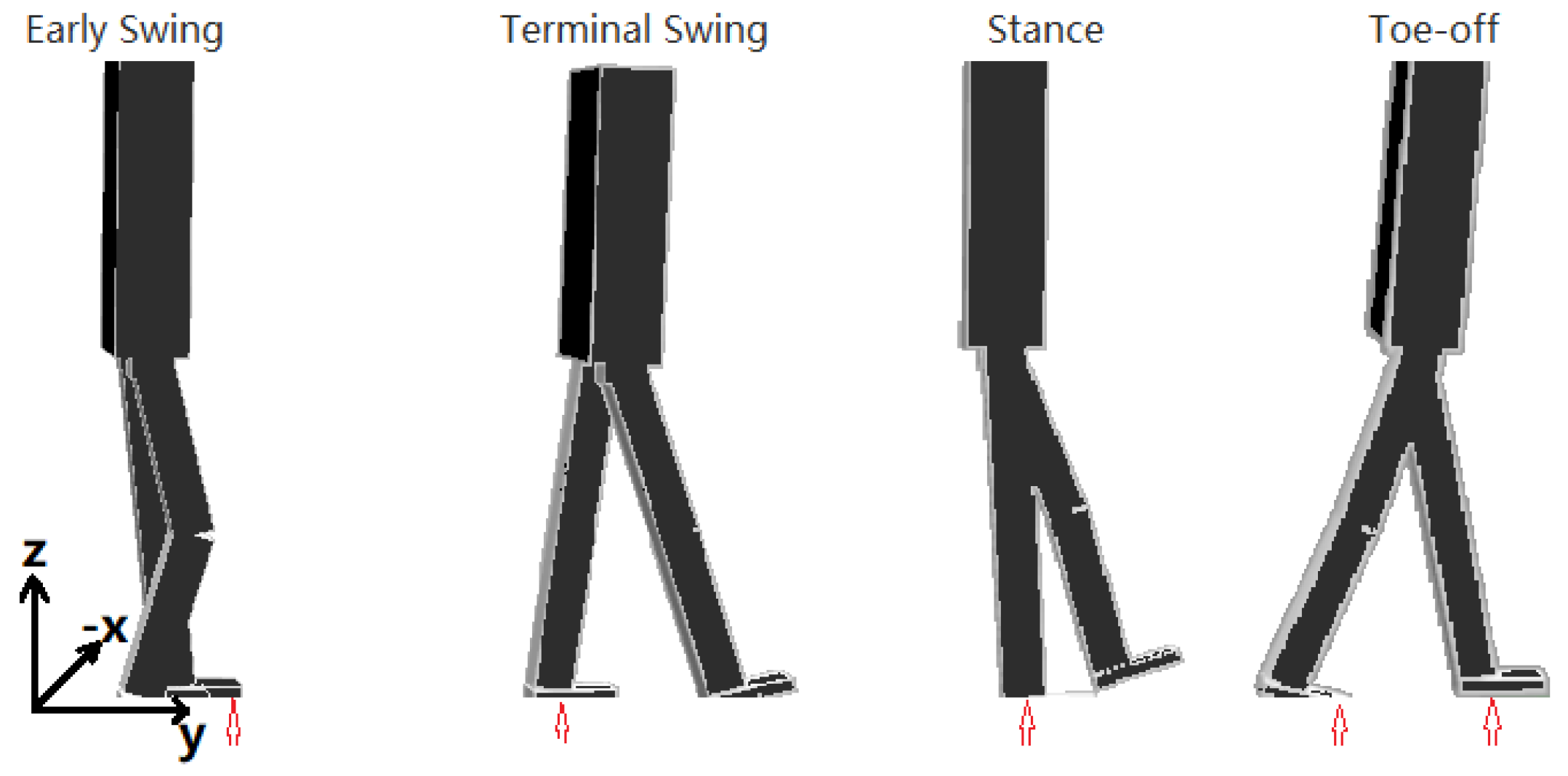
2.2. Target Locomotion
2.2.1. Early Swing Phase
2.2.2. Terminal Swing Phase
2.2.3. Stance Phase
2.2.4. Toe-Off Phase
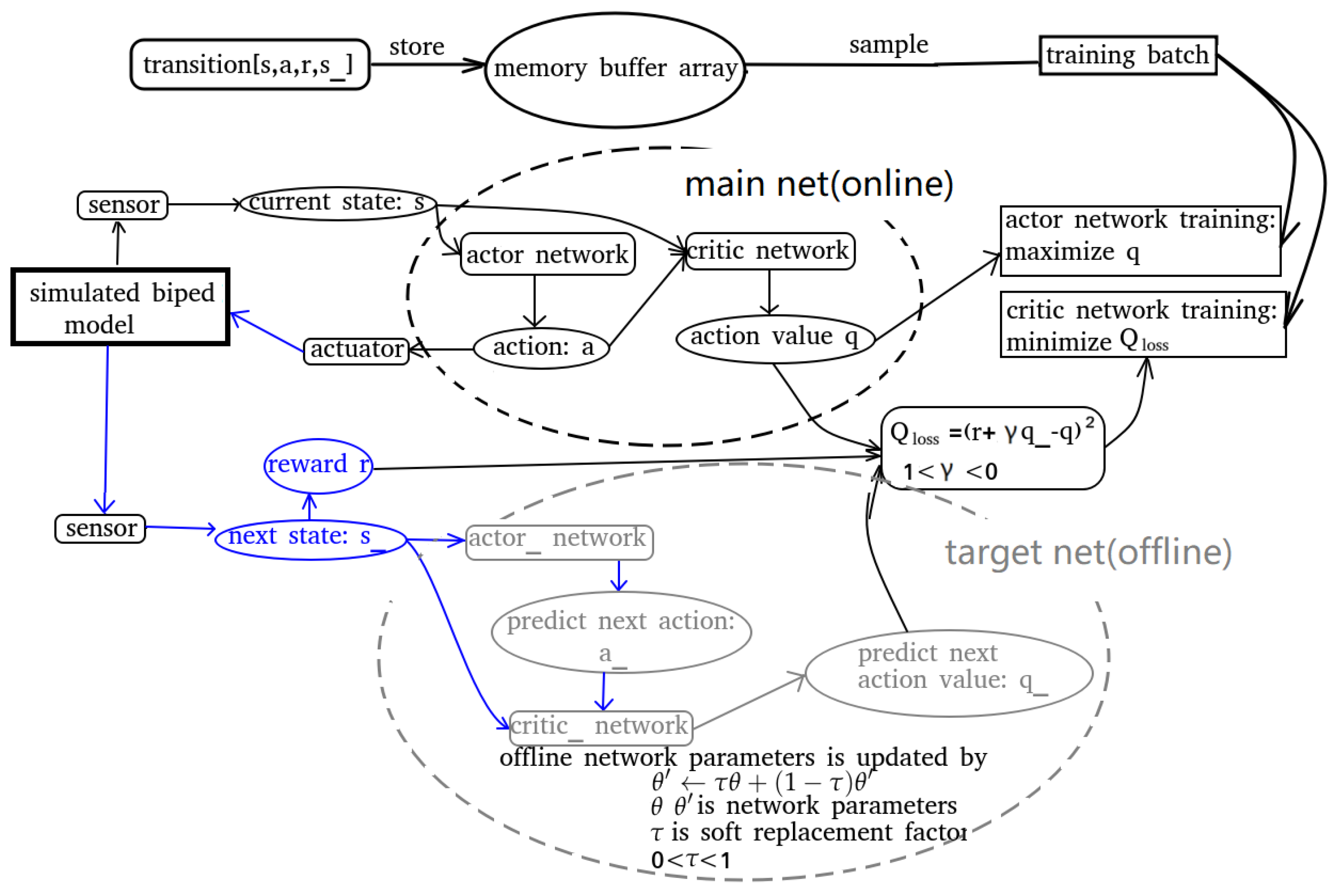
2.3. Control
2.3.1. Controller Architecture
2.3.2. Deep Deterministic Policy Gradient
2.3.3. Stance Controller
2.3.4. Ankle Torque Control
2.4. Simulation and Testing
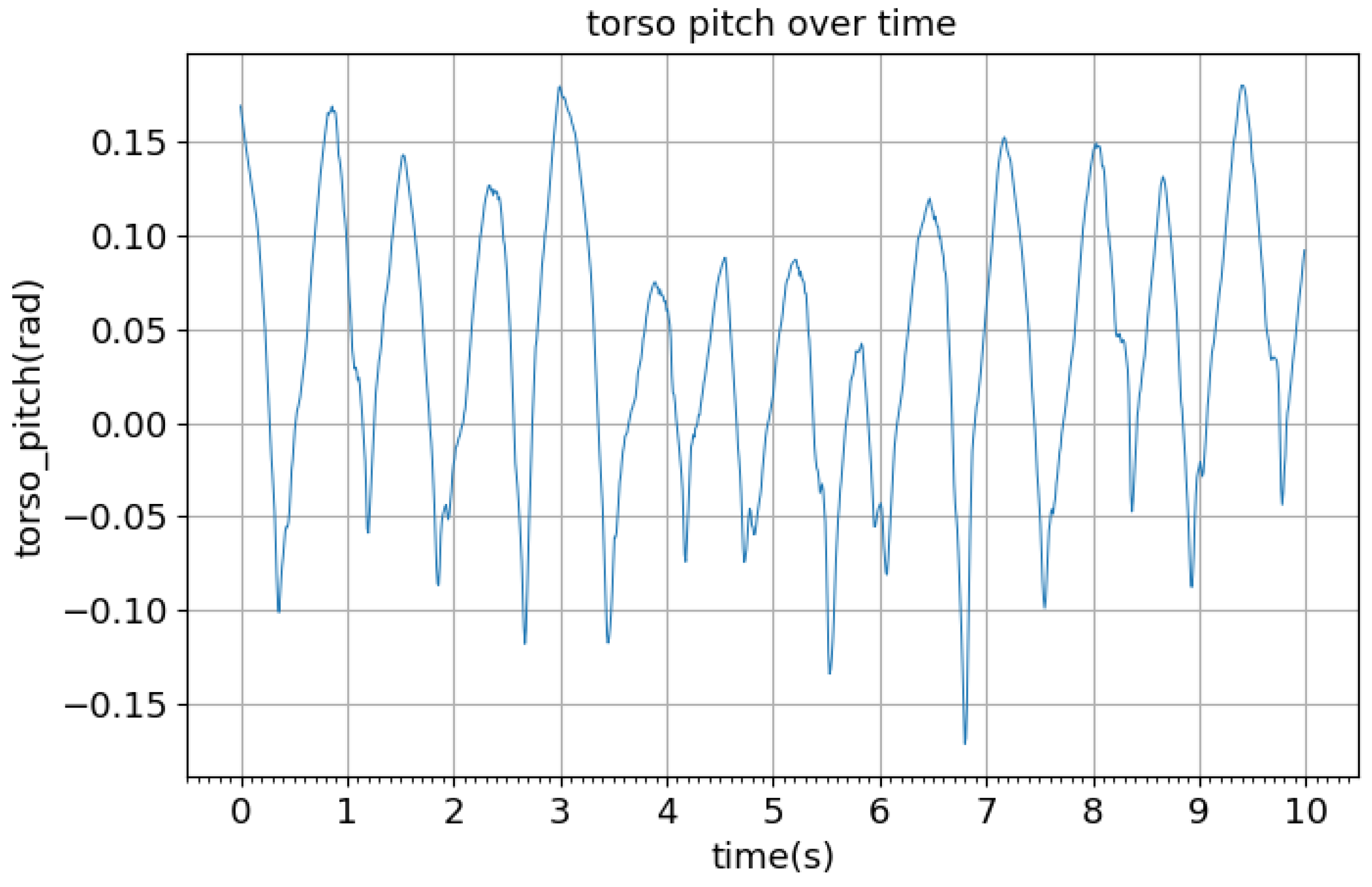
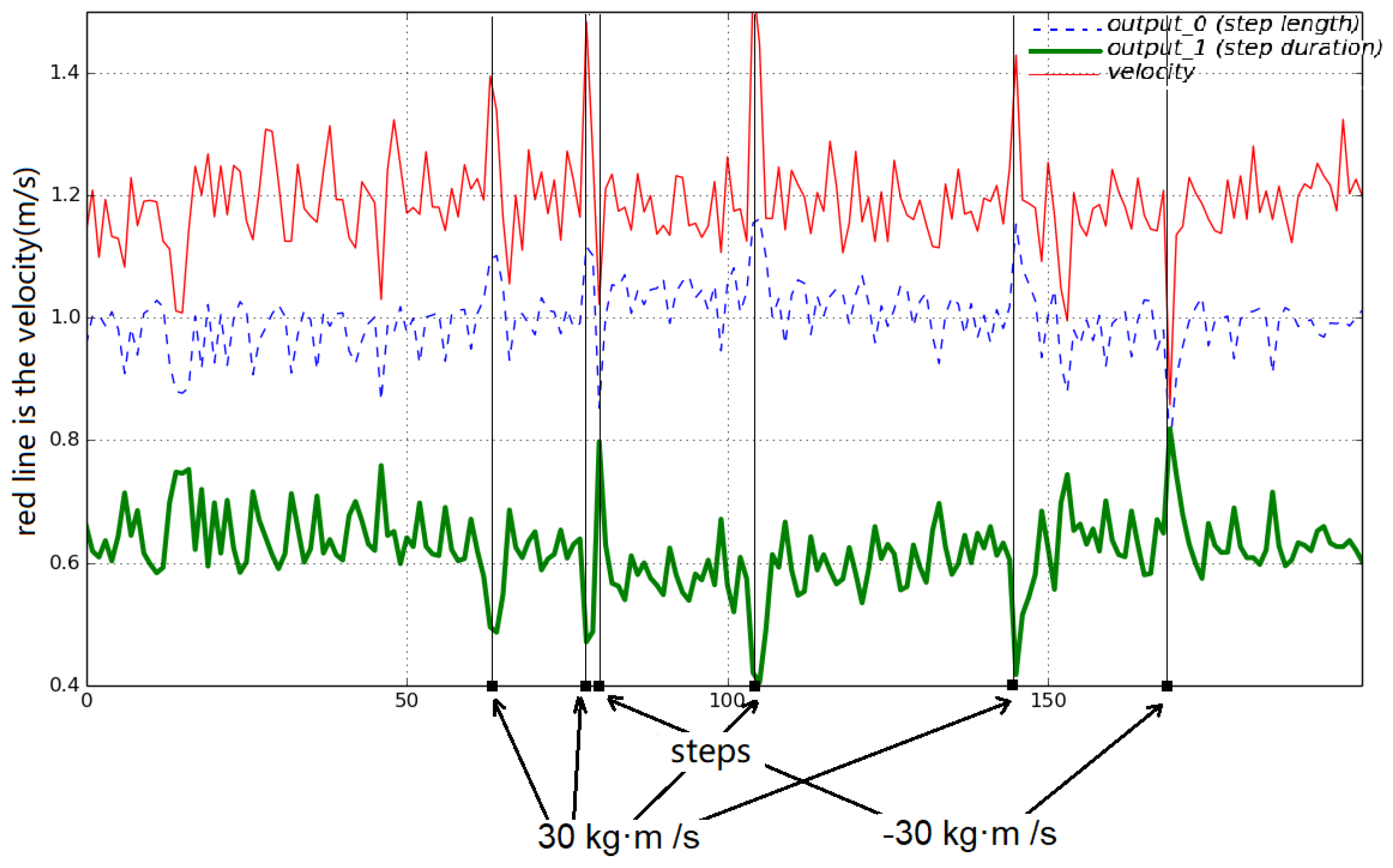
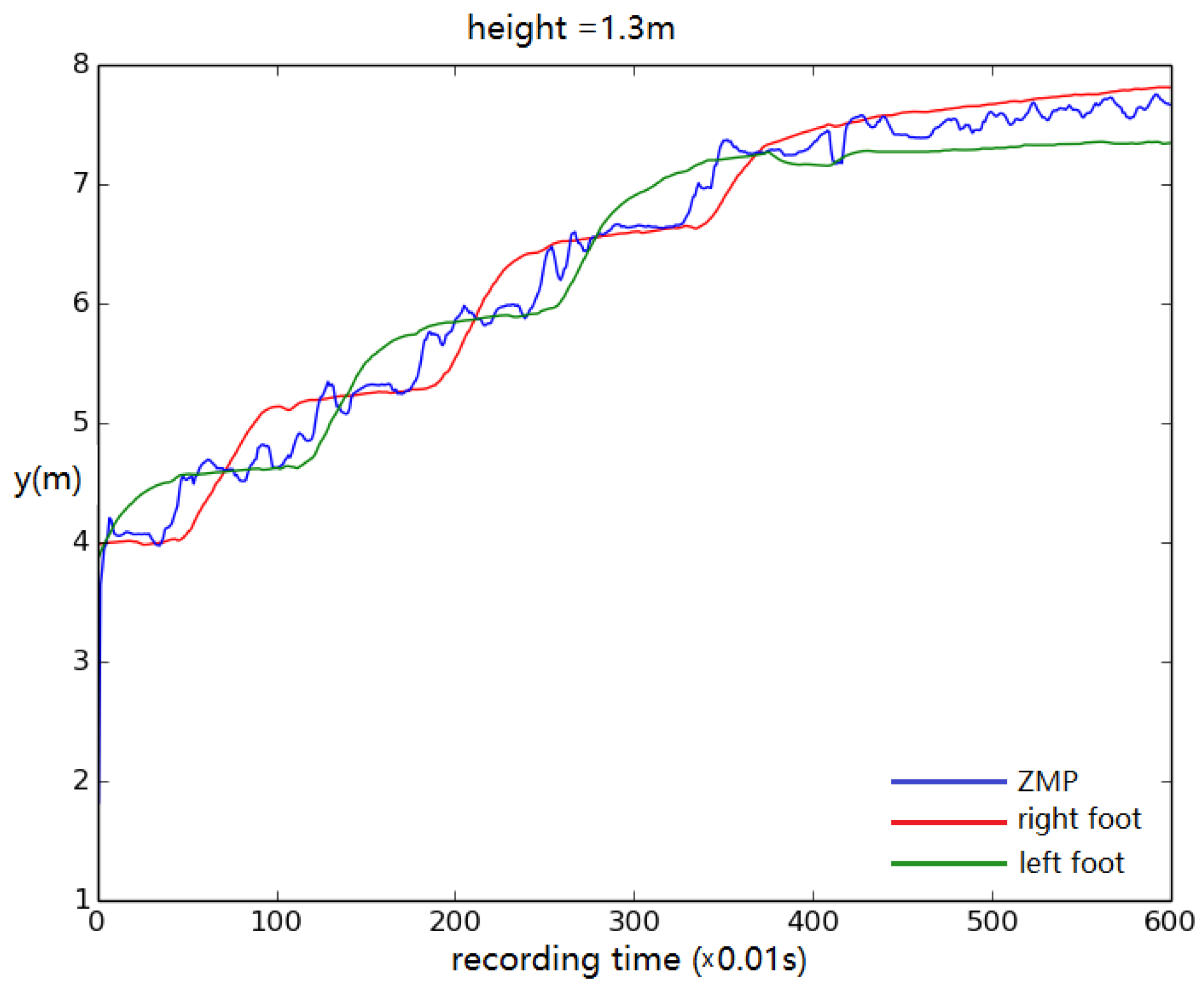
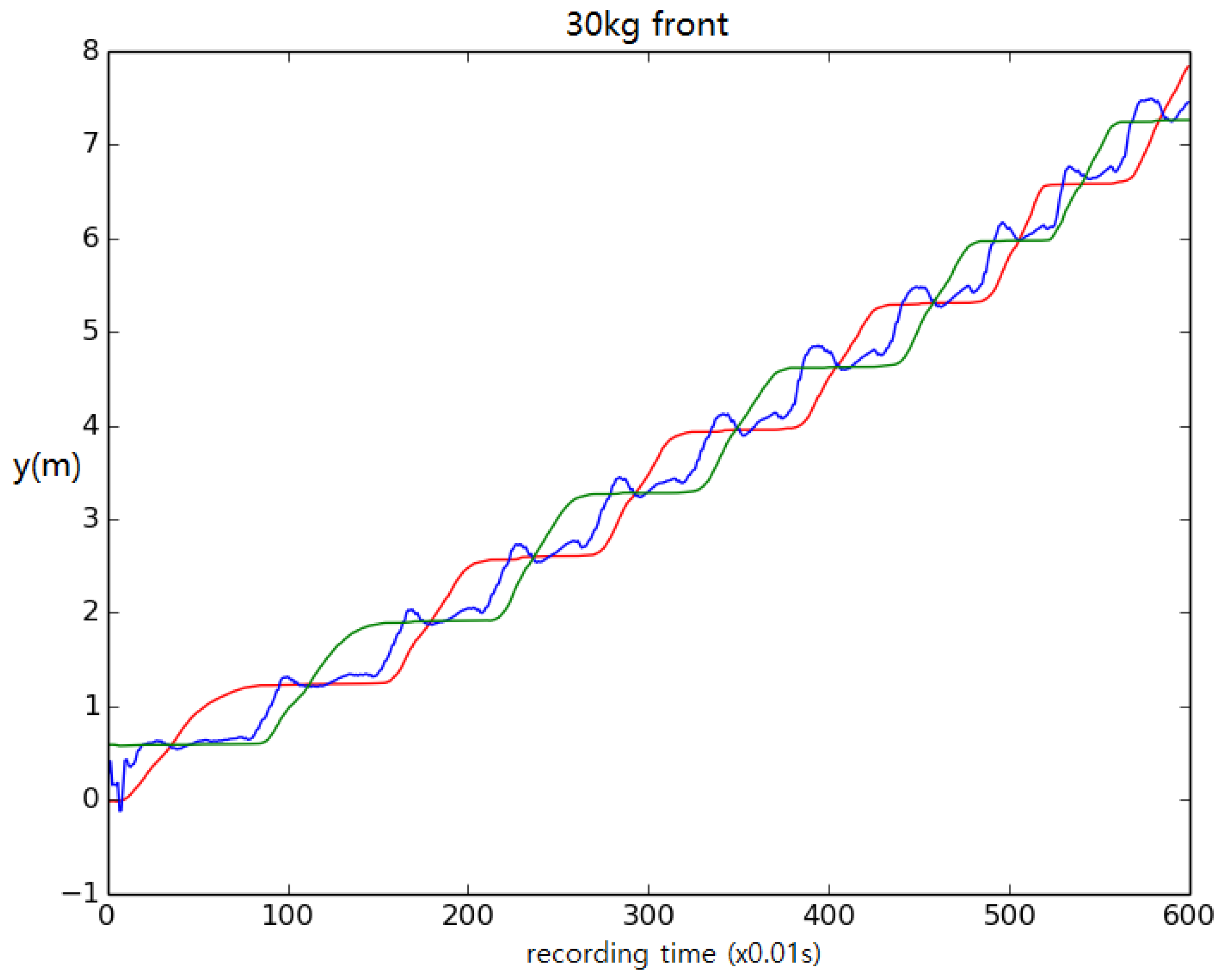
3. Results and Discussion
Robustness to Different Body Sizes and Payloads on the Torso
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Lonsberry, A.G.; Lonsberry, A.J.; Quinn, R.D. Deep dynamic programming: Optimal control with continuous model learning of a nonlinear muscle actuated arm. In Conference on Biomimetic and Biohybrid Systems; Springer: Berlin, Germany, 2017; pp. 255–266. [Google Scholar]
- Chang, S.R.; Nandor, M.J.; Li, L.; Kobetic, R.; Foglyano, K.M.; Schnellenberger, J.R.; Audu, M.L.; Pinault, G.; Quinn, R.D.; Triolo, R.J. A muscle-driven approach to restore stepping with an exoskeleton for individuals with paraplegia. J. Neuroeng. Rehabil. 2017, 14, 48. [Google Scholar] [CrossRef] [PubMed]
- Farris, R.J.; Quintero, H.A.; Goldfarb, M. Preliminary evaluation of a powered lower limb orthosis to aid walking in paraplegic individuals. IEEE Trans. Neural Syst. Rehabil. Eng. 2011, 19, 652–659. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Whitman, E.C.; Stilman, M. Whole-body trajectory optimization for humanoid falling. In Proceedings of the IEEE 2012 American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012; pp. 4837–4842. [Google Scholar]
- Luo, R.C.; Chen, C.H.; Pu, Y.H.; Chang, J.R. Towards active actuated natural walking humanoid robot legs. In Proceedings of the 2011 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Budapest, Hungary, 3–7 July 2011; pp. 886–891. [Google Scholar]
- Yamane, K. Systematic derivation of simplified dynamics for humanoid robots. In Proceedings of the IEEE 12th IEEE-RAS International Conference on Humanoid Robots (Humanoids 2012), Osaka, Japan, 29 November–1 December 2012; pp. 28–35. [Google Scholar]
- Li, T.; Rai, A.; Geyer, H.; Atkeson, C.G. Using deep reinforcement learning to learn high-level policies on the ATRIAS biped. arXiv, 2018; arXiv:1809.10811. [Google Scholar]
- Kuindersma, S.; Deits, R.; Fallon, M.; Valenzuela, A.; Dai, H.; Permenter, F.; Koolen, T.; Marion, P.; Tedrake, R. Optimization-based locomotion planning, estimation, and control design for the atlas humanoid robot. Auton. Robots 2016, 40, 429–455. [Google Scholar] [CrossRef]
- Kim, J.H.; Oh, J.H. Realization of dynamic walking for the humanoid robot platform KHR-1. Adv. Robot. 2004, 18, 749–768. [Google Scholar] [CrossRef]
- Yokoi, K.; Kanehiro, F.; Kaneko, K.; Fujiwara, K.; Kajita, S.; Hirukawa, H. Experimental study of biped locomotion of humanoid robot hrp-1s. In Experimental Robotics VIII; Springer: Berlin, Germany, 2003; pp. 75–84. [Google Scholar]
- Townsend, M.A. Biped gait stabilization via foot placement. J. Biomech. 1985, 18, 21–38. [Google Scholar] [CrossRef]
- Urata, J.; Nshiwaki, K.; Nakanishi, Y.; Okada, K.; Kagami, S.; Inaba, M. Online decision of foot placement using singular LQ preview regulation. In Proceedings of the 2011 11th IEEE-RAS International Conference on Humanoid Robots, Bled, Slovenia, 26–28 October 2011; pp. 13–18. [Google Scholar]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Sepulveda, F.; Wells, D.M.; Vaughan, C.L. A neural network representation of electromyography and joint dynamics in human gait. J. Biomech. 1993, 26, 101–109. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing atari with deep reinforcement learning. arXiv, 2013; arXiv:1312.5602. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Introduction to Reinforcement Learning; MIT Press Cambridge: Cambridge, MA, USA, 1998; Volume 135. [Google Scholar]
- Baird, L.C. Reinforcement learning in continuous time: Advantage updating. In Proceedings of the 1994 IEEE International Conference on Neural Networks (ICNN’94), Orlando, FL, USA, 28 June–2 July 1994; Volume 4, pp. 2448–2453. [Google Scholar]
- Silver, D.; Lever, G.; Heess, N.; Degris, T.; Wierstra, D.; Riedmiller, M. Deterministic policy gradient algorithms. In Proceedings of the International Conference on Machine Learning (ICML 2014), Beijing, China, 21–26 June 2014. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv, 2015; arXiv:1502.03167. [Google Scholar]
- Morimoto, J.; Doya, K. Acquisition of stand-up behavior by a real robot using hierarchical reinforcement learning. Robot. Auton. Syst. 2001, 36, 37–51. [Google Scholar] [CrossRef]
- Koenig, N.; Howard, A. Design and use paradigms for gazebo, an open-source multi-robot simulator. In Proceedings of the 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Sendai, Japan, 28 September–2 October 2004; Volume 3, pp. 2149–2154. [Google Scholar]
- Open Dynamics Engine. Available online: https://www.ode.org/ (accessed on 22 March 2019).
- Chandler, R.; Clauser, C.E.; McConville, J.T.; Reynolds, H.; Young, J.W. Investigation of Inertial Properties of the Human Body; Technical Report; Air Force Aerospace Medical Research Lab: Wright-Patterson Air Force Base, OH, USA, 1975. [Google Scholar]
- Hausdorff, J.M.; Peng, C.; Ladin, Z.; Wei, J.Y.; Goldberger, A.L. Is walking a random walk? Evidence for long-range correlations in stride interval of human gait. J. Appl. Physiol. 1995, 78, 349–358. [Google Scholar] [CrossRef] [PubMed]
- Song, S.; Geyer, H. Evaluation of a neuromechanical walking control model using disturbance experiments. Front. Comput. Neurosci. 2017, 11, 15. [Google Scholar] [CrossRef] [PubMed]
- Peng, X.B.; Berseth, G.; Van de Panne, M. Terrain-adaptive locomotion skills using deep reinforcement learning. ACM Trans. Graph. (TOG) 2016, 35, 81. [Google Scholar] [CrossRef]
- Vukobratović, M.; Borovac, B. Zero-moment point—Thirty five years of its life. Int. J. Humanoid Robot. 2004, 1, 157–173. [Google Scholar] [CrossRef]
- Bruno, S.; Oussama, K. Springer Handbook of Robotics; Springer: Berlin, Germany, 2008. [Google Scholar]
- Grewal, M.S. Kalman Filtering; Springer: Berlin, Germany, 2011. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Quigley, M.; Conley, K.; Gerkey, B.; Faust, J.; Foote, T.; Leibs, J.; Wheeler, R.; Ng, A.Y. ROS: An open-source robot operating system. In Proceedings of the ICRA Workshop on Open Source Software, Kobe, Japan, 12 May 2009; Volume 3, p. 5. [Google Scholar]
- Cashmore, M.; Fox, M.; Long, D.; Magazzeni, D.; Ridder, B.; Carrera, A.; Palomeras, N.; Hurtos, N.; Carreras, M. Rosplan: Planning in the robot operating system. In Proceedings of the Twenty-Fifth International Conference on Automated Planning and Scheduling, Jerusalem, Israel, 7–11 June 2015. [Google Scholar]












© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Lonsberry, A.G.; Nandor, M.J.; Audu, M.L.; Lonsberry, A.J.; Quinn, R.D. Implementation of Deep Deterministic Policy Gradients for Controlling Dynamic Bipedal Walking. Biomimetics 2019, 4, 28. https://doi.org/10.3390/biomimetics4010028
Liu C, Lonsberry AG, Nandor MJ, Audu ML, Lonsberry AJ, Quinn RD. Implementation of Deep Deterministic Policy Gradients for Controlling Dynamic Bipedal Walking. Biomimetics. 2019; 4(1):28. https://doi.org/10.3390/biomimetics4010028
Chicago/Turabian StyleLiu, Chujun, Andrew G. Lonsberry, Mark J. Nandor, Musa L. Audu, Alexander J. Lonsberry, and Roger D. Quinn. 2019. "Implementation of Deep Deterministic Policy Gradients for Controlling Dynamic Bipedal Walking" Biomimetics 4, no. 1: 28. https://doi.org/10.3390/biomimetics4010028
APA StyleLiu, C., Lonsberry, A. G., Nandor, M. J., Audu, M. L., Lonsberry, A. J., & Quinn, R. D. (2019). Implementation of Deep Deterministic Policy Gradients for Controlling Dynamic Bipedal Walking. Biomimetics, 4(1), 28. https://doi.org/10.3390/biomimetics4010028




