Design and Experimental Research of Knee Joint Prosthesis Based on Gait Acquisition Technology
Abstract
:1. Introduction
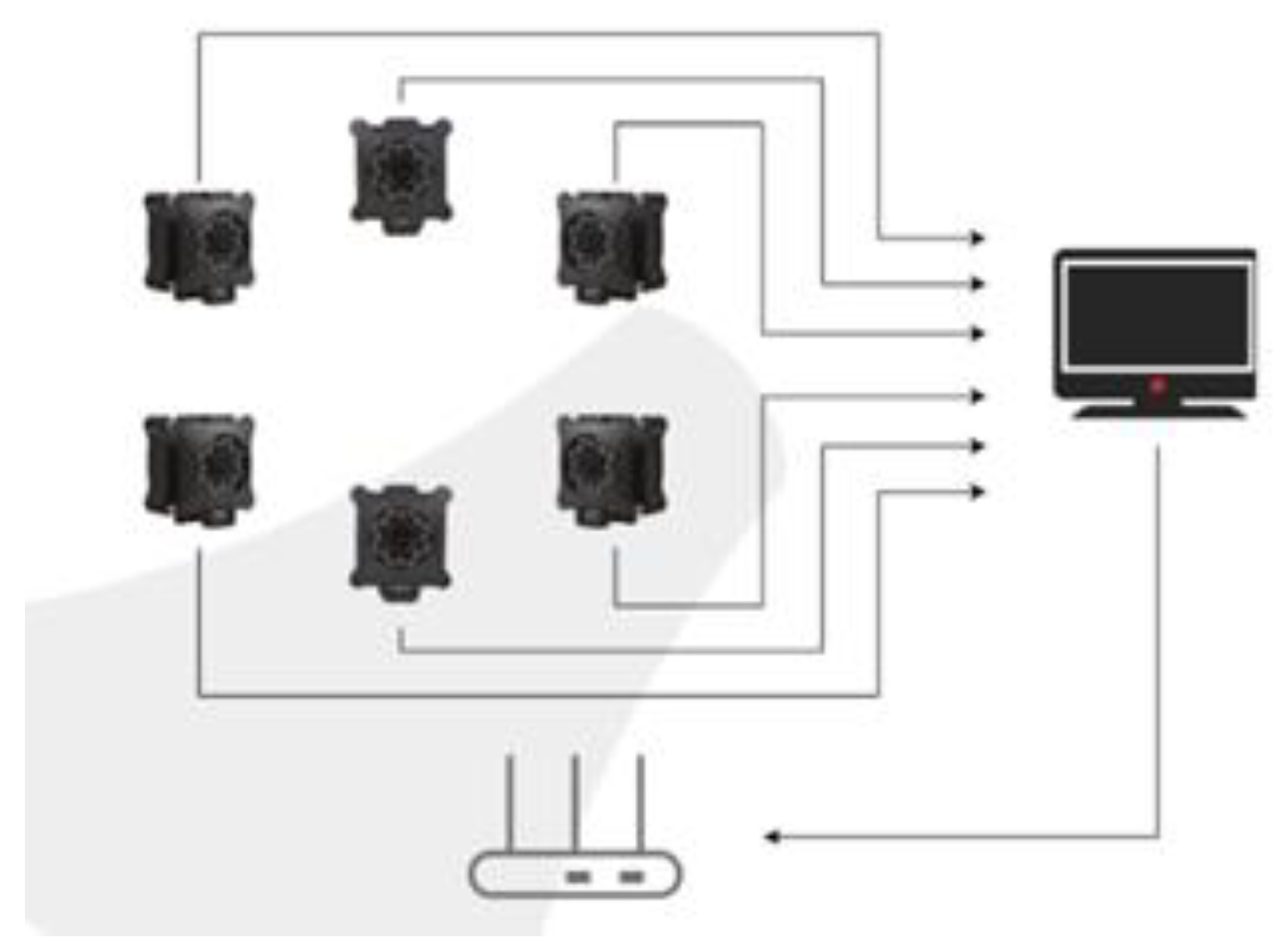
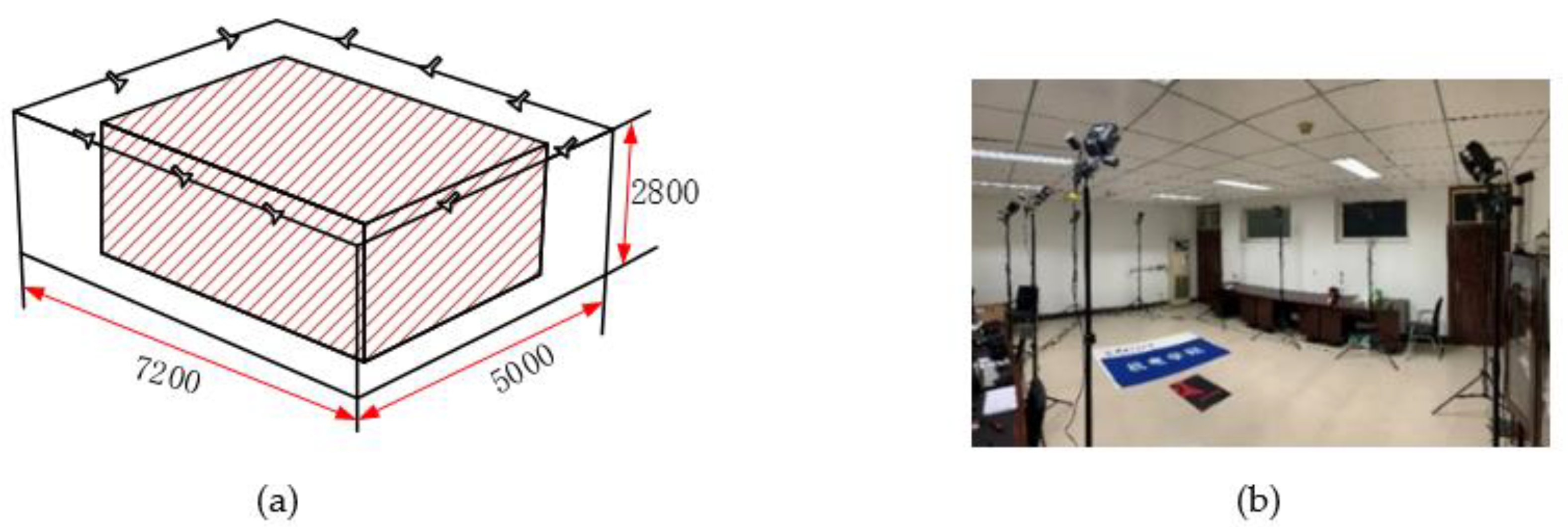
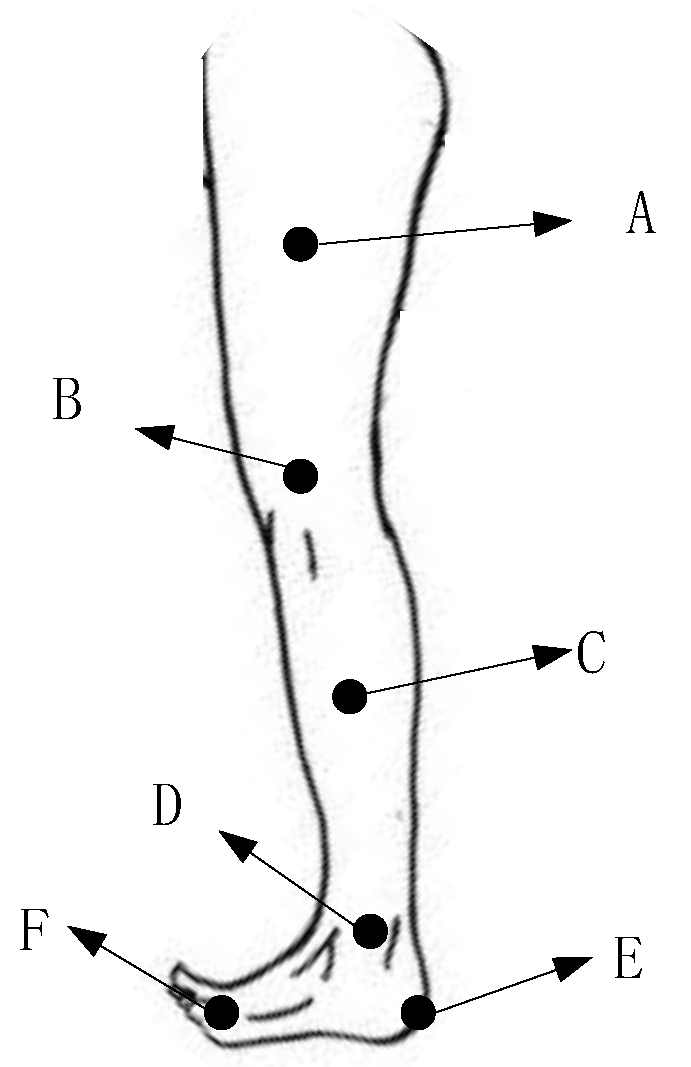
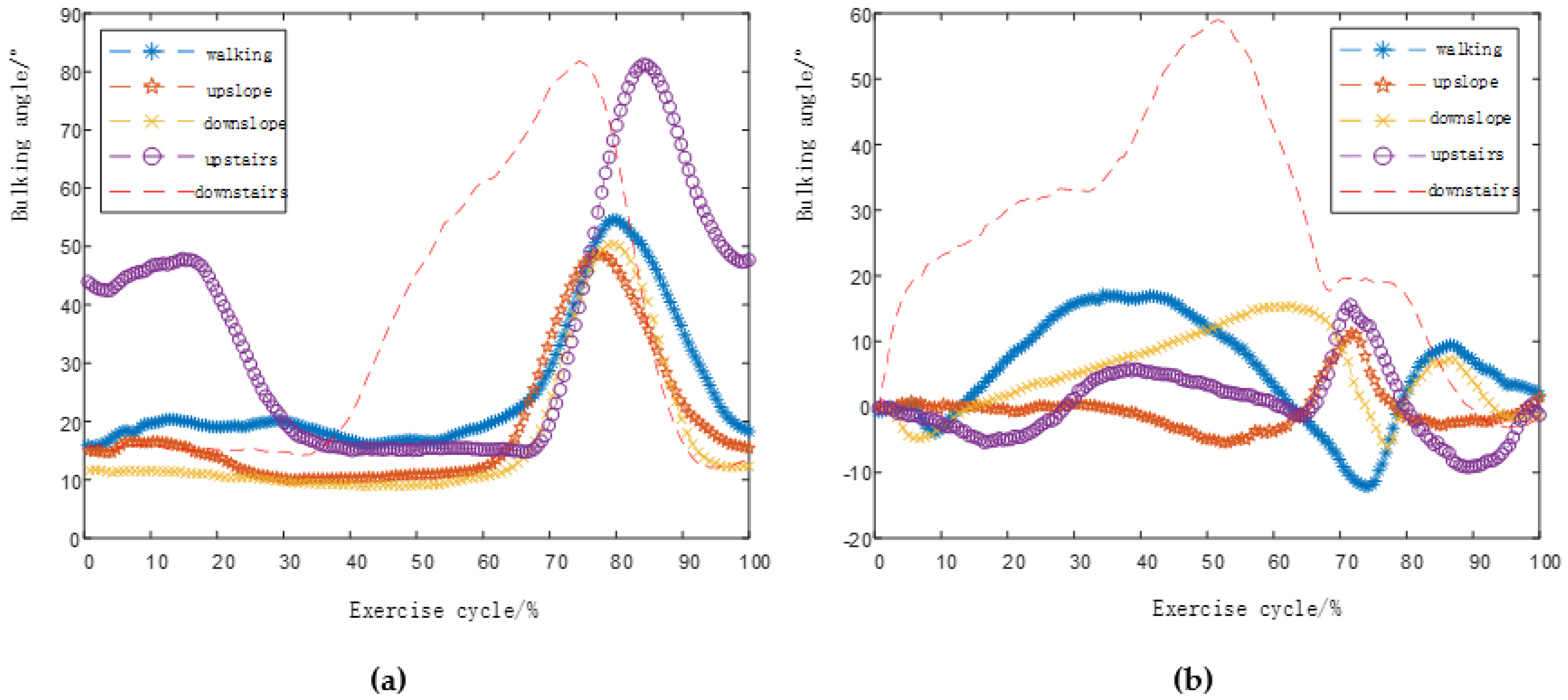
2. Data Collection and Characteristic Analysis of Human Lower Limb Movement
3. Mechanism Design and Optimization of Lower Limb Prostheses
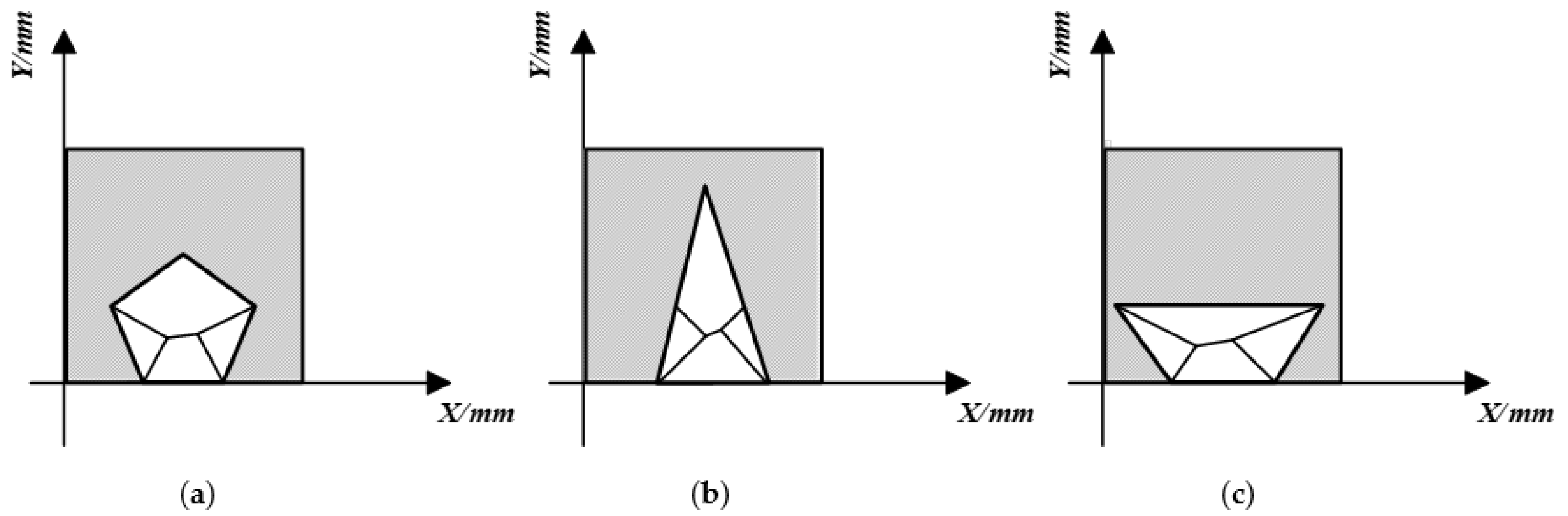
3.1. Mechanism Selection and Motion Analysis
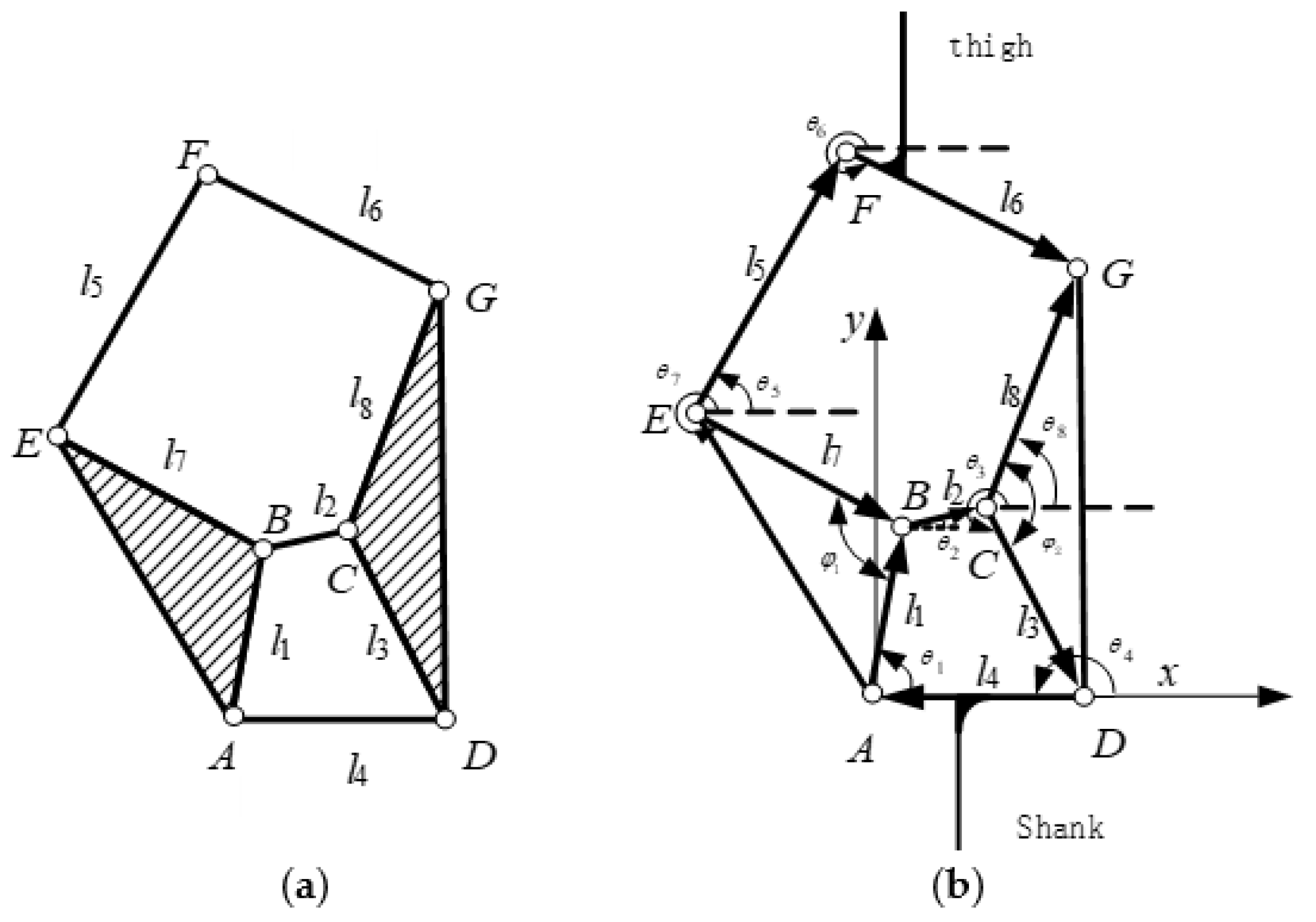
3.2. Optimal Design of Knee Joint Prosthesis with Six-Bar Mechanism
3.2.1. Vector Model of Six-Bar Knee Prosthetic Mechanism
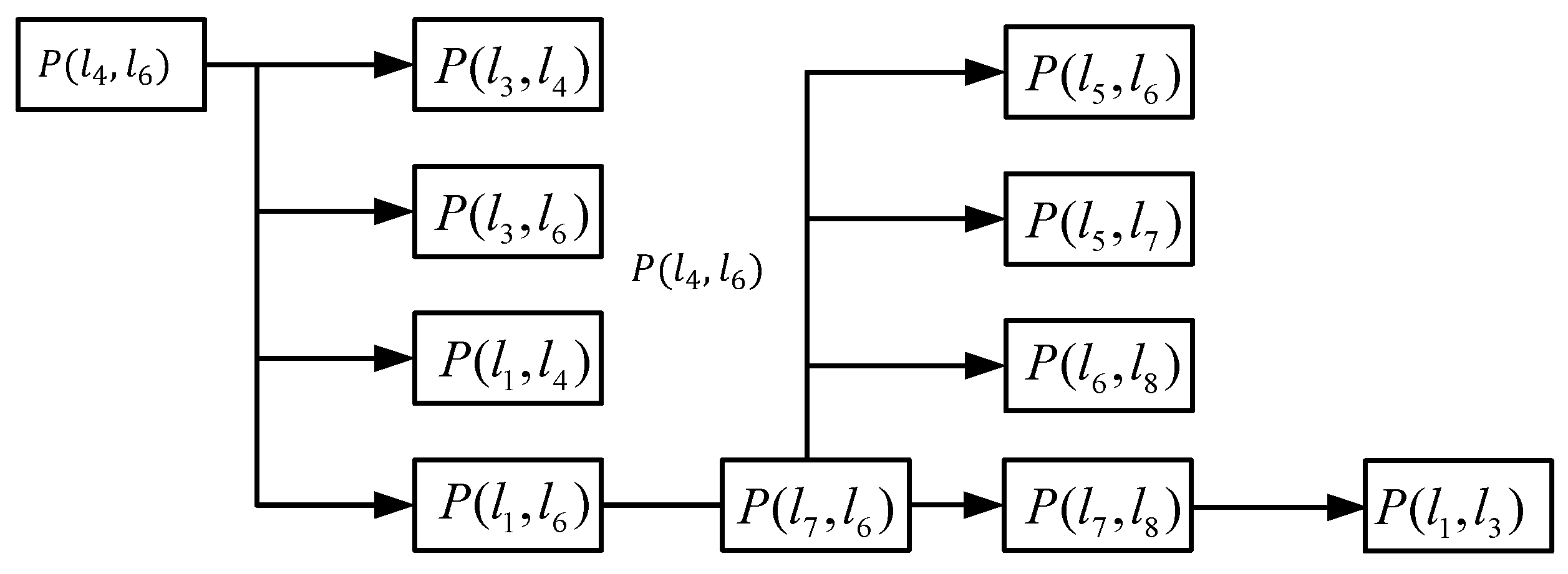
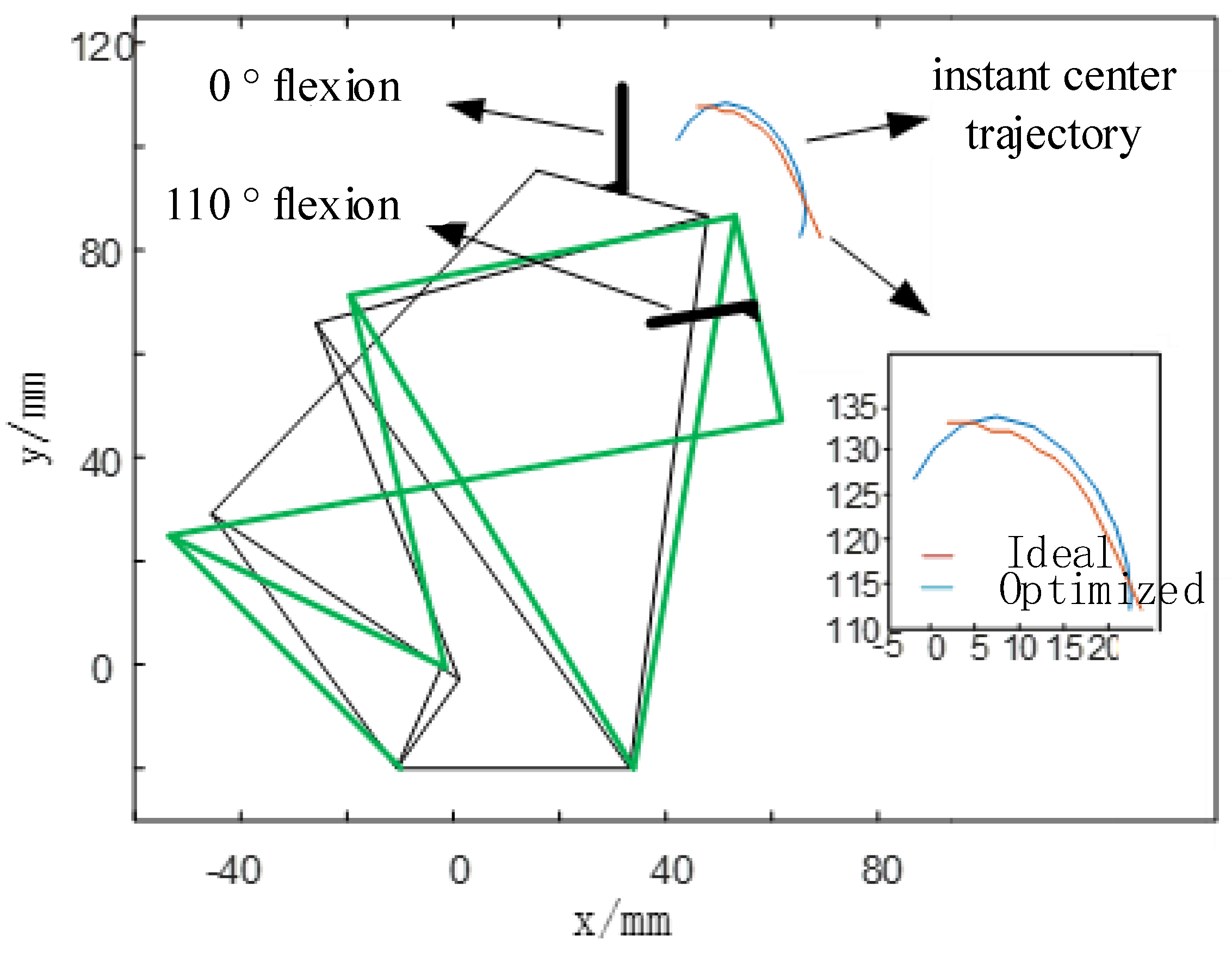
3.2.2. Analysis of the Instantaneous Center Trajectory of Six-Bar Prosthetic Knee Joint
3.3. Six-Bar Prosthetic Knee Joint Optimization Results and Motion Analysis
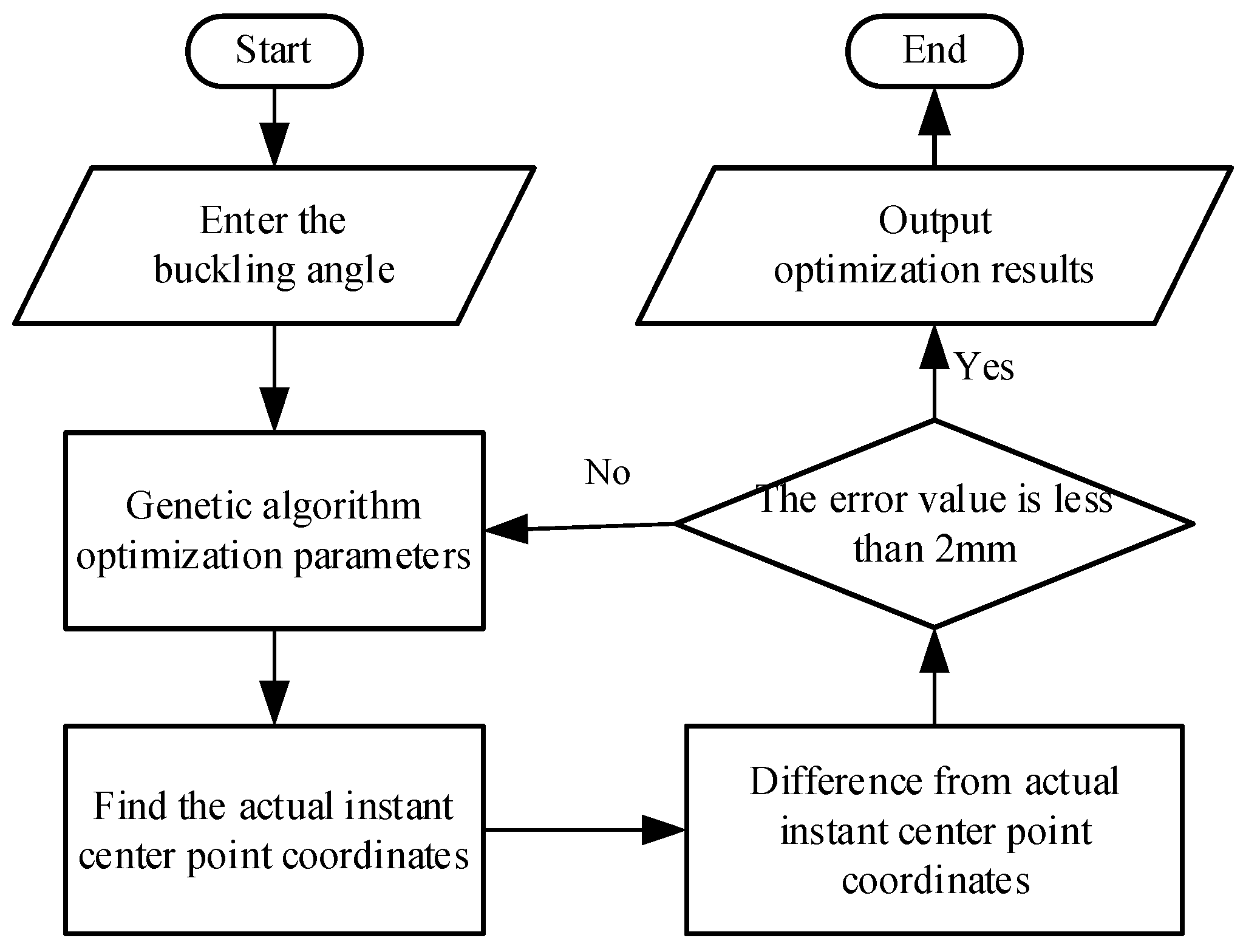
3.3.1. Parameter Optimization
3.3.2. Optimization Method
3.3.3. Optimization Results
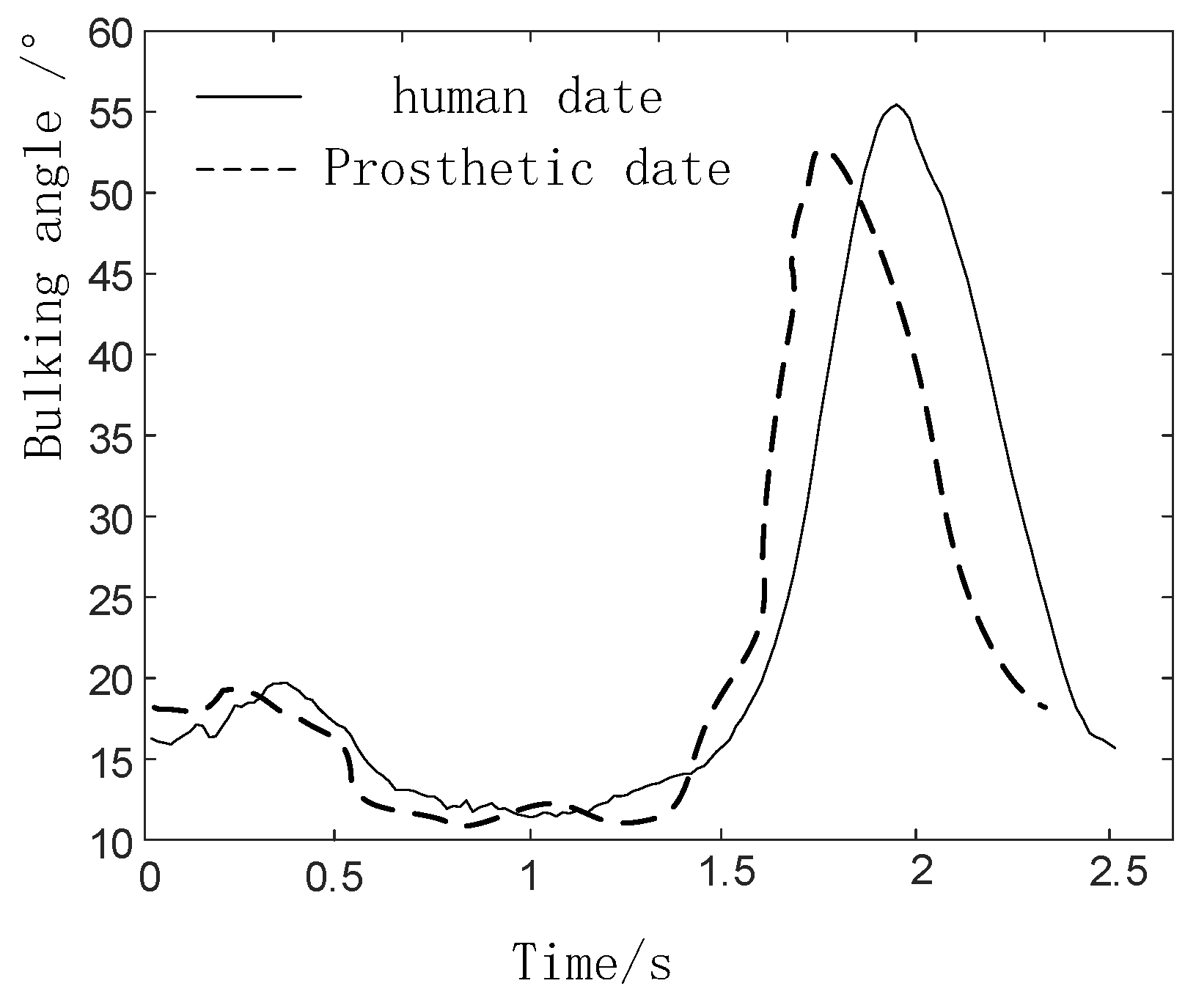
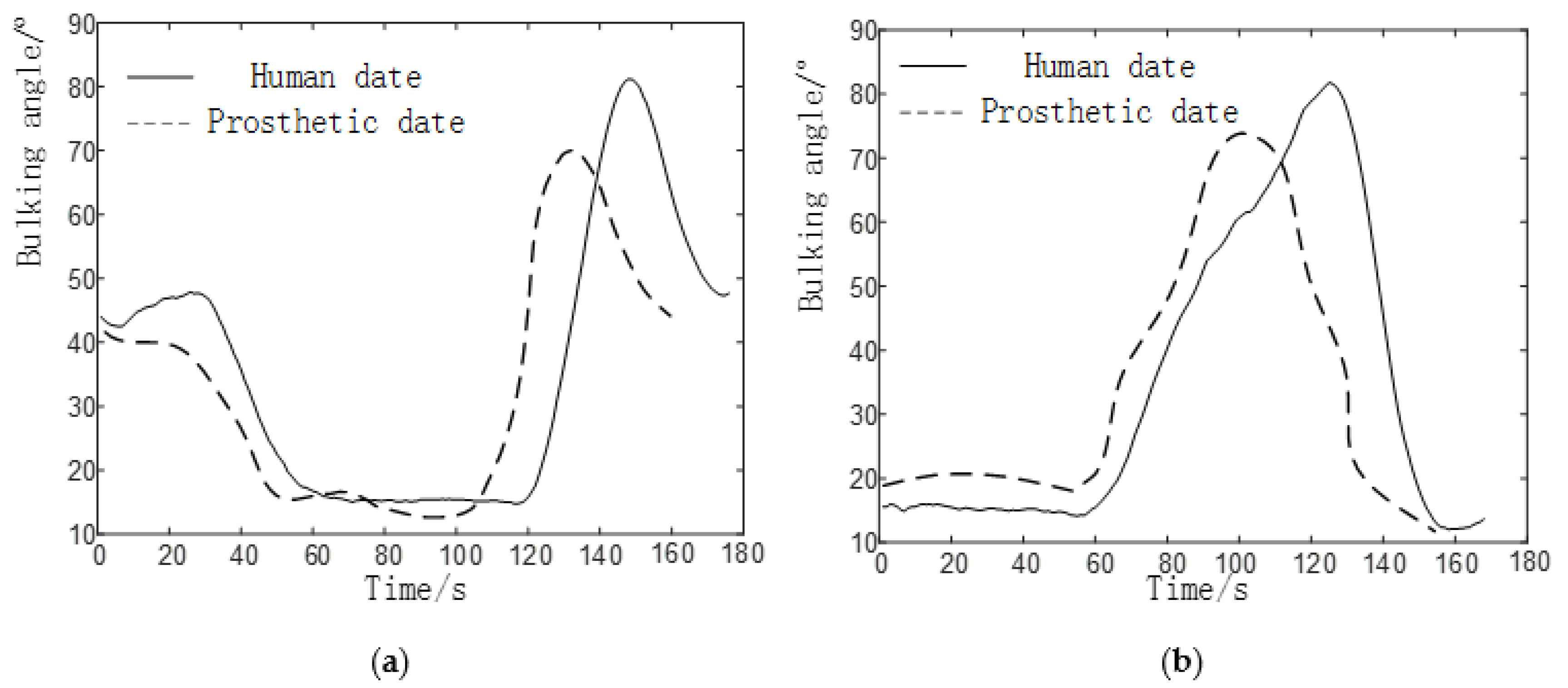
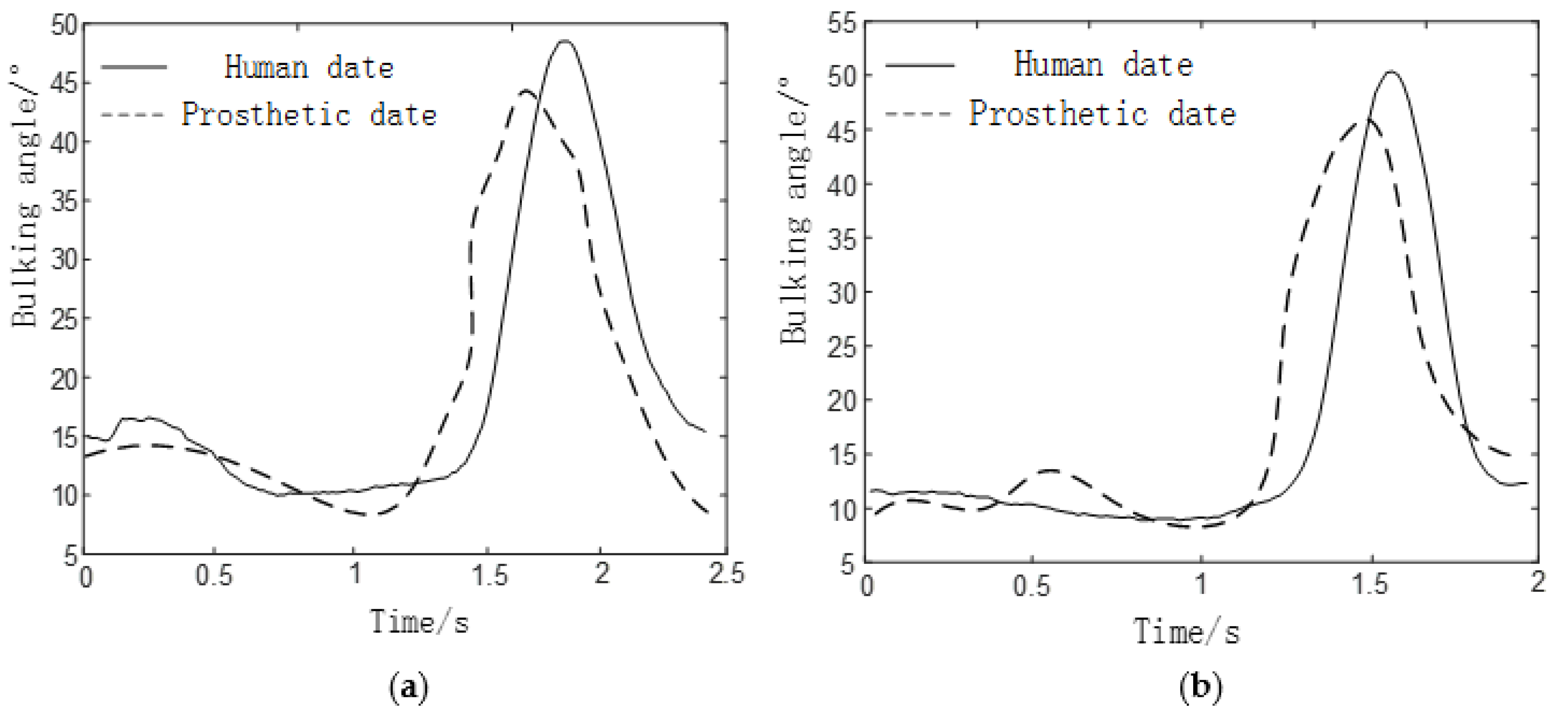
4. Experimental Research
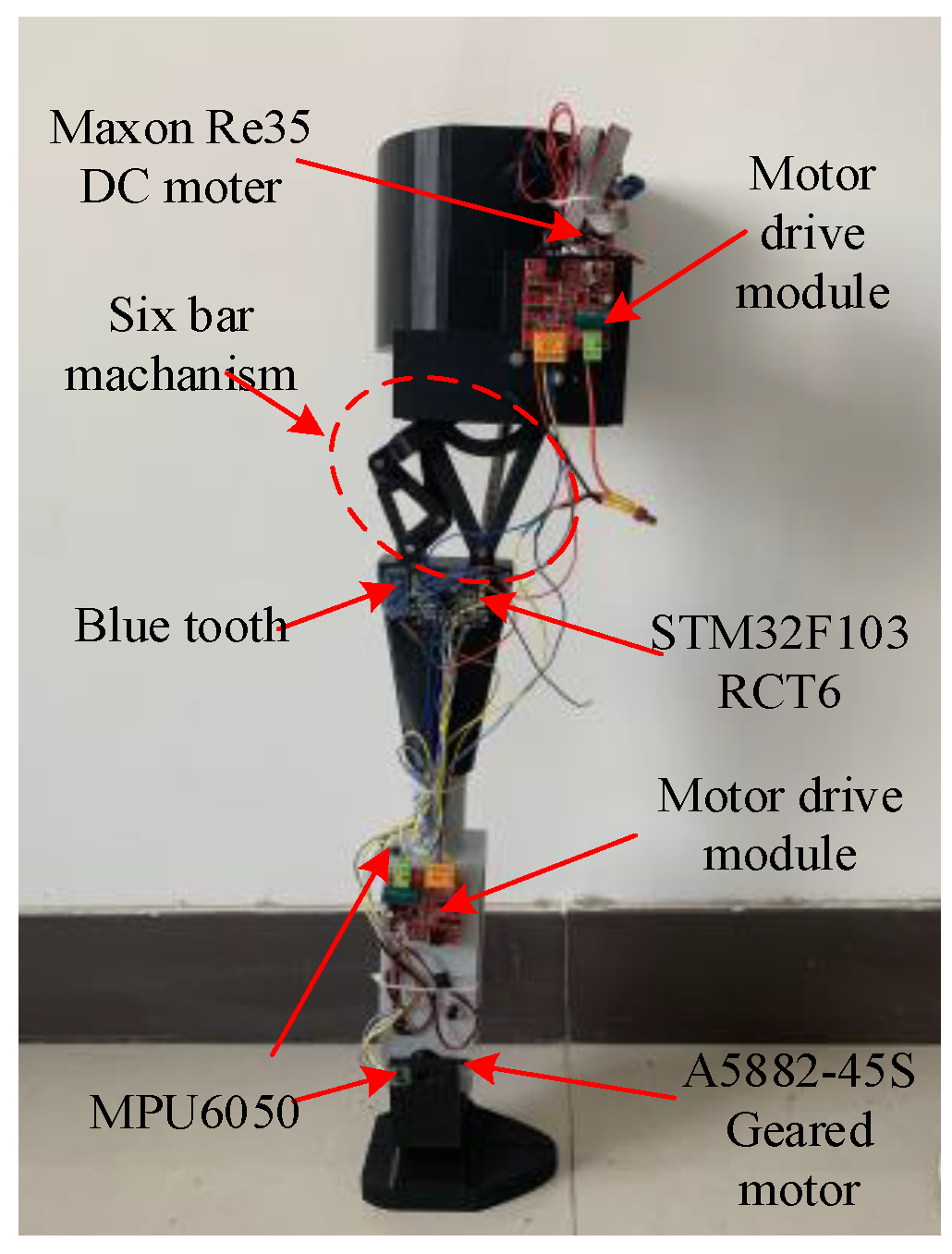
4.1. Experimental Prototype
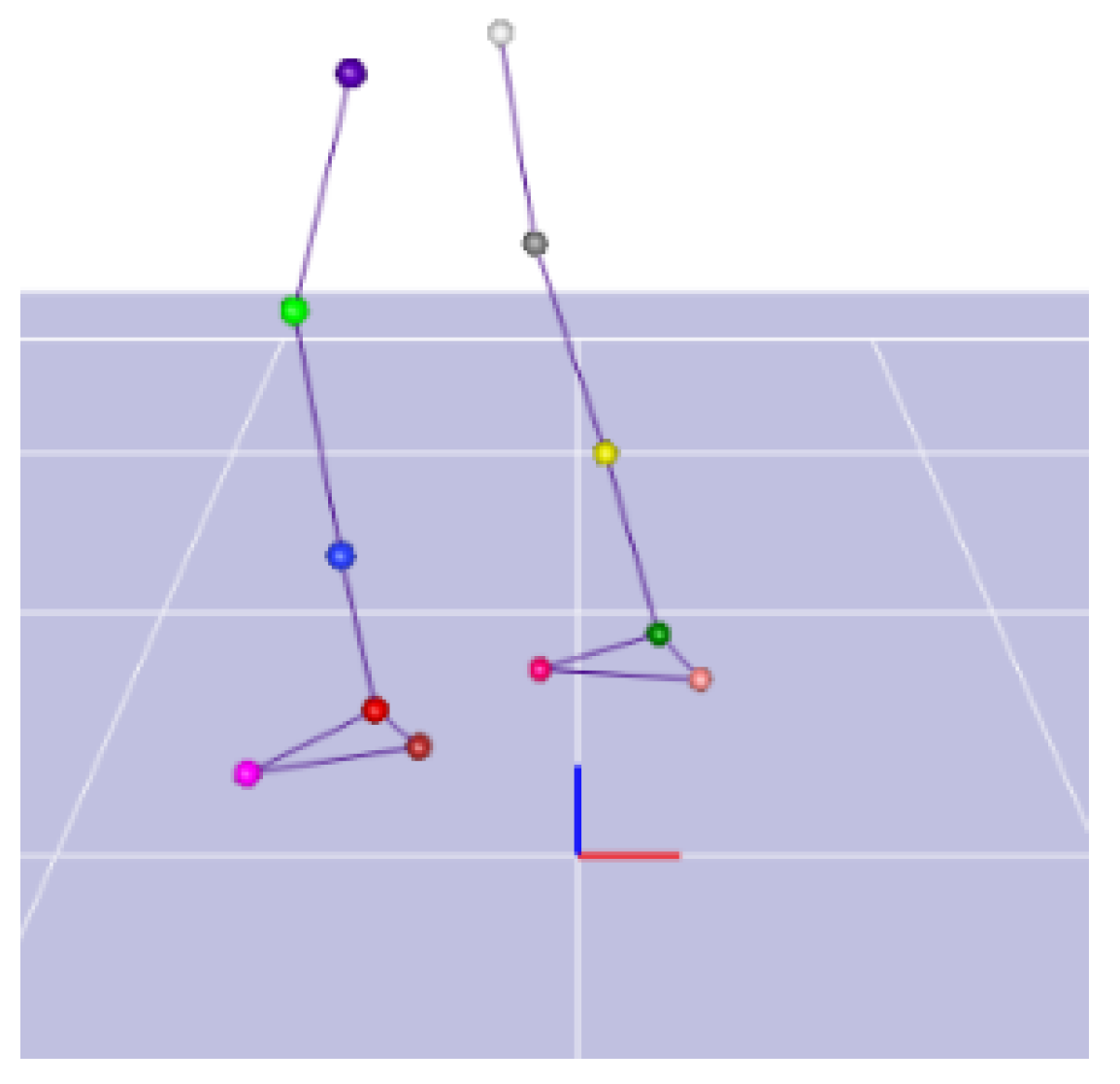
4.2. Experimental Process and Result Analysis
- The joint of a normal person provides a large driving torque(about 110Nm) in the standing phase. However, due to the insufficient strength of the component materials in this experiment, the joint prosthesis failed to provide a large driving torque in the standing phase.
- Due to the error between the actual weight of the prosthesis and the theoretical weight, the joint drive is insufficient, which has a certain negative impact on the result.
- The experimenter did not adapt well to the prosthesis and caused gait inconsistency.
- The error between the actual weight of the prosthesis and the theoretical weight.
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cooper, R.A.; Quatrano, L.A.; Stanhope, S.J.; Cavanagh, P.R.; Miller, F.; Kerrigan, D.C.; Esquenazi, A.; Harris, G.F.; Winters, J.M. Gait analysis in rehabilitation medicine—A brief report. Am. J. Phys. Med. Rehabil. 1999, 78, 278–280. [Google Scholar] [CrossRef] [PubMed]
- Larsen, P.K.; Simonsen, E.B.; Lynnerup, N. Use of Photogrammetry and Biomechanical Gait analysis to Identify Individuals. In Proceedings of the European Signal Processing Conference, IEEE, Nice, Italy, 31 August–4 September 2015. [Google Scholar]
- Hayashi, Y.; Tsujiuchi, N.; Koizumi, T.; Uno, R.; Matsuda, Y.; Tsuchiya, Y.; Inoue, Y. Gait motion analysis in the unrestrained condition of trans-femoral amputee with a prosthetic limb. IEEE Eng. Med. Biol. Soc. 2012, 2012, 3040–3043. [Google Scholar]
- Muro de la Herran, A.; García-Zapirain, B.; Méndez-Zorrilla, A. Gait Analysis Methods: An Overview of Wearable and Non-Wearable Systems, Highlighting Clinical Applications. Sensors 2014, 14, 3362–3394. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tanawongsuwan, R.; Bobick, A. Gait recognition from time-normalized joint-angle trajectories in the walking plane. In Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, CVPR, Kauai, HI, USA, 8–14 December 2001. [Google Scholar]
- Gabel, M.; Gilad-Bachrach, R.; Renshaw, E.; Schuster, A. Full body gait analysis with Kinect Engineering in Medicine & Biology Society. In Proceedings of the IEEE Engineering in Medicine and Biology Society, San Diego, CA, USA, 28 August–1 September 2012. [Google Scholar]
- Liu, T.; Inoue, Y.; Shibata, K. Development of a wearable sensor system for quantitative gait analysis. Measurement 2009, 42, 978–988. [Google Scholar] [CrossRef]
- Bamberg, S.J.M.; Benbasat, A.Y.; Scarborough, D.M.; Krebs, D.E.; Paradiso, J.A. Gait Analysis Using a Shoe-Integrated Wireless Sensor System. IEEE Trans. Inf. Technol. Biomed. 2008, 12, 413–423. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xiu-Feng, L.; Li-Quan, G.; Ji-Ping, W. Design of gait analysis system based on six-axis sensor. Transducer Microsyst. Technol. 2014, 33, 89–91. [Google Scholar]
- Chaparro-Rico, B.D.M.; Cafolla, D. Test-Retest, Inter-Rater and Intra-Rater Reliability for Spatiotemporal Gait Parameters Using SANE (an easy gait analysis system) as Measuring Instrument. Appl. Sci. 2020, 10, 5781. [Google Scholar] [CrossRef]
- Chaparro-Rico, B.D.M.; Cafolla, D.; Castillo-Castaneda, E.; Ceccarelli, M. Design of arm exercises for rehabilitation assistance. J. Eng. Res. 2020, 8, 203–218. [Google Scholar] [CrossRef]
- Inoue, K.; Wada, T.; Harada, R.; Tachiwana, S. Novel knee joint mechanism of transfemoral prosthesis for stair ascent. In Proceedings of the 13th International Conference on Rehabilitation Robotics (ICORR), IEEE, Seattle, WA, USA, 24–26 June 2013; pp. 1–6. [Google Scholar]
- Andrysek, J.; Klejman, S.; Torres-Moreno, R.; Heim, W.; Steinnagel, B.; Glasford, S. Mobility function of a prosthetic knee joint with an automatic stance phase lock. Prosthet. Orthot. Int. 2011, 35, 163–170. [Google Scholar] [CrossRef] [PubMed]
- Arelekatti, V.N.M.; Winter, A.G. Design of a fully passive prosthetic knee mechanism for transfemoral amputees in India. In Proceedings of the 14th IEEE International Conference on Rehabilitation Robotics, Singapore, 11–14 August 2015. [Google Scholar]
- Altamirano, A.; Leija, L.; Vera, A.; Muñoz, R.; Valentino, A. Low cost knee bionic prosthesis based on poly-centric mechanisms. In Proceedings of the 2012 Pan American Health Care Exchanges, Miami, FL, USA, 26–31 March 2012. [Google Scholar]
- Sun, Y.; Ge, W.; Zheng, J.; Dong, D. Design and evaluation of a prosthetic knee joint using the geared five-bar mechanism. IEEE Trans. Neural Syst. Rehabil. Eng. 2015, 23, 1031–1038. [Google Scholar] [CrossRef] [PubMed]
- Chaparro-Rico, B.D.M.; Cafolla, D.; Castillo-Castaneda, E.; Ceccarelli, M.D. NURSE-2 Do F Device for Arm Motion Guidance: Kinematic, Dynamic, and FEM Analysis. J. Nonlinear Sci. Appl. 2020, 10, 2139. [Google Scholar]
- Zhang, X.; Fu, H.; Wang, X.; Li, G.; Yang, R.; Liu, Y. Design of a novel bionic prosthetic knee joint. Assem. Autom. 2016, 36, 398–404. [Google Scholar] [CrossRef]


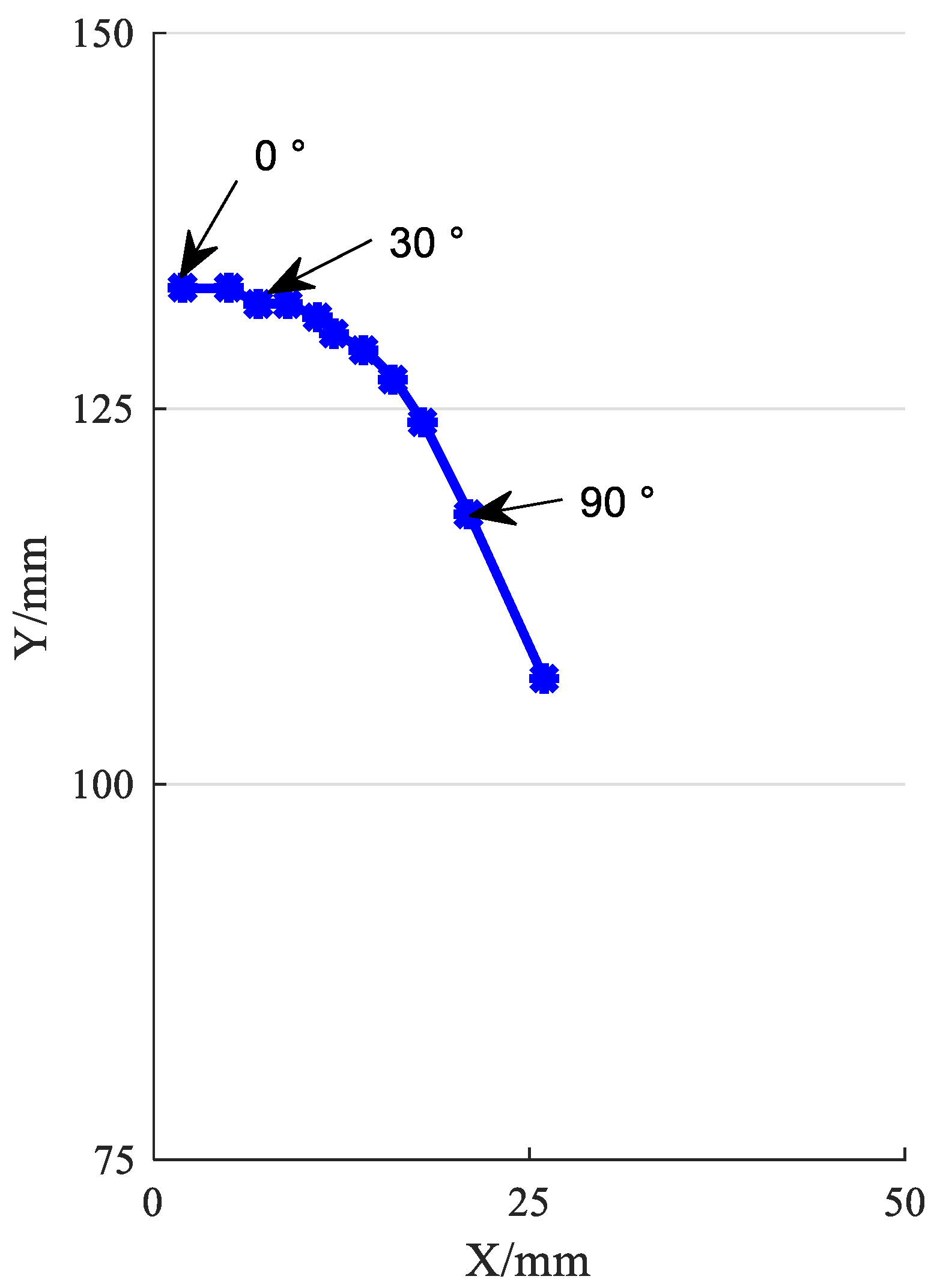

| Instantaneous Center Coordinates (mm) | Instantaneous Center Coordinates (mm) | ||
|---|---|---|---|
| 0 | (2133) | 10 | (5133) |
| 20 | (7132) | 30 | (9132) |
| 40 | (11,131) | 50 | (12,130) |
| 60 | (14,129) | 70 | (16,127) |
| 80 | (18,124) | 90 | (21,118) |
| 100 | (26,107) | 110 | (31,87) |
| Parameters | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| length | 28.7 | 76.9 | 96.7 | 51.4 | 116.6 | 27.8 | 63.5 | 90.8 | 17.69 | −1.4 | 24.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Wang, E.; Wang, M.; Liu, S.; Ge, W. Design and Experimental Research of Knee Joint Prosthesis Based on Gait Acquisition Technology. Biomimetics 2021, 6, 28. https://doi.org/10.3390/biomimetics6020028
Zhang Y, Wang E, Wang M, Liu S, Ge W. Design and Experimental Research of Knee Joint Prosthesis Based on Gait Acquisition Technology. Biomimetics. 2021; 6(2):28. https://doi.org/10.3390/biomimetics6020028
Chicago/Turabian StyleZhang, Yonghong, Erliang Wang, Miao Wang, Sizhe Liu, and Wenjie Ge. 2021. "Design and Experimental Research of Knee Joint Prosthesis Based on Gait Acquisition Technology" Biomimetics 6, no. 2: 28. https://doi.org/10.3390/biomimetics6020028
APA StyleZhang, Y., Wang, E., Wang, M., Liu, S., & Ge, W. (2021). Design and Experimental Research of Knee Joint Prosthesis Based on Gait Acquisition Technology. Biomimetics, 6(2), 28. https://doi.org/10.3390/biomimetics6020028





