Effect of the Structural Characteristics on Attachment-Detachment Mechanics of a Rigid-Flexible Coupling Adhesive Unit
Abstract
:1. Introduction
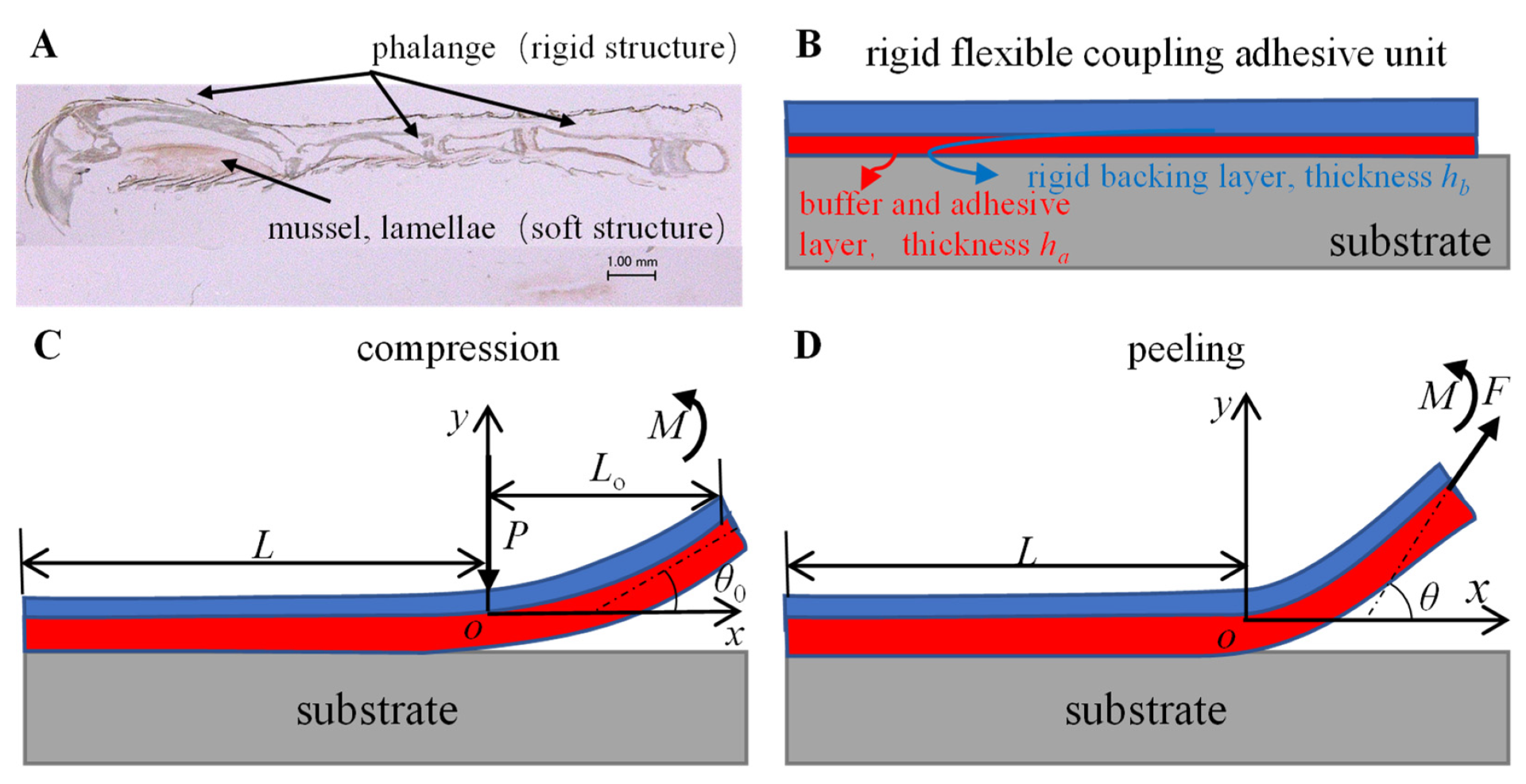
2. Modeling and Numerical Analysis of the Rigid-Flexible Coupling Adhesive Unit
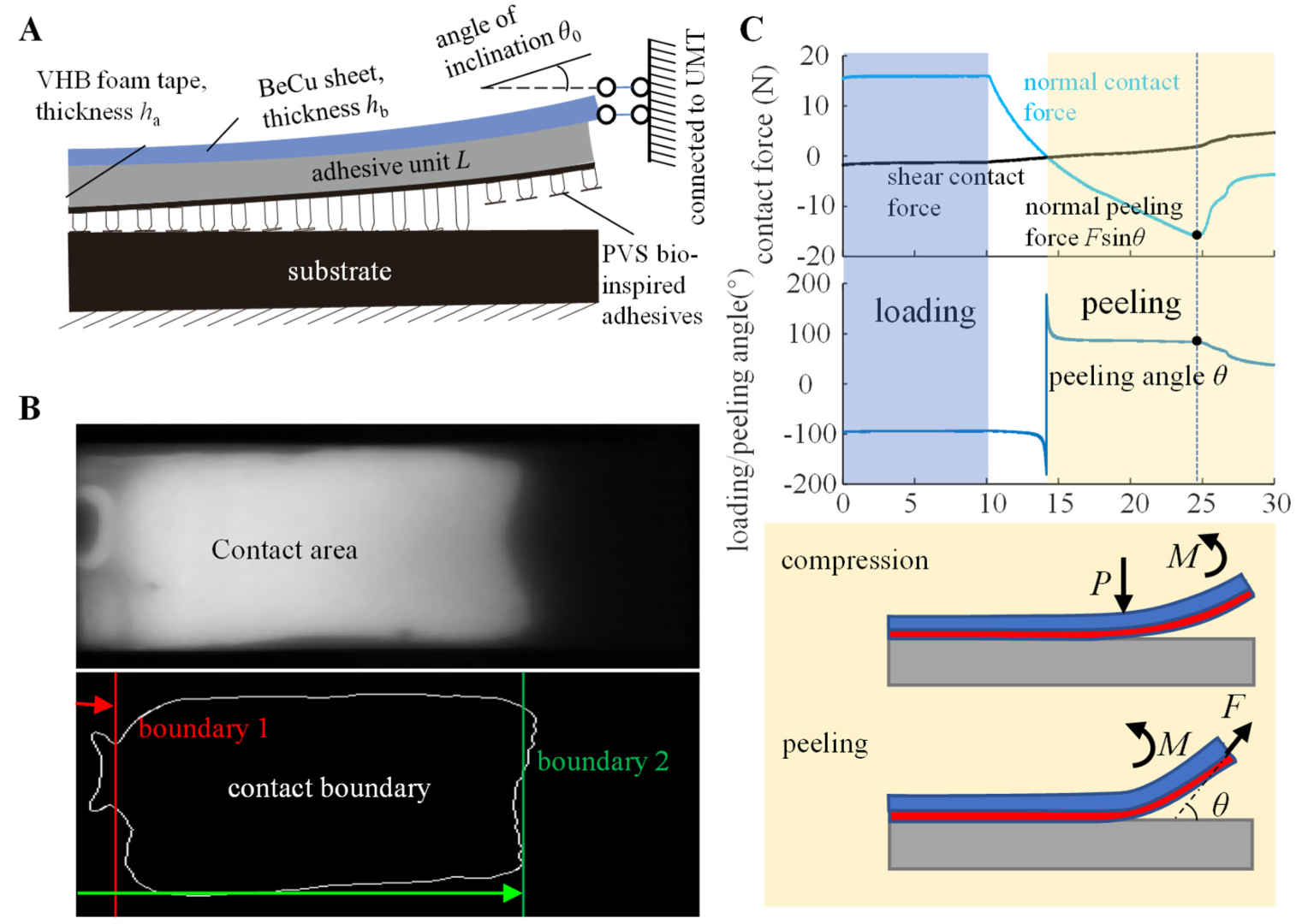
2.1. Mechanical Model
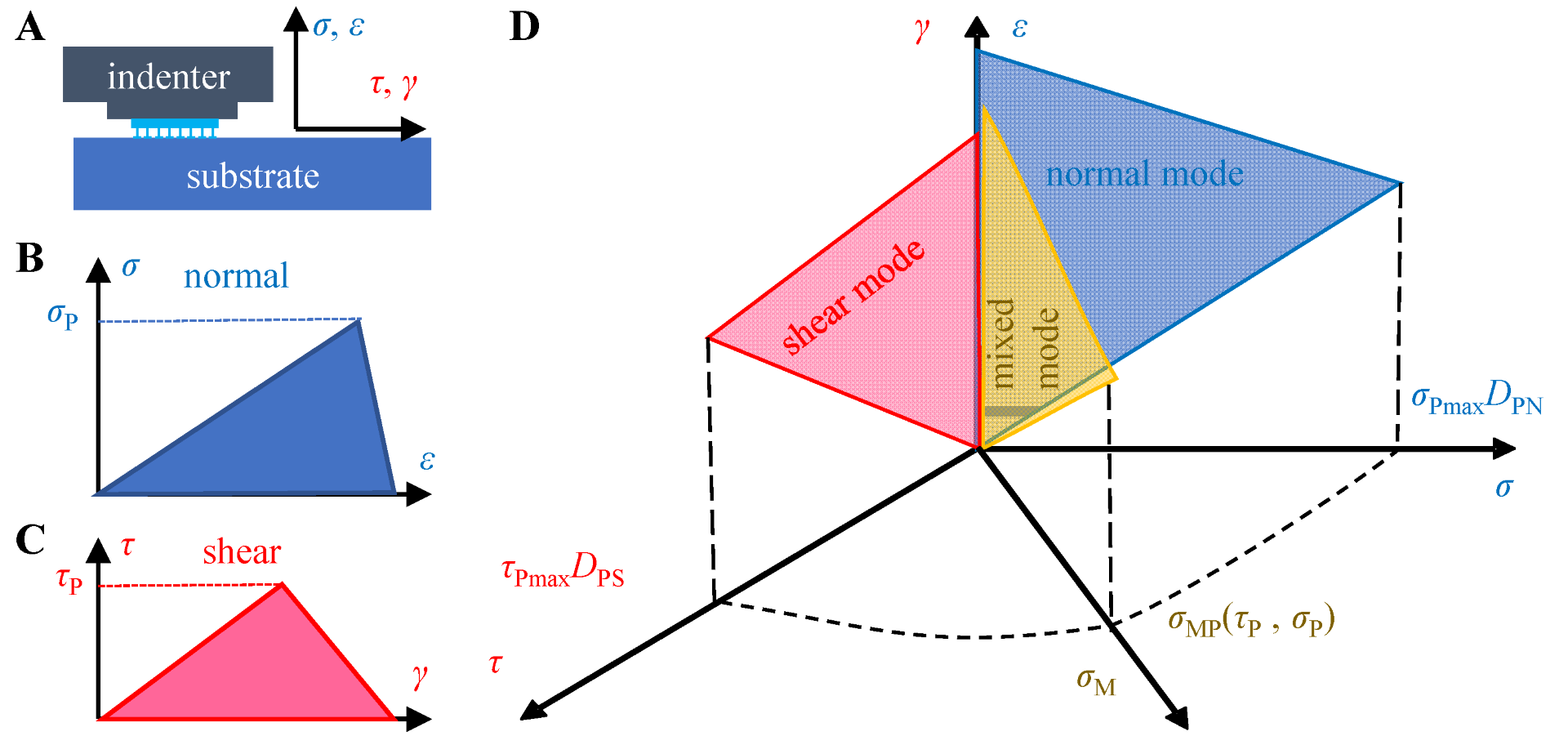
2.2. Traction Versus Separation Law
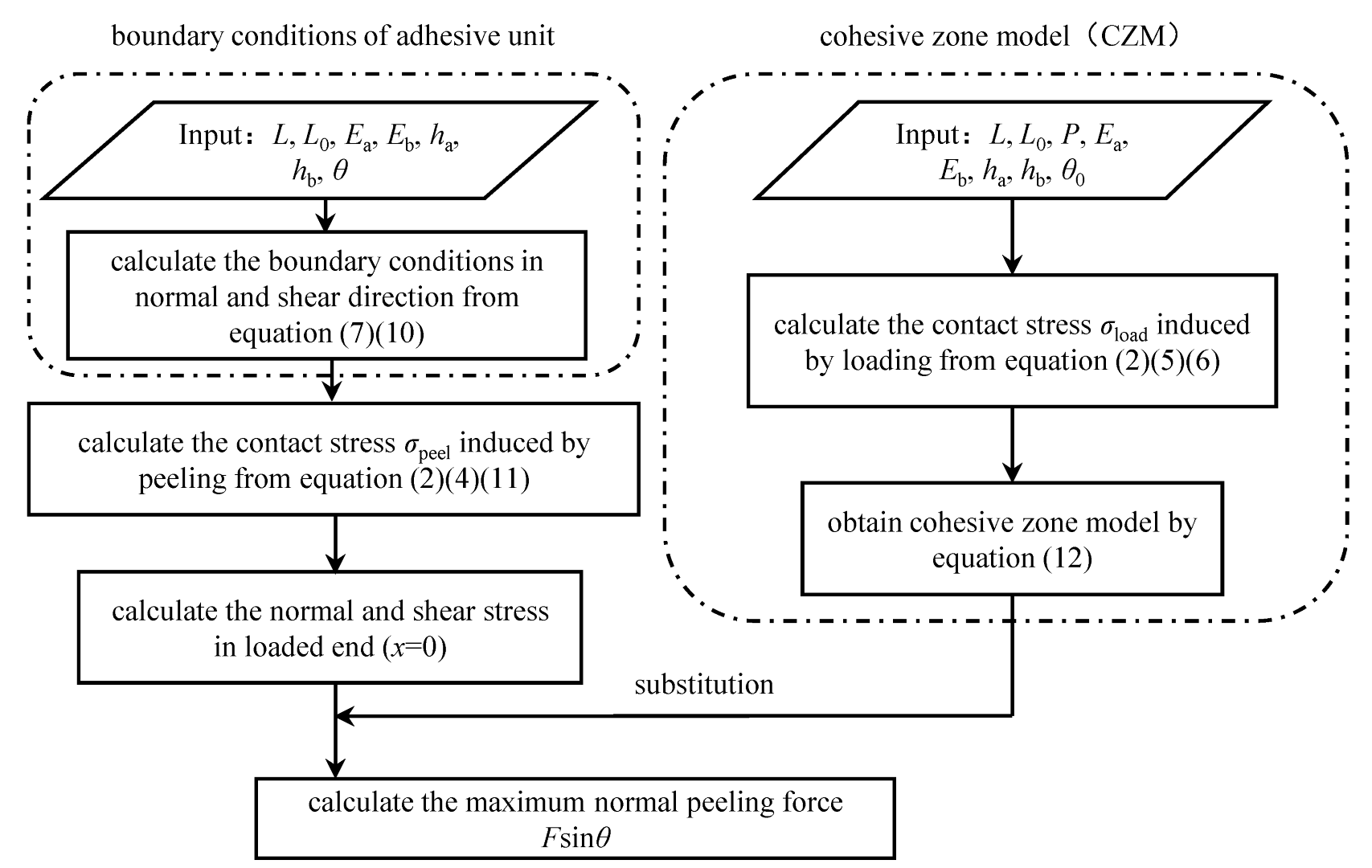
2.3. Mechanical Analysis Flow of Rigid-Flexible Coupling Adhesive Unit during the Compression and Peeling Process
3. Experiments and Methods
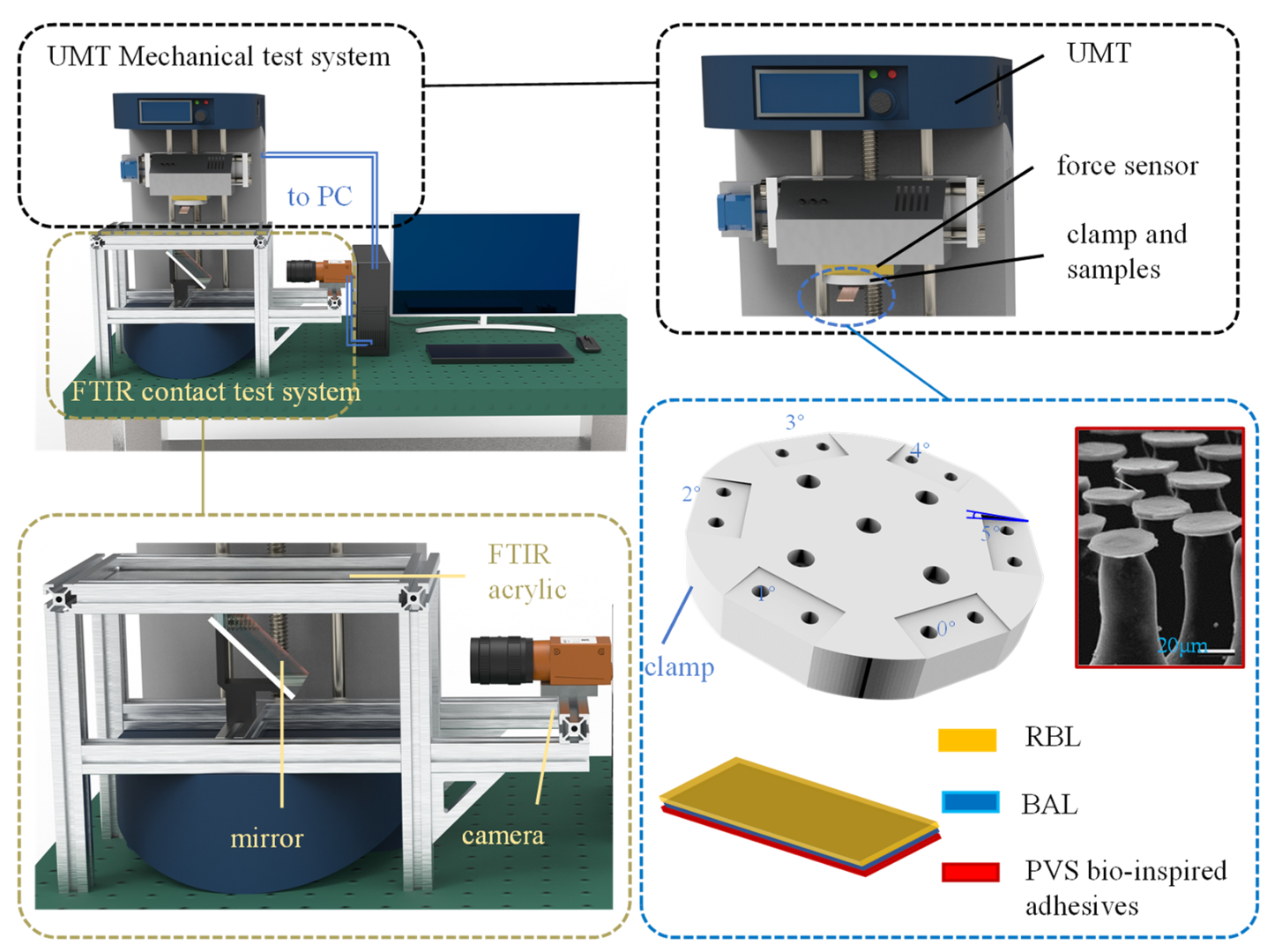
3.1. Simultaneous Test Method of the Quasi-Static Adhesion Mechanics and the Contact State
3.2. Working Conditions and Data Processing for the Attachment-Detachment Test of the Adhesive Unit
4. Result
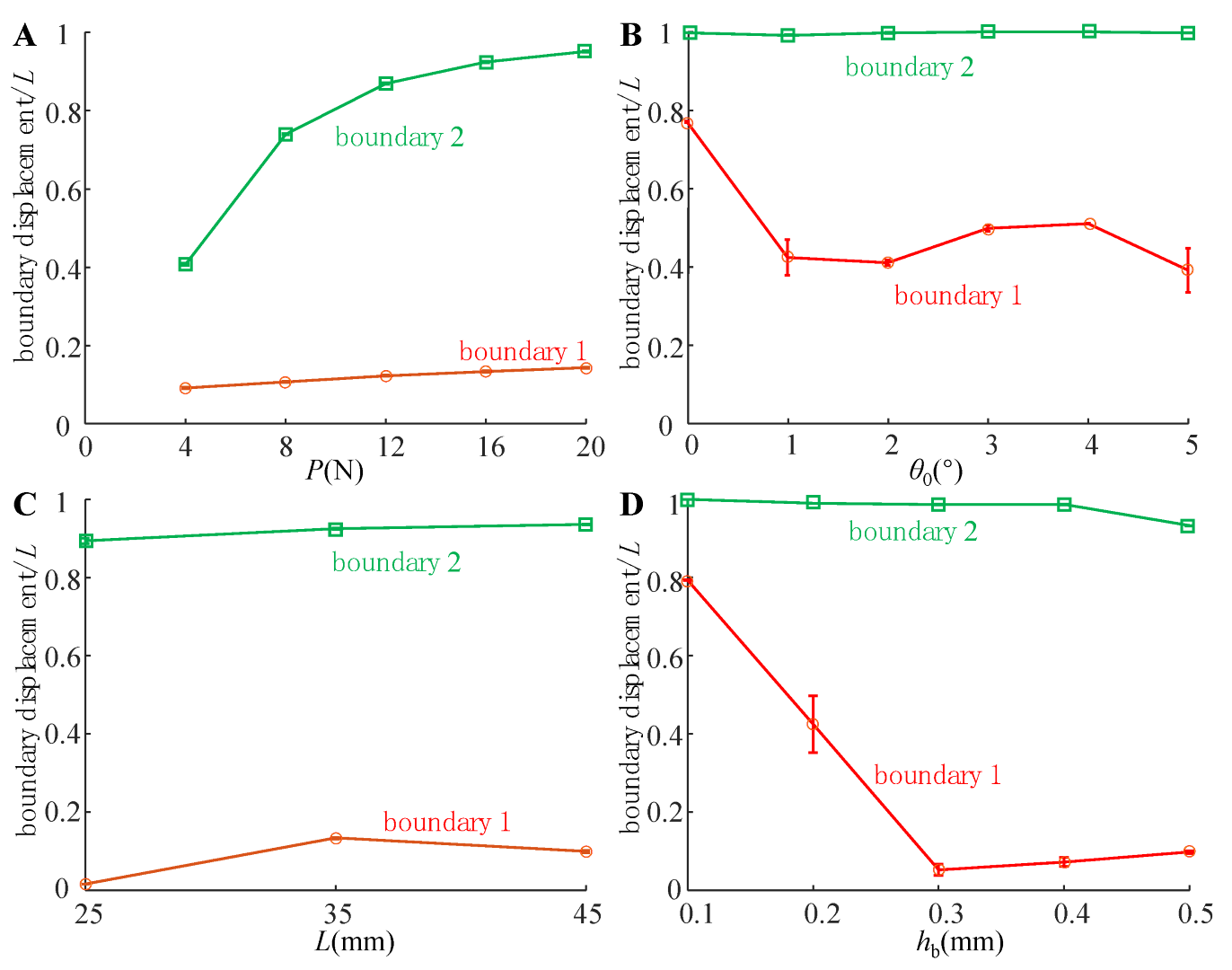
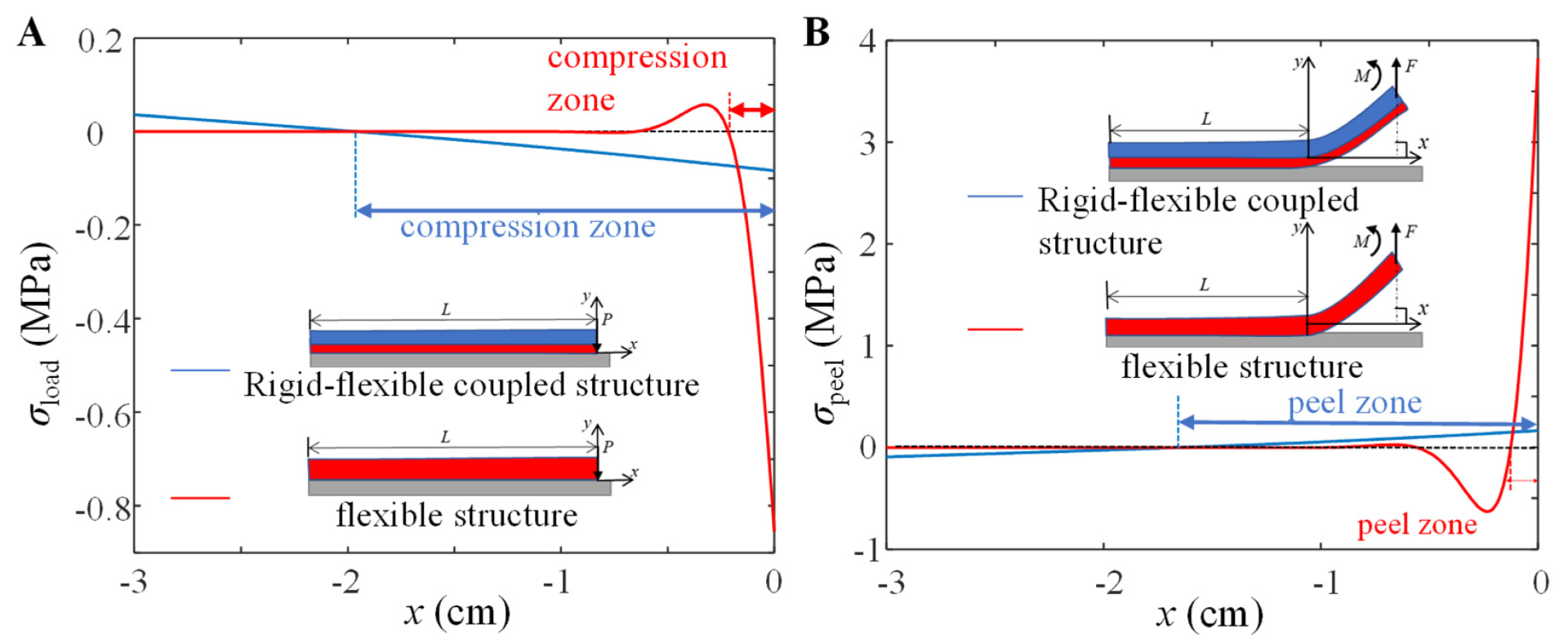
4.1. Compression State of the Adhesive Unit
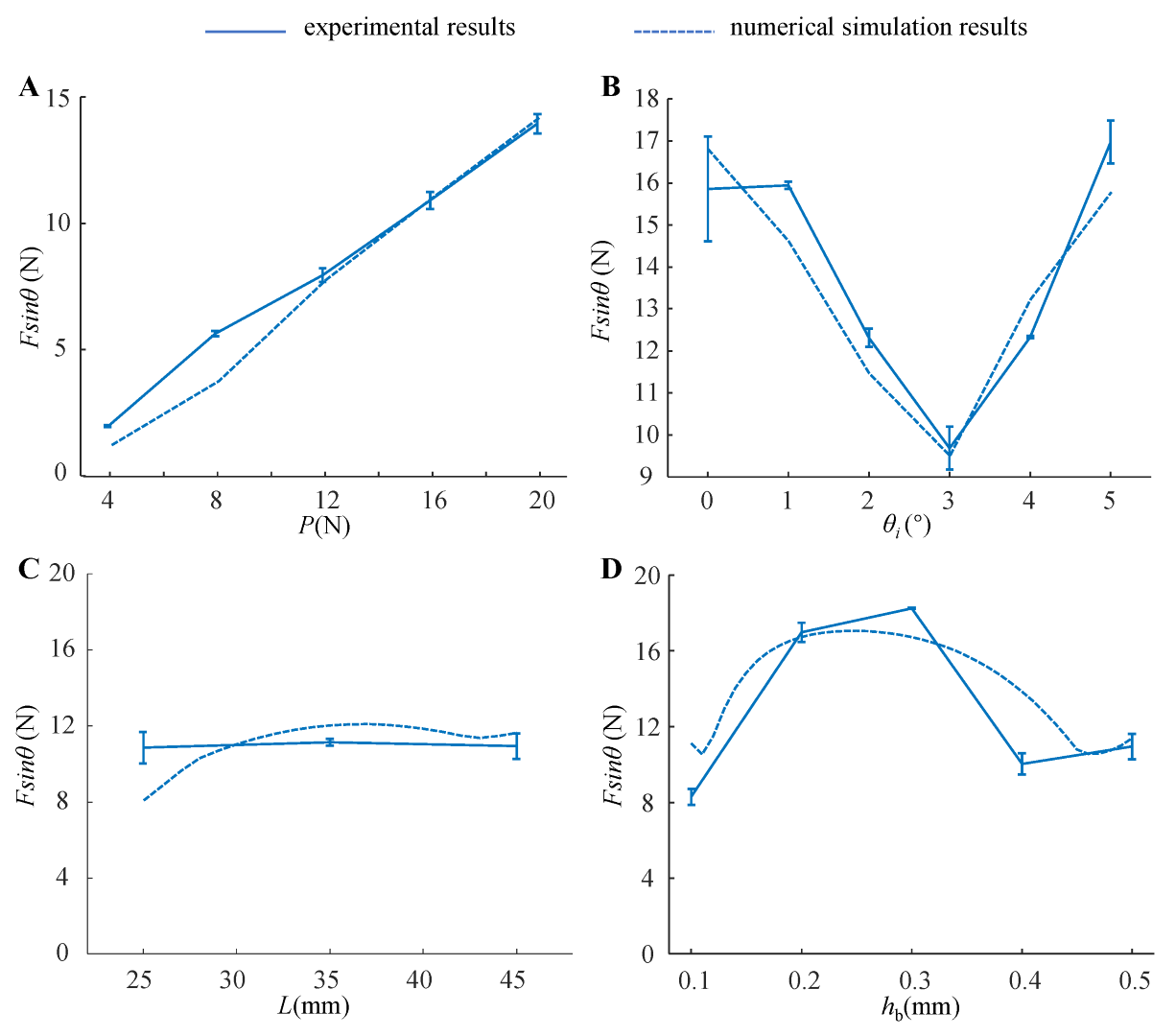
4.2. Peeling Behavior of the Adhesive Unit
5. Discussion
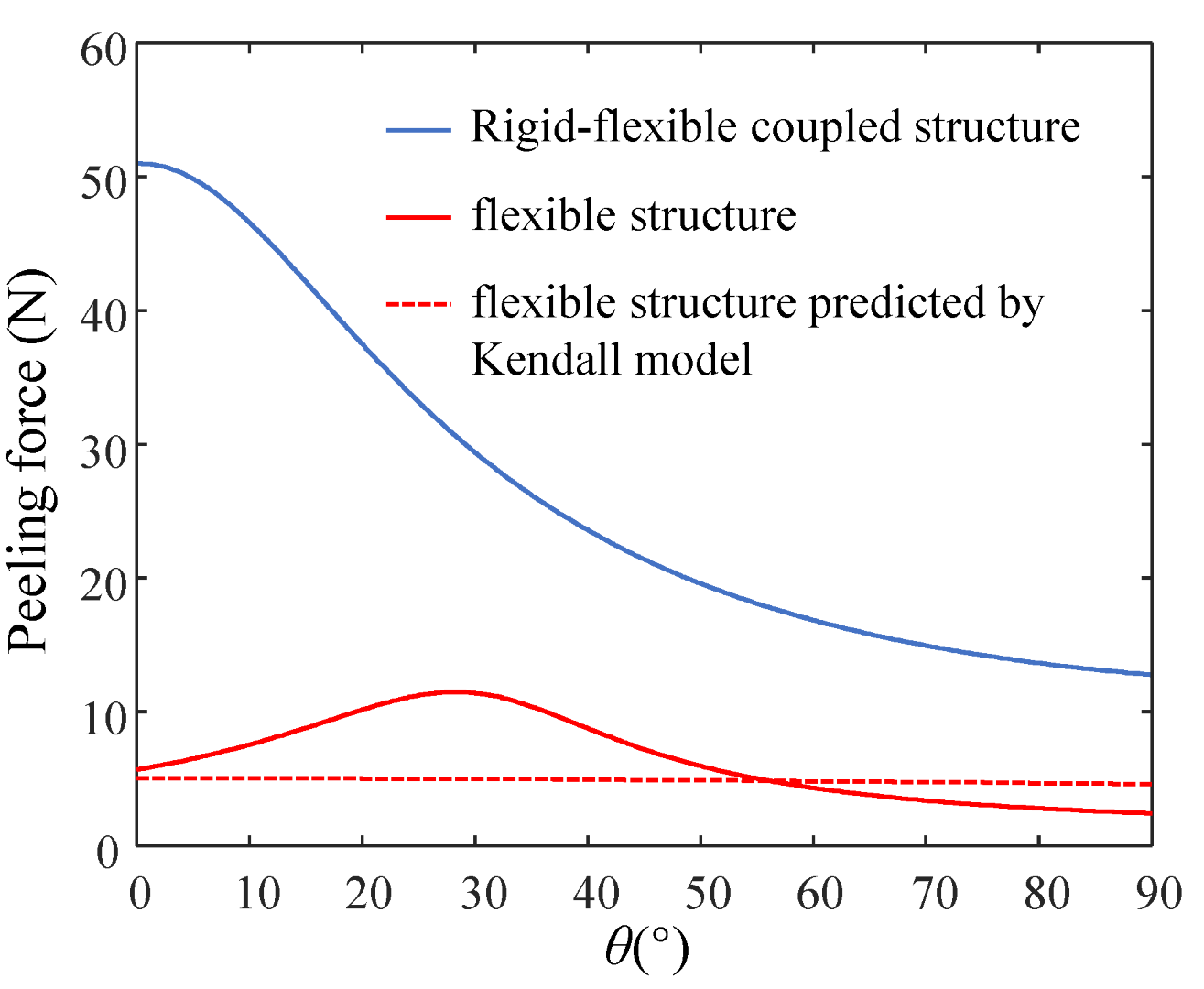
5.1. Comparison between Rigid-Flexible Coupling Adhesive Unit and Flexible Adhesive Unit
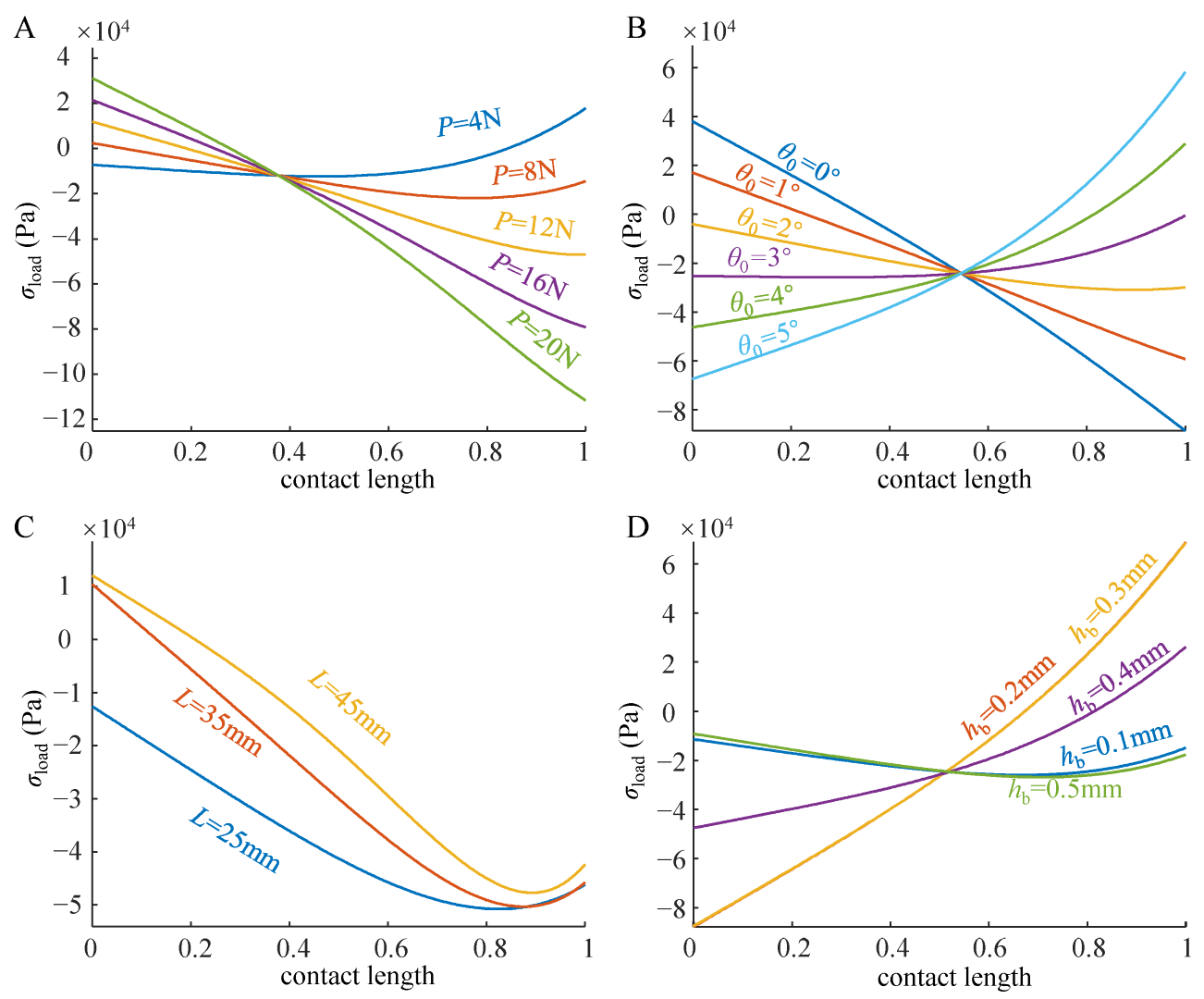
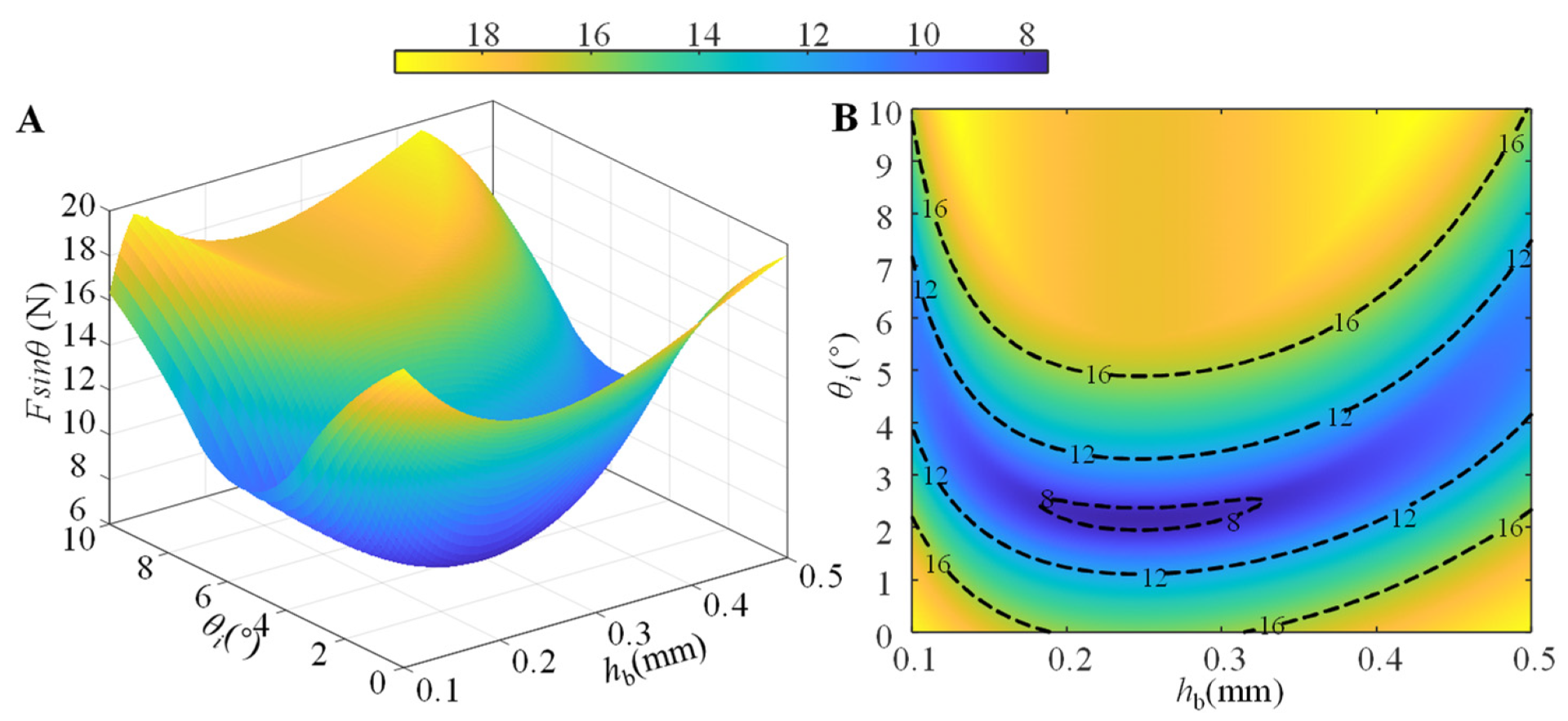
5.2. Relationship between the Structural Characteristics and the Normal Loading Capability
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Autumn, K.; Niewiarowski, P.H.; Puthoff, J.B. Gecko Adhesion as a Model System for Integrative Biology, Interdisciplinary Science, and Bioinspired Engineering. Annu. Rev. Ecol. Evol. Syst. 2014, 45, 445–470. [Google Scholar] [CrossRef]
- Lemetti, L.; Tersteegen, J.; Sammaljarvi, J.; Aranko, A.S.; Linder, M.B. Recombinant Spider Silk Protein and Delignified Wood Form a Strong Adhesive System. ACS Sustain. Chem. Eng. 2021, 10, 552–561. [Google Scholar] [CrossRef]
- Hu, H.; Tian, H.; Li, X.; Shao, J.; Ding, Y.; Liu, H.; An, N. Biomimetic Mushroom-Shaped Microfibers for Dry Adhesives by Electrically Induced Polymer Deformation. ACS Appl. Mater. Interfaces 2014, 6, 14167–14173. [Google Scholar] [CrossRef] [PubMed]
- Davies, J.; Haq, S.; Hawke, T.; Sargent, J. A practical approach to the development of a synthetic Gecko tape. Int. J. Adhes. Adhes. 2009, 29, 380–390. [Google Scholar] [CrossRef]
- Gorb, S.; Varenberg, M.; Peressadko, A.; Tuma, J. Biomimetic mushroom-shaped fibrillar adhesive microstructure. J. R. Soc. Interface 2007, 4, 271–275. [Google Scholar] [CrossRef] [PubMed]
- Parness, A.; Soto, D.; Esparza, N.; Gravish, N.; Wilkinson, M.; Autumn, K.; Cutkosky, M. A microfabricated wedge-shaped adhesive array displaying gecko-like dynamic adhesion, directionality and long lifetime. J. R. Soc. Interface 2009, 6, 1223–1232. [Google Scholar] [CrossRef] [PubMed]
- Tao, D.; Gao, X.; Lu, H.; Liu, Z.; Li, Y.; Tong, H.; Pesika, N.; Meng, Y.; Tian, Y. Controllable Anisotropic Dry Adhesion in Vacuum: Gecko Inspired Wedged Surface Fabricated with Ultraprecision Diamond Cutting. Adv. Funct. Mater. 2017, 27, 1606576. [Google Scholar] [CrossRef]
- Zhou, L.; Ren, L.; Chen, Y.; Niu, S.; Han, Z.; Ren, L. Bio-Inspired Soft Grippers Based on Impactive Gripping. Adv. Sci. 2021, 8, 2002017. [Google Scholar] [CrossRef]
- Autumn, K.; Majidi, C.; Groff, R.E.; Dittmore, A.; Fearing, R. Effective elastic modulus of isolated gecko setal arrays. J. Exp. Biol. 2006, 209, 3558–3568. [Google Scholar] [CrossRef]
- Russell, A.P. A contribution to the functional analysis of the foot of the Tokay, Gekko gecko (Reptilia: Gekkonidae). J. Zool. 1975, 176, 437–476. [Google Scholar] [CrossRef]
- Kwak, J.; Kim, T. A review of adhesion and friction models for gecko feet. Int. J. Precis. Eng. Manuf. 2010, 11, 171–186. [Google Scholar] [CrossRef]
- Zhou, M.; Pesika, N.; Zeng, H.; Tian, Y.; Israelachvili, J. Recent advances in gecko adhesion and friction mechanisms and development of gecko-inspired dry adhesive surfaces. Friction 2013, 1, 114–129. [Google Scholar] [CrossRef]
- Tian, Y.; Wan, J.; Pesika, N.; Zhou, M. Bridging nanocontacts to macroscale gecko adhesion by sliding soft lamellar skin supported setal array. Sci. Rep. 2013, 3, 1382. [Google Scholar] [CrossRef]
- Kendall, K. Interfacial dislocations spontaneously created by peeling. (Adhesive joint strength). J. Phys. D Appl. Phys. 1978, 11, 1519–1527. [Google Scholar] [CrossRef]
- Banea, M.D.; Da Silva, L.F. Adhesively bonded joints in composite materials: An overview. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2009, 223, 1–18. [Google Scholar] [CrossRef]
- Asbeck, A.; Dastoor, S.; Parness, A.; Fullerton, L.; Esparza, N.; Soto, D.; Heyneman, B.; Cutkosky, M. Climbing rough vertical surfaces with hierarchical directional adhesion. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 2675–2680. [Google Scholar] [CrossRef]
- Ko, H.; Yi, H.; Jeong, H.E. Wall and ceiling climbing quadruped robot with superior water repellency manufactured using 3D printing (UNIclimb). Int. J. Precis. Eng. Manuf. Technol. 2017, 4, 273–280. [Google Scholar] [CrossRef]
- Kim, S.; Spenko, M.; Trujillo, S.; Heyneman, B.; Santos, D.; Cutkosky, M. Smooth Vertical Surface Climbing with Directional Adhesion. IEEE Trans. Robot. 2008, 24, 65–74. [Google Scholar] [CrossRef]
- Wang, B.; Xiong, X.; Duan, J.; Wang, Z.; Dai, Z. Compliant Detachment of Wall-Climbing Robot Unaffected by Adhesion State. Appl. Sci. 2021, 11, 5860. [Google Scholar] [CrossRef]
- Jiang, H.; Hawkes, E.W.; Fuller, C.; Estrada, M.A.; Suresh, S.A.; Abcouwer, N.; Han, A.K.; Wang, S.; Ploch, C.J.; Parness, A.; et al. A robotic device using gecko-inspired adhesives can grasp and manipulate large objects in microgravity. Sci. Robot. 2017, 2, eaan4545. [Google Scholar] [CrossRef] [Green Version]
- Song, S.; Drotlef, D.-M.; Majidi, C.; Sitti, M. Controllable load sharing for soft adhesive interfaces on three-dimensional surfaces. Proc. Natl. Acad. Sci. USA 2017, 114, E4344–E4353. [Google Scholar] [CrossRef]
- Ruotolo, W.; Brouwer, D.; Cutkosky, M.R. From grasping to manipulation with gecko-inspired adhesives on a multifinger gripper. Sci. Robot. 2021, 6, eabi9773. [Google Scholar] [CrossRef] [PubMed]
- Federle, W.; LaBonte, D. Dynamic biological adhesion: Mechanisms for controlling attachment during locomotion. Philos. Trans. R. Soc. B Biol. Sci. 2019, 374, 20190199. [Google Scholar] [CrossRef] [PubMed]
- Zhou, M.; Tian, Y.; Pesika, N.; Zeng, H.; Wan, J.; Meng, Y.; Wen, S. The Extended Peel Zone Model: Effect of Peeling Velocity. J. Adhes. 2011, 87, 1045–1058. [Google Scholar] [CrossRef]
- Kendall, K. Thin-film peeling-the elastic term. J. Phys. D Appl. Phys. 1975, 8, 1449. [Google Scholar] [CrossRef]
- Persson, B.N.J.; Gorb, S. The effect of surface roughness on the adhesion of elastic plates with application to biological systems. J. Chem. Phys. 2003, 119, 11437–11444. [Google Scholar] [CrossRef]
- Meitl, M.A.; Zhu, Z.; Kumar, V.; Lee, K.J.; Feng, X.; Huang, Y.Y.; Adesida, I.; Nuzzo, R.G.; Rogers, J.A. Transfer printing by kinetic control of adhesion to an elastomeric stamp. Nat. Mater. 2005, 5, 33–38. [Google Scholar] [CrossRef]
- Da Silva, L.F.M.; Öchsner, A.; Adams, R.D. Handbook of Adhesion Technology; Springer: Berlin/Heidelberg, Germany, 2011; Volume 1. [Google Scholar]
- Greiner, C.; del Campo, A.; Arzt, E. Adhesion of Bioinspired Micropatterned Surfaces: Effects of Pillar Radius, Aspect Ratio, and Preload. Langmuir 2007, 23, 3495–3502. [Google Scholar] [CrossRef]
- Jiao, Y.; Gorb, S.; Scherge, M. Adhesion measured on the attachment pads of Tettigonia viridissima (Orthoptera, Insecta). J. Exp. Biol. 2000, 203, 1887–1895. [Google Scholar] [CrossRef]
- Kaelble, D.H. Theory and Analysis of Peel Adhesion: Bond Stresses and Distributions. Trans. Soc. Rheol. 1960, 4, 45–73. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, J. A generalized cohesive zone model of the peel test for pressure-sensitive adhesives. Int. J. Adhes. Adhes. 2009, 29, 217–224. [Google Scholar] [CrossRef]
- Yuan, H.; Chen, J.; Teng, J.; Lu, X. Interfacial stress analysis of a thin plate bonded to a rigid substrate and subjected to inclined loading. Int. J. Solids Struct. 2007, 44, 5247–5271. [Google Scholar] [CrossRef]
- Barenblatt, G.I. The Mathematical Theory of Equilibrium Cracks in Brittle Fracture. Adv. Appl. Mech. 1962, 7, 55–129. [Google Scholar]
- Paretkar, D.; Kamperman, M.; Martina, D.; Zhao, J.; Creton, C.; Lindner, A.; Jagota, A.; Mcmeeking, R.; Arzt, E. Preload-responsive adhesion: Effects of aspect ratio, tip shape and alignment. J. R. Soc. Interface 2013, 10, 20130171. [Google Scholar] [CrossRef]
- Lu, X.Z.; Teng, J.G.; Ye, L.P.; Jiang, J.J. Bond–slip models for FRP sheets/plates bonded to concrete. Eng. Struct. 2005, 27, 920–937. [Google Scholar] [CrossRef]
- Li, G.; Tan, K.H.; Fung, T.C.; Del Linz, P. Mode I fracture characterisation of FRP-concrete interfaces under dynamic loading. Compos. Struct. 2020, 254, 112824. [Google Scholar] [CrossRef]
- Li, G.; Tan, K.H.; Fung, T.C.; Yu, Q.J.; May, M. A coupled dynamic cohesive zone model for FRP-concrete mixed-mode separation. Compos. Struct. 2021, 268, 113872. [Google Scholar] [CrossRef]
- Wang, Y.; Lehmann, S.; Shao, J.; Sameoto, D. Adhesion Circle: A New Approach To Better Characterize Directional Gecko-Inspired Dry Adhesives. ACS Appl. Mater. Interfaces 2017, 9, 3060–3067. [Google Scholar] [CrossRef]
- Li, X.; Tao, D.; Lu, H.; Bai, P.; Liu, Z.; Ma, L.; Meng, Y.; Tian, Y. Recent developments in gecko-inspired dry adhesive surfaces from fabrication to application. Surf. Topogr. Metrol. Prop. 2019, 7, 023001. [Google Scholar] [CrossRef]
- Dugdale, D.S. Yielding of steel sheets containing slits. J. Mech. Phys. Solids 1960, 8, 100–104. [Google Scholar] [CrossRef]
- Dimitri, R.; Trullo, M.; De Lorenzis, L.; Zavarise, G. Coupled cohesive zone models for mixed-mode fracture: A comparative study. Eng. Fract. Mech. 2015, 148, 145–179. [Google Scholar] [CrossRef]
- Jiang, W.-G.; Hallett, S.R.; Green, B.G.; Wisnom, M.R. A concise interface constitutive law for analysis of delamination and splitting in composite materials and its application to scaled notched tensile specimens. Int. J. Numer. Methods Eng. 2007, 69, 1982–1995. [Google Scholar] [CrossRef]
- Schargott, M.; Popov, V.L.; Gorb, S. Spring model of biological attachment pads. J. Theor. Biol. 2006, 243, 48–53. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Dai, Z.; Wang, Z.; Full, R.J. Role of multiple, adjustable toes in distributed control shown by sideways wall-running in geckos. Proc. R. Soc. B Boil. Sci. 2020, 287, 20200123. [Google Scholar] [CrossRef] [PubMed]
- Eason, E.V.; Hawkes, E.W.; Windheim, M.; Christensen, D.L.; Libby, T.; Cutkosky, M.R. Stress distribution and contact area measurements of a gecko toe using a high-resolution tactile sensor. Bioinspir. Biomim. 2015, 10, 016013. [Google Scholar] [CrossRef] [PubMed]
- Pesika, N.S.; Tian, Y.; Zhao, B.; Rosenberg, K.; Zeng, H.; McGuiggan, P.; Autumn, K.; Israelachvili, J.N. Peel-Zone Model of Tape Peeling Based on the Gecko Adhesive System. J. Adhes. 2007, 83, 383–401. [Google Scholar] [CrossRef] [Green Version]
| RBL | BAL | PVS Adhesives | |
|---|---|---|---|
| Length (mm) | 30, 40, 50 | 30, 40, 50 | 30, 40, 50 |
| Width (mm) | 17 | 17 | 17 |
| elastic module | 128GPa | 18 MPa | ~3 MPa (bulk) |
| Poisson’s ratio | 0.35 | 0.49 | 0.49 |
| Thickness (mm) | 0.1, 0.2, 0.3, 0.4, 0.5 | 3 | 0.4 |
| Working Condition | Thickness of RBL hb (mm) | Length of the Unit L (mm) | Angle of Inclination θ0 (°) | Compression Force P (N) |
|---|---|---|---|---|
| working condition 1 (different P) | 0.5 | 35 | 5 | 4, 8, 12, 16, 20 |
| working condition 2 (different θ0) | 0.2 | 45 | 0, 1, 2, 3, 4, 5 | 16 |
| working condition 3 (different L) | 0.5 | 25, 35, 45 | 5 | 16 |
| working condition 4 (different hb) | 0.1, 0.2, 0.3, 0.4, 0.5 | 45 | 5 | 16 |
| Peeling Angle (°) (Mean ± sd) | Peeling Angle (°) (Mean ± sd) | Peeling Angle (°) (Mean ± sd) | Peeling Angle (°) (Mean ± sd) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Preload (N) | 4 | 109.3 ± 0.7 | angle of inclination (°) | 0 | 82.2 ± 0.3 | thickness of RBL (mm) | 0.1 | 74.7 ± 0.1 | adhesive unit length (mm) | 25 | 91.5 ± 0.1 |
| 8 | 103.8 ± 0.4 | 1 | 82.7 ± 0.4 | 0.2 | 87.4 ± 0.2 | 35 | 92.5 ± 0.1 | ||||
| 12 | 108.2 ± 0.8 | 2 | 89.4 ± 0.4 | 0.3 | 91.9 ± 0.4 | 45 | 93.8 ± 0.4 | ||||
| 16 | 106.7 ± 0.8 | 3 | 85.5 ± 1.0 | 0.4 | 102.4 ± 0.2 | ||||||
| 20 | 104.0 ± 0.4 | 4 | 84.7 ± 0.1 | 0.5 | 93.8 ± 0.4 | ||||||
| 5 | 87.4 ± 0.2 | ||||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Q.; Wang, L.; Weng, Z.; Wang, Z.; Dai, Z.; Chen, W. Effect of the Structural Characteristics on Attachment-Detachment Mechanics of a Rigid-Flexible Coupling Adhesive Unit. Biomimetics 2022, 7, 119. https://doi.org/10.3390/biomimetics7030119
Jiang Q, Wang L, Weng Z, Wang Z, Dai Z, Chen W. Effect of the Structural Characteristics on Attachment-Detachment Mechanics of a Rigid-Flexible Coupling Adhesive Unit. Biomimetics. 2022; 7(3):119. https://doi.org/10.3390/biomimetics7030119
Chicago/Turabian StyleJiang, Qijun, Liuwei Wang, Zhiyuan Weng, Zhouyi Wang, Zhendong Dai, and Weidong Chen. 2022. "Effect of the Structural Characteristics on Attachment-Detachment Mechanics of a Rigid-Flexible Coupling Adhesive Unit" Biomimetics 7, no. 3: 119. https://doi.org/10.3390/biomimetics7030119
APA StyleJiang, Q., Wang, L., Weng, Z., Wang, Z., Dai, Z., & Chen, W. (2022). Effect of the Structural Characteristics on Attachment-Detachment Mechanics of a Rigid-Flexible Coupling Adhesive Unit. Biomimetics, 7(3), 119. https://doi.org/10.3390/biomimetics7030119








