Multi-Joint Bionic Mechanism Based on Non-Circular Gear Drive
Abstract
1. Introduction
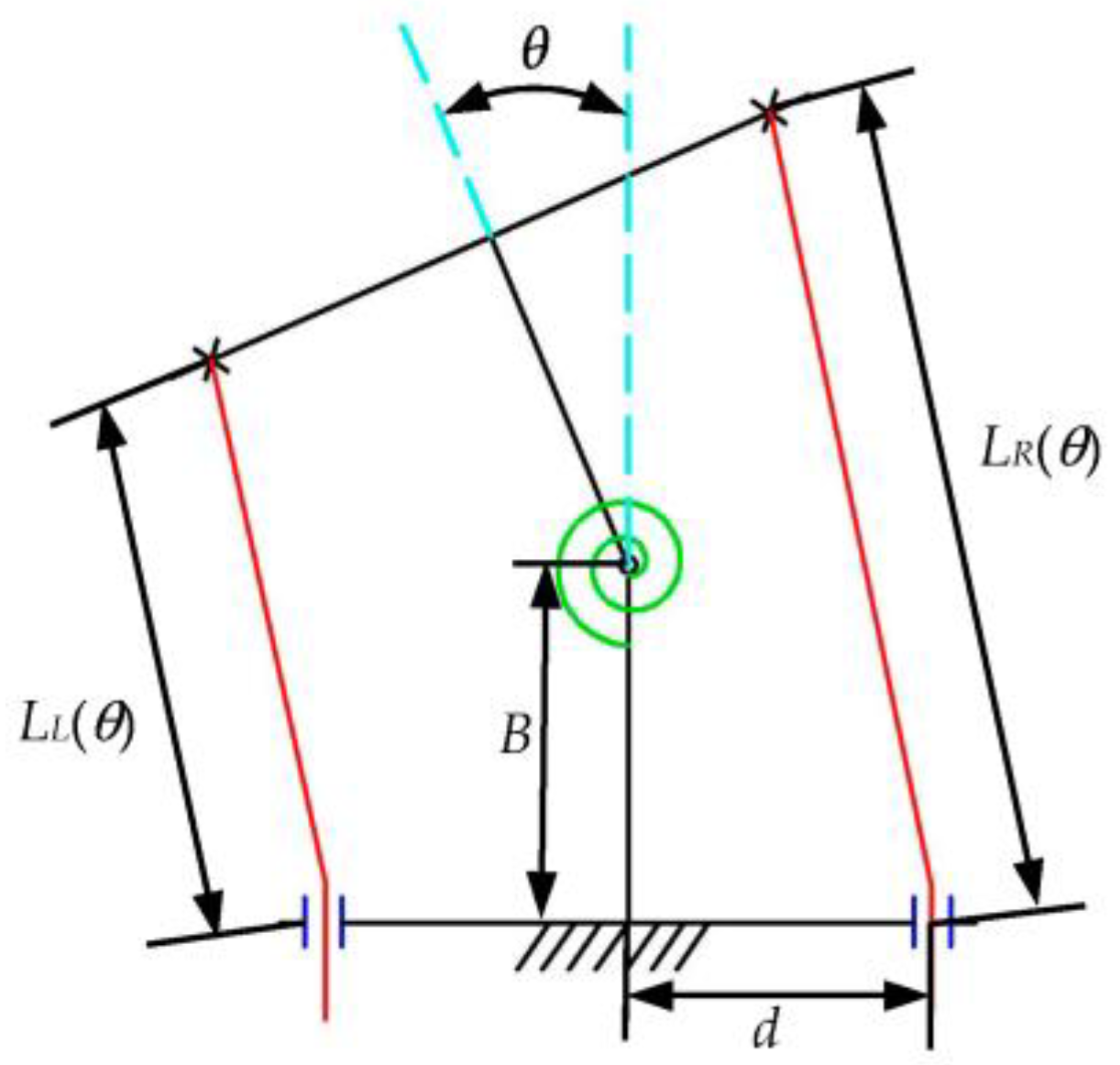
2. Principle of the Single-DOF Bending Mechanism
2.1. Single-DOF Simplest Bending Mechanism
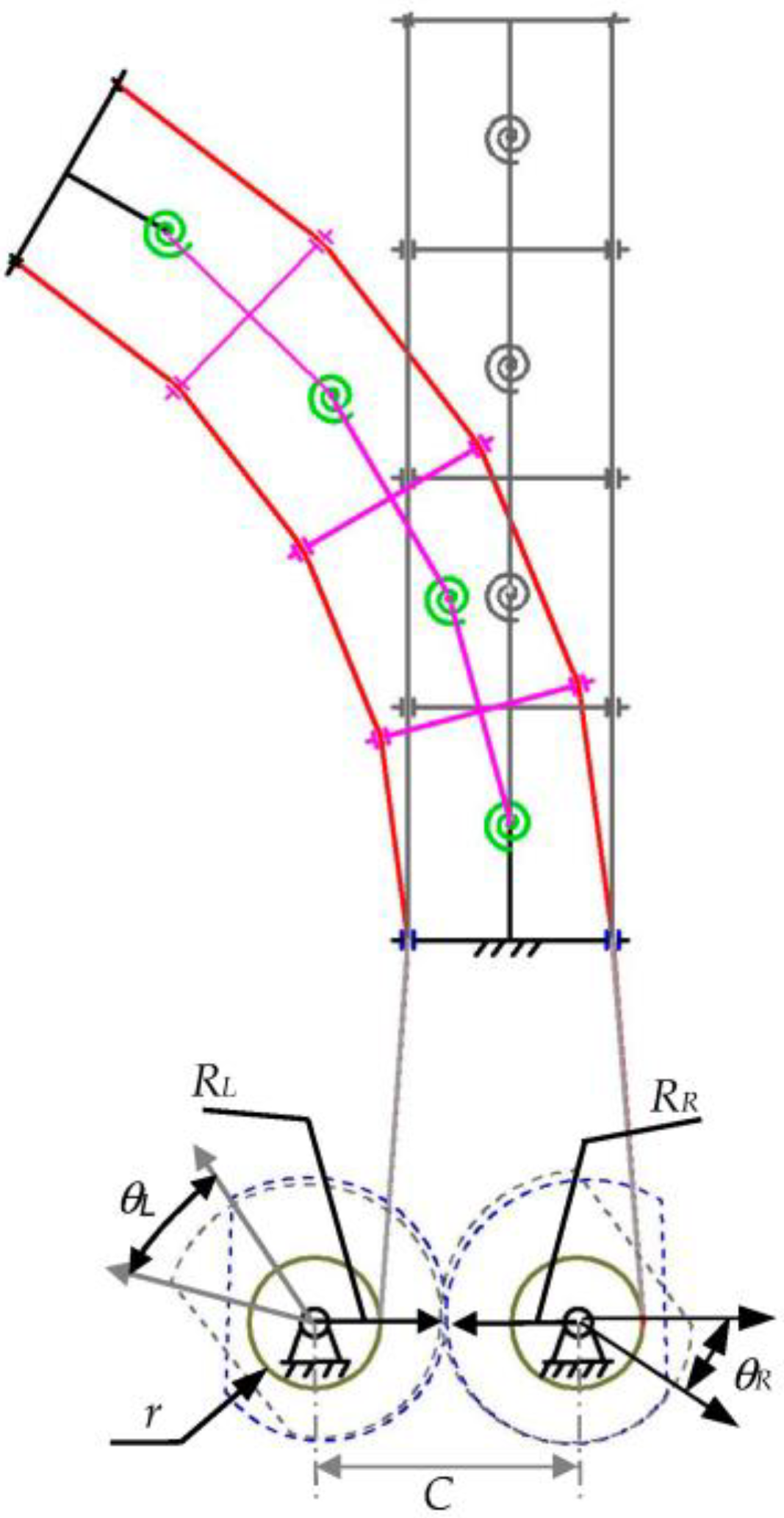
2.2. Single-DOF Multi-Joint Bending Mechanism
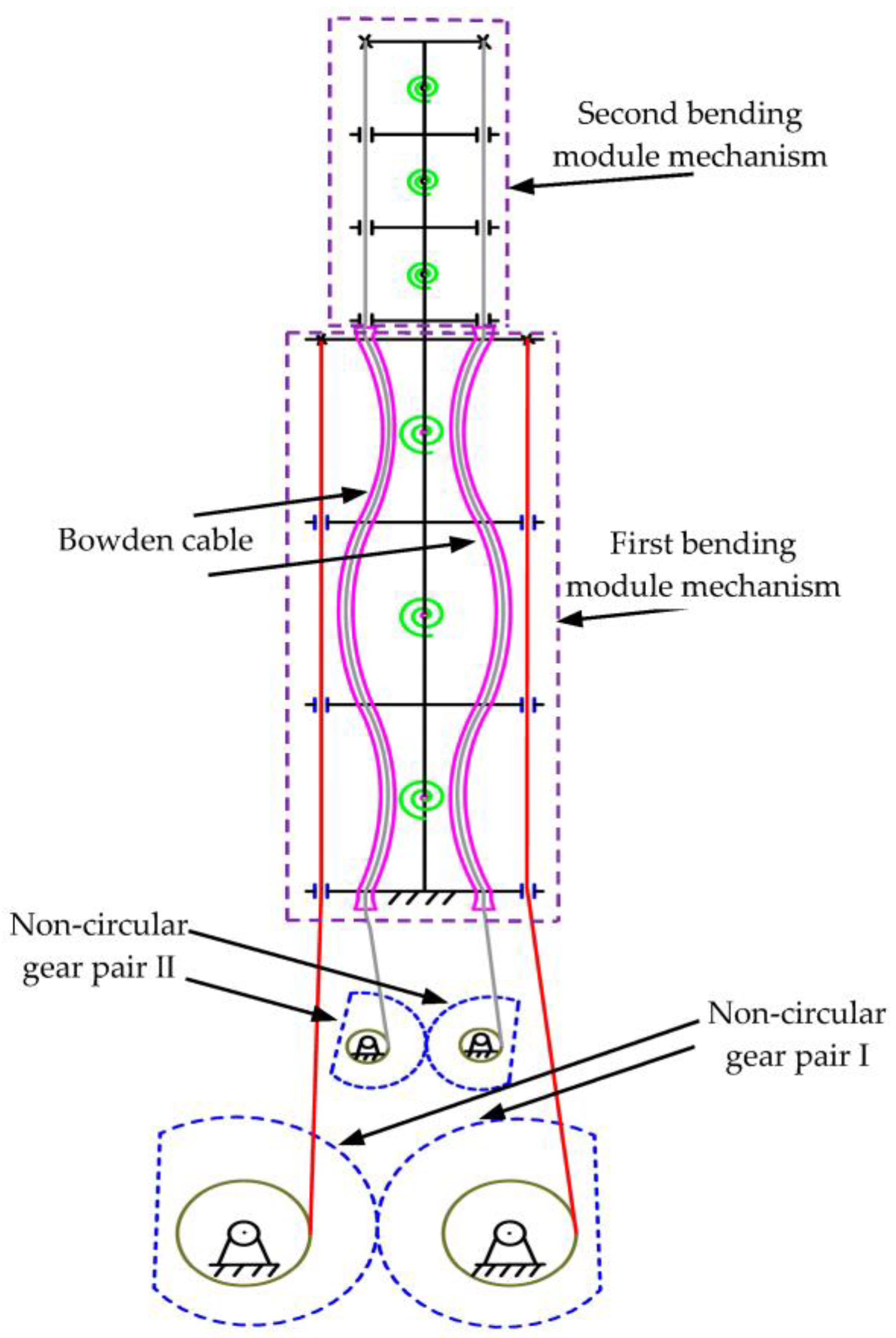
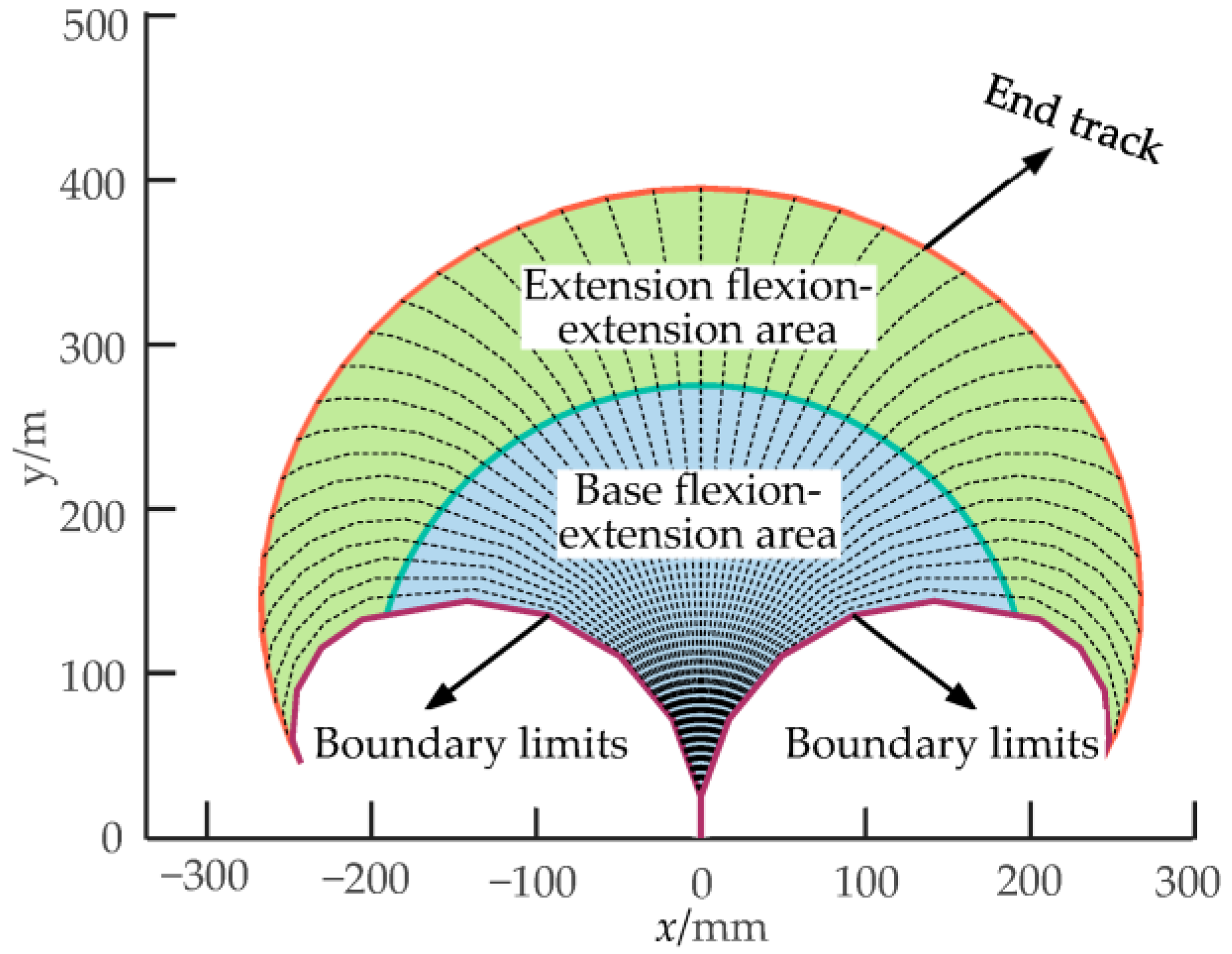
3. Multi-DOF Multi-Joint Bending Mechanism
4. Eliminate Backlash for Beveloid Non-Circular Gears
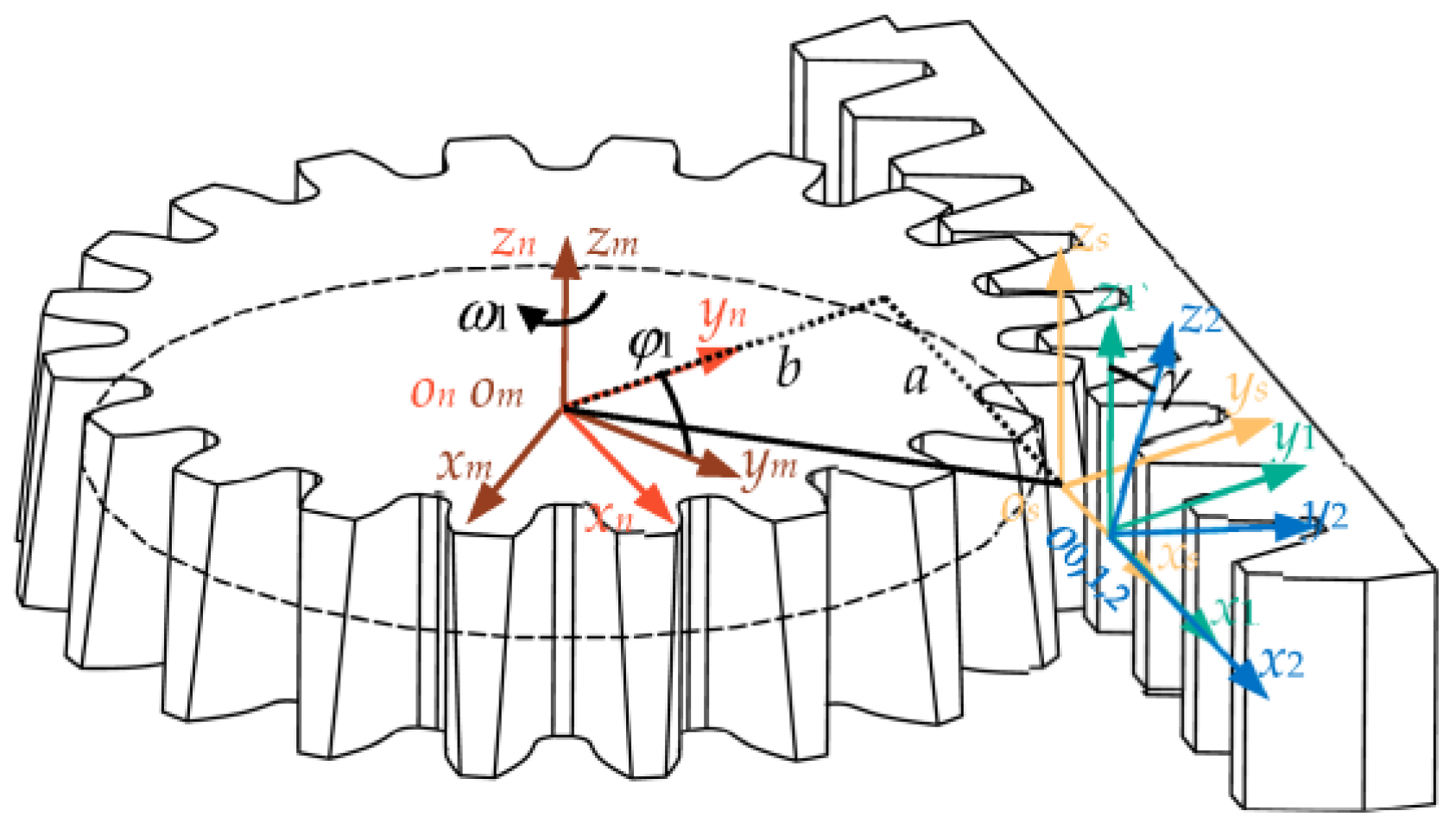
4.1. Eliminate Backlash Principle of Parallel-Shaft Beveloid Non-Circular Gears
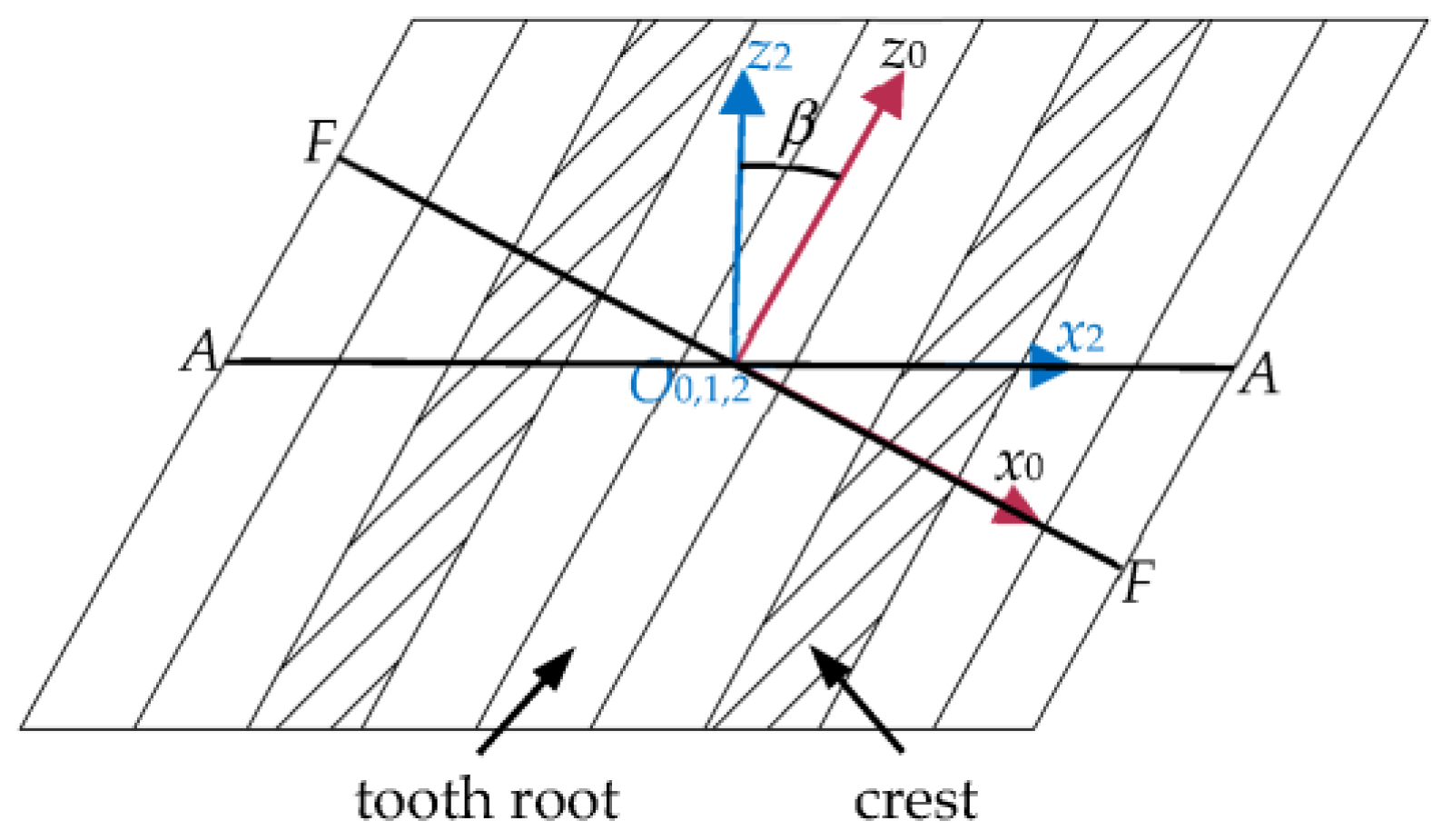
4.2. Enveloping Principle of Parallel-Shaft Beveloid Non-Circular Gears
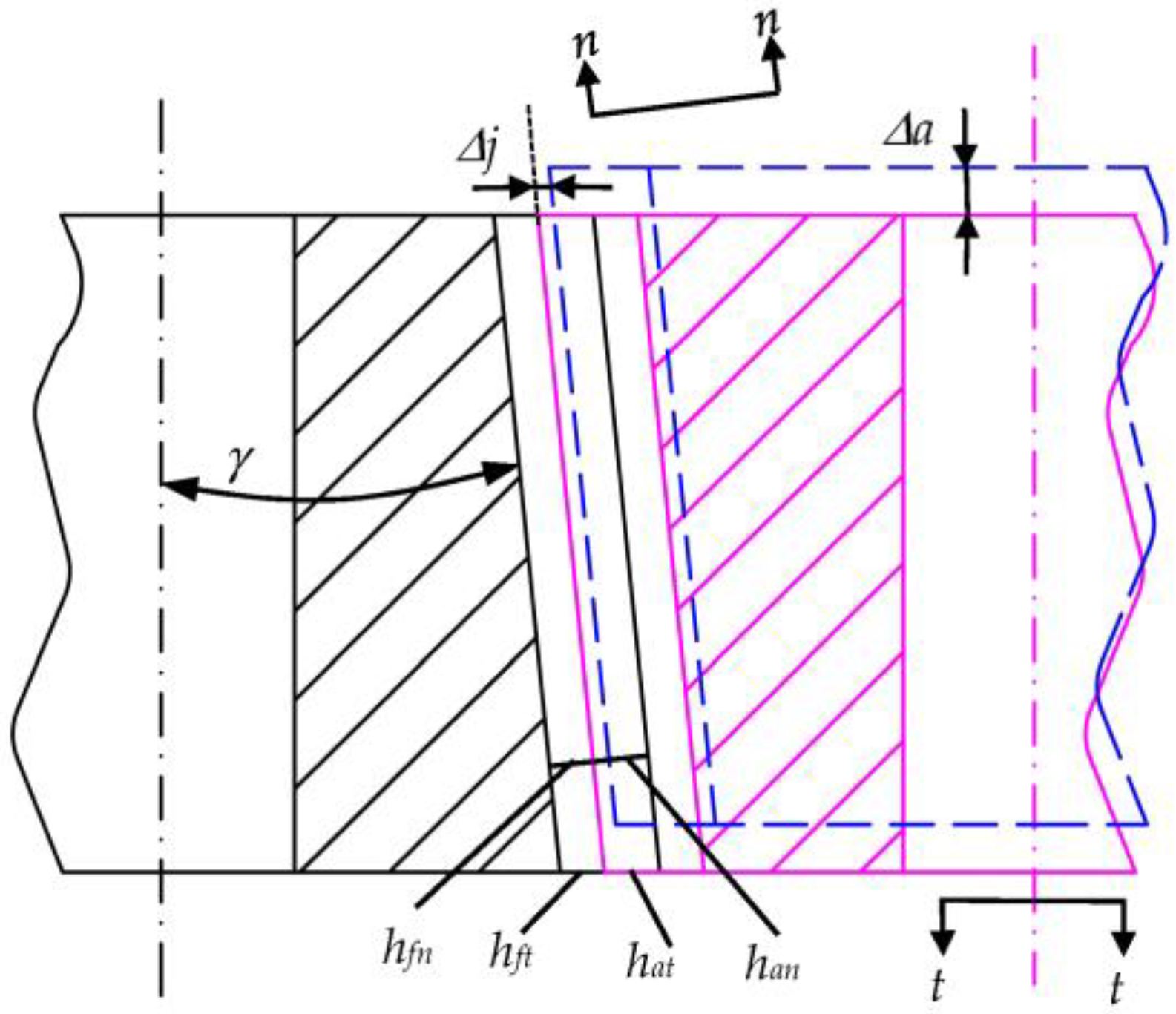
4.3. Parallel-Shaft Beveloid Non-Circular Gear Geometric Parameter Solution
5. Simulation and Test
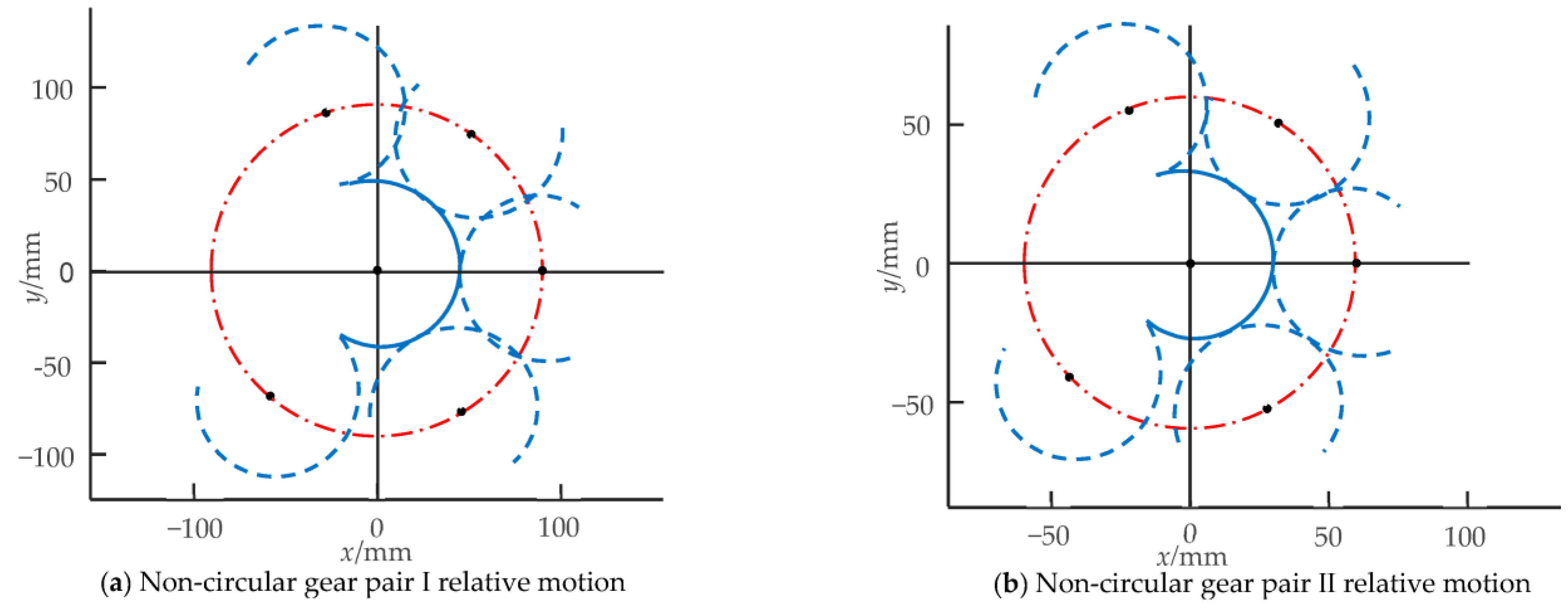
5.1. Non-Circular Gear Pitch Curve Calculation
5.2. Meshing Characteristics of the Tooth Surface without Installation Errors
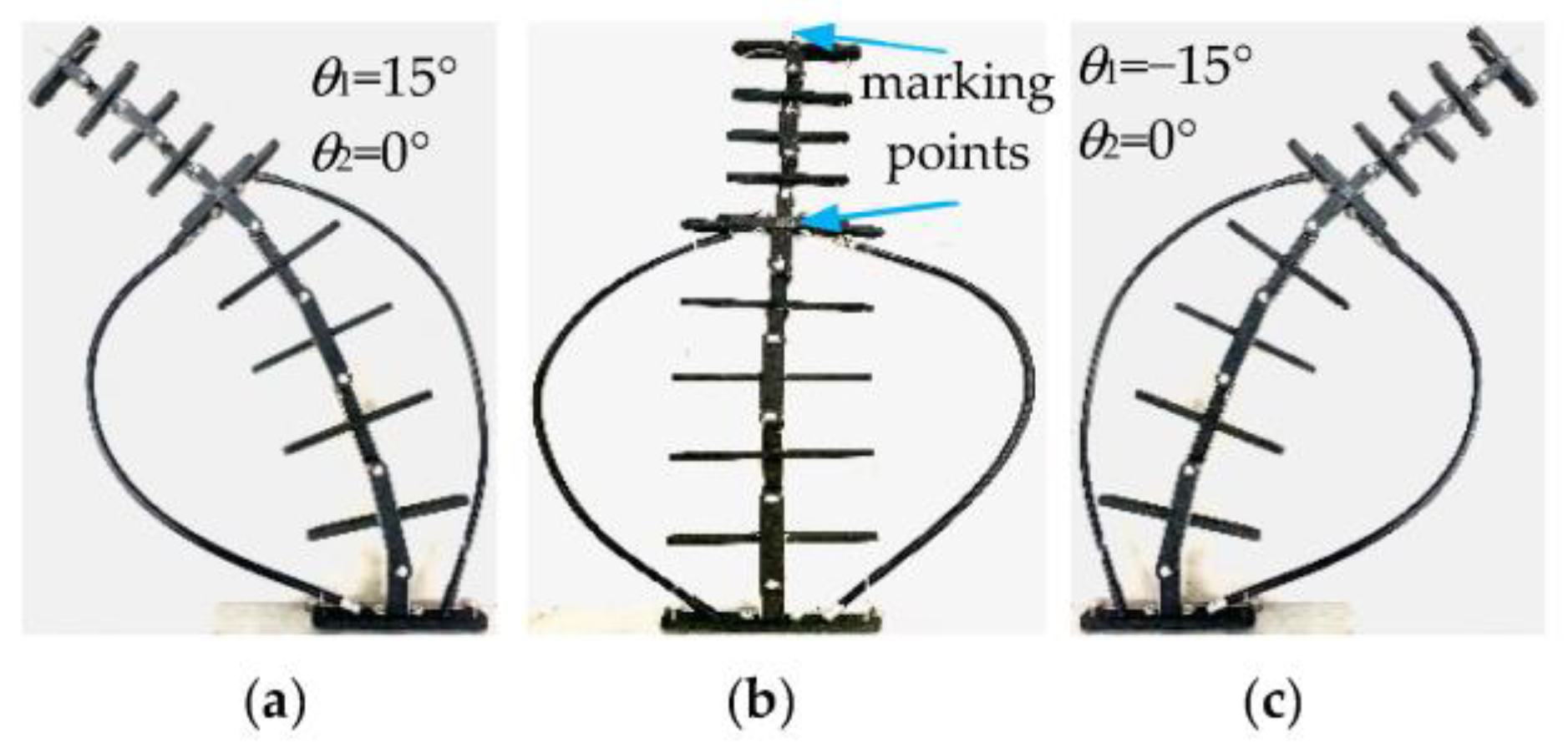
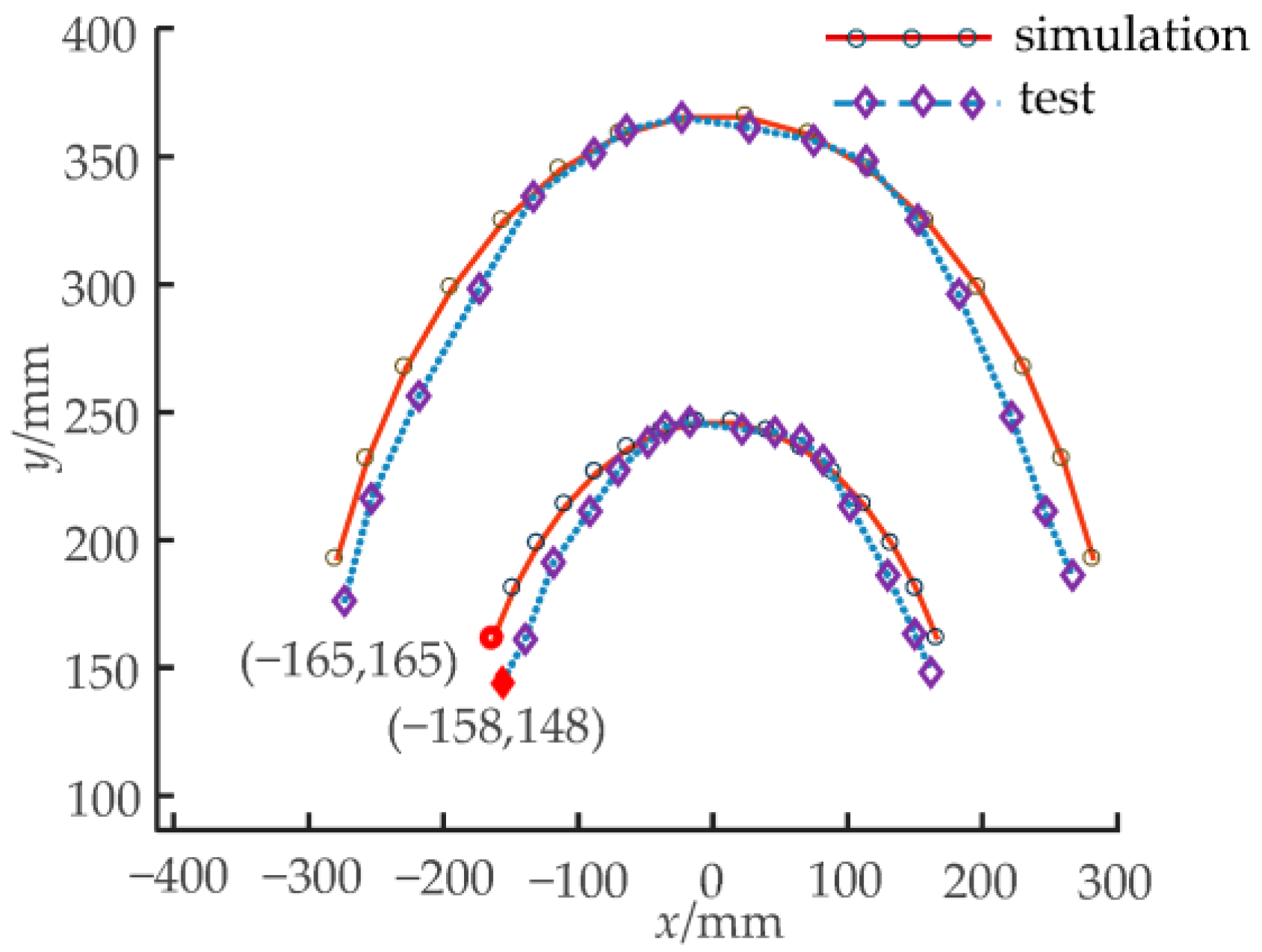
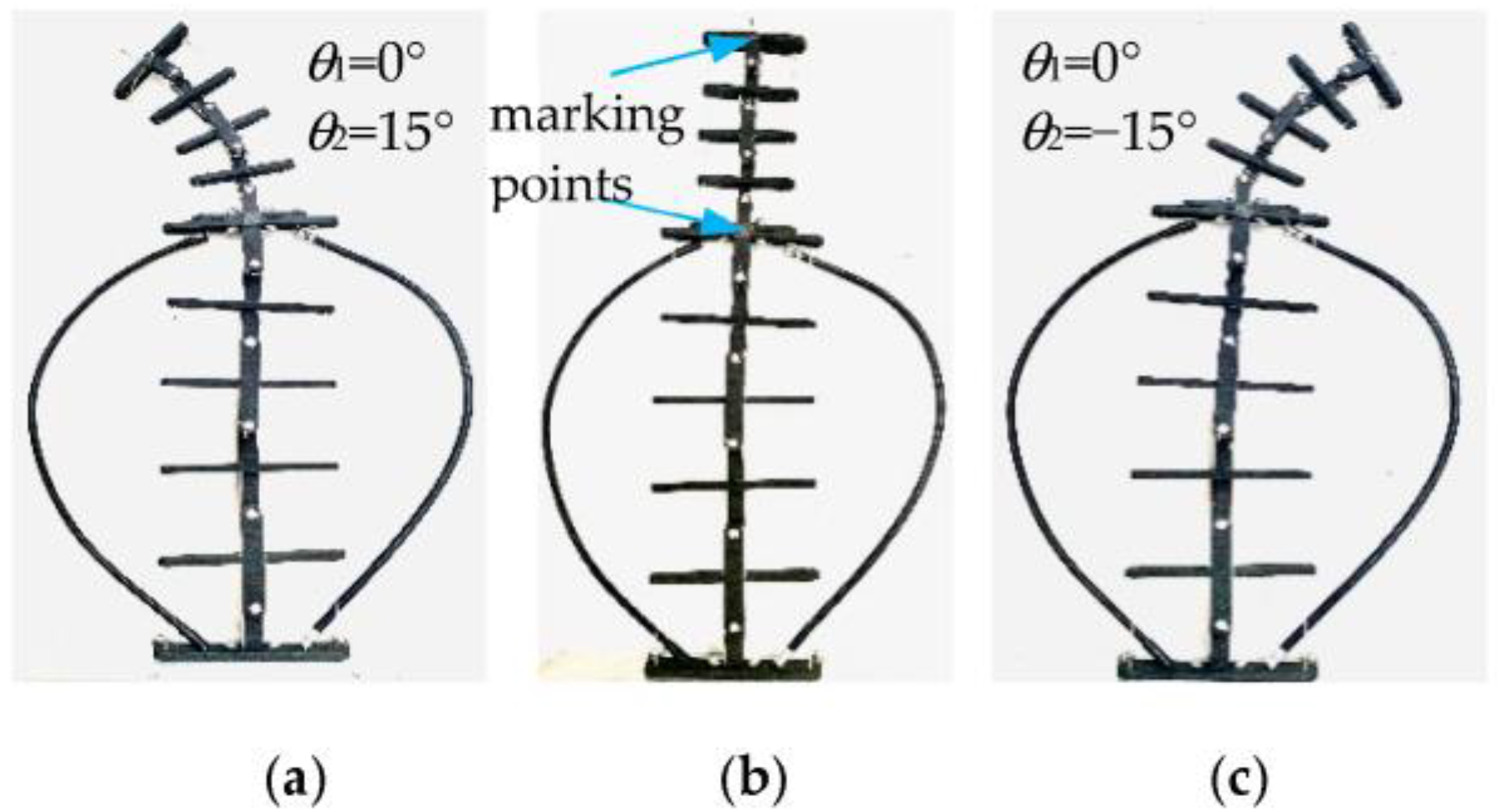
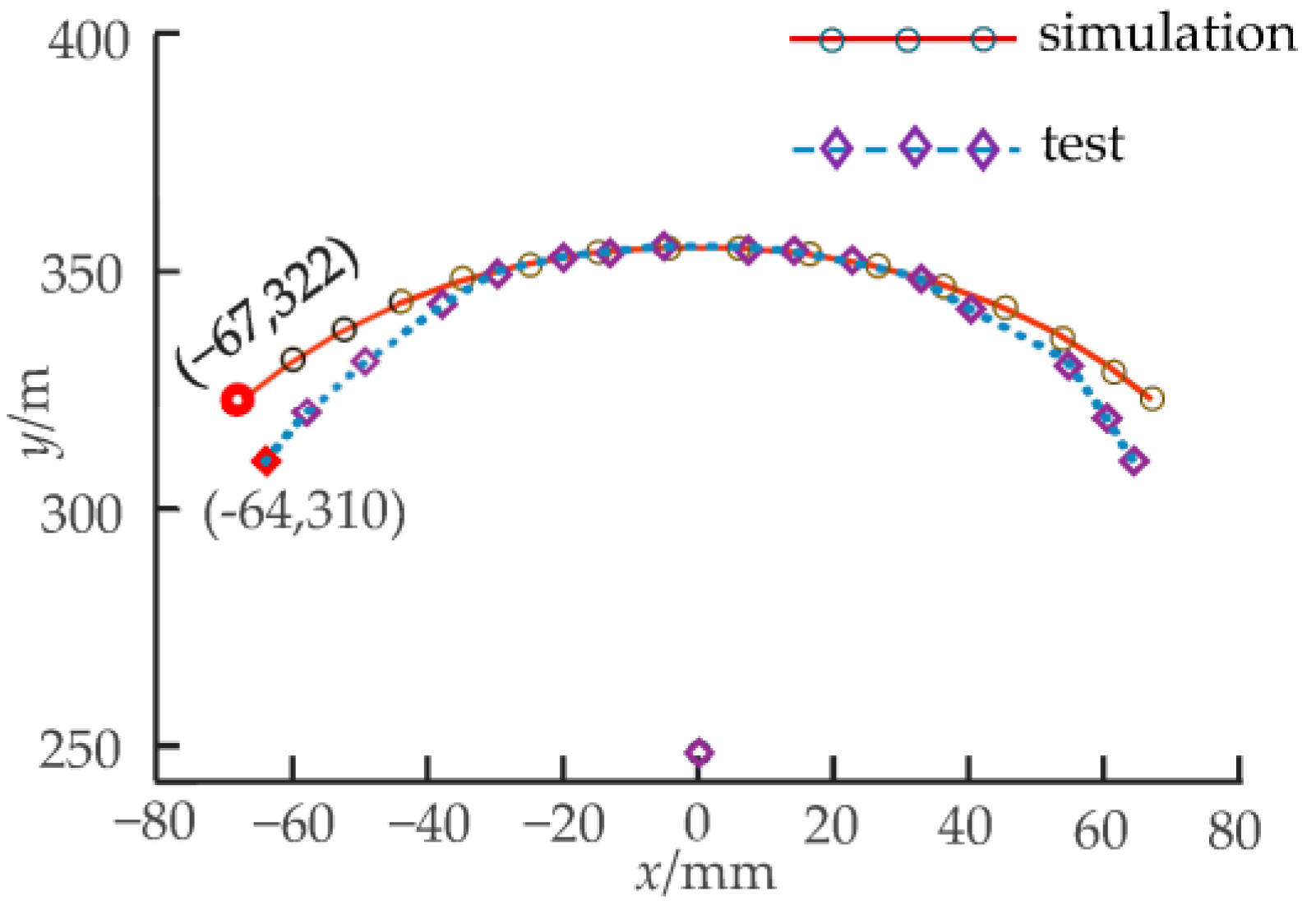
5.3. Workspace Comparison Test of Prototype
- (1)
- The stiffness of the torsion spring used in the prototype is too small to provide enough bending stiffness, so there is a certain error in the assumption of equal curvature of each joint in the bending process.
- (2)
- Due to the error of the initial position of the T-/cross-shaped component and the torsion spring, the hinge points of the multi-joint mechanism are not kept in a straight line at the initial position.
6. Conclusions
- (1)
- By designing the pitch curve of the non-circular gear matching the number of joints, the motion control of the multi-joint mechanism can be achieved by using only one motor, without detecting the angle of the cable wheel. This scheme can minimize the control difficulty of multi-joint mechanisms and reduce the system cost.
- (2)
- In order to solve the coupling problem of a two-DOF or multi-DOF multi-joint bending mechanism, a decoupling scheme driven by a Bowden line was proposed. This scheme can achieve the independent control of different bending modules of the bionic mechanism and improve the working space and flexibility of the bionic mechanism.
- (3)
- For high-precision multi-joint mechanisms, the backlash can be reduced by the relative axial movement of beveloid non-circular gears. The influence of hysteresis on the motion accuracy of multi-joint mechanisms can be eliminated.
- (4)
- The non-circular gear-driven multi-joint mechanism can provide a reliable and simple bionic spine for bionic robotic fish, bionic quadruped robots, etc. At the same time, the drive scheme based on non-circular gears can also be extended to cable-driven continuous mechanisms.
Author Contributions
Funding
Conflicts of Interest
References
- Lei, J.T.; Zhang, Y.W.; Rao, J.J. Research progress of rigid-soft coupled bionic spine of four-legged robot. Sci. Technol. Rev. 2020, 38, 35–49. [Google Scholar]
- Wang, A.Y.; Liu, G.J.; Wang, X.B.; Fu, B.B. Research progress and analysis of body/caudal fin propulsion model of bionic robotic fish. J. Mech. Eng. 2016, 52, 137–146. [Google Scholar] [CrossRef]
- Zhong, Y.; Li, Z.; Du, R. A novel robot fish with wire-driven active body and compliant tail. Trans. Mechatron. 2017, 22, 1633–1643. [Google Scholar] [CrossRef]
- Xue, Z.H.; Liu, J.G. Research review on space robotic arm control technology. Robotics 2022, 44, 108–128. [Google Scholar]
- Lina, Germany Festo Has Produced 3 More Bionic Robot Black Technologies: Tentacles, Elephant Trunks, Arms [EB/OL]. 2017. Available online: http://zhidx.com/p/77757.html (accessed on 1 April 2019).
- Lei, J.T.; Zhang, Y.W. Characteristics of biovaria stiffness of biometic organisms driven by pneumatic muscle fibers. J. Mech. Eng. 2022, 58, 1–12. [Google Scholar]
- Shen, S.; Lei, J.T.; Zhang, Y.W. Position/Stiffness control of aero-series elastic joints of bionic jumping robot. China Mech. Eng. 2021, 32, 1486–1493. [Google Scholar]
- Sun, K.Q.; Tian, Y.D. Numerical investigation of a bioinspired multi-segment soft pneumatic actuator for grasping applications. Mater. Today Commun. 2022, 31, 103449. [Google Scholar] [CrossRef]
- Yang, Q.; Zhang, L.; Bao, G.; Ruan, J. Pneumatic squirming robot based on flexible pneumatic actuator. Control Syst. Robot. 2005, 6042, 60422W. [Google Scholar]
- Liu, Z.Q.; Zhang, X.; Liu, H.W.; Chen, Y.; Huang, Y.; Chen, X. Kinematic modelling and experimental validation of a foldable pneumatic soft manipulator. Appl. Sci. 2020, 10, 1447. [Google Scholar] [CrossRef]
- Yuan, H.; Li, Z.; Wang, H.M.; Song, C.Z. Static modeling and analysis of continuum surgical robots. Int. Conf. Robot. Biomim. 2016, 10, 1109. [Google Scholar]
- Suh, J.; Kim, K.; Jeong, J.; Lee, J. Design considerations for a hyper-redundant pulley-less rolling joint with elastic fixtures. Trans. Mechatron. 2015, 20, 2841–2852. [Google Scholar] [CrossRef]
- Suh, J.; Kim, K. Harmonious cable actuation mechanism for soft robot joints using a pair of non-circular pulleys. J. Mech. Robot. 2018, 10, 061002. [Google Scholar] [CrossRef]
- Geng, H.; Guo, Z.F. Structural design and mechanical analysis of rope-driven super-redundant manipulator. Mach. Tool Hydraul. 2022, 50, 11–15. [Google Scholar]
- Wei, G.W.; Xu, Z.B.; Zhao, Z.Y. Design and kinematic simulation of linear drive continuous robotic arm. Mech. Transm. 2019, 43, 32–38+53. [Google Scholar]
- Wei, G.W. Space Continuous Robotic Arm Design and Kinematic Simulation; Changchun Institute of Optics Fine Mechanics and Physics, Chinese Academy of Sciences: Changchun, China, 2019. [Google Scholar]
- Amare, Z.; Zi, B.; Qian, S.; Du, J.; Ge, Q.J. Three-dimensional static and dynamic stiffness analyses of the cable driven parallel robot with non-negligible cable mass and elasticity. Mech. Based Des. Struct. Mach. 2017, 46, 455–482. [Google Scholar] [CrossRef]
- Lin, J.; Wu, C.Y.; Chang, J.L. Design and implementation of a multi-degrees-of-freedom cable-driven parallel robot with gripper. Int. J. Adv. Robot. Syst. 2018, 15, 1729881418803845. [Google Scholar] [CrossRef]
- Fan, X.; Wang, H.T.; Ding, L.; Xie, S. Bending deformation prediction method of soft actuators with pneumatic networks. China Mech. Eng. 2020, 31, 1108–1114. [Google Scholar]
- Santina, C.D.; Bicchi, A.; Rus, D. On an improved state parametrization for soft robots with piecewise constant curvature and its use in model based control. Robot. Autom. Lett. 2020, 5, 1001–1008. [Google Scholar] [CrossRef]
- Song, H.Z. Theoretical Analysis and Design Research Based on Variable Thickness Non-Circular Gear Transmission; Beijing University of Posts and Telecommunications: Beijing, China, 2016. [Google Scholar]

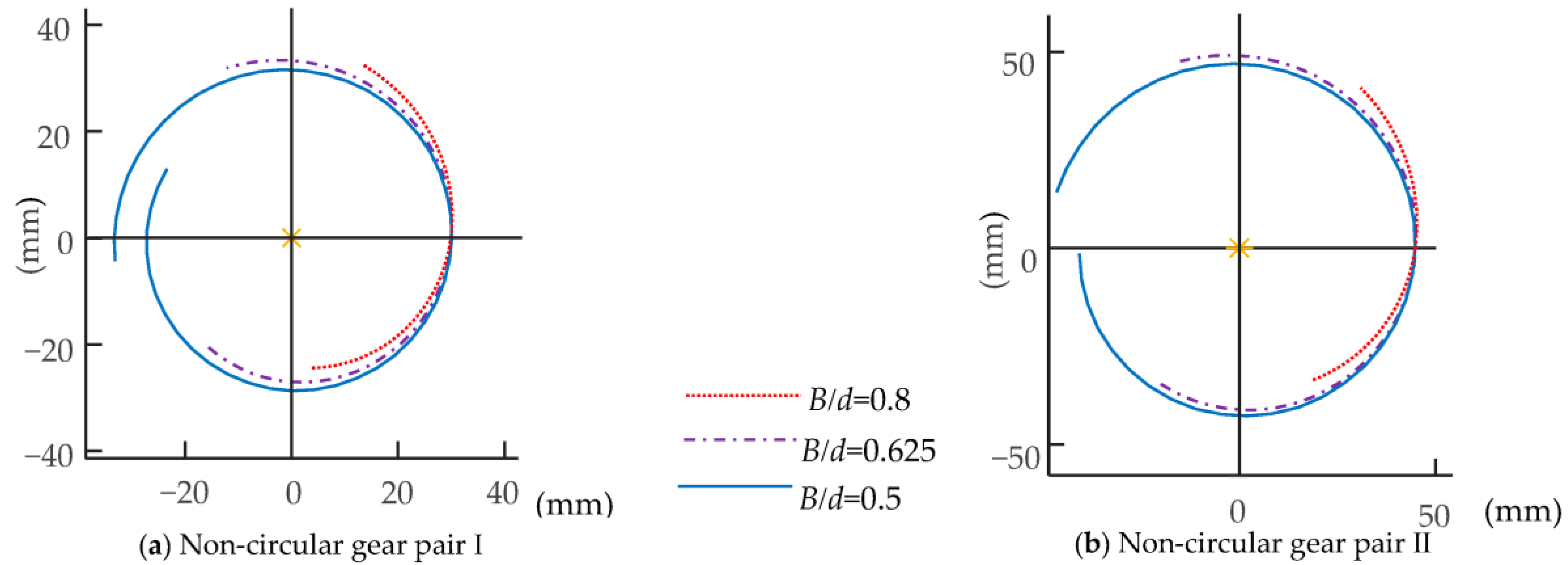


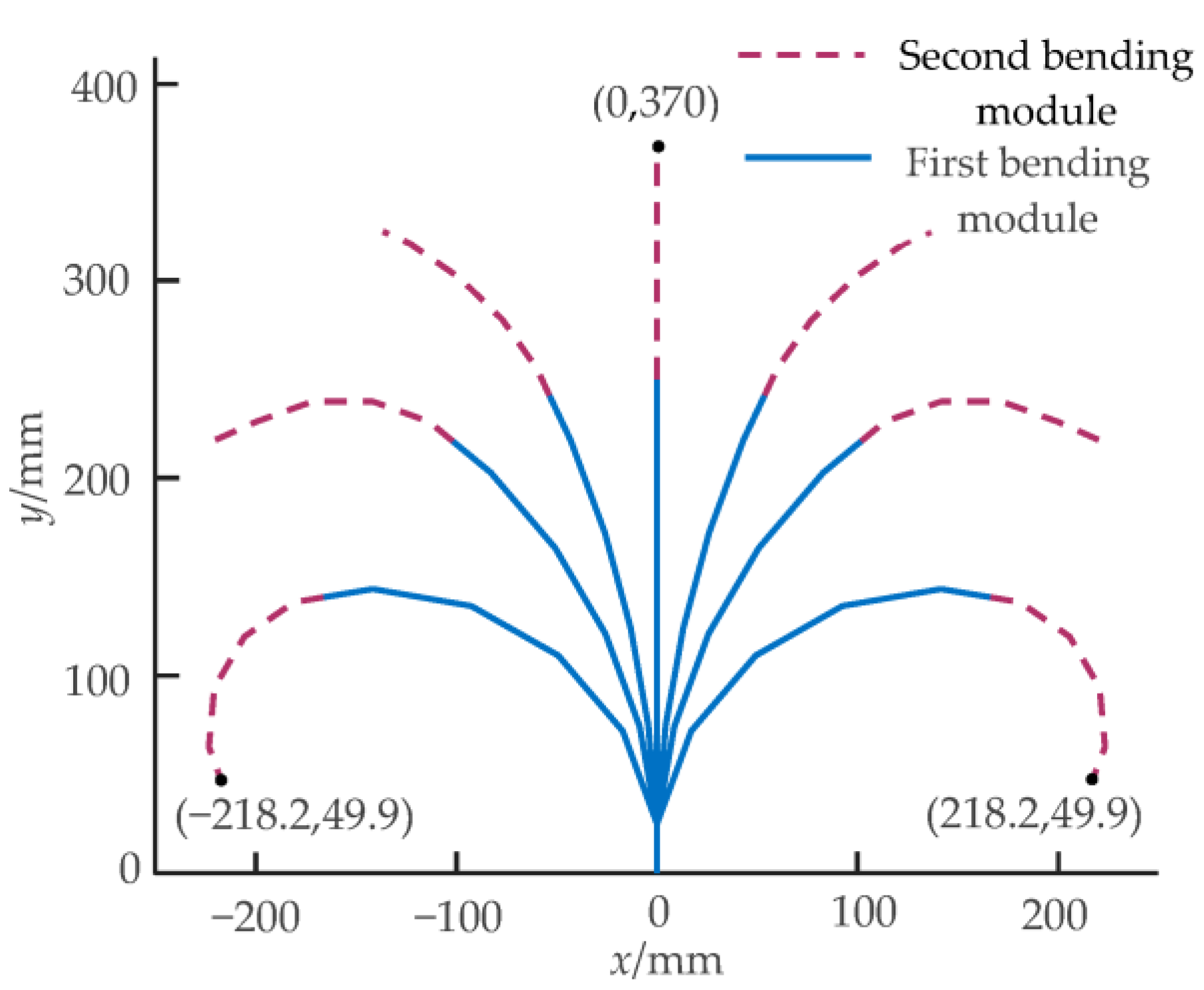

| First bending module mechanism | Cable wheel radius, r (mm) | 35 | ||
| Length of T-shaped component, B (mm) | 16 | 25 | 30 | |
| Length of cross-shaped component, 2B (mm) | 32 | 50 | 60 | |
| Width of cross-shaped component, 2d (mm) | 40 | 80 | 120 | |
| Component length ratio, B/d | 0.8 | 0.625 | 0.5 | |
| Total number of components, N | 5 | |||
| Center distance of non-circular gear, C (mm) | 90 | |||
| Second bending module mechanism | Cable wheel radius, r (mm) | 20 | ||
| Length of T-shaped component, B (mm) | 12 | 15 | 20 | |
| Length of cross-shaped component, 2B (mm) | 24 | 30 | 40 | |
| Width of cross-shaped component, 2d (mm) | 30 | 60 | 80 | |
| Component length ratio, B/d | 0.8 | 0.625 | 0.5 | |
| Total number of components, N | 4 | |||
| Center distance of non-circular gear, C (mm) | 60 | |||
| Working Condition | GearIration Angle (°) | GearIIration Angle (°) | First Module Bending Angle | Second Module Bending Angle |
|---|---|---|---|---|
| I | −88.9~81.9° | 0° | −15~15° | 0° |
| II | 0° | −74.7~68.9° | 0° | −15~15° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, D.; Zhang, T.; Cao, Y. Multi-Joint Bionic Mechanism Based on Non-Circular Gear Drive. Biomimetics 2023, 8, 272. https://doi.org/10.3390/biomimetics8030272
Liu D, Zhang T, Cao Y. Multi-Joint Bionic Mechanism Based on Non-Circular Gear Drive. Biomimetics. 2023; 8(3):272. https://doi.org/10.3390/biomimetics8030272
Chicago/Turabian StyleLiu, Dawei, Tao Zhang, and Yuetong Cao. 2023. "Multi-Joint Bionic Mechanism Based on Non-Circular Gear Drive" Biomimetics 8, no. 3: 272. https://doi.org/10.3390/biomimetics8030272
APA StyleLiu, D., Zhang, T., & Cao, Y. (2023). Multi-Joint Bionic Mechanism Based on Non-Circular Gear Drive. Biomimetics, 8(3), 272. https://doi.org/10.3390/biomimetics8030272





