Effect of Hindwings on the Aerodynamics and Passive Dynamic Stability of a Hovering Hawkmoth
Abstract
:1. Introduction
2. Materials and Methods
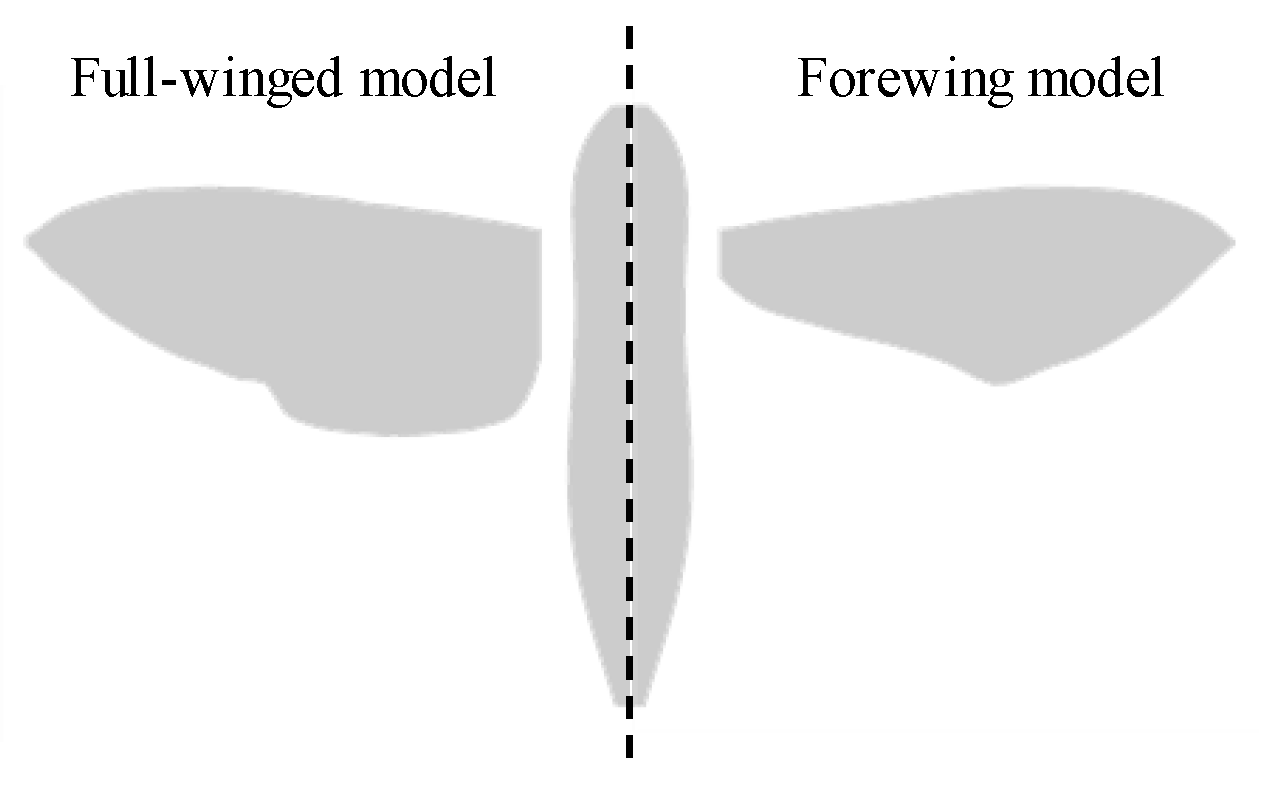
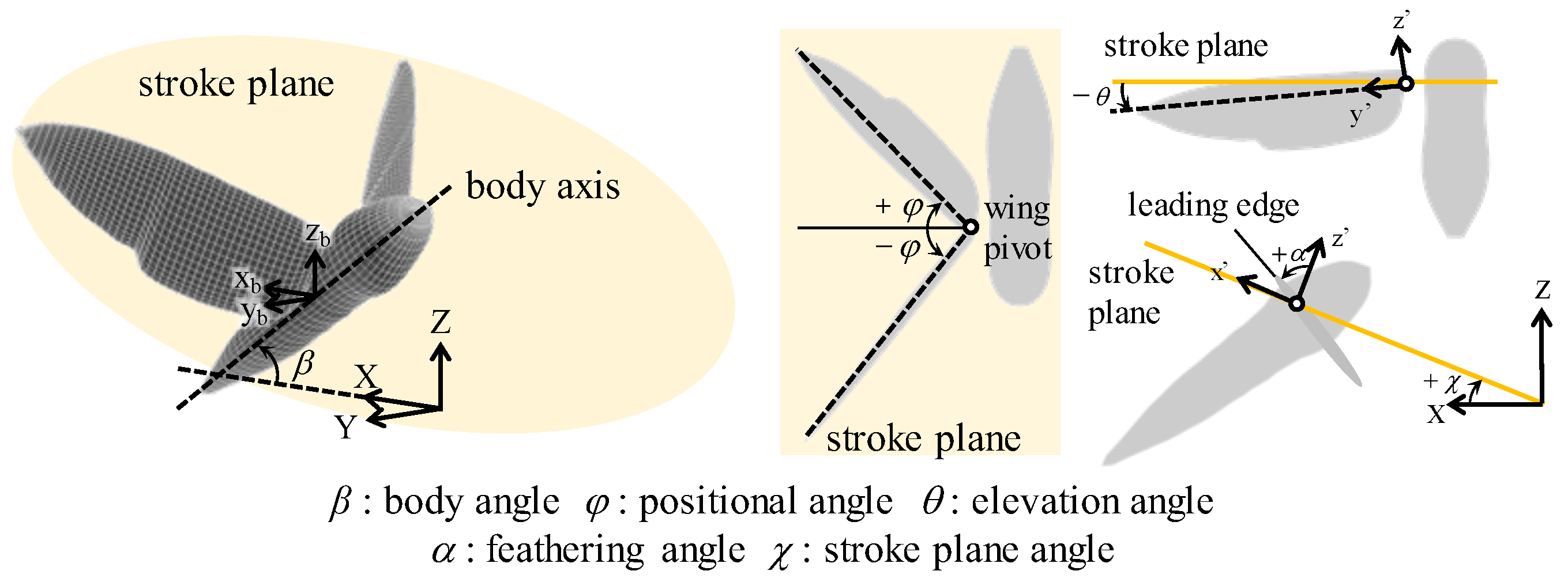
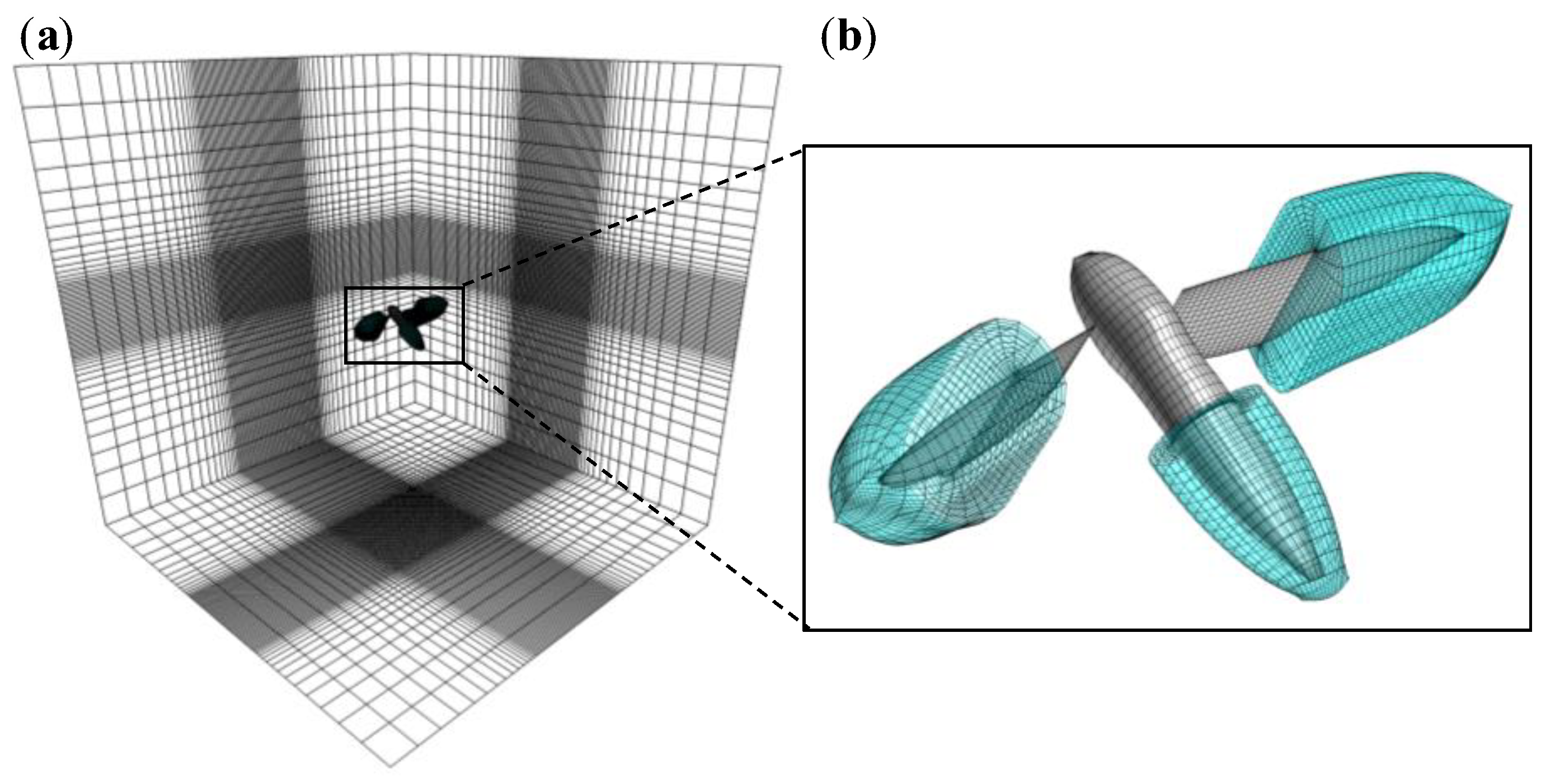
2.1. Morphological and Kinematic Model for a Hawkmoth with/without Hindwings
2.2. Numerical Model for Flow Field around a Flyer
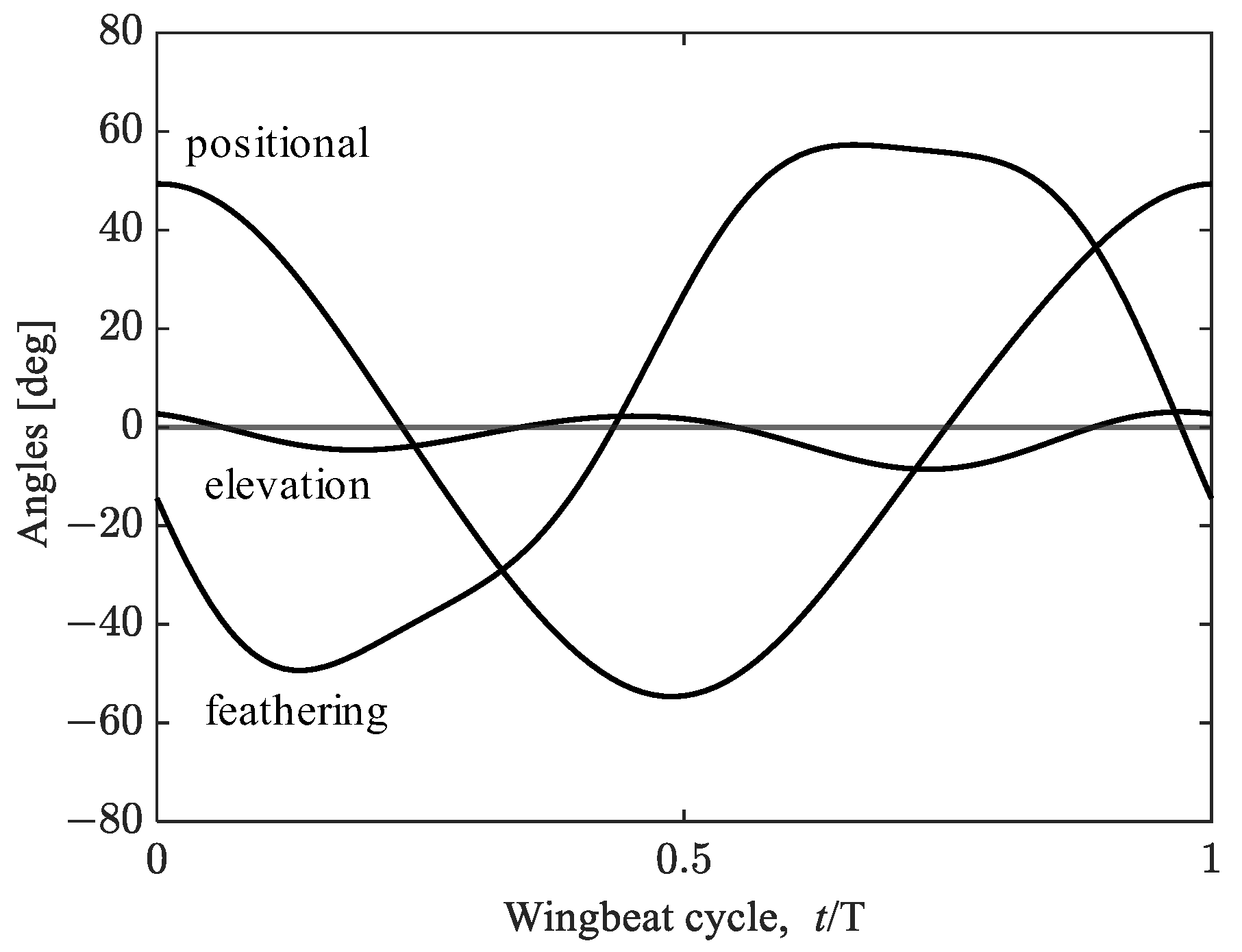
2.3. Wing Kinematics Modifications for Hovering Equilibrium Conditions
2.4. Numerical Model for Flight Dynamics: Equations of 3 DoF Motions
2.5. Nonlinear Stability Analysis Based on the Perturbation Theory
3. Results and Discussion
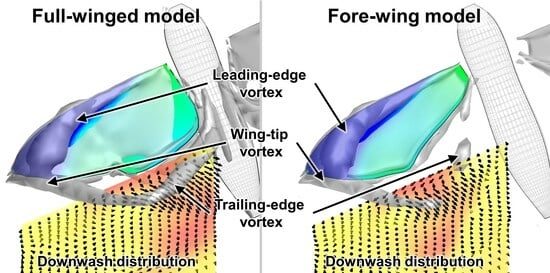
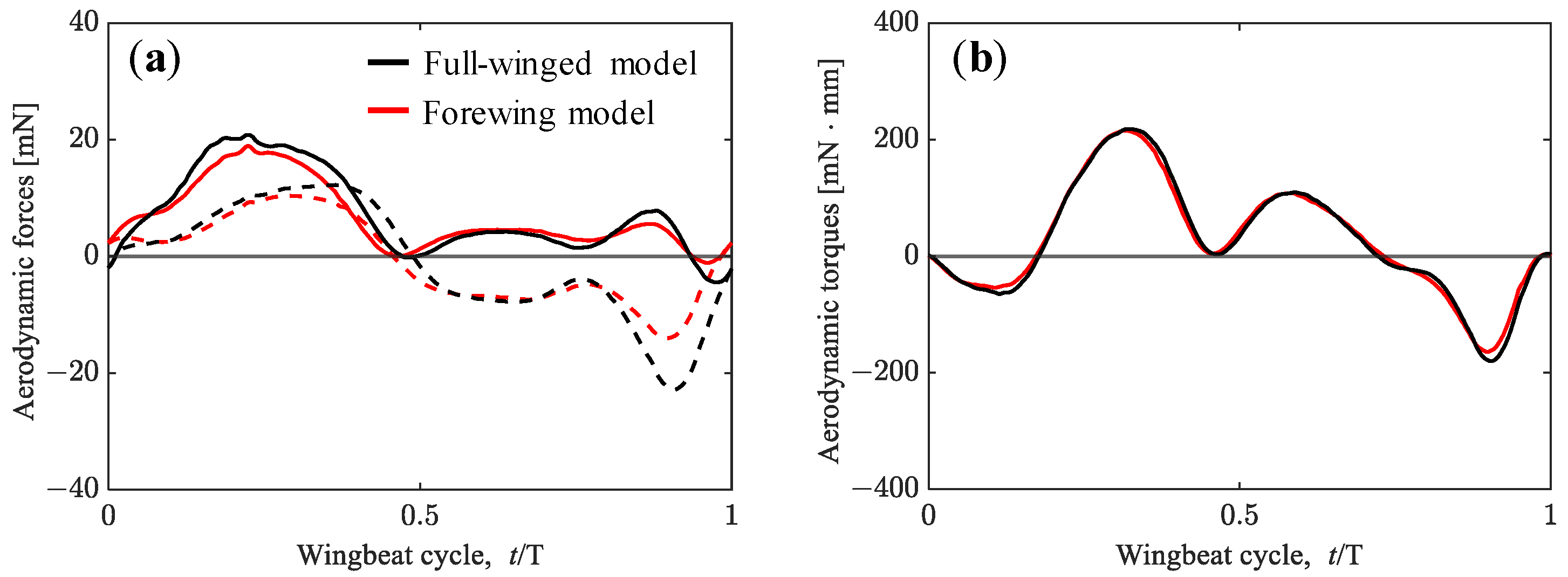
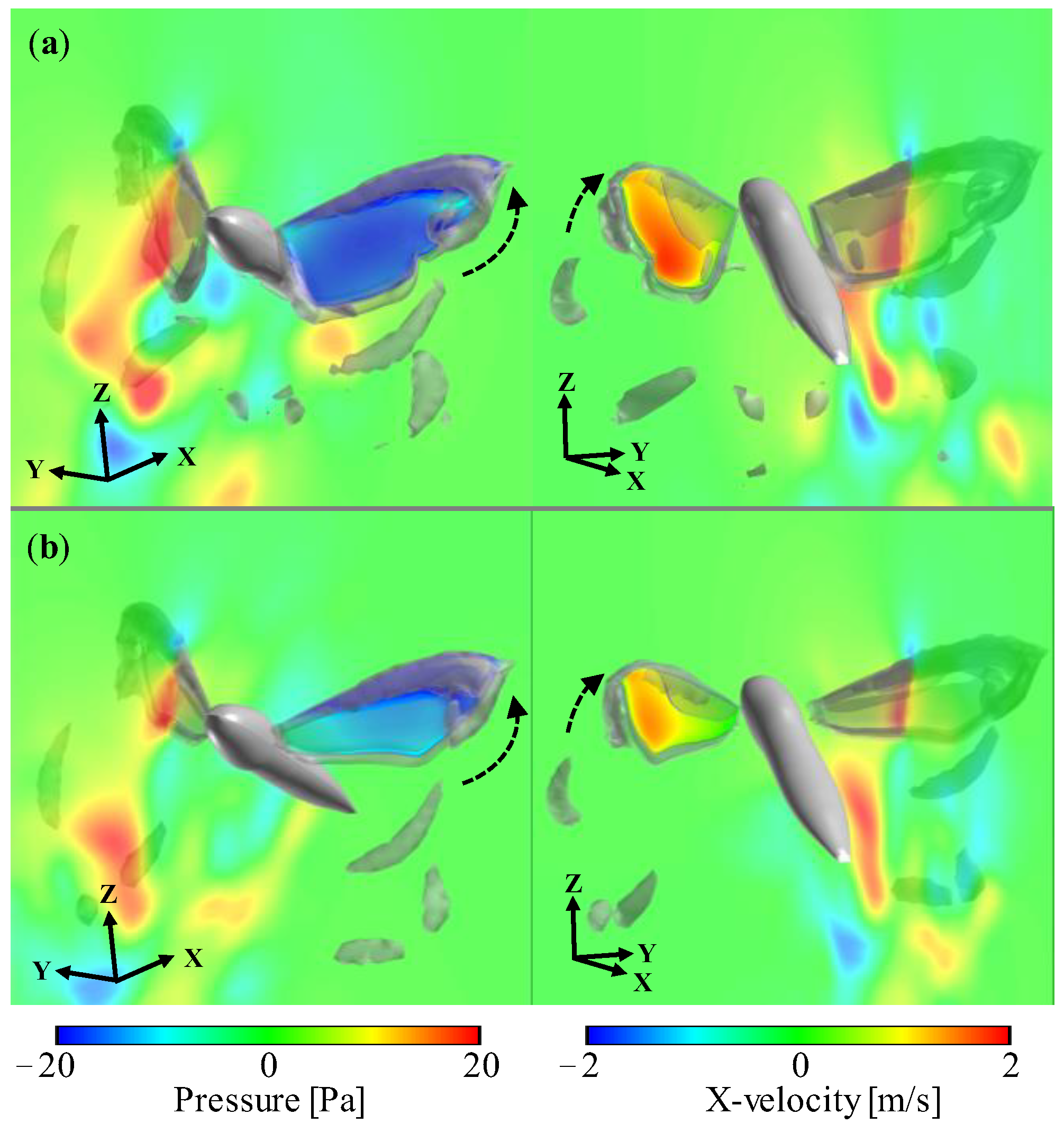
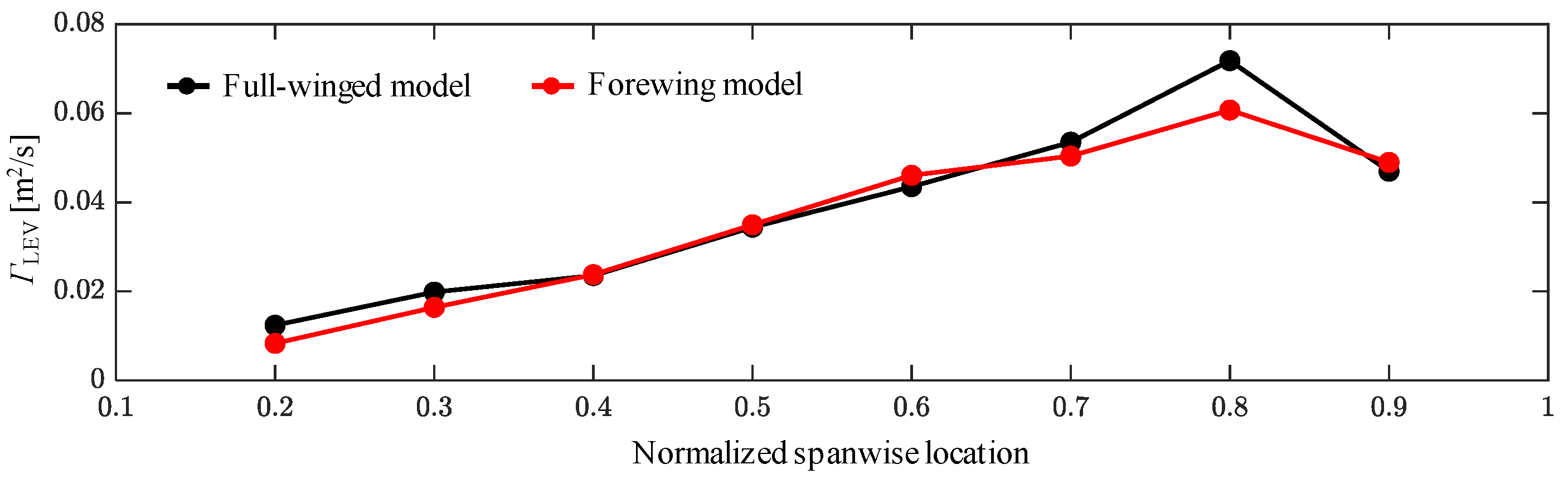
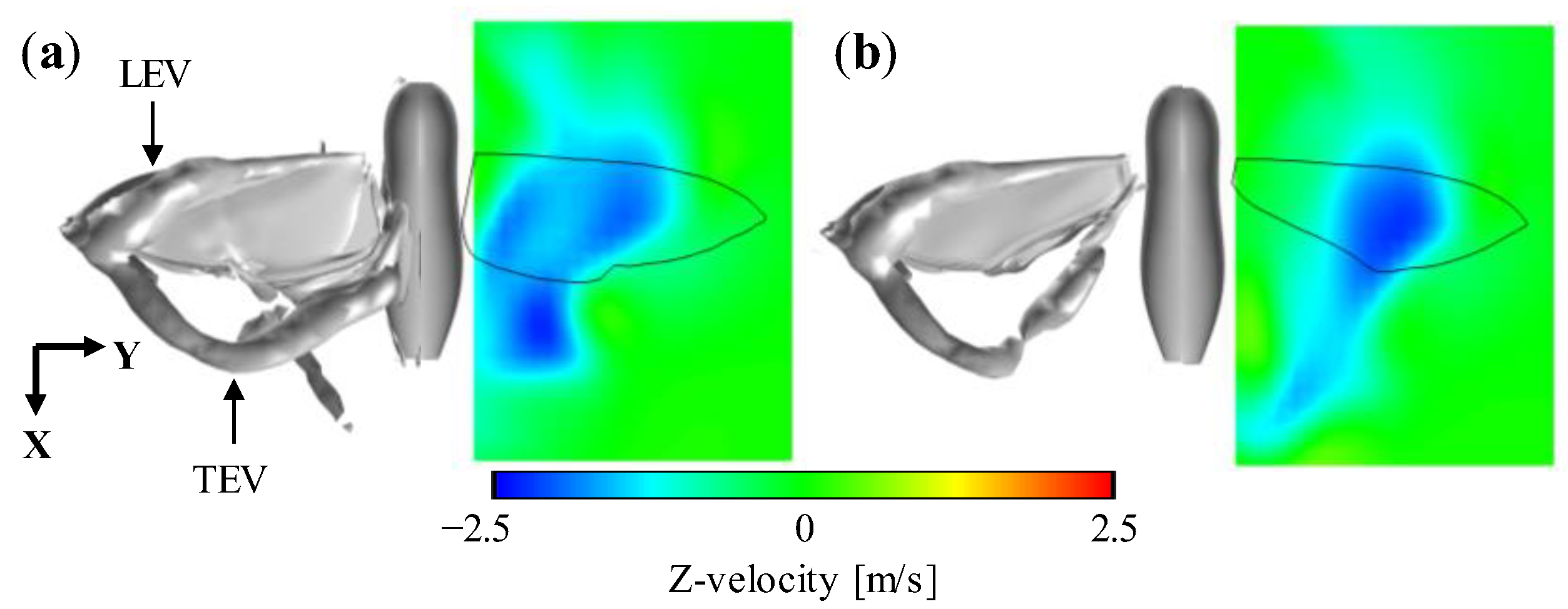
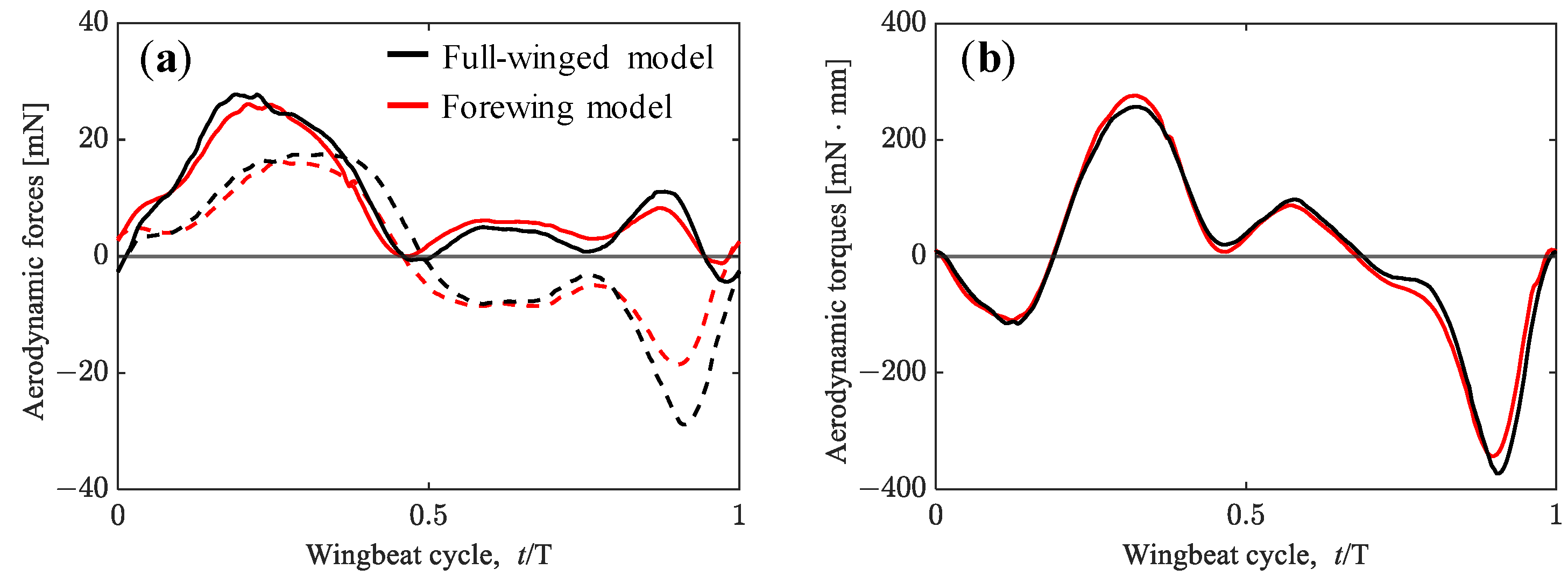
3.1. Aerodynamic Performance of a Hawkmoth with/without Hindwings
3.2. Hovering Equilibrium Condition
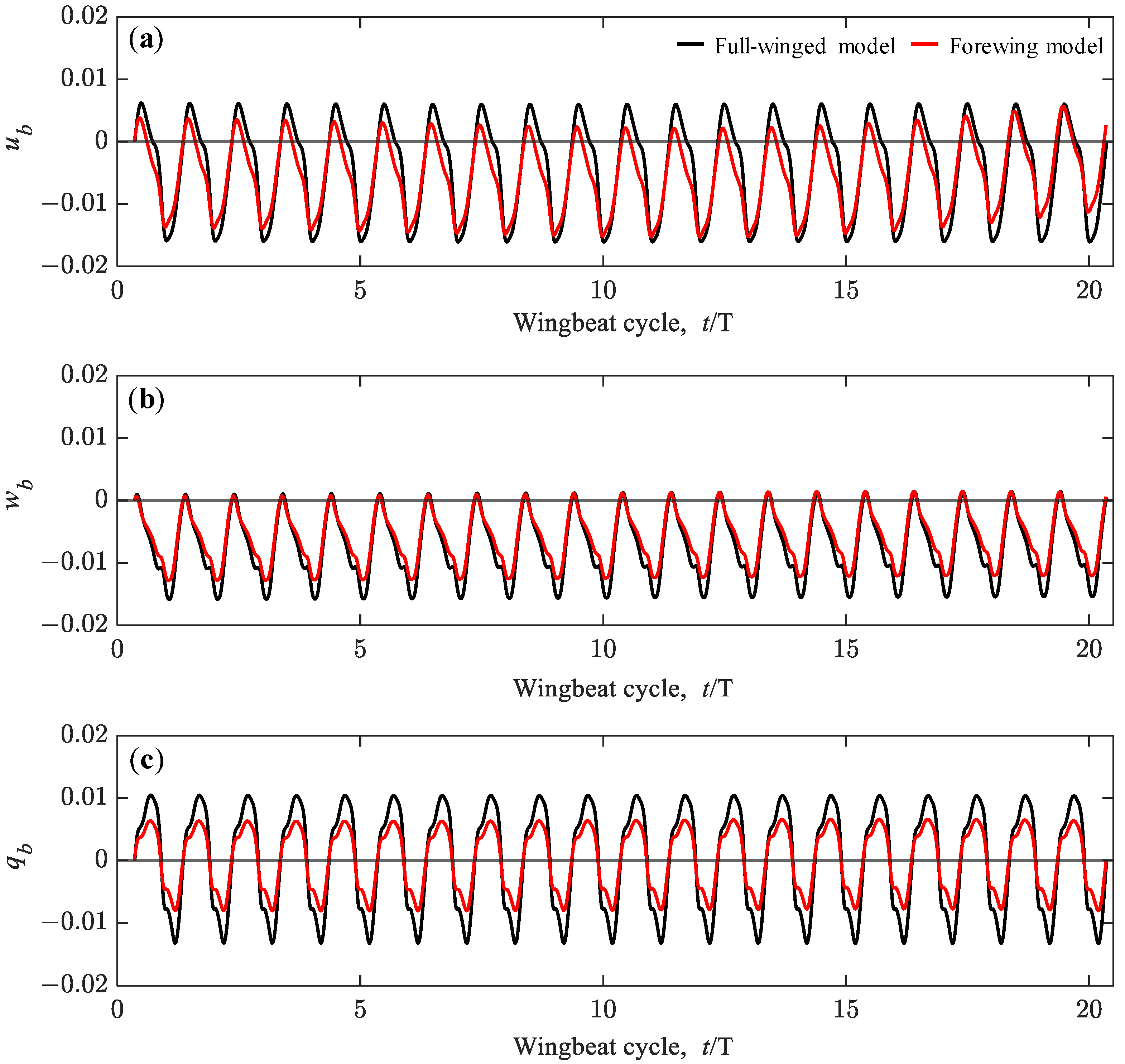
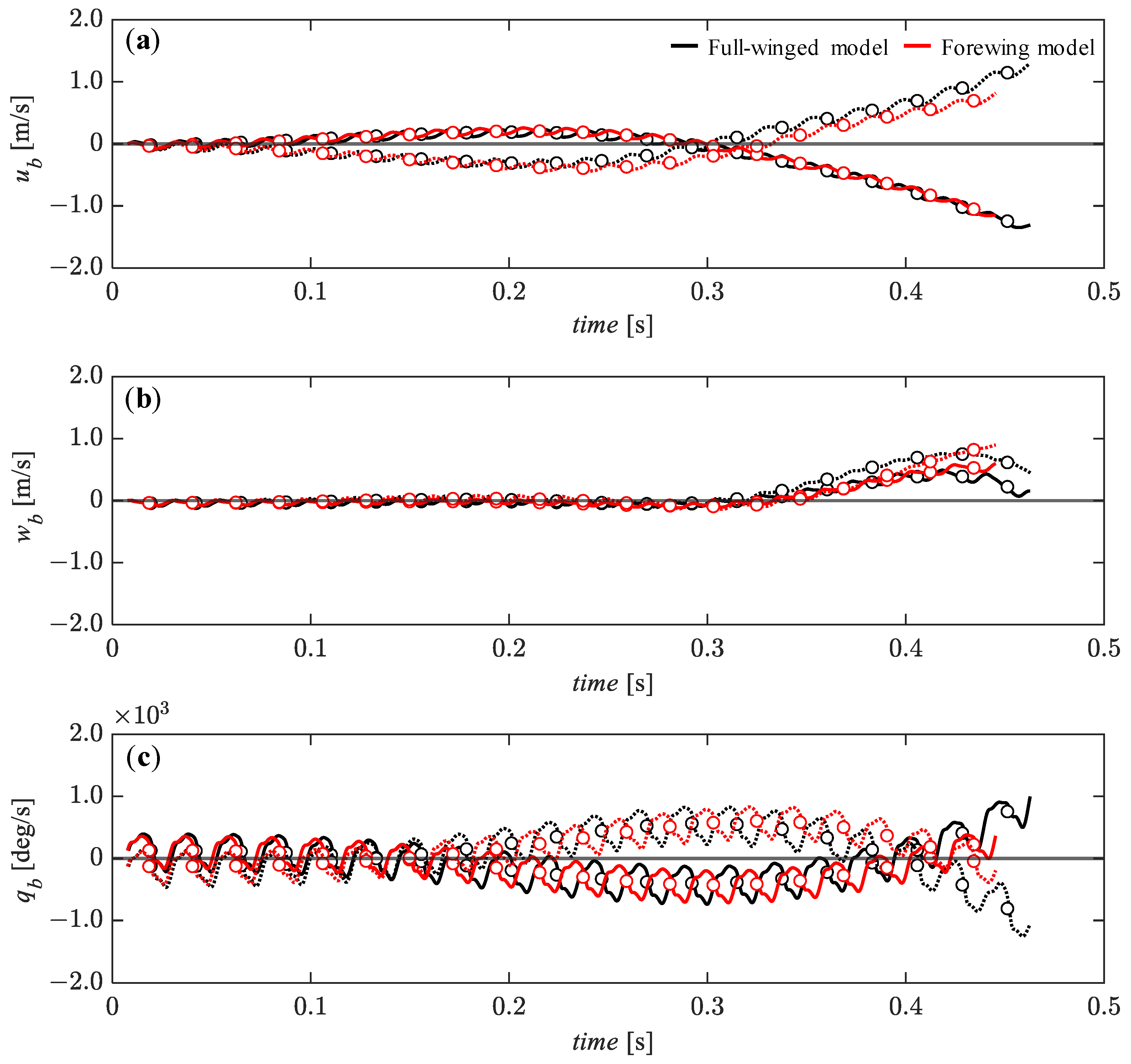
3.3. Passive Dynamic Stability with Relative Small Perturbations
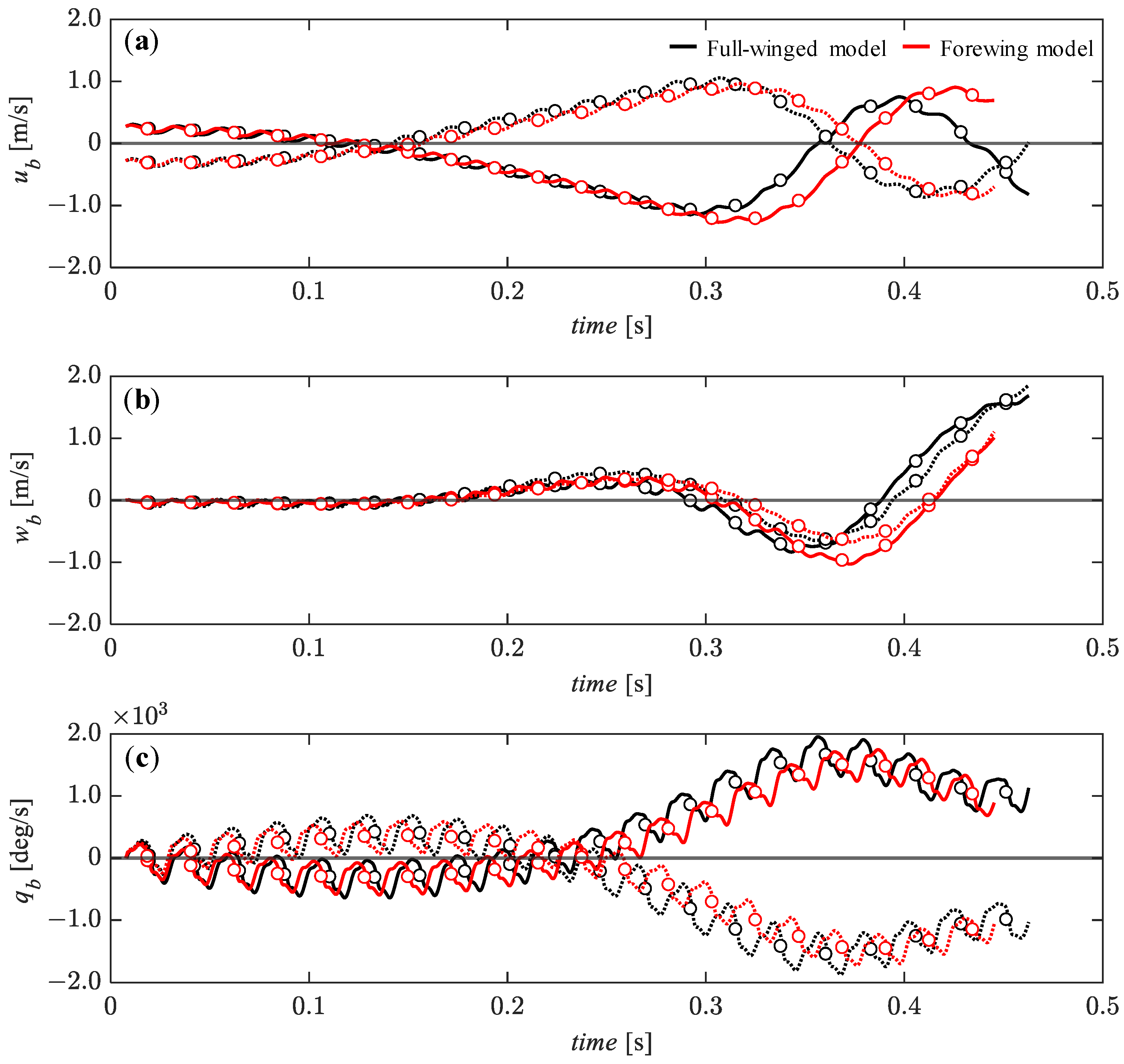
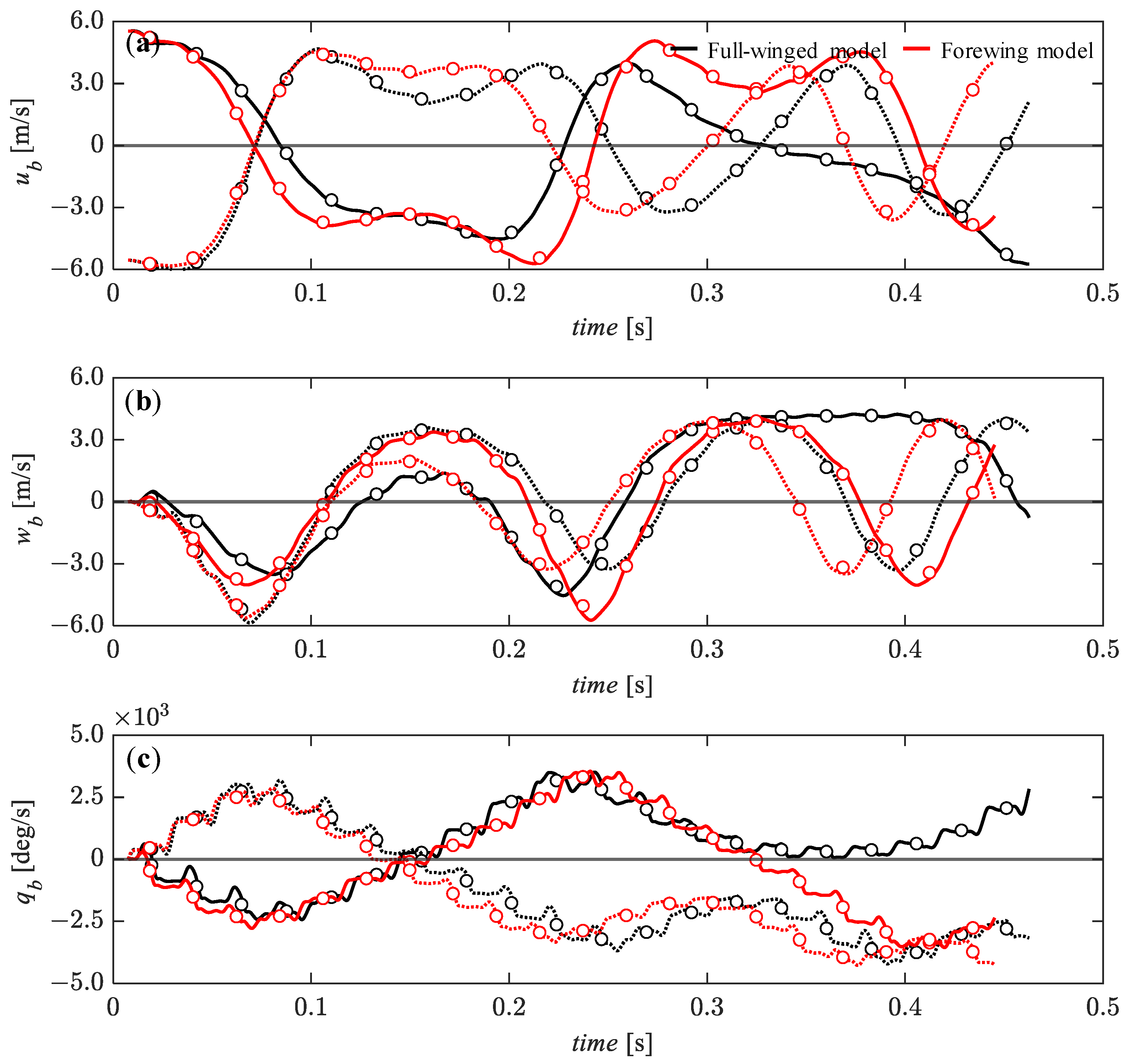
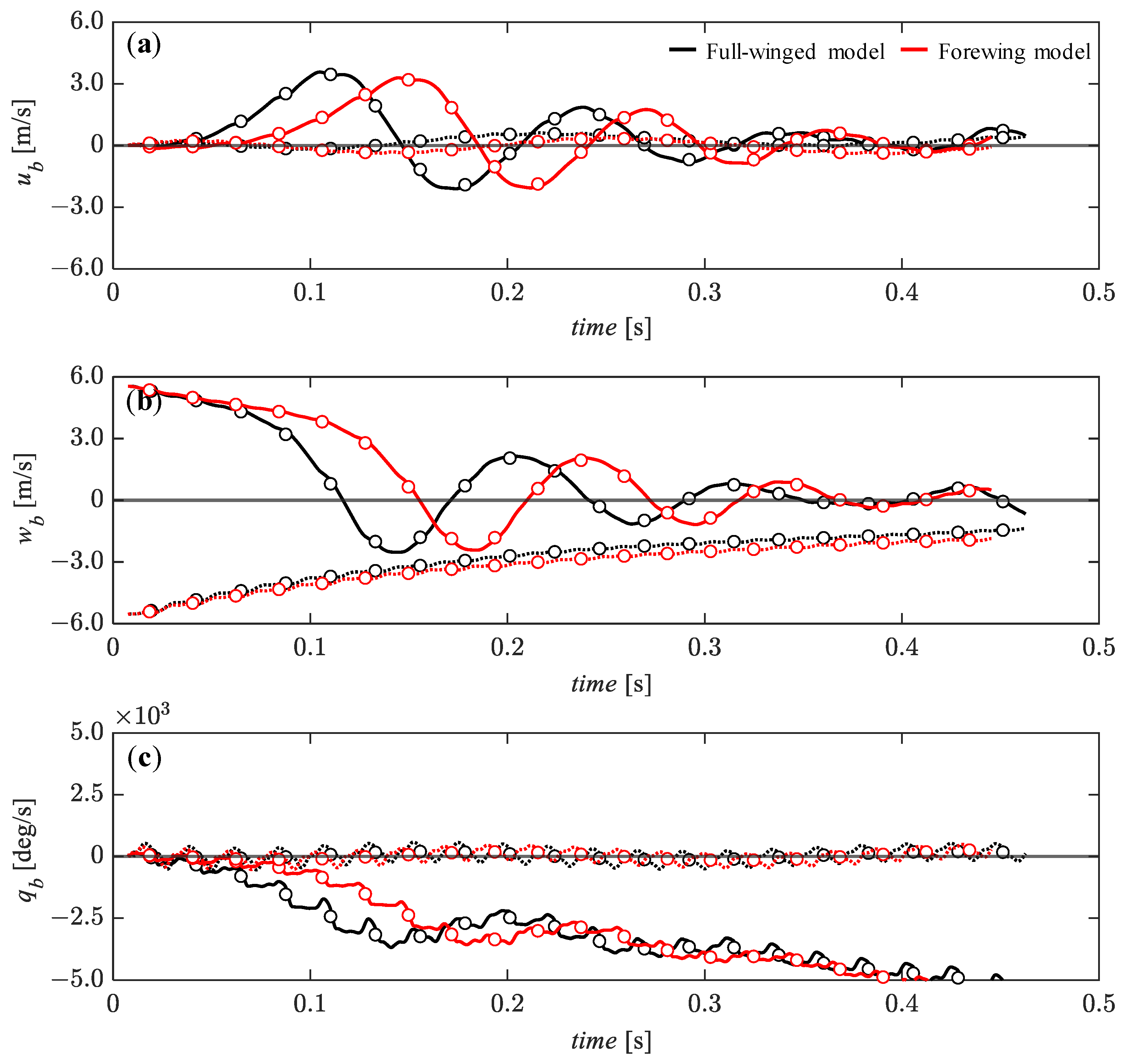
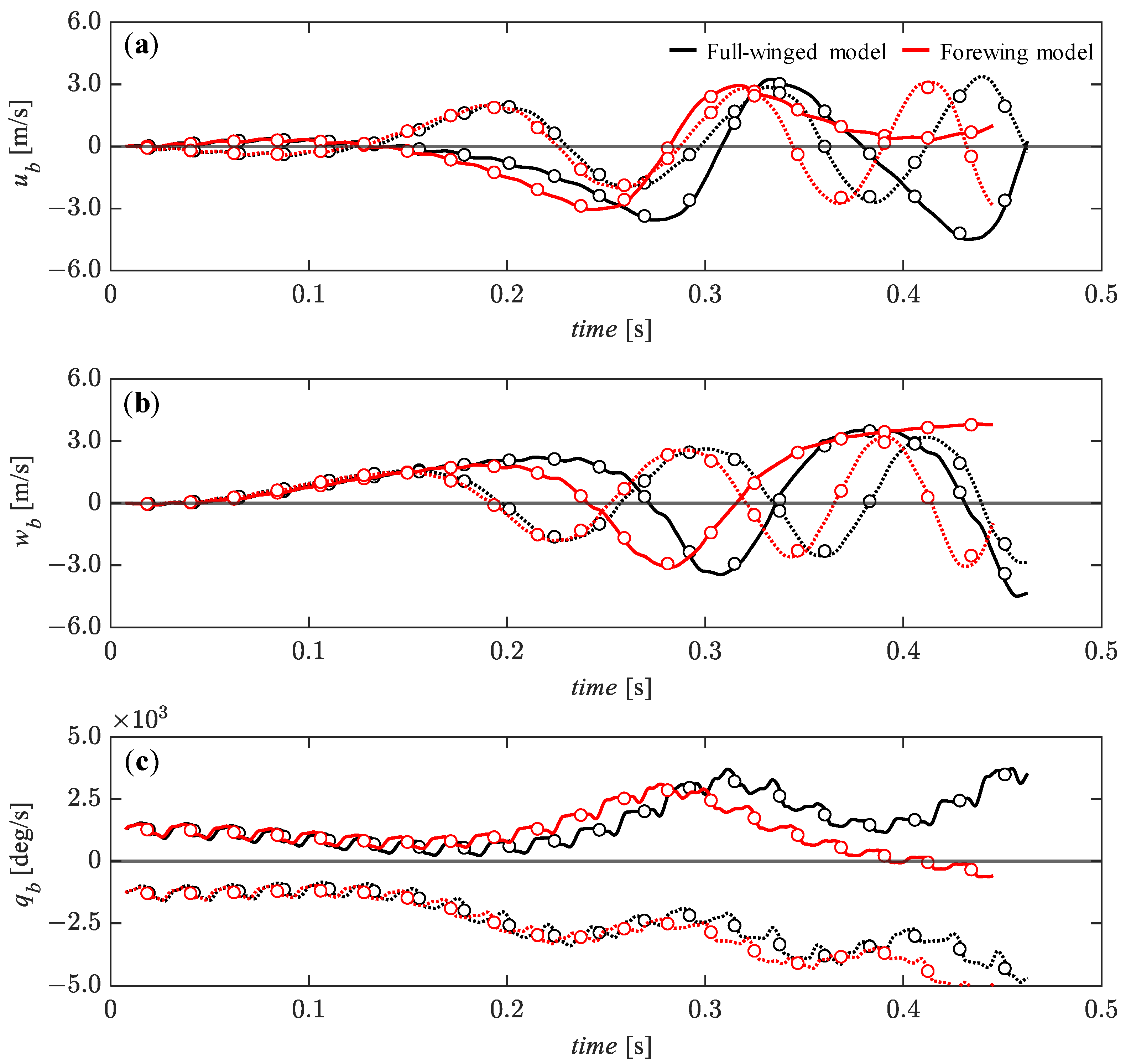
3.4. Passive Dynamic Stability with Relatively Large Perturbations
3.5. Effect of Hindwings on Passive Dynamic Stability
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rothstein, A. Drone; Bloomsbury Publishing: New York, NY, USA, 2015. [Google Scholar]
- Floreano, D.; Wood, R.J. Science, Technology and the Future of Small Autonomous Drones. Nature 2015, 521, 460–466. [Google Scholar] [CrossRef]
- Ellington, C.P.; Van Den Berg, C.; Willmott, A.P.; Thomas, A.L. Leading-Edge Vortices in Insect Flight. Nature 1996, 384, 626–630. [Google Scholar] [CrossRef]
- Dickinson, M.H.; Lehmann, F.-O.; Sane, S.P. Wing Rotation and the Aerodynamic Basis of Insect Flight. Science 1999, 284, 1954–1960. [Google Scholar] [CrossRef]
- Sane, S.P. The Aerodynamics of Insect Flight. J. Exp. Biol. 2003, 206, 4191–4208. [Google Scholar] [CrossRef]
- Chin, D.D.; Lentink, D. Flapping Wing Aerodynamics: From Insects to Vertebrates. J. Exp. Biol. 2016, 219, 920–932. [Google Scholar] [CrossRef]
- Sane, S.P.; Dickinson, M.H. The Aerodynamic Effects of Wing Rotation and a Revised Quasi-Steady Model of Flapping Flight. J. Exp. Biol. 2002, 205, 1087–1096. [Google Scholar] [CrossRef]
- Li, H.; Nabawy, M.R. Effects of Stroke Amplitude and Wing Planform on the Aerodynamic Performance of Hovering Flapping Wings. Aerospace 2022, 9, 479. [Google Scholar] [CrossRef]
- Phillips, N.; Knowles, K.; Bomphrey, R.J. Petiolate Wings: Effects on the Leading-Edge Vortex in Flapping Flight. Interface Focus 2017, 7, 20160084. [Google Scholar] [CrossRef]
- Phillips, N.; Knowles, K.; Bomphrey, R.J. The Effect of Aspect Ratio on the Leading-Edge Vortex over an Insect-like Flapping Wing. Bioinspir. Biomim. 2015, 10, 056020. [Google Scholar] [CrossRef]
- Berman, G.J.; Wang, Z.J. Energy-Minimizing Kinematics in Hovering Insect Flight. J. Fluid Mech. 2007, 582, 153–168. [Google Scholar] [CrossRef]
- Nabawy, M.R.; Crowther, W.J. Optimum Hovering Wing Planform. J. Theor. Biol. 2016, 406, 187–191. [Google Scholar] [CrossRef]
- Taylor, G.K. Mechanics and Aerodynamics of Insect Flight Control. Biol. Rev. 2001, 76, 449–471. [Google Scholar] [CrossRef]
- Elzinga, M.J.; Dickson, W.B.; Dickinson, M.H. The Influence of Sensory Delay on the Yaw Dynamics of a Flapping Insect. J. R. Soc. Interface 2012, 9, 1685–1696. [Google Scholar] [CrossRef]
- Taylor, G.K.; Thomas, A.L. Dynamic Flight Stability in the Desert Locust Schistocerca Gregaria. J. Exp. Biol. 2003, 206, 2803–2829. [Google Scholar] [CrossRef]
- Okamoto, M.; Sunada, S.; Tokutake, H. Stability Analysis of Gliding Flight of a Swallowtail Butterfly Papilio Xuthus. J. Theor. Biol. 2009, 257, 191–202. [Google Scholar] [CrossRef]
- Sun, M. Insect Flight Dynamics: Stability and Control. Rev. Mod. Phys. 2014, 86, 615–646. [Google Scholar] [CrossRef]
- Liang, B.; Sun, M. Dynamic Flight Stability of a Hovering Model Dragonfly. J. Theor. Biol. 2014, 348, 100–112. [Google Scholar] [CrossRef]
- Zhu, H.J.; Meng, X.G.; Sun, M. Forward Flight Stability in a Drone-Fly. Sci. Rep. 2020, 10, 1975. [Google Scholar] [CrossRef]
- Jantzen, B.; Eisner, T. Hindwings Are Unnecessary for Flight but Essential for Execution of Normal Evasive Flight in Lepidoptera. Proc. Natl. Acad. Sci. USA 2008, 105, 16636–16640. [Google Scholar] [CrossRef] [PubMed]
- Hedrick, T.L. Software Techniques for Two-and Three-Dimensional Kinematic Measurements of Biological and Biomimetic Systems. Bioinspir. Biomim. 2008, 3, 034001. [Google Scholar] [CrossRef] [PubMed]
- Noda, R. Aerodynamic Performance and Stability of Insect-Inspired Flights with Flexible Wings and Bodies. 2015. Available online: https://opac.ll.chiba-u.jp/da/curator/900119154/TLA_0195.pdf (accessed on 23 November 2023).
- Liu, H. Integrated Modeling of Insect Flight: From Morphology, Kinematics to Aerodynamics. J. Comput. Phys. 2009, 228, 439–459. [Google Scholar] [CrossRef]
- Lua, K.B.; Lai, K.C.; Lim, T.T.; Yeo, K.S. On the Aerodynamic Characteristics of Hovering Rigid and Flexible Hawkmoth-like Wings. Exp. Fluids 2010, 49, 1263–1291. [Google Scholar] [CrossRef]
- Gao, N.; Aono, H.; Liu, H. A Numerical Analysis of Dynamic Flight Stability of Hawkmoth Hovering. J. Biomech. Sci. Eng. 2009, 4, 105–116. [Google Scholar] [CrossRef]
- Phillips, N.; Knowles, K. Effect of Flapping Kinematics on the Mean Lift of an Insect-like Flapping Wing. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2011, 225, 723–736. [Google Scholar] [CrossRef]
- Fernández, M.J.; Springthorpe, D.; Hedrick, T.L. Neuromuscular and Biomechanical Compensation for Wing Asymmetry in Insect Hovering Flight. J. Exp. Biol. 2012, 215, 3631–3638. [Google Scholar] [CrossRef]
- Kassner, Z.; Dafni, E.; Ribak, G. Kinematic Compensation for Wing Loss in Flying Damselflies. J. Insect Physiol. 2016, 85, 1–9. [Google Scholar] [CrossRef]
- Vance, J.T.; Roberts, S.P. The Effects of Artificial Wing Wear on the Flight Capacity of the Honey Bee Apis Mellifera. J. Insect Physiol. 2014, 65, 27–36. [Google Scholar] [CrossRef]
- Willmott, A.P.; Ellington, C.P. The Mechanics of Flight in the Hawkmoth Manduca Sexta II. Aerodynamic Consequences of Kinematic and Morphological Variation. J. Exp. Biol. 1997, 200, 2723–2745. [Google Scholar] [CrossRef]
- Etkin, B. Dynamics of Atmospheric Flight; Wiley: New York, NY, USA, 1972. [Google Scholar]
- Gao, N.; Aono, H.; Liu, H. Perturbation Analysis of 6DoF Flight Dynamics and Passive Dynamic Stability of Hovering Fruit Fly Drosophila Melanogaster. J. Theor. Biol. 2011, 270, 98–111. [Google Scholar] [CrossRef]
- Combes, S.A.; Dudley, R. Turbulence-Driven Instabilities Limit Insect Flight Performance. Proc. Natl. Acad. Sci. USA 2009, 106, 9105–9108. [Google Scholar] [CrossRef]
- Liang, B.; Sun, M. Nonlinear Flight Dynamics and Stability of Hovering Model Insects. J. R. Soc. Interface 2013, 10, 20130269. [Google Scholar] [CrossRef] [PubMed]
- Taylor, G.K.; Żbikowski, R. Nonlinear Time-Periodic Models of the Longitudinal Flight Dynamics of Desert Locusts Schistocerca gregaria. J. R. Soc. Interface. 2005, 2, 197–221. [Google Scholar] [CrossRef]
- Ellington, C.P. The Aerodynamics of Hovering Insect Flight. II. Morphological Parameters. Phil. Trans. R. Soc. Lond. B 1984, 305, 17–40. [Google Scholar] [CrossRef]
- Van Den Berg, C.; Ellington, C.P. The Three–Dimensional Leading–Edge Vortex of a ‘Hovering’ Model Hawkmoth. Phil. Trans. R. Soc. Lond. B 1997, 352, 329–340. [Google Scholar] [CrossRef]
- Van Den Berg, C.; Ellington, C.P. The Vortex Wake of a ‘Hovering’ Model Hawkmoth. Phil. Trans. R. Soc. Lond. B 1997, 352, 317–328. [Google Scholar] [CrossRef]
- Willmott, A.P.; Ellington, C.P.; Thomas, A.L.R. Flow Visualization and Unsteady Aerodynamics in the Flight of the Hawkmoth, Manduca sexta. Phil. Trans. R. Soc. Lond. B 1997, 352, 303–316. [Google Scholar] [CrossRef]
- Hedenström, A.; Johansson, L.C.; Wolf, M.; Von Busse, R.; Winter, Y.; Spedding, G.R. Bat Flight Generates Complex Aerodynamic Tracks. Science 2007, 316, 894–897. [Google Scholar] [CrossRef]
- Chen, D.; Kolomenskiy, D.; Nakata, T.; Liu, H. Forewings Match the Formation of Leading-Edge Vortices and Dominate Aerodynamic Force Production in Revolving Insect Wings. Bioinspir. Biomim. 2017, 13, 016009. [Google Scholar] [CrossRef]
- Harbig, R.R.; Sheridan, J.; Thompson, M.C. Reynolds Number and Aspect Ratio Effects on the Leading-Edge Vortex for Rotating Insect Wing Planforms. J. Fluid Mech. 2013, 717, 166–192. [Google Scholar] [CrossRef]
- Lee, H.; Jang, J.; Wang, J.; Son, Y.; Lee, S. Comparison of Cicada Hindwings with Hindwing-Less Drosophila for Flapping Motion at Low Reynolds Number. J. Fluids Struct. 2019, 87, 1–22. [Google Scholar] [CrossRef]
- Birch, J.M.; Dickinson, M.H. Spanwise Flow and the Attachment of the Leading-Edge Vortex on Insect Wings. Nature 2001, 412, 729–733. [Google Scholar] [CrossRef]
- Chen, L.; Wang, L.; Zhou, C.; Wu, J.; Cheng, B. Effects of Reynolds Number on Leading-Edge Vortex Formation Dynamics and Stability in Revolving Wings. J. Fluid Mech. 2022, 931, A13. [Google Scholar] [CrossRef]
- Chen, L.; Zhou, C.; Werner, N.H.; Cheng, B.; Wu, J. Dual-Stage Radial–Tangential Vortex Tilting Reverses Radial Vorticity and Contributes to Leading-Edge Vortex Stability on Revolving Wings. J. Fluid Mech. 2023, 963, A29. [Google Scholar] [CrossRef]
- Zheng, L.; Hedrick, T.L.; Mittal, R. Time-Varying Wing-Twist Improves Aerodynamic Efficiency of Forward Flight in Butterflies. PLoS ONE 2013, 8, e53060. [Google Scholar] [CrossRef] [PubMed]
- Willmott, A.P.; Ellington, C.P. The Mechanics of Flight in the Hawkmoth Manduca Sexta I. Kinematics of Hovering and Forward Flight. J. Exp. Biol. 1997, 200, 2705–2722. [Google Scholar] [CrossRef]
- Sun, M.; Xiong, Y. Dynamic Flight Stability of a Hovering Bumblebee. J. Exp. Biol. 2005, 208, 447–459. [Google Scholar] [CrossRef] [PubMed]
- Lehnert, M.S. New Protocol for Measuring Lepidoptera Wing Damage. J. Lepid. Soc. 2010, 64, 29–32. [Google Scholar] [CrossRef]
- Rubin, J.J.; Hamilton, C.A.; McClure, C.J.W.; Chadwell, B.A.; Kawahara, A.Y.; Barber, J.R. The Evolution of Anti-Bat Sensory Illusions in Moths. Sci. Adv. 2018, 4, eaar7428. [Google Scholar] [CrossRef]
- Mistick, E.A.; Mountcastle, A.M.; Combes, S.A. Wing Flexibility Improves Bumblebee Flight Stability. J. Exp. Biol. 2016, 219, 3384–3390. [Google Scholar] [CrossRef]

| Full-Winged Model | Forewing Model | |
|---|---|---|
| Total mass [mg] | 956 | 946 |
| Wing area [mm2] | 443 | 325 |
| Mean chord length, Cm [mm] | 12.39 | 9.10 |
| Wing length, R [mm] | 35.76 | |
| Stroke plane angle [deg] | 36.36 | |
| Body length [mm] | 41.70 | |
| Body angle, β [deg] | 36.36 | |
| Measurement Model | Full-Winged Model | Forewing Model | |
|---|---|---|---|
| Amplitude center of the feathering angle [deg] | 7.36 | 11.86 (+4.5) | 10.66 (+3.3) |
| Flapping frequency, f [Hz] | 39.14 | 44.00 (+4.86) | 45.70 (+6.56) |
| Center of mass in Z-axis [mm] | 0 | −5.29 | −6.66 |
| Cycle-averaged horizontal force, Fx [mN] | −1.13 | −0.0019 | 0.012 |
| Cycle-averaged vertical force, Fz [mN] | 7.28 | 9.35 | 9.30 |
| Total weight [mN] | 9.38 | 9.38 | 9.28 |
| Cycle-averaged pitching torque, Ty [mN·mm] | 34.21 | −0.011 | 0.017 |
| Full-Winged Model | Forewing Model | |
|---|---|---|
| Cycle-averaged horizontal force, Fx [mN] | −1.13 | −0.80 (70%) |
| Cycle-averaged vertical force, Fz [mN] | 7.28 | 6.73 (93%) |
| Cycle-averaged pitching torque, Ty [mN·mm] | 34.21 | 28.53 (85%) |
| Wing area [mm2] | 443 | 325 (73%) |
| Second moment of wing area [mm4] | 1.41 × 10−7 | 1.31 × 10−7 (93%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noda, R.; Nakata, T.; Liu, H. Effect of Hindwings on the Aerodynamics and Passive Dynamic Stability of a Hovering Hawkmoth. Biomimetics 2023, 8, 578. https://doi.org/10.3390/biomimetics8080578
Noda R, Nakata T, Liu H. Effect of Hindwings on the Aerodynamics and Passive Dynamic Stability of a Hovering Hawkmoth. Biomimetics. 2023; 8(8):578. https://doi.org/10.3390/biomimetics8080578
Chicago/Turabian StyleNoda, Ryusuke, Toshiyuki Nakata, and Hao Liu. 2023. "Effect of Hindwings on the Aerodynamics and Passive Dynamic Stability of a Hovering Hawkmoth" Biomimetics 8, no. 8: 578. https://doi.org/10.3390/biomimetics8080578
APA StyleNoda, R., Nakata, T., & Liu, H. (2023). Effect of Hindwings on the Aerodynamics and Passive Dynamic Stability of a Hovering Hawkmoth. Biomimetics, 8(8), 578. https://doi.org/10.3390/biomimetics8080578