Design and Reality-Based Modeling Optimization of a Flexible Passive Joint Paddle for Swimming Robots
Abstract
1. Introduction
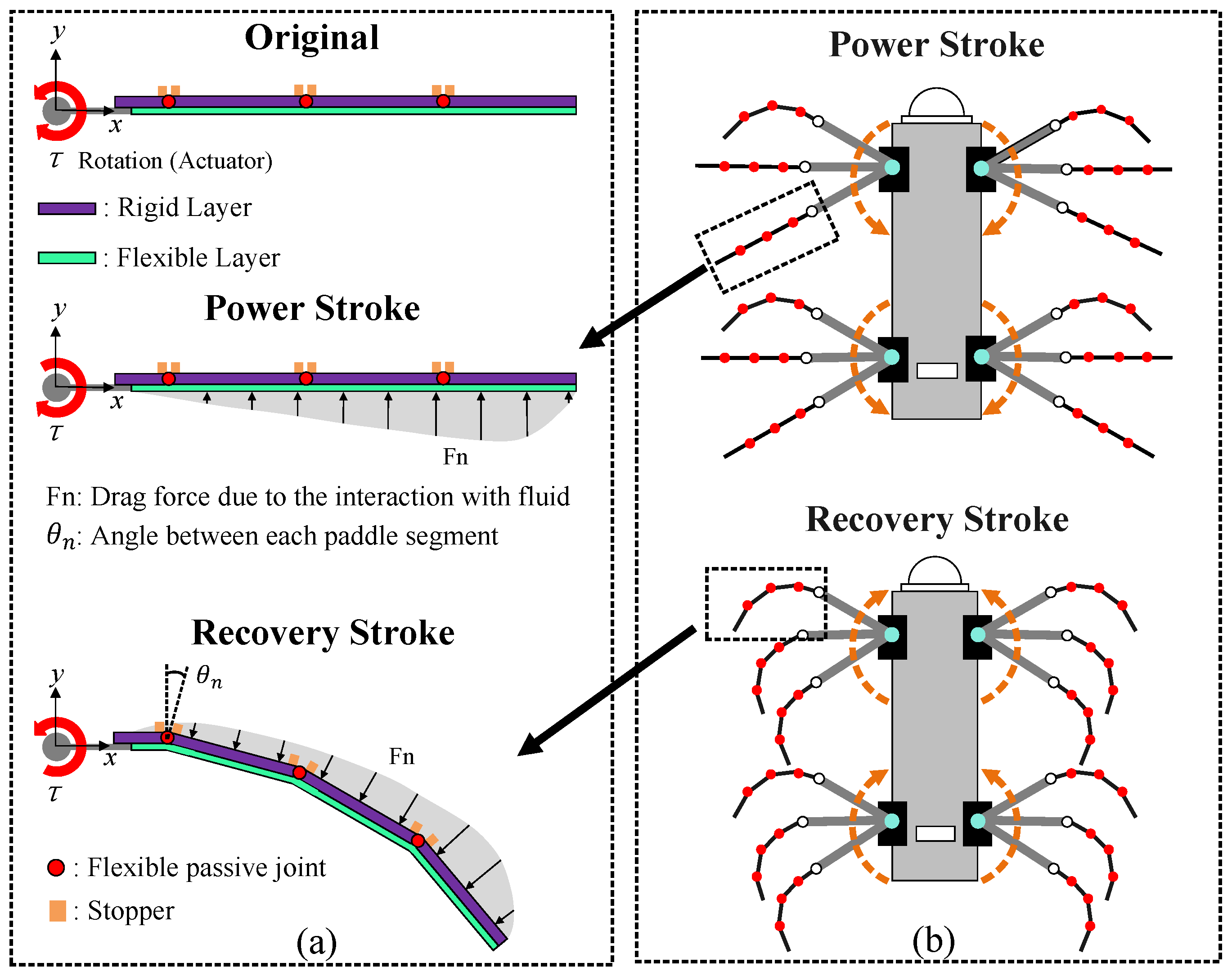
2. Flexible Passive Joint Paddle (FPJP) Design
3. Dynamics Modeling and System Identification
3.1. Dynamics Modeling
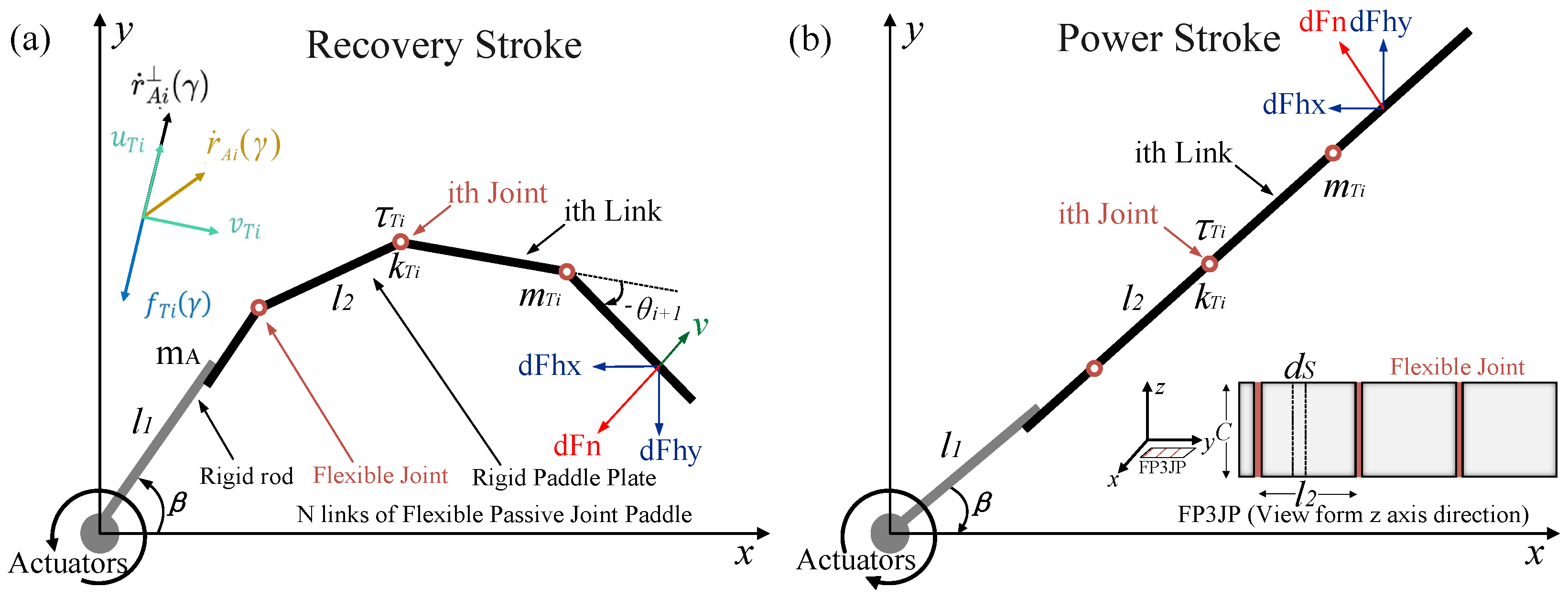
3.2. System Identification
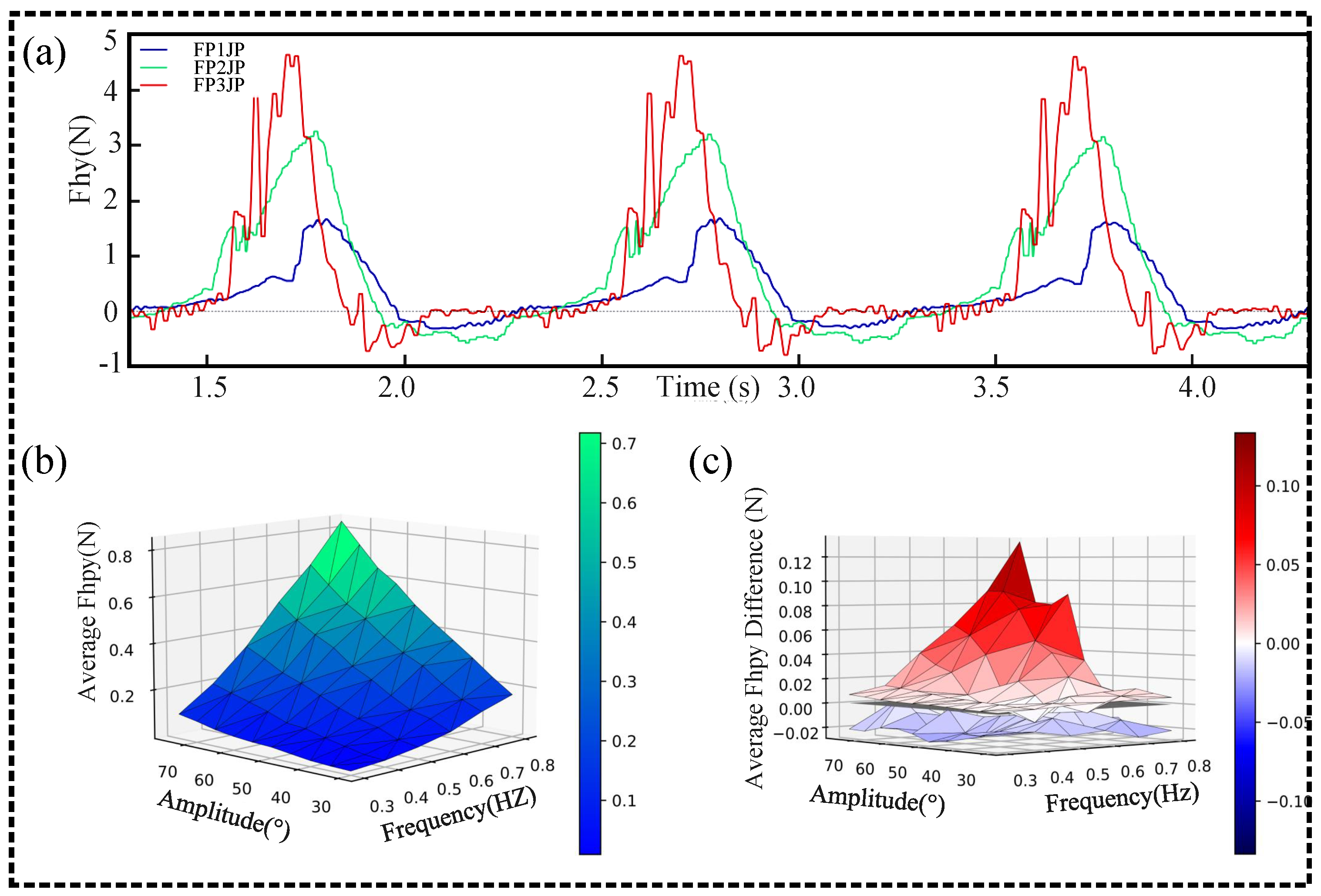
4. Optimization Method
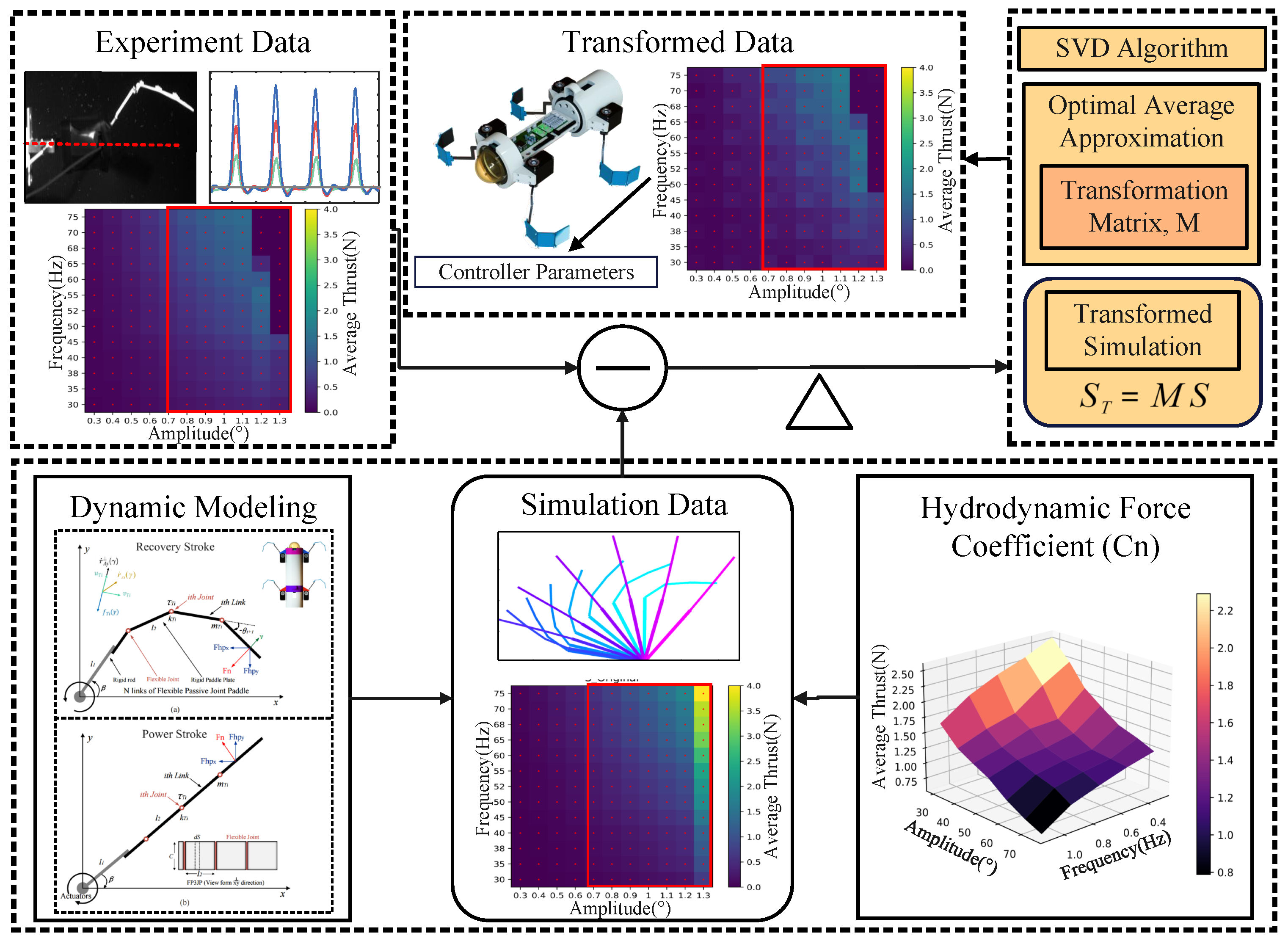
4.1. Effect of Hydrodynamic Coefficients on Simulation
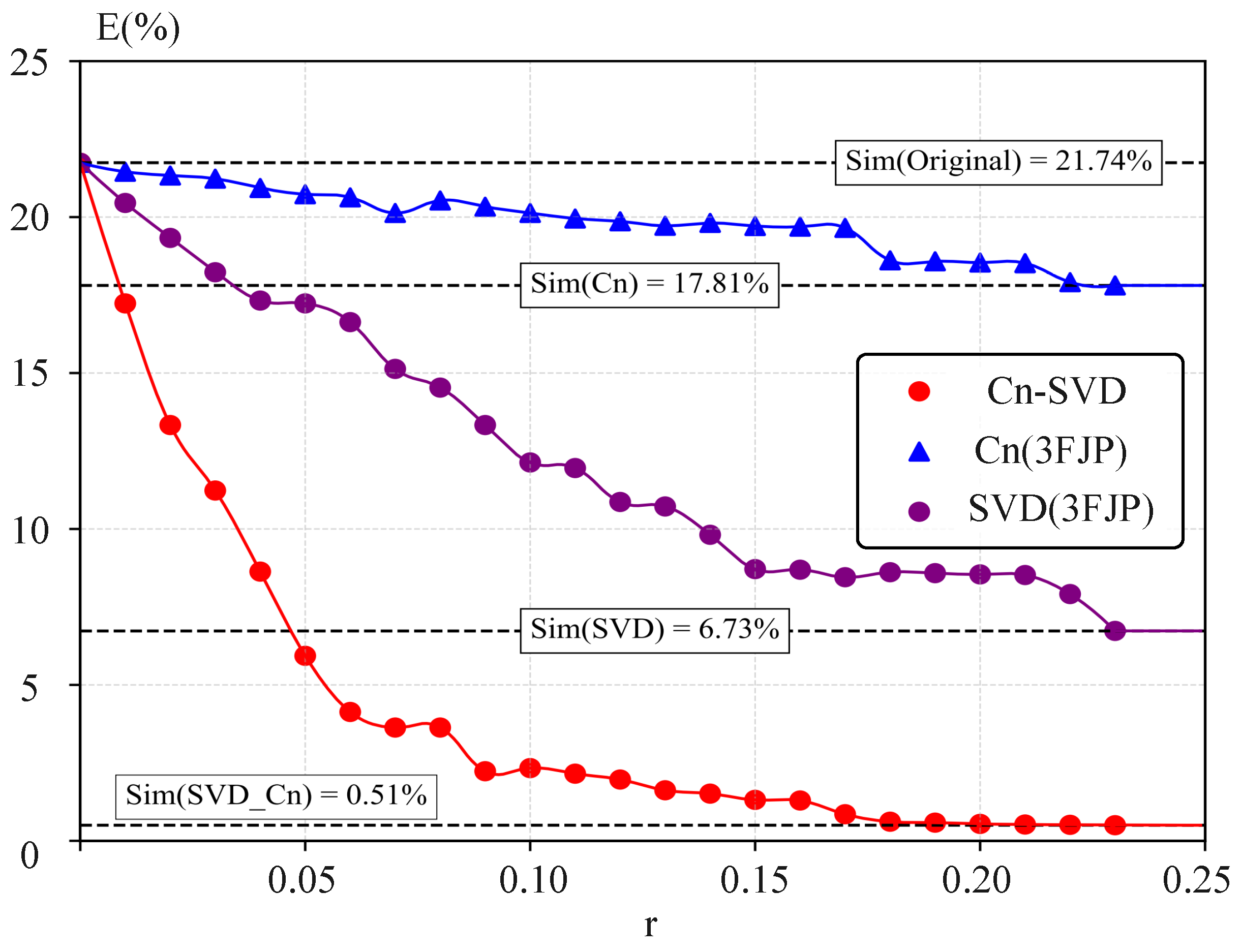
4.2. Simulation to Reality Transfer
| Algorithm 1: Least Squares Method for Simulation Revision |
|
4.3. Novel Semi-Empirical Data-Driven Model
5. Experimental Setup and Swimming Robot Prototype
5.1. Experimental Setup
5.2. Design of Diving Beetle Swimming Robot
| Component | Parameter | Value | Unit |
|---|---|---|---|
| Body | Mass | 2.5 | kg |
| Length | 0.426 | m | |
| Width | 0.569 | m | |
| Height | 0.110 | m | |
| FPJP | Servo arm length () | 0.010 | m |
| Mass () | 0.029 | kg | |
| Length () | 0.105 | m | |
| Width | 0.040 | m | |
| Hardware | Microcontroller | STM32F407 | |
| IMU | MPU6050(JY61) | ||
| Servomotors | XW540T40R | ||
| Communication module | APC220 | ||
| Battery | 11.1 | V |

6. Results and Discussion
6.1. Experiment A
6.2. Experiment B
7. Conclusions
8. Future Plans
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Grams, M.; Richter, S. Locomotion in Anaspides (Anaspidacea, Malacostraca)—insights from a morpho-functional study of thoracopods with some observations on swimming and walking. Zoology 2021, 144, 125883. [Google Scholar] [CrossRef]
- Shao, H.; Dong, B.; Zheng, C.; Li, T.; Zuo, Q.; Xu, Y.; Fang, H.; He, K.; Xie, F. Thrust Improvement of a Biomimetic Robotic Fish by Using a Deformable Caudal Fin. Biomimetics 2022, 7, 113. [Google Scholar] [CrossRef]
- Jia, X.; Chen, Z.; Petrosino, J.M.; Hamel, W.R.; Zhang, M. Biological Undulation Inspired Swimming Robot. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 4795–4800. [Google Scholar]
- Wang, J.; Zhu, Y.; Du, X.; Yang, G.; Hu, D. Theoretical and numerical studies on a five-ray flexible pectoral fin during labriform swimming. Bioinspir. Biomim. 2020, 15, 016007. [Google Scholar]
- Kwak, B.; Choi, S.; Bae, J. Development of a Stiffness-Adjustable Articulated Paddle and its Application to a Swimming Robot. Adv. Intell. Syst. 2023, 5, 2200348. [Google Scholar] [CrossRef]
- Chen, G.; Tu, J.; Ti, X.; Wang, Z.; Hu, H. Hydrodynamic model of the beaver-like bendable webbed foot and paddling characteristics under different flow velocities. Ocean Eng. 2021, 234, 109179. [Google Scholar]
- Kwak, B.; Bae, J. Toward Fast and Efficient Mobility in Aquatic Environment: A Robot with Compliant Swimming Appendages Inspired by a Water Beetle. J. Bionic Eng. 2017, 14, 260. [Google Scholar]
- Li, D.; Huang, S.; Tang, Y.; Marvi, H.; Tao, J.; Aukes, D.M. Compliant Fins for Locomotion in Granular Media. IEEE Rob. Autom. Lett. 2021, 6, 5984. [Google Scholar] [CrossRef]
- Chen, T.; Bilal, O.R.; Shea, K.; Daraio, C. Harnessing bistability for directional propulsion of soft, untethered robots. Proc. Natl. Acad. Sci. USA 2018, 115, 5698. [Google Scholar] [CrossRef]
- Kwak, K.; Bae, J. Design of hair-like appendages and comparative analysis on their coordination toward steady and efficient swimming. Bioinspir. Biomim. 2017, 12, 036014. [Google Scholar] [CrossRef]
- Voise, J.; Casas, J. The management of fluid and wave resistances by whirligig beetles. J. R. Soc. Interface 2009, 7, 343. [Google Scholar] [CrossRef]
- Kim, H.; Lee, J. Swimming Pattern Generator Based on Diving Beetles for Legged Underwater Robots. Int. J. Mater. Mech. Manuf. 2014, 2, 13. [Google Scholar]
- Pham, V.A.; Nguyen, T.T.; Lee, B.R.; Vo, T.Q. Dynamic Analysis of a Robotic Fish Propelled by Flexible Folding Pectoral Fins. Robotica 2019, 38, 699. [Google Scholar] [CrossRef]
- Xu, Y.; Hu, J.; Song, J.; Xie, F.; Zuo, Q.; He, K. A Novel Multiple Synchronous Compliant and Passive Propeller Inspired by Loons for Swimming Robot. In Proceedings of the 2022 IEEE International Conference on Robotics and Biomimetics, Xishuangbanna, China, 5–9 December 2022; pp. 563–568. [Google Scholar]
- Sharifzadeh, M.; Aukes, D.M. Curvature-Induced Buckling for Flapping-Wing Vehicles. IEEE/ASME Trans. Mechatron. 2021, 26, 503. [Google Scholar] [CrossRef]
- Boudrias, M.A. Are Pleopods Just “More Legs”? the Functional Morphology of Swimming Limbs in Eurythenes Gryllus (Amphipoda). J. Crustac. Biol. 2002, 22, 581. [Google Scholar]
- Jia, X.; Chen, Z.; Riedel, A.; Si, T.; Hamel, W.R.; Zhang, M. Energy-Efficient Surface Propulsion Inspired by Whirligig Beetles. IEEE Trans. Rob. 2017, 31, 1432. [Google Scholar]
- KWak, B.; Lee, D.; Bae, J. Comprehensive analysis of efficient swimming using articulated legs fringed with flexible appendages inspired by a water beetle. Bioinspir. Biomim. 2019, 14, 066003. [Google Scholar] [CrossRef]
- Junge, K.; Obayashi, N.; Stella, F.; Santina, C.D.; Hughes, J. Controlling Maneuverability of a Bio-Inspired Swimming Robot Through Morphological Transformation. IEEE Rob. Autom. Maga. 2022, 29, 78. [Google Scholar] [CrossRef]
- Howell, L.L. 21st Century Kinematics; Springer: London, UK, 2012; pp. 189–216. ISBN 978-1-4471-4509-7. [Google Scholar]
- Zuo, Q.; Xu, Y.; Xie, F.; Fang, H.; He, K.; Zhong, Y.; Li, Z. Designs of the Biomimetic Robotic Fishes Performing Body and/or Caudal Fin (BCF) Swimming Locomotion: A Review. J. Intell. Robot. Syst. 2022, 105, 41. [Google Scholar]
- Venkiteswaran, V.K.; Su, H.J. A Three-Spring Pseudorigid-Body Model for Soft Joints With Significant Elongation Effects. J. Mech. Robot. 2016, 8, 061001. [Google Scholar] [CrossRef]
- Wang, W.; Dai, X.; Li, L.; Gheneti, G.H.; Ding, Y.; Yu, J.; Xie, G. Three-Dimensional Modeling of a Fin-Actuated Robotic Fish with Multimodal Swimming. IEEE/ASME Trans. Mechatron. 2018, 23, 1641. [Google Scholar] [CrossRef]
- Thandiackal, R.; Melo, K.; Paez, L.; Herault, J.; Kano, T.; Akiyama, K.; Boyer, F.; Ryczko, D.; Ishiguro, A.; Ijspeert, A.J. Emergence ofrobust self-organized undulatory swimming based on local hydrodynamic force sensing. Sci. Robot. 2021, 6, 6354. [Google Scholar] [CrossRef]
- Obayashi, N.; Bosio, C.; Hughes, J. Soft Passive Swimmer Optimization: From Simulation to Reality Using Data-Driven Transformation. In Proceedings of the 2022 IEEE 5th International Conference on Soft Robotics (RoboSoft), Edinburgh, UK, 4–8 April 2022; pp. 328–333. [Google Scholar]
- Stella, F.; Obayashi, N.; Santina, C.D.; Hughes, J. An Experimental Validation of the Polynomial Curvature Model: Identification and Optimal Control of a Soft Underwater Tentacle. IEEE Rob. Autom. Lett. 2022, 7, 11410. [Google Scholar] [CrossRef]
- Obayashi, N.; Vicari, A.; Junge, K.; Shakir, K.; Hughes, J. Control and Morphology Optimization of Passive Asymmetric Structures for Robotic Swimming. IEEE Rob. Autom. Lett. 2023, 8, 1495. [Google Scholar] [CrossRef]
- Lu, B.; Zhou, C.; Wang, J.; Fu, Y.; Cheng, L.; Tan, M. Development and Stiffness Optimization for a Flexible-Tail Robotic Fish. IEEE Rob. Autom. Lett. 2022, 7, 834. [Google Scholar] [CrossRef]
- Simha, A.; Gkliva, R.; Kotta, Ü.; Kruusmaa, M. A Flapped Paddle-Fin for Improving Underwater Propulsive Efficiency of Oscillatory Actuation. IEEE Rob. Autom. Lett 2020, 5, 3176. [Google Scholar] [CrossRef]
- Jiang, M.; Yu, Q.; Gravish, N. Vacuum induced tube pinching enables reconfigurable flexure joints with controllable bend axis and stiffness. In Proceedings of the 2021 IEEE 4th International Conference on Soft Robotics (RoboSoft), New Haven, CT, USA, 12–16 April 2021; pp. 315–320. [Google Scholar]
- Wang, J.; McKinley, P.K.; Tan, X. Dynamic Modeling of Robotic Fish With a Base-Actuated Flexible Tail. J. Dyn. Syst. Meas. Control 2015, 137, 011004. [Google Scholar] [CrossRef]
- Nian, P.; Song, B.; Xuan, J.; Zhou, W.; Xue, D. Study on flexible flapping wings with three dimensional asymmetric passive deformation in a flapping cycle. Aerosp. Sci. Technol. 2020, 104, 105944. [Google Scholar] [CrossRef]
- Lou, J.; Yang, Y.; Wu, C.; Li, G.; Chen, T.; Ma, J. Underwater oscillation performance and 3D vortex distribution generated by miniature caudal fin-like propulsion with macro fiber composite actuation. Sens. Actuators A 2020, 303, 111587. [Google Scholar]
- Xie, F.; Zhong, Y.; Du, R.; Li, Z. Central Pattern Generator (CPG) Control of a Biomimetic Robot Fish for Multimodal Swimming. J. Bionic Eng. 2019, 16, 222. [Google Scholar]
- Song, J.; Zhong, Y.; Luo, H.; Ding, Y.; Du, R. Hydrodynamics of larval fish quick turning: A computational study. Proc. Inst. Mech. Eng. Part C 2017, 232, 2515. [Google Scholar] [CrossRef]
- Yan, Y.; Wang, X.; Qi, X.; Hou, J.; Chen, C.; Ma, J.; Xing, H.; Chen, Y.; Zhao, Y. Development of a Turtle-inspired Robot with Variable Stiffness Hydrofoils. In Proceedings of the 2022 IEEE International Conference on Mechatronics and Automation, Guilin, China, 7–10 August 2022; pp. 493–498. [Google Scholar]
- Bai, X.; Wang, Y.; Wang, R.; Wang, S.; Tan, M. Hydrodynamics of a Flexible Flipper for an Underwater Vehicle-Manipulator System. IEEE/ASME Trans. Mechatron. 2022, 27, 868. [Google Scholar]
- Jiang, Y.; Sharifzadeh, M.; Aukes, D.M. Shape Change Propagation Through Soft Curved Materials for Dynamically-Tuned Paddling Robots. In Proceedings of the 2021 IEEE 4th International Conference on Soft Robotics (RoboSoft), New Haven, CT, USA, 12–16 April 2021; pp. 230–237. [Google Scholar]
- Hughes, J.A.E.; Maiolino, P.; Iida, F. An anthropomorphic soft skeleton hand exploiting conditional models for piano playing. Sci. Robot. 2018, 3, 3098. [Google Scholar] [CrossRef]
- Chen, D.; Wu, Z.; Dong, H.; Tan, M.; Yu, J. Exploration of swimming performance for a biomimetic multi-joint robotic fish with a compliant passive joint. Bioinspir. Biomim. 2020, 16, 026007. [Google Scholar] [CrossRef]
- Liu, A.; Zhao, J.; Li, L.; Xie, G. Micro-Force measuring apparatus for robotic fish : Design, implementation and application. In Proceedings of the 27th Chinese Control and Decision Conference (2015 CCDC), Qingdao, China, 23–25 May 2015; pp. 4938–4943. [Google Scholar]
- Arun, K.S.; Huang, T.S.; Blostein, S.D. Least-Squares Fitting of Two 3-D Point Sets. IEEE Trans. Pattern Anal. Mach. Intell. 1987, 5, 698700. [Google Scholar] [CrossRef]
- Eggert, D.W.; Lorusso, A.; Fisher, R.B. Estimating 3-D rigid body transformations: A comparison of four major algorithms. Mach. Vis. Appl. 1997, 9, 272. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381395. [Google Scholar]
- Porez, M.; Boyer, F.; Ijspeert, A.J. Improved Lighthill fish swimming model for bio-inspired robots: Modeling, computational aspects and experimental comparisons. Inter. J. Rob. R. 2014, 33, 1322–1341. [Google Scholar]
- Youssef, S.M.; Soliman, M.; Saleh, M.A.; Mousa, M.A.; Elsamanty, M.; Radwan, A.G. Underwater Soft Robotics: A Review of Bioinspiration in Design, Actuation, Modeling, and Control. Micromachines 2022, 13, 110. [Google Scholar] [CrossRef]
- Chen, G.; Lu, Y.; Yang, X.; Hu, H. Reinforcement learning control for the swimming motions of a beaver-like, single-legged robot based on biological inspiration. Robot. Auton. Syst. 2022, 154, 104116. [Google Scholar] [CrossRef]
- Bal, C.; Koca, G.O.; Korkmaz, D.; Akpolat, Z.H.; Ay, M. CPG-based autonomous swimming control for multi-tasks of a biomimetic robotic fish. Ocean Eng. 2019, 189, 106334. [Google Scholar]
- Fan, J.; Du, Q.; Yu, Q.; Wang, Y.; Qi, J.; Zhu, Y. Corrigendum: Biologically inspired swimming robotic frog based on pneumatic soft actuators. Bioinspir. Biomim. 2020, 15, 046006. [Google Scholar]
- Wang, J.; Wu, Z.; Yan, S.; Tan, M.; Yu, J. Real-Time Path Planning and Following of a Gliding Robotic Dolphin Within a Hierarchical Framework. IEEE Trans. Veh. Technol. 2021, 70, 3243. [Google Scholar]
- Sun, Y.; Zong, C.; Pancheri, F.; Chen, T.; Lueth, T.C. Design of Topology Optimized Compliant Legs for Bio-Inspired Quadruped Robots. Sci. Rep. 2023, 13, 4875. [Google Scholar] [CrossRef]
- Li, Y.; Fish, F.; Chen, Y.; Ren, T.; Zhou, J. Bio-Inspired Robotic Dog Paddling: Kinematic and Hydro-Dynamic Analysis. Bioinspir. Biomim. 2019, 14, 066008. [Google Scholar] [CrossRef]




| Material | Parameter | Value | Unit |
|---|---|---|---|
| PA66 | Density | 1.14 | g/cm3 |
| Melting point | 260 | °C | |
| Young’s modulus | 2.7 | GPa | |
| Silicone | Density | 1.2 | g/cm3 |
| Melting point | 250 | °C | |
| Young’s modulus | 2 | MPa |
| Parameter | Meaning | Value | Unit |
|---|---|---|---|
| Rigid rod length | 105 | mm | |
| Paddle segment length | 35 | mm | |
| w | Paddle width | 40 | mm |
| Hydrodynamic coefficient | 1 | ||
| Mass of each paddle segment | 10 | g | |
| Mass of rigid rod | 16 | g | |
| Stiffness of the first joint | 0.032 | N·m/rad | |
| Stiffness of the second joint | 0.031 | N·m/rad | |
| Stiffness of the third joint | 0.031 | N·m/rad |
| Cn | SVD | Cn-SVD | ||||
|---|---|---|---|---|---|---|
| Maximum Error | Average Error | Maximum Error | Average Error | Maximum Error | Average Error | |
| r = 0.00 | 99.86% | 21.74% | 99.86% | 21.74% | 99.86% | 21.74% |
| r = 0.05 | 99.86% | 20.65% | 87.63% | 14.87% | 54.41% | 6.12% |
| r = 0.10 | 98.91% | 20.38% | 74.42% | 12.21% | 34.98% | 2.37% |
| r = 0.15 | 98.91% | 19.47% | 59.79% | 8.32% | 16.83% | 1.59% |
| r = 0.20 | 95.43% | 18.52% | 56.87% | 8.25% | 12.64% | 0.56% |
| r = 0.25 | 95.43% | 17.81% | 47.45% | 6.73% | 8.29% | 0.51% |
| Paddle Type | Control Parameters | Average Speed | Average Yaw Angle | Maximum Yaw Angle |
|---|---|---|---|---|
| FP3JP | 1.1 Hz, 75° | 0.323 m/s | 2.73° | 35.29° |
| FP3JP | 1.3 Hz, 75° | 0.142 m/s | 27.29° | 151.63° |
| FP1JP | 1.1 Hz, 75° | 0.279 m/s | 2.73° | 35.29° |
| FP1JP | 1.3 Hz, 75° | 0.126 m/s | 27.29° | 151.63° |
| FP3JP | 0.3 Hz, 30° | 0.093 m/s | 1.57° | 22.19° |
| FP1JP | 0.3 Hz, 30° | 0.082 m/s | 1.47° | 24.87° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, J.; Xu, Y.; Chen, P.; Xie, F.; Li, H.; He, K. Design and Reality-Based Modeling Optimization of a Flexible Passive Joint Paddle for Swimming Robots. Biomimetics 2024, 9, 56. https://doi.org/10.3390/biomimetics9010056
Hu J, Xu Y, Chen P, Xie F, Li H, He K. Design and Reality-Based Modeling Optimization of a Flexible Passive Joint Paddle for Swimming Robots. Biomimetics. 2024; 9(1):56. https://doi.org/10.3390/biomimetics9010056
Chicago/Turabian StyleHu, Junzhe, Yaohui Xu, Pengyu Chen, Fengran Xie, Hanlin Li, and Kai He. 2024. "Design and Reality-Based Modeling Optimization of a Flexible Passive Joint Paddle for Swimming Robots" Biomimetics 9, no. 1: 56. https://doi.org/10.3390/biomimetics9010056
APA StyleHu, J., Xu, Y., Chen, P., Xie, F., Li, H., & He, K. (2024). Design and Reality-Based Modeling Optimization of a Flexible Passive Joint Paddle for Swimming Robots. Biomimetics, 9(1), 56. https://doi.org/10.3390/biomimetics9010056





