Bionic Optimization Design and Fatigue Life Prediction of a Honeycomb-Structured Wheel Hub
Abstract
:1. Introduction
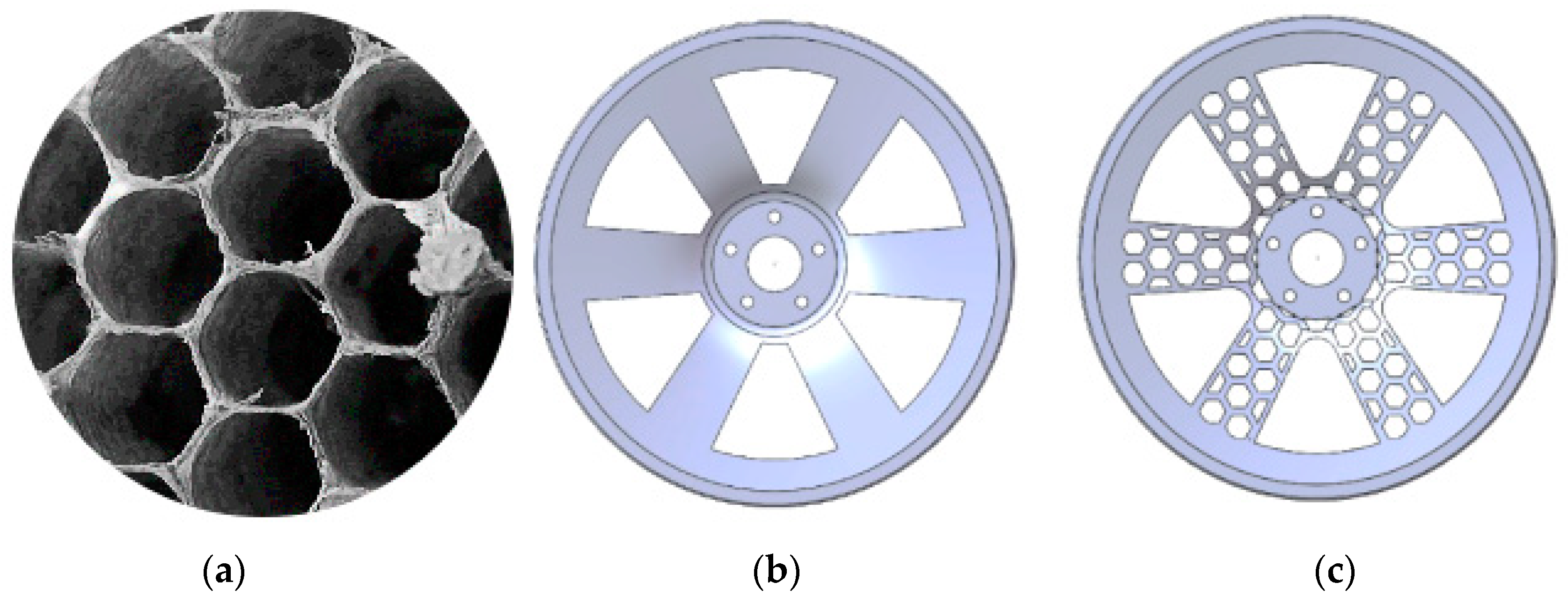
2. Biomimetic Hub Materials and Analytical Methods
2.1. Establishment of a Finite Element Model
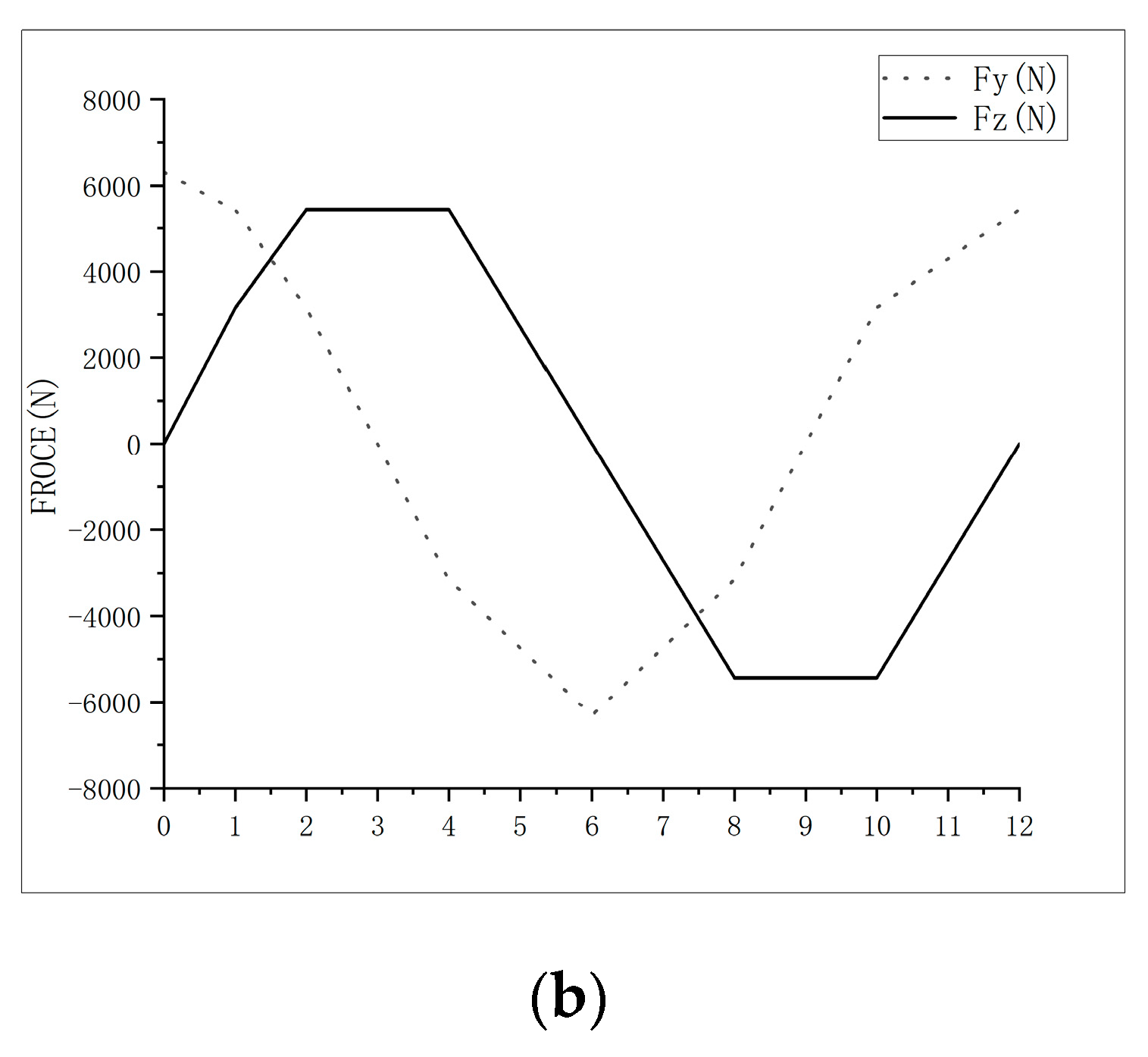
2.2. Load Calculation under Bending Conditions
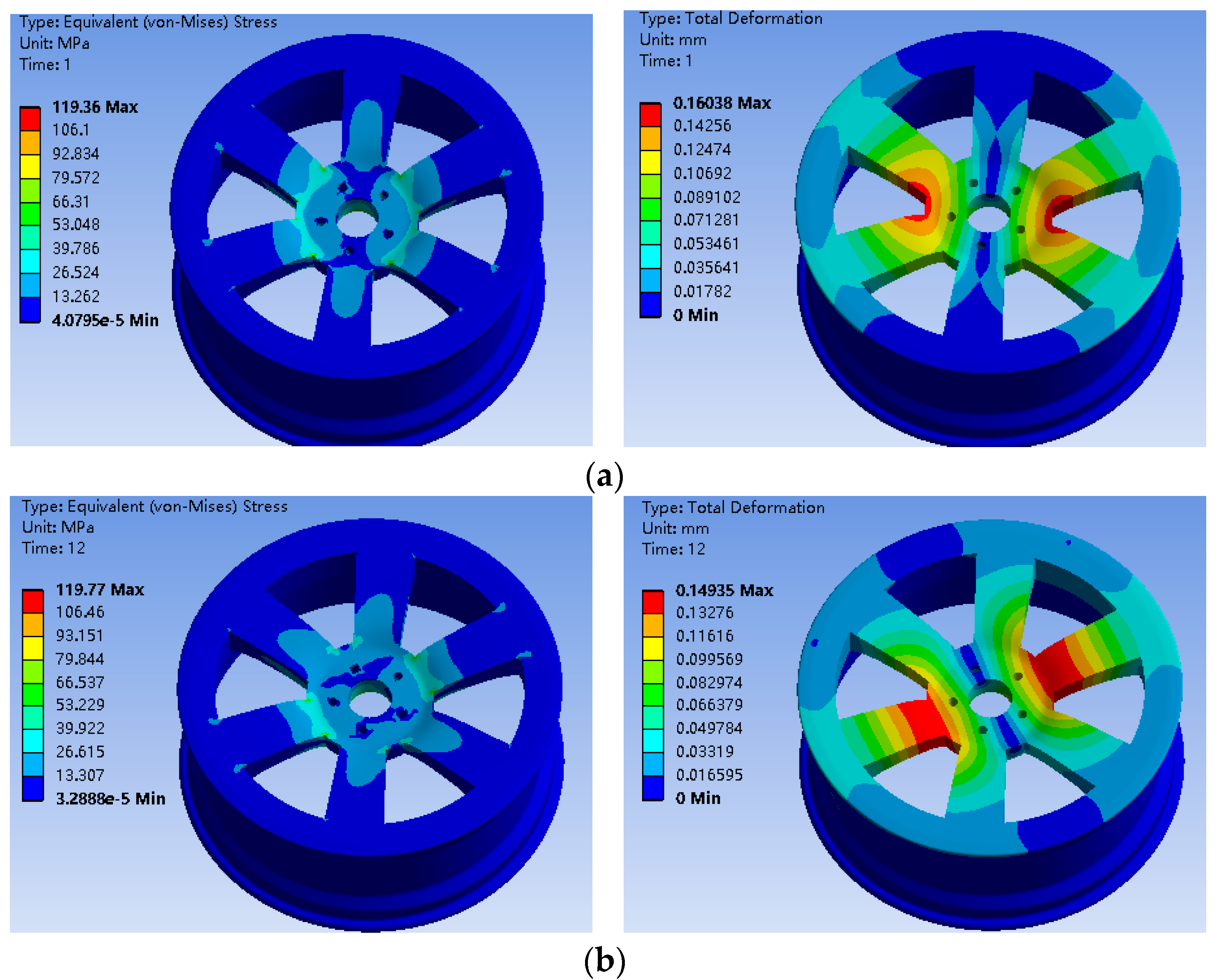
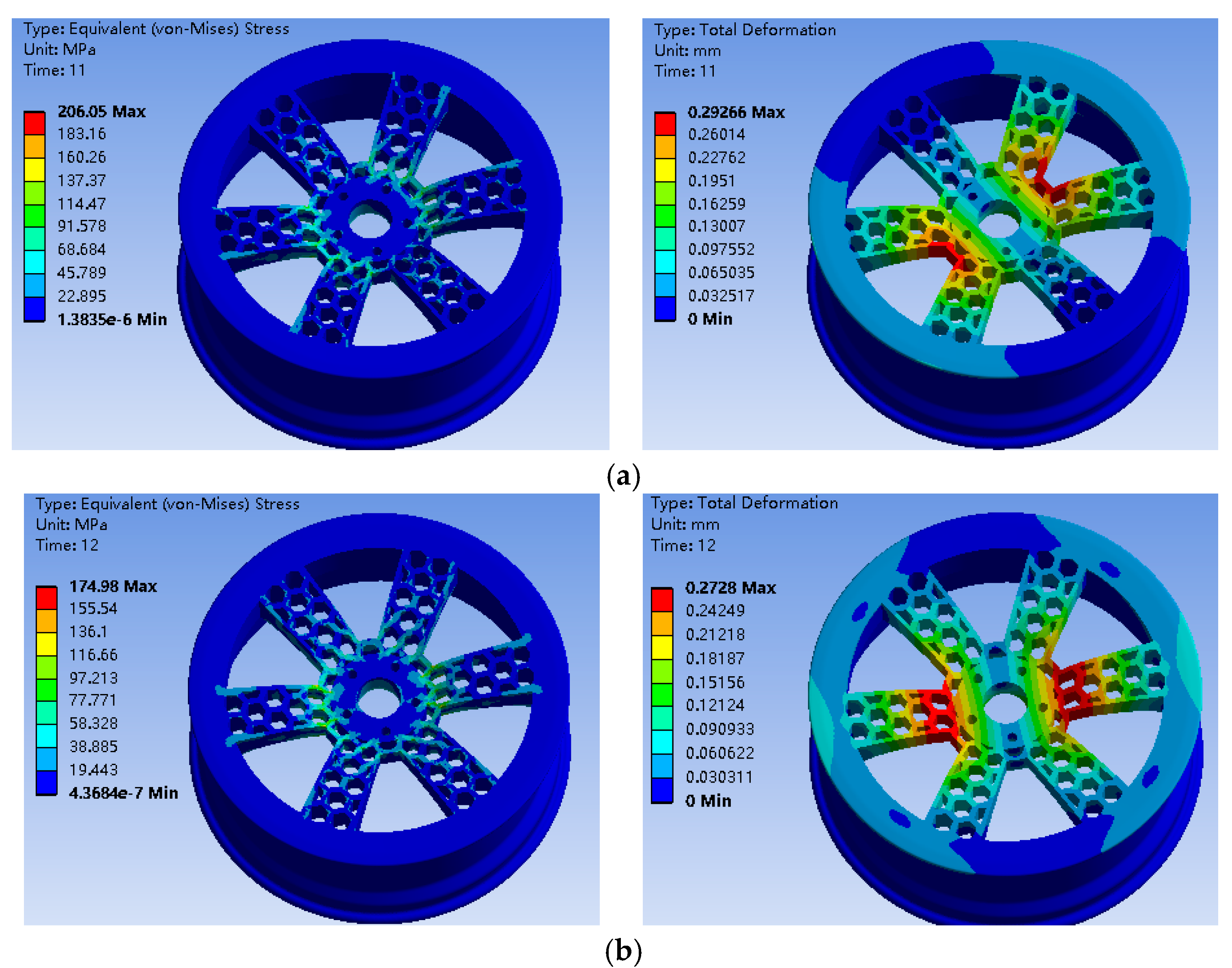
2.3. Stress Comparison between the Bionic Wheel of the Honeycombed Structure and Ordinary Wheel Hub
3. Bionic Hub Structure Optimization Design of the Honeycombed Structure
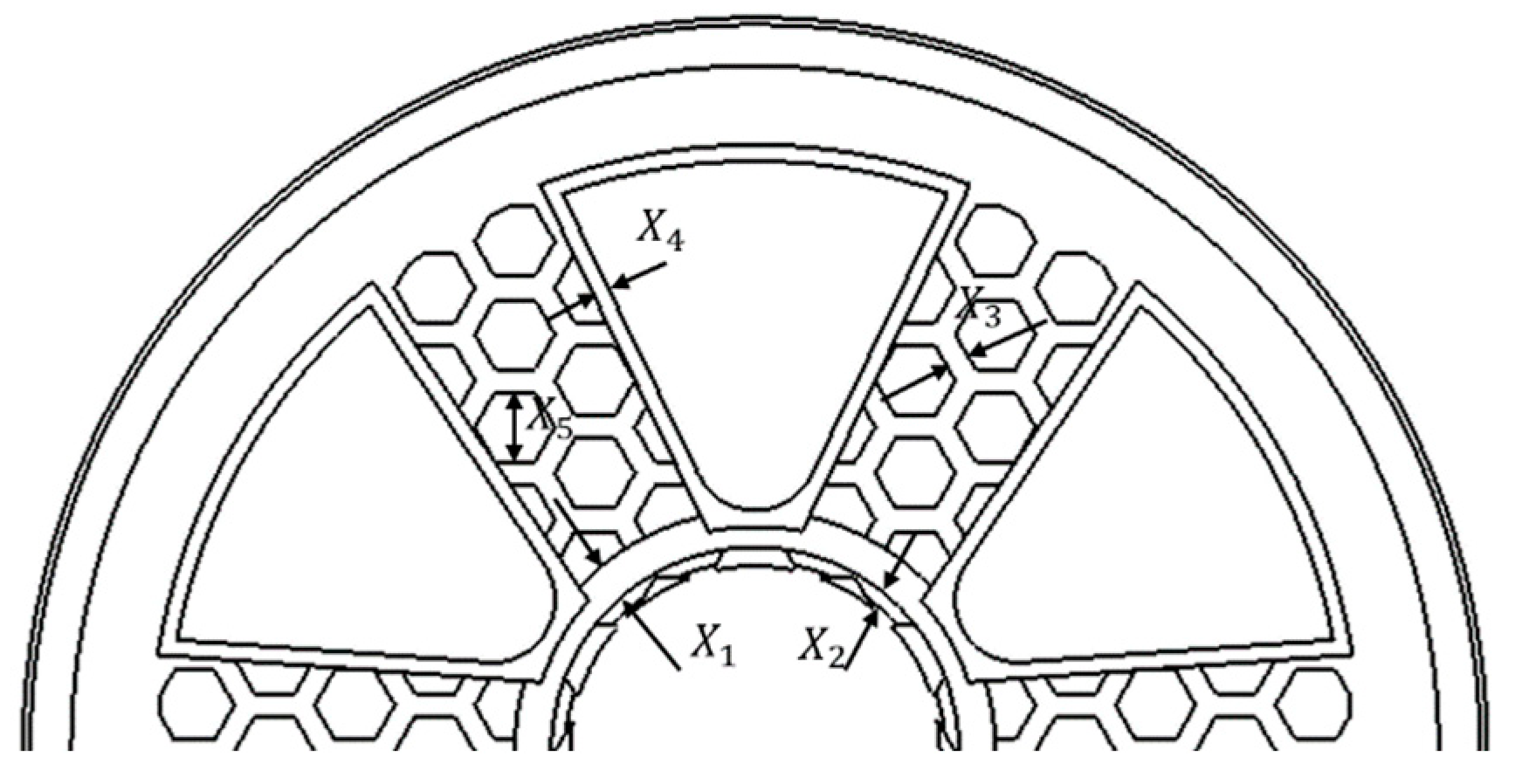
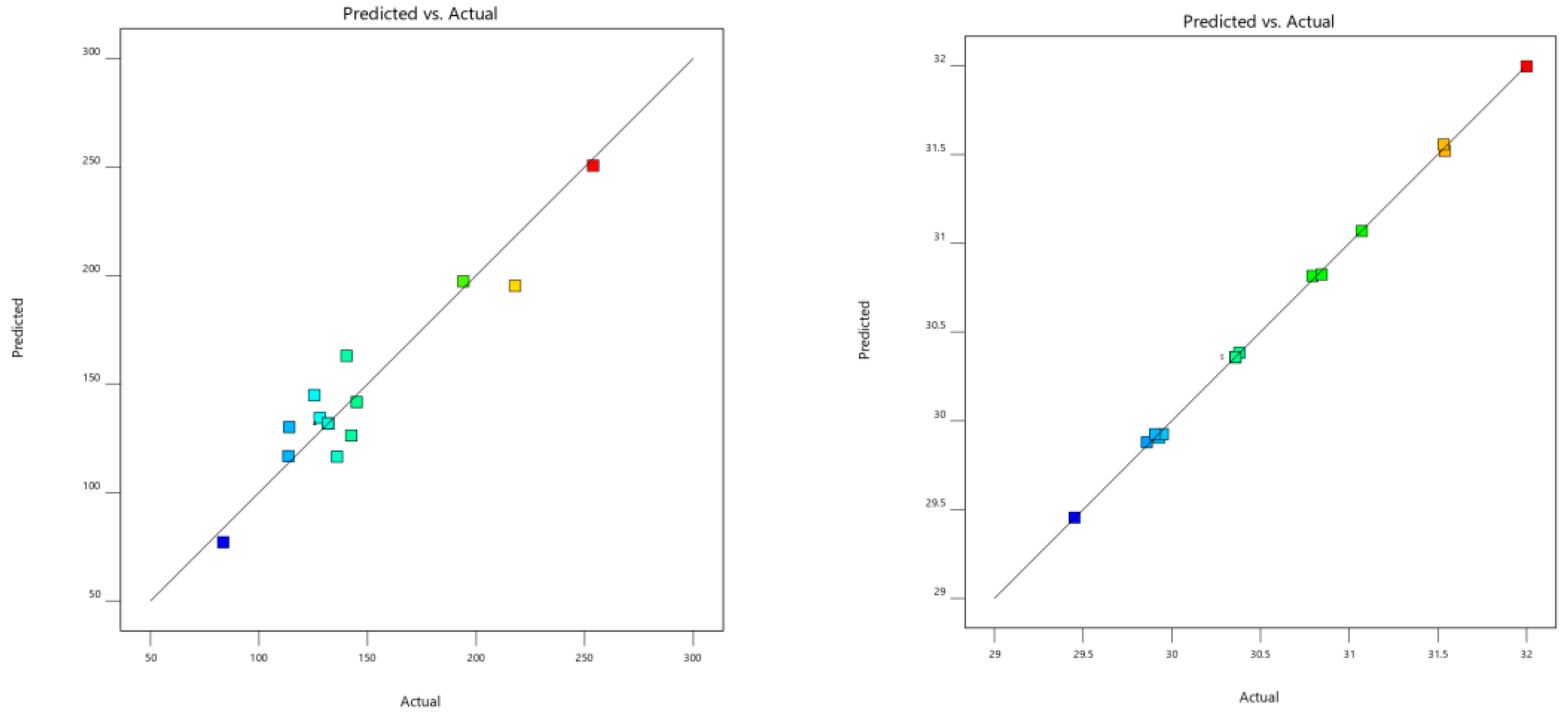
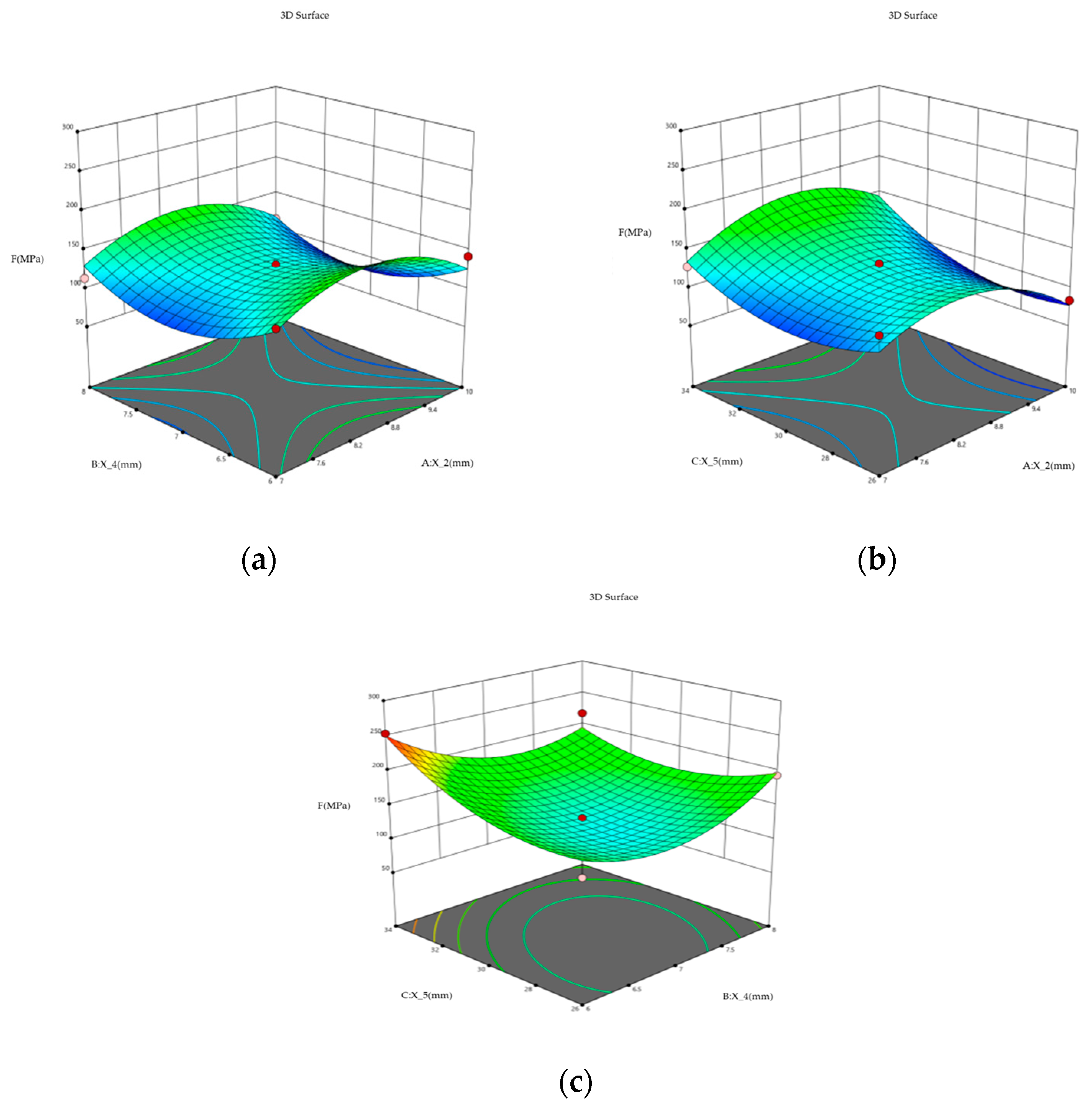
Response Surface Optimization Design of the Bionic Wheel Hub with a Honeycombed Structure
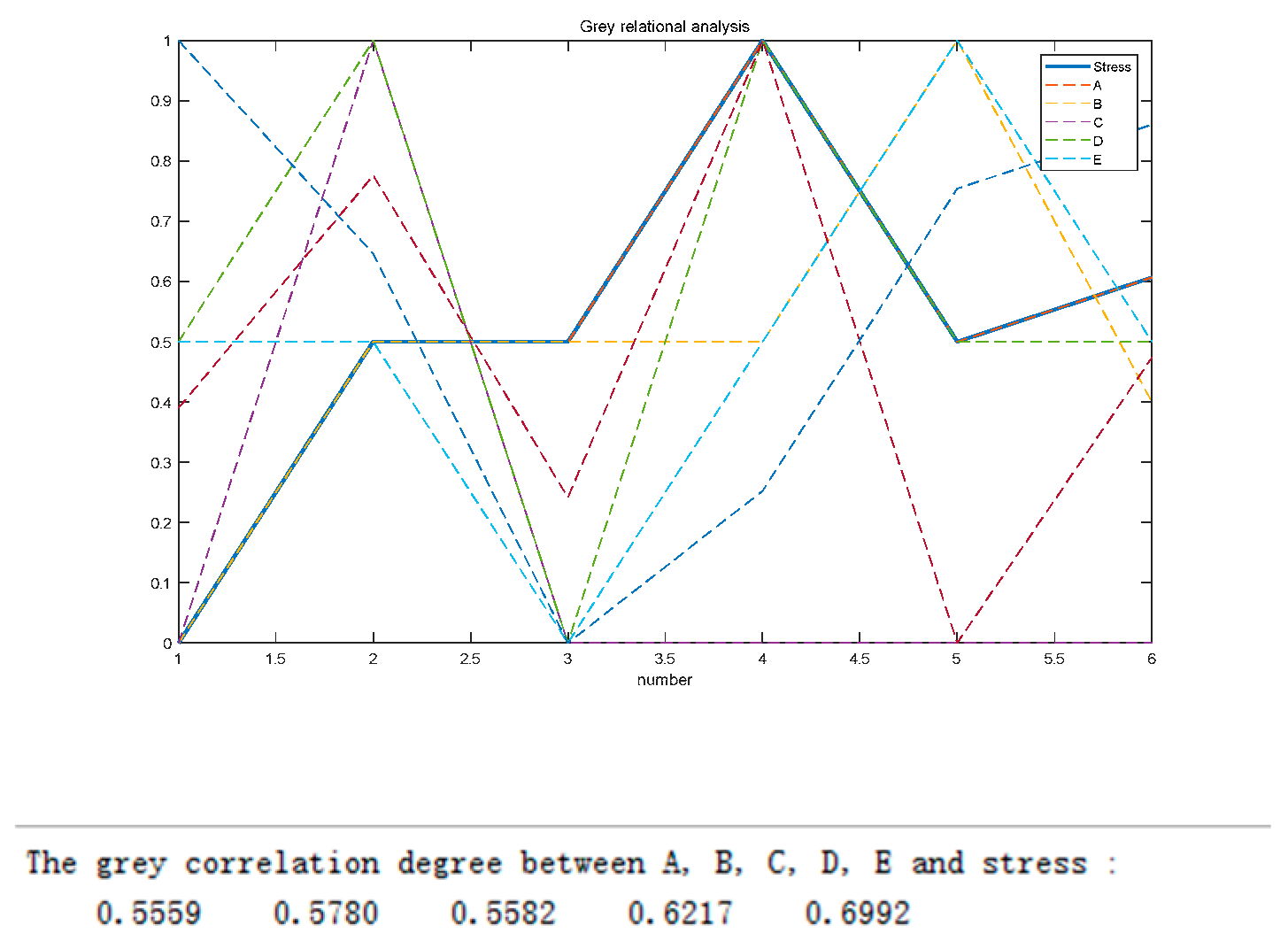
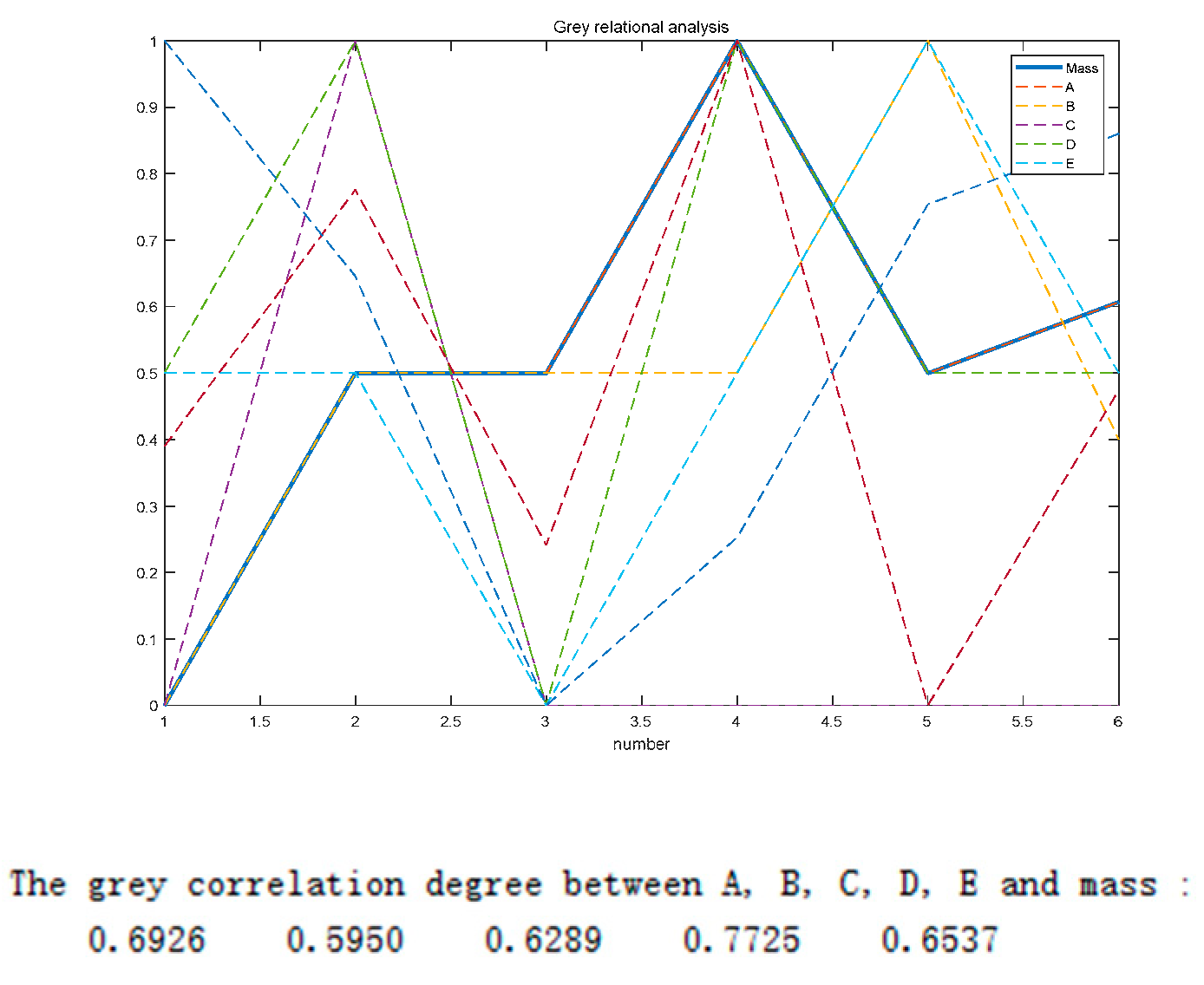
Gray Correlation Degree Analysis of Five Parameters with Wheel Hub Stress and Quality
4. Results
5. Conclusions
- (1)
- The optimization results demonstrated that the maximum stress under the response surface optimization method was 109.34 MPa, which was 8.7% lower than the maximum stress of an ordinary wheel hub at 119.77 MPa. This reduction highlights the effectiveness of optimization in alleviating wheel hub stress.
- (2)
- The mass of the ordinary wheel hub was 34.02 kg, whereas the mass of the optimized wheel hub was 29.89 kg, representing a reduction of 12.13%. The lightweight wheel hub not only improved fuel economy but also enhanced the vehicle’s handling performance.
- (3)
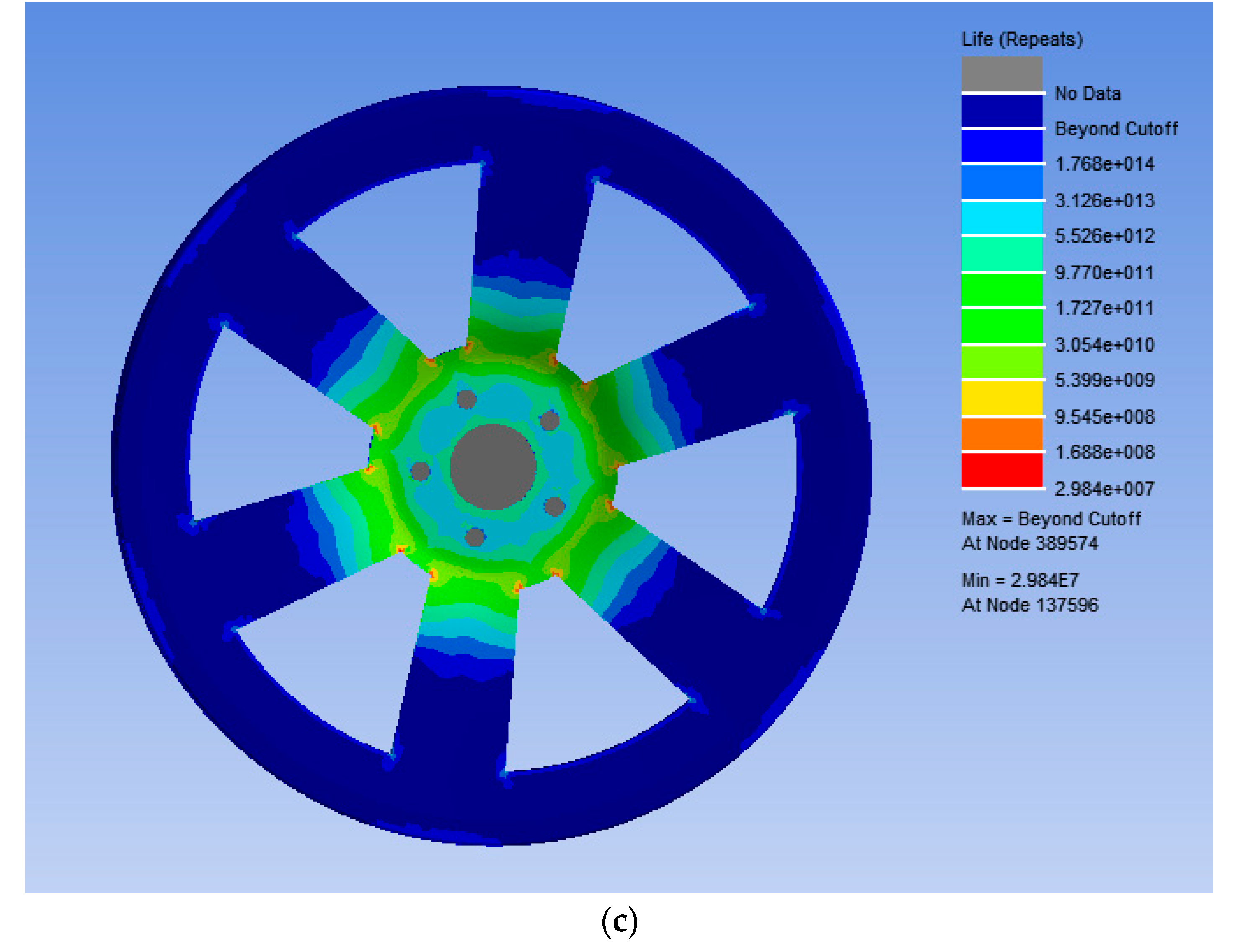
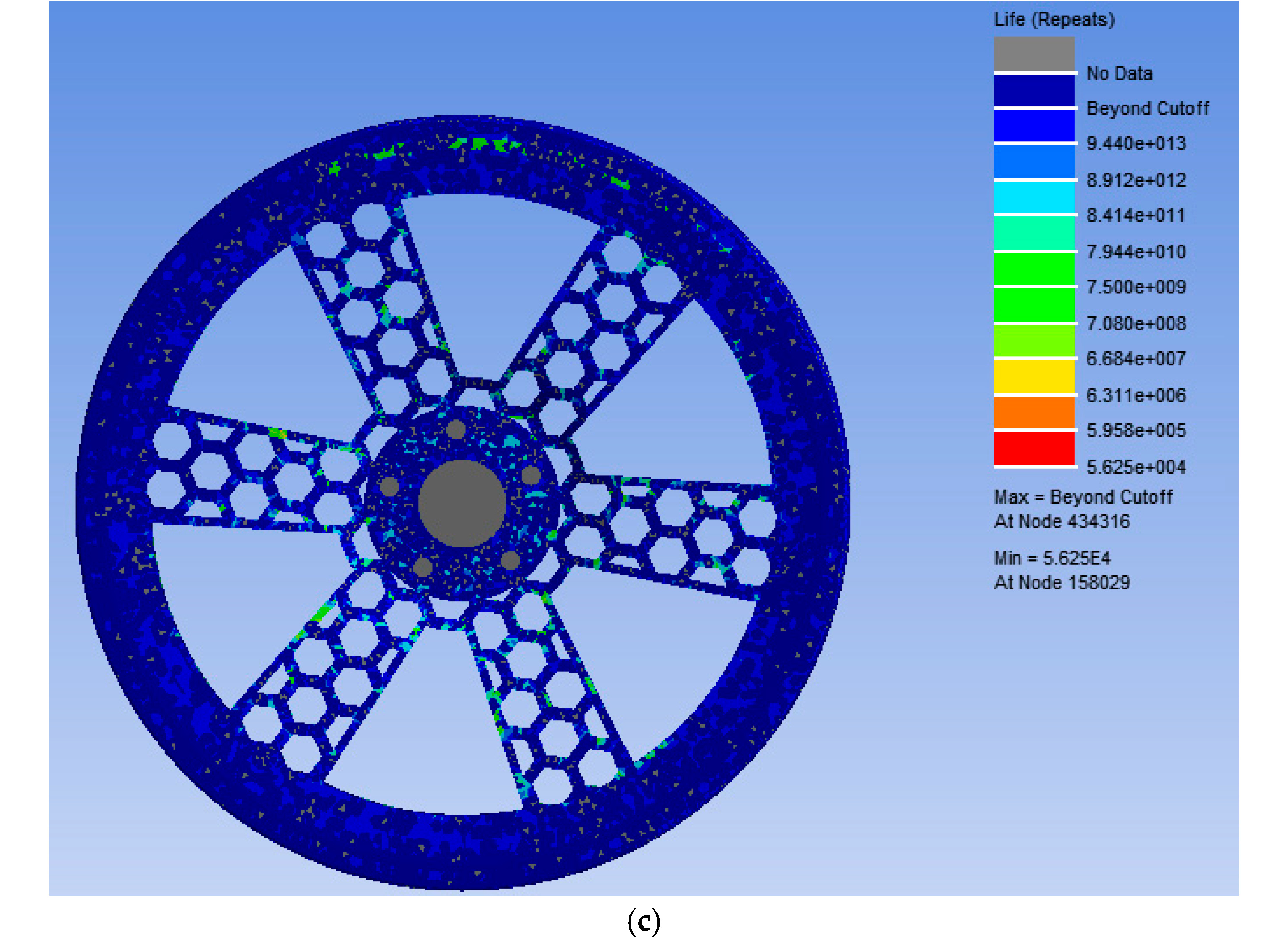
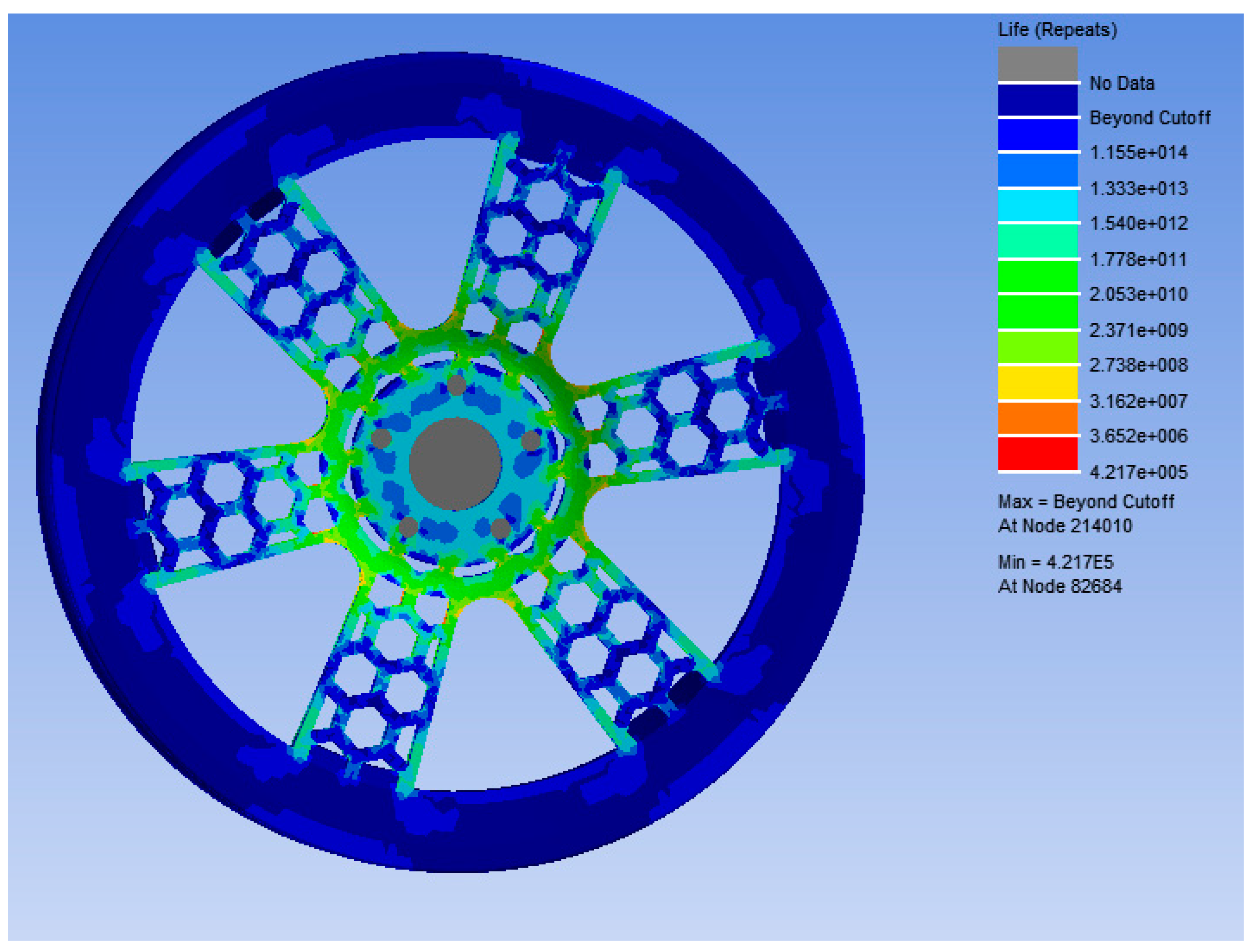
- The bending fatigue life of the bionic wheel with the optimized honeycombed structure was predicted. Under a stress of 109.34 MPa, the load cycles would be at least 421,700 at the connection with the half-shaft. This exceeded the design requirement of a strengthening coefficient of 1.6 and met the minimum cycle number for bending fatigue tests of wheel hubs as specified in GB/T 5334-2021.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Luo, S.-J.; Fu, Y.-T.; Zhou, Y.-X. Perceptual matching of shape design style between wheel hub and car type. Int. J. Ind. Ergon. 2012, 42, 90–102. [Google Scholar] [CrossRef]
- Acer, D.C.; Uzay, Ç.; Geren, N.; Akilli, H. Design and optimization of a Wheel Hub for Lightweight Efficiency Challenge Vehicles. In Proceedings of the International Advanced Researches & Engineering Congress 2017, Osmaniye, Turkey, 16–18 November 2017. [Google Scholar]
- Mohite, B. Stress analysis and optimization of front wheel hub. Int. J. Res. Appl. Sci. Eng. Technol. 2018, 6. [Google Scholar] [CrossRef]
- Shah, V.; Patel, P.; Keshav, M. Modeling and analysis of integrated wheel hub. J. Phys. Conf. Ser. 2022, 2256, 012035. [Google Scholar] [CrossRef]
- Barthlott, W.; Rafiqpoor, M.D.; Erdelen, W.R. Bionics and biodiversity–bio-inspired technical innovation for a sustainable future. Biomim. Res. Archit. Build. Constr. Biol. Des. Integr. Struct. 2016, 11–55. [Google Scholar] [CrossRef]
- Kindlein, W., Jr.; Guanabara, A.S. Methodology for product design based on the study of bionics. Mater. Des. 2005, 26, 149–155. [Google Scholar]
- Li, X.; Song, X.; Wang, Y.; Cao, X. Embedded type honeycomb structure surface mechanical properties of the study. Mech. Des. Manuf. 2024, 9, 331–334+339. [Google Scholar] [CrossRef]
- Rui, H.; Yumiao, C. Parametric design and Finite Element Analysis of automotive wheel hub based on morphological bionics. Ind. Des. 2023, 5, 26–29. [Google Scholar]
- Chen, Y.; Guo, C.; Li, L.; Ma, Y.; Ma, Y. Bionic lightweight design and optimization of wheel hub based on spider algae Structure. Mech. Manuf. Autom. 2019, 49, 90–94+100. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, X.; Zhang, L.; Song, J.; Sun, W. Lightweight design of hub under three working conditions based on Topological optimization. J. Phys. Conf. Ser. 2022, 2338, 012074. [Google Scholar] [CrossRef]
- Yun, Y.; Xudong, G.A.; Hao, W.; Kun, L.; Zongze, L. Dynamic Radial Fatigue Life Prediction of Wheel. Ordnance Ind. Autom. 2019, 38, 71–75. [Google Scholar]
- You, D.; Zhou, Z.; Hongjun, L.; Kelei, W. Mesh design of wing bionic surface based on Base structure method. J. Northwest. Polytech. Univ. 2022, 40, 271–280. (In Chinese) [Google Scholar]
- Zhang, Z.-F.; Zhang, J.-X.; Zhang, Y. Optimization Design of Ditcher based on Bionic Design Method. Comput. Integr. Manuf. Syst. 2022, 28, 1143–1149. [Google Scholar]
- Yihua, L. Lightweight Design of Car wheel hub Based on Finite Element Analysis. Spec. Purp. Veh. 2022, 9, 30–33. [Google Scholar]
- Song, G.; Zhu, Z.; Li, Y.; Wang, W. Numerical Simulation and Fatigue Life Analysis of Full-surface Wheel Radial Fatigue Test. Automot. Eng. 2017, 39, 556–560. [Google Scholar]
- Jiantao, W.; Li, S.; Qingying, L. Research on Parametric Model Construction for Bionic Modeling of Automotive wheel hub. Mach. Des. 2019, 36, 115–119. [Google Scholar]
- Wang, C.; Li, Y.; Zhao, W.; Zou, S.; Zhou, G.; Wang, Y. Structure design and multi-objective optimization of a novel crash box based on biomimetic structure. Int. J. Mech. Sci. 2018, 138–139, 489–501. [Google Scholar] [CrossRef]
- Wang, C.; Wu, F.; Liu, J.; Hui, L. Fatigue life prediction and experimental study of Aluminum alloy wheel hub considering damage accumulation. J. Mech. Strength 2023, 45, 970–976. [Google Scholar] [CrossRef]
- Tianci, L.; Dan, Z. Multi-objective Topology Optimization Design of Automotive Disc Brake. J. Jiangsu Univ. Technol. 2024, 30, 51–59. [Google Scholar]
- Chunyan, L.; Zhaolei, X.; Hejun, L.; Changdong, W. Multi-objective Topology Optimization Design of Automobile Suspension Control Arm. Mech. Electr. Eng. Technol. 2021, 50, 93–95+131. [Google Scholar]
- Onyibo, E.C.; Safaei, B. Application of finite element analysis to honeycomb sandwich structures: A review. Rep. Mech. Eng. 2022, 31, 192–209. [Google Scholar] [CrossRef]
- Shinde, T.; Jomde, A.; Shamkuwar, S.; Sollapur, S.; Naikwadi, V.; Patil, C. Fatigue analysis of alloy wheel using cornering fatigue test and its weight optimization. Mater. Today Proc. 2022, 62, 1470–1474. [Google Scholar] [CrossRef]
- Jimenez-Martinez, M. Manufacturing effects on fatigue strength. Eng. Fail. Anal. 2020, 108, 104339. [Google Scholar] [CrossRef]
- Saxena, G.; Chauhan, A.S.; Jain, R.; Gupta, I. Simulation and Optimization of wheel Hub and Upright of Vehicle: A Review. IOSR J. Mech. Civ. Eng. 2017, 14, 42–49. [Google Scholar] [CrossRef]
- Kokate, S.B.; Kulkarni, G.R. Material Optimization of Wheel Hub using Finite Element Analysis. Int. Res. J. Eng. Technol. 2019, 6, 7252–7258. [Google Scholar]
- Yetao, F.; Shuangfu, L.; Qian, W.; Xiao, L. Structure and Lightweight Design of wheel hub for Family Car. Times Automob. 2024, 2, 118–121. [Google Scholar]
- GB/T 5334-2021; Requirements and Test Methods for Bending and Radial Fatigue Performance of Passenger Car Wheels. Chinese Standard: Singapore, 2021.
- Leister, G. Passenger Car Tires and Wheels: Development-Manufacturing-Application; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Sonsino, C.M.; Breitenberger, M.; Krause, I.; Pötter, K.; Schröder, S.; Jürgens, K. Required Fatigue Strength (RFS) for evaluating of spectrum loaded components by the example of cast-aluminum passenger car wheels. Int. J. Fatigue 2021, 145, 105975. [Google Scholar] [CrossRef]
- Burande, D.H.; Kazi, T.N. Fatigue analysis of alloy wheel for passenger car under radial load. Int. J. Eng. Res. Gen. Sci. 2016, 4, 26–36. [Google Scholar]
- Zhanguang, Z.; Ganwei, C.A.; Zhaojun, L. Strength Analysis of Automobile Steel Rim with Bolt Preload. Mach. Des. Manuf. 2009, 8, 219–220. [Google Scholar]
- Jian, W.; Long, W.; Shizun, Z. Finite Element Analysis and Optimal Design of Aluminum Alloy wheel hub. J. Qingdao Univ. 2020, 35, 75–80. [Google Scholar]
- Bing, H.; Maotao, Z.; Yongjian, Z. Dynamic Bending Fatigue Life Prediction of Aluminum Alloy Wheel. Trans. Chin. Soc. Agric. Mach. 2008, 39, 208–210+196. [Google Scholar]
- Ma, C.; Lu, P.; Qiu, N.; Wang, X.; Qiu, W. Lightweight Design of Passenger Car wheel hub Based on Strength Topology Optimization. Mach. Des. Res. 2022, 38, 122–125+129. [Google Scholar] [CrossRef]
- Khuri, A.; Mukhopadhyay, S. Response surface methodology. Des. Anal. Exp. 2010, 2, 565–614. [Google Scholar] [CrossRef]
- Chelladurai, S.J.S.; Murugan, K.; Ray, A.P.; Upadhyaya, M.; Narasimharaj, V.; Gnanasekaran, S. Gnanasekaran, S. optimization of process parameters using response surface methodology: A review. Mater. Today Proc. 2021, 37, 1301–1304. [Google Scholar] [CrossRef]
- Kumar, R.; Katyal, P.; Mandhania, S. Grey relational analysis based multiresponse optimization for WEDM of ZE41A magnesium alloy. Int. J. Lightweight Mater. Manuf. 2022, 5, 543–554. [Google Scholar] [CrossRef]
- Pengcheng, L.; Qixun, W. Analysis and application of grey correlation degree. J. Salt Lake Res. 2001, 9, 48–51. [Google Scholar]
- Junjian, H.; Yong, W.; Yudong, Z.; Dengfeng, Z.; Wenbin., H.; Fang, Z. Lightweight design of Body in White Structure based on Adaptive Response Surface Method. Sci. Technol. Eng. 2019, 24, 3416–3425. (In Chinese) [Google Scholar]




| Material | Density (kg/m3) | Young’s Modulus (Pa) | Poisson’s Ratio (MPa) | Strength Limit |
|---|---|---|---|---|
| A356 Aluminum alloy | 2690 | 6.9 × 1010 | 0.33 | 290 |
| Material | Strengthening Factor | Minimum Cycle Number | Friction Coefficient |
|---|---|---|---|
| Lightweight aluminum alloy | 1.60 (optimization coefficient) | 100,000 | 0.7 |
| Number of Grids | 1.5 × 105 | 1.9 × 105 | 2.6 × 105 | 3.7 × 105 | 5.6 × 105 | 9.6 × 105 | 1.9 × 106 | 4.3 × 106 |
|---|---|---|---|---|---|---|---|---|
| Maximum Stress of the Hub (MPa) | 204.11 | 204.56 | 204.85 | 205.21 | 205.55 | 206.05 | 206.06 | 206.08 |
| Working Condition | Mass (kg) | Maximum Stress (MPa) | Displacement (mm) |
|---|---|---|---|
| Ordinary wheel hub 1 | 34.02 | 119.36 | 0.16 |
| Honeycomb-structured wheel hub 1 | 29.73 | 206.09 | 0.29 |
| Ordinary wheel hub 2 | 34.02 | 119.77 | 0.15 |
| Honeycomb-structured wheel hub 2 | 29.73 | 174.94 | 0.27 |
| Target Parameter | Variation Range (mm) |
|---|---|
| 14–17 | |
| 7–10 | |
| 8–12 | |
| 6–8 | |
| 26–34 |
| Finite Element Analysis | Response Surface Optimization Design | Error | |
|---|---|---|---|
| Mass (kg) | 31.17 | 29.89 | 4.2% |
| Stress (MPa) | 106.59 | 109.34 | 2.5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, N.; Liu, X.; Jiang, Y.; Liu, P.; Gao, Y.; Ding, H.; Zhao, Y. Bionic Optimization Design and Fatigue Life Prediction of a Honeycomb-Structured Wheel Hub. Biomimetics 2024, 9, 611. https://doi.org/10.3390/biomimetics9100611
Liu N, Liu X, Jiang Y, Liu P, Gao Y, Ding H, Zhao Y. Bionic Optimization Design and Fatigue Life Prediction of a Honeycomb-Structured Wheel Hub. Biomimetics. 2024; 9(10):611. https://doi.org/10.3390/biomimetics9100611
Chicago/Turabian StyleLiu, Na, Xujie Liu, Yueming Jiang, Peng Liu, Yuanyuan Gao, Hang Ding, and Yujun Zhao. 2024. "Bionic Optimization Design and Fatigue Life Prediction of a Honeycomb-Structured Wheel Hub" Biomimetics 9, no. 10: 611. https://doi.org/10.3390/biomimetics9100611
APA StyleLiu, N., Liu, X., Jiang, Y., Liu, P., Gao, Y., Ding, H., & Zhao, Y. (2024). Bionic Optimization Design and Fatigue Life Prediction of a Honeycomb-Structured Wheel Hub. Biomimetics, 9(10), 611. https://doi.org/10.3390/biomimetics9100611






