Finger Prosthesis Driven by DEA Pairs as Agonist–Antagonist Artificial Muscles
Abstract
:1. Introduction
2. Materials and Methods
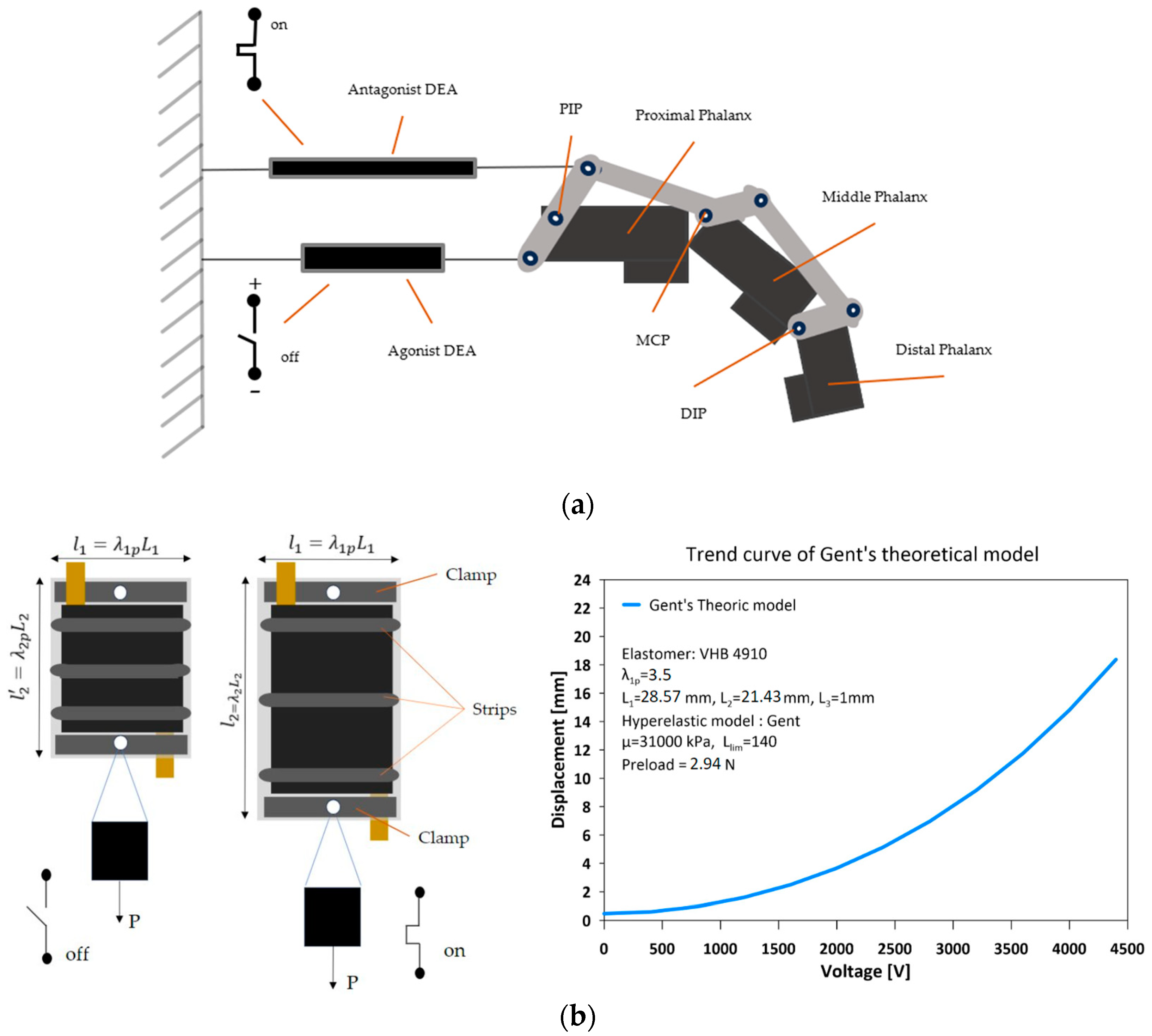
2.1. Finger FCDEA Setup
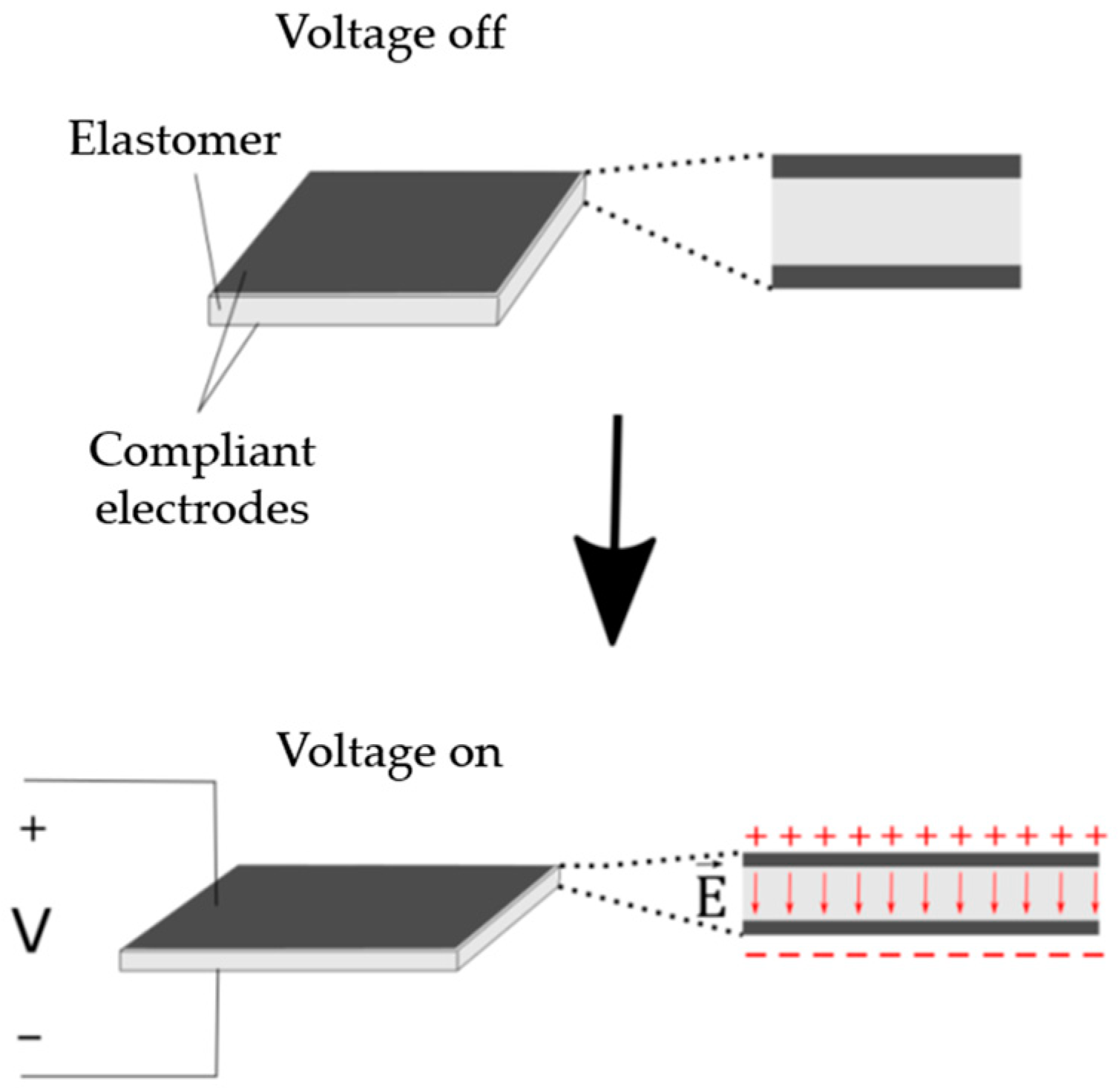
2.2. DEA Modeling
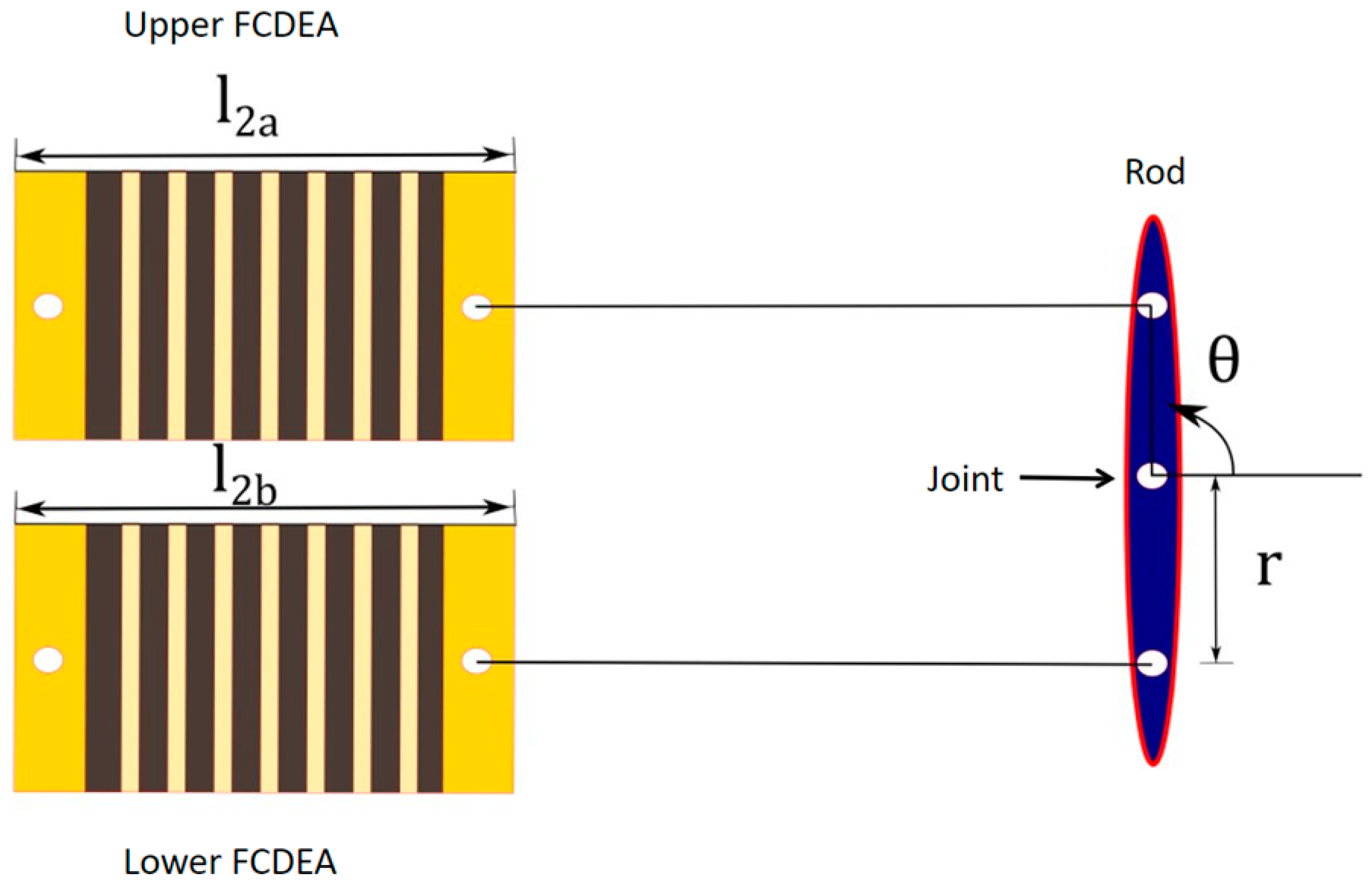
2.3. Finger Mechanism Modeling
2.4. FCDEA Finger Prototype
3. Results and Discussion
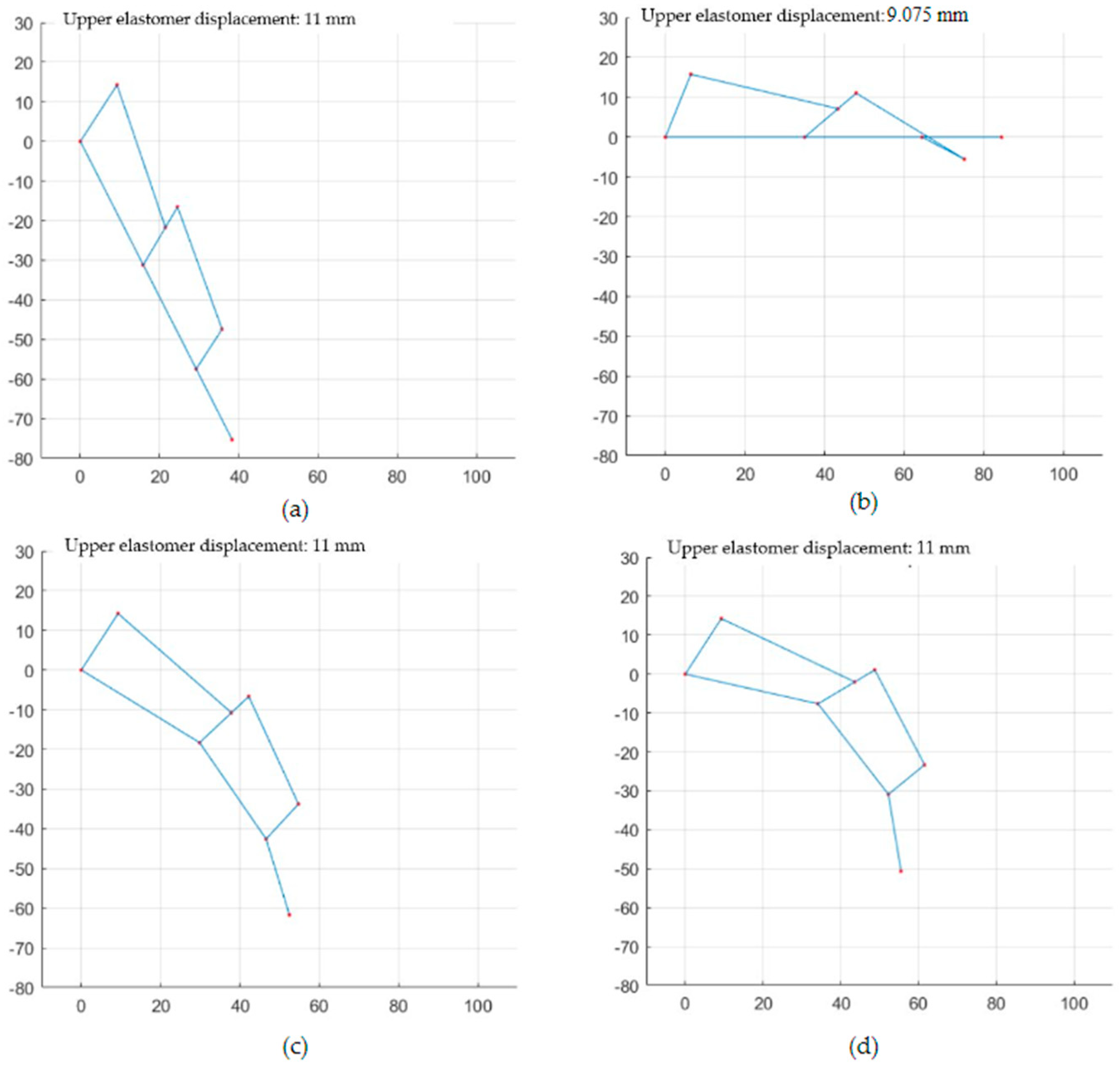
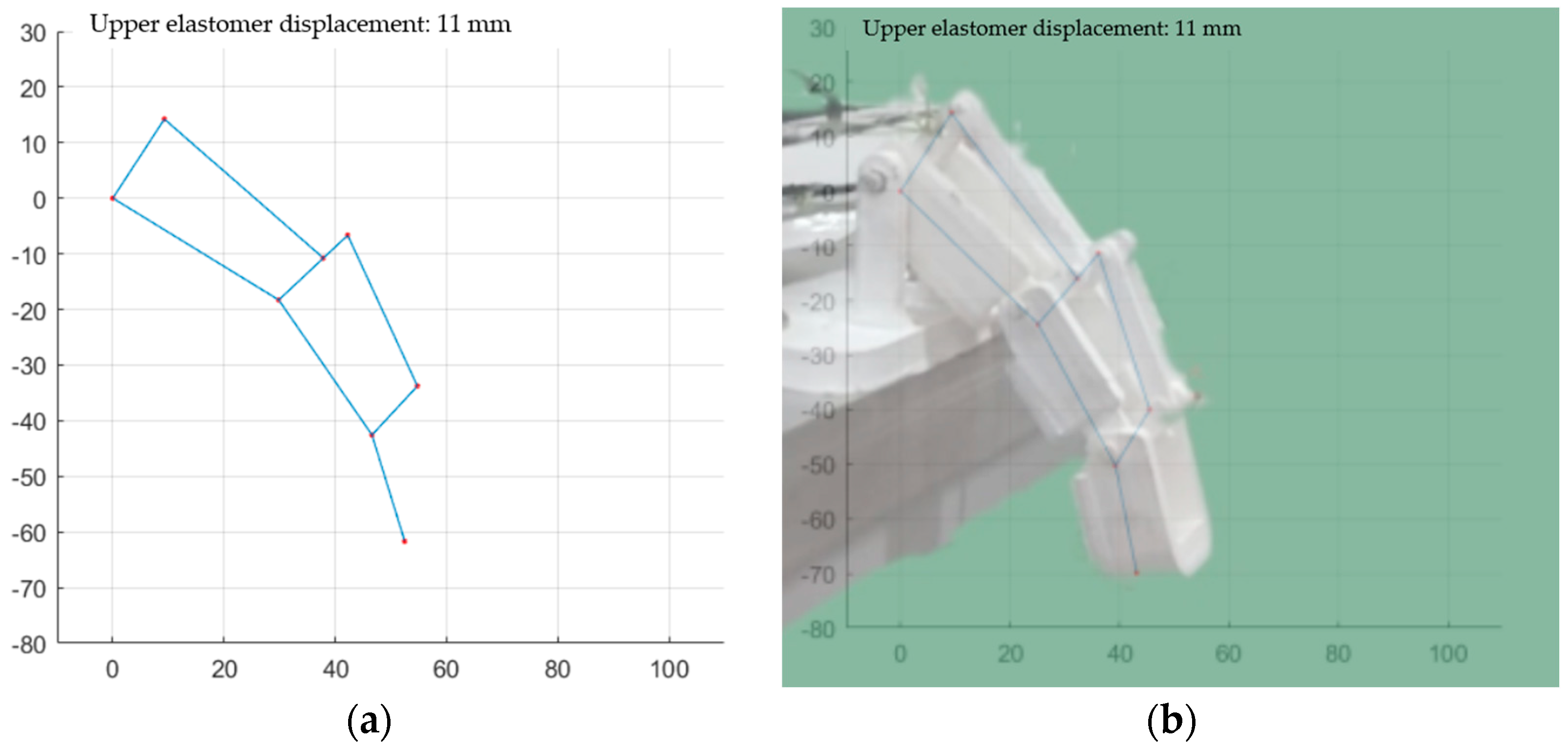
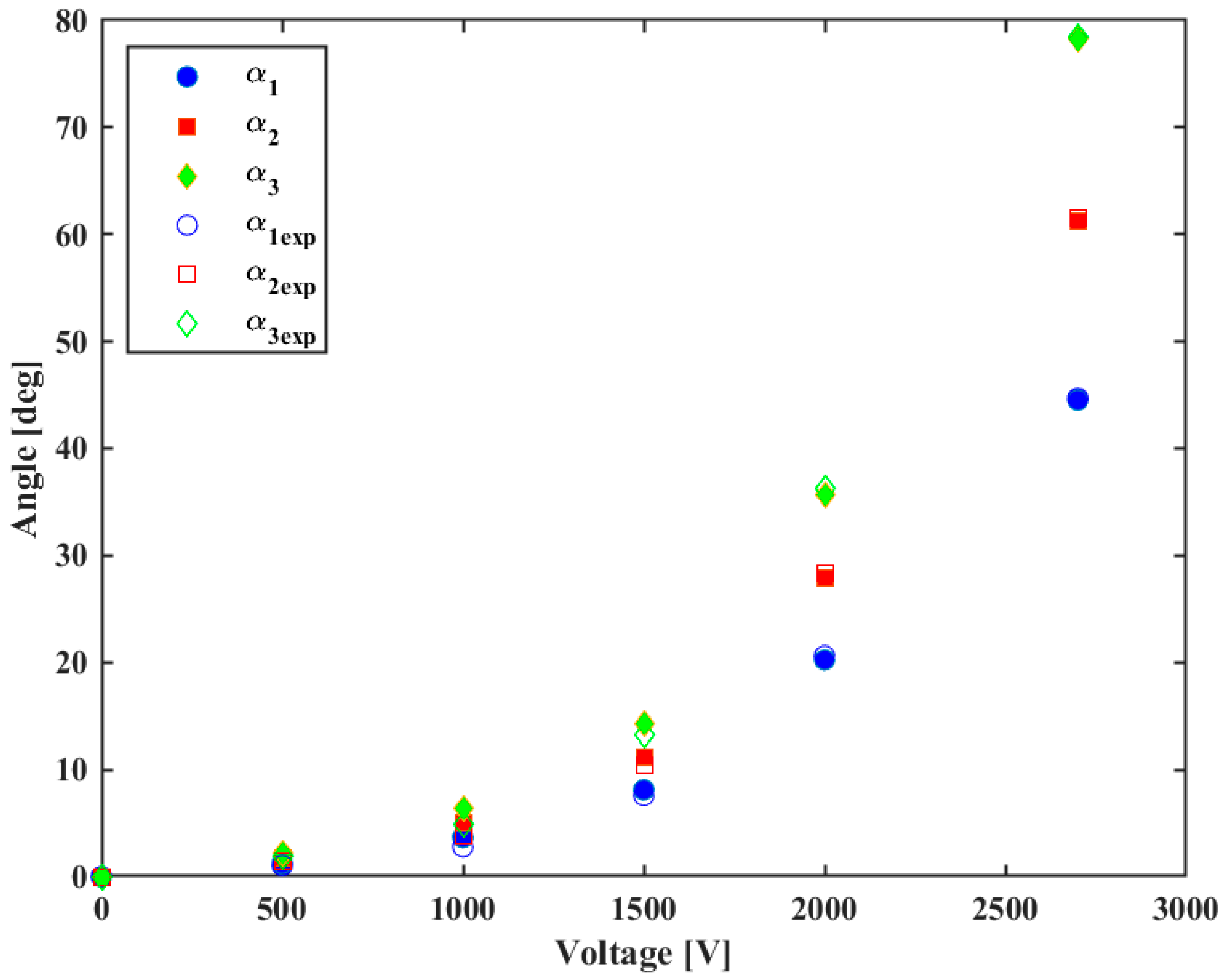
3.1. Finger Mechanism Simulation
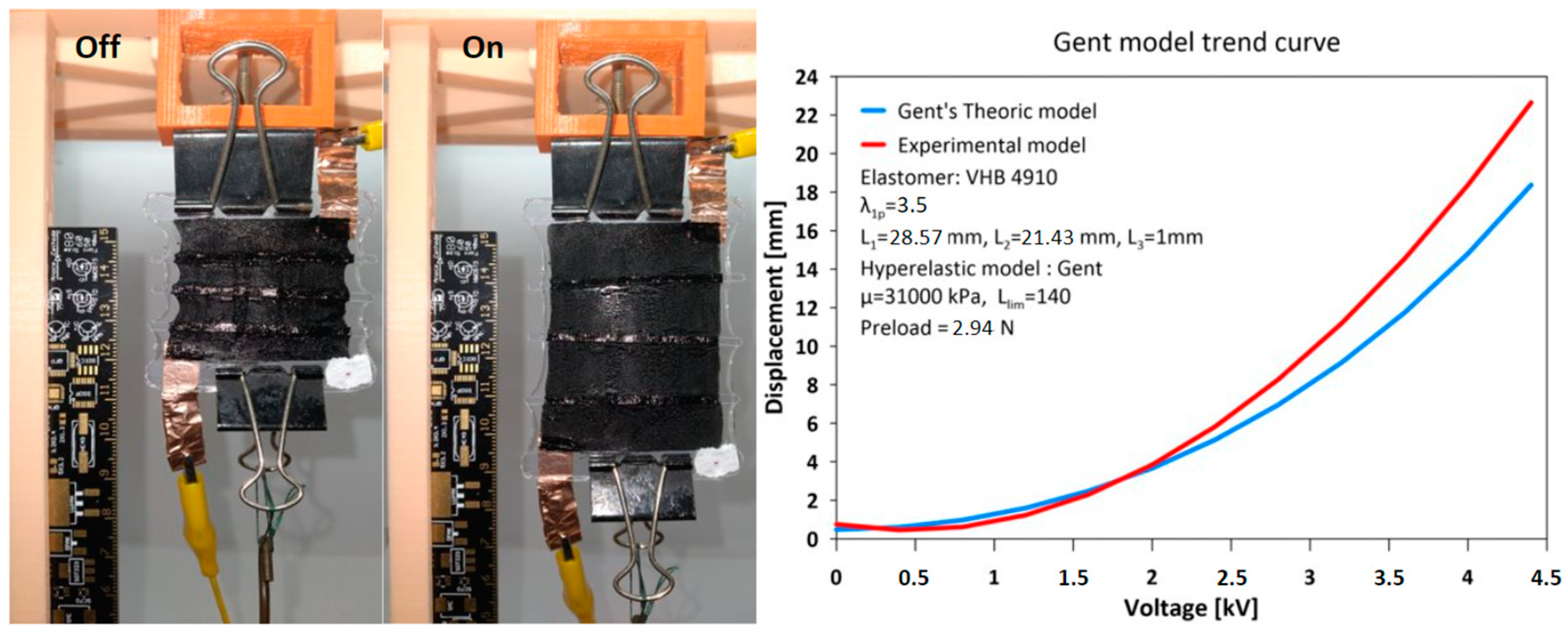
3.2. Expandable Linear Actuator
3.3. Physical Prototype
3.4. Gripping an Object
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Institute for Health Metrics and Evaluation. Global Burden of Disease Study 2019 (GBD 2019) Data Resources|GHDx 2019. Available online: https://ghdx.healthdata.org/gbd-2019 (accessed on 23 July 2023).
- Light, C.M.; Chappell, P.H. Development of a Lightweight and Adaptable Multiple-Axis Hand Prosthesis. Med. Eng. Phys. 2000, 22, 679–684. [Google Scholar] [CrossRef]
- Cao, W.; Chen, C.; Wang, D.; Wu, X.; Chen, L.; Xu, T.; Liu, J. A Lower Limb Exoskeleton with Rigid and Soft Structure for Loaded Walking Assistance. IEEE Robot. Autom. Lett. 2022, 7, 454–461. [Google Scholar] [CrossRef]
- Näf, M.B.; Junius, K.; Rossini, M.; Rodriguez-Guerrero, C.; Vanderborght, B.; Lefeber, D. Misalignment Compensation for Full Human-Exoskeleton Kinematic Compatibility: State of the Art and Evaluation. Appl. Mech. Rev. 2019, 70, 050802. [Google Scholar] [CrossRef]
- Andrade, R.M.; Sapienza, S.; Mohebbi, A.; Fabara, E.E.; Bonato, P. Overground Walking with a Transparent Exoskeleton Shows Changes in Spatiotemporal Gait Parameters. IEEE J. Transl. Eng. Health Med. 2024, 12, 182–193. [Google Scholar] [CrossRef]
- Youn, J.-H.; Jeong, S.M.; Hwang, G.; Kim, H.; Hyeon, K.; Park, J.; Kyung, K.-U. Dielectric Elastomer Actuator for Soft Robotics Applications and Challenges. Appl. Sci. 2020, 10, 640. [Google Scholar] [CrossRef]
- Zhang, J.; Sheng, J.; O’Neill, C.T.; Walsh, C.J.; Wood, R.J.; Ryu, J.-H.; Desai, J.P.; Yip, M.C. Robotic Artificial Muscles: Current Progress and Future Perspectives. IEEE Trans. Robot. 2019, 35, 761–781. [Google Scholar] [CrossRef]
- Brochu, P.; Pei, Q. Advances in Dielectric Elastomers for Actuators and Artificial Muscles. Macromol. Rapid Commun. 2010, 31, 10–36. [Google Scholar] [CrossRef] [PubMed]
- Novelli, G.L.; Andrade, R.M. Towards an Active Ankle-Foot Prosthesis Powered by Dielectric Elastomer Actuators in Antagonistic Pairs. In Proceedings of the 2021 International Symposium on Medical Robotics (ISMR), Atlanta, GA, USA, 17–19 November 2021; pp. 1–6. [Google Scholar]
- Lai, H.; Reid, K. Investigation of Dielectric Elastomer Human Energy Harvesting to Reduce Knee Joint Torque Deviation Due to Bracing. J. Rehabil. Assist. Technol. Eng. 2019, 6. [Google Scholar] [CrossRef] [PubMed]
- Novelli, G.L.; Vargas, G.G.; Andrade, R.M. Dielectric Elastomer Actuators as Artificial Muscles for Wearable Robots. J. Intell. Mater. Syst. Struct. 2023, 34, 1007–1025. [Google Scholar] [CrossRef]
- Maw, J.; Wong, K.Y.; Gillespie, P. Hand Anatomy. Br. J. Hosp. Med. 2016, 77, C34–C40. [Google Scholar] [CrossRef] [PubMed]
- Silva, R.C.; Lourenço, B.G.; Ulhoa, P.H.F.; Dias, E.A.F.; da Cunha, F.L.; Tonetto, C.P.; Villani, L.G.; Vimieiro, C.B.S.; Lepski, G.A.; Monjardim, M.; et al. Biomimetic Design of a Tendon-Driven Myoelectric Soft Hand Exoskeleton for Upper-Limb Rehabilitation. Biomimetics 2023, 8, 317. [Google Scholar] [CrossRef]
- de Andrade, R.M.; Fabriz Ulhoa, P.H.; Fragoso Dias, E.A.; Filho, A.B.; Vimieiro, C.B.S. Design and Testing a Highly Backdrivable and Kinematic Compatible Magneto-Rheological Knee Exoskeleton. J. Intell. Mater. Syst. Struct. 2023, 34, 653–663. [Google Scholar] [CrossRef]
- Hunter, I.W.; Lafontaine, S. A Comparison of Muscle with Artificial Actuators. In Proceedings of the Technical Digest IEEE Solid-State Sensor and Actuator Workshop, Hilton Head, SC, USA, 22–25 June 1992; pp. 178–185. [Google Scholar]
- Mirvakili, S.M.; Hunter, I.W. Artificial Muscles: Mechanisms, Applications, and Challenges. Adv. Mater. 2018, 30, 1704407. [Google Scholar] [CrossRef]
- Liang, W.; Liu, H.; Wang, K.; Qian, Z.; Ren, L.; Ren, L. Comparative Study of Robotic Artificial Actuators and Biological Muscle. Adv. Mech. Eng. 2020, 12, 1687814020933409. [Google Scholar] [CrossRef]
- Lu, T.; Shi, Z.; Shi, Q.; Wang, T.J. Bioinspired Bicipital Muscle with Fiber-Constrained Dielectric Elastomer Actuator. Extreme Mech. Lett. 2016, 6, 75–81. [Google Scholar] [CrossRef]
- Weiner, P.; Neef, C.; Shibata, Y.; Nakamura, Y.; Asfour, T. An Embedded, Multi-Modal Sensor System for Scalable Robotic and Prosthetic Hand Fingers. Sensors 2019, 20, 101. [Google Scholar] [CrossRef]
- De Arco, L.; Pontes, M.J.; Segatto, M.E.V.; Monteiro, M.E.; Cifuentes, C.A.; Díaz, C.A.R. Soft-Sensor System for Grasp Type Recognition in Underactuated Hand Prostheses. Sensors 2023, 23, 3364. [Google Scholar] [CrossRef] [PubMed]
- Nemoto, Y.; Ogawa, K.; Yoshikawa, M. F3Hand II: A Flexible Five-Fingered Prosthetic Hand Using Curved Pneumatic Artificial Muscles. In Proceedings of the 2020 IEEE/SICE International Symposium on System Integration (SII), Honolulu, HI, USA, 12–15 January 2020; pp. 99–104. [Google Scholar]
- Liu, S.; Van, M.; Chen, Z.; Angeles, J.; Chen, C. A Novel Prosthetic Finger Design with High Load-Carrying Capacity. Mech. Mach. Theory 2021, 156, 104121. [Google Scholar] [CrossRef]
- Saharan, L.; Wu, L.; Tadesse, Y. Modeling and Simulation of Robotic Finger Powered by Nylon Artificial Muscles. J. Mech. Robot. 2019, 12, 1–24. [Google Scholar] [CrossRef]
- Zhao, H.; O’Brien, K.; Li, S.; Shepherd, R.F. Optoelectronically Innervated Soft Prosthetic Hand via Stretchable Optical Waveguides. Sci. Robot. 2016, 1, eaai7529. [Google Scholar] [CrossRef] [PubMed]
- Allen, D.P.; Little, R.; Laube, J.; Warren, J.; Voit, W.; Gregg, R.D. Towards an Ankle-Foot Orthosis Powered by a Dielectric Elastomer Actuator. Mechatronics 2021, 76, 102551. [Google Scholar] [CrossRef]
- Hoss, L.; Marczak, R.J. A New Constitutive Model for Rubber-Like Materials. Mecánica Comput. 2010, 29, 2759–2773. [Google Scholar]
- Wissler, M.; Mazza, E. Mechanical Behavior of an Acrylic Elastomer Used in Dielectric Elastomer Actuators. Sens. Actuators Phys. 2007, 134, 494–504. [Google Scholar] [CrossRef]
- Gent, A.N. A New Constitutive Relation for Rubber. Rubber Chem. Technol. 1996, 69, 59–61. [Google Scholar] [CrossRef]
- Vo, V.T.K.; Ang, M.H.; Koh, S.J.A. Maximal Performance of an Antagonistically Coupled Dielectric Elastomer Actuator System. Soft Robot. 2021, 8, 200–212. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Kollosche, M.; Lu, T.; Kofod, G.; Suo, Z. Two Types of Transitions to Wrinkles in Dielectric Elastomers. Soft Matter 2012, 8, 8840–8846. [Google Scholar] [CrossRef]
- Kaltseis, R.; Keplinger, C.; Koh, S.J.A.; Baumgartner, R.; Feng Goh, Y.; Hoe Ng, W.; Kogler, A.; Tröls, A.; Chiang Foo, C.; Suo, Z.; et al. Natural Rubber for Sustainable High-Power Electrical Energy Generation. RSC Adv. 2014, 4, 27905–27913. [Google Scholar] [CrossRef]
- Cordella, F.; Ciancio, A.L.; Sacchetti, R.; Davalli, A.; Cutti, A.G.; Guglielmelli, E.; Zollo, L. Literature Review on Needs of Upper Limb Prosthesis Users. Front. Neurosci. 2016, 10, 209. [Google Scholar] [CrossRef]
- Kumar, D.K.; Jelfs, B.; Sui, X.; Arjunan, S.P. Prosthetic Hand Control: A Multidisciplinary Review to Identify Strengths, Shortcomings, and the Future. Biomed. Signal Process. Control 2019, 53, 101588. [Google Scholar] [CrossRef]
- Osu, R.; Franklin, D.W.; Kato, H.; Gomi, H.; Domen, K.; Yoshioka, T.; Kawato, M. Short- and Long-Term Changes in Joint Co-Contraction Associated with Motor Learning as Revealed from Surface EMG. J. Neurophysiol. 2002, 88, 991–1004. [Google Scholar] [CrossRef]
- Ajiboye, A.B.; Weir, R.F. Muscle Synergies as a Predictive Framework for the EMG Patterns of New Hand Postures. J. Neural Eng. 2009, 6, 036004. [Google Scholar] [CrossRef] [PubMed]







| Metric | Skeletal Striated Muscle | Dielectric Elastomer |
|---|---|---|
| Maximum deformation (%) | 40 | 142 (linear) |
| Maximum tension (MPa) | 0.35 | 7.7 |
| Maximum deformation rate (%/s) | 50 | 450 |
| Work density (kJ/m3) | 40 | 3500 |
| Specific power (kW/kg) | 0.28 | 3.6 |
| Efficiency (%) | 40 | 80 |
| Metric | Elastomer |
|---|---|
| Eletrical Voltage (V) | 3500 |
| 3.50 | |
| (mm) | 28.57 |
| (mm) | 21.43 |
| (mm) | 11.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
da Silva, A.B.S.; Mendes, G.E.P.; Bragato, E.S.; Novelli, G.L.; Monjardim, M.; Andrade, R.M. Finger Prosthesis Driven by DEA Pairs as Agonist–Antagonist Artificial Muscles. Biomimetics 2024, 9, 110. https://doi.org/10.3390/biomimetics9020110
da Silva ABS, Mendes GEP, Bragato ES, Novelli GL, Monjardim M, Andrade RM. Finger Prosthesis Driven by DEA Pairs as Agonist–Antagonist Artificial Muscles. Biomimetics. 2024; 9(2):110. https://doi.org/10.3390/biomimetics9020110
Chicago/Turabian Styleda Silva, Alexandre B. S., Gabriel E. P. Mendes, Eduardo S. Bragato, Guilherme L. Novelli, Marina Monjardim, and Rafhael M. Andrade. 2024. "Finger Prosthesis Driven by DEA Pairs as Agonist–Antagonist Artificial Muscles" Biomimetics 9, no. 2: 110. https://doi.org/10.3390/biomimetics9020110
APA Styleda Silva, A. B. S., Mendes, G. E. P., Bragato, E. S., Novelli, G. L., Monjardim, M., & Andrade, R. M. (2024). Finger Prosthesis Driven by DEA Pairs as Agonist–Antagonist Artificial Muscles. Biomimetics, 9(2), 110. https://doi.org/10.3390/biomimetics9020110






