Design and Control of a Tendon-Driven Robotic Finger Based on Grasping Task Analysis
Abstract
:1. Introduction
2. Related Work
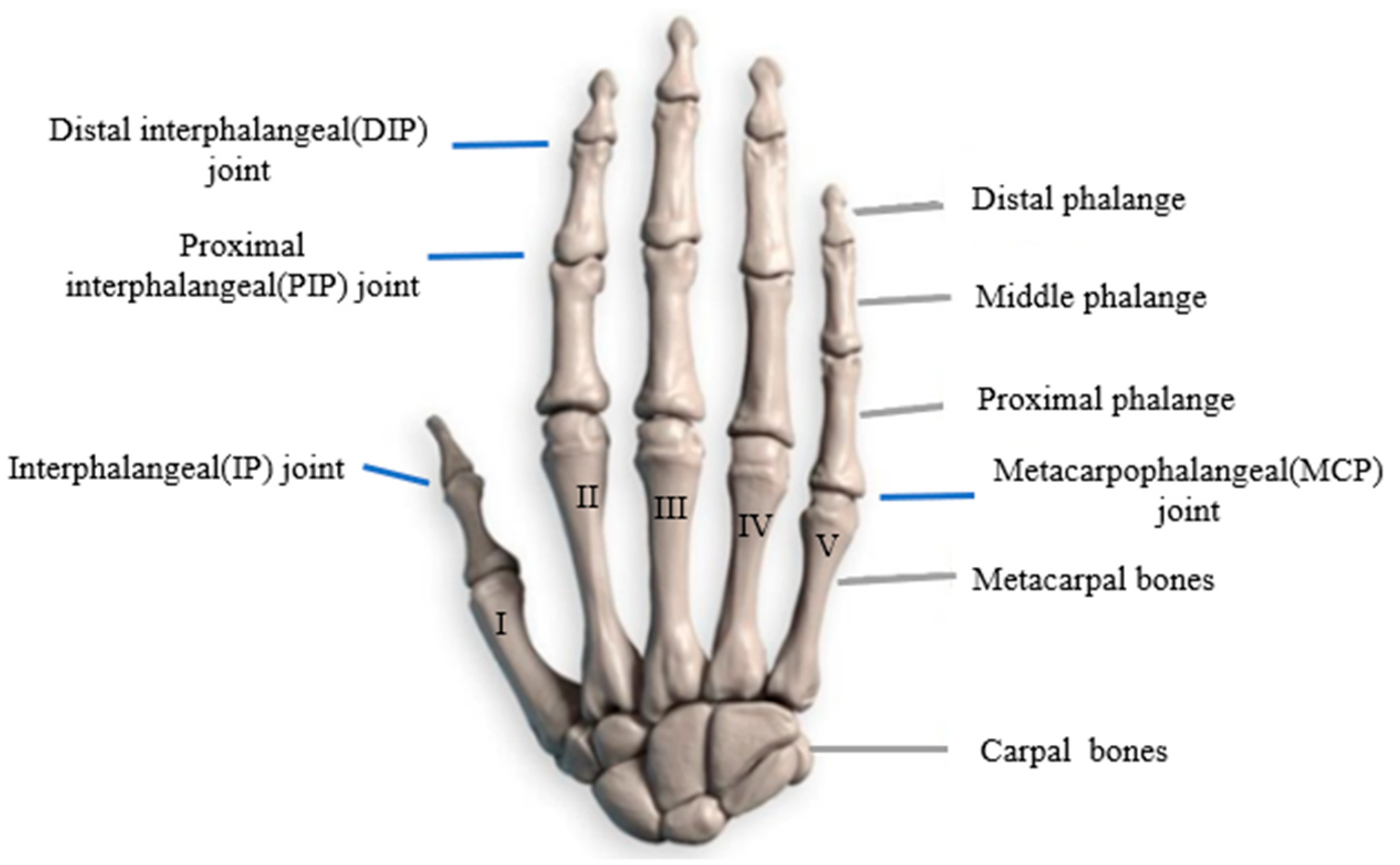
- Extrinsic tendons originate from muscles in the forearm and travel through the wrist to the fingers. These include the flexor and extensor tendons, which control the bending and straightening of the fingers.
- Intrinsic tendons originate from muscles within the hand itself. These include the lumbricals and interossei muscles, which fine-tune finger movements and contribute to the hand’s dexterity by enabling precise adjustments in finger positioning.
- (1)
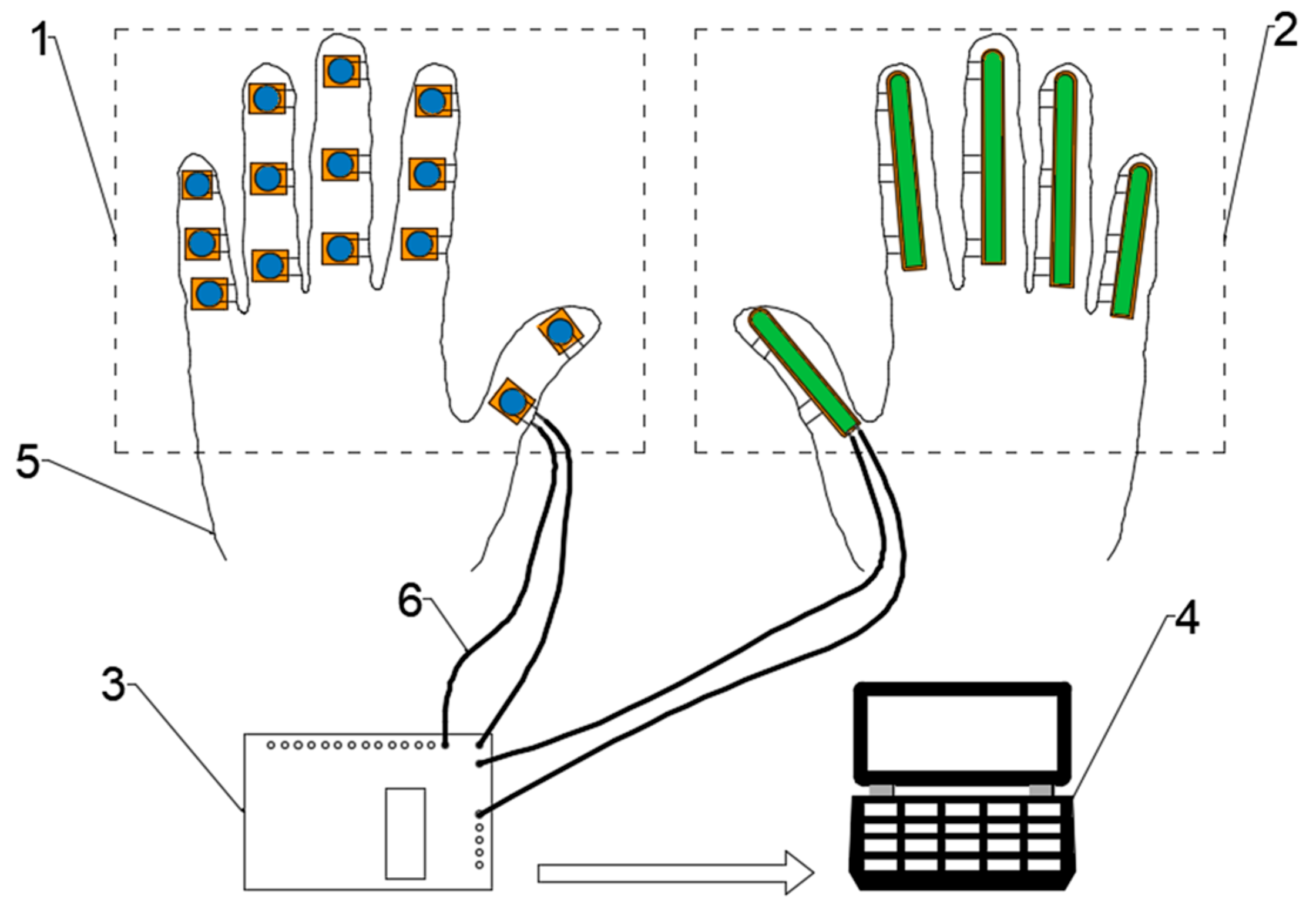
- A data collection glove is designed to collect the typical grasping tasks. The hand manipulation characteristics, finger end pressure, and finger joint bending angle are obtained through experiments based on the Feix grasping spectrum.
- (2)
- A series of contact motion characteristic comparison experiments were conducted on a tendon-driven finger with 12 different tendon pathways. These experiments revealed distinct output performance characteristics for each of the tendon pathways. The findings provide valuable insights that can inform the design and control strategies for future tendon-driven hands.
3. Human Hand Manipulation Characteristics
3.1. Structural Characteristics of the Human Hand
3.2. Experimental Design of Human Hand Manipulation Characteristics
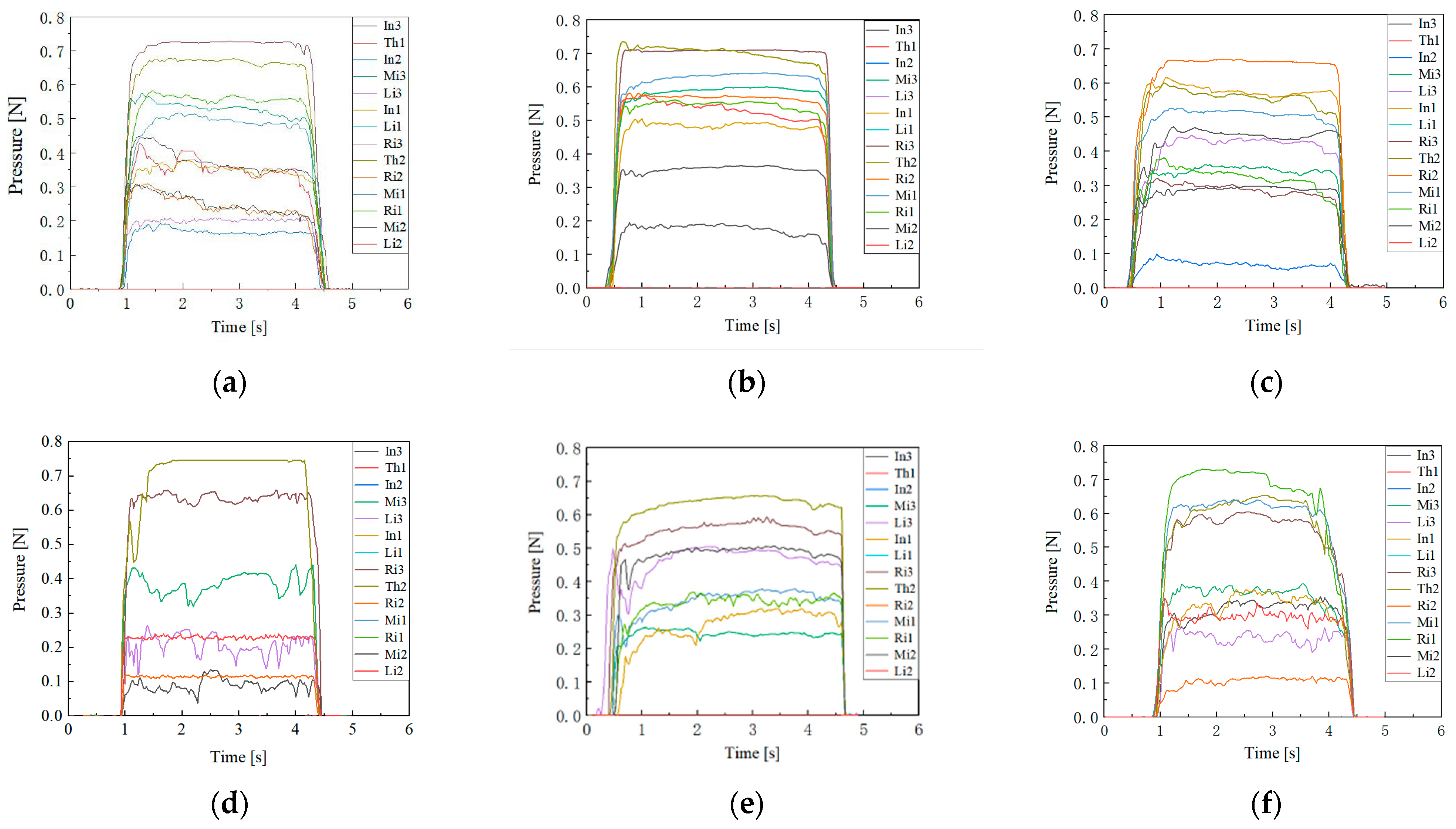
3.3. Analysis of Finger End Pressure
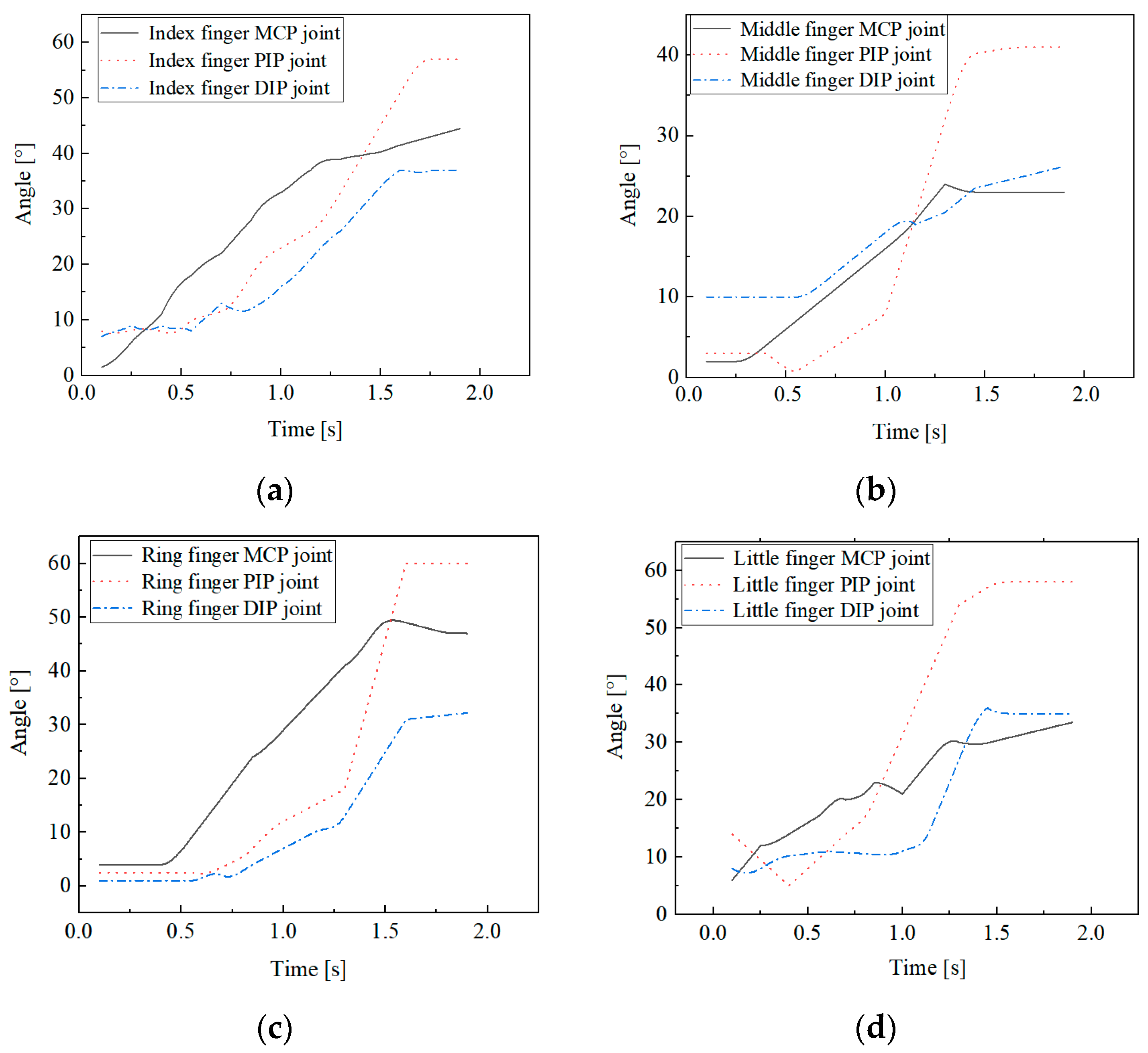
3.4. Analysis of Finger Joint Bending Angle
4. Mechanical Analysis
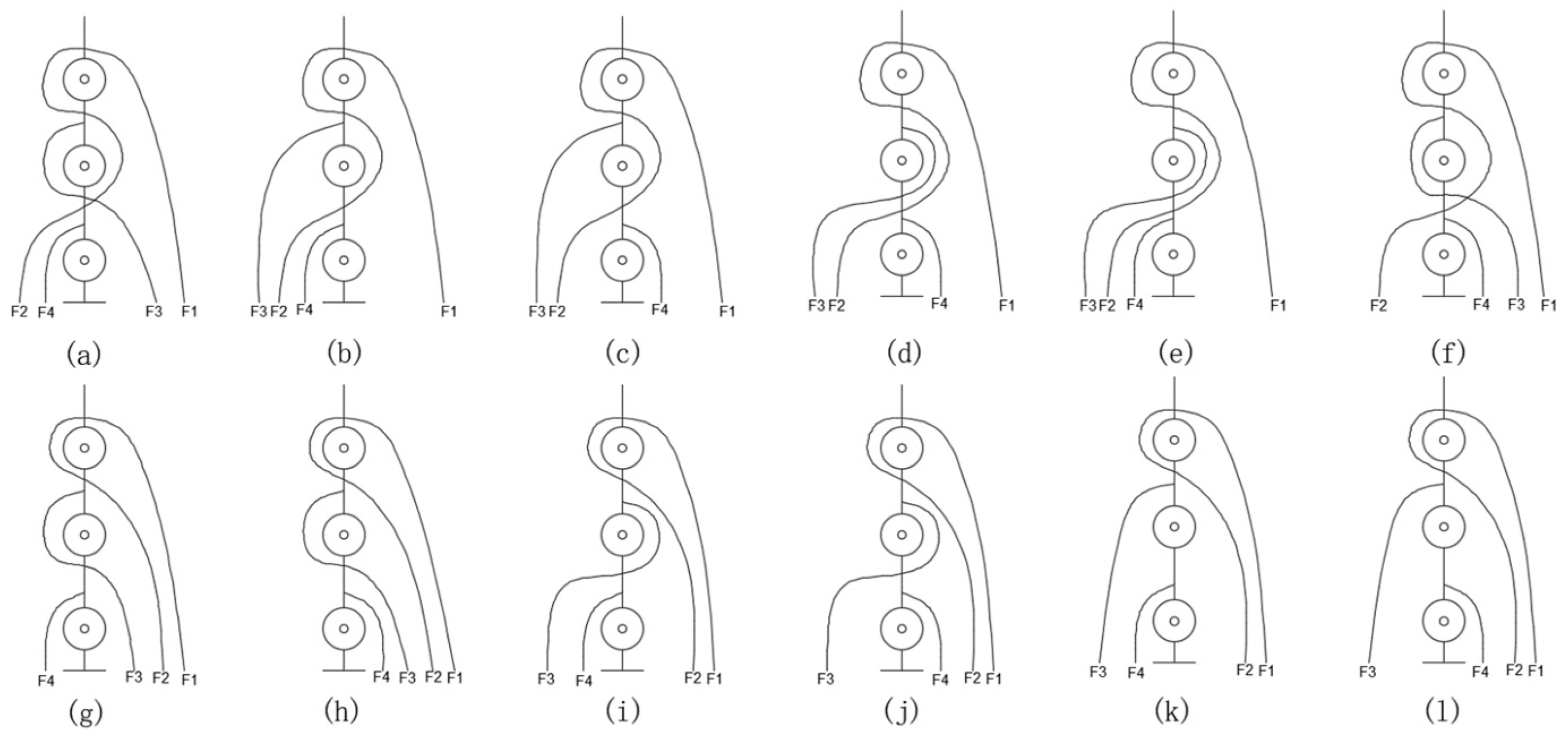
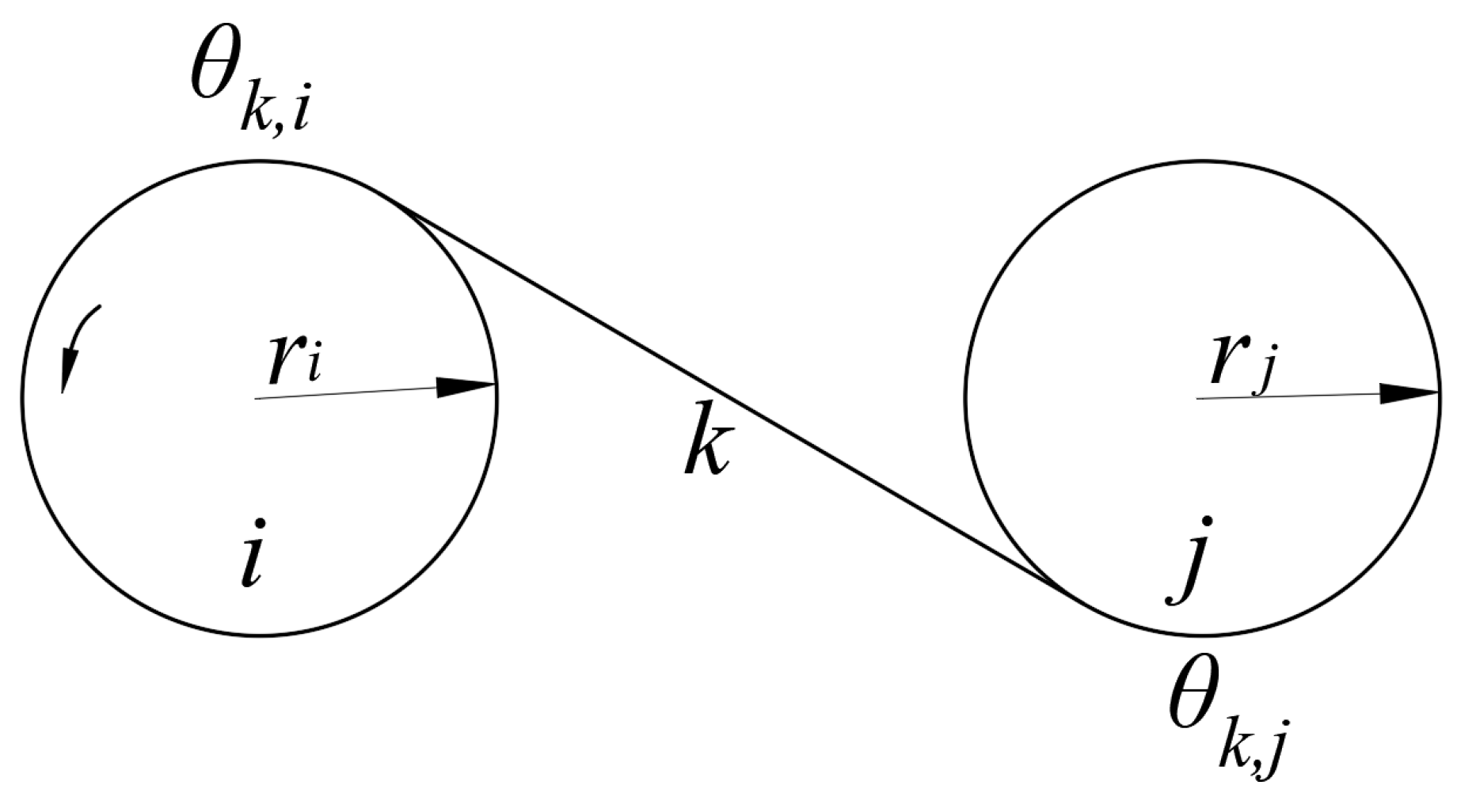
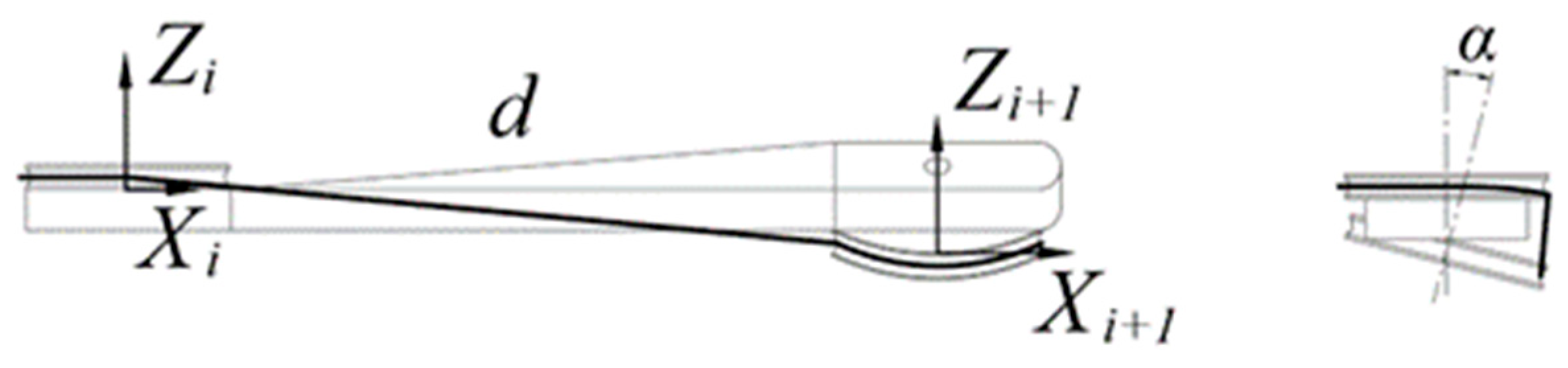
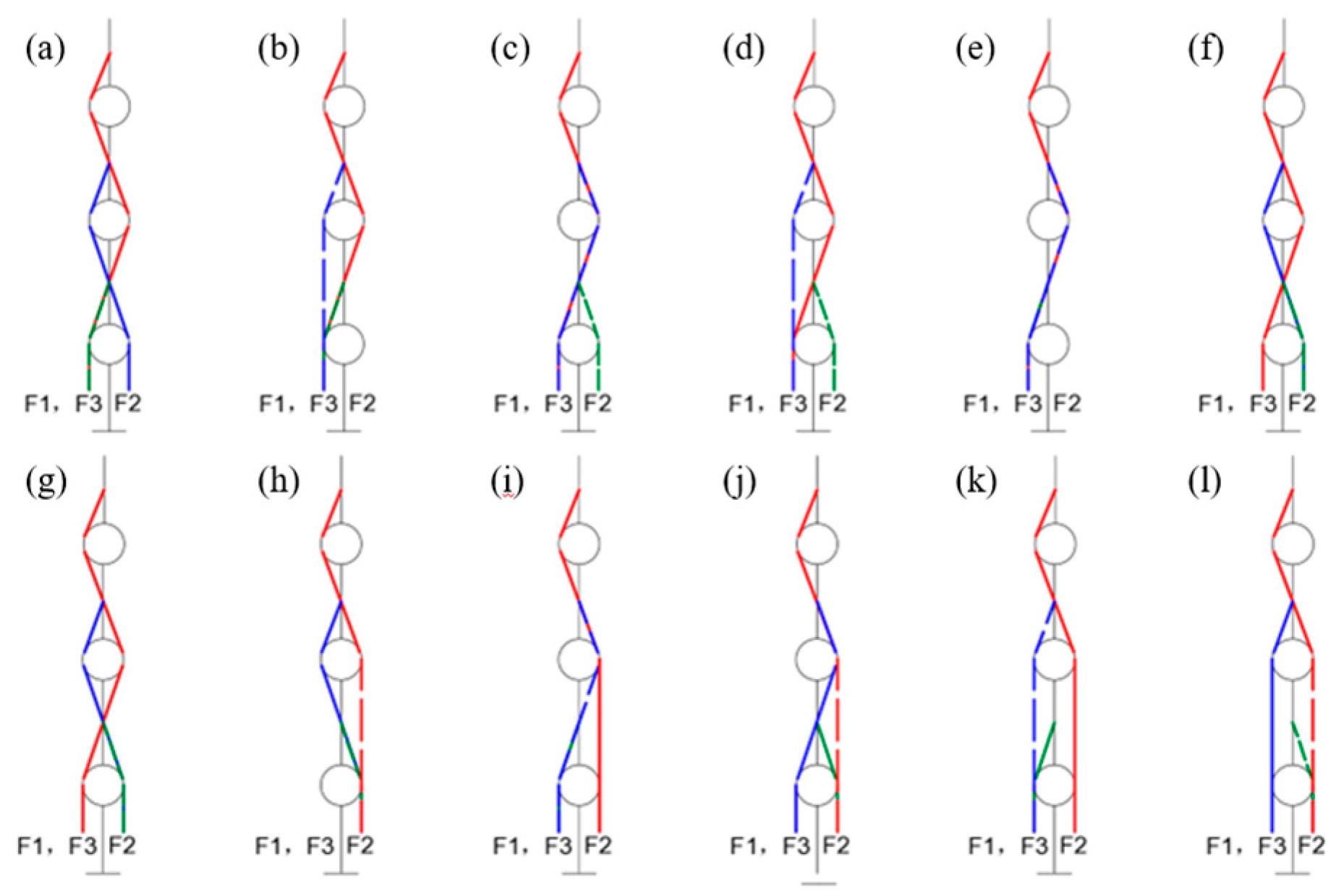
4.1. Tendon Path Design
- The direction of the axis of each finger joint is positive when it points outward from the plane of the hand.
- When a downward force is applied at the end of a tendon, if the pulley rotates counterclockwise around the joint axis, the force is positive; otherwise, it is negative.
- Each row must have at least two non-zero elements with opposite signs, ensuring that each joint of the finger can rotate in both directions.
- Swapping any two columns is equivalent to renaming the two tendons, which does not affect the overall functionality of the tendon-driven system.
- All zero elements in the structure matrix should be in the upper right corner of the matrix.
- Changing the sign of every element in any row does not affect the general characteristics of the matrix, which is equivalent to changing the positive direction of the joint axis.
- The rank of the structure matrix corresponds to the degrees of freedom of the system. For a system with ii tendons and jj degrees of freedom, at least one submatrix formed by deleting (i − j)(i − j) columns must have a non-zero determinant. If i = j + 1i = j + 1, then the determinant of the submatrix formed by deleting any column must be non-zero.
- If two structure matrices become identical after changing the sign of each element or rearranging some columns, they are considered structurally isomorphic. Structurally, isomorphic tendon pathways are regarded as the same.
4.2. Structure Design of the Tendon-Driven Finger
4.3. The Tendon Tension Model
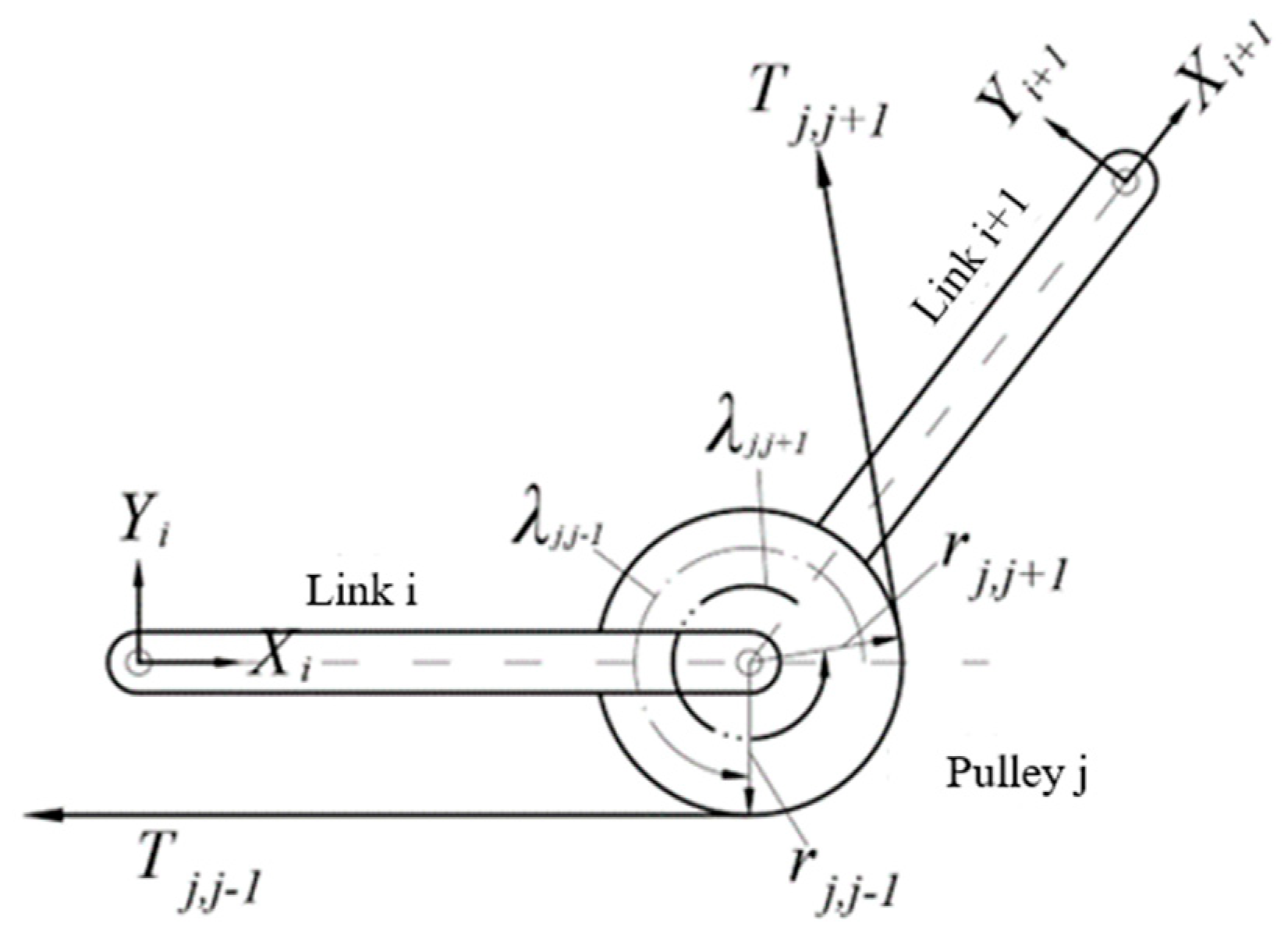
4.4. Force Analysis of a Pulley
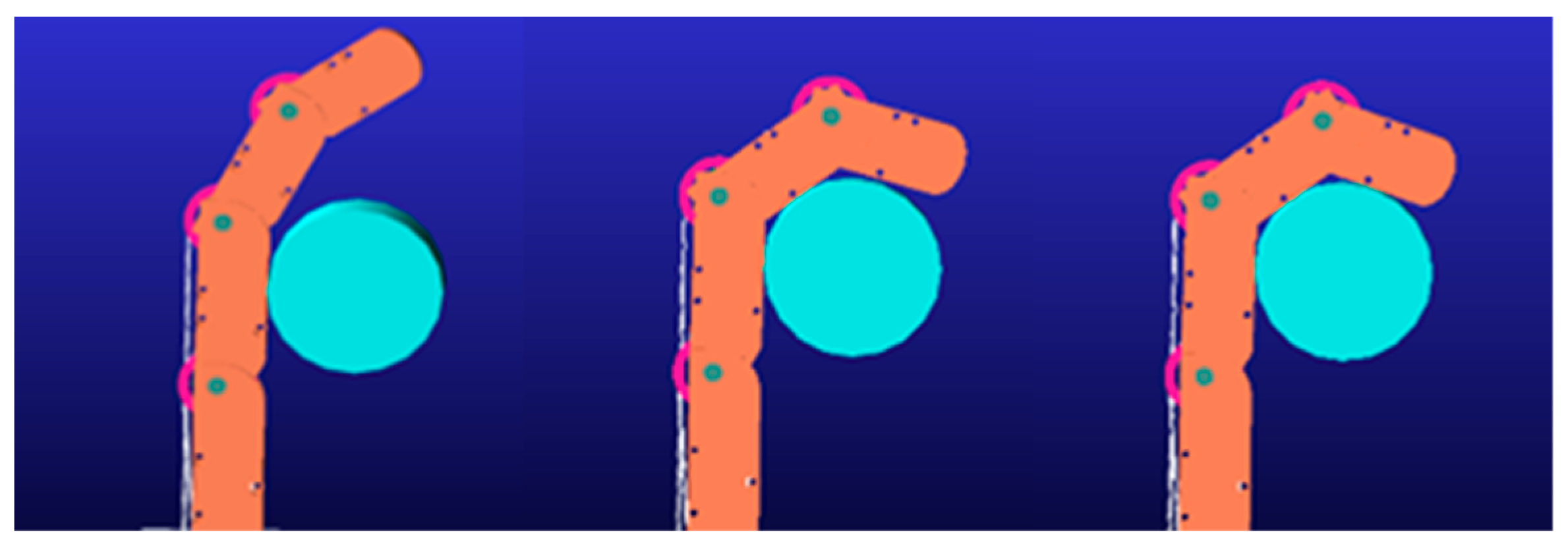
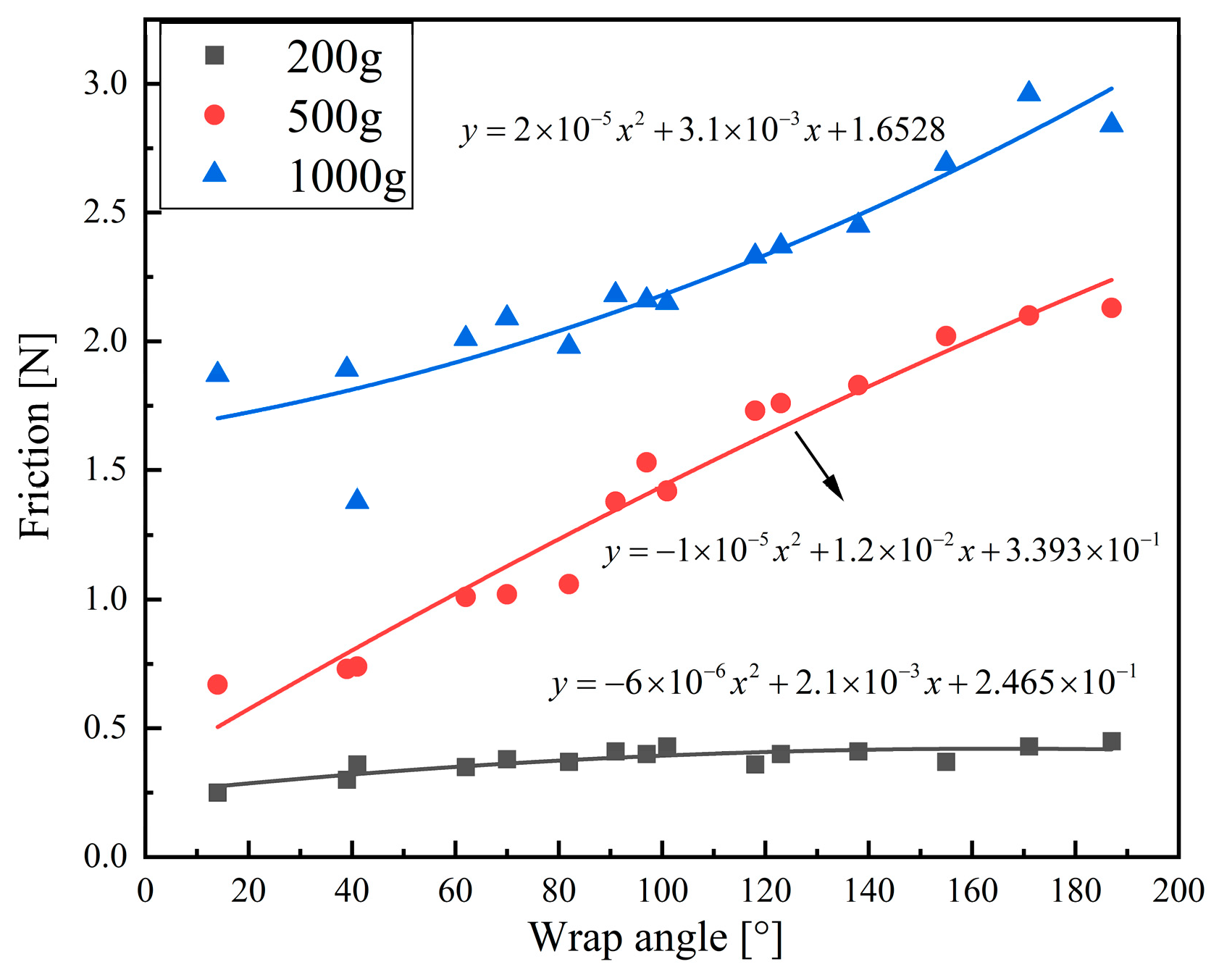
5. Experiments and Simulation of Tendon-Driven Fingers
6. Conclusions
- Drawing insights from human hand dexterity, we developed a data acquisition glove capable of capturing fingertip pressure and joint bending angles during Feix motion spectrum-based grasping tasks. This glove facilitated the collection of data on human hand characteristics when grasping different objects. From this analysis, we established human hand operational feature metrics, including fingertip pressure distribution and joint rotation angular velocity. These metrics provided a reference framework for evaluating the performance of tendon-driven fingers with 12 different tendon pathways.
- An experimental platform is designed for tendon-driven fingers to validate their performance. We evaluated various finger drive schemes and tendon transmission configurations, opting for the N + 1 drive and pulley-based tendon transmission. Validation experiments, as well as comparative motion characteristic experiments, are conducted for the 12 designed tendon pathways. The results revealed distinct performance characteristics for each pathway. Notably, pathway 4 exhibited the least fluctuation in tendon tension. Pathways 2, 11, and 12 met the contact pressure distribution requirements for the index finger, ring finger, and little finger, respectively. Pathway 1 satisfied the angular velocity metrics for finger joint rotation. Pathway 5 achieved the highest motion accuracy. Pathway 12 had the lowest friction losses.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, U.; Jung, D.; Jeong, H.; Park, J.; Jung, H.-M.; Cheong, J.; Choi, H.R.; Do, H.; Park, C. Integrated Linkage-Driven Dexterous Anthropomorphic Robotic Hand. Nat. Commun. 2021, 12, 7177. [Google Scholar] [CrossRef]
- Su, H.; Mariani, A.; Ovur, S.E.; Menciassi, A.; Ferrigno, G.; De Momi, E. Toward Teaching by Demonstration for Robot-Assisted Minimally Invasive Surgery. IEEE Trans. Autom. Sci. Eng. 2021, 18, 484–494. [Google Scholar] [CrossRef]
- Su, H.; Zhang, J.; She, Z.; Zhang, X.; Fan, K.; Zhang, X.; Liu, Q.; Ferrigno, G.; De Momi, E. Incorporating Model Predictive Control with Fuzzy Approximation for Robot Manipulation under Remote Center of Motion Constraint. Complex Intell. Syst. 2022, 8, 2883–2895. [Google Scholar] [CrossRef]
- Zhang, W.; Che, D.; Liu, H.; Ma, X.; Chen, Q.; Du, D.; Sun, Z. Super Under-actuated Multi-fingered Mechanical Hand with Modular Self-adaptive Gear-rack Mechanism. Ind. Robot Int. J. 2009, 36, 255–262. [Google Scholar] [CrossRef]
- Wang, C.; Sun, Y.; Xu, J.; Liu, X.; Zhou, X.; Chen, X. The Design and Development of an Anthropomorphic Worm-Gear Driven Robotic Hand: BIT-JOCKO. In Proceedings of the 2019 IEEE 4th International Conference on Advanced Robotics and Mechatronics (ICARM), Toyonaka, Japan, 3–5 July 2019; pp. 426–431. [Google Scholar]
- Liu, Q.; Gu, X.; Tan, N.; Ren, H. Soft Robotic Gripper Driven by Flexible Shafts for Simultaneous Grasping and In-Hand Cap Manipulation. IEEE Trans. Autom. Sci. Eng. 2021, 18, 1134–1143. [Google Scholar] [CrossRef]
- Yan, J.; Zheng, H.; Sun, F.; Liu, H.; Song, Y.; Fang, B. C-Shaped Bidirectional Stiffness Joint Design For Anthropomorphic Hand. IEEE Robot. Autom. Lett. 2022, 7, 12371–12378. [Google Scholar] [CrossRef]
- Liu, H.; Wu, K.; Meusel, P.; Seitz, N.; Hirzinger, G.; Jin, M.H.; Liu, Y.W.; Fan, S.W.; Lan, T.; Chen, Z.P. Multisensory Five-Finger Dexterous Hand: The DLR/HIT Hand II. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 3692–3697. [Google Scholar]
- Deng, E.; Tadesse, Y. A Soft 3D-Printed Robotic Hand Actuated by Coiled SMA. Actuators 2021, 10, 6. [Google Scholar] [CrossRef]
- Okada, T. Computer Control of Multijointed Finger System for Precise Object-Handling. IEEE Trans. Syst. Man Cybern. 1982, 12, 289–299. [Google Scholar] [CrossRef]
- Jacobsen, S.C.; Wood, J.E.; Knutti, D.F.; Biggers, K.B. The UTAH/M.I.T. Dextrous Hand: Work in Progress. Int. J. Robot. Res. 1984, 3, 21–50. [Google Scholar] [CrossRef]
- Vande Weghe, M.; Rogers, M.; Weissert, M.; Matsuoka, Y. The ACT Hand: Design of the Skeletal Structure. In Proceedings of the IEEE International Conference on Robotics and Automation, 2004. Proceedings. ICRA ’04. 2004, New Orleans, LA, USA, 26 April–1 May 2004; Volume 4, pp. 3375–3379. [Google Scholar]
- Vrochidou, E.; Tsakalidou, V.N.; Kalathas, I.; Gkrimpizis, T.; Pachidis, T.; Kaburlasos, V.G. An Overview of End Effectors in Agricultural Robotic Harvesting Systems. Agriculture 2022, 12, 1240. [Google Scholar] [CrossRef]
- Butterfass, J.; Hirzinger, G.; Knoch, S.; Liu, H. DLR’s Multisensory Articulated Hand. I. Hard- and Software Architecture. In Proceedings of the Proceedings. 1998 IEEE International Conference on Robotics and Automation (Cat. No.98CH36146), Leuven, Belgium, 20–20 May 1998; Volume 3, pp. 2081–2086. [Google Scholar]
- Narumi, S.; Huang, X.; Lee, J.; Kambara, H.; Kang, Y.; Shin, D. A Design of Biomimetic Prosthetic Hand. Actuators 2022, 11, 167. [Google Scholar] [CrossRef]
- Liu, R.; Zheng, H.; Hliboký, M.; Endo, H.; Zhang, S.; Baba, Y.; Sawada, H. Anatomically-Inspired Robotic Finger with SMA Tendon Actuation for Enhanced Biomimetic Functionality. Biomimetics 2024, 9, 151. [Google Scholar] [CrossRef]
- García-Córdova, F.; Guerrero-González, A.; Hidalgo-Castelo, F. Anthropomorphic Tendon-Based Hands Controlled by Agonist–Antagonist Corticospinal Neural Network. Sensors 2024, 24, 2924. [Google Scholar] [CrossRef]
- Nazma, E.; Mohd, S. Tendon Driven Robotic Hands: A Review. Int. J. Mech. Eng. Robot. Res. 2012, 1, 350–357. [Google Scholar]
- Treratanakulwong, T.; Kaminaga, H.; Nakamura, Y. Low-Friction Tendon-Driven Robot Hand with Carpal Tunnel Mechanism in the Palm by Optimal 3D Allocation of Pulleys. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 6739–6744. [Google Scholar]
- Friedl, W.; Chalon, M.; Reinecke, J.; Grebenstein, M. FRCEF: The New Friction Reduced and Coupling Enhanced Finger for the Awiwi Hand. In Proceedings of the 2015 IEEE-RAS 15th International Conference on Humanoid Robots (Humanoids), Seoul, Republic of Korea, 3–5 November 2015; pp. 140–147. [Google Scholar]
- Hong, H.; Ali, J.; Ren, L. A Review on Topological Architecture and Design Methods of Cable-Driven Mechanism. Adv. Mech. Eng. 2018, 10, 1687814018774186. [Google Scholar] [CrossRef]
- Morecki, A. Synthesis and Control of the Anthropomorphic Two-Handed Manipulator. Proc 10th Int Symp. Ind. Robots 1980, 461, 10003570226. [Google Scholar]
- Salisbury, J.K.; Craig, J.J. Articulated Hands: Force Control and Kinematic Issues. Int. J. Robot. Res. 1982, 1, 4–17. [Google Scholar] [CrossRef]
- Becker, J.C.; Thakor, N.V. A Study of the Range of Motion of Human Fingers with Application to Anthropomorphic Designs. IEEE Trans. Biomed. Eng. 1988, 35, 110–117. [Google Scholar] [CrossRef]
- Ozawa, R.; Kobayashi, H.; Hashirii, K. Analysis, Classification, and Design of Tendon-Driven Mechanisms. IEEE Trans. Robot. 2014, 30, 396–410. [Google Scholar] [CrossRef]
- Kim, Y.-J.; Yoon, J.; Sim, Y.-W. Fluid Lubricated Dexterous Finger Mechanism for Human-like Impact Absorbing Capability. IEEE Robot. Autom. Lett. 2019, 4, 3971–3978. [Google Scholar] [CrossRef]
- Giuffre, J.L.; Bishop, A.T.; Spinner, R.J.; Shin, A.Y. The Best of Tendon and Nerve Transfers in the Upper Extremity. Plast. Reconstr. Surg. 2015, 135, 617e–630e. [Google Scholar] [CrossRef]
- Naruse, M.; Trappe, S.; Trappe, T.A. Human Skeletal Muscle-Specific Atrophy with Aging: A Comprehensive Review. J. Appl. Physiol. 2023, 134, 900–914. [Google Scholar] [CrossRef]
- Sobinov, A.R.; Bensmaia, S.J. The Neural Mechanisms of Manual Dexterity. Nat. Rev. Neurosci. 2021, 22, 741–757. [Google Scholar] [CrossRef]
- Rombokas, E.; Theodorou, E.; Malhotra, M.; Todorov, E.; Matsuoka, Y. Tendon-Driven Control of Biomechanical and Robotic Systems: A Path Integral Reinforcement Learning Approach. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, St Paul, MN, USA, 14–18 May 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 208–214. [Google Scholar]
- Feix, T.; Romero, J.; Schmiedmayer, H.-B.; Dollar, A.M.; Kragic, D. The GRASP Taxonomy of Human Grasp Types. IEEE Trans. Hum.-Mach. Syst. 2016, 46, 66–77. [Google Scholar] [CrossRef]
- Su, H.; De Momi, E. Towards Human Activity Recognition Enhanced Robot Assisted Surgery. In Robot Design; Carbone, G., Laribi, M.A., Eds.; Mechanisms and Machine Science; Springer International Publishing: Cham, Switzerland, 2023; Volume 123, pp. 143–168. ISBN 978-3-031-11127-3. [Google Scholar]
- Chen, W.; Yu, C.; Tu, C.; Lyu, Z.; Tang, J.; Ou, S.; Fu, Y.; Xue, Z. A Survey on Hand Pose Estimation with Wearable Sensors and Computer-Vision-Based Methods. Sensors 2020, 20, 1074. [Google Scholar] [CrossRef]
- Takahashi, N.; Furuya, S.; Koike, H. Soft Exoskeleton Glove with Human Anatomical Architecture: Production of Dexterous Finger Movements and Skillful Piano Performance. IEEE Trans. Haptics 2020, 13, 679–690. [Google Scholar] [CrossRef]
- Yang, J.; Liu, W.; Yuan, J.; Mei, T. Hierarchical Soft Quantization for Skeleton-Based Human Action Recognition. IEEE Trans. Multimed. 2021, 23, 883–898. [Google Scholar] [CrossRef]
- Mnyusiwalla, H.; Triantafyllou, P.; Sotiropoulos, P.; Roa, M.A.; Friedl, W.; Sundaram, A.M.; Russell, D.; Deacon, G. A Bin-Picking Benchmark for Systematic Evaluation of Robotic Pick-and-Place Systems. IEEE Robot. Autom. Lett. 2020, 5, 1389–1396. [Google Scholar] [CrossRef]







| Object | Thumb | Index Finger | Middle Finger | Ring Finger | Little Finger |
|---|---|---|---|---|---|
| Sphere with 56 mm | 31% | 21% | 26% | 18% | 4% |
| Cylinder with 45 mm | 35% | 24% | 30% | 15% | 6% |
| Pencil with 7 mm | 28% | 25% | 25% | 12% | 10% |
| Disc with 90 mm | 41% | 14% | 15% | 17% | 13% |
| Rectangular prism 96 × 50 × 36 mm | 39% | 21% | 24% | 10% | 6% |
| Small rectangular prism | 21% | 29% | 33% | 17% | 0 |
| Index Finger | Middle Finger | Ring Finger | Little Finger | |
|---|---|---|---|---|
| Metacarpophalangeal (MCP) joint | 39.97° | 45.13° | 49.85° | 29.13° |
| Proximal interphalangeal (PIP) joint | 62.60° | 69.38° | 70.40° | 62.33° |
| Distal Interphalangeal (DIP) joint | 46.58° | 49.23° | 35.97° | 41.50° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, X.; Fu, H.; Shentu, B.; Wang, W.; Cai, S.; Bao, G. Design and Control of a Tendon-Driven Robotic Finger Based on Grasping Task Analysis. Biomimetics 2024, 9, 370. https://doi.org/10.3390/biomimetics9060370
Zhou X, Fu H, Shentu B, Wang W, Cai S, Bao G. Design and Control of a Tendon-Driven Robotic Finger Based on Grasping Task Analysis. Biomimetics. 2024; 9(6):370. https://doi.org/10.3390/biomimetics9060370
Chicago/Turabian StyleZhou, Xuanyi, Hao Fu, Baoqing Shentu, Weidong Wang, Shibo Cai, and Guanjun Bao. 2024. "Design and Control of a Tendon-Driven Robotic Finger Based on Grasping Task Analysis" Biomimetics 9, no. 6: 370. https://doi.org/10.3390/biomimetics9060370
APA StyleZhou, X., Fu, H., Shentu, B., Wang, W., Cai, S., & Bao, G. (2024). Design and Control of a Tendon-Driven Robotic Finger Based on Grasping Task Analysis. Biomimetics, 9(6), 370. https://doi.org/10.3390/biomimetics9060370






